Abstract
Motivation: Recent advances in technology have dramatically increased the availability of protein–protein interaction (PPI) data and stimulated the development of many methods for improving the systems level understanding the cell. However, those efforts have been significantly hindered by the high level of noise, sparseness and highly skewed degree distribution of PPI networks. Here, we present a novel algorithm to reduce the noise present in PPI networks. The key idea of our algorithm is that two proteins sharing some higher-order topological similarities, measured by a novel random walk-based procedure, are likely interacting with each other and may belong to the same protein complex.
Results: Applying our algorithm to a yeast PPI network, we found that the edges in the reconstructed network have higher biological relevance than in the original network, assessed by multiple types of information, including gene ontology, gene expression, essentiality, conservation between species and known protein complexes. Comparison with existing methods shows that the network reconstructed by our method has the highest quality. Using two independent graph clustering algorithms, we found that the reconstructed network has resulted in significantly improved prediction accuracy of protein complexes. Furthermore, our method is applicable to PPI networks obtained with different experimental systems, such as affinity purification, yeast two-hybrid (Y2H) and protein-fragment complementation assay (PCA), and evidence shows that the predicted edges are likely bona fide physical interactions. Finally, an application to a human PPI network increased the coverage of the network by at least 100%.
Availability: www.cs.utsa.edu/∼jruan/RWS/.
Contact: Jianhua.Ruan@utsa.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Recent advances in high-throughput techniques, such as yeast two-hybrid (Y2H) and tandem affinity purification, have enabled the production of a large amount of protein–protein interaction (PPI) data (Gavin et al., 2006; Krogan et al., 2006; Tarassov et al., 2008; Yu et al., 2008). These PPI data can be modelled by networks, where nodes in networks represent proteins and edges between the nodes represent physical interactions between proteins. These networks, together with other high-throughput functional genomics data, are offering unprecedented opportunities for both biological and computational scientists to understand the cell at a systems level (Przulj, 2011). For example, global analysis of PPI networks has revealed important connections between topology and function (Han et al., 2004; Jeong et al., 2001; Yu et al., 2007). PPI networks have also been used for predicting gene functions, functional pathways or protein complexes, with both supervised and unsupervised methods (Asthana et al., 2004; Bader and Hogue, 2002; Chua et al., 2006; Friedel et al., 2009; King et al., 2004; Lee et al., 2008; Sharan et al., 2007; Ulitsky and Shamir, 2009; Wang et al., 2007a; Wang et al., 2010). Furthermore, much effort has been devoted recently towards incorporating PPI networks to obtain a better mechanistic understanding of complex diseases and to improve the diagnosis and treatment of diseases (Chuang et al., 2007; Hannum et al., 2009; Hidalgo et al., 2009; Ideker and Sharan, 2008; Kim et al., 2011).
However, the growing size and complexity of PPI networks poses multiple challenges to biologists. First, PPI networks often have a high false-positive rate and an even higher false-negative rate (Huang et al., 2007). Second, PPI networks are typically sparse, partially because of the high false-negative rate, which places a hurdle for algorithms that rely on neighbour information, for example, in gene function prediction (Chua et al., 2006; Sharan et al., 2007). Third, PPI networks are known to have skewed degree distribution, meaning that they have more than expected quantity of hub genes. Such hub nodes can often reduce the performance of existing graph theoretic algorithms (e.g. for predicting protein complexes) that were often designed for networks with relatively uniform degree distributions.
In this article, we present a novel method to improve the quality of a given PPI network by computationally predicting some new interactions and removing spurious edges. It is worth noting that our idea is purely based on the topology of the network, with no additional biological information involved. This ensures that our algorithm can be easily combined with other algorithms that have already been developed for predicting protein complexes or performing PPI-based studies. There are also several studies that attempt to combine additional biological information, such as gene ontology and gene expression, with PPI network for protein complex prediction (Asthana et al., 2004; Ulitsky and Shamir, 2009; Wang et al., 2010). It should be straightforward to use our method in these approaches, by replacing the PPI network with our reconstructed PPI network.
To assess the performance of our algorithm, we tested it on three yeast PPI networks obtained with different experimental systems, and we examined the biological relevance of the results using multiple information sources, including gene ontology annotations, gene expression data, protein complexes, list of essential genes, conservation between species and a large collection of known physical interactions in the BioGRID database. Results show that the predicted PPIs have much higher functional relevance than the removed ones, and they are likely bona fide physical interactions. Comparison with several existing methods shows that the network reconstructed by our method has the highest overall quality. Furthermore, applying two independent graph clustering algorithms, we found that the reconstructed network has resulted in significantly improved prediction accuracy of protein complexes. Finally, an application to a human PPI network shows encouraging results.
2 METHODS
2.1 Rationale and related works
In recent years, many computational methods have been developed to predict missing links from networks (Fouss et al., 2007; Li and Horvath, 2007; Ruan and Zhang, 2006; Radicchi et al., 2004; Tong et al., 2006), and reviewed in (Lü and Zhou, 2011), some of which have been successfully applied to PPI networks. These methods basically fall into two categories: common neighbour based and distance based. The first type of methods is based on a simple yet effective idea—two nodes sharing many common neighbours are likely in the same module (Li and Horvath, 2007; Ruan and Zhang, 2006; Radicchi et al., 2004; Wang et al., 2007a). These methods may have limited value on PPI networks that are usually sparse. To circumvent this problem, Fang et al. (2011) generalized the idea to consider neighbours of greater path lengths and showed that the so-called ‘global geometric affinity’ (GGA) measurement can help predict new PPI.
The second type of methods measures the ‘distance’ between pairs of nodes in the network taking into consideration all alternative paths; popular examples include two algorithms based on random walks, namely, Euclidean commute time (ECT) (Fouss et al., 2007) and random walk with restart (RWR) (Tong et al., 2006). ECT measures the expected number of steps needed for a random walker to travel between two nodes as the distance between them, whereas RWR computes the probability for a random walker starting from node  to reach another node
to reach another node  . Performance of this type of methods may be significantly affected by hub nodes that are connected to many nodes in the network. Another method falling into this category is because of Kuchaiev et al. (2009), where they attempted to embed a PPI network into a low dimensional geometric space using multiple dimensional scaling (MDS), and assign edges to pairs of nodes that have short distances in the embedded space. While good performance was observed, this method may not work very well in general as it may not always be easy to find an accurate geometric embedding for a given PPI network.
. Performance of this type of methods may be significantly affected by hub nodes that are connected to many nodes in the network. Another method falling into this category is because of Kuchaiev et al. (2009), where they attempted to embed a PPI network into a low dimensional geometric space using multiple dimensional scaling (MDS), and assign edges to pairs of nodes that have short distances in the embedded space. While good performance was observed, this method may not work very well in general as it may not always be easy to find an accurate geometric embedding for a given PPI network.
In this work, we propose a novel method that can be considered as a generalization of the simple common neighbour-based method, combining ideas from the distance-based method. We hypothesize that two nodes having similar ‘distances’ (in the view of a random walker) to all other nodes in the network can potentially interact with each other. This idea is more general than the aforementioned two types of methods because it can not only predict links that are covered by the aforementioned two types of methods but can also predict links between nodes that are themselves far away from each other (for a random walker) and do not share any common neighbours. The basic idea of our method consists of three steps and is illustrated in Figure 1. First, a topological profile, which measures the ‘distances’ between a target node and all other nodes in the network, is calculated for each node. Second, similarities of topological profiles are calculated between every pair of nodes. In the final step, edges are created to connect nodes that are topologically similar. The framework is general, and each step can have multiple designing choices. Here, we propose a novel random walk procedure for computing topological profiles, which can handle hub nodes better than the existing random walk-based methods. We use simple ideas for the other two steps, leaving room for future improvements.
Fig. 1.
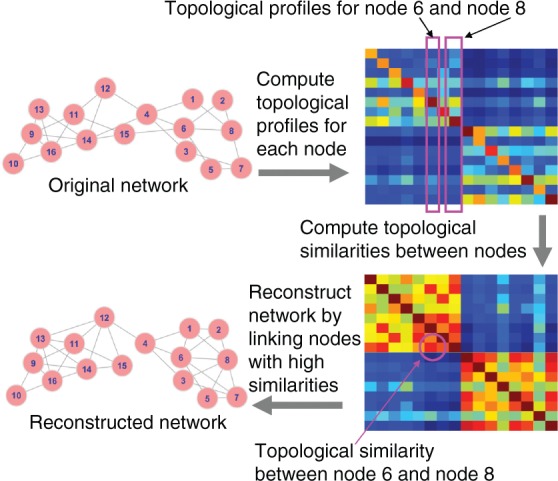
Basic idea of our method
2.2 Random walk with resistance
Let 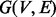 be an undirected graph representing a PPI network, with
be an undirected graph representing a PPI network, with 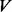 the set of nodes and
the set of nodes and 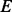 the set of edges (for convenience, a self-loop is also added for each node). For
the set of edges (for convenience, a self-loop is also added for each node). For 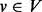 , let
, let 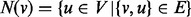 be the set of neighbours of
be the set of neighbours of  and
and 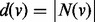 the degree of
the degree of  .
.
The simple random walk for one node on a graph  is a walk on
is a walk on  where the next node is chosen uniformly at random from the set of neighbours of the current node. Formally, when the random walker is at node
where the next node is chosen uniformly at random from the set of neighbours of the current node. Formally, when the random walker is at node  , the probability for her to move in the next step to the neighbour
, the probability for her to move in the next step to the neighbour  is
is 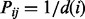 for
for 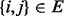 and
and 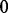 otherwise. Assume that a random walk is initiated at a node
otherwise. Assume that a random walk is initiated at a node  . Let
. Let 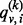 be the probability for the random walker sitting at node
be the probability for the random walker sitting at node  at a discrete time point
at a discrete time point 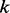 . Then, at time point
. Then, at time point 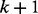 , the probability for the random walker taking the path from node
, the probability for the random walker taking the path from node 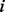 to node
to node 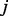 can be calculated as
can be calculated as
| (1) |
and the probability for the random walker to reach node 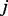 at time point
at time point 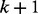 can be calculated as
can be calculated as
| (2) |
It is important to note that, under some mild conditions, with this simple random walk, the probability to reach node 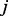 ,
, 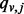 , converges to the same value regardless of the starting point
, converges to the same value regardless of the starting point  (Lovász, 1993). Therefore, the stationary probability distribution obtained from the simple random walk cannot be used directly to measure distance between nodes. To provide a measurement of the distance between two nodes in a network, several modifications have been proposed. For example, ECT measures the expected number of hops needed to travel between two nodes in the simple random walk (Fouss et al., 2007), whereas RWR attempts to bias the random walk to stay close to the starting node by teleporting the random walker to the starting node with a certain probability (Tong et al., 2006).
(Lovász, 1993). Therefore, the stationary probability distribution obtained from the simple random walk cannot be used directly to measure distance between nodes. To provide a measurement of the distance between two nodes in a network, several modifications have been proposed. For example, ECT measures the expected number of hops needed to travel between two nodes in the simple random walk (Fouss et al., 2007), whereas RWR attempts to bias the random walk to stay close to the starting node by teleporting the random walker to the starting node with a certain probability (Tong et al., 2006).
Here, we describe a random walk algorithm, named random walk with resistance (RWS), based on two key ideas: (i) we bias the random walker towards staying close to the starting point by adding a small amount of resistance on each edge of the network, and (ii) we introduce a condition to discourage the random walker from roaming into new territories via hub nodes, by adding additional resistance for a random walker to overcome when meeting a new node that she has never visited before. The algorithm can be best described as a modification to the simple random walk algorithm. Basically, we replace Equation (1) by
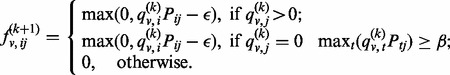 |
(3) |
The probability of reaching node 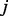 at time point
at time point 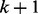 is then calculated by adding up the probabilities to enter
is then calculated by adding up the probabilities to enter 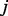 from all paths, and re-normalized so that the probability vector sums to 1:
from all paths, and re-normalized so that the probability vector sums to 1:
| (4) |
As in Equation (3), the algorithm first checks whether a destination node, 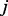 , is new to the random walker. If not, that is,
, is new to the random walker. If not, that is, 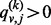 , the random walker will visit the node with probability
, the random walker will visit the node with probability 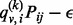 . The probability will be set to 0 if it is <0. Combined with the normalization step, the purpose of introducing the
. The probability will be set to 0 if it is <0. Combined with the normalization step, the purpose of introducing the  parameter is similar to the teleporting idea in RWR that biases the random walker to stay close to the starting node, so that the stationary probability vectors for different starting nodes are not always converged to the same values.
parameter is similar to the teleporting idea in RWR that biases the random walker to stay close to the starting node, so that the stationary probability vectors for different starting nodes are not always converged to the same values.
If the node 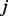 is new to the random walker, then an additional parameter,
is new to the random walker, then an additional parameter, 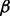 , is introduced to discourage the random walker from visiting the new node, unless there is at least one path for
, is introduced to discourage the random walker from visiting the new node, unless there is at least one path for  to enter
to enter 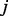 with sufficiently large probability. The main motivation for this step is to reduce the impact of hub nodes in the random walk process. Imagining that without the
with sufficiently large probability. The main motivation for this step is to reduce the impact of hub nodes in the random walk process. Imagining that without the 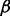 parameter, a random walker reaching a hub node will be able to travel, with the same probability, to all other nodes that are connected with the hub nodes, which may or may not be functionally related to the starting node. In contrast, with our algorithm, given the same scenario, the random walker would selectively prefer the nodes that are not only connected to the hub nodes but are also connected with the starting node via some alternative paths not involving the hub nodes. (See Supplementary Fig. S1 for a toy example).
parameter, a random walker reaching a hub node will be able to travel, with the same probability, to all other nodes that are connected with the hub nodes, which may or may not be functionally related to the starting node. In contrast, with our algorithm, given the same scenario, the random walker would selectively prefer the nodes that are not only connected to the hub nodes but are also connected with the starting node via some alternative paths not involving the hub nodes. (See Supplementary Fig. S1 for a toy example).
In our experiment,  is set to
is set to 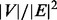 and
and 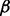 is set to
is set to 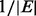 . This choice is based on an analysis of the minimum and average value of
. This choice is based on an analysis of the minimum and average value of 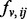 on each edge. Empirically, we have found that these two values perform well on multiple, both biological and non-biological, networks. Variations of these two values within a constant multiple do not significantly change the results.
on each edge. Empirically, we have found that these two values perform well on multiple, both biological and non-biological, networks. Variations of these two values within a constant multiple do not significantly change the results.
The aforementioned procedure is applied iteratively for each starting node. A random walker is considered to have reached its stationary distribution when the change of its probability to arrive at any node is less than a small cut-off value. In our experiment, all nodes converged in 5–20 iterations, which only took a few minutes on a personal computer.
2.3 Calculating topological similarity
After applying the aforementioned random walk procedure to the network, we have a 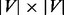 probability matrix, denoted as
probability matrix, denoted as 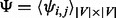 , where
, where 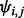 represents the probability for a random walker started at node
represents the probability for a random walker started at node  to reach node
to reach node 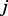 at convergence.
at convergence.
To magnify the difference between probability vectors from different nodes, we first obtain the median vector 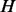 from all the vectors, where the
from all the vectors, where the 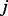 -th element of
-th element of 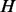 is defined as
is defined as 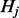 =median (
=median (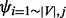 ). This median probability vector is similar to the stationary probability vector for the simple random walk. We then calculate the
). This median probability vector is similar to the stationary probability vector for the simple random walk. We then calculate the 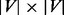 offset matrix
offset matrix  , where
, where 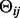 =
=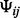 −
−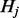 .
.
Finally, we calculate the Pearson correlation coefficient between each pair of rows or columns of the offset matrix as a measurement of topological similarity, 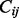 , between nodes. Empirically, we have found that using columns of the offset matrix as topological profiles, that is, letting
, between nodes. Empirically, we have found that using columns of the offset matrix as topological profiles, that is, letting 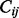 =pcc(
=pcc(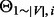 ,
, 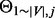 ), works slightly better than rows. Informally speaking, a row vector represents the information passed from a node to all nodes in the network, whereas a column vector represents the information that a node receives from the network; therefore, the latter is a more accurate way of describing the position of the node in the network.
), works slightly better than rows. Informally speaking, a row vector represents the information passed from a node to all nodes in the network, whereas a column vector represents the information that a node receives from the network; therefore, the latter is a more accurate way of describing the position of the node in the network.
2.4 Reconstructing PPI network
Finally, a network is reconstructed from the topological similarity matrix by connecting pairs of nodes whose similarity is above a certain threshold. Although more sophisticated methods are possible (e.g. Ruan, 2009), in this article, we choose to implement a simple strategy for easy evaluation and fair comparison to other methods: we simply pick a cut-off value so that the number of edges can be kept the same as in the original network. We will show that this simple strategy worked well. In Section 4, we discuss some future plans in improving cut-off selection, which should further improve the quality of the reconstructed network, and particularly, reduce the false-negative rate of PPI networks.
3 RESULTS AND DISCUSSION
For evaluation, we applied our algorithm to three yeast PPI networks obtained from different technologies: tandem-affinity purification (Krogan et al., 2006), Y2H (Yu et al., 2008) and protein-fragment complementation assay (Tarassov et al., 2008). In Sections 3.1–3.3, we discuss results on the Krogan dataset, which is the largest, and in Sections 3.4 and 3.5, we present some comparative analysis of the three datasets. In Section 3.6, we present an application to a human PPI network.
3.1 Reconstructed PPI network has better functional relevance
We performed a random walk on the Krogan PPI network, which covers 2708 genes with 7123 edges, and derived a modified PPI network by choosing 7123 potential connections with the highest similarities (see Section 2). Within the modified network, 2870 (40%) edges are new (and the same number of edges in the original network has been removed). To evaluate the functional relevance of the newly predicted edges, we resort to several types of sources, including gene ontology, gene expression, essentiality, known protein complexes and conservation of interactions in other species. To facilitate discussion, we call the group of edges present in the original network ‘before’ group, and that in the modified network ‘after’ group. Furthermore, ‘new’ edges designate the edges that are in ‘after’ but not ‘before’ group, ‘removed’ edges are ‘before’ but not ‘after’. Finally, those present in both ‘before’ and ‘after’ are called ‘confirmed’. We also generated random networks with a randomly rewiring procedure that preserves the degree of each node (Ruan and Zhang, 2008).
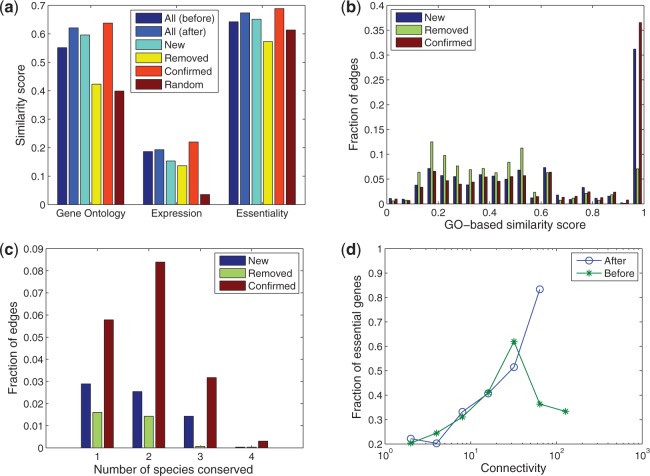
As interacting proteins are likely involved in similar biological processes, they are expected to have similar functional annotations in gene ontology and similar gene expression patterns across diverse conditions. Therefore, we measure the functional relevance between any pair of genes that are connected by an edge using the semantic similarity between the GO terms annotated with the proteins, using a popular method (Wang et al., 2007b; Yu et al., 2010). Results shown are based on the ‘molecular function’ branch of Gene Ontology. Using ‘biological process’ yielded similar values, and ‘cellular localization’ resulted in slightly lower but consistent values (Supplementary Fig. S2). We also measured the Pearson correlation coefficient between the gene expression profiles of every pair of genes, using the yeast stress response microarray data (Gasch et al., 2000). We used the average similarity of the pairs of nodes connected by an edge in a certain group to represent the functional relevance of that edge group. As shown in Figure 2a, the after group has a higher functional relevance than the before group based on both GO and gene expression. Moreover, the confirmed group has the highest functional similarity compared with the other groups, and the removed group is far lower than the new group. The standard error of these average measurements are all <10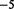 ; therefore, these differences are highly significant. Further investigation showed that the GO-based similarity is
; therefore, these differences are highly significant. Further investigation showed that the GO-based similarity is 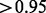 for
for 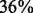 and
and 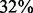 of the edges in the confirmed and new groups, respectively. In contrast, only
of the edges in the confirmed and new groups, respectively. In contrast, only 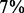 of removed edges have a GO-based similarity
of removed edges have a GO-based similarity 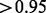 (Fig. 2b).
(Fig. 2b).
Fig. 2.
Results of our method on the Krogan PPI network. (a) Different edge groups are evaluated by GO-based similarity, gene expression correlation and co-essentiality. (b) Distribution of the GO-based similarity scores for three edge groups. (c) Fraction of conserved edges for three edge groups. (d) Relationship between connectivity and essentiality
Next, we used essential genes to compare different edge groups. The list of essential genes in yeast is retrieved from the Saccharomyces Genome Database (Dwight et al., 2004). As two interacting proteins may belong to the same protein complex, they tend to have the same essentiality. In other words, if one is (not) essential, the other is also expected to be (not) essential. As shown in Figure 2a, the percentage of the removed edges that share the same essentiality is actually lower than that of the randomly generated edges, which suggests that the removed edges are probably connecting genes in different complexes (also see Section 3.2). In contrast, the measurement for the new edges is close to that of the confirmed PPIs.
We also looked at the conservation of the edges in other species. We downloaded conserved PPIs between yeast and four species including Caenorhabditis elegans, fly, mouse and human from InteroLogFinder (http://www.interologfinder.org/) (Wiles et al., 2010). As shown in Figure 2c, a considerable fraction of confirmed edges are conserved in at least two other species. Although a small fraction of the removed edges are conserved in one or two species, they are rarely conserved in more than two species. In comparison, the new edges tend to be more conserved than the removed edges, although not as much as the confirmed ones. The conservation analysis also suggests that the predicted edges are bona fide physical interactions rather than functional links (see also Section 3.5).
Finally, it has been shown that genes with high connectivity in the PPI network tend to be more essential, but it is also known that connectivity and essentiality (percentage of genes that are essential) are only weakly correlated (Jeong et al., 2001). For example, Figure 1d shows that although the essentiality of genes is generally increasing for genes with low to intermediate degrees, the essentiality of genes with the highest degrees is relatively lower than expected by their degrees. Besides several possible explanations, it may be that some of the proteins with the highest degrees may be ‘sticky’ in the sense that they may seem to interact with many proteins under the experimental protocol, but these interactions do not exist in reality because the protein is poorly expressed or not co-expressed with the proteins they can potentially interact with. It can be seen that in the reconstructed network, essentiality and degree have a much better correlation (Fig. 2d).
In summary, using multiple independent sources of evidence, we have shown that the new edges have clearly higher functional relevance than the removed ones. These results suggest that our algorithm can indeed reduce the noise in PPI network and improve the network quality.
3.2 Reconstructed PPI network improves accuracy of protein complex prediction
We investigated whether the improved PPI network can also improve the prediction accuracy of protein complexes. We applied two network clustering algorithms to the original and modified PPI networks, and compared the predicted complexes with the MIPS known protein complexes (Mewes et al., 2006), which included 767 proteins in 170 known complexes after intersecting with the PPI network. Markov Clustering Algorithm (MCL) is a well-known graph clustering algorithm and has been shown to outperform other protein complex prediction algorithms in two independent evaluation studies (Brohee and van Helden, 2006; Vlasblom and Wodak, 2009). HQcut is a community discovery algorithm developed by one of the co-authors, based on the optimization of a so-called modularity function (Ruan and Zhang, 2008). For MCL, we set the inflation parameter to 1.8 as suggested by others (Brohee and van Helden, 2006). HQcut does not require any user-tuned parameters. To measure the accuracy of the prediction, we used the Fowlkes–Mallows index for comparing clustering (Fowlkes and Mallows, 1983; Meila, 2005). Formally, let 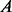 be the list of gene pairs that fall into the same complex in the set of predicted complexes and
be the list of gene pairs that fall into the same complex in the set of predicted complexes and 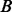 that in the set of known complexes, the prediction accuracy is measured by
that in the set of known complexes, the prediction accuracy is measured by 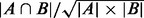 , where
, where 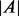 denotes the cardinality of the set
denotes the cardinality of the set 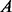 . As shown in Figure 3a, the prediction accuracy is significantly improved for both MCL and HQcut, demonstrating that the improvement is general. Moreover, as the MIPS database of known protein complexes only covers
. As shown in Figure 3a, the prediction accuracy is significantly improved for both MCL and HQcut, demonstrating that the improvement is general. Moreover, as the MIPS database of known protein complexes only covers 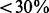 of the proteins in the PPI network, we measured the average pairwise functional similarity using gene ontology semantic similarity and co-expression (see Section 3.1) between every pair of nodes that are predicted to be in the same complex. Again, it is shown that the results are improved significantly in the modified network for both MCL and HQcut (Fig. 3a).
of the proteins in the PPI network, we measured the average pairwise functional similarity using gene ontology semantic similarity and co-expression (see Section 3.1) between every pair of nodes that are predicted to be in the same complex. Again, it is shown that the results are improved significantly in the modified network for both MCL and HQcut (Fig. 3a).
Fig. 3.
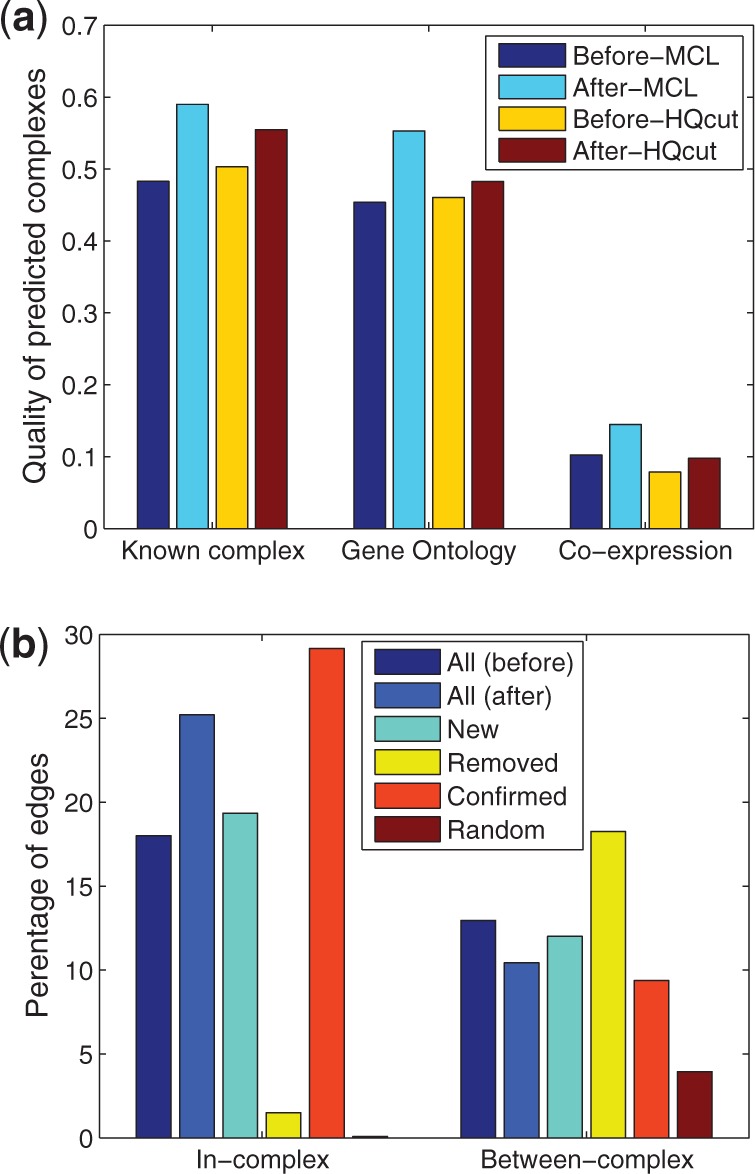
Evaluation of our method based on protein complexes. In (a), the original PPI network (before) or the reconstructed counterpart (after) is partitioned using two algorithms (MCL and HQcut) for protein complex predictions. Each prediction is then evaluated by its similarity (F–M index, see main text) to MIPS known complexes, by the average gene ontology similarity between pairs of nodes in the same complex, or by average gene co-expression correlation between pairs of nodes in the same complex. In (b), different edge groups are evaluated for the fraction of edges connecting edges in the same or different MIPS known protein complexes
To further investigate why the reconstructed network can result in better prediction accuracy of protein complexes, we directly compared different edge groups for the fraction of edges that are connecting genes in the same known complex (in-complex) versus those that are in different known complexes (between-complex). Indeed, as shown in Figure 3b, the new edges have much higher in-complex probability and lower between-complex probability compared with the removed edges, whereas the confirmed edges have the highest in-complex probability and lowest between-complex probability. Therefore, it is likely that the reconstructed PPI network can be combined with any existing protein complex prediction algorithm and improves its accuracy. Figure 4 shows the changes to the PPI network relevant for two known protein complexes. The prediction for the Arp2/3 complex is improved in the after network, because connectivity is increased within the complex, and many between-complex edges are removed. Interestingly, for the anaphase-promoting complex (APC) complex, our algorithm not only removed several external edges and added many in-complex edges but also predicted interactions between a non-member protein, MND2 and the complex members. It turns out that MND2 is indeed a member of the APC complex (Hall et al., 2003).
Fig. 4.
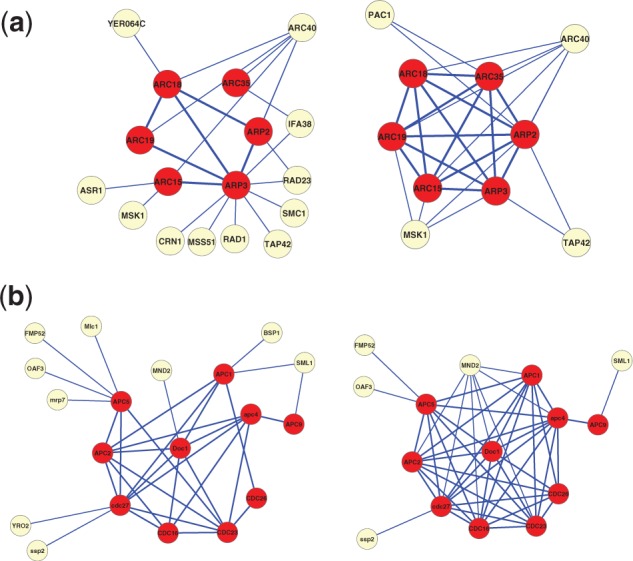
Subnetworks for (a) Arp2/3 protein complex and (b) APC protein complex. The subnetworks contain interactions among known members (dark) of MIPS protein complexes and their direct neighbours (light) in the original Krogan PPI network (left) or the reconstructed network with our method (right)
3.3 Comparisons with previous methods
We compared our algorithm with four existing methods, namely, ECT (Fouss et al., 2007), RWR (Tong et al., 2006), MDS (Kuchaiev et al., 2009) and GGA (Fang et al., 2011). The ECT and RWR methods are well known in data mining and network analysis communities, whereas the MDS and GGA methods were recently proposed to improve the quality of PPI networks (see Section 2.1). As all four algorithms calculate some topology-based similarity scores for pairs of nodes, and then use different (ad hoc) approaches to determine cut-offs, for a fair comparison, here, we simply took the top 7123 pairs of genes having the highest scores as the predicted PPIs. Table 1 shows the change to the network introduced by each method. We then compared the functional relevance of the reconstructed PPI networks. As shown in Figure 5, the PPI network reconstructed by our method has the highest GO similarity, highest fraction of in-complex edges and lowest fraction of between-complex edges. In fact, our algorithm is the only method that shows consistent improvement over the original network using all four criteria. For example, RWR improved GO similarity scores and the fraction of in-complex edges, but at the same time reduced the co-expression scores and increased between-complex edges. GGA resulted in lower co-expression scores. The network reconstructed by ECT has slightly higher co-expression than the network reconstructed by our method, but its GO similarity score is much lower than the original network, and it has a decreased fraction of in-complex edges and an increased fraction of between-complex edges. MDS resulted in degraded functional relevance scores according to all measurements except between-complex edges.
Table 1.
Changes to network statistics by different algorithms
| Network property | RWS | RWR | ECT | MDS | GGA |
|---|---|---|---|---|---|
| Number of nodes/edges before | 2708/7123 | 2708/7123 | 2708/7123 | 2708/7123 | 2708/7123 |
| Number of nodes/edges after | 2549/7123 | 2708/7123 | 2016/7123 | 2241/7123 | 2173/7123 |
| Number of replaced edges | 2870 (40.3%) | 2795 (39.2%) | 5671 (79.6%) | 5468 (76.8%) | 4712 (66.2%) |
Fig. 5.
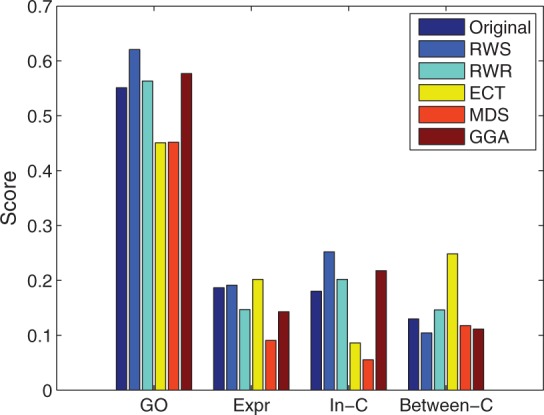
Comparison with other algorithms. GO: gene ontology-based similarities; Expr: gene co-expression (Pearson correlation coefficient); In-C: fraction of edges that are in-complex; Between-C: fraction of edges that are between-complex
3.4 Applicability to other types of PPI networks
We also applied our method to two other datasets, obtained by Yu et al. (2008) and Tarassov et al. (2008), using Y2H and protein-fragment complementation assay (PCA), respectively. Although the affinity purification (AP) technique used in Krogan et al. (2006) is designed to capture co-complex memberships, Y2H and PCA directly detect binary interactions and were shown to have higher false-negative rate but lower false-positive rate than AP (Yu et al., 2008; Tarassov et al., 2008).
The original Yu and Tarassov networks cover 1278 and 1124 genes with 1641 and 2513 edges, respectively, excluding self-interacting edges. With our method, we were able to replace (predict and remove) 706 (43.0%) and 1203 (47.9%) of the edges for the two networks, respectively. As shown in Figure 6, the evaluation results based on Gene Ontology for these two datasets and the evaluation results based on co-expression for the Yu data set are consistent with those for the Krogan dataset, confirming the general applicability of our method to PPI networks regardless of the experimental systems used to infer them. On the other hand, the differences between the predicted and removed edges are smaller in Yu/Tarassov data than in Krogan data. In fact, for the Tarassov data, the removed edges have slightly better co-expression than the predicted ones; nevertheless, both are lower than the confirmed edges and significantly higher than the randomly predicted ones. These deviations from the Krogan dataset likely reflect the lower false-positive rate of the Y2H and PCA data compared with AP data (Tarassov et al., 2008, Yu et al., 2008). As our results consistently showed that the removed edges have much higher functional relevance than random predictions, chances are that many of the removed edges are not really false positives—they just tend to contain more false-positive edges than the confirmed group of edges. To reiterate, we chose to keep the original number of edges in the predicted networks to facilitate an unbiased comparison of different approaches, as otherwise changing parameters may significantly alter and bias the evaluation outcomes. In practice, because of the high false-negative rate in PPI networks, especially for Y2H and PCA based networks, one would prefer to choose a lower similarity threshold to make more predictions and remove fewer edges than we have done here. As mentioned in Section 2 and later in Section 4, we are aware of and are developing better ways to select cut-offs to improve the coverage of PPI networks, which will be presented elsewhere.
Fig. 6.
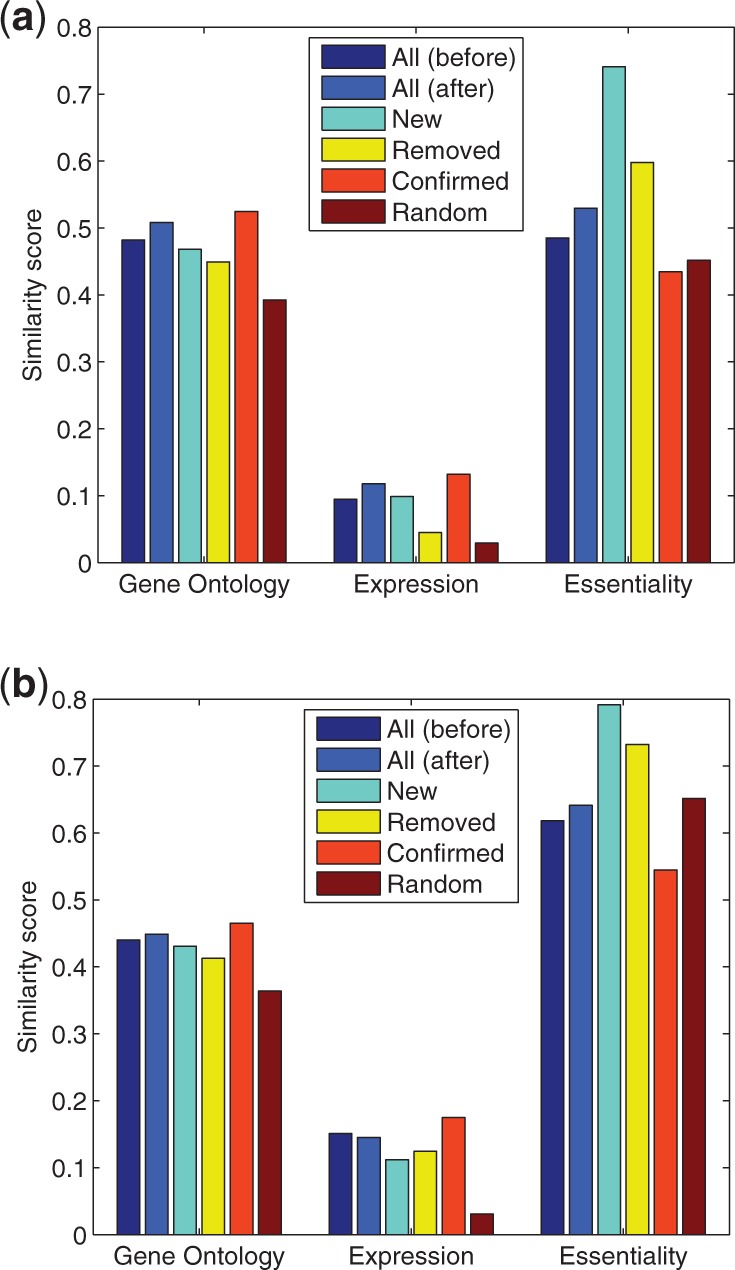
Results of our algorithm on additional yeast PPI datasets from (a) Yu et al., 2008 and (b) Tarassov et al. 2008, evaluated by functional relevance scores based on gene ontology, gene expression and gene essentiality
Similarly, as in Krogan data, the predicted edges in Yu/Tarassov data have higher co-essentiality than the removed edges, suggesting that the predicted ones are more likely to be in-complex than the removed ones. On the other hand, although the confirmed edges in Krogan data have high co-essentiality, those in the Yu/Tarassov data have much lower co-essentiality, indicating that a large portion of between-complex edges in these two datasets are preserved by our algorithm. As shown in Yu et al. (2008), Y2H and PCA usually detect more between-complex edges than AP. Our algorithm nicely preserved this property.
3.5 Predicted edges are bona fide physical interactions
Finally, it is interesting to ask whether the edges predicted by our algorithm are bona fide physical interactions or simply functional interactions. To answer this question, we validated the edges predicted by our algorithm on the three yeast datasets using the physical interactions present in the BioGRID database (Stark et al., 2011). It is known that different PPI assay techniques have different characteristics and produce complementary, largely disjoint, results (Tarassov et al., 2008; Yu et al., 2008). We, therefore, classified the PPIs in BioGRID into four categories according to the experimental systems: AP, Y2H), PCA and other. Note that each PPI in BioGRID may have been captured by multiple experiments and, therefore, appear in multiple categories. The three datasets we used, Krogan, Yu and Tarassov, were generated by the first three systems, respectively, and are all present in the BioGRID database. To ensure fair comparison, before evaluating results for a particular dataset (e.g. Krogan), BioGRID entries from the corresponding publication were removed (as otherwise the validation rate for the confirmed or removed group for the Krogan dataset would be 100%).
Table 2 shows the number and fraction of edges in different groups validated by BioGRID, using all physical interactions (column ‘All’) or using edges detected by specific experimental systems (columns ‘AP’, ‘Y2H’, ‘PCA’ and ‘other’). When all physical interactions are considered, for all three datasets, the confirmed edges always have the highest validation rate compared with the other edge groups. The validation rates for predicted/removed edges are lower than that of the confirmed ones but significantly higher than the random ones (<1% in all cases). For Krogan data, the predicted edges have a much higher validation rate than the removed ones, whereas for Tarassov and Yu data, the validation rates for the predicted edges are similar as or lower than that for the removed ones. These results suggest that the predicted edges in all three datasets are likely bona fide physical interactions, and reconfirm that the removed ones are not necessarily false-positive results, especially for Y2H and PCA-based data, which are known to have lower false-positive rate than AP (Tarassov et al., 2008; Yu et al., 2008). Therefore, it may be preferred to have a lower cut-off to increase the coverage of PPI networks, as discussed in Section 3.4. Overall, Krogan data has the highest percentage of validated predictions (36.0% or 1033/2870), compared with Yu and Tarassov data, which have 9.2% (65/706) and 11.2% (135/1203) predicted edges validated by BioGRID, respectively (but see later in the text). As the BioGRID PPI data may still have a high false-negative rate, the real validation rate is likely underestimated.
Table 2.
Validation by BioGRID, breaking down according to experimental systemsa
| BioGRID physical interactions |
||||||
|---|---|---|---|---|---|---|
| Edge group | Number of edges | All | AP | Y2H | PCA | Other |
| BioGRID | 73 929 | 73 929 (1.00) | 52 842 (0.71) | 9303 (0.12) | 5237 (0.07) | 13 080 (0.18) |
| Krogan | ||||||
| Predicted | 2870 | 1033 (0.36) | 983 (0.34) | 134 (0.05) | 35 (0.01) | 180 (0.06) |
| Removed | 2870 | 412 (0.14) | 393 (0.14) | 48 (0.02) | 16 (0.01) | 67 (0.02) |
| Confirmed | 4253 | 2732 (0.64) | 2682 (0.63) | 595 (0.14) | 165 (0.04) | 770 (0.18) |
| Random | 7123 | 54 (0.01) | 33 (0.00) | 13 (0.00) | 1 (0.00) | 13 (0.00) |
| Yu | ||||||
| Predicted | 706 | 65 (0.09) | 52 (0.07) | 35 (0.05) | 4 (0.01) | 20 (0.03) |
| Removed | 706 | 114 (0.16) | 53 (0.07) | 85 (0.12) | 3 (0.00) | 19 (0.03) |
| Confirmed | 935 | 405 (0.43) | 304 (0.33) | 290 (0.31) | 35 (0.04) | 169 (0.18) |
| Random | 1641 | 7 (0.00) | 3 (0.00) | 1 (0.00) | 0 (0.00) | 3 (0.00) |
| Tarassov | ||||||
| Predicted | 1203 | 135 (0.11) | 96 (0.08) | 39 (0.03) | 23 (0.02) | 42 (0.03) |
| Removed | 1203 | 109 (0.09) | 81 (0.07) | 22 (0.02) | 15 (0.01) | 26 (0.02) |
| Confirmed | 1333 | 352 (0.26) | 301 (0.23) | 143 (0.11) | 34 (0.03) | 121 (0.09) |
| Random | 2536 | 24 (0.01) | 18 (0.01) | 2 (0.00) | 1 (0.00) | 6 (0.00) |
aValues in parentheses are fractions of edges validated.
We also validated our results using the BioGRID PPIs within each specific category. Interestingly, it seems that the different characteristics in different experimental systems are carried over to the predicted edges. For example, the predicted edges for Krogan data are mostly validated by the AP-based interactions in BioGRID. Moreover, although Y2H only covers 12.6% of edges in BioGRID, it accounts for 53.9% (35/65) of the validated predictions in Yu data. Similarly, PCA only contributes 7.1% of the edges in BioGRID, but accounts for 17.0% (23/135) of the validated predictions in Tarassov data. Therefore, the relatively low validation rate for the Yu and Tarassov data can be partially explained by the insufficient presence of Y2H and PCA data in the BioGRID database.
3.6 Application to human PPI network
Finally, we apply our method to predict novel interactions in the human PPI network downloaded from the Human Protein Reference Database (HPRD, version 9) (Keshava Prasad et al., 2009). The largest connected component of this network contains 9205 nodes and 36 720 edges. We first tried to use the idea to retain the same number of edges, which causes 24 187 (65.9%) edges to be replaced. To evaluate this result, we calculated gene ontology-based similarity and gene co-expression for different edge groups, following the same logic as in Section 3.1. The gene expression data used for this purpose is downloaded from M DB and contains 878 normal (non-diseased) tissue samples from the Affymetrix Human U133A platform, following the parameters suggested by the developers (Cheng et al., 2010). Figure 7 shows the validation results. Similar as for the yeast data set, the reconstructed network has improved scores using both criteria. Although the confirmed edges have the highest similarities scores, the predicted ones have better scores than the removed ones, and both are significantly better than random predictions.
DB and contains 878 normal (non-diseased) tissue samples from the Affymetrix Human U133A platform, following the parameters suggested by the developers (Cheng et al., 2010). Figure 7 shows the validation results. Similar as for the yeast data set, the reconstructed network has improved scores using both criteria. Although the confirmed edges have the highest similarities scores, the predicted ones have better scores than the removed ones, and both are significantly better than random predictions.
Fig. 7.
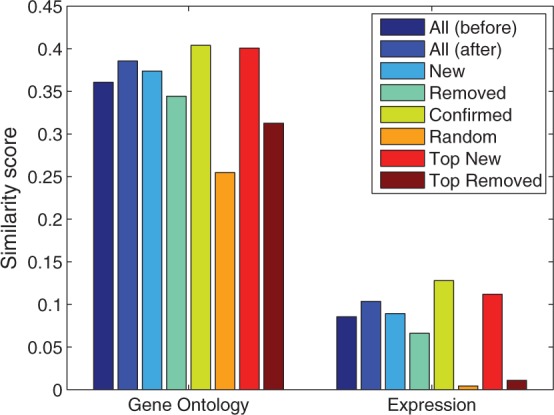
Results of our algorithm on human PPI network, evaluated by functional relevance scores based on gene ontology, gene expression. See main text for definitions of top new and top removed
On the other hand, because of the high replacement rate (65.9%), and the non-trivial functional and gene co-expression similarity scores, we suspect that most of the removed edges are probably true interactions. Therefore, we further investigated the distribution of the topological similarity scores for the PPIs in the original network, which clearly follow a bimodal distribution (Supplementary Fig. S3). Therefore, we used topological similarity score  0.2 to select 4309 edges to be treated as high-confidence false-positive edges (top removed), and topological similarity score
0.2 to select 4309 edges to be treated as high-confidence false-positive edges (top removed), and topological similarity score  0.9 to select 3802 edges as high-confidence false-negative edges (top new) and evaluated them using gene ontology and gene co-expression. As shown in Figure 7, the high-confidence false-positive edges have close-to-random gene co-expression (0.01), and low GO-based similarity. In contrast, the average GO-based similarity score for the high-confidence false-negative edges are almost as high as the confirmed edges, and they have high co-expression. These results indicate that the topological similarity scores can be used to prioritize edges for further validation. In fact, as shown in Figure 8, with as many as 35 000 (50 000) predicted edges, the average gene co-expression (GO similarity) of interacting genes are as good as that in the original PPI network, indicating that we can increase the coverage of the HPRD human PPI network by at least 100%.
0.9 to select 3802 edges as high-confidence false-negative edges (top new) and evaluated them using gene ontology and gene co-expression. As shown in Figure 7, the high-confidence false-positive edges have close-to-random gene co-expression (0.01), and low GO-based similarity. In contrast, the average GO-based similarity score for the high-confidence false-negative edges are almost as high as the confirmed edges, and they have high co-expression. These results indicate that the topological similarity scores can be used to prioritize edges for further validation. In fact, as shown in Figure 8, with as many as 35 000 (50 000) predicted edges, the average gene co-expression (GO similarity) of interacting genes are as good as that in the original PPI network, indicating that we can increase the coverage of the HPRD human PPI network by at least 100%.
Fig. 8.
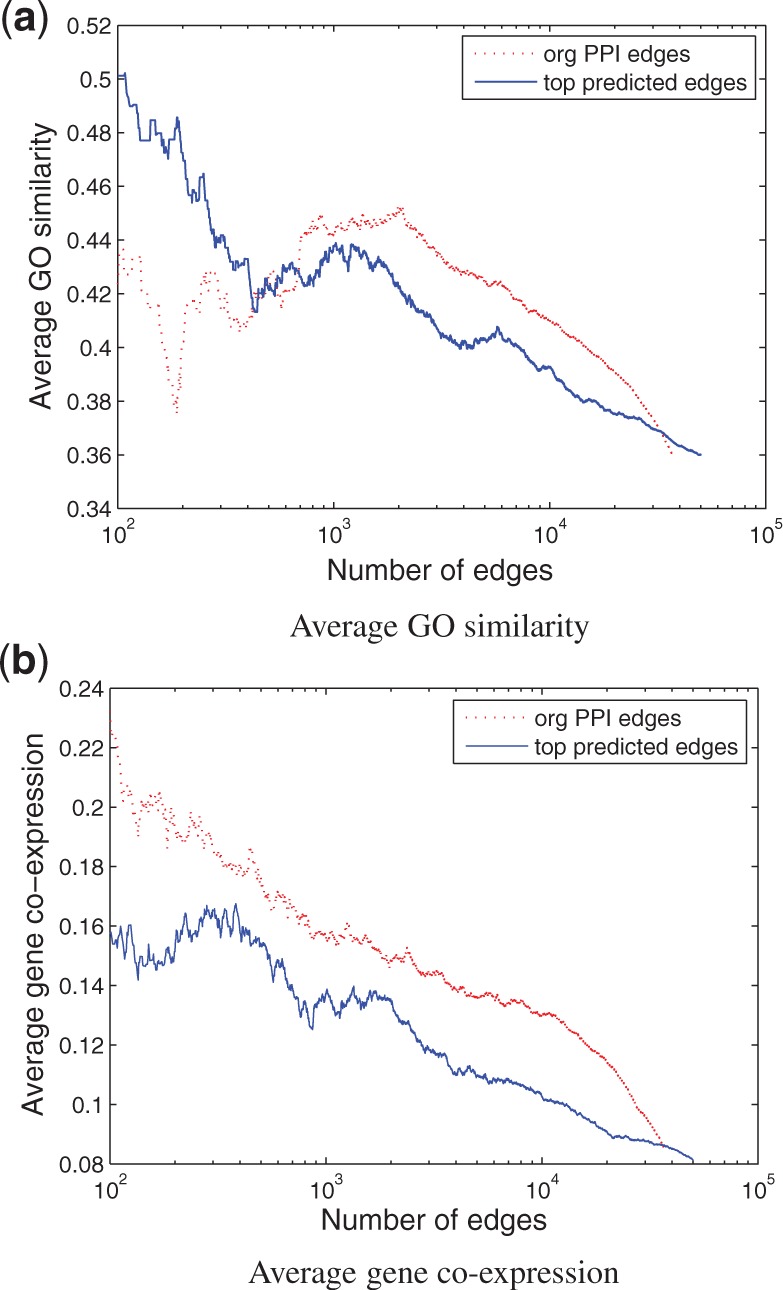
Quality of top predicted human PPIs as compared with that of the original PPIs. Predicted/original PPIs are ranked by their topological similarity scores. All edges above a particular rank are then used to calculate the average GO similarity score (a) or average gene co-expression (b)
4 CONCLUSIONS
In this article, we have presented a novel network topology-based algorithm to improve the quality of PPI networks, which in turn can improve the prediction accuracy of protein complexes. The key idea of our algorithm is that two proteins sharing some high-order topological similarities, which are measured by a novel random walk-based procedure, are likely interacting with each other and may belong to the same protein complex. Overall, the reconstructed yeast PPI network have much higher biological relevance than the original network, and better quality than those reconstructed by several existing algorithms, assessed by multiple types of information, including gene ontology, gene expression, essentiality and conservation between species. The reconstructed network has also resulted in significantly improved protein complex prediction accuracy using two different algorithms. Furthermore, our method is applicable to PPI networks obtained with different experimental systems, such as Y2H, affinity purification based and protein-fragment complementation assay, and evidence shows that the predicted edges are likely bona fide physical interactions. Finally, an application to a human PPI network increased the coverage of the network by at least 100%.
Our method may be improved in several directions. For example, to derive a network from the topology-based similarity matrix, we have used a simple cut-off-based strategy to maintain the number of edges in the original network. We made this choice to facilitate a fair evaluation of different network reconstruction/clustering algorithms. In fact, we have found that many edges with similarity slightly below the cut-off also have higher biological relevance than those removed, as shown in the human data. This is also biologically understandable—the original PPI network has a higher false-negative rate than false-positive rate (Huang et al., 2007; Kuchaiev et al., 2009). In future work, it may be worthwhile to develop methods that can guide the selection of a more appropriate cut-off that would allow more functionally relevant edges being included without introducing too many false-positive edges. One possible way is to examine the distribution of the similarity scores of the original edges and non-edges and determine what edge weights might represent a good separation.
Supplementary Material
ACKNOWLEDGEMENT
The authors would like to thank Saleh Tamim for his assistance in obtaining the human microarray data. We also thank the anonymous reviewers for their insightful comments that have significantly improved this manuscript.
FUNDING
NIH (SC3GM086305, R01CA152063, U54CA113001, G12MD007591 (Computational Systems Biology Core)), NSF (IIS-1218201, IOS-0848135).
Conflict of Interest: none declared.
REFERENCES
- Asthana S, et al. Predicting protein complex membership using probabilistic network reliability. Genome Res. 2004;14:1170–1175. doi: 10.1101/gr.2203804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader G, Hogue C. Analyzing yeast protein-protein interaction data obtained from different sources. Nat. Biotechnol. 2002;20:991–997. doi: 10.1038/nbt1002-991. [DOI] [PubMed] [Google Scholar]
- Brohee S, van Helden J. Evaluation of clustering algorithms for protein-protein interaction networks. BMC Bioinformatics. 2006;7:488. doi: 10.1186/1471-2105-7-488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng W-C, et al. Microarray meta-analysis database (m2db): a uniformly pre-processed, quality controlled, and manually curated human clinical microarray database. BMC Bioinformatics. 2010;11:421. doi: 10.1186/1471-2105-11-421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chua HN, et al. Exploiting indirect neighbours and topological weight to predict protein function from protein-protein interactions. Bioinformatics. 2006;22:1623–1630. doi: 10.1093/bioinformatics/btl145. [DOI] [PubMed] [Google Scholar]
- Chuang HY, et al. Network-based classification of breast cancer metastasis. Mol. Syst. Biol. 2007;3:140–140. doi: 10.1038/msb4100180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dwight S, et al. Saccharomyces genome database: underlying principles and organisation. Brief. Bioinform. 2004;5:9–22. doi: 10.1093/bib/5.1.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang Y, et al. Global geometric affinity for revealing high fidelity protein interaction network. PLoS ONE. 2011;6:e19349. doi: 10.1371/journal.pone.0019349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fouss F, et al. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation. IEEE Trans. Knowl. Data Eng. 2007;19:355–369. [Google Scholar]
- Fowlkes E, Mallows C. A method for comparing two hierarchical clusterings. J. Am. Stat. Assoc. 1983;78:553–569. [Google Scholar]
- Friedel C, et al. Bootstrapping the interactome: unsupervised identification of protein complexes in yeast. J. Comput. Biol. 2009;16:1–17. doi: 10.1089/cmb.2009.0023. [DOI] [PubMed] [Google Scholar]
- Gasch A, et al. Genomic expression programs in the response of yeast cells to environmental changes. Mol. Biol. Cell. 2000;11:4241–4257. doi: 10.1091/mbc.11.12.4241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gavin A, et al. Proteome survey reveals modularity of the yeast cell machinery. Nature. 2006;440:631–636. doi: 10.1038/nature04532. [DOI] [PubMed] [Google Scholar]
- Hall MC, et al. Mnd2 and swm1 are core subunits of the saccharomyces cerevisiae anaphase-promoting complex. J. Biol. Chem. 2003;278:16698–16705. doi: 10.1074/jbc.M213109200. [DOI] [PubMed] [Google Scholar]
- Hannum G, et al. Genome-wide association data reveal a global map of genetic interactions among protein complexes. PLoS Genet. 2009;5:e1000782. doi: 10.1371/journal.pgen.1000782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han J-DJ, et al. Evidence for dynamically organized modularity in the yeast protein-protein interaction network. Nature. 2004;430:88–93. doi: 10.1038/nature02555. [DOI] [PubMed] [Google Scholar]
- Hidalgo C, et al. A dynamic network approach for the study of human phenotypes. PLoS Comput. Biol. 2009;5:e1000353. doi: 10.1371/journal.pcbi.1000353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang H, et al. Where have all the interactions gone? Estimating the coverage of two-hybrid protein interaction maps. PLoS Comput. Biol. 2007;3:e214. doi: 10.1371/journal.pcbi.0030214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ideker T, Sharan R. Protein networks in disease. Genome Res. 2008;18:644–652. doi: 10.1101/gr.071852.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeong H, et al. Lethality and centrality in protein networks. Nature. 2001;411:41–42. doi: 10.1038/35075138. [DOI] [PubMed] [Google Scholar]
- Keshava Prasad TS, et al. Human protein reference database–2009 update. Nucleic Acids Res. 2009;37:D767–D772. doi: 10.1093/nar/gkn892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y, et al. Identifying causal genes and dysregulated pathways in complex diseases. PLoS Comput. Biol. 2011;7:e1001095. doi: 10.1371/journal.pcbi.1001095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King A, et al. Protein complex prediction via cost-based clustering. Bioinformatics. 2004;20:3013–3020. doi: 10.1093/bioinformatics/bth351. [DOI] [PubMed] [Google Scholar]
- Krogan N, et al. Global landscape of protein complexes in the yeast saccharomyces cerevisiae. Nature. 2006;440:637–643. doi: 10.1038/nature04670. [DOI] [PubMed] [Google Scholar]
- Kuchaiev O, et al. Geometric de-noising of protein-protein interaction networks. PLoS Comput. Biol. 2009;5:e1000454. doi: 10.1371/journal.pcbi.1000454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K, et al. Protein networks markedly improve prediction of subcellular localization in multiple eukaryotic species. Nucleic Acids Res. 2008;36:e136. doi: 10.1093/nar/gkn619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li A, Horvath S. Network neighborhood analysis with the multi-node topological overlap measure. Bioinformatics. 2007;23:222–231. doi: 10.1093/bioinformatics/btl581. [DOI] [PubMed] [Google Scholar]
- Lovász L. Random walks on graphs: a survey. Combinatorics, Paul Erdős is Eighty. 1993;2:1–46. [Google Scholar]
- Lü L, Zhou T. Link prediction in complex networks: a survey. Physica A. 2011;390:1150–1170. [Google Scholar]
- Meila M. Comparing clusterings: an axiomatic view. ICML ’05: Proceedings of the 22nd International Conference on Machine Learning; New York, NY. ACM Press; 2005. pp. 577–584. [Google Scholar]
- Mewes H, et al. MIPS: analysis and annotation of proteins from whole genomes in 2005. Nucleic Acids Res. 2006;34:D169–D172. doi: 10.1093/nar/gkj148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Przulj N. Protein-protein interactions: making sense of networks via graph-theoretic modeling. Bioessays. 2011;33:115–123. doi: 10.1002/bies.201000044. [DOI] [PubMed] [Google Scholar]
- Radicchi F, et al. Defining and identifying communities in networks. Proc. Natl Acad. Sci. USA. 2004;101:2658–2663. doi: 10.1073/pnas.0400054101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruan J, Zhang W. Identification and evaluation of weak community structures in networks. Proceedings National Conference on Artificial Intelligence (AAAI-06); Boston, MA, AAAI press. 2006. pp. 470–475. [Google Scholar]
- Ruan J, Zhang W. Identifying network community structures with a high resolution. Phys. Rev. E. 2008;77:016104. doi: 10.1103/PhysRevE.77.016104. [DOI] [PubMed] [Google Scholar]
- Ruan J. A fully automated method for discovering community structures in high dimensional data. Proceedings of IEEE International Conference on Data Mining (ICDM-09); Miami, FL, IEEE. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharan R, et al. Network-based prediction of protein function. Mol. Syst. Biol. 2007;3:88. doi: 10.1038/msb4100129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark C, et al. The BioGRID interaction database: 2011 update. Nucleic Acids Res. 2011;39:D698–D704. doi: 10.1093/nar/gkq1116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarassov K, et al. An in vivo map of the yeast protein interactome. Science. 2008;320:1465–1470. doi: 10.1126/science.1153878. [DOI] [PubMed] [Google Scholar]
- Tong H, et al. Fast random walk with restart and its applications. Proceedings of the Sixth International Conference on Data Mining; 2006. ICDM ’06. Washington, DC, IEEE Computer Society, pp. 613–622. [Google Scholar]
- Ulitsky I, Shamir R. Identifying functional modules using expression profiles and confidence-scored protein interactions. Bioinformatics. 2009;25:1158–1164. doi: 10.1093/bioinformatics/btp118. [DOI] [PubMed] [Google Scholar]
- Vlasblom J, Wodak S. Markov clustering versus affinity propagation for the partitioning of protein interaction graphs. BMC Bioinformatics. 2009;10:99. doi: 10.1186/1471-2105-10-99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, et al. Consistent dissection of the protein interaction network by combining global and local metrics. Genome Biol. 2007a;8:R271. doi: 10.1186/gb-2007-8-12-r271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, et al. A new method to measure the semantic similarity of go terms. Bioinformatics. 2007b;23:1274–1281. doi: 10.1093/bioinformatics/btm087. [DOI] [PubMed] [Google Scholar]
- Wang J, et al. Recent advances in clustering methods for protein interaction networks. BMC Genomics. 2010;11(Suppl. 3):S10. doi: 10.1186/1471-2164-11-S3-S10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiles A, et al. Building and analyzing protein interactome networks by cross-species comparisons. BMC Syst. Biol. 2010;4:36. doi: 10.1186/1752-0509-4-36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu G, et al. Gosemsim: an R package for measuring semantic similarity among go terms and gene products. Bioinformatics. 2010;26:976–978. doi: 10.1093/bioinformatics/btq064. [DOI] [PubMed] [Google Scholar]
- Yu H, et al. The importance of bottlenecks in protein networks: correlation with gene essentiality and expression dynamics. PLoS Comput. Biol. 2007;3:e59. doi: 10.1371/journal.pcbi.0030059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, et al. High-quality binary protein interaction map of the yeast interactome network. Science. 2008;322:1158684–1158110. doi: 10.1126/science.1158684. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.