Mapping the Timing, Pace, and Scale of the Fertility Transition in Brazil

Demographers attempting to generalize about the nature of the shift from high to low fertility have often mapped the course of the transition across different subpopulations within a region or country. The European Fertility Project (Coale and Watkins 1986) offers perhaps the most influential example. Maps of fertility indicators had a prominent place in the project’s summary volume and in the individual volumes on specific countries. Sequences of maps have been important to more recent studies of the “second demographic transition” in Europe and the United States (Lesthaeghe and Neels 2002; Lesthaeghe and Neidert 2006, 2009), as well as to analyses of the historical demographic transition in a number of developing countries (Bocquet-Appel et al. 2002; Weeks et al. 2000).

One limitation of previous efforts to map fertility transitions is that spatial units have often been quite large. For example, in the case of the European Fertility Project, Guinnane and others have argued that the timing and pace of fertility change at the provincial level resulted from disparate patterns in provincial subpopulations (Brown and Guinnane 2007; Casterline 2001; Guinnane et al. 1994). They claim that a more fine-grained analysis would present a different picture of transition timing and of the relevance of socioeconomic covariates.

Availability of large microdata samples from successive censuses for a number of countries now makes it possible to construct fertility estimates for smaller and more homogeneous spatial units in populations that lack a historical series of complete vital registration. But even with large census samples, data for small spatial units may be sparse. One way to overcome that limitation is to take advantage of the underlying spatial correlation in fertility. If neighboring regions tend to have similar levels of fertility, then the spatial structure of regions can be used to “borrow strength from neighbors” when estimating a region’s transition path.

In this article, we chart the path of fertility levels from 1960 to 2000 in over 500 small regions of Brazil, by fitting a separate logistic curve to census estimates of the total fertility rate for each region. This enables us to map the fertility transition and to answer questions regarding: 1) variation in the pretransitional level of fertility, 2) the speed of earlier as compared to later transitions, 3) prevailing social and economic conditions at the onset of fertility decline, and 4) where and when the fertility transition may end in Brazil.

After a brief introduction to the Brazilian context, we turn to methods. We first review the use of logistic curves in demography and describe the Bayesian method used to estimate these curves from sparse and frequently noisy data. We then present the estimates and assess their implications for some of the main hypotheses and stylized facts about the timing and speed of the fertility transition. Finally, we compare model forecasts for 2005 to estimates from the recently completed National Survey of Demography and the Health of Women and Children. We close with reflections on what our fine-grained mapping exercise reveals about the fertility transition in Brazil and, by implication, elsewhere.

Brazil 1960–2000

Brazil is geographically large, culturally heterogeneous, and economically unequal, making it an interesting case study for the spatial distribution of the fertility transition. Its population is much larger than that of any European country, numbering over 140 million at the midpoint of the four decades from 1960 to 2000. Most of its fertility transition took place in these four decades, with the national TFR falling from about 6.3 births per woman to about 2.3. The national TFR is now below replacement (Ministério da Saúde 2008). Although Brazil’s aggregate demographic trajectory was smooth, local fertility transitions were highly variable, beginning in some parts of the country well before 1960 from relatively low initial levels, and in other regions after 1980 from quite high levels.

In 1960 Brazil’s immense land area, challenging topography, and colonial institutional legacy made for a decentralized and disconnected collection of states, with strong local identities and considerable regional autonomy. The rapid spread of electrification, mass media, highways, and air transport have made Brazil a much more connected country today.

Brazil is commonly divided into five main census regions (macroregions): North, Northeast, Central-West, Southeast, and South. Regional differences in the level of economic development, transportation infrastructure, communications, and health and education services remained pronounced over the four decades (Diniz 1995). The Southeast and South accounted for most of the increasing number of formal jobs, production, and consumption. Parallel to the industrial development occurring in the South and Southeast was an expansion of the agrarian frontier and agricultural modernization in the South and the Central-West. Industrialization and agricultural modernization followed at least a decade later in the Northeast and North (the latter region mostly covered by the Amazon rainforest).

These were turbulent decades in both political and economic terms. A military coup in 1964 replaced a democratic government with an authoritarian regime; democratic rule was eventually restored in 1988. Economic growth was rapid from 1968 to 1973, but then waned, becoming stagnant in the 1980s and uneven in the remaining years of the twentieth century. The annual rate of inflation increased from around 16 percent per annum in 1960 to near hyperinflationary rates in the early 1990s, followed by much lower rates in the late 1990s (Baer 1995).

Data

Microdata for this study are from population censuses of Brazil taken in 1960, 1970, 1980, 1991, and 2000. Fertility data come from long-form questionnaires applied to a 25 percent sample in 1960, 1970, and 1980 and to around 12.5 percent of the population in 1991 and 2000. For each census from 1970 on, we have the number of children born in the year preceding the census for all women of reproductive age. We used this information to construct age-specific fertility rates for each microregion (defined below) at each point in time. We then adjusted these rates based on the enumeration of children under age 5 years, corrected using local child survivorship estimates. Because the 1960 census did not include data on current fertility, we estimated the TFR for 1960 from the number of children age 0–4 years in each location, assuming that the local age pattern of fertility was the same as in 1970.¹

While over the five censuses our sample includes data from more than 26 million women of reproductive age, the number of women sampled per microregion and census varies widely across location and time—from 151 (Pontes e Lacerda, Mato Grosso 1960) to 663,455 (city of São Paulo 1980). Also, data for 1960 are incomplete. For historical administrative reasons, there are nine states (around 17 percent of the total population) for which no 1960 microdata are available. Data are missing for all of the states in the North, two states in the Northeast (Maranhão and Piauí), one in the Southeast (Espírito Santo), and one in the South (Santa Catarina).

The spatial units called microregions are defined by the Brazilian Census Bureau on the basis of economic homogeneity and commercial transportation links. In our mapping analysis, we constructed 502 areas with unchanging boundaries across the period 1960–2000 that closely approximate the official 1991 microregions and are uniquely identifiable from the (changing) geographic codes on all five censuses.²

This is an unusually long series of census microdata, and the geographic identifiers are more detailed than those usually provided with census records. However, in addition to the missing states in 1960, there are two other critical limitations of our fertility measures. First, because of the small number of women of childbearing age in many of the microregions, estimated TFRs are subject to considerable sampling variation, especially in the earlier censuses. Second, because these are census records, the quality of the registration of small children and the accuracy of responses to questions about surviving children and date of last live birth are subject to various kinds of errors. Moreover, there is no guarantee that the pattern of errors will be the same across censuses or even across regions within a census.

The logistic curve—A schematic model for fertility transition

We estimate a separate logistic curve for the path of the TFR in each of Brazil’s 502 microregions. The logistic function has most often been used to represent population growth, but fertility and mortality transitions can also be modeled with logistic curves³ (Marchetti, Meyer, and Ausubel 2004). One attractive feature of the logistic curve is that its four parameters closely match the classic formulation of the demographic transition: for each variable there is an initial level, a final level, a time location, and a speed.

The United Nations has used logistic curves to project fertility since 2002. In stark contrast to the approach we take here, which uses hundreds of distinct transition paths for regions within a single country, the UN projects national fertility for every country using only one of three possible logistic paths, based on “the combined experience of all countries that underwent fertility decline between 1950 and 2000” (United Nations 2004).⁴

Despite this extensive use, there is little evidence as to when and where a logistic curve adequately represents the fertility experience of individual populations. Such phenomena as the post–World War II baby boom in most industrialized countries, substantial tempo-induced swings in the TFR in such countries as Italy and Korea, and recent “stalls” in fertility at above-replacement levels in such countries as Kenya and Peru would lead one to doubt its universal applicability (Bongaarts 2006). However, if logistic time paths fit the data for our microregions reasonably well, they would provide useful summary indexes of the timing and speed of local fertility transitions, and of the pre- and post-transitional levels of local fertility.

Estimating the logistic curve for small regions

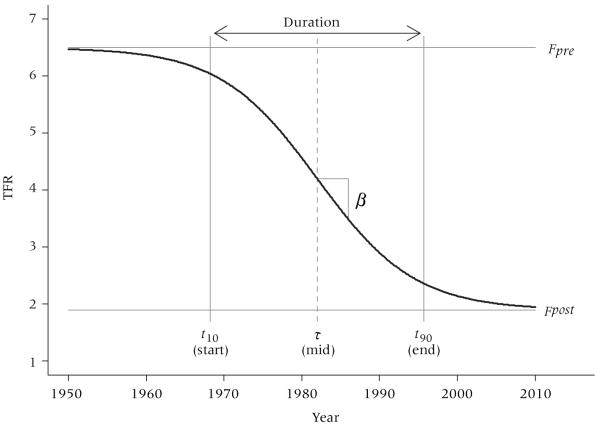
In our application to Brazilian transition data, we specify a logistic curve, as in Figure 1, for each of the country’s 502 microregions. We hereafter refer to these microregions as regions and index them by i=1,…,502. We assume that the TFR in region i at time t, F_i(t), is given by

$$F_i\left(t\right)={\mathit{Fpost}}_i+({\mathit{Fpre}}_i-{\mathit{Fpost}}_i)∕(1+e^{-{\beta }_i(t-{\tau }_i)})$$

where Fpre_i and Fpost_i are the initial and final levels of TFR along a transition path; τ_i is the halfway point of the fertility transition (i.e., the time at which the transition is 50 percent complete in region i); and β_i represents transition speed. The parameter β_i is necessarily negative, with larger absolute values representing more rapid fertility declines. To facilitate estimation and interpretation, we also use a common reparameterization, in which the speed and timing parameters (β,τ) are replaced with the times at which the transition is 10 percent and 90 percent complete (t₁₀ = τ + ln(9)/β, t₉₀ = τ – ln(9)/β). In this reparameterized version we refer to t₁₀, t₉₀, and t₉₀ – t₁₀ as the Start, End, and Duration of the transition, respectively.

FIGURE 1. Logistic model of fertility transition applied to microregions in Brazil.

NOTE: Starting from a pretransition level Fpre, TFR declines toward a new level Fpost. Times t₁₀, θ, and t₉₀ are the points at which the transition is 10 percent, 50 percent, and 90 percent complete. Duration = t₉₀–t₁₀. (Curve as drawn shows a stylized transition in TFR from 6.5 to 1.9, centered around 1982.)

In any of our parameterizations there are four constants for each curve and at most five census estimates of the TFR (1960, 1970, 1980, 1991, 2000). Thus, we have 4 × 502 = 2,008 logistic parameters, which is only slightly less than the number of available TFR estimates. As noted above, TFR estimates include measurement errors inherent in census data and sometimes include considerable sampling error.

To estimate a large number of region-specific parameters from sparse data, we must impose additional structure on the model. However, we do this in a manner that also lets us discern the true variability in local fertility trends. We begin by postulating that the true time path of TFR in each region follows a distinct four-parameter logistic curve like that in Figure 1. We then assume that census TFR calculations represent noisy estimates of these true values, with sampling variance inversely proportional to the number of women surveyed (see the likelihood function in the Appendix).

We model each logistic parameter as a function of regional educational levels and region-specific random effects. For example,

$${\mathit{Fpre}}_i=\underset{\text{National average}}{{\alpha }_{\mathit{Fpre}}}+\underset{\text{Regional education effect}}{{\delta }_{\mathit{Fpre}}(E{d}_i-\stackrel{‒}{Ed})}+\underset{\text{Regional random effect}}{{\epsilon }_{\mathrm{Fpre},i}},i=1,\dots 502,$$

with equivalent expressions for the other three logistic parameters.⁵ Educational levels may vary sharply between neighboring regions—for example, between high levels in a state capital and low levels in the surrounding hinterland. In contrast, we assume that other factors affecting logistic parameters (ε terms) are likely to vary smoothly over space. However, by using a Bayesian model, we do not specify how smoothly, nor where any hills and valleys will be. We favor spatial smoothness by using a prior distribution for the random effects (as described in the Appendix), which takes higher values when spatially adjacent ε terms are more similar. This model structure combines a traditional regression approach with spatial smoothing, and attempts to pull logistic parameters away from noisy or erroneous values by borrowing strength from both geographical and educational neighbors.

Results

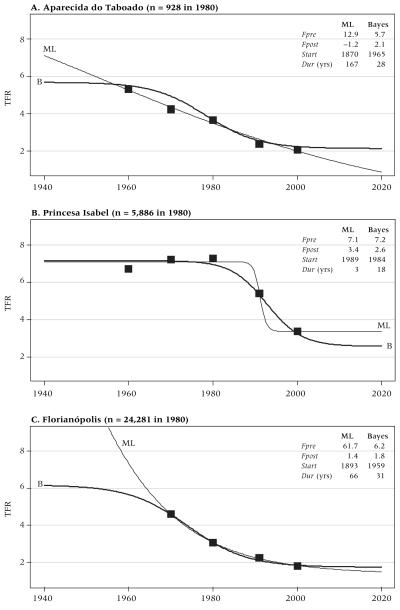
Before presenting our estimates for all 502 regions in thematic maps, we briefly review sample fits for three selected regions. These cases illustrate how Bayesian estimates of transition paths can differ substantially from maximum-likelihood (ML) methods that do not draw on information from neighbors.

Bayesian estimates of logistic parameters (i.e., posterior means) and the fitted curve (heavy line) for the selected regions are shown in Figure 2, along with the local TFR estimates from census data (points) and a standard maximum-likelihood logistic fit to the time series of regional fertility (light line). Because the ML fits do not use information from spatial or educational neighbors, comparing them to the Bayesian fits helps us understand how borrowing strength across regions affects the final estimates.

FIGURE 2. Bayesian (B) and maximum likelihood (ML) logistic curves of fertility transition for three selected microregions in Brazil.

NOTE: Points are census estimates of local TFR.

The first case (Panel A) is Aparecida do Taboado, a region in the state of Mato Grosso do Sul that had only 928 women of reproductive age in its 1980 census sample. The five TFR estimates seem to have fallen, by chance, onto a nearly straight line, which leads the ML procedure to implausible estimates of the logistic parameters, including an estimated start date of 1870 and a negative value for Fpost. The Bayesian procedure, on the other hand, yields a curve that represents a compromise between the local data and the data for the region’s geographical and educational neighbors. It does not fit the four local data points as well, but its parameters are far more plausible. Because Aparecida has a below-average population size, the Bayesian estimator gives less weight to local data and borrows more information than average from neighboring regions.

The second example (Panel B) is Princesa Isabel, a region in the state of Paraíba with a larger population. Here the ML procedure yields far more plausible estimates of the initial and final fertility levels. However, there is limited information from which to estimate transition timing because there is only one midtransition observation, and ML consequently produces an extremely small and implausible duration estimate of three years. The Bayesian procedure, in comparison, yields a curve that fits the data points nearly as well but has much more reasonable parameters, including a duration of 18 years.

Panel C for Florianópolis, the capital city of the state of Santa Catarina, illustrates a case for which Bayesian and ML estimates differ by a wide margin even when census samples are large. Because there are no 1960 data for Santa Catarina, we have only four data points, and their trajectory offers little indication of when and from what level the transition began. The ML procedure yields an implausible estimate of the duration of the transition (66 years) and an absurd pretransitional level of TFR (61.7); the Bayesian procedure provides sensible estimates of these parameters by drawing on the experience of neighbors, while sacrificing only a small amount of fit to the local data.

Not surprisingly, deviations of Bayesian estimates from census TFRs tend to be larger when regional populations are small. Bayesian and ML estimates also tend to diverge more widely in small places, because the former sacrifices local fit in order to conform better to fertility patterns in spatial and educational neighbors. Table 1 illustrates these differences, showing how fitting errors vary by local sample size and fitting method. On average, fits are better in more populous regions with larger census samples. Fitting errors from the Bayesian model (which balances local fit against neighborhood smoothness) are about twice as large as errors from the ML model (which only maximizes local fit). However, average TFR fitting errors are small in both methods, suggesting that the cost of Bayesian smoothing is small when compared to the benefits of the greater plausibility and reduced variability in local estimates.

TABLE 1. Fit and plausibility of maximum likelihood and Bayesian estimators of logistic parameters, by quartiles of 1980 sample size.

	Quartile
	I	II	III	IV
Sample size
No. of microregions	126	125	125	126
Minimum sample size	157	3,805	7,133	12,737
Maximum sample size	3,804	7,132	12,736	663,455
Root mean squared fitting error
Maximum likelihood	.13	.08	.07	.05
Bayesian	.27	.17	.13	.10
No. of regions with implausible parameters
Maximum likelihood	46	34	25	40
Bayesian	0	0	0	6

NOTE. Local estimates are “implausible” unless all of the following obtain: Fpre lies in the range [4,10], Fpost in [1,4], Start in [1900,∞], Duration in [10,50].

Table 1 also summarizes the tradeoffs between plausibility and fitting errors. In the table we define a set of logistic parameters as implausible unless they lie in the following ranges: Fpre in [4,10], Fpost in [1,4], Start in [1900,∞], and Duration in [10,50]. Table 1 shows the number of locations for which ML and Bayesian parameter estimates fall outside of these ranges, by quartiles of 1980 sample size. Under our definition, ML fits are implausible in 145 of the 502 regions and in over one third of the smallest locations (Quartile I). In contrast, Bayesian estimates are implausible in only six locations.⁶ Like Figure 2, Table 1 illustrates how Bayesian modeling allows estimation of realistic, highly localized trends from sparse data, without large sacrifices in the accuracy of local fits.

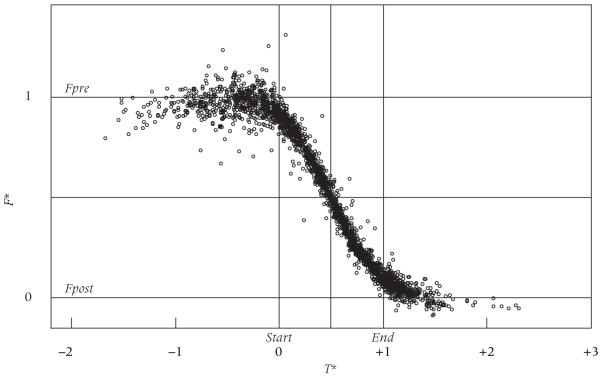
To visualize the overall utility and applicability of the logistic model, Figure 3 plots all of the Brazilian census TFR observations using common scales based on local logistic parameters. The essentially “logistic” nature of the Brazilian transitions is revealed by the symmetry evident in this aggregate plot, by the acceleration and deceleration of decline, and by the plateaus at both ends.⁷

FIGURE 3. Observed TFRs for all regions and times, standardized using local logistic parameters.

NOTE: T* = (year–Start_i)/(End_i–Start_i); F* = (TFR–Fpost_i)/(Fpre_i–Fpost_i). See endnote 7.

Overall, logistic curves fit the observed local data well: estimated curves follow the observed TFRs closely, and the smoothed trends provide reasonable compromises between local data and neighboring data. The more difficult question is whether the estimated parameters truly reflect the timing and speed of the fertility transition in each region, as well as the pre- and post-transitional levels of fertility in those regions. We return to this central question in the discussion, but it is clear that estimated parameters can be misleading in the rare cases where the transition began before the first available census or where a stall occurred in either the first or last observed decade.

Maps of the fertility transition

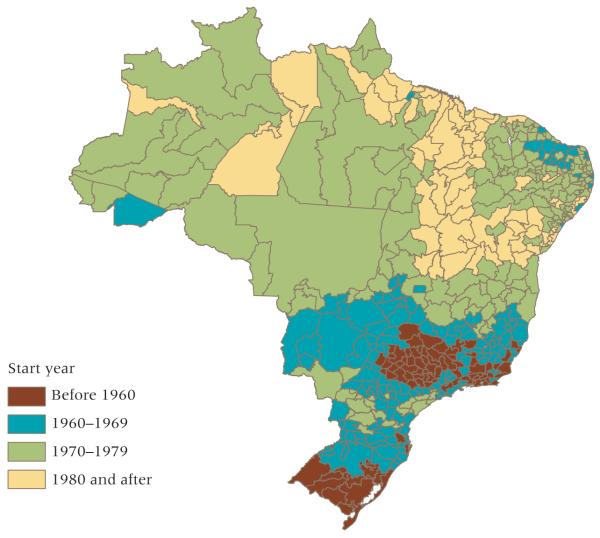
Although we cannot be sure about start dates for regions that began the fertility transition before 1960, grouping regions by start date still provides much interesting information about the way fertility decline spread throughout Brazil. Figure 4 maps regions by t₁₀ values, which we interpret as the starting times for local transitions. Fertility transition began in small clusters of the South and Southeast before 1960 and gradually spread to the rest of the country over the next 30 years. The regions with start dates in the 1960s were located mainly in the South and Southeast, but also included a few regions in the Northeast. The regions with start dates in the 1970s were predominantly in the Northeast and Central-West, while the regions with start dates after 1980 were mostly in the North and the interior Northeast.

FIGURE 4.

Bayesian estimates of the start year of fertility transition (t₁₀)

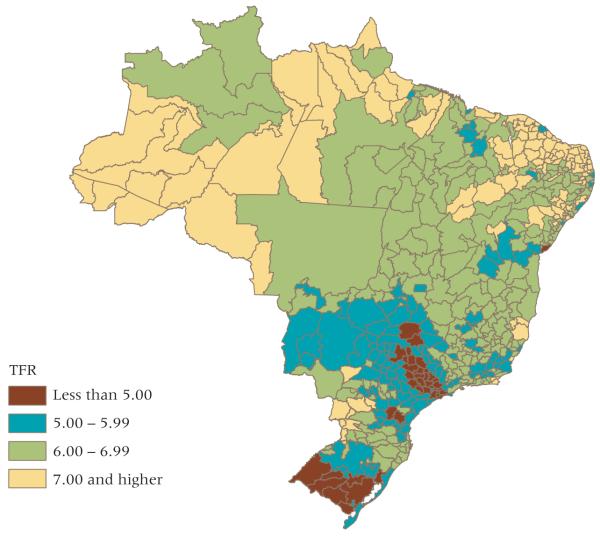
Figure 5 illustrates Bayesian estimates of pretransitional fertility levels, Fpre, grouped by integer values 5, 6, and 7. Virtually all of the regions with Fpre < 5 were in the South and Southeast, and most had a start date earlier than 1960.⁸ A minority of regions with low Fpre had a start date after 1960, including São Paulo and several other cities. Here, it is plausible that the late start and low Fpre may be an artifact of a stall between 1960 and 1970 brought about by large migratory inflows from high-fertility regions. But the general pattern is similar to Figure 4—Fpre values below 6 are found in the South and Southeast, where the transition began, and the values greater than 7 are found in the North and Northeast.

FIGURE 5.

Bayesian estimates of pretransitional fertility levels (Fpre)

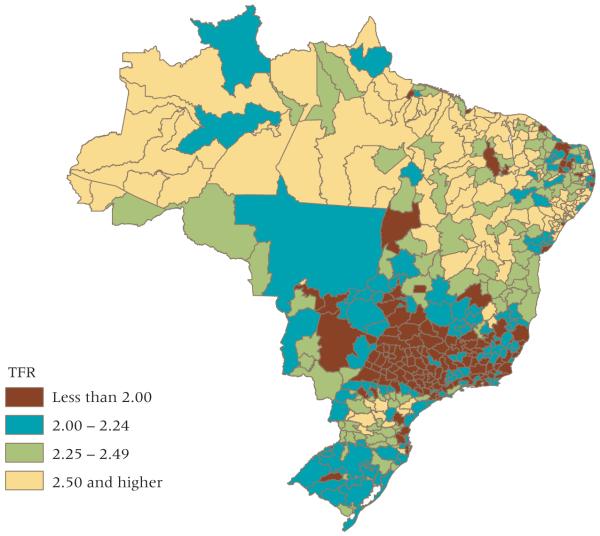
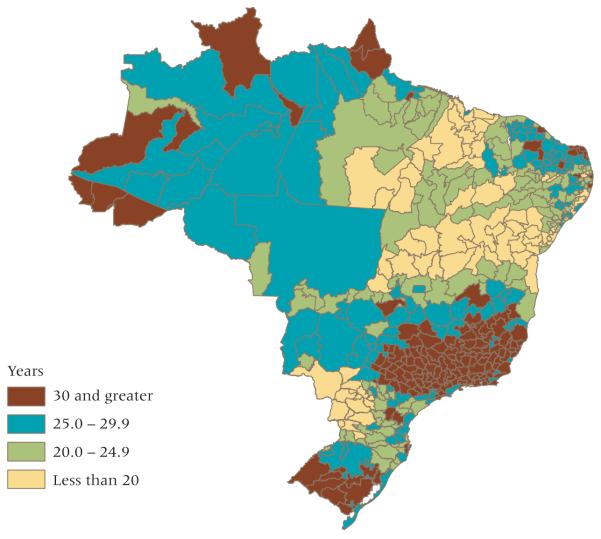
We see much less variation in the estimates of Fpost, which are shown in Figure 6. Ninety percent of all regions had an estimated TFR between 1.7 and 2.8. Places with values below 2.0 were mostly in the middle of the country, with a few such places in both the South and Northeast. The highest Fpost values (greater than 2.5) were found in the North and Northeast, where the transition started later and from a high pretransitional level of fertility. The final map, Figure 7, shows the duration of the fertility transition. The slowest transitions were in the South and Southeast, and the fastest in parts of the North, in the interior Northeast, and in the western parts of the state of Paraná in the South.

FIGURE 6.

Bayesian estimates of post-transitional fertility levels (Fpost)

FIGURE 7.

Bayesian estimates of the duration of fertility transition (t₉₀–t₁₀)

These map data, summarized in Table 2, allow us to test some of the generalizations about the demographic transition in the literature. The table shows the mean values of Fpre, Fpost, and Duration for regional transitions beginning in each of six periods. Estimates of Fpre increase monotonically across the first five of the start periods, while the Fpost estimates do so across all six periods. On the other hand, the Duration of the transition declines monotonically with the start date. Thus, in the case of Brazil, it is clear that later transitions are faster, start from higher TFR levels, and end at higher TFR levels than early transitions.

TABLE 2. Median values of estimates of Fpre, Fpost, and Duration by estimated start year.

Start year	No. of regions	Fpre	Fpost	Duration (years)
Before 1960	88	5.4	1.9	36
1960–64	77	6.1	2.0	31
1965–69	83	6.4	2.2	27
1970–74	85	6.8	2.3	26
1975–79	100	6.8	2.5	23
1980 or later	69	6.7	2.6	19

The fertility transition and the level of socioeconomic development

Our results also provide several ways to examine the relationship between fertility transition and indicators of socioeconomic development. In the hierarchical model that we used to estimate the transition curves, we assessed, in addition to the individual regional path parameters, the way in which these local parameters were correlated with the regional level of female education. We postulated that Fpre, Start, and Duration would all be related to the level of education in 1970 and that Fpost would be related to the level of education in 2000. Table 3 shows these estimated education effects.

TABLE 3. Effect of education on fertility transition.

(a) Posterior means of coefficients
Parameter	Global (α)	Education effect (δ)	Interpretation
Fpre	6.36	−0.55	more education in 1970 ⇒ lower
Fpost	2.26	−0.27	more education in 2000 ⇒ lower
Start	1970	−4.6	more education in 1970 ⇒ earlier
Duration	27	3.9	more education in 1970 ⇒ longer

(b) Implied logistic parameters across education distribution (excluding spatial effects)
	Education level
	min	25%ile	median	75%ile	max
Fpre	7.3	6.8	6.5	5.9	4.7
Fpost	3.3	2.6	2.2	2.0	1.5
Start	1978	1974	1971	1966	1956
Duration	20	24	26	30	39

NOTE: See model on page 288 for definitions of α and δ.

As we might have expected on the basis of the maps, both the pre- and post-transitional levels of fertility were inversely related to education. The effect was about twice as large for the pretransitional level. There were also pronounced, but opposite, education effects on the start date and the duration of the transition. The magnitude of these effects can be seen in the second panel of Table 3, which shows how the parameters vary by a region’s position in the education distribution. These effects are large and clearly in line with the variation in the parameters evident in the maps.

Perhaps the most controversial and longest-standing question about fertility and development concerns the level of development at the start of the transition. Results in Table 3 and Figure 4 provide unambiguous, if unsurprising, evidence that fertility declined earlier in places with higher education levels in 1970, but they do not tell us about the absolute levels of education or other indicators at the start of a region’s transition.

To identify the development threshold for fertility decline and to determine whether this threshold changed over time, where possible we have interpolated the values of four socioeconomic indicators at each region’s estimated starting time (t_10,i).⁹ The indicators are (1) mean years of education for women of reproductive age, (2) the percent of households with electricity, (3) the percent of households in an urban area, and (4) the percent of the labor force in the primary sector. In Table 4 we show median values for these indicators at the start of regional fertility transitions, disaggregated by five-year periods of t₁₀. To clarify the importance of differences across start times, we also include in the last row the inter-quartile ranges for the four indicators across all of the available (region, census) pairs. Some shifting over time from more urban to more rural (and agricultural) places is apparent, and there is a small decline followed by a later increase in both education and electrification. However, given the spread of these indicators across places and times, the stability of the median values across the different starting periods is remarkable. Thus, our results provide little indication of a meaningful decline in the development threshold for the onset of fertility decline, at least during the last three quarters of the transition.

TABLE 4. Median values of development indicators at estimated start year, plus inter-quartile range (IQR) of indicators over all 1960–2000 region and census observations.

Start year (t10)	n	Median
		Education (yrs)	Electrification (%)	Urbanization (%)	Primary sector (%)
1960–64	63	2.1	30	41	65
1965–69	68	1.9	22	37	69
1970–74	85	1.8	17	32	73
1975–80	100	1.9	22	34	70
1980–	69	2.3	27	32	74
IQR over all  region and census  observations	2,405	1.5–4.8	22–87	33–71	22–72

Logistic curves as forecasts: Projecting fertility beyond the 2000 census

Recent national fertility surveys and vital registration allow us to see how closely extrapolated logistic curves for regions correspond to actual out-of-sample fertility levels, specifically those for calendar year 2005. Because the last TFR estimate from which these curves were estimated came from the 2000 census, and was therefore centered on a point about 2.5 years before the census, these comparisons involve projecting the logistic curves slightly more than seven years past the last data point. For the five macroregions and for Brazil as a whole, Table 5 illustrates comparisons between the TFR projections aggregated across the respective regions and TFRs estimated from the Pesquisa Nacional de Demografia e Saúde da Criança e da Mulher [National Survey of Demography and the Health of Women and Children] (PNDS-2006) carried out in late 2006 and early 2007¹⁰ (Ministério da Saúde 2008).

TABLE 5. Projected and observed TFR for selected major regions and Brazil, 2005.

Region	Projected	Observed
North	2.5	2.3
Northeast	2.3	2.0
Southeast	1.9	1.7
South	2.1	1.7
Central-West	2.0	1.8
Brazil	2.1	1.8

A substantial difference is seen between the projected and observed TFR in each macroregion and at the national level. The difference is largest in the Northeast and South. Clearly, the leveling off of fertility near or slightly above replacement that was detected by our logistic estimation appears to have been a pervasive “false bottom” that gave way in the following years.¹¹ In the next section we consider possible interpretations of this discrepancy between the projected and observed rates for 2005 and the implications of our results for generalizations regarding the fertility transition.

Discussion

With a few caveats, we believe that using Bayesian methods to fit highly localized logistic models for fertility transitions is useful and informative. The local logistic curves fit most of the TFR data for individual Brazilian regions well, and Bayesian methods sensibly balance local information with information from spatial and educational neighbors. Our approach was not fully successful, however, in the minority of places where fertility decline began long before the period covered by census observations or where fertility decline stalled between 1960 and 1970.¹²

For the majority of locations, a Bayesian model seems to provide useful estimates of logistic parameters that yield new evidence with which to consider generalizations regarding the fertility transition. Regarding the level from which the transition began, as in many other studies we found considerable variation across places. In Brazil, however, the estimated pretransitional TFR was highly correlated with the 1970 level of female education and with the transition’s start date. The factors responsible for the increase in the level of pretransitional fertility across successive transitions will require further research, but it seems to us that the earliest transitions in the South and Southeast of Brazil began from pretransitional patterns that incorporated later and less universal marriage, and that might be considered more “European,” in comparison with the pretransitional patterns that prevailed in the North and Northeast.¹³

While it is clear that later transitions started from higher levels of fertility than did earlier ones, our analysis provides little support for the claim that the development threshold for transition onset declines over time. There was no clear trend in the levels of women’s education, electrification, urbanization, and primary-sector employment at the estimated start date for the declines beginning in successive five-year periods following 1960. In this respect, our results differ from one of the main findings of Bongaarts and Watkins’s cross-country analysis (1996).¹⁴

The clearest and perhaps most important generalization from our results concerns the speed of the transition. The early transitions in Brazil were, on average, much slower than later transitions. Indeed, according to our logistic parameter estimates, the mean duration of the transition was almost twice as long for transitions beginning before 1960 as it was for those beginning after 1980. Also, because later transitions began from much higher fertility levels, their annual declines in TFR were especially large. The average speed of the later regional transitions in Brazil was similar to that of Hong Kong, the fastest national transition ever recorded (Casterline 2001).

These results do not match the description of the fertility transition in which the threshold for fertility “within a region” declines over time because followers at an earlier stage of development adopt the behavior of leaders as a result of diffusion or social interaction (Bongaarts and Watkins 1996). On the other hand, the results are highly consistent with Watkins’s assessment of the European experience, wherein the differentials in fertility across regions within a country diminished greatly over the course of the transition, presumably because of the homogenizing effects of modernization (Watkins 1991). The role of mass communications, television in particular, has been identified as an important homogenizing force that operated in Brazil from the late 1960s onward, particularly after the spread of signals via satellite from 1980 onward (Faria 1989; Faria and Potter 1999; Rios-Neto 2001). Another reason for the difference in speed between earlier and later declines may have been the increasing availability and acceptability of modern contraception (Martine 1996).

The last, and perhaps most provocative, question raised by our results concerns the reasons why fertility over wide areas of Brazil seems to have plateaued at or near replacement level toward the end of the century, and then to have fallen considerably over the next seven years. We can only speculate about the factors that led to what seems, in retrospect, to have been a premature and remarkably simultaneous deceleration in fertility decline across the country. One possible influence is the sudden end of near-hyperinflation, brought about by a new economic plan (the Plano Real) started in 1994 (Sachs and Zini 1996). This economic policy led to an increase in real incomes among the poorest sectors of the population. However, the evidence suggests that wanted fertility went down, not up, after 1996, making an income effect an unlikely explanation.¹⁵

Another possibility is that the post-2000 fall in Brazil’s fertility was brought about by the ending of a tempo effect caused by temporary shifts in the age pattern of childbearing toward younger ages (Bongaarts and Feeney 1998; Rodriguez 2006). Bongaarts (2006) identified a change in the timing of union formation as a likely influence on the stalls he found in three other Latin American countries: Colombia, the Dominican Republic, and Peru. There is indeed evidence that the timing of childbearing and union formation shifted during the 1990s in Brazil, with a resulting increase in fertility in the 15–19 age group (Cavenaghi and Berquó 2005). The effect of such a shift on period fertility is a temporary increase if the trend is not continued, as it appears it was not in Brazil according to the most recent national survey (Ministério da Saúde 2008).

A third possible contributor to the deceleration in fertility decline in the late 1990s was restricted access to contraception. Although the prevalence of female sterilization in Brazil in the late 1990s was among the highest in the world (EngenderHealth 2002), demand for this method far exceeded its supply, especially among women without private health insurance (Potter et al. 2003). After the mid-1990s significant changes occurred in public-sector policies and programs for delivering contraceptive services, and although these changes did not lead to greater access to female sterilization, they did expand access to other methods.¹⁶ Moreover, these policies were implemented together with an ambitious program to expand local-level family health care (Facchini et al. 2006) and the expansion of a huge conditional cash-transfer program (Paes-Sousa and Vaitsman 2007) that increased the reach of the government’s provision of family planning methods to people with limited resources (UNFPA 2008). These efforts may have contributed to the substantial narrowing of the difference between actual and wanted fertility that occurred between 1996 and 2006, shifting the asymptote for the fertility transition to a level closer to desired family size.

Conclusion

We close by reflecting on what we learned about the fertility transition in Brazil by observing it through the lens of our Bayesian logistic model. First, by using a method that retains small geographic units and borrows strength from neighbors, we have gained a deeper understanding of the timing of fertility decline than could be obtained by other methods. This analysis has directed attention to early declines that would have been invisible with larger geographic aggregates and has posed new questions regarding the forces that brought about these declines. Second, our analysis illuminates large differences in pretransitional fertility levels and in the speed of decline, and highlights how the component parts of the national decline differ in magnitude and timing from the overall trend. Finally, these results draw attention to an apparent stall in fertility decline in the late 1990s. This slowdown did not meet the usual definition of a stall (no decline over, say, a five-year period) and might well have gone undetected in aggregate birth histories from national surveys or in the time series of fertility rates generated by an incomplete vital registration system.

Our analysis demonstrates that the logistic model provides a useful description of both national and local patterns during the fertility transition. However, it also reinforces the lesson that logistic curves are not reliable guides for forecasting fertility, and it demonstrates the kinds of unexpected irregularities that may arise in countries at the tail end of the transition. The main value of the curves in this application was to map the principal features of the Brazilian fertility transition in considerable detail and thus to uncover regularities and patterns in the timing, pace, and scale of the transition, and in the relations of these different aspects of the transition to social and economic development. It would be interesting to know whether similar micro-patterns exist in other large countries undergoing fertility transition.

Appendix: Bayesian techniques

Spatial smoothing in disease mapping

Bayesian techniques have found wide application in spatial statistics, especially for increasing the signal-to-noise ratio in estimates of disease rates for small areas. In such applications, the main interest is in the relative risk of rare phenomena occurring in different regions of a country. The main problem is that standard estimates may be greatly influenced by sampling variability (Clayton and Kaldor 1987), so that the resulting maps provide a poor representation of the underlying geographic variation in disease risk. The Bayesian remedy has been to smooth estimates by imposing a “plausible structure of spatial relatedness” and modeling the entire set of relative risks collectively as a spatial stochastic process (Bernardinelli and Montomoli 1992). Estimates are displaced from unbiased but unstable local maximum-likelihood levels toward regional geographical means in a way that achieves a good compromise between the information available for a given region and the information from its (presumably similar) neighbors.

This class of problems lends itself to a hierarchical Bayesian model in which we suppose that the local parameters are related but we have only a vague idea about the strength of the relationship. The challenge of estimating such a large number of parameters with a series of moving, local neighborhoods for each region can be solved with the powerful but computationally intensive Markov Chain Monte Carlo (MCMC) methods for sampling distributions that were developed in the 1990s (Gelfand et al. 1990; Gelfand and Smith 1990; Gelman et al. 1995).

Application to fertility transition data

In this analysis we closely follow the methods developed for disease mapping. However, our problem is more complex because it involves estimating four parameters, rather than one, for each region. The goal is the same: to produce reliable estimates that preserve as much as possible of the underlying geographic variation in parameters.

As in any Bayesian analysis, we use a standard likelihood model for the probability of the observed data given certain values, together with a prior that quantifies our initial knowledge or beliefs about parameters. The prior, in the form of a probability distribution, assigns higher weights to parameter sets that we know or believe to be more likely before examining the data. In our analysis, the most important feature of the prior is spatial smoothness: a priori, a set θ of 502 × 4 = 2,008 local logistic parameters is more likely if values for neighboring locations are similar, and less likely if they are not. By Bayes’s Theorem, the product of the sample likelihood and the prior determines a probability distribution for the parameters, conditional on the observed data:

$$\underset{\mathit{POSTERIOR}}{P(\theta \mid \mathrm{TFR}\text{estimates})}\infty \underset{\mathit{LIKELIHOOD}(\approx FIT)}{L(\mathrm{TFR}\text{estimates}\mid \theta )}\cdot \underset{\mathit{PRIOR}(\approx \text{SMOOTHNESS})}{f\left(\theta \right)}$$

Thus logistic parameters are more likely a posteriori when they (1) fit the local TFR data well in each microregion and (2) are similar in spatially adjacent regions. The first objective comes from the likelihood function L(TFR|θ); the second comes from the prior f(θ), which assigns higher probability to smoother maps. Bayesian estimation compromises between these two possibly competing objectives by searching for parameters with a high posterior density.

Complete details about the data, likelihood function, and priors are available in the online archive at «http://schmert.net/BayesLogistic». The essential features are (1) location- and time-specific quadratic penalties for lack of fit that are larger for big local samples

$$n_{it}{[F_{it}-{\widehat{F}}_{it}\left(\theta \right)]}^2$$

and (2) quadratic penalties for lack of similarity in the kth logistic parameter between neighboring locations i and j

$${[{\theta }_{ik}-{\theta }_{jk}]}^2$$

Penalties of type (1) are summed over all places and times to produce the (log) likelihood for a specific parameter set θ. Similarly, penalties of type (2) are summed over all pairs of neighbors and all four components of the logistic curve to produce a (log) prior.

The compromise between local fit and map smoothness has two important features. First, it links parameters across space. If regions i and j are neighbors, our prior says that a parameter pair such as (Fpost_i, Fpost_j) is more likely when (Fpost_i – Fpost_j)² is small. Thus, for example, lower levels of estimated fertility in i would lower the best estimate of Fpost_i in order to improve the fit in i, but would also lower the best estimate of Fpost_j in order to maintain neighborly similarity. In a third region k that borders j (but not i), Fpost_k estimates would also be affected by differences in i ’s fertility, albeit more indirectly through the prior assumption that parameters in j and k are likely to be similar. The reverse also happens, so that fertility levels in k and j affect parameter estimates in i. Thus local estimators borrow strength from data in neighboring regions, and to a lesser extent from neighbors of neighbors, and so on. The result is a set of estimates that compromise between matching local data and smoothing fits using broader regional averages.

A second valuable feature of the Bayesian approach is that it borrows strength selectively. In regions with large populations and less noisy data, the penalties for lack of fit are larger and the likelihood function has a stronger effect on the posterior. In such regions neighborly similarity becomes relatively less important, and fertility in nearby regions has less effect on local estimates. For locations with small census samples and noisy data, the opposite is true: the smoothness objective dominates, and Bayesian estimators borrow information more heavily from neighbors and do more smoothing. In short, the Bayesian procedure relies almost exclusively on local information to fit time trends for areas with large samples, but borrows much more information from neighbors for areas with small samples.

Our model is hierarchical, with local logistic parameters varying systematically with local educational levels. As a consequence, the Bayesian procedure borrows information across regions with similar educational levels and similar map locations.

The posterior is a complex multivariate distribution over more than 2,000 parameters. Bayesian inference proceeds by generating random samples from the posterior distribution, in order to learn which sets of parameters θ represent good compromises that fit the data well while also smoothing the resulting map. From these posterior samples we make inferences about parameters.¹⁷

We generated posterior distribution samples using WinBUGS 1.4, the commonly used software package/language for MCMC estimation of Bayesian models (Lunn et al. 2000). More details, including programs and data necessary to replicate our results, are available in the online archive at «http://schmert.net/BayesLogistic».