Explaining why Gleevec is a specific and potent inhibitor of Abl kinase

Abstract

Tyrosine kinases present attractive drug targets for specific types of cancers. Gleevec, a well-known therapeutic agent against chronic myelogenous leukemia, is an effective inhibitor of Abl tyrosine kinase. However, Gleevec fails to inhibit closely homologous tyrosine kinases, such as c-Src. Because many structural features of the binding site are conserved, the molecular determinants responsible for binding specificity are not immediately apparent. Some have attributed the difference in binding specificity of Gleevec to subtle variations in ligand–protein interactions (binding affinity control), whereas others have proposed that it is the conformation of the DFG motif, in which ligand binding is only accessible to Abl and not to c-Src (conformational selection control). To address this issue, the absolute binding free energy was computed using all-atom molecular dynamics simulations with explicit solvent. The results of the free energy simulations are in good agreement with experiments, thereby enabling a meaningful decomposition of the binding free energy to elucidate the factors controlling Gleevec’s binding specificity. The latter is shown to be controlled by a conformational selection mechanism and also by differences in key van der Waals interactions responsible for the stabilization of Gleevec in the binding pocket of Abl.

Tyrosine kinases are crucial to cellular signaling pathways regulating cell growth, and for this reason, they represent attractive drug targets for curing certain types of cancers. The development of kinase inhibitors is, however, challenging because of the high sequence conservation of the kinase ATP-binding site, the major site targeted by these small molecules. The difficulties encountered by these efforts are displayed most clearly by Gleevec (Novartis), a potent inhibitor of Abl tyrosine kinase (1). Gleevec is one of the most successful drugs against chronic myelogenous leukemia (2), a pathological condition that is caused by mutations leading to a constitutively activated Abl kinase (3, 4). The remarkable effectiveness of Gleevec raised the hope that one might be able to develop novel kinase inhibitors for specific cancers. The situation is nonetheless complicated by the fact that Gleevec displays a much lower inhibitory effect on c-Src for unclear reasons, even though these two tyrosine kinases display a high degree of sequence identity (47%) and similar structural scaffolds (Fig. 1). From this perspective, understanding the molecular basis for the binding specificity of Gleevec is likely to hold important lessons for the rational design of kinase inhibitors in general.

Fig. 1.

Structural comparison of Abl and c-Src in the Gleevec-bound kinase domain.

The X-ray crystallographic structure of the Abl kinase in complex with Gleevec revealed an important clue to understand the molecular basis of binding specificity explaining the binding specificity of Gleevec to Abl (5). A short motif composed of the residues Asp-Phe-Gly near the N-terminal region of the activation loop (A-loop) adopted an unusual conformation referred to as “DFG-out,” giving rise to a previously unobserved inactive conformational state of the catalytic domain. This binding mode contributing to the selectivity of Gleevec to Abl has been further confirmed by a solution NMR study (6). The binding of Gleevec to the DFG-out conformation appears to prevent the transition to the conformationally active form of the kinase, hence causing inhibition. Because the DFG-out conformation had never been observed previously with other related tyrosine kinases of the Src family, it was initially thought that this inactive conformation was only accessible to Abl kinase, leading to the suggestion that the low binding affinity of Gleevec to c-Src might reflect its inability to adopt a DFG-out conformation. However, the latter was subsequently observed in an X-ray structure of c-Src in the DFG-out inactive conformation in complex with Gleevec (7), thus ruling out this possibility. Therefore, despite the extensive experimental studies and the X-ray structures of Abl and c-Src, the basic question remains unanswered: Why is Gleevec a specific and potent inhibitor of Abl but not of c-Src? Two distinct mechanisms, binding affinity and conformational selection, have been invoked to explain the differences in the binding specificity of Gleevec. In the first, it is hypothesized that specificity arises primarily from differences in binding affinities caused by subtle variations in the residue sequence of the binding pocket presented by Abl and c-Src in the DFG-out conformation. In the second, it is proposed that the DFG-out conformation, although being accessible to both kinases, incurs a higher free energy penalty in c-Src compared with Abl.

Although a contrast can be drawn between the binding affinity and conformational selection mechanisms, both are necessarily oversimplified. Nevertheless, it is difficult to achieve a deeper understanding of the underlying mechanism of the binding specificity of Gleevec without a detailed dissection of the equilibrium association constant or absolute (standard) binding free energy, ΔG_eq⁽°⁾, in terms of all the thermodynamic contributions associated with the protein conformational change and ligand binding. Achieving this directly by experimental means is difficult because critical contributions remain essentially “hidden” from direct experimental measurements. Computations based on atomic models offer a virtual, albeit approximate, route to address these issues. The binding of tyrosine-kinase inhibitors to target kinases has been the object of a number of computational studies (8–14). So far, two computational studies have presented evidence supporting the view that Gleevec binding specificity to Abl and c-Src is controlled by conformational selection (11, 14). However, the absolute binding free energy of Gleevec, ΔG_eq⁽°⁾, has never been calculated within a single and consistent computational model and methodology, and the origin of binding specificity of Gleevec ultimately remains unresolved despite previous efforts. In the present study, we report complete computations of the absolute binding free energies of Gleevec to the catalytic domain of Abl and c-Src kinases using detailed all-atom molecular dynamics (MD) simulations with explicit solvent molecules. The computations allow the identification of the molecular determinants of ligand-protein recognition controlling the binding specificity of Gleevec, thereby permitting an objective evaluation of the previously proposed mechanisms. The study demonstrates that the MD simulations, when combined with a rigorous step-by-step formulation of absolute binding free energy, together with extensive sampling methodologies, can provide critical information underlying protein-ligand binding to help guide rational de novo drug design.

Results and Discussion

All the free energy contributions must be accounted for to draw definitive conclusions about the mechanism underlying the binding specificity of Gleevec to Abl and c-Src kinases (i.e., DFG-flip conformational change and ligand affinity). An effective strategy is to identify all the slow degrees of freedom first, and then to control them deliberately during alchemical free energy perturbation (FEP)/MD simulations using special techniques, such as umbrella sampling (US) (15–17). In the present situation, the flip of the DFG motif from “in” to “out” is a very slow conformational change, occurring on a time scale on the order of tens of microseconds, and it is necessary to treat this process separately from the alchemical FEP/MD simulations. In addition, the conformation of Gleevec, a fairly large ligand, is controlled via a biasing restraint potential based on the rmsd relative to the bound configuration (18). Accordingly, the present computations proceed along two main stages, as described in Methods.

Free Energy Landscape of DFG Flip in Abl and c-Src.

The first task is to determine the relative free energy associated with the conformational change of the DFG motif. This is carried out by calculating the potential of mean force (PMF) with respect to two pseudodihedral angles controlling the DFG-flip using umbrella sampling MD simulations (details are provided in Methods). The choice of the two pseudodihedral angles for Abl and c-Src, referred to as χ₁ and χ₂, was suggested from previous studies of the DFG-flip using the string method, a computational technique to determine the pathway of conformational transitions (19). The 1D-PMF of Fig. 2 was obtained by integration of the Boltzmann factor of the 2D-PMF over the variable associated with the side-chain rotation of the aspartate residue (Fig. S1 shows the calculated 2D-PMFs for the DFG-flip in Abl and c-Src). The overall stability of the out vs. in conformation of the DFG motif, ΔG_in→out = [G_out − G_in], is estimated to be 1.4 kcal/mol for Abl and 5.4 kcal/mol for c-Src. This shows that there is an inherent conformational selection phenomenon and that the inactive DFG-out conformation is more stable in Abl than in c-Src. Previous computational results based on metadynamics found a ΔG_in→out of 4.0 kcal/mol and 6.0 kcal/mol for Abl and c-Src, respectively (14), confirming that the DFG flip is more costly in c-Src than in Abl.

Fig. 2.

One-dimensional PMF of DFG-flip in Abl (red line) and c-Src (blue line) as a function of χ ≡ Ala380C β-Ala380C α-Asp381C α-Asp381C γ (Abl numbering).

Binding Free Energy of Gleevec to the DFG-Out Conformation.

The second task is to determine the absolute binding free energy of Gleevec from a bulk solution to the binding pockets of Abl and c-Src with the DFG motif in the out configuration. Table 1 summarizes the various free energy contributions to the binding affinity of the ligand with the kinases [progression of the free energy during successive FEP/λ-replica exchange molecular dynamics (REMD) cycles is shown in Fig. S2]. When the DFG motif is in the out conformation, the absolute binding free energy of Gleevec to Abl kinase and c-Src is estimated be to −10.8 kcal/mol and −6.8 kcal/mol, respectively (these numbers include the contribution for restricting the ligand conformations calculated from the rmsd PMF). This shows that when the two kinases are in the DFG-out conformation, Abl provides a more favorable binding pocket than c-Src.

Table 1.

Absolute binding free energy of Gleevec to tyrosine kinases (kcal/mol)

Kinase	Repulsion	Dispersion	Electrostatics	Interaction	Trans/rot	Gleevec conformation	DFG-out conformation	Total
Abl	1.2	−29.4	0.5	−27.7	5.6	11.3	1.4	−9.4
c-Src	4.0	−23.0	0.1	−18.9	4.6	7.5	5.4	−1.4

Trans/rot, the free energy cost associated with the loss of translational and rotational freedom upon ligand binding.

Binding Specificity of Gleevec for Abl and c-Src Kinases.

The total standard binding free energies of Gleevec, ΔG⁽°⁾, accounting for the thermodynamic contributions associated with the conformational change of the DFG-flip in apo kinase (ΔG_in→out) and the ligand-binding free energy to the DFG-out conformation, are −9.4 kcal/mol and −1.4 kcal/mol for Abl and c-Src, respectively. The measured inhibitory potency of the drug for unphosphorylated Abl and c-Src is 0.013 μM and 31.1 μM, respectively, corresponding to a standard binding affinity of −10.8 kcal/mol and −6.2 kcal/mol, respectively (7, 20). The poorer agreement for c-Src may be due to the fact that 13 residues from the A-loop, unresolved in the X-ray structure, were modeled from the inactive conformation. Additional computations with alternative conformations for the A-loop indicate that this can have an impact on the relative stability of the DFG-flip conformation, as well as on the binding affinity of Gleevec. Ultimately, one should also consider the possibility that Gleevec might be able to bind to alternative kinase conformations. For example, it has been observed that Gleevec and one analog bind to the homologous Syk kinase and c-Src, respectively, in the DFG-in conformation (21). Nevertheless, although it would be interesting to calculate the binding affinity of Gleevec for the “Syk-like” DFG-in kinase conformation employing the computational methodology used in the present study, there are strong indications that the DFG-out binding mode of Gleevec to c-Src, which is considered here, leads to the most stable complex (5, 6).

The calculations support both proposed mechanisms, the conformational selection of the DFG-flip as well as the binding affinity of Gleevec for the inactive DFG-out conformation, because both make thermodynamic contributions enhancing the preference of Gleevec for Abl over c-Src. To test the reliability of the computations further, the binding free energy of Gleevec to unphosphorylated Lck was calculated as a control (Fig. S3). The calculated total binding free energy is −7.8 kcal/mol, comprising −0.4 kcal/mol for the conformational change of the DFG-flip in the apo kinase and −7.4 kcal/mol for the ligand-binding free energy to the DFG-out conformation, which is in excellent agreement with experimental data obtained by measuring the inhibitory constants (K_i = 0.43 μM, corresponding to a binding free energy of −8.7 kcal/mol). This control strengthens our confidence in the computational methodology to help determine the molecular determinants of binding specificity. The computational results are sufficiently accurate to suggest that analysis of the thermodynamic contributions to ΔG⁽°⁾ will provide meaningful information about the molecular determinants of the binding specificity of Gleevec with Abl and c-Src.

Free Energy Components.

The staged alchemical FEP/λ-REMD strategy used here naturally separates the interaction free energy of the ligand with its surrounding (bulk solvent and protein) into three contributions associated with the repulsive, dispersive, and electrostatic components of the biomolecular force field between the ligand and the environment (Fig. S4). The net free energy contribution from the repulsive interaction is 1.2 kcal/mol and 4.0 kcal/mol for Abl and c-Src, respectively, implying a modest penalty for inserting the large ligand into the binding cleft and expelling ∼20–30 water molecules (Fig. S5). Similarly, the contribution of electrostatic interactions nearly cancels out on average, indicating that changes in hydrogen-bonding, charge–charge, and charge–dipolar interactions in the binding pockets are offset by the loss of solvent–ligand interactions in bulk solution. In contrast, the total free energy contribution from the van der Waals dispersion is of considerable magnitude, and it is equal to −29.4 kcal/mol and −23.0 kcal/mol for Abl and c-Src, respectively.

A striking feature of the van der Waals dispersive free energy contribution shown in Fig. S4 is the near-perfect linear dependent with respect to the thermodynamic coupling parameter, λ_dis. This means that the ensemble of configurations is not significantly altered by the van der Waals interaction. The implication is that such a free energy component can be accurately represented by a simple difference between end-point averages. This important property of the van der Waals dispersive free energy contribution will be exploited to determine the contributions from different kinase residues and solvent effect to the binding affinity of Gleevec (see below). It is interesting to note that the linear progression of the dispersive free energy is considerably steeper when Gleevec is in the binding pocket rather than in bulk water. This is consistent with the higher density of attractive van der Waals interaction centers in the protein cavity compared with bulk solution. It is for this reason that maximizing the molecular weight of the ligand, while respecting shape complementarity to the binding pocket, is critically important for providing a substantial gain in attractive van der Waals protein–ligand interactions on ligand transfer from the bulk phase.

Although the above free energy decomposition shows that a ligand gains much favorable interaction by moving from bulk solution to the binding pocket, there is obviously a considerable loss of motional freedom of the ligand associated with this process. In the field of ligand docking/scoring, it is customary to associate such free energy cost with a loss of “conformational entropy.” This concept, however, often remains poorly defined at the statistical mechanical level because the true entropy ΔS arising from a proper thermodynamic decomposition of the free energy in terms of entropy, ΔG = ΔH − TΔS, incorporates a multitude of effects. One advantage of the present approach is that the free energy contributions associated with restriction on the translation, orientation, and conformation of Gleevec on binding to the kinases can be quantitatively evaluated (15, 17, 18). The loss of translational and rotational freedom of Gleevec on binding to the kinases leads to a free energy cost of 5.6 kcal/mol and 4.6 kcal/mol for Abl and c-Src, respectively. The free energy contribution due to the loss of the conformational flexibility from bulk solution to the binding pocket is calculated explicitly by integration of the PMFs of Gleevec in bulk solution, as well as in the kinase-binding pocket, as a function of the rmsd relative to the bound conformation of the ligand, yielding 11.3 kcal/mol and 7.5 kcal/mol in Abl and c-Src, respectively. Such a large contribution does not correspond to a “strain” energy of the flexible ligand but to the cost associated with the loss of conformational freedom on binding. The PMFs as a function of rmsd relative to the bound conformation of the ligand are shown in Fig. 3. The PMF of Gleevec in bulk water is broader than that in the kinase-binding pocket, consistent with the notion that the ligand has more freedom to explore a wide range of conformation in bulk solution.

Fig. 3.

PMFs of rmsd of Gleevec in bulk solution (black line) and in the binding sites of Abl (red line) and c-Src (blue line).

Determinants of Specificity.

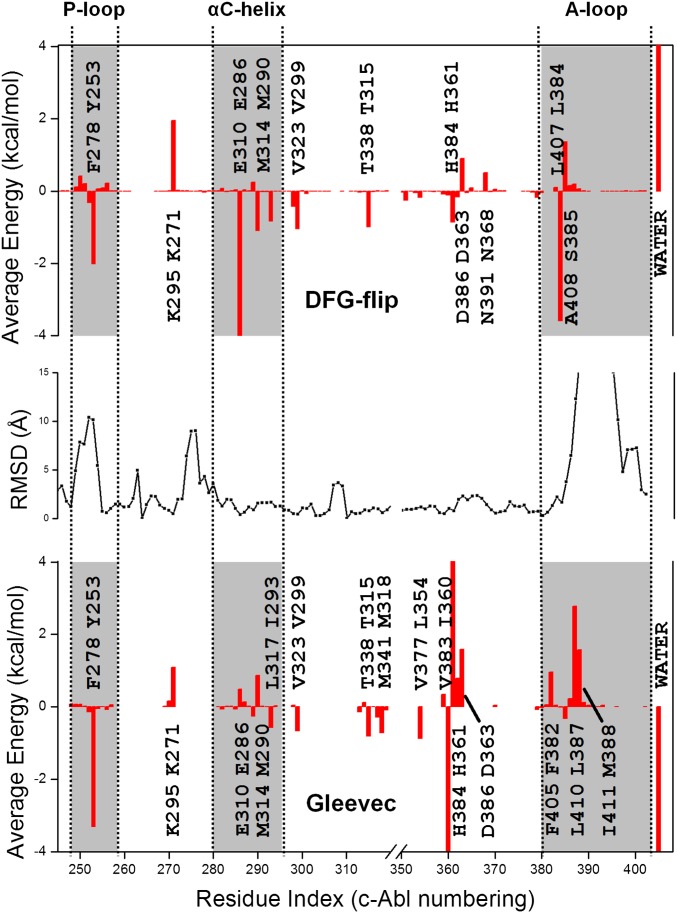
To display the key residues contributing favorably to the binding, the average interaction energy between the ligand and each active site residue in the kinase systems was determined from the configurations extracted from the trajectories saved during the FEP simulations. The results are shown in Fig. 4 (Bottom) and Fig. S6, and data are listed in Table S1. The residual decomposition analyses show that the total van der Waals protein–ligand interactions in the Abl-binding site are more favorable by −3.9 kcal/mol relative to c-Src (value obtained by summing up all the individual contributions in Table S1), although the various contributions are broadly distributed over many residues. Tyr253 makes one of the largest contributions enhancing ligand binding in Abl, although the corresponding phenylalanine residue in c-Src (Phe278) contributes negligibly. This large difference between two chemically very similar residues is explained by the difference in the structure of the phosphate-binding loop (P-loop) in the bound complexes. As shown in Fig. 1, the P-loop in Abl exhibits a kinked W-shaped conformation, acting as a lid to hold the ligand. In Abl, Tyr253 anchors the W-shaped conformation of the loop by forming hydrogen-bonding interactions with the side chain and backbone amide group of the Asn322 residue in the C-lobe. Furthermore, Gly249 and Gln252 at the ends of the P-loop are hydrogen-bonded with each other via their backbone atom, further stabilizing the kinked loop conformation. All these interactions contribute to stabilize the conformation of the P-loop in Abl that brings Tyr253 into proximity to the pyridinyl ring and pyrimidine moiety group of the ligand to make favorable van der Waals contacts. A similar interaction, however, is not observed in the case of c-Src because the P-loop maintains an extended conformation during the simulations. Similar observations about the impact of different P-loop conformations on the recognition of Gleevec to Abl and c-Src have been made by Seeliger et al. (22) and Dar et al. (23).

Fig. 4.

(Top) Difference in the average interaction energies of the DFG-flip ΔΔE between Abl and c-Src as a function of residue index. ΔΔE is defined as [E(DFG-out, c-Abl) − E(DFG-in, c-Abl)] − [E(DFG-out, c-Src) − E(DFG-in, c-Src),] where E represents the average interaction energy of a conformation in a kinase (calculated over 500 structures). Residues with a ||ΔΔE|| greater than 0.5 kcal/mol are marked explicitly, and their corresponding indices in the sequence are also shown. In the text boxes displaying residue indices, Abl residues are on the top and c-Src residues are at the bottom. The ΔΔE values of residues ranging from index 320–350 or larger than 402 were negligible (not shown). The ΔΔE of water, which is 9.36 kcal/mol, is truncated to fit within the plot. (Middle) rmsd between Abl and c-Src X-ray structures (truncated at 15 Å). (Bottom) Difference in the average interaction kinase–ligand interaction energies ΔE between Abl and c-Src as a function of residue index. ΔE is defined as [E(Abl) − E(Src)], where E represents the average interaction energy of Gleevec with a given kinase (calculated over 550 structures). The ΔE values of Ile360, His361, and water (−8.22, 7.14, and −7.32 kcal/mol, respectively) were truncated at 4 kcal/mol to fit within the plot.

A similar analysis of the individual interactions was carried out to probe the contribution of each residue of the kinase domain to the conformational equilibration of the DFG motif in the apo kinases. The results are shown in Fig. 4 (Top). The difference in the average van der Waals and electrostatic interaction energies of the residues of the DFG motif from the rest of the kinase domain for the in and out conformations is calculated [i.e., ΔE = E(DFG-out) − E(DFG-in)]; negative values indicate that a residue in Abl contributes to the stabilization of the inactive DFG-out conformation relative to the same residue in c-Src. The average interactions of the residues of the DFG motif (Asp381, Phe382, and Gly383) with the P-loop, αC-helix, and A-loop all contribute to make the flipped DFG-out conformation more favorable in Abl than in c-Src (more information is given in Fig. S7). Tyr253, in the P-loop, provides one of the largest interactions favoring the DFG-out conformation in Abl. This arises mainly from the stabilizing van der Waals interactions formed with the phenylalanine side chain of the DFG motif in the flipped DFG-out conformation (this interaction is negligible for both kinases in the DFG-in conformation). This stabilizing interaction is not present in c-Src because the P-loop adopts an extended conformation (the rmsd of this region is on the order of 10 Å; Fig. 4, Middle). In the αC-helix, Glu286 significantly favors the DFG-out conformation in Abl due to a repulsive electrostatic interaction with the carboxylic and carbonyl groups of the DFG aspartate residue that is present in the DFG-in conformation (Fig. S8). This repulsive interaction is actually present in both kinases, but it appears to be significantly alleviated only for Abl when it adopts the DFG-out conformation, thereby resulting in a differential stabilizing effect only in this case. In the A-loop, Leu384 plays the most important role in differentiating the energetic cost of the flipped conformation in Abl and c-Src. The stabilization arises mainly from electrostatic interactions between the backbone amide group of Leu384 and the backbone carbonyl group of Asp381, as well as from van der Waals interactions between the side chains. Lys271 is another residue that affects the conformational stability of the DFG motif via electrostatic interactions, although it acts in the opposite direction by differentially favoring the DFG-out conformation of c-Src. In the DFG-in conformation, the positively charged side chain of Lys271 forms a salt bridge with the carboxylate group of Asp381, which is then broken in the DFG-out conformation with an unfavorable energetic cost that is larger in Abl than in c-Src.

Kuriyan and coworkers (7) have attempted to increase the sensitivity of the c-Src kinase domain to Gleevec by substituting certain key residues that are adjacent to the drug-binding site by the corresponding residues in Abl. However, none of the swapped residues significantly increases the structural stability of c-Src bound to Gleevec, except for F405A (in the DFG motif of c-Src), which is expected to destabilize the DFG-in inactive conformation of c-Src. This underlines important structural differences between Abl and c-Src, even when the implicated residues are similar. For example, Tyr253 enhances ligand binding in Abl, but the correspondingly similar Phe278 in c-Src does not provide favorable interactions because of the considerable difference in the conformation of the P-loop. For the same reason, Tyr253 makes favorable interactions with the residues of the DFG motif favoring the inactive out conformation in Abl kinase, but these interactions are not present in c-Src. Thus, differences in the residue sequence as well as in the 3D structure of the P-loop in the neighborhood of the DFG motif are responsible for the difference in the stabilization of the DFG-out conformation in Abl and c-Src. An intriguing question is whether it would possible for these regions of c-Src kinase to adopt more closely the conformation observed in Abl. Although a full sampling of the conformational propensity of the A-loop in these kinases is beyond the scope of this analysis, two empirical scores widely used in comparative modeling, Atomic Non-Local Environment Assessment (ANOLEA) (24) and QMEAN (25, 26), can shed some light on this issue. Constructing a homology model of c-Src in the DFG-out conformation using the X-ray structure of inactivated Abl as a template, the empirical structural scores indicate that the quality of these regions in the c-Src homology structures is below the acceptable threshold (Figs. S9 and S10). This means that according to the empirical scores, Abl does not provide a good template for some regions of c-Src. The loops in c-Src cannot adopt the conformation observed in Abl, and single point mutations are unlikely to succeed in making c-Src more Abl-like.

Ionization State of Ligand and Protein Residues.

Several molecular groups in Gleevec could potentially alter their ionization state as a function of pH. The piperazinyl group is possibly the most critical because it can carry a net positive charge (as shown in Fig. S2). Its pK_a has been determined to be 7.7 by means of macroscopic pH potentiometric titrations and microscopic NMR-pH titrations (27), indicating that Gleevec can be either neutral or positively charged under physiological conditions. There is a strong indication that Gleevec is also protonated when it is bound to the kinases. In the crystal structure of Abl in complex with Gleevec, the nitrogen atom of the piperazinyl group makes hydrogen-bond contacts with the carbonyl oxygen atoms of Ile360 and His361, a configuration that would be unlikely if the group was deprotonated. A similar configuration is observed in the Gleevec-bound c-Src complex, where the corresponding hydrogen-binding acceptor residues are Val383 and His384. Together, these findings support the notion that under physiological conditions, the piperazinyl group is predominantly protonated and Gleevec carries a net positive charge in the bound complex with tyrosine kinases. This enables hydrogen-bonding interactions of Gleevec with the backbone carbonyl of specific residues in the binding pocket. The notion that Gleevec is protonated in the kinase-binding pockets is also supported by independent MD simulation studies (28).

The protonation state of the aspartate residue of the DFG motif has been proposed to have an important impact on the DFG-flip conformational change, although the protonation is believed to affect mainly the kinetics of the transition rather than the relative thermodynamic stability of the DFG-in and DFG-out conformations (29). Indeed, additional PMF calculations indicate that protonation of the DFG aspartate residue does not fundamentally alter the active-inactive conformational equilibrium of the DFG motif, which is estimated to be 1.0 kcal/mol in Abl and 5.5 kcal/mol in c-Src. However, no definitive conclusion can be drawn from the information provided by the PMFs about the flipping rate of the DFG motif and how it might be affected by the protonation of the aspartate. Nevertheless, it is most likely that this residue is deprotonated in the bound complex with the kinases. According to the X-ray structures of Abl kinase and c-Src with bound Gleevec, the aspartate side chain of the DFG motif forms hydrogen bonds with a backbone amide group and two water molecules, a configuration that is only consistent with a deprotonated carboxylate group. Furthermore, similar configurations are observed in additional X-ray structures of tyrosine kinases in complex with Gleevec, including c-Kit (30) and Lck (31). In further support for this conclusion, the pK_a values of the DFG aspartate residue of Abl and c-Src in the DFG-out inactive conformation have been estimated to be within a range of 3–4 using the empirical PROPKA method (14). To examine the impact of the ionizing groups in Gleevec binding specificity further, the electrostatic contributions to the binding free energy of Gleevec (protonated/neutral) to Abl kinase (with the DFG aspartate neutral/deprotonated) were calculated using alchemical FEP/λ-REMD. The results show that unless Gleevec is protonated and the aspartate of the DFG motif is deprotonated, there is a loss of favorable binding affinity on the order of 1–2 kcal/mol. Together, all these results converge to support the notion that Gleevec is protonated (positively charged) and the aspartate of the DFG motif is deprotonated (negatively charged) in the bound complex of Abl and c-Src kinases.

Conclusion

The calculated absolute binding free energies of Gleevec to Abl and to c-Src are in excellent agreement with experiments, offering a virtual route to identify the key molecular factors responsible for the binding specificity of Gleevec that are not easily accessible otherwise. The calculations herein demonstrate that the specificity of Gleevec is controlled both via a conformational selection mechanism and by inherent differences in affinity.

The calculated free energy landscapes describing the DFG-flip conformational change show that Abl has the intrinsic ability to stabilize the DFG-out conformation favorably even in the absence of Gleevec, whereas c-Src incurs a considerable free energy cost for adopting the DFG-out conformation. This finding is further supported by the residual decomposition results that the P-loop, αC-helix, and A-loop of apo Abl significantly enhance the stabilization of the DFG motif in the inactive out conformation before binding Gleevec, relative to c-Src kinase. Conformational selection has been suggested as an explanation for the preference of Gleevec binding to Abl and c-Src (7, 28, 32, 33).

Gleevec also has a different affinity for the inactive DFG-out conformation binding pocket of the two kinases. Free energy decomposition reveals that the attractive van der Waals dispersive interaction between the complementary protein and ligand surfaces is the main driving force leading to the formation of the complex. It is notably stronger in the Abl/Gleevec complex relative to the c-Src/Gleevec complex. An apparent requirement for tyrosine kinase to bind Gleevec optimally is to optimize the attractively dispersive energy of the aliphatic/aromatic residues in the drug-binding pocket. Abl kinase achieves this, for example, by uniquely forming a kinked P-loop inward of the binding pocket to position the phenol side chain of Tyr253 precisely to form favorable van der Waals interactions with the 2-phenylaminopyrimidine moiety of Gleevec. These interactions are not present in c-Src. Thus, Abl mutations that lead to a wrong orientation of the P-loop residues relative to the pyridine group of Gleevec or mutations that alter the composition of residue 253 would be expected to alter the Gleevec binding affinity (32, 34–38).

The conclusion from the present computational study that both conformational selection and binding affinity are responsible for Gleevec’s binding specificity reconciles these two views by shedding some light on the apparent inconsistencies. It will be of interest to extend the present set of free energy calculations to various kinase inhibitors to quantify the importance of these two factors on binding specificity.

The present study demonstrates that a computational strategy based on all-atom free energy simulations has the ability to address quantitative issues about the physical and molecular bases for the design of specific inhibitors of tyrosine kinases. It is our hope that the insight gained by such computations will facilitate the discovery and design of novel lead compounds and that the free energy methods will play an increasing role in structural-based drug design to combat kinase inhibitor resistance and prolong the effectiveness of treatment in patients.

Methods

Umbrella sampling (US) simulations were first carried out to calculate the PMF for the DFG-flip in apo Abl and c-Src and determine the relative free energy associated with this conformational transition in the two kinases. Alchemical FEP/λ-REMD simulations using a step-by-step reversible work staging procedure were then carried out to determine the binding affinity of Gleevec (restrained around its bound conformation using an rmsd biasing potential) to Abl and c-Src kinases in the DFG-out conformation. To characterize the DFG-flip conformational transition, the Abl active DFG-in [Protein Data Bank (PDB) ID code 2F4J] (39) and c-Src active DFG-in (PDB ID code 1Y57) (40) X-ray structures were adopted. For the alchemical absolute binding free energy calculations, the Gleevec-bound Abl (PDB ID code 1IEP) (41) and c-Src (PDB ID code 2OIQ) (7) X-ray structures (both with the DFG motif in the inactive out conformation) were used. All the structures used in the DFG-flip simulations as well as in the ligand-binding FEP/MD calculations were unphosphorylated. The simulation systems comprise about 40,000–45,000 atoms. The all-atom CHARMM force field PARAM22 (42) with the CMAP backbone dihedral (43, 44) was used for the protein residues and ion species, and water was represented by the three-point-charge TIP3P (45) model. The topology and parameter files used to represent the potential function of Gleevec were taken from a study by Aleksandrov and Simonson (28). MD simulations were carried out at constant temperature and pressure of 300 K and 1 atm, respectively, with a time step of 2 fs. All bonds involving hydrogen atoms were considered to their equilibrium distances, and the TIP3P water geometry was kept rigid using the SHAKE algorithm (46). Long-range electrostatic interactions were treated using the particle-mesh Ewald method (47) with a real-space cutoff of 14 Å. All the kinase systems were equilibrated for at least 25–30 ns using NAMD (48). All the umbrella sampling simulations for the DFG-flip were carried out using NAMD. The absolute binding free energies were carried out with the PERT module of CHARMM on the basis of the staged alchemical FEP/MD simulation protocol with biasing restraints that was introduced previously (15, 16, 49–51; reviewed in ref. 52). The approach was recently extended to a global REMD scheme with respect to the thermodynamic coupling parameters “λ,” implemented in the parallel-parallel REPDSTR of CHARMM (53, 54). The absolute binding free energy was computed using 25 independent alchemical FEP/λ-REMD runs, representing a total of 5.5 ns of sampling for each system. The results begin to converge after a few runs and appear to fluctuate around a mean value after 15 runs. The data points of the last 5 runs were collected to compute the block average of the absolute binding free energies of Gleevec with the kinases, yielding the reported values. The results from the FEP and US simulations were unbiased using the weighted histogram analysis method (55, 56).