Caulobacter chromosome in vivo configuration matches model predictions for a supercoiled polymer in a cell-like confinement

Abstract

We measured the distance between fluorescent-labeled DNA loci of various interloci contour lengths in Caulobacter crescentus swarmer cells to determine the in vivo configuration of the chromosome. For DNA segments less than about 300 kb, the mean interloci distances, 〈r〉, scale as n^0.22, where n is the contour length, and cell-to-cell distribution of the interloci distance r is a universal function of r/n^0.22 with broad cell-to-cell variability. For DNA segments greater than about 300 kb, the mean interloci distances scale as n, in agreement with previous observations. The 0.22 value of the scaling exponent for short DNA segments is consistent with theoretical predictions for a branched DNA polymer structure. Predictions from Brownian dynamics simulations of the packing of supercoiled DNA polymers in an elongated cell-like confinement are also consistent with a branched DNA structure, and simulated interloci distance distributions predict that confinement leads to “freezing” of the supercoiled configuration. Lateral positions of labeled loci at comparable positions along the length of the cell are strongly correlated when the longitudinal locus positions differ by <0.16 μm. We conclude that the chromosome structure is supercoiled locally and elongated at large length scales and that substantial cell-to-cell variability in the interloci distances indicates that in vivo crowding prevents the chromosome from reaching an equilibrium arrangement. We suggest that the force causing rapid transport of loci remote from the parS centromere to the distal cell pole may arise from the release at the polar region of potential energy within the supercoiled DNA.

Bacterial chromosomes are vastly longer than their cells, and in vivo chromosomal organization is only partially understood (1). The in vivo DNA is negatively supercoiled, it forms plectoneme structures with random-sized branches (2, 3), and the nucleoid is compacted by nucleoid-associated proteins (4). Fluorescent-labeled bacterial chromosomal loci exhibit random motion within a confined domain (5–8). In the Caulobacter swarmer cell, the chromosomal parS site, 8 kb away from the origin of replication initiation (Cori), is anchored at the flagellated pole (9), and the rest of the chromosome is organized such that the average position of loci along the length of the cell is proportional to their distance on the chromosome from parS (10). Fluorescent-labeled chromosomal loci positions in Escherichia coli cells also show a linear ordering along the cell length (11, 12).

Physical insights into equilibrium and dynamic polymer behavior can be inferred from the relationship between observable structural quantities and the length of the polymer (13, 14). For example, the random-walk nature of polymer molecules frequently leads to the mean interloci distance 〈r〉 obeying a scaling relationship 〈r〉 ∼ n^ν, where n is the contour length between segments and ν is a scaling exponent. The scaling exponent ν varies with the choice of the solvent, the presence of confinement, the interactions with neighboring polymer segments and macromolecular entities, polymer topology, and other physical contributors (13, 14).

Grosberg et al. (15) postulated that a confined chromosome becomes fixed in an unknotted “crumbled-globule” state that is dynamically arrested and unable to explore all possible configurations. Because the structural configuration is effectively frozen in this state, this conformation exhibits structural “freezing.” If the crumpled-globule model applies, this structural state would exhibit a broad range of variability from cell to cell (15). The original formulation of the crumpled globule model predicted a single scaling exponent ν = 1/3, corresponding to a tightly packed globule configuration that persists over multiple hierarchies of compaction (15). This theoretical model has been used to determine how spatial proximity maps relate to the architecture of the human genome (16). The observed linear arrangement (i.e., ν = 1) of chromosomal loci within the elongated Caulobacter nucleoid (10) deviates from the original crumpled-globule model (15), and supercoiling of the DNA may alter the local and global arrangement of the packaged chromosome due to the branched nature of plectonemic coils (17). Understanding the physics basis for the observed scaling is critical in interpreting the role of structural freezing for in vivo chromosomal processes including gene regulation, recombination, and chromosome segregation.

Here, we report the compaction characteristics of Caulobacter DNA in vivo within swarmer cells where chromosome replication is not active. Swarmer cell DNA is confined within a cylindrical cell envelope about 0.5 μm in diameter (18) and about 2.3 μm in length. We examine here the impact of supercoiling and confinement on the in vivo DNA compaction statistics. Our results show that the compaction of the swarmer cell DNA is consistent with theoretical predictions for a branched polymer confined in a cylindrical space. Furthermore, we show (i) that Brownian dynamics simulations of the segregation of a supercoiled DNA polymer within an elongated confinement results in a configuration with random branching that exhibits scaling behaviors comparable to our experimental measurements and (ii) that the experimental cell-to-cell variability of interloci distances is consistent with structural freezing. Analysis of the correlation of the lateral positions of fluorescent-labeled loci at varying distance shows that the correlation declines by half over a distance of 0.16 μm along the length of the cell.

Results

Statistics of Interloci Distances of Caulobacter Swarmer Cell DNA Scale with Exponent 0.22.

We determined the DNA compaction characteristics by observing the interloci distance between fluorescent-labeled DNA segments as a function of the segment contour length. We analyzed three sets of strains that each have two fluorescent-labeled loci separated at varying distances on the chromosome. Two of these strain sets had one locus at or near the parS centromere and another locus between 5 and 2,046 kb from the first locus, either on the right or left arm of the chromosome. The third strain set had one locus 605 kb away from parS on the right arm and a second locus at varying distances between 10 and 874 kb from this locus. The loci were labeled by fluorescence tagging of the proteins that specifically bind to a locus of interest (SI Appendix, SI Methods).

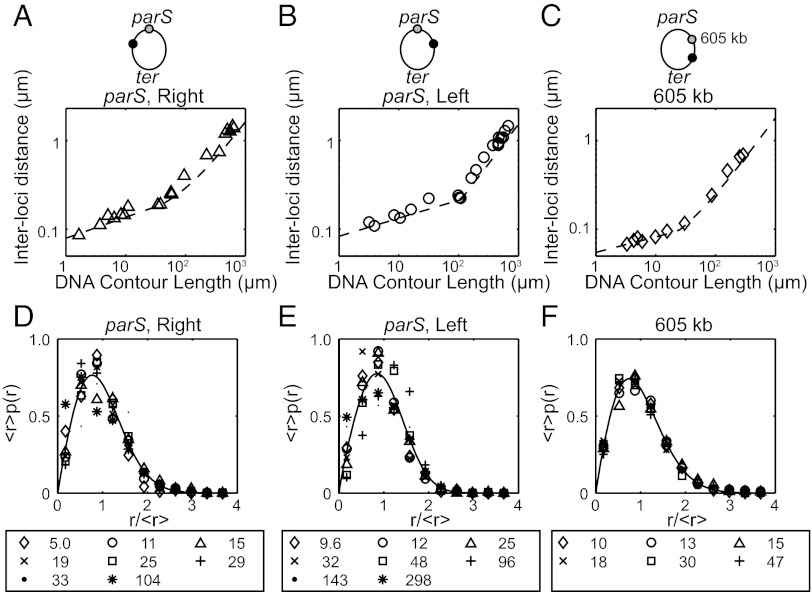
We synchronized Caulobacter cells and imaged cell samples collected at the swarmer cell stage using fluorescence microscopy. We measured the distance between the two labeled loci in each cell to obtain the distribution of distances between the ends of the end-labeled segments in from 267 to 2,100 cells (SI Appendix, SI Image Analysis, Fig. S1, and Table S1). The cyan fluorescent protein (CFP) and yellow fluorescent protein (YFP) images were taken sequentially with the minimum time between images (<4 s) that our system allowed and with exposures in the range of 0.4–1.0 s. The Caulobacter chromosome is virtually frozen during the time interval of the measurement (SI Appendix, SI Image Analysis). Fig. 1 A–C shows log-log plots of the mean interloci distances as a function of the segments’ contour lengths for each strain set; in each set, the shorter interloci distances scale as (contour length)^ν, with ν in the range 0.19–0.26; for longer interloci distances, the distance is proportional to the contour length as reported in ref. 10 (Fig. 1 A–C; SI Appendix, Table S2).

Fig. 1.

Mean interloci distance of DNA segments in vivo. (A–C) Mean interloci distances of DNA segments are plotted on a log-log scale as a function of contour length of the segment. (A and B) parS reference locus and the other loci on the right (A) and left (B) arm, respectively. (C) A 605-kb reference locus and other loci between 610 and 1,474 kb. Each plot shows a linear regime above and a scaling regime below an inflection point. Two curves (〈r〉 ∼ n^ν and 〈r〉 ∼ n) were fit to the data in each regime to determine the scaling exponents. The exponents for the shorter length scale are (A) 0.26 ± 0.07, (B) 0.22 ± 0.04, and (C) 0.19 ± 0.09. (SI Appendix, Table S2) (D–F) Before plotting, the interloci distances (r) were rescaled by dividing by the contour length (n) raised to the power of ν determined in A–C. The resulting plots were fit by a curve of the form y = ax^bexp(−cx^δ); the fitting parameters are given in SI Appendix, Table S3. The value of the plot symbols shown at the bottom of each strain set indicates the distance on the chromosome in kilobases between centers of the two loci. The result was the probability density functions of the rescaled interloci distance data sets as shown.

Following Grosberg et al. (15), we assume the distribution of the interloci distance p(r, n) is a function of (r/n^ν) for n shorter than 100–300 kb. Thus, the distribution of r for different n will fall on the same curve when r is divided by n^ν. Fig. 1 D–F shows this scaling relation holds for our three strain sets. The solid line in the figures is a fit of the combined rescaled distributions by the function p(x) = ax^bexp(−cx^δ), where x = r/n^ν. The parameters are a = 1.26–1.68, b = 0.88–0.97, c = 0.52–0.91, and δ = 1.82–2.57 (SI Appendix, Table S3). The value b is close to 1, consistent with an excluded volume effect. The Gaussian form proposed in ref. 15 is consistent with our experimental fits using this general function, because the data sets in SI Appendix, Table S3 bracket the value δ = 2.

The mean interloci distance for segments near parS is larger than for equivalent segment lengths near 605 kb, so these parS proximal DNA segments are less compacted than the segments near 605 kb, although the scaling parameter is nearly the same in both locations. We reported elsewhere (19) that (i) variable amounts of newly synthesized DNA are transported along with the parS site from the replisome to the distal pole by a mechanism involving a ParA structure extending from that pole, and (ii) newly synthesized DNA remote from the parS site is transported by a different mechanism. These differences in the history of the labeled DNA segments in the strain sets with labeled loci near parS vs. the strain sets with labeled loci near 605 kb might explain differences in the compaction characteristics of the strain sets. However, the consistency of the scaling parameter ν over the three strain sets suggests that polymer physics characteristics of the DNA are the major determinant of the chromosome structure.

Brownian Dynamics Simulation of Supercoiled Polymer in an Elongated Cylindrical Confinement.

Several features of our experimental observations align with predictions from polymer physics theory; however, we believe that recognition of DNA supercoiling effects is essential for interpretation of our data. We performed Brownian dynamics simulations of segregation of a supercoiled polymer, modeled as a discrete wormlike chain with twist, into an elongated cylindrical confinement to investigate the relevant DNA polymer structural properties (SI Appendix, SI Image Analysis).

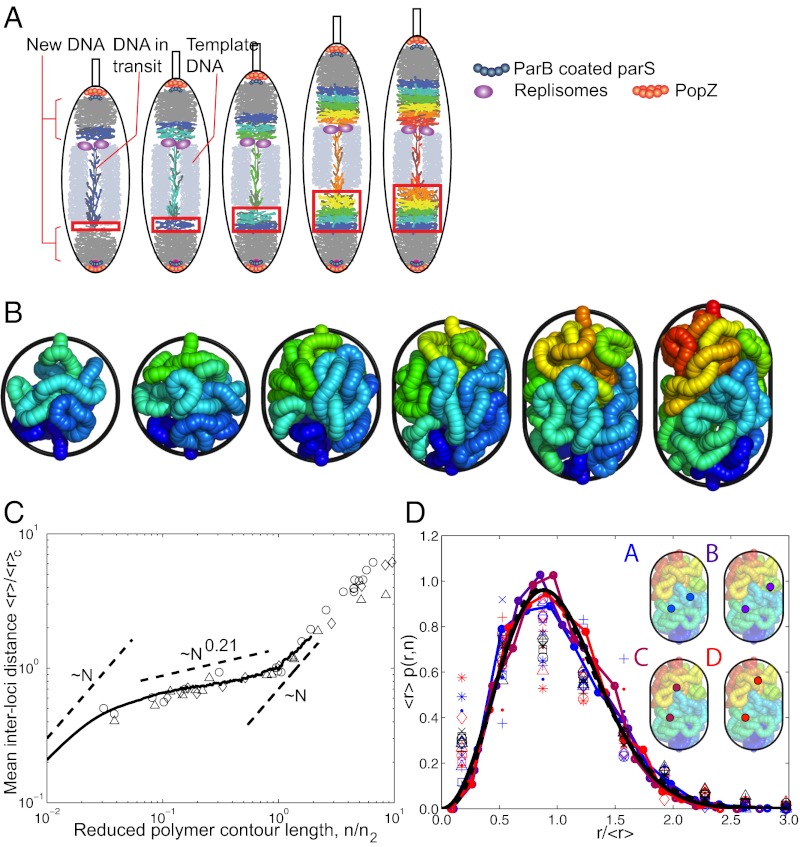
Both arms of the newly replicated chromosome are moved from the replisome to the distal pole in parallel after they emerge from the respective replisomes (Fig. 2A). In the simulation, we show just one polymeric structure emerging at the top and expanding into the polar region, forming twisted plectonemic structures as it fills the available space behind the old chromosome. As chromosome replication progresses, the template chromosome is continuously drawn into the replisomes, so that the polar space available for the newly replicated chromosome continuously increases. This effect is simulated by progressive elongation of the confinement. The physical model for the DNA in the simulation captures essential mechanical properties and steric interactions that dominate the behavior of such a supercoiled polymer within a cell-like confinement. By focusing on these physical mechanisms, we determined the dominant physical properties of a polymer that would result in observations consistent with our experiments without obscuring the behaviors of interest.

Fig. 2.

Brownian dynamics simulation of the compaction and organization of newly replicated and supercoiled DNA. (A) Diagram shows an interval during progression of DNA transport during chromosome replication where the newly replicated DNA is being transported through the template DNA (light gray) and stored at the distal pole. The template DNA is being continuously drawn into the replisomes, and the new DNA fills the polar space “behind” the template DNA created by the removal of that DNA and ongoing cell growth. The red rectangle represents the region of confinement treated in the simulation. (B) Snapshots of the polymer at successive time points in a run (note this is not to scale, SI Appendix, SI DNA Simulation. (C) Average interloci distance 〈r〉 as a function of the contour length n. Relevant scaling behavior 〈r〉 ∼ n^ν is displayed as dashed curves for the short-, intermediate-, and long-length regimes. (D) Time-averaged interloci distance distribution p(r, n) vs. the rescaled separation r/〈r〉 for four different interloci contour length. (Inset) Snapshots illustrating the separation corresponding to the four contour lengths. Dashed and solid black curves are theoretical fits to our simulation data.

In our Brownian dynamics simulations, a supercoiled polymer is injected into a cylindrical space with hemispherical caps in a scenario comparable to newly replicated DNA being transported through the template DNA and stored at a cell pole (19) (Fig. 2A). Fig. 2B shows stages in progression of the polymer stowage process (Movie S1). The in vivo DNA configuration corresponding to the start of the simulation results from action of a ParA structure that extends from the distal pole toward the replisome until it connects with ParB proteins bound to DNA in the vicinity of the parS centromere (19–22) (Fig. 2A). The ParA structure is thought to be depolymerized by interaction with ParB (20–23), resulting in transport of the parS site and a highly variable amount of surrounding DNA to the distal pole where it is anchored to polar PopZ (19, 24, 25) (Fig. 2A). Ultrahigh-resolution light microscopy shows that the ParA structure extends along the midline of the cell through the middle of the “old” template chromosome (20). This situation is approximated in the first frame of the simulation movie where the DNA at the top of the frame is emerging from the template DNA and extending to its polar anchor.

In the simulation, new polymer is incrementally inserted into the chamber with a slight twist added to each increment, resulting in the final supercoiled structure (Fig. 2B) (SI Appendix, SI Image Analysis). The twisted and folded DNA polymer structure is a consequence of random Brownian forces in the simulation, so each simulation run produces a unique outcome. Each simulation is averaged over a long time trajectory (Movie S2) to ensure that a time-averaged structure results. The mean interloci distances and interloci distance distributions reported are an average over 240 runs.

We analyzed the simulated polymer datasets as in our analysis of the experimental data (Fig. 1). Fig. 2C shows rescaled interloci distances 〈r〉/〈r〉_c versus rescaled interloci contour length, n/n_c, from the simulation datasets. The cross-over contour length n_c and cross-over interloci distance 〈r〉_c identify where the scaling of the interloci distance versus contour length transitions to the long-length linear regime; thus, the rescaled plot (Fig. 2C) transitions to the long-length linear regime at 〈r〉/〈r〉_c = 1 and n/n_c = 1. We also include the rescaled data as the dots in Fig. 2C.

The interloci distance exhibits three scaling regimes. The smallest length scale regime shows a mean interloci distance that scales as N^v with v = 1. This short-length regime persists until the length reaches the average length of a plectonemic supercoil, which is determined by the polymer twist and bend rigidity, as well as the degree of supercoiling. The intermediate-length regime exhibits a scaling exponent in the range v = 0.21 ± 0.03 (v = 0.21 scaling indicated by dashed curve in Fig. 2C). This regime corresponds to lengths larger than a single plectoneme but smaller than the diameter of the confinement. The long-length regime has a scaling exponent of v = 1 and begins at lengths comparable to the confinement diameter. Assuming the shortest interloci contour length in the experiments (n > 1 μm) is substantially larger than the average plectoneme length, the simulated polymer approximates the general properties observed for the DNA in the cell: the shorter lengths exhibit a scaling exponent v ∼ 0.21, and the longer lengths transition to a linear regime with v = 1.

Fig. 2D shows distributions of rescaled interlocus distance (r/〈r〉, where 〈r〉 is averaged over the 240 simulations) for four contour lengths. The measured interloci distance distributions are the dots in Fig. 2D. The inset images are simulation snapshots highlighting loci with contour-length separations corresponding to the four displayed data sets. The distributions all collapse onto a single curve, as did the rescaled DNA segments (Fig. 1E). We fit the simulated interlocus distance distribution to the functional form p(x) = ax^bexp(−cx^δ), where x = r/〈r〉. Using a least-squares fit to the four simulated distributions, we determine the parameter values to be b = 2.84 ± 0.31, c = 2.42 ± 0.48, and δ = 1.48 ± 0.15 (Fig. 2C, dashed curve). Grosberg et al. (15) postulated the form of the distribution for a crumpled globule to be Gaussian with δ = 2. Fitting our simulated distributions while fixing δ = 2 results in the parameters b = 2.09 ± 0.05 and c = 1.34 ± 0.03. This Gaussian fit is the solid curve in Fig. 2C, which is virtually indistinguishable from the dashed curve. Therefore, our simulations exhibit a broad interloci distance distribution consistent with the Gaussian form p(r,n) ∼ exp[−c(r/〈r〉)²] observed in our experiments and consistent with the crumpled globule model (15). This Gaussian form is distinct from the Gaussian distribution of a random walk in that it scales the separation by a power law that is not the typical n^1/2 that reflects the sum of uncorrelated random steps in the walk.

Although a simulation is not a direct replication of the intracellular DNA organization, it represents quite well the behavioral characteristics of a supercoiled polymer being injected into a cylindrical space that are dictated by general considerations of polymer physics (13, 14, 17). The properties of the simulated structures and their final configurations show striking similarity with our observations of in vivo properties of DNA segments. This observation corroborates our conclusion that the supercoiled DNA in the Caulobacter swarmer cell is structured as densely packed plectonemic structures.

Correlation of the Lateral Positions of Two Loci Is ∼0.8 when the Loci Have Similar Longitudinal Positions and Declines by 50% over 0.16 μm Along the Cell.

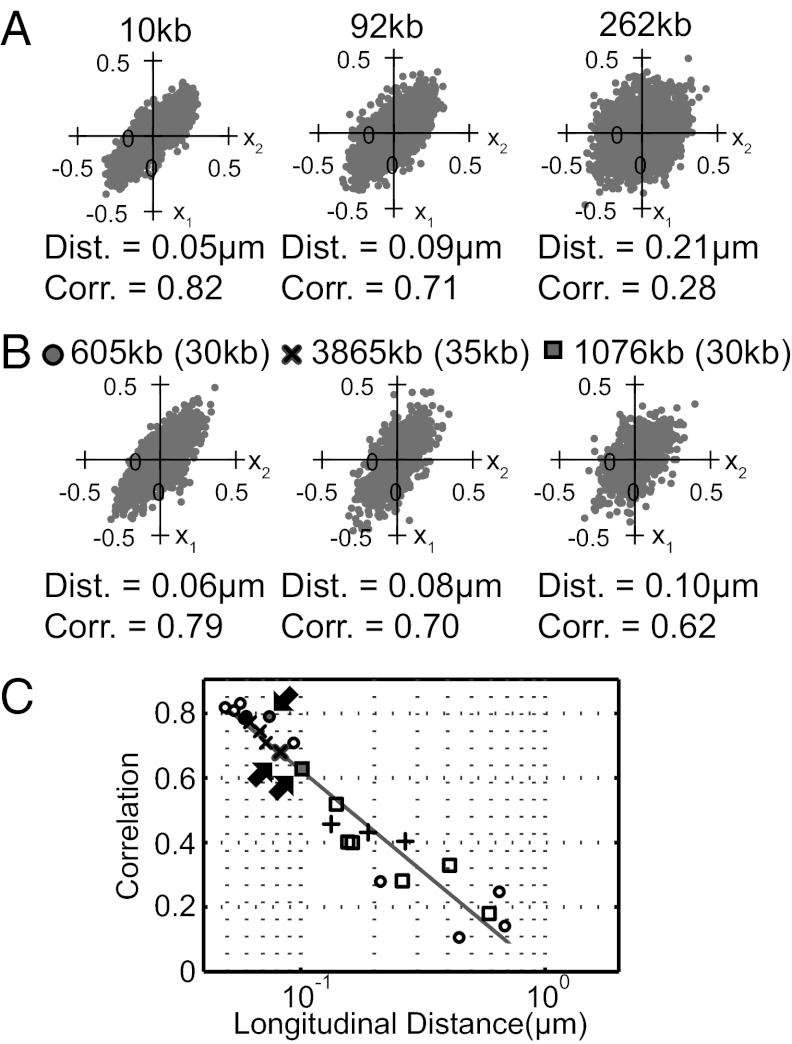
We measured the correlation of the lateral (i.e., along the short axis of the cell) positions of two chromosomal loci at various distances from each other in swarmer cells. In Fig. 3A, each scatter plot shows lateral positions of a locus at 605 kb (x₁) and another locus (x₂) at a distance specified above the plot. (Scatter plots for strain sets with a labeled 605 kb locus are in SI Appendix, Fig. S2B.) The lateral positions of the loci separated by short distances are correlated, and the correlation drops as the distance increases. We performed the same measurement for the three different strain sets, each labeling different regions of the chromosome (near 605, 3,865, and 1,076 kb). Fig. 3B shows the lateral position correlation for three sets of loci at different chromosomal positions but with each set of loci separated by about 30 kb. Lateral correlation for these three strains ranged from 0.62 to 0.79, demonstrating that two loci at the same genomic distance from each other can have notably different correlations if located at different positions on the chromosome (SI Appendix, Fig. S2A). In Fig. 3C, the correlations of the lateral positions for all strains are plotted vs. the average longitudinal separation of the loci along the cell (circles: 605 kb, crosses: 3,865 kb, squares: 1,076 kb). The figure shows that longitudinal physical distance between the two loci determines the correlation of the lateral position (Fig. 3C). The correlation of the closest two loci (separated by 1.7 kb on the genome and 0.05 μm along the cell) is ∼0.8, and it drops to 0.2 at ∼0.8 μm (SI Appendix, Table S4). The relation between the correlation C and the longitudinal distance l is fitted by C = alog(l) + C_0, where a = −0.63 ± 0.04 and C₀ = 0.16 ± 0.01. Thus, the correlation of the lateral positions of the loci drops by half when the longitudinal distance between the loci increases by 0.16 μm.

Fig. 3.

Correlation of lateral loci positions vs. their longitudinal separation. (A) Scatter plots of the lateral positions of three locus pairs are shown. (Upper) Genomic distance between the two labeled loci; (Lower) distance between the loci along the cell length and the lateral position correlation coefficients. (B) Scatter plots of the lateral positions of loci pairs that are approximately equally distant from each other and located at various positions on the chromosome. On the top of each plot, the chromosomal locations of one of the labeled loci and the genomic distance between the pairs (in parentheses) are shown. The symbol shapes at the top of each plot are used to designate the corresponding three points in the plot in C indicated by arrows. (C) Correlation of the lateral positions of two chromosomal loci as a function of their distance along the cell in micrometers. Different symbols represent data for different reference positions (circles: 605 kb, crosses: 3,865 kb, squares: 1,076 kb). Plus symbols mark the correlation between two loci on different arms. Arrows indicate the three strains in B.

We labeled two loci on different arms that are approximately the same physical distance away from the cell pole and measured the correlation of their lateral positions. The lateral positions of these were also positively correlated (C = ∼0.4), and the dependence of the correlation on the longitudinal separation was comparable to loci on the same arm (Fig. 3C, +).

It is significant that the high lateral correlation is determined by proximity as indicated by close longitudinal position in the cell rather than proximity as measured in kilobase distance between the loci. For two loci on the same strand, the smallest separations were in the ∼10-kb range, which allows for the possibility of great variation in physical separation depending on folding of the connecting DNA segment. However, if, by chance, that folding is quite compact and the two loci appear close longitudinally, it is no surprise their lateral correlation is high (C ∼ 0.8; Fig. 3) What about the loci on different arms? The two newly synthesized arms are transported through a crowded region as they go through the template DNA. This movement takes several minutes and affords ample opportunity for entanglement of the two strands (19). Because the two new strands come from different replisomes that operate asynchronously, there is no reason to expect that loci at similar distances (in kilobases) from the origin will be entangled in phase. However, when they are (as is likely when the loci are observed at nearly the same longitudinal distance), then their lateral distance is highly correlated as for loci on the same arm. This lateral correlation would only occur if the two arms are entangled and stored together in the polar region.

Discussion

Here, we report that chromosome organization in Caulobacter swarmer cells is consistent with theoretical predictions for organization of a polymer within a cell-like confinement. We reported previously that the organization of parS-proximal DNA immediately after replication and during transport is also consistent with predictions of polymer physics models (19), suggesting that many aspects of the supercoiled DNA structure are established and lead to compaction shortly after the new DNA strands emerge from the replisomes.

The Caulobacter swarmer cell DNA is supercoiled and confined within a cylindrical compartment much smaller than its unconfined radius of gyration. A polymer in a good solvent (e.g., DNA in water) and confined within a long, narrow cylinder of diameter D is predicted theoretically to exhibit two scaling regimes for the interloci distance 〈r〉 vs. the interloci contour length n (14). Short contour lengths, where 〈r〉 ≪ D, obey 〈r〉 ∼ n^ν with a scaling exponent v = 3/5 that corresponds to a self-avoiding random walk in three dimensions. For segment contour lengths much greater than D, the scaling exponent becomes v = 1, indicative of an effectively elongated structure. These observations were specific to a linear polymer within an uncapped cylindrical confinement. The exponent ν ∼ 1 we observed for longer DNA segments is consistent with the long-length scaling for a polymer in a cylindrical confinement (14); however, the behavior we observe in vivo is probably dependent on the polar anchoring of the DNA in Caulobacter (20) rather than the steric-swelling mechanism that dominates behavior for a polymer in a tube (14).

Another proposal for the long-length behavior suggests that steric exclusion of globular domains within the chromosome leads to an effectively elongated structure (26). The variance in the distance between a chromosomal locus and the origin of replication in E. coli exhibits a linear scaling with the genomic length (27), suggesting the chromosomal fiber exhibits a linear-elastic behavior at large length scales.

Our experimental short-length scaling parameter is slightly less than the theoretical scaling parameter of v = 0.25 for the mean interloci distance of a noninteracting randomly branched polymer (17, 28). Effective branching of the DNA may arise from negative supercoiling promoting formation of plectonemes (twisted coiled structures) in a manner structurally similar to a branched polymer (29). A self-avoiding randomly branched polymer exhibits a scaling parameter v = 0.5 (17, 28), larger than the ideal scaling due to polymer swelling from intersegment interactions. The confinement imposed by the Caulobacter cell wall (∼0.5 μm diameter) is sufficiently large that plectoneme branching can occur (for lengths >3 kb), yet the crowding results in correlation lengths that are shorter than the plectonemic branches. As in a concentrated polymer solution, self-interaction has little impact on the average polymer properties. In our simulations, the observed scaling exponent is consistently smaller than the ideal value of v = 0.25. Because the ideal scaling corresponds to the maximum entropy state, the reduction in the observed scaling parameter implies the chain does not achieve the thermodynamically preferred state.

For a linear chain, the scaling parameter is reduced from v = 0.5 in the maximum-entropy state to the value v = 0.33 in the dynamically arrested crumpled-globule state. A detailed treatment of a branched crumpled globule remains to be developed; however, we anticipate that the scaling exponent should be less than the ideal scaling of v = 0.25. Although the experimental v value is indeed less than 0.25, further experimental and theoretical work is needed to confirm this.

The observed long-length scaling of v = 1 corresponds to the chain segments being elongated along the length of the cell. If the chain behaved as an ideal polymer, the linear scaling would only be observed if the unconfined radius of gyration was significantly smaller than the length of the cell. If the unconfined radius of gyration substantially exceeds the cell length, the ideal polymer chain would fill the confinement as a random walk, leading to a long-length scaling exponent v = 0 and no observed regime where v = 1, regardless of whether the chain is anchored at the poles. The highly confined Caulobacter genome would not exhibit the long-length scaling v = 1 if the chain was not dynamically arrested and could achieve the maximum entropy state that corresponds to ideal chain statistics at both short and long length scales.

The application of equilibrium theory to interpret the polymer behavior requires the polymer chain to be capable of exploring all thermodynamically viable configurations within the time scale of observation. If equilibrium is achieved within the cells, a time-averaged property would be equal to an ensemble-averaged property, and there would be no cell-to-cell variability in these intracellular average properties. If cell-to-cell variability is observed in interloci distances, it implies there has been structural freezing during the establishment of the chromosome structure. Notably, structural freezing does not imply the DNA is incapable of undergoing local equilibration; rather, this implies that at intermediate scales and above, the chain is incapable of appreciably reorganizing at time scales that are biologically relevant. The crumpled globule model offers critical insight into the broad distribution of interloci distances we observed in the cell-to-cell averages. Grosberg et al. (15) predicted p(r, n) will have a Gaussian distribution p(r, n) ∼ exp[−r²/(2〈r²〉)] (15), which agrees with our observations.

Topo IV permits strand passage in vivo, which is important in decatenation and relaxation of positive supercoils. The basal activity of Topo IV could in principle facilitate facile DNA reorganization through strand passage, although this is not necessarily required for such motion to occur. Strand passage is likely to permit short length-scale reorganization, involving DNA segments that are both spatially and genomically close to each other. However, Topo IV may have limited capacity to facilitate large-scale reorganization, because strand passage of distal segments is less likely to occur. Further investigations are necessary to fully determine the role of Topo IV in chromosome organization and dynamics for cells in the quiescent state.

Large-scale supercoil domains have been previously observed in E. coli (3, 30, 31), with a typical size of 10,000 bp. The domain size is probably defined by either the length scale where entanglements persist or by structural proteins that contact multiple DNA sites. For example, the SMC proteins cross-link DNA segments in a dynamic fashion and may play a role in defining supercoil domains. Protein-induced cross-linking may confer a large-scale rigidity to the nucleoid fiber (27), impacting its organization and structural fluctuations. Further study is necessary to determine the role of DNA-binding proteins in defining the local and global supercoiled organization of the chromosome and their effect on dynamic reorganization.

After transport of the parS centromere and nearby DNA from the replisomes to the distal pole the DNA is anchored at the pole (19, 20, 25, 32). The cytoplasmic space near the pole is thought to be relatively free of the template DNA owing to both the retraction of that DNA as it is drawn into the replisome and the growth in cell length. The new DNA will inevitably be spatially confined as it is transported through the template DNA. Several theoretical, simulation, and experimental studies have examined the situation where strands of DNA emerge from a constrained (low entropy) region into a less constrained (higher entropy) region. These studies show that the partially confined DNA will be pulled from the more confined to the less-confined, higher-entropy region by actions of Brownian motion and diffusion (33–35). In each reported case, the specific rates and final configuration depend on the geometric details of the two regions. In our case, there is the added factor of supercoiling so that emergence of the new DNA from the template DNA into the more open cis-polar cytoplasmic region will allow the DNA to form higher levels of plectonemic structure (secondary and tertiary coiling). These structures are presumably lower energy and higher entropy states that would accentuate the pulling of the DNA from the confined region into the polar region, leading to the stored configuration that we observe. The behavior displayed by the DNA in the simulation suggests that the stored energy in the supercoiled DNA drives the expansion and coiling of the DNA as it emerges from the midst of the template chromosome. This model leads us to propose that the motivating force for the rapid transport observed by Hong and McAdams (19) for loci remote from the parS site arises from the release of potential energy within the supercoiled DNA as it emerges into the more open polar region.

Our polymer model for DNA within the Caulobacter cell reflects the physical impact of steric exclusion, confinement, and twist-induced supercoiling, and our simulation results substantiate the physical arguments posed above regarding the structural arrangement of the Caulobacter chromosome. The average interloci distance (i.e., averaged over both time and ensemble) exhibits a short-length regime with ν ∼ 0.25, followed by a long-length regime with ν ∼ 1 (Fig. 2C). Furthermore, the time-averaged interloci distance exhibits a broad variability across the ensemble of simulations (which is analogous to an ensemble of cells), consistent with the proposed Gaussian form for p(r, n) (15).

Although additional factors, particularly the nucleoid associated proteins, organize and compact the DNA, our results here and in ref. 19 show that the physical properties of the DNA polymer play a major, and perhaps the dominant, role in the organization of DNA in vivo.

Methods

Fluorescence microscopy followed by computer image analysis was used to determine intracellular location of labeled loci. Segregation of a supercoiled polymer, modeled as a discrete wormlike chain with twist, into a cell-like confinement was modeled using Brownian dynamics simulations. Details regarding reagents, protocols, microscopy, data analysis, and simulations are in SI Appendix.