Summary
Background and objectives
Risk factor analysis of long-term graft survival in kidney transplant recipients is usually based on Cox regression models of time to first occurrence of doubling of serum creatinine or graft loss (DSCGL). However, death is a competing cause of failure, and censoring patients who die could bias estimates. We therefore compared estimates of time to first event versus estimates that included death as a competing risk and recurrent events.
Design, setting, participants, & measurements
A Cox regression analysis of 1997–2002 data from the Assessment of Lescol in Renal Transplant (ALERT) trial population identified an eight-factor risk model, by analyzing time to first occurrence of DSCGL. The same factors were re-analyzed, allowing for death as competing. The probability of survival free of DSCGL was estimated; and two recurrent models (marginal and conditional) were used for time to events.
Results
Creatinine, systolic BP, and HLA-DR mismatches lost 33%–46% of their strength of association with DSCGL when death was included as a competing risk. Small changes were observed if recurrent events were analyzed in the marginal model.
Conclusion
The relationship between serum creatinine and DSCGL was attenuated when death was considered as a competing risk; inclusion of recurrent events had little effect. These findings have important implications for analysis and trial design in populations at high mortality risk.
Introduction
In renal transplant recipients, progressive graft dysfunction and failure have major implications for individual patients and for health care providers. Understanding the determinants of graft failure and of recurrent failure in patients who lose successive grafts is therefore of paramount importance. Existing analyses have been limited to the determinants of first (or a single) graft failure and have not addressed the issue of recurrent events with or without the competing risk of graft failure due to death. Put simply, the determinants of graft failure are also shared with risk factors for death, so when patient data are censored for death in conventional risk factor analyses, we neglect this relationship and potentially introduce bias into the overall analysis.
In this study we analyzed the determinants of graft dysfunction and failure, including multiple recurrent events. This strategy has previously been used to study rejection episodes, but not graft failure, in kidney transplantation (1) and has also been used in other disease areas (2–4). We used two approaches that address different aspects of recurrent events: a marginal approach covering the total burden of renal disease and a conditional approach, whereby the interrelationship between risk factor associations are taken into account. We also analyzed death as a competing event, recognizing that death and graft failure share common risk factors, thus limiting the bias inherent in models that censor death in the analysis (5–7). For the marginal approach, we followed the method of Wei et al. (8), which analyzes all recurrent events simultaneously, without conditioning for prior events.
Our analysis was based on 7-year extended follow-up data from the Assessment of Lescol in Renal Transplant (ALERT) study database. The aim was to compare the difference between risk factor patterns for the first occurrence of doubling of serum creatinine or graft loss (DSCGL) after randomization versus that of the total burden of repeated DSCGL, and versus a conditional model in which time from start to each event is counted and both start and end times for each recurrent event are used in the analyses. We also explored the effects of analyzing death as a competing risk on the risk factor associations for DSCGL, and we examined a model in which both competing risk and conditional recurrent events were modeled. Finally, we calculated lifetime risk estimates for achieving specified ages without having developed DSCGL or dying, focusing on the effect of different serum creatinine levels at baseline.
Materials and Methods
Study Groups
The ALERT study has been described and reported previously (9–11). This randomized trial of fluvastatin, 40–80 mg/d, versus placebo in 2102 renal transplant recipients with a composite primary cardiovascular endpoint was performed between 1997 and 2002. The main trial lasted for 5 years and was followed by a 2-year extension phase in which all patients were offered fluvastatin, 80 mg/d. The mean duration of follow-up in the complete, extended study was 6.7 years. All cardiovascular and renal endpoints were verified by an independent endpoint committee. In the current analysis, the main endpoint of interest was DSCGL, a composite renal endpoint comprising severe graft dysfunction (doubling of serum creatinine) and graft loss. Patients were male or female, were 30–75 years of age, had stable graft function, and had received a renal transplant more than 6 months (average, 5.1 years) before randomization. Patients were assessed every 6 months via analysis of serum lipids, creatinine, creatine kinase, liver enzymes, IL-6 (human IL-6 immunoassay [R&D Systems Inc., Minneapolis, MN]), and high-sensitivity C-reactive protein (Roche Diagnostics GmbH, Mannheim, Germany).
The study adhered to the International Conference of Harmonization guidelines for Good Clinical Practice and the Declaration of Helsinki. The clinical and research activities being reported are consistent with the Principles of the Declaration of Istanbul. All participants gave written informed consent, and the Ethics Committee at participating centers approved the trial.
Statistical Analyses
We first compared descriptive statistics in patients with or without DSCGL to identify potential risk factors. Such factors as systolic BP, serum creatinine, diabetes mellitus, and smoking were included in the model as forced factors. The time to first occurrence of DSCGL was then analyzed by a stepwise Cox regression analysis that included the potential risk factors listed in Table 1, as well as risk factors for renal endpoints identified in previous analyses (7). A P value < 0.20 was used to select factors, and P<0.05 was the cutoff for final inclusion in the model. Many factors were highly correlated, and we therefore used the ratio of total cholesterol to HDL cholesterol, systolic BP, and the natural logarithm of C-reactive protein as the single risk factors for lipids, BP, and inflammation. Risk associations were described as hazard ratios (with their 95% confidence intervals) and corresponding P values. Standard Cox regression modeling was then performed, stratified by number of recurrent events and using the “robust estimation procedure” in which SEMs of regression estimates are calculated (12). For the marginal method, risk factor estimates for any among recurrent events (total burden of renal disease) were our main focus. We also used a conditional recurrent event model, in which times from start to first event, from first event to second event, from second event to third event, and so forth were recorded on the time axis from baseline (13). In this model, the risk set of patients with a first event influences the risk set for the second or subsequent events. Estimates are thus equal only for the time to first event but will differ for subsequent events.
Table 1.
Baseline risk factors according to presence or absence of doubling of serum creatinine or graft loss during 7 years of follow-up
| Risk Factor | DSCGL (n=438) | No DSCGL (n=1664) | P Value |
|---|---|---|---|
| Categorical variables, n (%) | |||
| Women | 140 (32.0) | 575 (34.6) | 0.34 |
| History of coronary heart disease | 41 (9.4) | 160 (9.6) | 0.93 |
| Diabetes mellitus | 96 (21.9) | 300 (18.0) | 0.07 |
| Smoking | 124 (28.3) | 265 (15.9) | <0.001 |
| History of left ventricular hypertrophy | 71 (16.4) | 240 (14.6) | 0.37 |
| Number of transplants | 0.06 (trend) | ||
| 1 | 364 (83.1) | 1430 (86.0) | |
| 2 | 59 (13.5) | 200 (12.0) | |
| 3 | 15 (3.4) | 33 (2.0) | |
| Hypertension | 348 (79.5) | 1227 (73.7) | 0.02 |
| HLA-DR mismatches | 0.001 (trend) | ||
| 0 | 117 (27.8) | 545 (33.9) | |
| 1 | 214 (50.8) | 825 (51.3) | |
| 2 | 90 (21.4) | 238 (14.8) | |
| Treatment for rejections | 224 (51.7) | 678 (41.3) | <0.001 |
| Continuous variables, mean ± SD | |||
| Age (yr) | 47.4±10.7 | 50.3±10.9 | <0.001 |
| LDL cholesterol (mmol/L) | 4.21±1.06 | 4.12±1.01 | 0.10 |
| HDL cholesterol (mmol/L) | 1.24±0.43 | 1.36±0.45 | <0.001 |
| Triglycerides (mmol/L)a | 2.10±1.48 | 1.90±1.20 | <0.001 |
| Total cholesterol/HDL cholesterol ratio | 5.90±2.36 | 5.28±2.21 | <0.001 |
| Time last transplant (mo)a | 4.96±5.53 | 4.40±4.96 | 0.011 |
| Systolic BP (mmHg) | 149.3± 20.9 | 142.5±18.1 | <0.001 |
| Diastolic BP (mmHg) | 87.2±11.6 | 85.2±9.6 | <0.001 |
| Body mass index (kg/m2) | 25.6±4.8 | 25.9±4.4 | 0.22 |
| Creatinine (μmol/L)a | 170.0±84.0 | 127.0±47.0 | <0.001 |
| Calcium (mmol/L) | 2.41±0.16 | 2.43±0.16 | 0.17 |
| Phosphate (mmol/L) | 1.18±0.27 | 1.15±0.23 | 0.02 |
| Proteinuria (g/24 hr)a | 0.38±0.87 | 0.15±0.24 | <0.001 |
| Hemoglobin (g/dl) (n=1685) | 13.0±1.95 | 13.65±1.73 | 0.007 |
| LnCRP (mg/L) (n=1913) | 1.52±4.66 | 1.43±4.53 | 0.5 |
DSCGL, doubling of serum creatinine or graft loss; LnCRP, natural logarithm of high sensitive C-reactive protein.
Median and inter quartile range.
Risk factor analysis for DSCGL, including death as a competing risk, was performed using the method of Fine and Gray (5). A time to first DSCGL model differs from a model in which time to death is also competing. In the standard Cox model of time to first DSCGL, any preceding deaths are usually censored. This precludes DSCGL from occurring, making the exposure time shorter than it would have been had death not occurred. As a result, the rate of DSCGL, defined as the number of DSCGL events divided by total exposure time, will be biased upward because of the smaller denominator, thereby overestimating the probability that DSCGL would occur within a certain time. This bias increases if the absolute risk of death increases.
In a competing risk model, time to death is no longer censored but rather modeled by a separate Cox model with time to death as the endpoint. The model rationale is that two time variables are defined: T1 = time to first DSCGL and T2 = time to death (censoring is ignored for reasons of simplicity). What we observe is the minimum of these variables. The bivariate distribution of these variables, and particularly their correlation, is required in the competing risk analysis, but unfortunately this joint distribution cannot be identified from the data. However, if h1(t) represents the hazard for first DSCGL and h2(t) is the hazard for death, both can be estimated separately from Cox modeling, as can the sum of the two (h(t)=h1(t)+h2(t)). The statistical model then consists of two Cox models with separate endpoints, and estimates of both hazards can be made.
By combining these models it is possible to make an unbiased estimate of the probability of surviving to a given age (t) without DSCGL (S(t)= ∏(1−h1(tj) −h2(tj)), where products (∏) are taken for both types. event time points (tj is less than or equal to the specified obtained age). This is an important question for the patient and the clinician: What is the probability of an individual patient reaching, for example, age 70 years without DSCGL? The results were displayed graphically as the cumulative incidence of DSCGL with and without adjustment for competing mortality risk. For illustrative purposes, we used a high and a low level of serum creatinine as the strongest risk factor for DSCGL.
This approach does not provide information on the risk of DSCGL in patients who die before any such event, but risk factor associations with DSCGL can be provided for all patients, irrespective of whether they die or not. However, the model depends on the assumption that the two endpoints are independent before death or DSCGL occurs, after adjustment for risk factors included in the model. If DSCGL occurs, risk of death is drastically increased, but that situation is not relevant here. The effect of competing risk will depend on the degree of competition by death, becoming progressively more important as absolute risk of death increases. Over and above these considerations, associations with risk factors may differ when these two models are compared; however, the magnitude and direction of differences may vary according to the observed data, depending on how these factors are associated with both DSCGL and mortality.
We ultimately combined the competing risk model with the conditional recurrent event model, counting the time to end of follow-up from the time of each recurrent event to the time of death in patients who subsequently died. For a typical patient in the ALERT study (mean age at entry to the trial, 50 years), we estimated the probability of surviving without occurrence of DSCGL according to age at the end of follow-up for three levels of the most important risk factor, serum creatinine at baseline (110 μmol/L, 144 μmol/L [mean value], and 190 μmol/L). Other risk factors were set to their mean value. This analysis was performed using the competing-risk model for time to first event. All analyses were performed using SPSS software, version 18.0 (SPSS Inc., Chicago, IL), and Stata software, version 12.0 (Stata Corp., Cary, NC).
Results
Time to First DSCGL as Outcome
Overall, DSCGL occurred once after randomization in 438 patients, twice in 126 patients, three times in 15 patients, four times in 2 patients, and five times in 1 patient. These numbers were lower when analysis was restricted to patients with complete data for all risk factors. Baseline risk factors in patients with at least one occurrence of DSCGL versus those with no occurrences during 7 years of follow-up are shown in Table 1. The strongest risk factors were young age, serum creatinine, HLA-DR mismatches, smoking, systolic BP, proteinuria, history of treated acute rejection episodes, low hemoglobin concentration, and elevated lipid levels (specifically, total cholesterol/HDL cholesterol ratio, HDL cholesterol, and triglycerides). With the exception of lipid levels, these are all well recognized risk factors for graft failure. Diabetes did not achieve statistical significance for DSCGL (P=0.074).
In the stepwise Cox proportional hazards regression model, we identified eight risk factors based on 299 events in 1487 patients with complete risk factor information (hemoglobin concentration was the most common missing factor). These factors (defined in references 9–11) were smoking, systolic BP, serum creatinine, diabetes mellitus, time since last transplantation, degree of HLA mismatch (three categories), hemoglobin, and proteinuria. Age and lipid levels were not included in the final model because of their intercorrelation with other strong risk factors, such as serum creatinine and smoking.
Baseline risk factors were compared between patients with complete data and those with incomplete data: Seventeen percent and 22%, respectively, were smokers (P=0.001); 20% and 15% had diabetes mellitus (P=0.005), and mean time since last transplantation was 5.0 and 5.4 years (P=0.004). No other risk factor was close to being significantly different between the patients with and those without a complete baseline dataset. The global risk of DSCGL was therefore similar in the two populations (hazard ratio, 0.86; 95% confidence interval, 0.70–1.05; P=0.14). Table 2 shows the results when death was treated as a competing risk. This had the effect of reducing the strength of association of several factors, notably serum creatinine, systolic BP, and HLA-DR mismatch. Factors such as smoking, proteinuria, diabetes, and hemoglobin were affected to only a minor extent.
Table 2.
Time to first doubling of serum creatinine or graft loss with or without inclusion of death as a competing event, by baseline risk factors
| Risk Factor | Hazard Ratio per Unit Difference (95% CI) | P Value |
|---|---|---|
| Without competing risk of death | ||
| Smoking | 2.04 (1.57–2.64) | <0.001 |
| Systolic BP (mmHg) | 1.18 (1.06–1.30) | 0.003 |
| Creatinine | 1.98 (1.88–2.20) | <0.001 |
| Diabetes mellitus | 1.21 (0.91–1.60) | 0.19 |
| Time since last transplant | 1.15 (1.03–1.29) | 0.03 |
| HLA mismatch 1 | 1.45 (1.10–1.91) | 0.009 |
| HLA mismatch 2 | 1.64 (1.17–1.91) | 0.004 |
| Hemoglobin | 0.78 (0.69–0.88) | <0.001 |
| Proteinuria (score) | 1.30 (1.24–1.37) | <0.001 |
| With competing risk of death | ||
| Smoking | 2.01 (1.51–2.66) | <0.001 |
| Systolic BP (mmHg) | 1.12 (1.00–1.28) | 0.05 |
| Creatinine | 1.57 (1.30–1.88) | <0.001 |
| Diabetes mellitus | 1.14 (0.85–1.54) | 0.24 |
| Total time since transplant | 1.16 (0.95–1.39) | 0.22 |
| HLA mismatch 1 | 1.35 (1.03–1.76) | 0.01 |
| HLA mismatch 2 | 1.31 (0.87–1.95) | 0.28 |
| Hemoglobin | 0.89 (0.81–0.92) | 0.001 |
| Proteinuria (score) | 1.33 (1.24–1.42) | <0.001 |
There were 299 cases during 7 years of follow-up out of 1487 patients with complete data. CI, confidence interval.
Figure 1 shows the cumulative incidence of DSCGL with and without adjustment for the competing risk of total mortality when a patient has a high serum creatinine level (190 μmol/L) or a low level (140 μmol/L). For the low level, adjustment for competing risk of death was associated with a small reduction in DSCGL; for the higher level, adjustment for competing risk of death was associated with a small increase from a higher baseline level.
Figure 1.
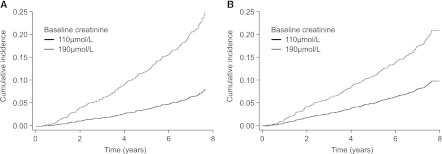
Cumulative incidence of doubling of serum creatinine or graft loss (DSCGL) by time with and without adjustment for competing risk by total mortality. The curves show the relationships for high (190 μmol/L) and low (110 μmol/L) serum creatinine levels.
Recurrent DSCGL
Time to Any DSCGL as an Outcome.
We first examined recurrent events, using the marginal model to examine first and subsequent DSCGL simultaneously. Thus, we investigated whether risk factors measured at baseline would predict any DSCGL and whether there was a difference between time to first event and time to any event. The upper section of Table 3 shows hazard ratios in the recurrent model based on a total of 407 cases of DSCGL. All risk factor associations were estimated with greater precision (i.e., smaller confidence intervals), indicating highly significant and robust associations, except for diabetes. The degree of association between risk factors and any DSCGL was approximately the same as for the first event.
Table 3.
Time to doubling of serum creatinine or graft loss counted as recurrent events according to the marginal method (8) and according to the conditional method with clock set to previous event at the next event, by baseline risk factors
| Method and Risk Factor | Hazard Ratio per Unit Difference (95% CI) | P Value |
|---|---|---|
| Marginal method | ||
| Smoking | 1.97 (1.56–2.47) | <0.001 |
| Systolic BP | 1.16 (1.04–1.28) | 0.007 |
| Creatinine | 1.98 (1.79–2.09) | <0.001 |
| Diabetes mellitus | 1.21 (0.94–1.54) | 0.14 |
| Time since last transplant | 1.13 (1.04–1.23) | 0.006 |
| HLA mismatch 1 | 1.34 (1.07–1.69) | 0.01 |
| HLA mismatch 2 | 1.54 (1.14–2.07) | 0.005 |
| Hemoglobin | 0.82 (0.73–0.91) | <0.001 |
| Proteinuria (score) | 1.30 (1.23–1.38) | <0.001 |
| Conditional (time from event to event) | ||
| Smoking | 2.05 (1.56–2.71) | <0.001 |
| Systolic BP (mmHg) | 1.10 (0.96–1.28) | 0.13 |
| Creatinine | 1.98 (1.79–2.09) | <0.001 |
| Diabetes mellitus | 1.25 (0.92–1.69) | 0.15 |
| Time since last transplant | 1.14 (1.02–1.27) | 0.02 |
| HLA mismatch 1 | 1.44 (1.09–1.90) | 0.01 |
| HLA mismatch 2 | 1.75 (1.23–2.49) | 0.002 |
| Hemoglobin | 0.74 (0.65–0.84) | <0.001 |
| Proteinuria (score) | 1.30 (1.21–1.40) | <0.001 |
| Competing risk and conditional model (combined) | ||
| Smoking | 1.67 (1.18–2.35) | 0.004 |
| Systolic BP (mmHg) | 0.98 (0.84–1.12) | 0.7 |
| Creatinine | 1.45 (1.24–1.61) | <0.001 |
| Diabetes mellitus | 0.86 (0.59–1.23) | 0.4 |
| Time since last transplant | 1.10 (0.95–1.27) | 0.22 |
| HLA mismatch 1 | 1.24 (0.90–1.71) | 0.19 |
| HLA mismatch 2 | 1.17 (0.74–1.86) | 0.51 |
| Hemoglobin | 0.73 (0.62–0.87) | <0.001 |
| Proteinuria (score) | 1.35 (1.27–1.44) | <0.001 |
There were 407 cases during 7 years of follow-up out of 1487 patients with complete data. CI, confidence interval.
Conditional Model.
In the conditional model that was used, time to first event is the same as for a standard Cox model, but all times to subsequent events are counted from event to event along the time axis from baseline. The main point of interest is in the dynamics from event to event. The middle section of Table 3 shows that the relationships changed only for systolic BP, for which the association weakened markedly with use of the conditional approach.
The lower section of Table 3 depicts the results when both the conditional approach and competing risk by death were taken into account. This weakened smoking as a risk factor, and only proteinuria and hemoglobin retained their strength of association.
Probability of Surviving without DSCGL.
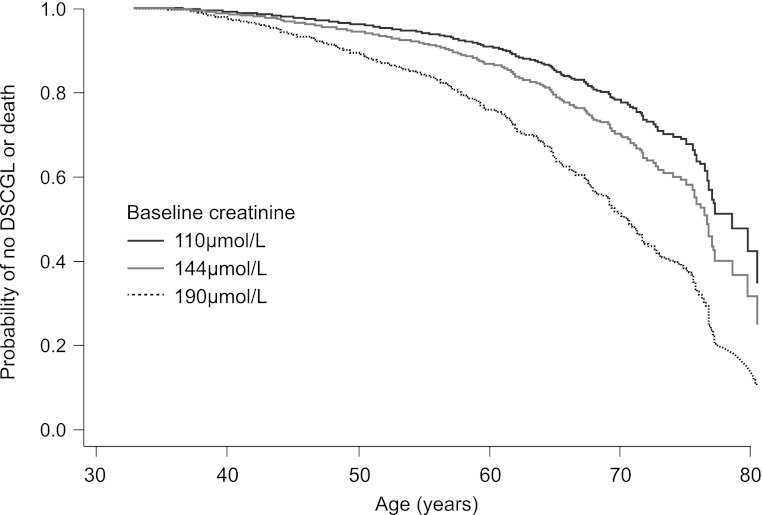
Baseline serum creatinine was, predictably, the strongest risk factor for DSCGL. Because DSCGL and death share risk factors, and age is the most important risk factor for mortality, we examined the interaction between achieved age and serum creatinine on estimated probabilities of death and DSCGL. Other risk factors were set to their mean value. Figure 2 shows the probabilities of reaching a given age free of DSCGL when baseline serum creatinine is 110 μmol/L, 144 μmol/L (the mean value at study entry), and 190 μmol/L. Thus, for an average patient in the trial (age 50 years), the probabilities of reaching age 60 years and of remaining event-free are 91%, 88%, and 78%, respectively, for the three chosen levels of renal function. Similarly, the probabilities of reaching age 70 years and remaining event-free are 79%, 71%, and 52%, respectively; for 80 years of age, the probabilities are 42%, 32%, and 16%.
Figure 2.
Estimated probability of achieving a given age free of doubling of serum creatinine or graft loss (DSCGL). Results are reported according to three baseline serum creatinine concentrations for an otherwise “average” participant in the Assessment of Lescol in Renal Transplant (ALERT) trial.
Discussion
This study shows that allowing for the competing risk of death in a risk factor study of first DSCGL in stable renal transplant recipients yields different risk associations compared with a standard model. Serum creatinine was the most susceptible to competing risk adjustments, losing 40% of its associated strength when adjusted for death. This is likely to reflect the fact that poor renal function is the leading risk factor for graft failure, but it shows a weaker association with risk of mortality. At the start of follow-up, the effect of competition is small because mortality is low. With time, however, the effect of competing risk increases. This is analogous to the situation in which a confounding variable becomes stronger with time, which usually results in weakening of the regression association across the whole follow-up period. However, the confounding effect of mortality is more complex because individual risk factors are associated to a varying degree to competing outcomes simultaneously and the net effect is difficult to predict.
The analyses revealed similar effects for other established risk factors—HLA-DR mismatches and time since transplantation—but not for proteinuria. The association of smoking with DSCGL changed a little when death was included as a competing risk, which may reflect the fact that the primary effect of smoking is on mortality rather than on graft loss. The degree of “confounding” by competing risk may thus be smaller. Systolic BP also reduced its association with DSCGL despite its known association with several types of cardiovascular event, such as coronary heart disease, heart failure, and stroke. A smaller change was seen for the association between hemoglobin concentration and DSCGL, possibly because it is associated with a series of cardiovascular causes of death (14,15) and with cancer.
Baseline serum creatinine, the major risk factor for graft dysfunction and failure, showed a constant association with outcome when the global burden of all renal events was analyzed, indicating that it has an important effect on recurrent events, as described by others (16). The same pattern was observed for other risk factors. The results were not influenced significantly by the use of a conditional model. Even if the risk set from the first event influences the risk set of later events, these effects were minor and had little effect on the overall pattern of risk factors. In addition, the marginal model is dominated by first events, so there were few differences between the two recurrent models. In the combined model, proteinuria and hemoglobin retained or slightly increased their association with DSCGL, but both creatinine and smoking showed somewhat weaker associations with this outcome.
The inclusion of healthy patients in the ALERT population may result in differences from a registry population of renal transplant recipients (17), given the better than predicted survival of patients in the study. Graft survival was also good, with a lower than expected risk of DSCGL. This was especially true for patients with preserved renal function. Thus, an ALERT patient (age 50 years on average) with a baseline serum creatinine level of 110 μmol/L had a 42% predicted chance of reaching 80 years without renal failure or death.
The statistical analysis of competing risk depends on the assumption of independence between death and DSCGL. This cannot be tested because DSCGL cannot occur after death. However, by adjusting for common risk factors, our analyses show a clearer relationship between risk factors that influence graft function based on long-term DSCGL. We have shown different results depending on the model assumptions and endpoints used, raising the question of which method is optimal. It is clear that in populations with a high mortality rate, as is the case in patients with kidney disease, analyses by competing risk seem to give a closer description of events, and it seems more appropriate to include competing risk in the model than ignoring it. Likewise, if there are substantial numbers of recurrent endpoints, it seems inappropriate to limit reporting of data to risk factor associations for the first event rather than to also consider the global burden of multiple events.
The clinician should be aware of situations in which competing risk may give biased results if analyzed by a standard Cox regression analysis for time to first DSCGL. This will be the case when the risk of death is high (for example, >3% per year during at least 5 years of follow-up). In the ALERT trial, the mortality marginally exceeded this rate, but such high mortality would be more typical in hemodialysis patients or in patients with severely impaired kidney function. The difference in regression coefficients between a simple time to first event Cox model and one that includes competing risk is not unexpected because these are two different models of the real world: One ignores the fact that competing risk by death before DSCGL takes place by censoring patients at time of death, whereas the other tries to model the competing risk so that times to both endpoints are incorporated into the same model.
We did not force age and sex into the model but rather restricted the choice of variables to those with established etiologic or clinical relevance. According to this strategy, age did not retain statistical prediction. Moreover, because age was used in the calculations of event-free probabilities, age could not be included as a cofactor. Sex was not significant in the univariate analysis and was also not used in the model. The overall aim was not to find an optimal model but to compare different model approaches with a realistic set of risk factors.
Selection of healthy patients may limit the generalization of the analyses. The fact that patients were selected on the basis of stable graft function is a major factor likely to be associated with good outcomes. Thus, these results may apply only to similar transplant populations. The statistical modeling of competing events rests on the assumption of independence between death and DSCGL before either event occurs. This is probably more realistic in a multivariate model, which adjusts for baseline risk factor levels. However, this assumption is not testable. Moreover, many deaths took place after first DSCGL, so only 135 deaths were included in the competing risk analysis. In a hemodialysis population, where mortality is much higher, the effects of competing risk would have played a larger role. In the combined conditional recurrent and competing model, all recurrent events were treated equally with respect to competing risk (i.e., no allowance was made for possible differing degree of competition with the various recurrent events).
Overall, this study demonstrates an alternative approach to multivariate analyses in renal transplant recipients that is appropriate for other renal populations in whom the mortality rate is high and mortality shares risk factors with renal events. The inclusion of death as a competing risk allows the clearer identification of primary risk factors for renal events and is an approach that is likely to be of general relevance in populations with a high mortality rate. A high competing risk may also affect sample size considerations and should be taken into account in the planning of new studies.
Disclosures
I.H. has received steering committee fees from Roche. B.C.F. has received consulting fees from AstraZeneca, Novartis, Roche, and Wyeth; lecture fees from AstraZeneca, Novartis, and Roche; and grant support from Novartis, Roche, Merck-Schering-Plough, and Wyeth. A.G.J. has received consulting and lecture fees and has been a member of data monitoring, end-point, and steering committees for Novartis, Roche, Wyeth, Pfizer, and Astellas. A.H. has received lecture fees from Novartis, Roche, and Amgen. H.H. has received consulting fees from Novartis, AstraZeneca, and Schering-Plough and lecture fees from Novartis and AstraZeneca.
Acknowledgments
The ALERT trial was sponsored by Novartis Pharma AG.
Footnotes
Published online ahead of print. Publication date available at www.cjasn.org.
References
- 1.Cook RJ, Lawless JF: Marginal analysis of recurrent events and a terminating event. Stat Med 16: 911–924, 1997 [DOI] [PubMed] [Google Scholar]
- 2.Wei LJ, Glidden DV: An overview of statistical methods for multiple failure time data in clinical trials. Stat Med 16: 833–839, discussion 841–851, 1997 [DOI] [PubMed] [Google Scholar]
- 3.Metcalfe C, Thompson SG: Wei, Lin and Weissfeld’s marginal analysis of multivariate failure time data: Should it be applied to a recurrent events outcome? Stat Methods Med Res 16: 103–122, 2007 [DOI] [PubMed] [Google Scholar]
- 4.Tikkanen MJ, Szarek M, Fayyad R, Holme I, Cater NB, Faergeman O, Kastelein JJP, Olsson AG, Larsen ML, Lindahl C, Pedersen TR, IDEAL Investigators : Total cardiovascular disease burden: Comparing intensive with moderate statin therapy insights from the IDEAL (Incremental Decrease in End Points Through Aggressive Lipid Lowering) trial. J Am Coll Cardiol 54: 2353–2357, 2009 [DOI] [PubMed] [Google Scholar]
- 5.Fine JP, Gray RJ: A proportional hazards model for the subdistribution of a competing risk. J Am Stat Assoc 94: 496–509, 1999 [Google Scholar]
- 6.Shastri S, Tangri N, Tighiouart H, Beck GJ, Vlagopoulos P, Ornt D, Eknoyan G, Kusek JW, Herzog C, Cheung AK, Sarnak MJ: Predictors of sudden cardiac death: A competing risk approach in the hemodialysis study. Clin J Am Soc Nephrol 7: 123–130, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dahle DO, Mjøen G, Oqvist B, Scharnagl H, Weihrauch G, Grammer T, März W, Abedini S, Norby GE, Holme I, Fellström B, Jardine A, Holdaas H: Inflammation-associated graft loss in renal transplant recipients. Nephrol Dial Transplant 26: 3756–3761, 2011 [DOI] [PubMed] [Google Scholar]
- 8.Wei LJ, Lin DY, Weissfeld L: Regression analysis of multivariate incomplete failure time data by modelling marginal distributions. J Am Stat Assoc 84: 1065–1073, 1989 [Google Scholar]
- 9.Holdaas H, Fellström B, Jardine AG, Holme I, Nyberg G, Fauchald P, Grönhagen-Riska C, Madsen S, Neumayer HH, Cole E, Maes B, Ambühl P, Olsson AG, Hartmann A, Solbu DO, Pedersen TR: Assessment of LEscol in Renal Transplantation (ALERT) Study Investigators: Effect of fluvastatin on cardiac outcomes in renal transplant recipients: A multicentre, randomised, placebo-controlled trial. Lancet 361: 2024–2031, 2003 [DOI] [PubMed] [Google Scholar]
- 10.Holdaas H, Fellström B, Cole E, Nyberg G, Olsson AG, Pedersen TR, Madsen S, Grönhagen-Riska C, Neumayer HH, Maes B, Ambühl P, Hartmann A, Staffler B, Jardine AG, Assessment of LEscol in Renal Transplantation (ALERT) Study Investigators : Long-term cardiac outcomes in renal transplant recipients receiving fluvastatin: The ALERT extension study. Am J Transplant 5: 2929–2936, 2005 [DOI] [PubMed] [Google Scholar]
- 11.Fellström B, Holdaas H, Jardine AG, Nyberg G, Grönhagen-Riska C, Madsen S, Neumayer HH, Cole E, Maes B, Ambühl P, Olsson AG, Staffler B, Pedersen TR, Assessment of Lescol in Renal Transplantation Study Investigators : Risk factors for reaching renal endpoints in the assessment of Lescol in renal transplantation (ALERT) trial. Transplantation 79: 205–212, 2005 [DOI] [PubMed] [Google Scholar]
- 12.Lin DY, Wei LJ: The robust inference for the Cox proportional hazards model. J Am Stat Assoc 84: 1074–1078, 1989 [Google Scholar]
- 13.Prentice RL, Williams BJ, Peterson AV: On the regression analysis of multivariate failure time data. Biometrika 68: 373–379, 1981 [Google Scholar]
- 14.Gagnon DR, Zhang T-J, Brand FN, Kannel WB: Hematocrit and the risk of cardiovascular disease—the Framingham study: a 34-year follow-up. Am Heart J 127: 674–682, 1994 [DOI] [PubMed] [Google Scholar]
- 15.Holme I, Aastveit AH, Hammar N, Jungner I, Walldius G: High blood hemoglobin concentration as a risk factor of major atherosclerotic events in 114,159 healthy men and women in the Apolipoprotein Mortality RISk study (AMORIS). Ann Med 44: 476–486 [DOI] [PubMed] [Google Scholar]
- 16.Pascual M, Theruvath T, Kawai T, Tolkoff-Rubin N, Cosimi AB: Strategies to improve long-term outcomes after renal transplantation. N Engl J Med 346: 580–590, 2002 [DOI] [PubMed] [Google Scholar]
- 17.Schaeffner ES, Födinger M, Kramar R, Frei U, Hörl WH, Sunder-Plassmann G, Winkelmayer WC: Prognostic associations between lipid markers and outcomes in kidney transplant recipients. Am J Kidney Dis 47: 509–517, 2006 [DOI] [PubMed] [Google Scholar]