Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Feb 4;3:1203. doi: 10.1038/srep01203

Dynamics and Thermodynamics beyond the critical point

F A Gorelli 1,2, T Bryk 3,4, M Krisch 5, G Ruocco 6,1, M Santoro 7, T Scopigno 6,1,a
PMCID: PMC3563038  PMID: 23383373

Abstract

Sudden changes in the dynamical properties of a supercritical fluid model have been found as a function of pressure and temperature (T/Tc = 2–5 and P/Pc = 10–103), striving with the notion of a single phase beyond the critical point established by thermodynamics. The sound propagation in the Terahertz frequency region reveals a sharp dynamic crossover between the gas like and the liquid like regimes along several isotherms, which involves, at sufficiently low densities, the interplay between purely acoustic waves and heat waves. Such a crossover allows one to determine a dynamic line in the phase diagram which exhibits a very tight correlation with a number of thermodynamic observables, showing that the supercritical state is remarkably more complex than thought so far.

The supercritical fluid has since ever1, until recently, been considered as a unique state with intermediate properties of the liquid and gas phases. The thermodynamical observables show a continuous evolution along any P-T path in supercritical conditions. This fact is supported by the traditional view on liquid and gas as phases of the same symmetry, implying that these phases cannot be distinguished above the critical point where they do not coexist. On the other hand, this view assumes that physics of fluids is entirely determined by their structure. Modern approaches to liquid theory clearly show that this is not always the case. Dynamics plays often a crucial role. Early in 2005 L. Xu and collaborators have pointed out that the diffusion coefficient of water undergoes a non-Arrhenius (“fragile”) to Arrhenius (“strong”) crossover accompanying a thermodynamic liquid-liquid transition in the so called “no-man's land” i.e. not accessible by current experimental techniques2.

More recently, it has been discovered that subtle but remarkable changes in supercritical fluids do occur in the positive sound dispersion (PSD)3,4,5. These changes posses the potential to part the phase diagram in a gas like and a liquid like region.

PSD is a phenomenon ascribed to the presence of one or more relaxation processes consisting in the increase of the sound velocity when the sound frequency is close to the relaxation frequency. In fact the relaxation processes time scale, τ, marks the border between the “viscous liquid-like” dynamic (for ωL(Q)τ ≪1, where ωL and Q are the sound frequency and wave vector, respectively) to the “elastic solid-like” one (ωL(Q)τ≫1). Correspondingly, the longitudinal sound velocity undergoes a transition (PSD) from its “low” frequency adiabatic limit cS to its “infinite” frequency limit c∞ > cS. This effect has been observed in a wealth of liquids and glasses with typical relaxation frequency of the order of THz in simple liquids. On the other hand, PSD has never been observed so far in gases6,3. Recently, PSD has been observed in supercritical fluids such as Argon (critical parameters Tc = 150.87 K and Pc = 4.898 MPa) and Oxygen (Tc = 154.6 K and Pc = 5.050 MPa) along isothermal lines, showing a cusp (discontinuity in the first derivative) as a function of pressure. This allows to define the high and low density supercritical fluids as liquid-like and gas like supercritical fluids, respectively3,5. Based on such results, it has been proposed that the onset of PSD takes place in correspondence with the maxima of constant pressure specific heat cP, defining the so called Widom line7, which establishes a tight link between dynamics (PSD) and thermodynamics5 (cP). Unfortunately, in that case the study was performed along an isotherm at high temperature (T/Tc = 3.8), where the maximum of cP is no longer visible and the Widom line could be only extrapolated. A recent study indeed identified a dynamic crossover at the Widom line at lower temperatures where the maxima in cP are still very well visible, based on anomalies in the self-diffusion coefficient and the excess two body entropy8. These results are at ease with previous findings of our group on the dynamic crossover related to collective modes. On the other hand, our view has been challenged by recent theoretical investigations. In one of these works9 it has been found that the extrema of different thermodynamic functions rapidly smear out above the critical point; this led the authors to question the potential link between dynamics and thermodynamics in the supercritical state, and to suggest the separation between liquid-like and gas-like regions to be rather determined by dynamics alone. The crossover in PSD of a model supercritical fluid was indeed assigned to a universal dynamic (Frenkel) line, where the equality between the relaxation time and the minimum period of transverse quasiharmonic waves holds10. Unfortunately, PSD was not calculated, hence the advanced relationship between the potential dynamic crossover and the Frenkel line remains at the level of an interesting speculation calling for further investigations. Another possible way to identify two regions in the supercritical phase builds on the appearance of some elasticity upon crossing an aggregation line11. In addition, an alternative definition of the Widom line in terms of the loci of maxima of the volume of the correlation length was recently advanced12. Interestingly, this line does not follow the slope of any response function extrema except in the close vicinity of the critical point, where it indeed follows the cP maxima. This result adds a further call for a definitive clue on what is the right thermodynamic observable -if any- to correlate with the dynamic crossover.

Results

All this matter motivated us to deeply investigate what we think to be a milestone in the physics of the elusive supercritical state, i.e. the potential link between dynamics and thermodynamics. Specifically, based on molecular dynamics (MD) computer simulations, we investigated the onset of PSD along several isotherms down to temperatures where the line of maxima of cP is well defined. In fact, we discovered that the onset of PSD occurs along this line up to temperatures where the maximum of cP is still well defined and along the common minima of thermal diffusivity, DT, and kinematic shear viscosity, ν, at higher temperatures (note that kinematic longitudinal and shear viscosity DL and ν are related to the shear and bulk viscosity coefficients ηS and ηB as: DL = (4/3ηS + ηB)/ρ, and ν = ηS/ρ, where ρ is the density). The lines of extrema of these three observables are very close each others at sufficiently low temperatures, where maxima of cP are well defined. Remarkably, we found that at sufficiently low densities in the gas-like regime, up to the dynamic crossover to the liquid-like regime, there is a strong interplay between purely acoustic waves and heat waves. These findings led us to the quantitative characterization of both types of wave properties, along with the quantitative determination of the crossover.

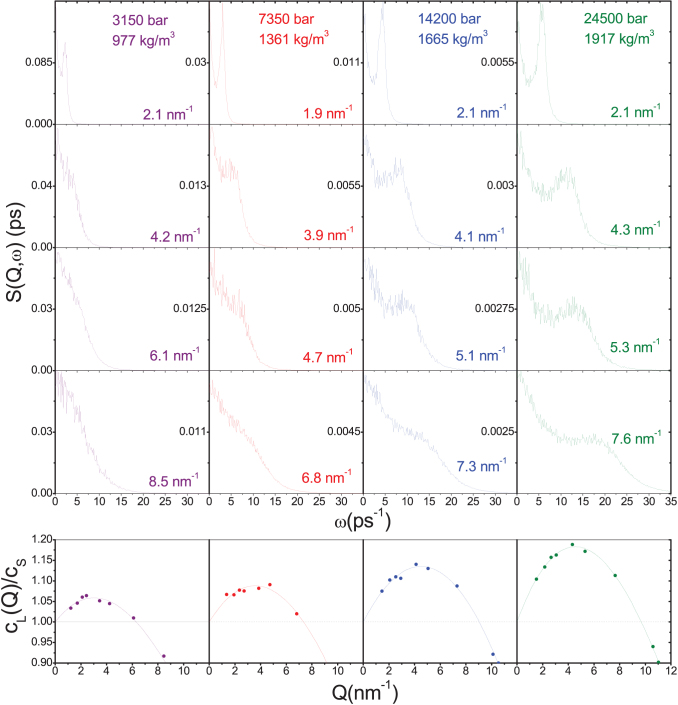
Some S(Q, ω)s simulated on Ar at 700 K at four selected pressure and Q values are reported in figure 1, upper panel. The acoustic peak is increasingly more pronounced at high densities and small Q values. The corresponding sound dispersion cL(Q) values have been divided by the adiabatic sound velocity value cS (figure 1, lower panel). In case of no PSD this ratio must be equal to 1 at small Qs and to monotonically decrease at higher Qs on approaching the Q value of the first sharp diffraction peak (FSDP) of the static structure factor S(Q), resembling the bending of dispersion curves in crystals on approaching the Brillouin zone boundaries. On the other hand, when PSD is present, as it is the case here, the cL(Q)/cS ratio is expected to tend to 1 at very small Qs, to show a maximum upon increasing Q and then again to decrease at higher Qs on approaching the FSDP. PSD, i.e. the value of this maximum has been estimated by fitting a cubic polynomial function to the cL(Q)/cS ratio to account for finite Q sampling. The maximum takes place at around 3–5 nm−1, i.e. at the lengthscale ~2π/Q*, where the inverse of structural relaxation time τ(Q) equals the acoustic frequency Ω(Q). This occurs at all the investigated pressures and the amount of PSD decreases on lowering density. Similar evolutions have been obtained along the other isotherms.

Figure 1.

Figure 1

Open in a new tab

Upper panel: S(Q, ω) spectra obtained from MD simulations on supercritical Ar at four selected pressure (density) and Q values, at 700 K. Lower panel: cL(Q)/cS ratio at the same pressures. The dispersions (dots) have been fitted to a cubic polynom for a better estimation of the maximum. The cS values have been obtained from NIST23 up to the density corresponding to 10 Kbar, and extrapolated above this density using the formula: cS(m/s) = 501.1174 + 0.17806·ρ(kg/m3) + 4.32538(10-4·ρ(kg/m3)2. We propose this extrapolation as, on the basis of NIST23 data for Ar at 700 K, it results that in the whole range of available data (from 50 to 10000 bar, (33.866 to 1506.5 kg/m3) the sound speed shows a quadratic dependence on density with very good approximation (within about 0.1%).

Density evolution of PSD is reported in Figure 2. Along all isotherms PSD shows a kink, being constant at low densities and increasing linearly at high densities. The extrapolation of the linear behaviour to low densities allows to estimate the density at which PSD is expected to vanish if coupling to the structural relaxation process was the only underlying, relevant mechanism; this density marks the onset of this kind of PSD or, in other words, the dynamic crossover between the gas-like and the liquid-like regime. On the other hand, the non-vanishing plateau in PSD at low densities indicates that for ρ→0 some mechanism other than structural relaxation must exist. In order to shed light on potential mechanisms of PSD we used a thermo-viscoelastic model considering the possible propagation of heat and sound waves and the coupling between them13. A powerful method in the framework of generalized hydrodynamics is the approach of Generalized Collective Modes (GCM), representing acoustic excitations coupled to non-hydrodynamic processes as dynamic eigenmodes14,15. The GCM approach explained correctly the “fast sound” phenomenon in disparate mass binary liquid alloys and predicted conditions of existence of non-hydrodynamic excitations like optic-like modes, heat waves etc16,17. In Figure 3 (left frames) we show the frequency of acoustic modes and heat waves, as functions of Qs, at four selected densities at T = 363 K. Heat waves were known to exist in solids as “second sound” excitations18,19,20 while in liquids heat waves similarly to transverse sound waves cannot propagate on macroscopic distances21. This fact is reflected in the Q dependence of the frequency of heat waves vanishing at some finite Qh value; heat waves can exist on spatial scales not larger than roughly 2π/Qh. The dependence of sound dispersion on density shown in Fig. 3 gives evidence that below 5 nm−1 the deviation from the hydrodynamic dispersion law reduces with decreasing density. For low densities, however, there is also a strong increase of the deviation from the hydrodynamic dispersion around 10 nm−1, that is responsible of the overall PSD causing the plateau observed in Figure 2. We suggest that the origin of this increase at around 10 nm−1 for low-density states may be connected with heat waves because in this Q region at low density we observed the strong increase of their contributions to the S(Q,ω) (Figure 3, right frames). These contributions (mode strengths) were obtained fit-free from the eigenvectors associated with acoustic and heat excitations. In the long-wavelength limit they tend to the values predicted by hydrodynamics22. At high density the strength of the contribution of heat waves to the S(Q,ω) is negligible, whereas it strongly increases upon decreasing density. This implies that at low densities, beyond the hydrodynamic region there exist two branches of strongly coupled acoustic-heat excitations, which in turn causes strong deviation from the hydrodynamic dispersion for the high-frequency branch.

Figure 2.

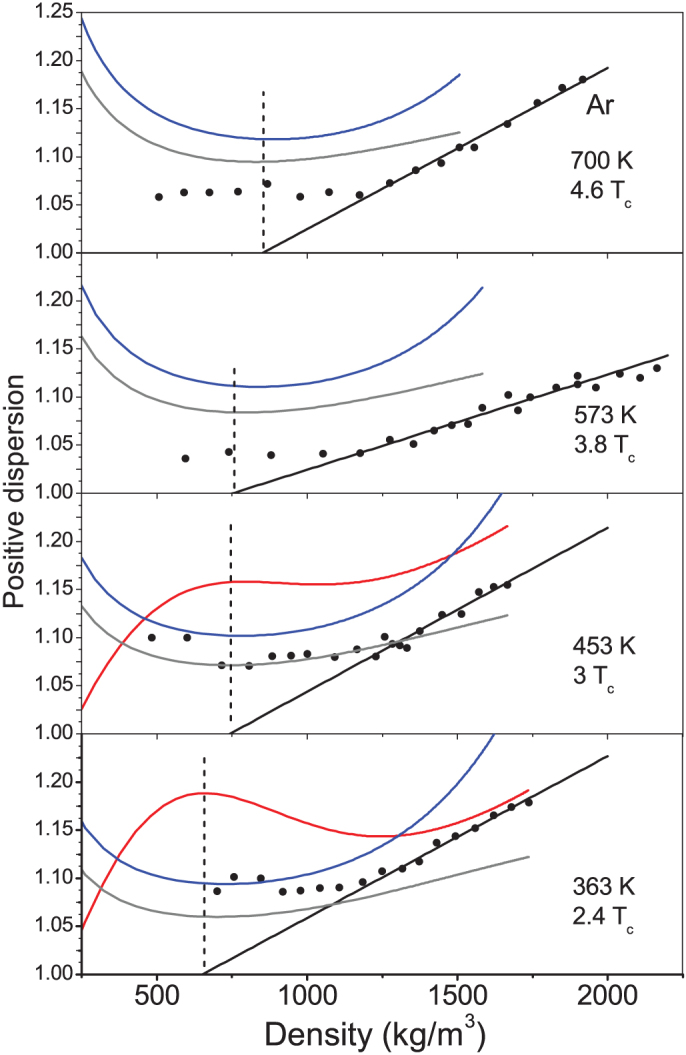
Figure 2

Open in a new tab

Density evolution (dots) of the PSD (max cL(Q)/cS) at the four isotherms of this study. A linear behaviour has been fitted through the high density data points, whose intercept with the horizontal line of value 1 marks the onset of PSD, i.e. the dynamic crossover between the gas-like and the liquid-like regimes. The other lines have been obtained using NIST data for Argon23 (corresponding y axes are arbitrarily rescaled) and represent: cP (red), DT (grey) and ν (blue). The extrema of these lines correspond to the dynamic crossover marked by the onset of PSD.

Figure 3.

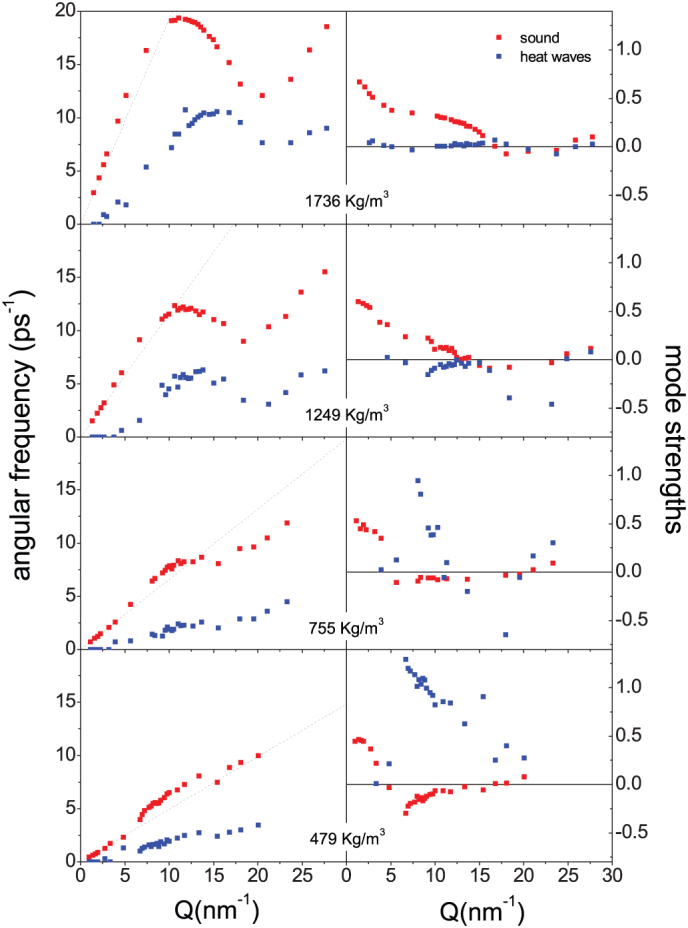
Figure 3

Open in a new tab

Dispersion and mode strengths in S(Q, ω)s of two types of collective excitations in supercritical Ar at T = 363 K as follows from the fit-free analysis based on GCM approach. Left frames: dispersion of acoustic excitations (red) and non-hydrodynamic heat waves (green) at four selected densities. Dashed lines correspond to the hydrodynamic dispersion. Right frames: mode strengths of the corresponding propagating modes. In the long-wavelength limit heat waves do not exist, while the hydrodynamic value for the sound mode strength is 1/γ, where the ratio of specific heats γ varies from 1.43 to 2.16 for the highest and the lowest density, respectively.

Discussion

The reduced phase diagram (P/Pc-T/Tc) for Argon is reported in figure 4. It shows the simulation points (open dots) and the points where structural relaxation related PSD vanishes (full stars), according to the linear extrapolation of high density data as discussed above. Lines emanating from the critical point have been obtained from NIST data23: the red, blue and grey lines are obtained from extrema of cP, ν and DT, respectively. These are among all possible lines emanating from the critical point and which can be considered as extensions of the liquid-vapour coexistence line into the supercritical fluid region. The line of maxima of cP can be traced up to about 450 K (T/Tc = 2.98), as above this temperature these maxima severely smear out. On the other hand, the minima of DT and ν are still observable, even if broad, up to the highest temperature of this study (700 K, T/Tc = 4.64). The lines of extrema of cP, DT and ν are very close each other. Stars indicating the onset of PSD lie very close to these lines, putting the link between the dynamic crossover and thermodynamics on a very solid background. Indeed, the very existence of such a relationship has been the matter of what now appears to be a correct intuition in our previous works3,5, where the relevant marker was thought to be only the line of cP maxima. On the other hand, the fact that this line is not defined far from the critical point, where cP maxima are not visible, made the connection between the onset of PSD and thermodynamics rather limited. Now, the connection between the dynamic crossover and the lines of DT and ν minima, which are well defined also very far from the critical point, makes the link between dynamics and thermodynamics quite robust and general. Interestingly, the non monotonic density dependence of longitudinal kinematic viscosity, DT and ν has a remarkable consequence. These quantities define the hydrodynamic relaxation times for longitudinal and transverse dynamics of supercritical fluids22. The Q-width of the hydrodynamic regime, where collective excitations and relaxation processes have strictly hydrodynamic behaviour, depends on inverse of kinematic viscosities and DT24,25. Recently the estimates for the hydrodynamic Q-range were proved by IXS experiments26. Hence, the minimum in the density dependence of these quantities corresponds to the widest Q-range of the hydrodynamic regime at given temperature, which in turn we found corresponding to the dynamic crossover observed in this work. Within this context, one may wonder how the crossover in the positive sound dispersion, established by this work to be the key parameter which allows to identify two different “phases”, one gas- and the other liquid-like, relates to the behaviour of diffusion coefficient, playing a role in distinguishing two different liquid phases in water2. In the water case, Kumar et al27,28. identify the liquid-liquid transition reporting the breakdown of a linear dependence of the diffusivity as a function of the inverse structural relaxation time 1/τα. By virtue of the Maxwell relation, in turn, they eventually put forward the breakdown of the Stokes-Einstein relation. Although fascinating, this latter step relies on the assumption of a constant “infinite shear modulus”, the proportionality factor between diffusivity and 1/τα. The present work addresses the non constant behaviour of positive dispersion as function of the thermodynamic coordinates in the case of the gas-liquid transition in supercritical fluids, precisely the deviation of infinite frequency elastic properties from their hydrodynamic limit. It strongly suggests, therefore, that the amplitude of the structural relaxation was the dynamical observable related to the Widom line, rather than the relaxation time itself. This observation seems to indicate that the two phenomenon (liquid-liquid-transition in water and gas-liquid transition in supercritical fluids), both related to the Widom line, may be not based on the same physics. In summary, we discovered two striking features in density dependence of PSD in supercritical fluids: i) linear behaviour of PSD at sufficiently high densities, that extrapolates right to the density of cP, DT and ν extrema; ii) a plateau in the density behaviour of PSD for ρ→0, clearly indicating that this observable is originated by an additional collective process along with structural relaxation. The detailed analysis of dynamic eigenmodes and their contributions to S(Q,ω)s revealed a novel effect of non-hydrodynamic heat waves on sound dispersion in low-density supercritical fluids. We quantitatively identified the dynamic crossover in a supercritical fluid model, at several temperatures, between the low density gas-like regime and the high density liquid-like regime, based on the analysis of collective modes with mesoscopic/microscopic wavelengths. In this framework, the unique role of heat thermal waves along with their interplay with sound waves have been unveiled. A remarkable outcome of this study is that the dynamic crossover shows a very tight correlation with the extrema of thermodynamic response functions and transport coefficients as cP, DT and ν, defining a narrow region emanating from the critical point, as emphasized in reference29. This gives a new dimension to a recent work where a crossover in single particle dynamics was identified at the line of maxima of cP in a supercritical model fluid8, in turns anticipated by similar results in the different context of the liquid-liquid transition in water. The deep link between dynamics and thermodynamics beyond a critical point is now rationalized on a very general background.

Figure 4.

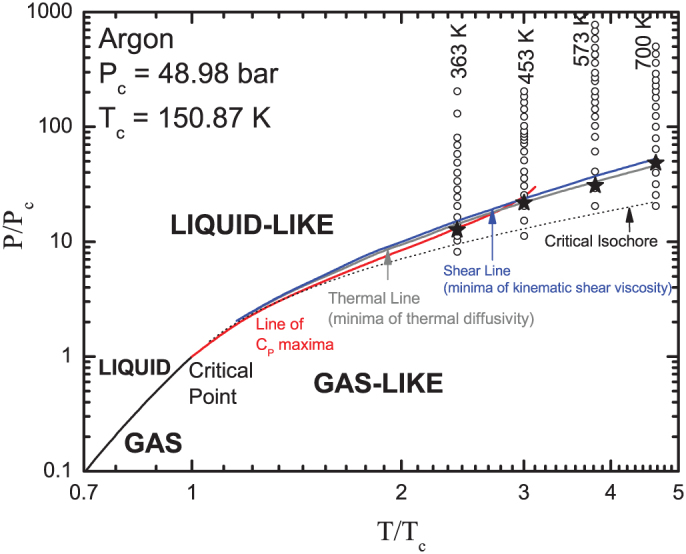
Figure 4

Open in a new tab

Reduced phase diagram (P/Pc -T/Tc) for Argon. Open dots: P-T points used in MD simulations. Stars: onset of PSD at the four isotherms, based on linear extrapolation of the PSD data points to low densities (see figure 2). Lines (obtained from NIST23): loci of the extrema of cP (red), DT (grey) and ν (blue). Dotted line: critical isochore.

Methods

Molecular dynamics simulations were carried out on supercritical Argon at different densities at T = 363, 453, 573 and 700 K. The corresponding pressures were obtained from NIST23 up to 1 GPa and, above this pressure, as: n(g/cm3) = A + B·log(P(GPa)), where A = −1.41806 g/cm3 and B = 9.42809·10−4 g/cm3 at 700 K, while the values at 573 K are reported elsewhere5. MD was done on the standard microcanonical ensemble for 2000 particles interacting through an ab initio potential30,31 with 12 Å cutoff radius. We checked, at a few densities, that the same results are obtained with 4000 particles and 20 Å cutoff radius. The production runs were of 600000 time steps, for small densities they were extended up to 1.2 mln time steps, each one of 2 fs. The energy drift over each production run was not higher than 0.2% that gave evidence of very good energy conservation in MD simulations. All of the calculated thermodynamic quantities agree with the values provided by the NIST23 within 1%. Transport coefficients reported in Fig. 2, such as DT and ν were taken from the same NIST23 database.

Every sixth timestep we sampled spatial Fourier transforms of density of particles n(Q,t), density of mass-current J(Q,t), and energy density e(Q,t) from the instantaneous positions ri(t), velocities vi(t) and single-particle energies εi(t) of N particles as follows:

graphic file with name srep01203-m1.jpg

These densities represent fluctuations of conserved quantities and are the main dynamic variables for hydrodynamic description of liquid dynamics. The density-density time correlation functions 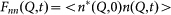Inline graphic, where the asterisk means complex conjugation, were calculated from the MD time evolution of n(Q,t), and additional averages were performed over the all possible directions of wave vectors corresponding to the same wave number Q. Numerical Fourier transform was used to obtain from the calculated density-density time correlation functions the dynamic structure factors S(Q,ω) and longitudinal current spectral functions JL(Q,ω) = (ω/Q)2S(Q,ω). The longitudinal sound velocity cL(Q) is obtained as cL(Q) = ωL(Q)/Q, where ωL(Q) is the sound frequency and it corresponds to the frequency of the maximum of JL(Q,ω)5. For analysis of contributions from collective modes to dynamic structure factors we applied the approach of Generalized Collective Modes (GCM)14,15, that consists in solving the matrix form of generalized Langevin equation in terms of dynamic eigenmodes that can exist in the system. The MD-derived time evolution of dynamic variables was used to calculate for each wave number the matrix elements of generalized hydrodynamic matrix T(Q)14,15. The eigenvectors associated with each eigenvalue were used to calculate the Q-dependent contributions (mode strengths) to dynamic structure factors.

Author Contributions

F.A.G., T.B., M.K., G.R., M.S. & T.S. designed research, performed research, wrote, reviewed and approved the manuscript. T.B. performed the numerical simulations.

Acknowledgments

Two of us, F.A.G. and M.S., have been supported by the European Community (LENS Contract FP7 G.A.No. 228334 LASERLABEUROPE). T.S. has received funding from the European Research Council under the European Community's Seventh Framework Program (FP7/2007–2013)/ERC grant Agreement No. 207916.

References

  1. Zemanski M. W. in:Heat and Thermodynamics, (MacGraw-Hill, New York, 1968). [Google Scholar]
  2. Xu L. et al. Relation between the Widom line and dynamic crossover in systems with a liquid-liquid phase transitions. Proc Natl Acad Sci USA 102, 16558–16562 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Gorelli F. A., Santoro M., Scopigno T., Krisch M. & Ruocco G. Liquidlike behavior of supercritical fluids. Phys Rev Lett 97, 245702 (2006). [DOI] [PubMed] [Google Scholar]
  4. Gorelli F. A. et al. Inelastic x-ray scattering from high pressure fluids in a diamond anvil cell. Appl. Phys. Lett. 94, 074102 (2009). [Google Scholar]
  5. Simeoni G. G. et al. The Widom's line as the crossover between liquid-like and gas-like behaviour in supercritical fluids. Nature Physics 6, 503 (2010). [Google Scholar]
  6. Cunsolo A. et al. Dynamics of Dense Supercritical Neon at the Transition from Hydrodynamical to Single Particle Regimes. Phys Rev Lett 80, 3515 (1998). [Google Scholar]
  7. Widom B. in Phase Transitions and Critical Phenomena, Domb C., Green M. S., eds. (Academic, 1972). [Google Scholar]
  8. Han S. Anomalous change in the dynamics of a supercritical fluid. Phys. Rev. E 84, 051204 (2011). [DOI] [PubMed] [Google Scholar]
  9. Brazhkin V. V. & Ryzhov V. N. Van der Waals supercritical fluid: Exact formulas for special lines. J Chem Phys 135, 084503 (2011). [DOI] [PubMed] [Google Scholar]
  10. Brazhkin V. V., Fomin Y. D., Lyapin A. G., Ryzhov V. N. & Trachenko K. Two liquid states of matter: a dynamic line on a phase diagram. Phys Rev E 85, 031203 (2012). [DOI] [PubMed] [Google Scholar]
  11. Bonn D., Ross D., Hachem S., Gridel S. & Meunier J. Percolation transition in Coulombic near-critical binary liquids,. Europhys. Lett. 58, 74 (2002). [Google Scholar]
  12. May H. O. & Mausbach P. Riemannian geometry study of vapor-liquid phase equilibria and supercritical behavior of the Lennard-Jones fluid. Phys Rev E 85, 031201 (2012). [DOI] [PubMed] [Google Scholar]
  13. Akcasu A. Z. & Daniels E. Fluctuation analysis in simple fluids. Phys Rev A 2, 962–975 (1970). [Google Scholar]
  14. De Schepper I. M. et al. Hydrodynamic time correlation functions for a Lennard-Jones fluid,. Phys. Rev. A 38, 271 (1988). [DOI] [PubMed] [Google Scholar]
  15. Mryglod I. M., Omelyan I. P. & Tokarchuk M. V. Generalized collective modes for the Lennard-Jones fluid. Mol. Phys. 84, 235 (1995). [Google Scholar]
  16. Bryk T. & Mryglod I. Collective dynamics in binary liquids: spectra dependence on mass ratio. J Phys: Cond Matt 17, 413–427 (2005). [Google Scholar]
  17. Bryk T. Non-hydrodynamic collective modes in liquid metals and alloys. Eur Phys J Spec Top 196, 65–83 (2011). [Google Scholar]
  18. Narayanamurti V. & Dynes R. C. Observation of second sound in bismuth. Phys Rev Lett 28, 1461–1465 (1972). [Google Scholar]
  19. Koreeda A., Takano R. & Saikan S. Second sound in SrTiO3. Phys Rev Lett 99, 265502 (2007). [DOI] [PubMed] [Google Scholar]
  20. Pohl D. W. & Irniger V. Observation of Second Sound in NaF by Means of Light Scattering. Phys Rev Lett 36, 480–483 (1976). [Google Scholar]
  21. Joseph D. D. & Preziosi L. Heat waves. Rev Mod Phys 61, 41–73 (1989). [Google Scholar]
  22. Hansen J. P. & McDonald I. R. in: Theory of Simple Liquids, Third Edition (Academic Press, Elsevier, 2006). [Google Scholar]
  23. Retrieved July 3, 2012, from NIST Chemistry WebBook, http://webbook.nist.gov/chemistry/.
  24. Bryk T. et al. Collective excitations in supercritical fluids: Analytical and molecular dynamics study of “positive” and “negative” dispersion. J Chem Phys 133, 024502 (2010). [DOI] [PubMed] [Google Scholar]
  25. Scopigno T. et al. Hard sphere-like dynamics in a non hard sphere liquid. Phys Rev Lett 94, 155301 (2005). [DOI] [PubMed] [Google Scholar]
  26. Bencivenga F. & Cunsolo A. The dispersive behavior of collective excitations in fluids: An experimental test for the generalized collective modes theory,. J Chem Phys 136, 114508 (2012). [DOI] [PubMed] [Google Scholar]
  27. Kumar P. et al. Relation between the Widom line and the breakdown of the Stokes–Einstein relation in supercooled water. Proc Natl Acad Sci 104, 9575–9579 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Xu L. et al. Appearance of a Fractional Stokes-Einstein Relation in Water and a Structural Interpretation of Its Onset. Nature Physics 5, 565–569 (2009). [Google Scholar]
  29. Brazhkin V. V. & Trachenko K. What separates a liquid from a gas? Phys. Today 65, 11, 68 (2012). [Google Scholar]
  30. Woon D. E. Accurate modeling of intermolecular forces: A systematic Moller-Plesset study of the argon dimer using correlation consistent basis sets. Chem Phys Lett 204, 29–35 (1993). [Google Scholar]
  31. Bomont J. M., Bretonnet J. L., Pfleiderer T. & Bertagnolli H. Structural and thermodynamic description of supercritical argon with ab initio potentials . J Chem Phys 113, 6815 (2000). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES