Abstract
Hall elements are by far the most widely used magnetic sensor. In general, the higher the mobility and the thinner the active region of the semiconductor used, the better the Hall device. While most common magnetic field sensors are Si-based Hall sensors, devices made from III-V compounds tend to favor over that based on Si. However these devices are more expensive and difficult to manufacture than Si, and hard to be integrated with signal-processing circuits for extending function and enforcing performance. In this article we show that graphene is intrinsically an ideal material for Hall elements which may harness the remarkable properties of graphene, i.e. extremely high carrier mobility and atomically thin active body, to create ideal magnetic sensors with high sensitivity, excellent linearity and remarkable thermal stability.
Magnetic sensors are devices capable of sensing a magnetic field and extracting information from it. Among them, Hall elements are by far the most widely used. More than two billion Hall elements are manufactured annually, and used in such fields ranging from computers to sewing machines, automobiles to aircraft, machine tools to medical equipment, and industrial applications to scientific detecting1,2,3,4,5. Hall devices exploit the galvanomagnetic effects due to the Lorentz force on charge carriers in a semiconductor, and transform a magnetic signal into an electric signal. In general, the higher the mobility of the semiconductor used, and the thinner the active region, the better the Hall device5. While most common magnetic field sensors are Si-based Hall sensors, devices made from III-V compounds, and particularly narrow-gap, high-mobility compounds such as InSb, tend to favor over that based on Si6,7,8,9, and ultra-high sensitivity Hall devices have also been realized based on two-dimensional-electron-gas (2DEG) which combines ultra-high carrier mobility with thin activebody6,10,11. However these devices are more expensive and difficult to manufacture than Si, and hard to be integrated with signal-processing circuits for extending function and enforcing performance6,7,8,9,10,11.
Graphene has been considered as a promising material for electronics applications in recent years, largely due to its extremely thin body and ultra-high carrier mobility12. Extensive investigations have been carried out on graphene field-effect transistors (G-FETs) which hold promise for radio-frequency applications12,13. However G-FETs currently perform no better than conventional transistors based on silicon or III-V compound semiconductors12. This may be largely attributed to the fact that the graphene device fabrication technology is still immature and falls far behind the conventional semiconductor technology, and this completely offsets the material advantages of graphene. In principle a more predictable electronics application of graphene should focus on a kind of simple device which only requires a very simple fabrication process while takes the full advantages of the remarkable physical properties of graphene. Compared with FET and other electrical devices12,14,15. Hall element is much simpler in device structure and is thus much easier to fabricate. The performance of a Hall element is mainly dependent on the electric properties of the material, most importantly on carrier mobility and concentration1,2,3,4,5,6, rather than on fabrication technology. Since graphene is born with extremely high room temperature carrier mobility and atomically thin body, it is an ideal material for building high-performance Hall elements. In addition, since FET based integrated circuits (ICs) can also be fabricated on graphene12,13, the function of Hall elements can be further enhanced in the future by combining them with those ICs on the same chip. It is thus nature to conclude that graphene could be the ideal material for building high-performance Hall elements and ICs with lower cost and better performance than conventional Hall devices, leading perhaps to the first field of mass electronic applications for graphene.
Although Hall effects including quantum Hall effects of graphene were intensively studied from the viewpoints of physical interests16, the performance of graphene Hall structure as a device aiming for sensor applications was hardly investigated. Recently a graphene magnetometer based on magnetoresistance effect was demonstrated, with potential applications in such fields as scanning probe magnetometry and magnetic storage17,18. Micro-sized Hall devices were also fabricated using graphene and important parameters including sensitivity and resolution were studied19,20. However, limited by the quality of the graphene used and not optimized device geometry and contact resistance, a low field resolution of 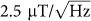 was reported20 which lags far behind that achieved by low-noise silicon-on-insulator Hall device of about
was reported20 which lags far behind that achieved by low-noise silicon-on-insulator Hall device of about 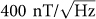 . In principle high quality graphene should be an ideal conductive channel for building Hall elements. Here we show, by utilizing the methods for growing and transferring high quality and large area graphene which we developed recently21, graphene Hall elements (GHEs) with higher performances than conventional Hall elements in all important aspects, including higher sensitivity and resolution, higher linearity, lower driving voltage, wider temperature range and better thermal stability can be realized and batch-fabricated. In addition, key performances of GHEs, in particular sensitivity, are controllable during the fabricating process of the devices according to the needs of desired applications. In this letter we show that graphene is intrinsically an ideal material for Hall elements which may harness the remarkable properties of graphene, i.e. extremely high carrier mobility and atomically thin active body, to create ideal magnetic sensors with high sensitivity of more than 1200 V/AT, excellent linearity of less than ±2% for magnetic field of up to 2T and remarkable thermal stability from 2 K to 400 K. In addition, graphene Hall elements can be batch-fabricated with low cost and readily integrated with integrated circuits (ICs) for signal-amplifying and processing.
. In principle high quality graphene should be an ideal conductive channel for building Hall elements. Here we show, by utilizing the methods for growing and transferring high quality and large area graphene which we developed recently21, graphene Hall elements (GHEs) with higher performances than conventional Hall elements in all important aspects, including higher sensitivity and resolution, higher linearity, lower driving voltage, wider temperature range and better thermal stability can be realized and batch-fabricated. In addition, key performances of GHEs, in particular sensitivity, are controllable during the fabricating process of the devices according to the needs of desired applications. In this letter we show that graphene is intrinsically an ideal material for Hall elements which may harness the remarkable properties of graphene, i.e. extremely high carrier mobility and atomically thin active body, to create ideal magnetic sensors with high sensitivity of more than 1200 V/AT, excellent linearity of less than ±2% for magnetic field of up to 2T and remarkable thermal stability from 2 K to 400 K. In addition, graphene Hall elements can be batch-fabricated with low cost and readily integrated with integrated circuits (ICs) for signal-amplifying and processing.
Results
A macro GHE with a channel length and width larger than 100 μm was firstly fabricated on a large area graphene on Si/SiO2 substrate. The macro GHE was then used to construct a graphene Gauss meter as a high sensitivity magnetic detector (see supplementary information for detailed description of the Gauss meter). After calibrated by a high sensitivity commercial Gauss meter, the graphene Gauss meter was used to map a two-dimensional non-uniform magnetic field. The output Hall voltages of the GHE were recorded at various positions of the magnetic field, and the magnetic field strength at corresponding position was compared with that measured by using the commercial Gauss meter. Quantitative analysis reveals that the Hall voltage of the GHE is linearly dependent on the magnetic field strength as measured by the commercial Gauss meter with very small fluctuations (Fig. 1a), and the GHE can thus be used as a Gauss meter after calibration through the measured linear relation to yield a two-dimensional map of magnetic field distribution as shown in Fig. 1b. This map is very similar to that mapped using the commercial Gauss meter in which a high sensitivity InSb Hall element is used as the magnetic detector (see Fig. S1f in supplementary information). The small difference between the two maps may come from the positioning differences between the two measurements which were carried out manually and the performance fluctuation of the GHE where the graphene channel was exposed directly to air during the measurement process.
Figure 1. Macro GHE as the detector of a Gauss meter.
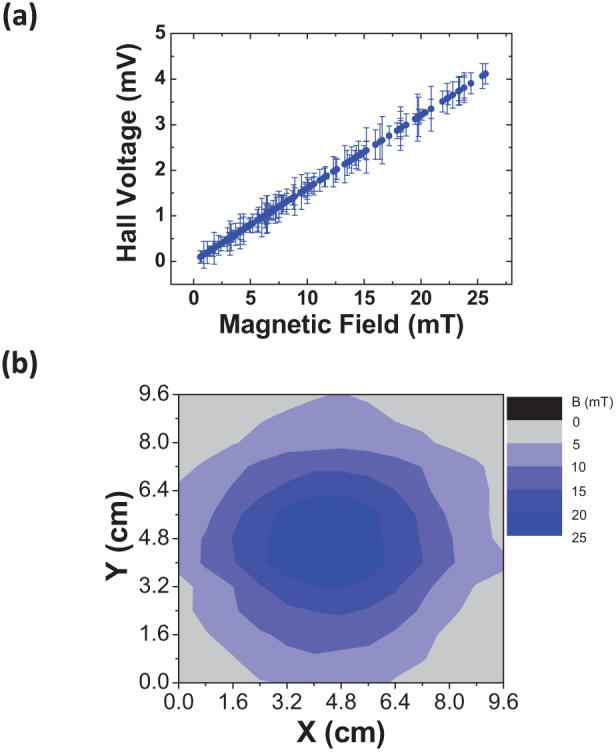
(a) Output Hall voltages of a GHE sampled at different points of an external magnetic field as a function of field strength measured by a commercial high sensitivity Gauss meter. (b) Two-dimensional map of the external magnetic field measured using the calibrated GHE.
Comparing to macro Hall elements, micro Hall elements with channel shorter than 10 μm afford higher density and higher spatial resolution1,4. Micro GHEs were fabricated on a Si/SiO2 substrate with a size of about 2 cm×2 cm (Fig. 2a), which was covered with a transferred high-quality graphene21. Over 400 GHEs were batch-fabricated on the 2 cm×2 cm substrate with approximately 50% yield. While not yet wafer-scaled, the procedure used here may in principle be scaled up to yield wafer-scale graphene material grown and devices fabrication process with higher yield than 50%.
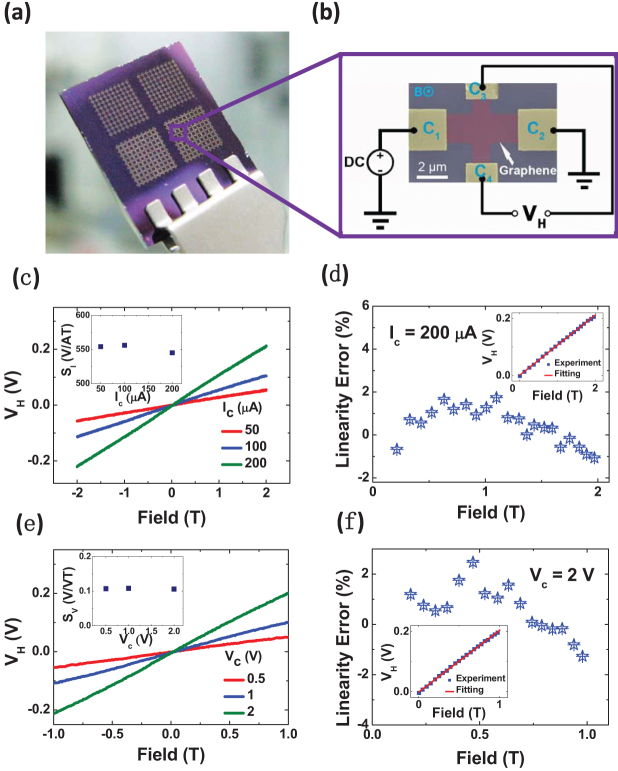
Figure 2. Batch-fabricated micro GHEs and their room temperature characteristics.
(a) Optical image showing GHEs arrays on a Si/SiO2 chip. (b) SEM image showing one of the GHEs of (a) and related Hall testing circuitry. (c) Hall voltage versus magnetic field measured in current mode. Inset: current-related sensitivity. (d) Linearity error of the GHE working in current mode and in a magnetic field ranging from 0 to 2 T. Inset: a typical linear fitting of the Hall voltage versus magnetic field. (e) Hall voltage versus magnetic field in voltage mode. Inset: voltage-related sensitivity. (f) Linearity error of the GHE working in voltage mode and in a magnetic field ranging from 0 to 1 T. Inset: a typical linear fitting of the Hall voltage versus magnetic field.
Figure 2b presents a scanning electron microscopic (SEM) image showing a typical cross-shaped micro GHE, which is a four-terminal device with two pairs of electrodes contacting four terminals of the graphene Hall cross. One pair electrodes (C1 and C2) are designed for current or voltage supply, and the other pair (C3 and C4) are for Hall voltage measurement. When an external magnetic field B is applied normal to the graphene plane, with the graphene channel being biased either with a constant current or voltage supply over C1 and C2, a Hall voltage is developed over C3 and C4 which depends linearly on the strength of the magnetic field as a result of the Hall effect, i.e. VH = SAB, where SA is the absolute sensitivity of the Hall element5,6. In principle GHEs can be used as magnetometers if the detailed electrical characteristics of the devices are known.
A Hall element can be used either in constant-current-supply or current mode, or in constant-voltage-supply or voltage mode. The Hall voltage generated in current mode can be written as1,6
and in voltage mode
where 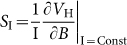 and
and 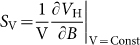 are current-related sensitivity and voltage-related sensitivity respectively, and I or V is the constant current or voltage supplied. The sensitivity of a sensor represents its ability to respond to a signal to be measured (here a magnetic field), and is one of the key performance parameters of the Hall element1,2,3,4,5,6,7,8,9,10,11.
are current-related sensitivity and voltage-related sensitivity respectively, and I or V is the constant current or voltage supplied. The sensitivity of a sensor represents its ability to respond to a signal to be measured (here a magnetic field), and is one of the key performance parameters of the Hall element1,2,3,4,5,6,7,8,9,10,11.
We first consider the current mode which is the most widely used mode for conventional Hall elements, since this mode may effectively avoid the degradation of device linearity induced by the magnetoresistance effect. When a GHE is measured in current mode, its output Hall voltage as a function of the magnetic field is shown in Fig. 2c. This figure shows clearly that the output Hall voltage increases linearly with increasing supply current and magnetic field ranging from −2 T to 2 T, suggesting a very large measurement range for magnetic field. The slopes of the VH-B curves give the absolute sensitivity SA of the GHE, which increases also linearly with bias current. Normalizing the absolute sensitivity SA with the bias current, the current-related sensitivity SI of the GHE is obtained and shown in the inset of Fig. 2c. The current-related sensitivity of the micro-GHE exceeds 550 V/AT at room temperature. As a comparison, for a typical conventional Hall devices1, these values are around 100 V/AT for silicon Hall plates fabricated by the standard bulk CMOS IC technology5, and typically 200 V/AT for GaAs (for example the standard GaAs Hall element provided by Asahi Kasei Corporation has a sensitivity 200 V/AT), but may approach 700 V/AT for 2DEG-based Hall devices1.
Linearity, an important performance parameter of Hall devices, determines the accuracy of measured result and is quantitatively described by a linearity error defined as7
where VH0 is the best linear fitted value to the measured Hall voltages VH at a given magnetic field. The data shown in Fig. 2d are obtained by linear fitting VH - B curves (e.g. those shown in Fig. 2c) for various magnetic field strengths ranging from 0 to 2 T. The linearity error lies within ±2%, suggesting that the GHE is a highly linear Hall element in current mode over a large magnetic field range.
The voltage mode is another operation mode of Hall devices. But few conventional Hall elements can directly work in this mode with high linearity over a wide range of magnetic fields as a result of the magnetoresistance effect. This is particularly so for the physical magnetoresistance effect, which results from the mobility spread of the charge carriers around the Fermi energy and usually scales up with magnetic field via a square relationship5,7. The output Hall voltage as a function of the magnetic field in voltage mode is given in Fig. 2e, showing clearly that the output Hall voltage increases linearly with increasing magnetic field and also with the supply voltage. The slope of the VH-B curve gives the absolute sensitivity SA of the GHE, and voltage-related sensitivity SV of the GHE is obtained to be about 0.1 V/VT through normalizing SA with bias voltage, as shown in the inset of Fig. 2e.
For real applications the linearity is perhaps the most concerned parameter for Hall elements working in voltage mode, since the linearity is usually degraded seriously due to the magnetoresistance effect in conventional Hall elements. While in GHEs, VH is hardly affected by the effect, which is a result of the absence of the physical magnetoresistance in graphene in the Coulomb scattering range (see supplementary information). The inset of Fig. 2f shows that the Hall voltage VH may be linearly fitted with B excellently well for a wide range of magnetic field from 0 to 1 T, and typically the linearity error is within ±2%. This small error should be compared with the typical value of about 10% for 2DEGs Hall elements at magnetic field less than 0.1 T10. GHEs thus afford excellent linearity over a wide magnetic field range in voltage mode, in which the use of Hall elements are indeed more convenient and economic than in current mode. Operating in voltage mode, GHEs are not only simpler to power, but also show better stability than in current mode. As a typical example, Fig. 2S of supplementary information shows back gate voltage dependence of both the voltage-related and current-related sensitivities. It is obvious that the voltage-related sensitivity shows a much weaker dependence on the back gate (or on environment) than the current-related sensitivity. This is because the carrier density is a much more sensitive parameter to the gate voltage or environment than the carrier mobility. It should be pointed out that our GHE is still far from being optimized both on device geometry and fabricating process, which leaves a large space for further improvements. A simple derivation shows that the sensitivity of a Hall element is strongly dependent on carrier density or mobility, and to a good approximation current and voltage related sensitivities of a Hall element can be written as1,6
where q is the elemental charge, W and L are the width and length, and ns and μ are the sheet carrier density and carrier mobility of the graphene channel respectively. Therefore the sensitivity of the GHE can be improved by decreasing ns or increasing carrier mobility μ, and also by optimizing the geometry of the device.
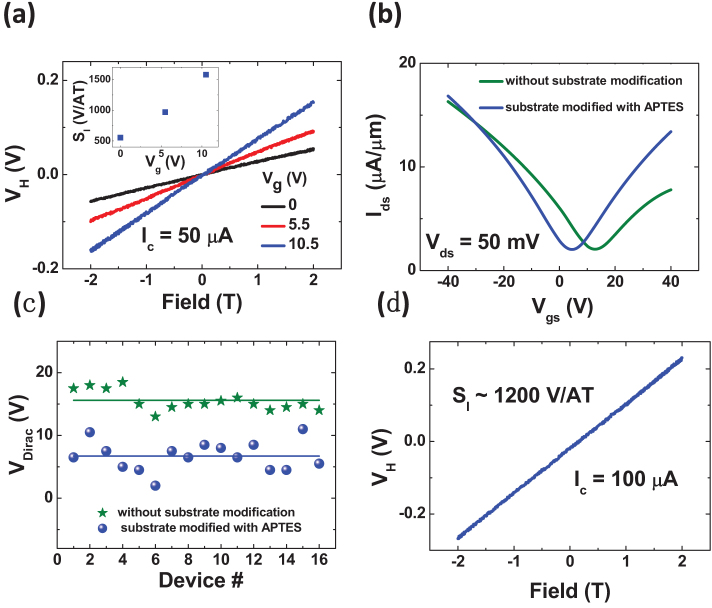
For a typical graphene channel, carrier density ns can in principle be controlled by applying a voltage Vg on the back gate12, i.e. the Si substrate here, then the current sensitivity SI of the GHE can be adjusted through gate voltage as shown in Fig. 3a. Since the Dirac voltage of the GHE is about 13 V (Fig. 3b), the carrier density (or device current) may be significantly reduced by applying a positive gate voltage smaller than 13 V on the back gate. The inset of Fig. 3a shows that SI increases from 550 V/AT at Vg = 0 V to about 1500 V/AT at Vg = 10.5 V, while corresponding carrier density decreases from 1×1012/cm2 to about 4×1011/cm2. Although gate voltage can be easily used to adjust the sensitivity of the GHE, the use of an additional large voltage on the back gate would bring great inconvenience to device fabrication and applications19. Alternatively we may emulate the back gate effect by surface or substrate modification. It is by now well established that the Dirac voltage of a graphene Hall device can be adjusted through modifying the surface of Si/SiO2 substrate with 3-aminopropyltriethoxysilane (APTES) before graphene was transferred onto the surface22. Figure 3b compares the transfer characteristics of a GHE with and without the additional modification treatment of the surface. This figure shows clearly that the GHE with APTES modification exhibits a smaller Dirac voltage and larger transconductance than that without surface modification. Thirty-two Hall elements were fabricated and measured, and half of the devices were fabricated on functionalized Si/SiO2 substrate. Statistical results (Fig. 3c) show that the Dirac voltage can be reduced systematically from 15.5 V to 6.7 V by the additional modification process (all transfer curves of the two groups of devices are shown in Fig. S3 in supplementary information). The current sensitivity of the GHE is improved up to 1200 V/AT for the GHE fabricated on functionalized surface (Fig. 3d) which is much larger than that of most commercial Hall elements.
Figure 3. Controlled Dirac point voltage and Hall elements sensitivity.
(a) Hall voltage versus magnetic field in current mode and at varying back gate voltage. Inset: current-related sensitivity as a function of the back gate voltage. (b) Transfer characteristics of two typical GHEs at a bias of 50 mV. The olive curve represents the GHE being fabricated through the normal process, and the blue curve represents that being fabricated on a substrate which was modified by APTES before graphene was transferred. (c) Statistical comparison of Dirac point voltages of GHEs with or without substrate modification. (d) Hall voltage versus magnetic field of a typical GHE with APTES modification in current mode without applying back gate voltage.
To further demonstrate the potential of GHEs in real applications, we tested nine APTES-treated micro GHEs in atmosphere conditions. The performance of the nine tested devices is similar to that tested in vacuum conditions (see the detailed in supplementary information). The current-related sensitivity at room temperature ranges from 645 V/AT to 1180 V/AT, with an average value of 850 V/AT [Figure S4(b)]. The voltage-related sensitivity ranges from 0.2 V/VT to 0.35 V/VT, with an average value of about 0.3 V/VT [Figure S4(d)]. The Hall mobility extracted based on equation (5) is found to distribute around 5000 cm2/V·s [Figure S4(d)], suggesting that our CVD graphene samples are of high quality. It should be noted that the tests were performed in air within 1 hour. Longer exposure time of the devices in air may result in contamination of graphene channel by possible organic or water molecules, and as a result degradation of the devices performance may occur. Further passivation technique is needed so as to deliver stable and repeatable performance of GHEs.
Graphene devices are also intrinsically low noise devices23. The combination of high sensitivity and low noise of graphene devices23 may in principle lead to very high resolution, i.e. minimum detectable field Bmin, and in our case this is less than 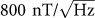 at operation frequency of 3 kHz (see e.g. Figure S5 of supplementary information). The resolution achieved here presents a significant improvement on that achieved previously19,20 which is larger than
at operation frequency of 3 kHz (see e.g. Figure S5 of supplementary information). The resolution achieved here presents a significant improvement on that achieved previously19,20 which is larger than 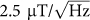 even at higher operation frequency and lower temperature. Increasing the operation frequency up to 4.5 MHz, Bmin can be improved to about
even at higher operation frequency and lower temperature. Increasing the operation frequency up to 4.5 MHz, Bmin can be improved to about 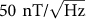 . Normalized by the device width, the resolution of the GHE is about 100 pT·mm/Hz1/2 which is much smaller than that of most conventional Hall elements1. In principle the sensitivity and resolution of the GHE can be further improved by optimizing substrate and growth conditions24,25. It is well known that for graphene it is possible to lower ns to about 1.2×1011 cm−2 and to improve μ up to about 100,000 cm2/V·s.24,25 Then SI of a GHE can in principle be improved up to 5000 V/AT, which is significantly larger than that of any conventional Hall elements, and a SV of up to about 7 V/VT (the maximum effective width-to-length ratio ~0.7 has been taken into account5, which limits the maximum voltage related sensitivity as SVmax~0.7 µ) which also compares favorably with the best Hall devices based on InP, InAs or even 2DEG1,2,3,4,5,6,7,8,9,10,11. The ultra-high normalized resolution (Bmin·W) of up to 4 pT·mm/Hz1/2 can also be expected in the GHE at room temperature (detailed estimating process is described in the Methods section), which points to the potential detection of an extremely weak field of picotesla.
. Normalized by the device width, the resolution of the GHE is about 100 pT·mm/Hz1/2 which is much smaller than that of most conventional Hall elements1. In principle the sensitivity and resolution of the GHE can be further improved by optimizing substrate and growth conditions24,25. It is well known that for graphene it is possible to lower ns to about 1.2×1011 cm−2 and to improve μ up to about 100,000 cm2/V·s.24,25 Then SI of a GHE can in principle be improved up to 5000 V/AT, which is significantly larger than that of any conventional Hall elements, and a SV of up to about 7 V/VT (the maximum effective width-to-length ratio ~0.7 has been taken into account5, which limits the maximum voltage related sensitivity as SVmax~0.7 µ) which also compares favorably with the best Hall devices based on InP, InAs or even 2DEG1,2,3,4,5,6,7,8,9,10,11. The ultra-high normalized resolution (Bmin·W) of up to 4 pT·mm/Hz1/2 can also be expected in the GHE at room temperature (detailed estimating process is described in the Methods section), which points to the potential detection of an extremely weak field of picotesla.
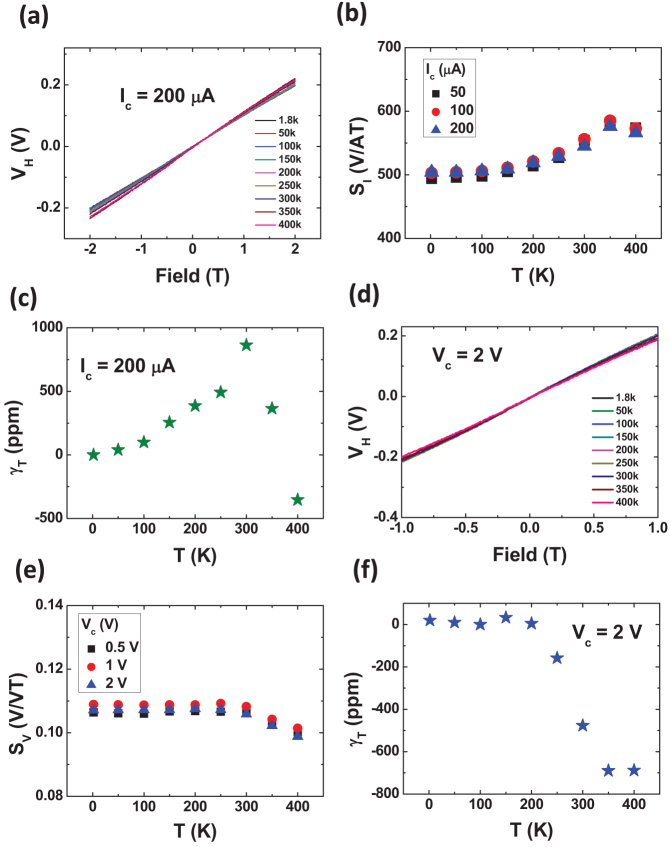
In addition to high sensitivity and linearity, excellent stability over a wide temperature range is also crucial for high performance Hall elements, and will significantly extend the application fields of Hall elements26. Figure 4a shows the output Hall voltage as a function of the magnetic field at a range of temperatures from 1.8 K to 400 K (the upper limit of our measurement instrument, see Methods section) and different bias currents. The near perfect linearity of the Hall voltage as a function of magnetic field is seen to hardly depend on temperature. The current-related sensitivity SI as a function of temperature is shown in Fig. 4b. The sensitivity is seen to increase, from 494 V/AT at 1.8 K, with increasing temperature and peak at about 580 V/AT at 350 K, and then decreases with temperature. The temperature coefficient of the sensitivity is defined as26,27,28
where S denotes either the absolute sensitivity or the current/voltage-related sensitivity. The temperature coefficient γT of the GHE operating in current mode remains below 800 ppm·K−1 over a wide temperature range from 1.8 K to 400 K (Fig. 4c). As a comparison, Hall elements made from high mobility InSb usually has a much larger temperature coefficient of −2000 ppm·K−1 at 300 K4.
Figure 4. Temperature performance of GHE.
(a) Hall voltage versus magnetic field in current mode (with a drive current of 200 μA) and over a wide temperature range from 1.8 K to 400 K. (b) The corresponding current-related sensitivities at various temperatures and (c) the related temperature coefficients. (d) Hall voltage versus magnetic field working in voltage mode (with a drive voltage of 2 V) and over a wide temperature range from 1.8 K to 400 K. (e) The corresponding voltage-related sensitivities at various temperatures and (f) the related temperature coefficients.
The output Hall voltage of the GHE is also measured as a function of the magnetic field in voltage mode at a bias of 2 V for various temperatures ranged from 1.8 K to 400 K (Fig. 4d). It is important to note that the VH-B curves at different temperature almost coincide with each other, suggesting that the behavior of the GHE is extremely stable within the ~400 K temperature range in voltage mode (Fig. 4e). The temperature coefficients of the GHE in voltage mode are found to be smaller than 700 ppm·K−1 from 1.8 K to 400 K (Fig. 4f). In particular, the temperature coefficient is as low as 30 ppm·K−1 below 200 K, which is much better than that of all published conventional Hall elements with typical temperature coefficient of around 1000 ppm·K−1 4,26,27,28. On the other hand, the offset voltage is also found to hardly change over a wide temperature range from 1.8 K to 400 K, which fluctuates between −4 mV and −5 mV (see Fig. S6 of supplementary information). The equivalent magnetic induction offset field Bo,eq (defined as Voffset/SA,) is then about −2 mT, which is much smaller than that of Si Hall elements (usually larger than 10 mT) and comparable to that of InGaAs-based Hall element (typically 2 mT)3. Since Bo,eq is inversely proportional to carrier mobility, further reduction in Bo,eq to sub milli-tesla range can be expected for GHEs.
The excellent thermal stability of GHE is originated from the intrinsic properties of graphene. It is well known that the thermal stability of a Hall element is determined by the temperature dependence of carrier density in current mode and mobility in voltage mode. For a conventional semiconductor, intrinsic carrier concentration is dependent on temperature T via an exponential law, i.e. ni~exp(AT) (A being a constant), while carrier concentration in graphene is dependent on temperature much more weakly via a power law29, i.e. ni∝T2. Therefore, in principle GHE will exhibit better thermal stability than conventional Hall element in current mode. The temperature dependent carrier density and mobility of a typical GHE are shown in Fig. 5a. At temperature range from 400 K to 1.8 K, carrier density changes about 17% from about 1.27×1012/cm2 to 1.07×1012/cm2. In contrast, carrier mobility shows hardly any change and remains as a constant value from 1.6 K to 300 K, and changes less than 7% from 2700 cm2/V·s at 300 K to 2500 cm2/V·s at 400 K. Since the carrier mobility in our GHE is below 3000 cm2/V·s, the mobility is limited mainly by the Coulomb scattering mechanisms, which is almost independent of temperature30,31,32, suggesting excellent thermal stability of GHEs in voltage mode.
Figure 5. Temperature characteristics of graphene Hall elements and comparison with commercialized Hall elements supplied by Asahi Kasei Microdevices (AKM) Corporation.
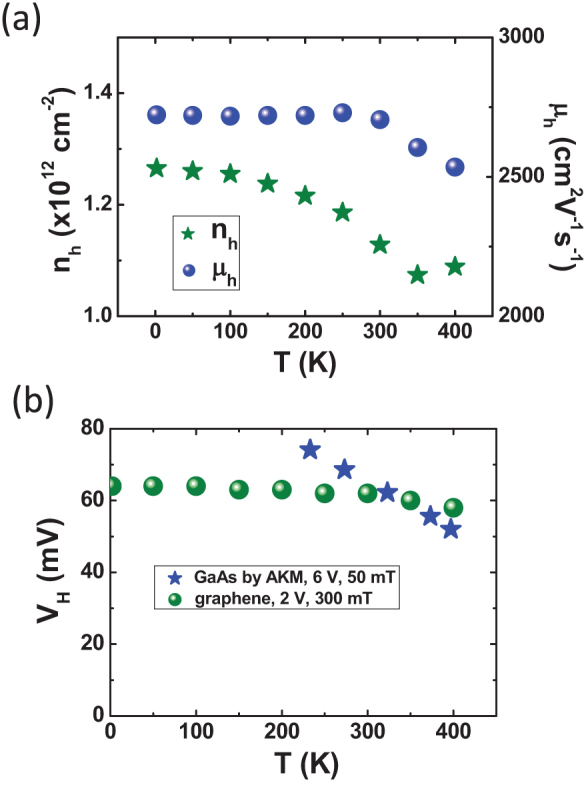
(a) Temperature dependent carrier density and Hall mobility of a typical GHE. Carrier mobility was retrieved under B = 1 T. (b) Temperature dependent Hall voltage of graphene (green spheres) and GaAs (blue stars) Hall elements in voltage mode. The voltage supplies are 2 V and 6 V, and the magnetic fields are 300 mT and 50 mT for graphene and GaAs Hall elements respectively. The specification for the commercial AKM GaAs Hall element is HG-106C-2U.
Excellent thermal stability over a wide temperature range from 1.8 K to 400 K is crucial for many applications of high performance Hall elements in such fields as aircraft, spacecraft, military, oil and gas industries1,2,3,26,28. In a conventional semiconductor, carrier density and mobility are both temperature sensitive and the thermal stability of the corresponding Hall element is generally poor26,27,28. Low thermal drift is usually realized by heavily doping the semiconductor, but doping reduces mobility and increases carrier density leading to a lowered sensitivity of the Hall device. Compromise usually has to be made between low thermal drift and high sensitivity. In contrast, in graphene both carrier density and mobility depend only weakly on temperature30,31,32. The GHE thus exhibits a much better thermal stability than that of the conventional Hall device, and this is especially so when the GHE is used in voltage mode (Fig. 5b). In principle the GHE can have low carrier density and high mobility simultaneously over a wide temperature range, which represents a significant advantage over all commercial Hall devices as shown in Fig. S7 in supplementary information.
In summary, graphene is an ideal material for building high-performance general purpose Hall elements with low cost and in large-scale. Compared with conventional Hall elements, the sensitivity of our GHE is as high as that of the bests based on 2DEG, and the sensitivity could potentially be further improved significantly by optimizing fabricating process. The combination of high sensitivity and low noise of graphene devices leads to ultra-high resolution, and in principle GHEs could be used for detecting extremely low magnetic field. The graphene Hall device also presents excellent linearity over a wide magnet field, especially in voltage mode. In addition, because in graphene both carrier density and mobility depend only weakly on temperature, GHE can operate linearly at ultra-wide temperature range at least from 1.8 K to 400 K simultaneously with high sensitivity and low thermal drift, extending the application field of GHE significantly. Last but not the least, methods for growing and transferring high quality graphene have been developed, providing possibility for large-scale fabrication of GHEs which take the full advantages of the excellent electric properties of graphene. In addition, the GHE fabrication process is low cost, compatible with that of signal-processing circuits, and may be carried out on different substrate, such as ultra-light material or flexible substrate. Graphene Hall devices are therefore general purpose high-performance magnetometers which can potentially satisfy most kinds of requirements for a wide range of applications, and potentially ideal substitutes for conventional Hall elements.
Methods
Graphene growth and transfer
Graphene was synthesized on a 50 µm thick polycrystalline Pt (with purity of 99.95%) film at 1070°C. Firstly, Pt film was heated to 1070°C under a constant flow of 300 sccm H2 in a quartz tube in 50 mins by a Lindberg/Blue furnace. Secondly, a mixture of 5 sccm CH4 and 700 sccm H2 was introduced into the quartz tube to growth graphene. The growth time was usually 15 mins, which we found is enough for graphene to fully covering the Pt metal surface. Finally, a fast cooling process was taken by simply pulling the quartz tube out till the sample was no longer in the heating region of the furnace. The synthesized graphene was transferred to the SiO2/Si substrate by the bubbling transfer method described by Gao et al.19. The thickness of the SiO2 layer is 285 nm.
Device fabrication
The patterns of metal contacts and pads of the graphene Hall element were defined by electron beam lithography (EBL) on poly methyl methacrylate (PMMA). A 5 nm Ti/45 nm Au metal stack was then deposited by electron beam evaporation (EBE), followed by a lift-off process in acetone. The graphene was tailored to rectangle geometry by EBL on PMMA followed by developing and oxygen plasma etching.
Fabrication of Gauss meter
The graphene Gauss meter is mainly composed of three parts, i.e. a magnetic-field-sensitive probe, a power supply of the probe, and a voltmeter which is used to measure the Hall voltage generated by the probe. The key component of the probe is a macro graphene Hall element fabricated by the processes described in the main text. The chip carrying the graphene Hall element was placed on a printed circuit board (PCB), with all the four metal contacts connected to the electrical wires on the PCB board by thin gold threads with a diameter of 50 µm. In addition, small amount of indium was used to soldering gold threads with metal leads where necessary. The power supply was made by two batteries in series, with a total constant voltage output of 3.0 V. The voltmeter used is Agilent 34410A Digit Millimeter.
Surface modification of APTES
The surface modification using APTES was done in two steps. First, the SiO2/Si substrate was treated to be hydrophilic in piranha solution (H2O2: H2SO4 = 1: 3) for 5 minutes at room temperature, rinsed with DI water and dried by nitrogen. Then, the substrate was transferred to the APTES solution (APTES: IPA = 1 : 100). After a reaction time of 10 minutes, the SiO2/Si substrate was taken out, rinsed with IPA and dried by nitrogen.
Estimating the resolution limit of GHE
The resolution of a Hall element can be written as 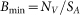 , where NV is the voltage noise spectral density at the device output, and SA is the absolute sensitivity of the Hall element10. To be simple, we will only consider thermal noise, which is usually the dominant noise spectrum at high frequencies. Then, we have
, where NV is the voltage noise spectral density at the device output, and SA is the absolute sensitivity of the Hall element10. To be simple, we will only consider thermal noise, which is usually the dominant noise spectrum at high frequencies. Then, we have 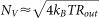 , in which kB is the Boltzmann constant, T is temperature and Rout is the output resistance of the Hall element, i.e. the resistance measured between C3 and C4 as in figure 2(b). The absolute sensitivity is estimated through
, in which kB is the Boltzmann constant, T is temperature and Rout is the output resistance of the Hall element, i.e. the resistance measured between C3 and C4 as in figure 2(b). The absolute sensitivity is estimated through 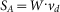 , which is a result of the balance between the Hall electric field and the Lorentz force. Here W is the width of the Hall plate and vd is the drift velocity of the charge carriers. As a result, we have
, which is a result of the balance between the Hall electric field and the Lorentz force. Here W is the width of the Hall plate and vd is the drift velocity of the charge carriers. As a result, we have 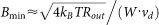 . It's clear that material with higher saturation drift velocity vsat has greater potential in building Hall elements with higher resolution. Notice that even the longitude of the Hall plate is stressed with high electric field and the velocity of the charge carriers tends to saturate, Rout may be still estimated by the diffusive model with
. It's clear that material with higher saturation drift velocity vsat has greater potential in building Hall elements with higher resolution. Notice that even the longitude of the Hall plate is stressed with high electric field and the velocity of the charge carriers tends to saturate, Rout may be still estimated by the diffusive model with  , where we suppose the effective width-to-length ratio related with Rout is typically 1. Thus resolution of GHE normalized by channel width can be given by
, where we suppose the effective width-to-length ratio related with Rout is typically 1. Thus resolution of GHE normalized by channel width can be given by 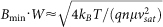 . It's very clear that both high mobility and high saturation velocity of carriers in graphene will contribute to decrease the minimum detectable magnetic field, or similarly improve the resolution. Using room temperature reference value in high-quality graphene, including μ = 5 m2/V·s, vsat = 4×105 m/s, and density = 1×1012 cm−2, we can obtain
. It's very clear that both high mobility and high saturation velocity of carriers in graphene will contribute to decrease the minimum detectable magnetic field, or similarly improve the resolution. Using room temperature reference value in high-quality graphene, including μ = 5 m2/V·s, vsat = 4×105 m/s, and density = 1×1012 cm−2, we can obtain 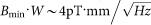 .
.
Temperature dependent Hall measurement
The device test was carried out in a modified MPMS (SQUID) VSM 7 Tesla System, with which a maximum 7-independent-port electrical signal measurement was possible. The constant voltage or current source of the graphene hall device was supplied by a lock-in amplifier Li5640 by nF cooperation, which also measures the hall voltage generated by the hall device but at different aux ports. The resolution of the hall voltage measurement is 1 mV. The back gate voltage was supplied by Keithley 2400 Source Meter. A 30 minutes in situ annealing in the vacuum chamber of the MPMS system at 400 K was carried out before any electrical measurement.
Author Contributions
Z.Z. and L.M.P. designed the experiment, H.X. and R.S. performed the growth and transfer of graphene, device fabrication and characterization. H.X. and Z.W. performed the noise measurement of GHE. H.X., Z.Z. and L.M.P. analysed the data and co-wrote the manuscript. All authors discussed the results and commented on the manuscript.
Supplementary Material
Supporting materials
Acknowledgments
This work was supported by the Ministry of Science and Technology of China (Grant Nos. 2011CB933001 and 2011CB933002), and Special Financial Grant from the China Postdoctoral Science Foundation (Grant No. 2012T50020). The authors would like to thank Prof. L. Lv and Dr. F. Yang for providing laboratory facilities for some of the electrical measurements reported in this work.
References
- Boero G., Demierre M., Besse P. A. & Popovic R. S. Micro-Hall devices: performance, technologies and applications. Sensors and Actuators A 106, 314–320 (2003). [Google Scholar]
- Ripka P. & Janosek M. Advances in Magnetic Field Sensors. IEEE Sensors Journal 10, 1108–1116 (2010). [Google Scholar]
- Popovic P. S., Flanagan J. A. & Besse P. A. The Future of magnetic Sensors. Sensor and Actuators A 56, 39–55 (1996). [Google Scholar]
- Mihajlovic G., Xiong P., von Molnar S., Ohtani K., Ohno H., Field M. & Sullivan G. J. Detection of single magnetic bead for biological applications using an InAs quantum-well micro-Hall sensor. Appl. Phys. Lett., 87, 112502 (2005). [Google Scholar]
- Popovic R. S. Hall Effect Devices, Second Edition, Institute Physics Publishing, 2004. [Google Scholar]
- Heremans J. . Solid State Magnetic Field Sensors and Applications. J. Phys. D: Appl. Phys. 26, 1149–1168 (1993). [Google Scholar]
- Hara T., Mihara M., Toyoda N. & Zama M. Highly Linear GaAs Hall Devices Fabricated by Ion Implantation. IEEE Transactions on Electron Devices ED-29, 78–82 (1982). [Google Scholar]
- Shibasaki I. Mass production of InAs Hall elements by MBE. Journal of Crystal Growth 175/176, 13–21(1997). [Google Scholar]
- Berus T., Oszwaldowski M. & Grabowski J. High quality Hall sensors made of heavily doped n-InSb epitaxial films. Sensors and Actuators A1 16, 75–78 (2004). [Google Scholar]
- Kunets V. P., Black W. T., Mazur Y. I., Guzun D., Salamo G. J., Goel N., Mishima T. D., Deen D. A., Murphy S. Q. &. Santos M. B. Highly Sensitive Micro-Hall Devices Based on Al0.12In0.88Sb/InSb Heterostructures. J. Appl. Phys. 98, 014506 (2005). [Google Scholar]
- Bando M., Ohashi T., Dede M., Akram R., Oral A., Park S. Y., Shibasaki I., Handa H. & Sandhu A. High sensitivity and multifunctional micro-Hall sensors fabricated using InAlSb/InAsSb/InAlSb heterostructures. J. Appl. Phys. 105, 073909 (2009). [Google Scholar]
- Schwierz F. Graphene Transistor. Nature Nanotechnol 5, 487–496 (2010). [DOI] [PubMed] [Google Scholar]
- Lin Y. M., Valdes-Garcia A., Han S. J., Farmer D. B., Meric I., Sun Y. N., Wu Y. Q., Dimitrakopoulos C., Grill A., Avouris P. & Jenkins, Keith A. Wafer-Scale Graphene Integrated Circuit. Science 332, 1294–1297 (2011). [DOI] [PubMed] [Google Scholar]
- Schedin F., Geim A. K., Morozov S. V., Hill E. W., Blake P., Katsnelson M. I. & Novoselov K. S. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 6, 652–655 (2007). [DOI] [PubMed] [Google Scholar]
- Mueller T., Xia F. & Avouris P. Graphene photodetectors for high-speed optical communications. Nature Photonics 4, 297–301 (2010). [Google Scholar]
- Novoselov K. S., Jiang Z., Zhang Y., Morozov S. V., Stormer H. L., Zeitler U., Maan J. C., Boebinger G. S., Kim P. & Geim A. K. Room-Temperature Quantum Hall Effect in Graphene. Science 315, 1379 (2007). [DOI] [PubMed] [Google Scholar]
- Pisana S., Braganca P. M., Marinero E. E. & Gurney B. A. Tunable Nanoscale Graphene Magnetometers. Nano Lett 10, 341–346 (2010). [DOI] [PubMed] [Google Scholar]
- Lu J. M., Zhang H. J., Shi W., Wang Z., Zheng Y., Zhang T., Wang N., Tang Z. K. & Sheng P. Graphene Magnetoresistance Device in van der Pauw Geometry. Nano Lett 11, 2973–2977 (2011). [DOI] [PubMed] [Google Scholar]
- Tang C. C., Li M. Y., Li L. J., Chi C. C. & Chen J. C. Characteristics of a sensitive micro-Hall probe fabricated on chemical vapor deposited graphene over the temperature range from liquid-helium to room temperature. Applied Physics Letters 99, 112107 (2011). [Google Scholar]
- Panchal V., Cedergren K., Yakimova R., Tzalenchuk A., Kubatkin S. & Kazakova O. Small epitaxial graphene devices for magnetosensing applications. Journal of Applied Physics 111, 07E509 (2012). [Google Scholar]
- Gao L. B., Ren W. C., Xu H. L., Jin L., Wang Z. X., Ma T., Ma L. P., Zhang Z. Y., Fu Q., Peng L. M., Bao X. H. & Cheng H. M. Repeated growth and bubbling transfer of graphene with millimetre-size single-crystal grains using platinum. Nature Comm 3, 3,699 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J., Jo S. B., Yu Y. J., Kim Y., Yang W., Lee W. H., Kim H. H., Hong B. H., Kim P., Cho K. & Kim, Kwang S. Single-Gate Bandgap Opening of Bilayer Graphene by Dual Molecular Doping. Adv. Mater. 24, 407–411 (2012). [DOI] [PubMed] [Google Scholar]
- Moon J. S., Curtis D., Zehnder D., Kim S., Gaskill D. K., Jernigan G. G., Myers-Ward R. L., Eddy C. R., Campbell P. M., Lee K.-M. & Asbeck P. Low-phase-noise Graphene FETs in Ambipolar RF applications. IEEE Electron Device Letters 32, 270–272 (2011). [Google Scholar]
- Du X., Skachko I., Barker A. & Andrei E. Y. Approaching ballistic transport in suspended graphene. Nature Nanotechnol 3, 491–495 (2008). [DOI] [PubMed] [Google Scholar]
- Dean C. R., Young A. F., Meric I., Lee C., Wang L., Sorgenfrei S., Watanabe K., Taniguchi T., Kim P., Shepard K. L. & Hone J. Boron nitride substrates for high-quality graphene electronics. Nature Nanotechnol 5, 722–726 (2010). [DOI] [PubMed] [Google Scholar]
- Jankowski J., El-Ahmar S. & Oszwaldowski M. Hall Sensors for Extreme Temperatures. Sensors 11, 876–885 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunets V. P., Dobbert J., Mazur Y. I., Salamo G. J., Muller U., Masselink W. T., Kostial H. & Wiebicke E. Low Thermal Drift in Highly Sensitive doped channel Al0.3Ga0.7As/GaAs/In0.2Ga0.8As Micro-Hall Element. Journal of Materials Science: Materials in Electronics 19, 776–782 (2008). [Google Scholar]
- Lu H., Sandvik P., Vertiatchikh A., Tucker J. & Elasser A. High temperature Hall effect sensors based on AlGaN/GaN heterojunctions. J. Appl. Phys. 99, 114510 (2006). [Google Scholar]
- Fang T., Konar A., Xing H. L. & Jena D. Carrier statistics and quantum capacitance of graphene sheets and ribbons. Applied Physics Letters 91, 092109 (2007). [Google Scholar]
- Adam S., Hwang E. H., Galitski V. M. & Das Sarma S. A Self-consistent Theory for Graphene Transport. Proc. Nat. Acad. Sci. USA 104, 18392–18397 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J.-H., Jang C., Adam S., Fuhrer M. S., Williams E. D. & Ishigami M. Charged-Impurity Scattering in Graphene. Nat. Phys. 4, 377–381 (2008). [Google Scholar]
- Zhu W. J., Perebeinos V., Freitag M. & Avouris P. Mobilities and electrostatic potential in monolayer, bilayer, and trilayer graphene. Phys. Rev. B 80, 235402 (2009). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting materials