Robust Detection and Identification of Sparse Segments in Ultra-High Dimensional Data Analysis

Summary

Copy number variants (CNVs) are alternations of DNA of a genome that results in the cell having a less or more than two copies of segments of the DNA. CNVs correspond to relatively large regions of the genome, ranging from about one kilobase to several megabases, that are deleted or duplicated. Motivated by CNV analysis based on next generation sequencing data, we consider the problem of detecting and identifying sparse short segments hidden in a long linear sequence of data with an unspecified noise distribution. We propose a computationally efficient method that provides a robust and near-optimal solution for segment identification over a wide range of noise distributions. We theoretically quantify the conditions for detecting the segment signals and show that the method near-optimally estimates the signal segments whenever it is possible to detect their existence. Simulation studies are carried out to demonstrate the efficiency of the method under different noise distributions. We present results from a CNV analysis of a HapMap Yoruban sample to further illustrate the theory and the methods.

1. INTRODUCTION

Structural variants in the human genome (Sebat et al., 2004; Feuk et al., 2006), including copy number variants (CNVs) and balanced rearrangements such as inversions and translocations, play an important role in the genetics of complex disease. CNVs are alternations of DNA of a genome that results in the cell having a less or more than two copies of segments of the DNA. CNVs correspond to relatively large regions of the genome, ranging from about one kilobase to several megabases, that are deleted or duplicated. Analysis of CNVs in developmental and neuropsychiatric disorders (Feuk et al., 2006; Walsh et al., 2008; Stefansson et al., 2008; Stone et al., 2008) and in cancer (Diskin et al., 2009) has led to the identification of novel disease-causing mutations, thus contributing important new insights into the genetics of these complex diseases. Changes in DNA copy number have also been highly implicated in tumor genomes; most are due to somatic mutations that occur during the clonal development of the tumor. The copy number changes in tumor genomes are often referred to as copy number aberrations (CNAs). In this paper, we focus on the CNVs from the germline constitutional genome where most of the CNVs are sparse and short (Zhang et al., 2009).

CNVs can be discovered by cytogenetic techniques, array comparative genomic hybridization (Urban et al., 2006) and by single nucleotide polymorphism (SNP) arrays (Redon et al., 2006). The emerging technologies of DNA sequencing have further enabled the identification of CNVs by next-generation sequencing (NGS) in high resolution. NGS can generate millions of short sequence reads along the whole human genome. When these short reads are mapped to the reference genome, both distances of paired-end data and read-depth (RD) data can reveal the possible structure variations of the target genome (for reviews, see Medvedev et al. (2009) and Alkan et al. (2011)). The mapping distances between pair-ends of reads provide better power to detect small- to medium size insertions/deletions (indels) or CNVs (Medvedev et al., 2009; Alkan et al., 2011). In this approach, two paired reads are generated at an approximately known distance in the donor genome and pairs mapping at a distance that is substantially different from the expected length, or with anomalous orientation, suggest structural variants. Methods based on the mapping distances often involve finding the clusters of reads that show anomalous mapping (Chen et al., 2009). Instead of mapping the short reads onto the reference genome, one can also perform whole genome de novo assembly and align the de novo assemblies of two genomes in order to identify gaps and segmental rearrangements in pair-wise alignments (Li et al., 2011). However, this approach requires data from two genomes.

Another important source of information useful for inferring CNVs from reads alignment is the read depth. The RD data are generated to count the number of reads that cover a genomic location or a small bin along the genome which provide important information about the CNVs that a given individual carries (Shendure and Ji, 2008; Medvedev et al., 2009). When the genomic location or bin is within a deletion, one expects to observe a smaller number of read counts or lower mapping density than the background read depth. In contrast, when the genomic location or bin is within an insertion or duplication, one expects to observe a larger number of read counts or higher mapping density. Therefore, these RDs can be used to detect and identify the CNVs. The read-depth data provide more reliable information for large CNVs and CNVs flanked by repeats, where accurate mapping reads is difficult. The read depth data also provide information on CNVs based on the targeted sequences where only targeted regions of the genome are sequenced (Nord et al., 2011).

In this paper, we consider the problem of CNV detection and identification based on the read depth data from the next generation sequencing. Several methods have been developed for such read depth data. Yoon et al. (2009) developed an algorithm for read depth data to detect CNVs, where they convert the read count of a window into a Z-score by subtracting the mean of all windows and dividing by the standard deviation and identify the CNVs by computing upper-tail and lower-tail probabilities by using a normality assumption on the RD data. The windows are then selected based on the extreme values of these probabilities controlling for the genome-wide false-positive rates. Abyzov et al. (2011) developed an approach to first partition the genome into a set of regions with different underlying copy numbers using mean-shift technique and then merge signal and call CNVs by performing t-tests. Xie and Tammi (2009), Chiang et al. (2009) and Kim et al. (2010) developed methods for CNV detection based on read depth data when pairs of samples are available. The basic idea underlying these two methods is to convert the counts data into ratios and then apply existing copy number analysis methods developed for array CGH data such as the circular binary segmentation (CBS) (Olshen et al., 2004) for CNV detection. Methods have also been developed for CNV detections in cancer cells (Ivakhno et al., 2010; Miller et al., 2011) based on the RD data.

One common feature of these existing methods is to make a certain parametric distribution assumption on the RD data. However, the distribution of the RD data is in general unknown due to the complex process of sequencing. Some recent literature assumes a constant read sampling rate across the genome and Poisson distribution or negative-binomial distribution for the read counts data (Xie and Tammi, 2009; Cheung et al., 2011). However, due to GC content, mappability of sequencing reads and regional biases, genomic sequences obtained through high throughput sequencing are not uniformly distributed across the genome and therefore the counts data are likely not to follow a Poisson distribution (Li et al., 2010; Miller et al., 2011; Cheung et al., 2011). The feature of the NGS data also changes with the advances of sequencing technologies. To analyze such data, classical parametric methods do not work well. It is crucial for these methods to specify the distribution of their test statistics, which depends on the data distribution. Misspecified data distribution can lead to a complete failure of these methods. Although some data distributions can be estimated by nonparametric methods, popular nonparametric methods such as permutation are often computationally expensive and not feasible for ultra-high dimensional data. Therefore, robust methods that are adaptive to unknown data distributions and computationally efficient at the same time are greatly needed. The goal of the present paper is to develop such a robust procedure for CNV identification based on NGS data and to study its properties.

In this paper, we assume that a long linear sequence of noisy data {Y₁, …, Y_n} is modeled as

$$Y_i={\alpha }_i+{\xi }_i,{\alpha }_i=\{\begin{array}{cc}{\mu }_j,\hfill & i\in I_j\text{for some}j\in \{1,\dots q\},\hfill \\ \hfill & 0,\text{otherwise}\hfill \end{array}\phantom{\}}1\le i\le n,$$ (1)

where q = q_n is the number of signal segments, possibly increasing with n, I₁, … I_q are disjoint intervals representing signal segments, μ₁,… μ_q are unknown constants, and ξ₁, …, ξ_n are i.i.d. random errors with median 0. Here positive μ_i implies duplication or insertion and negative mean implies deletion. Let $\mathbb{I}=\{I_1,\dots I_q\}$ denote the set of all segment intervals. For the problem of CNV detection based on the NGS data, Y_i is the guanine-cytosine (GC) content-adjusted RD counts at genomic location or bin i, which can be regarded as continuous when coverage of the genome is sufficiently high, for example greater than 20 (Yoon et al., 2009; Abyzov et al., 2011). This model describes the phenomenon that some signal segments are hidden in the n noisy observations. The number, locations, mean values of the segments, and the distribution of the random errors are unknown.

The problem of segment detection and identification can be separated into two steps. The first step is to detect the existence of such signal segments, i.e. to test

$$H_0:\mathbb{I}=\varnothing \text{against}{H}_1:\mathbb{I}\ne \varnothing ,$$

and the second step is to identify the locations of the segments if there are any. A procedure called the likelihood ratio selection (LRS) (Jeng et al., 2010) has recently been developed to treat the above problem in the case of Gaussian noise. Under the Gaussian and certain sparsity assumptions, the LRS has been shown to be optimal in the sense that it can separate the signal segments from noise whenever the segments are identifiable. However, when the noise distribution is heavy-tailed, the LRS may fail and provide a large number of misidentifications. To tackle this difficulty, in the present paper we introduce a computationally efficient method called robust segment identifier (RSI), which provides a robust and near-optimal solution for segment identification over a wide range of noise distributions. As an illustration, we generate 1000 observations based on Cauchy (0, 1), and set the signal segment at [457 : 556] with a positive mean. Figure 1 compares the LRS with the RSI. In this example, the LRS fails to work at all by identifying too many false segments, while the RSI, on the other hand, provides a good estimate of the signal segment even when the noise distribution is unknown and heavy-tailed.

Fig. 1.

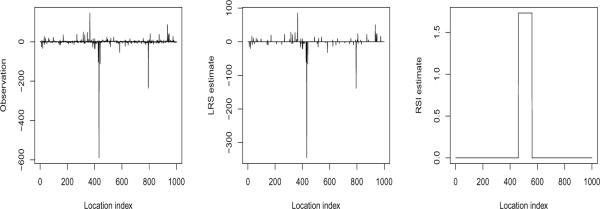
Effects of long-tailed error distribution on segment identification. Left plot: Data with Cauchy noise and a signal segment at [457 : 556]. Middle plot: Intervals identified and estimated interval means by LRS. Right plot: Interval identified and estimated means by RSI.

A key step of the RSI is a local median transformation, where the original observations are first divided into T small bins with m observations in each bin and then the median values of the data in these bins are taken as a new data set. The central idea is that the new data set can be well approximated by Gaussian random variables for a wide collection of error distributions. After the local median transformation, existing detection and identification methods that are designed for Gaussian noise can then be applied to the new data set. Brown et al. (2008) and Cai and Zhou (2009) used local medians to turn the problem of nonparametric regression with unknown noise distribution into a standard Gaussian regression. Here we use the local median transformation for signal detection and identification that is robust over a large collection of error distributions, including those that are heavy-tailed. Local median transformations or other local smoothing procedures have been applied in analysis of microarray data for data normalization (Quackenbush, 2002).

To elucidate the effect of data transformation in the simplest and cleanest way, we begin by considering the detection part of our problem, which is to test H₀ against H₁. We propose a robust segment detector (RSD), which applies the generalized likelihood ratio test (GLRT) to the transformed data. Arias-Castro et al. (2005) shows that the GLRT is an optimal procedure for detecting a single segment with constant length in the Gaussian noise setting. We find here that the RSD is an near-optimal procedure for the transformed data when the bin size m is properly chosen. The key condition for the RSD to be successful is that some segment I_j has its mean and length roughly satisfying ${\mu }_j\sqrt{\mid I_j\mid }>\sqrt{\text{log}n}∕\left(\sqrt{2}h\left(0\right)\right)$ and the noise density satisfies the Lipschitz condition, where h(0) is the noise density at 0. Clearly, a larger value of h(0), which corresponds to a more concentrated noise distribution, results in a more relaxed condition. This result agrees with our intuition that detection of signal segments should be easier if the noise distribution is more concentrated.

The RSD can detect the existence of signal segments with unknown noise distribution. However, it does not tell where the signal segments are. For segment identification, we propose a procedure called robust segment identifier (RSI), which first transforms the data by binning and taking local medians, then applies the LRS procedure on the transformed data. Unlike the RSD, which searches through all possible intervals after the data transformation, the RSI utilizes the short segment structure and considers only short intervals with length less than or equal to L, where L is some number much smaller than T. Furthermore, the data transformation step significantly reduces the dimension from n to T. These together make the RSI a computationally efficient method to handle ultra-high dimensional data. It is shown that the RSI provides robust identification results for a large collection of noise distributions, and it is a near-optimal procedure for the transformed data when m and L are properly chosen.

The rest of the paper is organized as follows. Section 2 introduces the data transformation technique and the robust segment detector (RSD). The robust segment identification procedure RSI is proposed and its theoretical properties are studied in Section 3. Numerical performance of RSI is investigated in Section 4 using simulations and is compared with the performances of LRS and CBS. We then present results in Section 5 from an analysis of sequence data of one individual from the 1000 Genomes Project (http://www.1000genomes.org/). We conclude with a discussion in Section 6. The proofs are detailed in the Appendix.

2. Data Transformation and Robust Detection

In this section, we first introduce the local median transformation to tackle the problem of unknown and possibly heavy-tailed noise distribution. After the transformation the data can be well approximated by Gaussian random variables. A robust segment detection procedure is then developed to reliably separate H₀ from H₁ over a wide range of noise distributions.

2.1. Local median transformation

Let Y₁, … Y_n be a sequence of observed data generated from Model (1) with an unknown noise distribution. We assume there are q sparse and short signal segments in the observed data and the number of observations n is very large. The goal is to detect and identify these q segments. In order to do so, we first equally divide the n observations into T = T_n groups with m = m_n observations in each group. De ne the set of indices in the k-th group as J_k = {i : (k − 1)m + 1 ≤ i ≤ km}, and generate the transformed dataset as

$$X_k=\text{median}\{Y_i:i\in J_k\},1\le k\le T.$$ (2)

Set

$${\eta }_k=\text{median}\{{\xi }_i:i\in J_k\},1\le k\le T,$$ (3)

then the medians X_k can be written as

$$X_k={\theta }_k+{\eta }_k,1\le k\le T,$$ (4)

where

$${\theta }_k=\{\begin{array}{cc}{\mu }_j,\hfill & J_k\subseteq i_j\text{for some}{I}_j,\hfill \\ {\mu }_k^{\ast }\in [0,{\mu }_j],\hfill & J_k\cap I_j\ne \varnothing \text{for some}{I}_j\text{and}{J}_k⊈I_j,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

After the local median transformation, the errors ξ_i in the original observations are re-represented by η_k. The main idea is that η_k can be well approximated by Gaussian random variable for a wide range of noise distributions. Specifically, we assume that the distribution of ξ_i is symmetric about 0 with the density function h satisfying h(0) > 0 and

$$\mid h\left(y\right)-h\left(0\right)\mid \le C_{y^2}$$ (5)

in an open neighborhood of 0. This assumption is satisfied, for example, by the Cauchy distribution, the Laplace distribution, the t distributions, as well as the Gaussian distribution. A similar assumption is introduced in Cai and Zhou (2009) in the context of nonparametric function estimation. The distributions of η_k are approximately normal. This can be precisely stated in the following lemma.

Lemma 2.1. Assume (1), (5), and transformation (4), then η_k can be written as

$${\eta }_k=\frac{1}{2h\left(0\right)\sqrt{m}}{Z}_k+\frac{1}{\sqrt{m}}{\zeta }_k,$$ (6)

where $Z_k\stackrel{iid}{~}N(0,1)$ and ζ_k are independent and stochastically small random variables satisfying Eζ_k = 0, and can be written as

$${\zeta }_k={\zeta }_{k1}+{\zeta }_{k2}$$

with

$$E{\zeta }_{k1}=0\mathit{and}E\mid {\zeta }_{k1}{\mid }^l\le C_l{m}^{-l},$$ (7)

$$P({\zeta }_{k2}=0)\ge 1-C\text{exp}(-am)$$ (8)

for some a > 0 and C > 0, and all l > 0.

The proof of this lemma is similar to that of Proposition 1 in Brown et al. (2008) and that of Proposition 2 in Cai and Zhou (2009), and is thus omitted. The key fact is that η_k can be well approximated by $Z_k∕\left(2h\left(0\right)\sqrt{m}\right)$, which follows N(0, 1/(4h²(0)m)), so that after the data transformation in (4), existing methods for Gaussian noise can be applied to X_k, 1 ≤ k ≤ T. It will be shown that by properly choosing the bin size m, a robust procedure can be constructed to reliably detect the signal segments. We note that the noise variance for the transformed data, 1/(4h²(0)m), can be easily estimated and the estimation error does not affect the theoretical results. So we shall assume h(0) to be known in the next section. Estimation of h(0) is discussed in Section 3.

2.2. Robust segment detection

Our first goal is signal detection, i.e., we wish to test $H_0:\mathbb{I}=\varnothing$ against $H_1:\mathbb{I}=\varnothing$. When the noise distribution is Gaussian, the GLRT, which applies a thresholding procedure on the extreme value of the likelihood ratio statistics of all possible intervals, has been proved to be an optimal procedure in Arias-Castro et al. (2005). However, the threshold used by the GLRT may perform poorly on non-Gaussian data. We propose the RSD, which applies a similar procedure to the transformed data, and we show that the RSD provides robust results over a wide range of noise distributions satisfying (5). For simplicity of presentation, we assume that μ_i > 0, for i = 1, …, q. When both positive and negative signal segments exist, a simple modification is to replace the relevant quantities with their absolute values.

The RSD procedure can be described as follows. After the local median transformation, define for any interval $\tilde{I}$

$$X\left(\tilde{I}\right)=\sum _{k\in \tilde{I}}{X}_k∕\sqrt{\mid \tilde{I}\mid ,}$$ (9)

and threshold

$${\lambda }_n=\sqrt{2\text{log}n}∕\left(2h\left(0\right)\sqrt{m}\right).$$ (10)

The RSD rejects H₀ when ${\text{max}}_{\tilde{I}\in {\mathbb{J}}_T}X\left(\tilde{I}\right)>{\lambda }_n$, where ${\mathbb{J}}_T$ is the collection of all possible intervals in {1, …, T}.

Note that the threshold λ_n is chosen by analyzing the distribution of $X\left(\tilde{I}\right)$ under the null hypothesis H₀. By (6), we have

$$X\left(\tilde{I}\right)=\frac{Z\left(\tilde{I}\right)}{2h\left(0\right)\sqrt{m}}+\frac{\zeta \left(\tilde{I}\right)}{\sqrt{m}}\text{under}{H}_0,$$ (11)

were

$$Z\left(\tilde{I}\right)=\sum _{k\in \tilde{I}}{Z}_k∕\sqrt{\mid \tilde{I}\mid }\text{and}\zeta \left(\tilde{I}\right)=\sum _{k\in \tilde{I}}{\zeta }_k∕\sqrt{\mid \tilde{I}\mid }.$$

Since ζk are stochastically small random variables according to Lemma 2.1, ${\text{max}}_{\tilde{I}\in {\mathbb{J}}_T}\zeta \left(\tilde{I}\right)$ should be much smaller than ${\text{max}}_{\tilde{I}\in {\mathbb{J}}_T}Z\left(\tilde{I}\right)$ for large m. The following lemma provides the asymptotic bounds for both ${\text{max}}_{\tilde{I}\in {\mathbb{J}}_T}\zeta \left(\tilde{I}\right)$ and ${\text{max}}_{\tilde{I}\in {\mathbb{J}}_T}Z\left(\tilde{I}\right)$.

Lemma 2.2. Assume (1), (5), and transformation (4) with m = log^1+b n for some b > 0. For the collection ${\mathbb{J}}_T$ of all the possible intervals in {1, …, T}, we have

$$P\left(\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}\zeta \left(\tilde{I}\right)>a\sqrt{\text{log}T}∕m\right)\le \frac{C}{\sqrt{\text{log}T}}{T}^{-C},$$ (12)

for some a > 4 and C > and

$$P\left(\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}Z\left(\tilde{I}\right)>\sqrt{\text{2 log}T}\right)\le \frac{C}{\sqrt{\text{log}T}}.$$ (13)

Lemma 2.2 and (11) imply that the threshold on ${\text{max}}_{\tilde{I}\in {\mathbb{J}}_T}X\left(\tilde{I}\right)$ should be approximately that of ${\text{max}}_{\tilde{I}\in {\mathbb{J}}_T}Z\left(\tilde{I}\right)∕2h\left(0\right)\sqrt{m}$, Which is log $\sqrt{2\text{log}T}∕\left(2h\left(0\right)\sqrt{m}\right)$ We set the threshold slightly more conservatively. The following theorem shows the control of family-wise type I error.

Theorem 2.1. Assume (1), (5), and transformation (4) with m = log^1+b n for some b > 0. For the collection ${\mathbb{J}}_T$ of all the possible intervals in {1, …, T},

$$P_{H_0}(\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}X\left(\tilde{I}\right)>{\lambda }_n)\le \frac{C}{\sqrt{\text{lot}T}}\to 0,T\to \infty .$$

Note that the above bound $C∕\sqrt{\text{log}T}$ converges to 0 quite slowly. To better control the family-wise type I error, we can increase λ_n a little to $\sqrt{2(1+{∊}_n)\text{log}n}∕\left(2h\left(0\right)\sqrt{m}\right)$ for some ε_n = o(1). This small increase does not change the theoretical results in this paper.

When there exist segmental signals that are strong enough, the RSD with threshold λ_n can successfully detect their existence while controlling the family-wise type I error. This is shown in the following theorem.

Theorem 2.2. Assume (1), (5), and transformation (4) with m = log^1+b n for some b > 0. If there exists some segment $I_j\in \mathbb{I}$ that satisfies

$$\mid I_j\mid ∕m\to \infty .$$ (14)

and

$${\mu }_j\sqrt{\mid I_j\mid }\ge \sqrt{2(1+∊)\text{log}n}∕\left(2h\left(0\right)\right)$$ (15)

for some ε > 0, then RSD has the sum of the probabilities of type I and type II errors going to 0.

Condition (14) guarantees that the difference between |I_j|/m and the cardinality of {J_k : J_k ⊆ I_j} is negligible. Condition (15) shows the requirement for the signal strength of some segment I_j, which is a combined effect of μ_j and |I_j|. Note that this condition is easier to satisfy for a bigger h(0), which corresponds to a more concentrated noise distribution. This agrees with our intuition that the detection of signal segments should be easier if the observation noises are more concentrated.

Next we characterize the situation when RSD cannot have asymptotically vanishing type I and type II errors. In fact, in this situation, no testing procedure works.

Theorem 2.3. Assume (1), (5), and transformation (4) with m = log^1+b n for some b > 0. If $\text{log}\mid \mathbb{I}\mid =o\left(\text{log}n\right)$, and for all segments I_j ∈ $I_j\in \mathbb{I}$,

$$\log \mid I_j\mid =o\left(\log n\right),$$ (16)

$${\mu }_j\sqrt{\mid I_j\mid }\le \sqrt{2(1-∊)\log n}∕\left(2h\left(0\right)\right)$$ (17)

for some ε > 0, then no testing procedure constructed on the transformed data X₁, …, X_T has the sum of the probabilities of type I and type II errors going to 0.

The results in Theorem 2.2 and 2.3 imply that RSD is an near-optimal procedure to detect short signal segments based on X₁, …, X_T. It can successfully separate H₀ and H₁ based on the transformed data whenever there exists some testing procedure that is able to do so.

The RSD is robust over a wide range of noise distributions when assumption (5) is satisfied. On the other hand, in the special case when the Gaussian assumption does hold for the noise distribution, the GLRT procedure specifically designed for this case is more efficient. The GLRT rejects H₀ if ${\text{max}}_{\tilde{I}\in {\mathbb{J}}_n}Y\left(\tilde{I}\right)>\sqrt{2\text{log}n}$, where ${\mathbb{J}}_n$ is the collection of all possible intervals in {1, …, n} and $Y\left(\tilde{I}\right)={\Sigma }_{i\in \tilde{I}}{Y}_i∕\sqrt{\mid \tilde{I}\mid }$ We have the following proposition.

Proposition 2.1. Assume (1) and ξ_i ~ N(0, 1). If there exists some segment $I_j\in \mathbb{I}$ that satisfies

$${\mu }_j\sqrt{\mid I_j\mid }\ge \sqrt{2(1+∊)\log n}$$ (18)

for all ε > 0, then the GLRT built on the original Y_i has the sum of the probabilities of type I and type II errors going to 0. On the other hand, if log q = o(log n), and for all segments $I_j\in \mathbb{I}$,

$$\log \mid I_j\mid =o\left(\log n\right),$$ (19)

$${\mu }_j\sqrt{\mid I_j\mid }\le \sqrt{2(1-∊)\log n,}$$ (20)

for some ε > 0, then no testing procedure has the sum of the probabilities of type I and type II errors going to 0.

This proposition generalizes Theorems 2.1 and 2.2 in Arias-Castro et al. (2005). By comparing Proposition 2.1 with Theorem 2.2 and 2.3, we can see the exact power loss due to the local median transformation if noise distribution is known to be Gaussian. Note that when ξ_i ~ N(0, 1), condition (5) is satisfied with $h\left(0\right)=1∕\sqrt{2\pi }\approx 0.4$. If we use the transformed data, the detection bound of ${\mu }_j\sqrt{I_j}$ is $\sqrt{2\text{log}n}∕\left(2h\left(0\right)\right)\approx 1.25\times \sqrt{2\text{log}n}$, where $\sqrt{2\text{log}n}$ is the corresponding bound for the original data. Therefore, the power loss is due to the stronger condition on ${\mu }_j\sqrt{I_j}$. However, a significant advantage of the RSD is that it automatically adapts to a wide range of unknown noise distributions, while the GLRT procedure specifically designed for the Gaussian case may fail completely if the noise distribution is heavy-tailed.

3. Robust Segment Identification

In this section we turn to segment identification, which is to locate each $I_j\in \mathbb{I}$ when the alternative hypothesis is true. Recall the model $y_i={\alpha }_i+{\xi }_i$, where ${\alpha }_i={\mu }_j{1}_{\{i\in I_j\}}$ for some $I_j\in \mathbb{I}$. In this section, we define $\underset{¯}{s}={\text{min}}_{I_j\in \mathbb{I}}\mid I_j\mid ,\stackrel{‒}{s}={\text{max}}_{I_j\in \mathbb{I}}\mid I_j\mid$, and $\underset{¯}{d}={\text{min}}_{I_j\in \mathbb{I}}\left\{\text{distance between}{I}_j\text{and}{I}_{j+1}\right\}$, and assume

$$\underset{¯}{s}\ge {\log }^{2}n\mathrm{and}\log \overline{s}=o\left(\log n\right),$$ (21)

which means that the lengths of the signal segments are neither too long nor too short. Examples of such segments include these that have $\mid I_j\mid ={\text{log}}^{a}n,a\ge 2$. Further, assume

$$\log q=o\left(\log n\right),$$ (22)

which implies that the number of signal segments are less than n^b for any b > 0.

To identify each $I_j\in \mathbb{I}$, a computationally efficient method, called the robust segment identifier (RSI), is proposed. RSI first transforms data by (4) and then applies a similar procedure as the LRS to the transformed data. The selected intervals have their statistics X(Î) defined in (9) pass certain thresholds and achieve local maximums. The RSI is computationally efficient even for ultra-high dimensional data. The transformation step significantly reduces the dimension by a factor of m. Further, the second step utilizes the short-segment structure and only considers intervals with length ≤ L/m, where L is some number much smaller than n.

The ideal threshold for RSI should be the same as that of RSD, which is λ_n defined in (10). However, h(0) is usually unknown in practice and needs to be estimated. By Lemma 2.1, $1∕\left(2h\left(0\right)\sqrt{m}\right)$ is approximately the standard deviation σ of the transformed noise η_k, which can be estimated accurately when signals are sparse. One such robust estimator is the median absolute deviation (MAD) estimator:

$$\widehat{\sigma }=\frac{\mathrm{median}\mid X_k-\mathrm{median}\left(X_k\right)\mid }{0.6745}.$$ (23)

Therefore, we can set the data-driven threshold for the RSI at

$${\lambda }_n^{\ast }=\widehat{\sigma }\sqrt{2\log n}.$$ (24)

The algorithm of RSI for a fixed L, can be stated as follows.

Step 1: Transform data by (4). Let ${\mathbb{J}}_T\left(L\right)$ be the collection of all possible subintervals in {1, . . . ,T} with interval length ≤ L/m.

Step 2: Let j = 1. Define ${\mathbb{I}}^{\left(j\right)}=\{\tilde{I}\in {\mathbb{J}}_T\left(L\right):X\left(\tilde{I}\right)>{\lambda }_n^{\ast }\}$, where X(Ĩ) and ${\lambda }_n^{\ast }$ are defined as in (9) and (24).

Step 3: Let $I_j^{\ast }={\text{arg max}}_{\tilde{I}\in \mathbb{I}\left(j\right)}X\left(\tilde{I}\right)$ and update ${\mathbb{I}}^{(j+1)}={\mathbb{I}}^{\left(j\right)}\backslash \{\tilde{I}\in {\mathbb{I}}^{\left(j\right)}:\tilde{I}\cap I_j^{\ast }\ne \varnothing \}$.

Step 4: Repeat Step 3–4 with j = j + 1 until ${\mathbb{I}}^{\left(j\right)}$ is empty.

Step 5: For each $I_j^{\ast }$ generated above, let $l_j=(\text{first element in}{I}_j^{\ast }-1)\times m+1$ and $r_j=\text{last element in}{I}_j^{\ast }\times m$, and denote ${\widehat{I}}_j=\{l_j,\dots ,r_j\}$.

Denote the collection of selected intervals as $\widehat{\mathbb{I}}=\{{\widehat{I}}_1,{\widehat{I}}_2,\dots \}$. If $\widehat{\mathbb{I}}\ne \varnothing$, we reject the null hypothesis and identify the signal segments by all the elements in $\widehat{\mathbb{I}}$. Note that the above RSI procedure is designed for positive signal segments (μ_j > 0). When both positive and negative signal segments exist, a simple modification is to replace the X(Ĩ) in step 2 and 3 with |X(Ĩ)|.

We now show that with m and L chosen properly, the RSI consistently estimates the segmental signals if they are strong enough. Define the dissimilarity between any pair of $\widehat{I}\in \widehat{\mathbb{I}}$ and $I\in \mathbb{I}$ as

$$D(\widehat{I},I)=1-\mid \widehat{I}\cap I\mid ∕\sqrt{\mid \widehat{I}\mid \mid I\mid }.$$ (25)

It is clear that $0\le D(\widehat{I},I)\le 1$ with $D(\widehat{I},I)=1$ indicating disjointness and $D(\widehat{I},I)=0$ indicating complete identity. The following theorem presents estimation consistency of the RSI for $\mathbb{I}$.

Theorem 3.1. Assume (1), (5), and transformation (4) with m = log^1+bn for 0 < b < 1. Suppose that $\widehat{\sigma }$ is an $n^{\gamma }$-consistent estimator of the standard deviation of η_k for some γ > 0, and L satisfies

$$\overline{s}\le L<\underset{¯}{d},\mathrm{and}\log L=o\left(\log n\right).$$ (26)

If (15) is stasfied for all $I_j\in \mathbb{I}$, then the RSI is consistent for $\mathbb{I}$ in the sense that

$$P_{H_0}(\mid \widehat{\mathbb{I}}\mid >0)+P_{H_1}(\underset{I_j\in \mathbb{I}}{\max }\underset{{\widehat{I}}_j\in \widehat{\mathbb{I}}}{\min }D({\widehat{I}}_j,I_j)>{\delta }_n)\to 0$$ (27)

for some δ_n = o(1).

The asymptotic result (27) essentially says that both the probability of having at least one false positive and the probability of some signal segments not being matched well by any of the selected intervals are asymptotically small. Condition (26) provides some insights on the selection of L. The range $[\stackrel{‒}{s},\underset{¯}{d})$ is very large when signal segments are relatively short and rare as in the applications we are interested. The second part log L = o(log T) is satisfied, if, for instance, L = log^a T for a ≥ 0. More discussions and some sensitivity study on L for the original LRS procedure in the Gaussian case can be found in Jeng et al. (2010).

Recall Theorem 2.3, which shows that when signals are very sparse, no testing procedure based on the transformed data can separate H₀ and H₁ if, for all $I_j\in \mathbb{I}$, ${\mu }_j\sqrt{\mid I_j\mid }\le \sqrt{2(1-∊)\text{log}n}∕\left(2h\left(0\right)\right)$. This implies that the RSI is an near-optimal identification procedure for the transformed data when m and L are properly chosen. In other words, the RSI consistently estimates the signal segments whenever it is possible to detect their existence based on the transformed data.

4. Simulation Studies

We evaluate the finite-sample behavior of the RSI through simulation studies and compare its performance with the performances of LRS and another popular procedure, circular binary segmentation (CBS) (Olshen et al., 2004).

4.1. Performance of RSI under different noise distributions

We generate ξ_i from a set of t-distributions with degrees of freedom 1, 3, and 30, where t(1) is the standard Cauchy distribution, which has heavy tails. As the degree of freedom increases, the tails get thinner, and the t-distribution approaches to the standard normal. Nevertheless, the t-distributions satisfy the general assumption in (5). We set the sample size at n = 5 × 10⁴, the number of segments at $\mid \mathbb{I}\mid =3$, the lengths of the segments at |I₁| = 100, |I₂| = 40 and |I₃| = 20, respectively, and the signal mean for all segments at μ = 1.0, 1.5, and 2.0, respectively. We randomly select three locations for the segments and generate the data from

$$Y_i=\alpha +{\xi }_i,$$

i = 1, …, n, where α = μ if i is in some signal segment, and α = 0 otherwise.

We apply the RSI on Y_i with m = 20, L = 120, and ${\lambda }_n=\widehat{\sigma }\sqrt{2\text{log}T}$, where $\widehat{\sigma }$ is calculated as in (23). Figure 2 shows the histograms of the original data Y_i ∈ [−60, 60] with t(1) noise and μ = 1, and that of the transformed data X_k. Clearly, even though the original distribution is far from being Gaussian, the transformed data is close to be normally distributed. In this case, m = 20 is large enough to stabilize the noise. More discussions on the choice of m are given in Section 4.3.

Fig. 2.

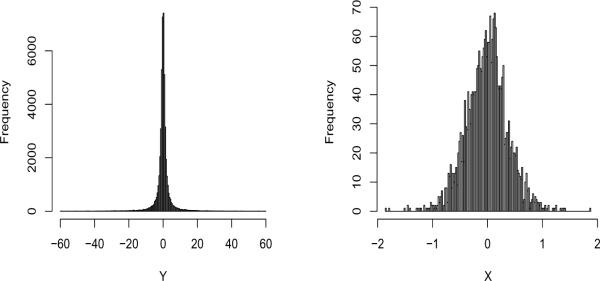
Simulated data. Left: histogram of the original data Y_i with t(1) noise and μ = 1. Right: histogram of the transformed data X_k.

As used in Jeng et al. (2010), the identification accuracy of RSI is measured by two quantities, D_j and #O, where D_j measures how well the signal segment I_j is estimated, and #O counts the number of over-selections. In detail, for each signal segment I_j, define

$$D_j=\underset{\widehat{I}\in \widehat{\mathbb{I}}}{\min }D(\widehat{I},I_j),$$

where $D(\widehat{I},I_j)$ is defined in (25). Obviously, smaller D_j represents better matching between I_l and some estimate $\widehat{I}\in \widehat{\mathbb{I}}$, and D_j = 0 iff $I_j=\widehat{\mathbb{I}}$. Define

$$\#O=\#\{\widehat{I}\in \widehat{\mathbb{I}}:\widehat{I}\cap I_j=\varnothing ,{\forall }_j=1,\dots ,q\}.$$

So #O is a non-negative integer, and #O = 0 if there are no over-selected intervals. Note that according to Theorem 3.1, ${\mu }_j\sqrt{\mid I_j\mid }$ should be at least $\sqrt{\text{log}n}∕\left(\sqrt{2}h\left(0\right)\right)\approx 7.307$ for segment I_j to be consistently estimated by RSI in this example.

We repeat the simulations 50 times to calculate D_j and #O. The medians of D₁, …, D_q, and #O are reported in Table 1 with estimated standard errors. To estimate the standard errors of the medians, we generate 500 bootstrap samples out of the 50 replication results, then calculate a median for each bootstrap sample. The estimated standard error is the standard deviation of the 500 bootstrap medians. Table 1 shows that the RSI provides quite accurate estimation for any of the signal segments when μ is large enough. In all the cases, the over-selection error is controlled very well. It also shows that larger μ is needed for shorter segments, which agrees with our theoretical results. More importantly, the results are very stable over different noise distributions.

Table 1.

Simulation results: medians of Dj and #O for RSI with m = 20 and L = 6. In Tables 1–3, the estimated standard errors based on the bootstrap appear in parentheses.

		D 1(|I1|=100)	D 2(|I2|=40)	D 3(|I3|=20)	#O
t(1)	μ = 1.0	0.080(0.015)	1.000(0.026)	1.000(0.000)	2.000(0.330)
	μ = 1.5	0.087(0.003)	0.184(0.017)	1.00(0.000)	2.000(0.260)
	μ = 2.0	0.087(0.009)	0.150(0.020)	0.423(0.220)	2.000(0.140)
t(3)	μ = 1.0	0.087(0.005)	1.000(0.270)	1.000(0.000)	0.000(0.000)
	μ = 1.5	0.060(0.009)	0.175(0.029)	1.000(0.000)	0.000(0.000)
	μ = 2.0	0.050(0.008)	0.150(0.016)	0.293(0.019)	0.000(0.000)
t(30)	μ = 1.0	0.070(0.014)	1.000(0.32)	1.000(0.000)	0.000(0.000)
	μ = 1.5	0.065(0.012)	0.175(0.021)	1.000(0.245)	0.000(0.000)
	μ = 2.0	0.050(0.010)	0.175(0.019)	0.250(0.028)	0.000(0.000)

4.2. A comparison with LRS and CBS

In the second set of simulations, we compare the performance of RSI with that of the original LRS and CBS under different noise distributions. All the parameters are chosen the same as in the previous simulations except that μ is fixed at 2.0. Further, the maximum interval length L for the original LRS is set at 45. Table 2 shows that in the cases of t(1) and t(3), the LRS has lower power and a large number of over-selections, while RSI remains very stable. In contrast, CBS fails to select any true intervals. When noise distribution is t(30), which is very close to Gaussian, both LRS and CBS outperform RSI with better power and better identification of the signal segments. However, RSI still performs reasonably well and has no over-selection. This agrees with our theoretical results in Section 2.2.

Table 2.

Simulation comparisons of RSI, LRS, and CBS, where both homogeneous and heterogeneous noises are considered. Homogenous noise is generated from the t-distribution with degrees of freedom 1, 3, and 30. Heterogeneous noise is generated from a mixture of N(0, 1) and N(0, σ²), where σ ~ Gamma(2, τ). μ is fixed at 2.0.

	RSI		LRS		CBS
	D 2(|I2|=40)	#O	D 2(|I2|=40)	#O	D 2(|I2|=40)	#O
t(1)	0.163(0.024)	2(0.2)	0.340(0.054)	3882(6.6)	1.000(0.000)	0(0.0)
t(3)	0.125(0.028)	0(0.0)	0.025(0.006)	467(4.4)	1.000(0.000)	0(0.0)
t(30)	0.125(0.018)	0(0.0)	0.000(0.001)	2(0.0)	0.006(0.006)	0(0.0)
τ = 0.5	0.125(0.015)	2(0.4)	0.013(0.005)	37(3.1)	0.180(0.006)	4(0.6)
τ = 1.0	0.113(0.022)	12(0.6)	0.000(0.006)	227(6.1)	1.000(0.010)	10(1.1)
τ = 1.5	0.125(0.016)	26(0.8)	0.000(0.006)	461(10.9)	1.000(0.000)	8(1.1)

We next consider the case when the errors have heterogeneous variances along the genome. The baseline noise is generated from N(0, 1). We randomly select 100 intervals with length of 50 and generate heterogeneous noise in these intervals. In each interval, the noises follow N(0, σ²), where σ is generated from Gamma(2, τ) with τ = 0.5, 1 and 1.5. Note that the noise variances are constant within an interval but different for different intervals. The bottom half of Table 2 shows the comparison of the three procedures. RSI still has the best overall performance. It results in smaller numbers of over-selections than LRS and better power than CBS. However, as the noise variance increases, RSI can result in more over-selections.

The computation is more expensive for LRS, especially for the t(1) and t(3) cases, because a large number of intervals pass the threshold of LRS. On the other hand, RSI is computationally much more efficient because the data transformation step regularizes the noise and also reduces the dimension from n to T.

4.3. Choice of m

The third set of simulations evaluate the effect of the bin size m on the performance of the RSI. We use the same simulation setting as in the first set of simulations except that μ is fixed at 2.0, m takes values of 10, 20, and 40.

Table 3 shows that there is a trade-off between the power and over-selection when m varies. Smaller m results in better power but more over-selections, especially when the noise distribution has heavy tail. The greater power is due to finer binning, which preserves the signal information better. On the other hand, when m is large, it is possible that none of the original observations in segments with length less than m is kept in the transformed data, such as the case when m = 40 and I₃ = 20. However, if m is too small, the Gaussian approximation of the transformed noise is not accurate enough to overcome the effect of the heavy-tailed noise on segment selection, which in term leads to more over-selections in the case of t(1) and m = 10.

Table 3.

Simulation results: effect of bin size m on the performance the RSI. μ is fixed at 2.

		D 1(|I1|=100)	D 2(|I2|=40)	D 3(|I3|=20)	#O
t(1)	m = 10	0.035(0.009)	0.10(0.018)	0.184(0.033)	19.000(0.850)
	m = 20	0.087(0.009)	0.15(0.020)	0.423(0.220)	2.000(0.140)
	m = 40	0.101(0.006)	0.25(0.056)	1.000(0.024)	0.000(0.000)
t(3)	m = 10	0.030(0.004)	0.088(0.015)	0.150(0.033)	1.000(0.220)
	m = 20	0.050(0.008)	0.150(0.016)	0.293(0.019)	0.000(0.000)
	m = 40	0.087(0.006)	0.293(0.041)	1.000(0.250)	0.000(0.000)
t(30)	m = 10	0.020(0.007)	0.075(0.008)	0.150(0.018)	0.000(0.000)
	m = 20	0.050(0.010)	0.175(0.019)	0.250(0.028)	0.000(0.000)
	m = 40	0.105(0.008)	0.293(0.035)	1.000(0.094)	0.000(0.000)

5. Application to Identification of CNVs Based on the NGS Data

To demonstrate our proposed methods, we analyze the short reads data on chromosome 19 of a HapMap Yoruban female sample (NA19240) from the 1000 Genomes Project. Let Y_i denote the GC content adjusted number of short reads that cover the base pair position i in the genome, for i = 1, …, n where n is very large. After the short reads are mapping to the reference human DNA sequences, we obtain the RD data at n = 54, 361, 060 genomic locations. Figure 3 (a) shows the read depth for the first 10, 000 observations of the data set. The median of the count number over all n sites is 30.

Fig. 3.

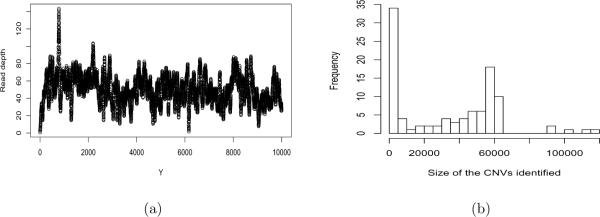
Analysis of the chromosome 19 data of individual NA19240 from the 1000 Genomes Project. (a): scatter plot of the first 10,000 observations; (b): histogram of the sizes of the CNVs identified in base pairs.

The statistical challenges for CNV detection based on NGS data include both ultra-high dimensionality of the data that requires fast computation and unknown distribution of the read depths data. A close examination of our data shows that the variance of the data is much larger than its mean, indicating that the standard Poisson distribution cannot be used for modeling these RD data.

We apply the proposed RSI with m = 400 and L = 150, which assumes that the maximum CNV based on our pre-processed data is 400 × 150 = 60, 000 base pairs (bps). This is sensible since typical CNVs include multi-kilobase deletions and duplications (McCarroll and Altshuler, 2007; Medvedev et al., 2009). We chose L=150 partially due to computational consideration. If the true CNVs are longer than the maximum allowable interval length, these intervals are often divided into several contiguous segments, we can then simply perform some post-processing to merge these segments into longer ones. The RSI selected 115 CNV segments, ranging from 400 to 75,991 bps in sizes, among these 24 are contiguous segments. After merging these contiguous segments, we obtained 101 CNVs, ranging from 400 to 125,440 bps in sizes with a median size of 38,860 bps. See Figure 3 (b) for the distributions of the sizes of CNVs identified. There are 8 CNVs of size of 400 bps, 4 CNVs of size of 800 bps and 4 CNVs of size of 1200 bps. These small CNVs are identified since we did not set a lower limit on the sizes of the CNVs.

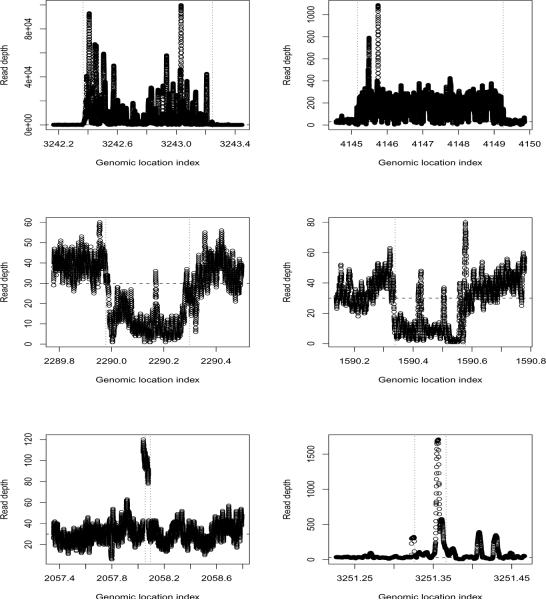
To visualize the CNVs identified by the RSI, Figure 4 shows six CNVs identified, including two duplications, two deletions, and two regions with the shortest CNVs. It is clear that these identified regions indeed represent the regions with different RDs than their neighboring regions. Examinations of the other CNV regions identified also show that these regions contain more or fewer reads than their neighboring regions, further indicating the effectiveness of the RSI procedure in identifying the CNVs.

Fig. 4.

Examples of CNV identified on chromosome 19 of NA19240 from the 1000 Genomes Project. Top two plots: duplications, regions with the highest scores; middle two plots: deletions, regions with the smallest scores; bottom two plots: the two shortest CNVs identified. For each plot, the horizontal line presents the median count of 30 and the vertical dashed lines represent the estimated CNV boundaries. For each plot, x-axis is the genomic location in base pairs/10,000.

Mills et al. (2011) recently reported a map of copy number variants based on whole genome DNA sequencing data from 185 human genomes from the 1000 Genomes Project, where both the RDs and the pair-end mapping distances were used for CNV identifications. Among the methods applied in Mills et al. (2011), three were based on the RDs data as we used in our data set. These three methods identified a total of 438, 332 and 615 CNVs on chromosome 19, respectively, based on the data from all 185 samples. Out of the 101 CNVs we identified for one single sample NA19240, 76 of them overlap with the CNVs reported in the CNV map of (Mills et al., 2011), indicating high sensitivity of our method in detecting the CNVs based on the RD data since our CNVs calls are based on data from only a single sample (NA19240). We are not able to make a direct comparison on CNV calls for this particular sample since the sample-level CNV calls are not available from the publication of Mills et al. (2011).

6. Conclusion and Further Discussion

Motivated by CNV analysis based on the read depth data generated by the NGS technology, we have studied the problem of segment detection and identification from an ultra long linear sequence of data with an unknown noise distribution. We have developed a robust detection procedure RSD and a robust segment identification procedure RSI, which are adaptive over a wide range of noise distributions and are near-optimal for the transformed data. The RSI procedure has been applied to identify the CNVs based on the NGS data of a Yoruban female sample from the 1000 Genomes Project. The CNV regions identified all show deviated read depths when compared to the neighboring regions. The key ingredient of our approaches is a local median transformation of the original data. This not only provides the basis for our algorithm and theoretical development, but also save a large amount of computational cost by greatly reducing the data dimension, which makes it particularly appealing for analyzing the ultra-high dimensional NGS data. As more and more NGS data are becoming available, we expect to see more applications of the RSI procedure in CNV identifications.

Model (1) does not require a specification of the noise distribution. However, we assume that the noises are i.i.d, which can be violated for the RD data. The noise distribution of the RD data is directly related to the uncertainty and errors inherent in the sequencing process and is the result of complex processing of noisy continuous fluorescence intensity measurements known as base-calling. Bravo and Irizarry (2010) showed that the complexity of the base-calling discretization process results in reads of widely varying quality within sequence samples and this variation in processing quality results in infrequent but systematic errors. Such errors can lead to violation of the i.i.d assumption for the RD data. While such errors can have great impact on analysis of single nucleotide polymorphisms and rare genetic variants, their impact on RD data distribution and CNV identification is not clear. Our simulations (Table 2) showed that when the noise has heterogeneous variances, RSI can still identify the correct CNVs unless the variance is very large.

The methods presented in this paper can be extended to more general settings, where one only needs to assume that the density function h of the noise satisfies

$${\int }_{-\infty }^{0}h\left(y\right)=1∕2,h\left(0\right)>0,\mathrm{and}h\left(y\right)\text{is Lipschits at}y=0.$$

Obviously, this assumption is more general than (5) (Brown et al., 2008). To accommodate this more general assumption, a larger m is needed for the robust methods developed in this paper. Our methods can also be extended to detect and identify general geometric objects in two-dimensional settings (Arias-Castro et al., 2005; Walther, 2010). Other interesting extensions include identification of CNVs shared among multiple individuals based on the NGS data and test for CNV associations. Our methods provide the basic tools for these extensions in order to consider structured signals with unknown and possibly heavy-tailed noise distributions.

Appendix: Proofs

In this appendix we present the proofs for Lemma 2.2, Theorem 2.1, 2.2, 2.3, and 3.1.

Proof of Lemma 2.2

(13) has been proved in Arias-Castro et al. (2005). We only need to show (12).

Decompose $\zeta \left(\tilde{I}\right)$ as $\zeta \left(\tilde{I}\right)={\zeta }_1\left(\tilde{I}\right)+{\zeta }_2\left(\tilde{I}\right)$, where ${\zeta }_1\left(\tilde{I}\right)={\sum }_{k\in \tilde{I}}{\zeta }_{k1}∕\sqrt{\mid \tilde{I}\mid }$ and ${\zeta }_2\left(\tilde{I}\right)={\sum }_{k\in \tilde{I}}{\zeta }_{k2}∕\sqrt{\mid \tilde{I}\mid }$. Then

$$P(\mid \zeta \left(\tilde{I}\right)\mid >x)\le P(\mid {\zeta }_1\left(\tilde{I}\right)\mid >x∕2)+P(\mid {\zeta }_2\left(\tilde{I}\right)\mid >x∕2).$$ (28)

Let A_k = mζ_k1, then by (7) in Lemma 2.1, EA_k = 0 and E|A_k|^l ≤ C_l for any l > 0. According to Lemma 2 in Zhou (2006), there exists some positive constant ∊′ such that for any 0 ≤ x ≤ ∊′ and interval $\tilde{I}$,

$$P(\mid \sum _{k\in \tilde{I}}{A}_k∕\sqrt{\mid \tilde{I}\mid }\mid >x)\le \stackrel{‒}{\Phi }\left(x\right)\exp \left(O(1∕\sqrt{\mid \tilde{I}\mid })\right),$$

where $\stackrel{‒}{\Phi }$ is the survival function of a standard normal random variable. Then we have

$$P(\mid {\zeta }_1\left(\tilde{I}\right)\mid >x∕2)\le P(\mid \sum _{k\in \tilde{I}}{A}_k∕\sqrt{\mid \tilde{I}\mid }\mid >xm∕2)\le C\stackrel{‒}{\Phi }(xm∕2)\le \frac{C}{xm}\exp (-x^2{m}^2∕8),$$ (29)

where the last step is by Miller's inequality. On the other hand, $\mid {\zeta }_2\left(\tilde{I}\right)\mid >x∕2$ implies that there exists some ζ_k2 such that $\mid {\zeta }_{k2}\mid >x∕\left(2\sqrt{\mid \tilde{I}\mid }\right)$, then

$$P(\mid {\zeta }_2\left(\tilde{I}\right)\mid >x∕2)\le TP(\mid {\zeta }_{\kappa 2}\mid >x∕2\sqrt{\mid \tilde{I}\mid })\le CT\text{exp}(-am)\le C{n}^{-C{\text{log}}^{b}n}$$ (30)

where the second inequality is by (8) and the last inequality is by the choice of m. Combine (28)–(30) we have

$$P(\mid \zeta \mid \left(\tilde{I}\right)>x)\le \frac{C}{xm}\text{exp}(-x^2{m}^2∕8)+C{n}^{-C{\text{log}}^{b}n},$$ (31)

and consequently

$$P(\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}\zeta \left(\tilde{I}\right)>x)\le T^{2}P(\mid \zeta \left(\tilde{I}\right)\mid >x)\le \frac{C}{xm}\text{exp}(2\text{log}T-x^2{m}^2∕8)+C{n}^{C{\text{log}}^{b}n}$$

Therefore, (12) follows by letting $x=a\sqrt{\text{log}T}∕m$ for some a > 4.

Proof of Theorem 2.1

Decompose $P_{H_0}\left({\text{max}}_{\tilde{I}\in {\mathbb{J}}_T}X\left(\tilde{I}\right)>{\lambda }_n\right)$ into two terms:

$$P_{H_0}\left(\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}X\left(\tilde{I}\right)>{\lambda }_n\right)=P_{H_0}(\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}X\left(\tilde{I}\right)>{\lambda }_n,\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}\le 5\sqrt{\text{logT/m}})+P_{H_0}(\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}X\left(\tilde{I}\right)>{\lambda }_n,\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}>5\sqrt{\text{logT/m}})$$

By (11) and (13), the first term

$$\begin{array}{cc}\hfill P_{H_0}(\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}X\left(\tilde{I}\right)>{\lambda }_n,\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}\le 5\sqrt{\text{logT}}∕m)& \le P(\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}Z\left(\tilde{I}\right)>\sqrt{2\text{log}n}-n\frac{10h\left(0\right)}{m}\sqrt{\text{log T}})\hfill \\ \hfill & \le P(\underset{\tilde{I}{\mathbb{J}}_T}{\text{max}}Z\left(\tilde{I}\right)>\sqrt{2\text{log T}}\le \frac{C}{\sqrt{\text{log}T}}).\hfill \end{array}$$

On the other hand, it is easy to show that the second term is bounded by ${\mathit{CT}}^{-C}∕\sqrt{\text{log}T}$ using (12). Result follows by combining the upper bounds of the two terms.

Proof of Theorem 2.2

Since Theorem 2.1 implies that the type I error of RSD goes to 0, all we need to show is

$${P_H}_1(\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}X\left(\tilde{I}\right)\le {\lambda }_n)\to 0$$ (32)

Suppose that under H₁ segment $I_j\in \mathbb{I}$ satisfies (14) and (15). Define ${\tilde{I}}_j$ to be the collection of the index of J_k such that J_k ⊆ I_j, i.e.

$${\tilde{I}}_j=\{\kappa :J_{\kappa }\subseteq I_j\},$$ (33)

then

$$\mid {\tilde{I}}_j\mid \le \lfloor \mid I_j\mid ∕m-1\rfloor >\mid I_j\mid ∕m-2,$$ (34)

and for each $k\in {\tilde{I}}_j$, θ_k = μ_j. This combined with (4) and (6) implies that

$$X_{\kappa }={\mu }_j+\frac{Z_{\kappa }}{2h\left(0\right)\sqrt{m}}+\frac{{\zeta }_{\kappa }}{\sqrt{m}},\kappa \in {\tilde{I}}_j,$$

which further implies that

$$X\left({\tilde{I}}_j\right)={\mu }_j\sqrt{\mid \tilde{I}\mid }+\frac{Z\left(\tilde{I}\right)}{2h\left(0\right)\sqrt{m}}+\frac{\zeta {\left(\tilde{I}\right)}_j}{\sqrt{m}}.$$

By (34), (14) and (15), we have

$$\mu \sqrt{\mid {\tilde{I}}_j\mid }\ge \frac{{\mu }_j\sqrt{\mid I_j\mid }}{\sqrt{m}}\sqrt{1-\frac{2m}{\mid I_j\mid }}\ge \frac{{\mu }_j\sqrt{\mid I_j\mid }}{\sqrt{m}}\sqrt{1-\frac{∊}{2(1+∊)}}\ge \frac{\sqrt{2(1+∊∕2)\text{log}n}}{2h\left(0\right)\sqrt{m}}$$

Then

$$\begin{array}{cc}\hfill & P_{H_1}(X\left({\tilde{I}}_j\right)\le {\lambda }_n)\hfill \\ \hfill \le & P(Z\left({\tilde{I}}_j\right)\le \sqrt{2\text{log}n}-\sqrt{2(1+∊∕2)\text{log}n}-2h\left(0\right)\zeta \left({\tilde{I}}_j\right))\hfill \\ \hfill \le & P(N(0,1)\le -\sqrt{2\text{log n}}-(\sqrt{(1+∊∕2}-1-\frac{\sqrt{2}h\left(0\right)∊}{m}))+P(\zeta \left({\tilde{I}}_j\right)<-\frac{∊\sqrt{\text{log}n}}{m})\hfill \\ \hfill \le & C{n}^{C{∊}^2},\hfill \end{array}$$ (35)

where the last inequality is by Miller's inequality and (31). (32) follows directly.

Proof of Theorem 2.3

Let $\stackrel{‒}{s}={\mathit{max}}_{I_j\in \mathbb{I}}\lceil \mid I_j\mid ∕m\rceil$ and ${\stackrel{‒}{I}}_j=\{k:J_k\cap I_j\ne \theta \}$. Assume (A) each ${\stackrel{‒}{I}}_j$ is in {$\{l_j\stackrel{‒}{s}+1,\dots ,(l_j+1)\stackrel{‒}{s}\}$} for some l_j, where ${\tilde{I}}_j$ is defined in (33). We show that no testing procedure has both type I and type II errors going to 0 under this situation. This is enough to show that no procedure has both type I and type II errors going to 0 without assuming (A). Let

$$W_i=(X_{l\stackrel{‒}{s}+1}+\dots +X_{(l+1)\stackrel{‒}{s}})∕\sqrt{\stackrel{‒}{s}},l=d,\dots ,\lfloor T∕\stackrel{‒}{s}\rfloor -1,$$

then W_l can be rewritten as

$$2h\left(0\right)\sqrt{m}{W}_l={\theta }_{\prime }^l+Z_{\prime }^l+2h\left(0\right){\zeta }_{\prime }^l$$

where $Z_l^{\prime }\stackrel{iid}{~}N(0,1)$, ${\zeta }_l^{\prime }=({\zeta }_{l\stackrel{‒}{s}+1}+\dots +{\zeta }_{(l+1)\stackrel{‒}{s}})∕\sqrt{\stackrel{‒}{s}}$, and ${\theta }_l^{\prime }=0$ at all but at most $\mid \mathbb{I}\mid$ positions where ${\theta }_l^{\prime }\le \sqrt{2(1-∊)\text{log}n}$ by (17).

By the well-known relationship between the L₁ distance and the Hellinger distance, it is enough to show that the Hellinger affinity between the distribution of $2h\left(0\right)\sqrt{m{W}_l}$ under the null and that under the alternative tends to 1 − o(1/n), i.e, define

$$g\left(x\right)=\frac{f_{Z_l^{\prime }+2h\left(0\right){\zeta }_l^{\prime }}(x-\sqrt{2(1-∊)\log n})}{f_{Z_l^{\prime }+2h\left(0\right){\zeta }_l^{\prime }}\left(x\right)},$$

where $f_{Z_l^{\prime }+2h\left(0\right){\zeta }_l^{\prime }}$ represents the density function of $Z_l^{\prime }+2h\left(0\right){\zeta }_l^{\prime }$, and it is enough to show

$$E\left[\sqrt{1-\nu +\nu g\left(X\right)}\right]=1-o(1∕n),$$

where $\nu =\mid \mathbb{I}\mid ∕\lfloor T∕\stackrel{‒}{s}\rfloor \le \mid \mathbb{I}\mid \cdot {\text{max}}_j\mid I_j\mid ∕n$ and $\mathcal{L}\left(X\right)=\mathcal{L}(Z_l^{\prime }+2h\left(0\right){\zeta }_l^{\prime })$. Further, define $D_n=\{\mid X\mid \le \sqrt{2\text{log}n}\}$. Then $E\left[\sqrt{1-\nu +\nu g\left(X\right)\cdot 1_{D_n}}\right]\le E\left[\sqrt{1-\nu +\nu g\left(X\right)}\right]\le 1$. Applying Taylor expansion gives

$$E\sqrt{1-\nu +\nu g\left(X\right)\cdot 1_{D_n}}=1-\frac{\nu }{2}E[g\left(X\right)\cdot 1_{D_n^c}]+\mathit{err},$$

where, by Cauchy-Schwarz inequality,

$$\mid \mathit{err}\mid \le C{\nu }^{2}E{[g\left(X\right)\cdot 1_{D_n}-1]}^2\le C{\nu }^2(E[g^2\left(X\right)\cdot 1_{D_n}]+1).$$

Now, by the range of ν and the conditions on $\mid \mathbb{I}\mid$ and max_j |I_j|, it is sufficient to show

$$E\left[g\left(X\right)1_{D_n^c}\right]=o\left(1\right)\mathrm{and}E\left[g^2\left(X\right)1_{D_n}\right]=o\left(n\right).$$

The following Lemma is implied by Lemma 3.1 in Cai et al. (2010).

Lemma 6.1.

$${\int }_{D_n^c}\varphi (x-\sqrt{2(1-∊)\text{log}n})dx=o\left(1\right)and{\int }_{D_n}\frac{{\varphi }^2(x-\sqrt{2(1-∊)\text{log}n})}{\varphi \left(x\right)}dx=o\left(n\right),$$

where ϕ is the density function of a standard normal random variable.

Then it is enough to show

$$E\left[g\left(X\right)1_{D_n^c}\right]={\int }_{D_n^c}\varphi (x-\sqrt{2(1-∊)\text{log}n})dx(1+o\left(1\right))+o\left(1\right)$$ (36)

and

$$E\left[g^2\left(X\right)1_{D_n}\right]={\int }_{D_n}\frac{{\varphi }^2(x-\sqrt{2(1-∊)\text{log}n})}{\varphi \left(x\right)}dx(1+o\left(1\right)).$$ (37)

Consider (36) first. By convolution,

$$\begin{array}{cc}\hfill E\left[g\left(X\right)1_{D_n^c}\right]& ={\int }_{D_n^c}{f}_{Z_l^{\prime }+2h\left(0\right){\zeta }_l^{\prime }}(x-\sqrt{2(1-∊)\text{log}n})dx\hfill \\ \hfill & ={\int }_{D_n^c}\left({\int }_{-\infty }^{\infty }{f}_{{\zeta }_l^{\prime }}\left(w\right)\varphi (x-\sqrt{2(1-∊)\text{log}n}-2h\left(0\right)w)dw\right)dx\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }{f}_{{\zeta }_l^{\prime }}\left(w\right)\left({\int }_{D_n^c}\varphi (x-\sqrt{2(1-∊)\text{log}n}-2h\left(0\right)w)dx\right)dw=\mathrm{I}+\mathrm{II},\hfill \end{array}$$

where

$$\text{I}={\int }_{\mid w\mid >4\sqrt{\text{log}n}∕m}{f}_{{\zeta }_l^{\prime }}\left(w\right)\left({\int }_{D_n^c}\varphi (x-\sqrt{2(1-∊)\text{log}n}-2h\left(0\right)w)dx\right)dw\le P(\mid {\zeta }_l^{\prime }\mid >4\sqrt{\text{log}n}∕m)\to 0$$

by (31), and

$$\begin{array}{cc}\hfill \text{II}& ={\int }_{\mid w\mid \le 4\sqrt{\text{log}n}∕m}{f}_{{\zeta }_l^{\prime }}\left(w\right)\left({\int }_{D_n^c}\varphi (x-\sqrt{2(1-∊)\text{log}n}-2h\left(0\right)w)dx\right)dw\hfill \\ \hfill & ={\int }_{\mid w\mid \le 4\sqrt{\text{log}n}∕m}{f}_{{\zeta }_l^{\prime }}\left(w\right)dw{\int }_{D_n^c}\varphi (x-\sqrt{2(1-∊)\text{log}n})dx+err\hfill \\ \hfill & ={\int }_{D_n^c}\varphi (x-\sqrt{2(1-∊)\text{log}n})dx(1+o\left(1\right))+err\hfill \end{array}$$

where the last step is by (31) again, and

$$\begin{array}{cc}\hfill \mid err\mid & \le C\frac{\sqrt{\text{log}n}}{m}\mid {\int }_{D_n^c}\varphi \prime (x-\sqrt{2(1-∊)\text{log}n})dx\mid {\int }_{\mid w\mid \le 4\sqrt{\text{log}n}∕m}{f}_{{\zeta }_l^{\prime }}\left(w\right)dw\hfill \\ \hfill & \le C\frac{\sqrt{\text{log}n}}{m}{n}^{-{(1-\sqrt{1-∊})}^2}\to 0.\hfill \end{array}$$

Summing up above gives (36).

Next, consider (37). By convolution again,

$$f_{z_l^{\prime }+2h\left(0\right){\zeta }_l^{\prime }}\left(x\right)={\int }_{-\infty }^{\infty }{f}_{{\zeta }_l^{\prime }}\left(w\right)\varphi (x-2h\left(0\right)w)dw=\mathrm{III}+\mathrm{IV}$$

where

$$\mathrm{III}={\int }_{\mid w\mid >4\sqrt{\text{log}n}∕m}{f}_{{\zeta }_l^{\prime }}\left(w\right)\varphi (x-2h\left(0\right)w)dw\le C{\int }_{\mid w\mid >4\sqrt{\text{log}n}∕m}{f}_{{\zeta }_l^{\prime }}\left(w\right)dw\le \frac{Cm}{\sqrt{\text{log}n}}{n}^{-2}$$

by (31). Note that in D_n, ϕ(x) ≥ Cn⁻¹, then III = o(ϕ(x)). Further, we have

$$\mathrm{IV}={\int }_{\mid w\mid \le 4\sqrt{\text{log}n}∕m}{f}_{{\zeta }_l^{\prime }}\left(w\right)\varphi (x-2h\left(0\right)w)dw=\varphi \left(x\right)(1+o\left(1\right))+er{r}_1,$$

where

$$\mid er{r}_1\mid \le C\frac{\sqrt{\text{log}n}}{m}\mid \varphi \prime \left(x\right)\mid {\int }_{\mid w\mid \le 4\sqrt{\text{log}n}∕m}{f}_{{\zeta }_l^{\prime }}\left(w\right)dw=o\left(\varphi \left(x\right)\right)$$

by the choice of m and the fact that |ϕ′(x)| ≤ Cϕ(x) for all x. Summing up above gives

$$f_{Z_l^{\prime }+2h\left(0\right){\zeta }_l^{\prime }}\left(x\right)=\varphi \left(x\right)(1+o\left(1\right))$$ (38)

in D_n. Similarly,

$$f_{Z_l^{\prime }+2h\left(0\right){\zeta }_l^{\prime }}(x-\sqrt{2(1-∊)\text{log}n})=\varphi (x-\sqrt{2(1-∊)\text{log}n})(1+o\left(1\right))$$ (39)

in D_n. Substitute (38) and (39) into the definition of E[g²(X)1_Dn] gives (37).

Proof of Theorem 3.1

It is sufficient to show that the set $\widehat{\mathbb{I}}$ of RSI satisfies

$$P_{H_0}(\mid \widehat{\mathbb{I}}\mid >0)\le \frac{C}{\sqrt{\text{log}T}}$$ (40)

and

$$P_{H_1}(\underset{I_j\in \mathbb{I}}{\text{max}}\underset{{\widehat{I}}_j\in \widehat{\mathbb{I}}}{\text{min}}D({\widehat{I}}_j,I_j)>{\delta }_n)\le Cq{n}^{-C{∊}^2}+Cq(\stackrel{‒}{s}∕m)(L∕m)n^{-C{\delta }_n^2}$$ (41)

for any δ_n such that $\sqrt{\text{log}q+\text{log}(\stackrel{‒}{s}∕m)+\text{log}(L∕m)}∕\sqrt{\text{log}n}⪡{\delta }_n⪡1$. Note that $\sqrt{\text{log}q+\text{log}(\stackrel{‒}{s}∕m)+\text{log}(L∕m)}∕\sqrt{\text{log}n}=o\left(1\right)$ under conditions (21), (22), (26), and the choice of m.

Consider (40) first. Since

$$P_{H_0}(\mid \widehat{\mathbb{I}}\mid >0)\le P_{H_0}(\underset{\tilde{I}\in {\mathbb{J}}_T\left(L\right)}{\text{max}}X\left(\tilde{I}\right)>{\lambda }_n^{\ast })\le P_{H_0}(\underset{\tilde{I}\in {\mathbb{J}}_T}{\text{max}}X\left(\tilde{I}\right)>{\lambda }_n^{\ast })$$

and ${\lambda }_n^{\ast }$ converges to λ_n at the order of $n^{\gamma }∕\sqrt{\text{log}n}$, then, by Theorem 2.1 and some routine calculation, (40) follows.

Next, we show (41). Since all the elements in ${\mathbb{J}}_T\left(L\right)$ can not reach more than one signal segments, the accuracy of estimating any $I_j\in \mathbb{I}$ by some element in $\widehat{\mathbb{I}}$ is not influenced by the estimation of other segments in $\mathbb{I}$. This means that the accuracy of estimating any $I_j\in \mathbb{I}$ is equivalent to the case when only segment I_j exists. De ne the following events:

$$A_j=\{{\mathbb{I}}^{\left(1\right)}\ne \varnothing \text{when only}{I}_j\text{exists}\},B_j=\{D({\widehat{I}}_1,I_j)\le {\delta }_n\},j=1,\dots ,q.$$

We have

$$\begin{array}{cc}\hfill P_{H_1}(\underset{I_j\in \mathbb{I}}{\text{max}}\underset{{\widehat{I}}_j\in \widehat{\mathbb{I}}}{\text{min}}D({\widehat{I}}_j,I_j)>{\delta }_n)& \le P(\exists I_j\in \mathbb{I}:A_j^c\cup (A_j\cap B_j^c))\hfill \\ \hfill & \le \sum _{j=1}^{q}P\left(A_j^c\right)+\sum _{j=1}^{q}P(B_j^c\mid A_j),\hfill \end{array}$$

and it is sufficient to show that for any j ∈ {1, …, q},

$$P\left(A_j^c\right)\le C{n}^{-C{∊}^2}$$ (42)

and

$$P(B_j^c\mid A_j)\le {\mathit{Cn}}^{-C}+C(\mid I_j\mid ∕m)(L∕m)n^{-C{\delta }_n^2}.$$ (43)

Consider (42) first. By the construction of ${\mathbb{I}}^{\left(1\right)}$,

$$P\left(A_j^c\right)=P(\underset{\tilde{I}\in {\mathbb{J}}_T\left(L\right)}{\text{max}}X\left(\tilde{I}\right)\le {\lambda }_n^{\ast },\text{only}{I}_j\text{exists})\le P(X\left({\tilde{I}}_j\right)\le {\lambda }_n^{\ast },\text{only}{I}_j\text{exists}),$$

where ${\tilde{I}}_j$ is defined in (33). By (35), the fact that ${\lambda }_n^{\ast }$ converges to λ_n at the order of $n^{\gamma }∕\sqrt{2\text{log}n}$ and some routine calculation, (42) follows.

Now consider (43). Define

$${\mathbb{K}}_T\left(L\right)=\{\tilde{I}\in {\mathbb{I}}^{\left(1\right)}:D(\tilde{I},{\tilde{I}}_j)>C{\delta }_n\}$$

for some C > 0. Since for an interval I, D(I, I_j) > δ_n implies $D(\tilde{I},{\tilde{I}}_j)>C{\delta }_n$, where $\tilde{I}$ is the collection of the index of J_k such that J_k ⊆ I, then $B_j^c$ implies $I_1^{\ast }\in {\mathbb{K}}_T\left(L\right)$, where $I_1^{\ast }$ is defined in the Step 3 of RSI algorithm. This further implies the existence of some $\tilde{I}\in {\mathbb{K}}_T\left(L\right)$ such that $X\left(\tilde{I}\right)\ge X\left({\tilde{I}}_j\right)$. Denote

$${\mathbb{K}}_0=\{\tilde{I}\in {\mathbb{K}}_T\left(L\right):\tilde{I}\cap {\tilde{I}}_j=\varnothing \},{\mathbb{K}}_1=\{\tilde{I}\in {\mathbb{K}}_T\left(L\right):\tilde{I}\ne {\tilde{I}}_j=\varnothing \}.$$

We have

$$P(B_j^c\mid A_j)\le P(\exists \tilde{I}\in {\mathbb{K}}_0:X\left(\tilde{I}\right)\ge X\left({\tilde{I}}_j\right),\mid {\mathbb{K}}_0\mid \le \mathit{CL}∕m+\text{log}n)+P(\mid {\mathbb{K}}_0\mid >\mathit{CL}∕m+\text{log}n)+P(\exists \tilde{I}\in {\mathbb{K}}_1:X\left(\tilde{I}\right)\ge X\left({\tilde{I}}_j\right))\le (\mathit{CL}∕m+\text{log}n)\cdot P(X\left(\tilde{I}\right)-X\left({\tilde{I}}_j\right)\ge 0,\tilde{I}\in {\mathbb{K}}_0)+P(\mid {\mathbb{K}}_0\mid >\mathit{CL}∕m+\text{log}n)+(\mid I_j\mid ∕m)\cdot (L∕m)\cdot P(X\left(\tilde{I}\right)-X\left({\tilde{I}}_j\right)\ge 0,\tilde{I}\in {\mathbb{K}}_1).$$

Since $\mid {\mathbb{K}}_0\mid ={\sum }_{\tilde{I}\in {\mathbb{J}}_T\left(L\right):\tilde{I}\cap {\tilde{I}}_j=\varnothing }1\{X\left(\tilde{I}\right)>{\lambda }_n^{\ast }\}$, which converges to ${\sum }_{\tilde{I}\in {\mathbb{J}}_T\left(L\right):\tilde{I}\cap {\tilde{I}}_j=\varnothing }P(X\left(\tilde{I}\right)>{\lambda }_n^{\ast })$ exponentially fast, and ${\sum }_{\tilde{I}\in {\mathbb{J}}_T\left(L\right):\tilde{I}\cap {\tilde{I}}_j=\varnothing }P(X\left(\tilde{I}\right)>{\lambda }_n^{\ast })\le CT(L∕m)P\left(Z(\tilde{I}>\sqrt{2\text{log}T})\right)\le CL∕m$, then we have

$$P(\mid {\mathbb{K}}_0\mid >\mathit{CL}∕m+\text{log}n)\le {\mathit{Cn}}^{-C}.$$

It is left to show

$$P(X\left(\tilde{I}\right)-X\left({\tilde{I}}_j\right)\ge 0,\tilde{I}\in {\mathbb{K}}_0)\le {\mathit{Cn}}^{-C}$$ (44)

and

$$P(X\left(\tilde{I}\right)-X\left({\tilde{I}}_j\right)\ge 0,\tilde{I}\in {\mathbb{K}}_1)\le {\mathit{Cn}}^{-C{\delta }_n^2}.$$ (45)

For (44), since $\tilde{I}\cap {\tilde{I}}_j=\varnothing$, then

$$X\left(\tilde{I}\right)\le {\mu }_j+\frac{Z\left(\tilde{I}\right)}{2h\left(0\right)\sqrt{m}}+\frac{\zeta \left(\tilde{I}\right)}{\sqrt{m}},$$

where the first term on the right shows up because there is at most one position in $\tilde{I}$ that can possibly has mean μ_j, and other positions have mean 0. On the other hand,

$$X\left({\tilde{I}}_j\right)={\mu }_j\sqrt{\mid {\tilde{I}}_j\mid }+\frac{Z\left({\tilde{I}}_j\right)}{2h\left(0\right)\sqrt{m}}+\frac{\zeta \left({\tilde{I}}_j\right)}{\sqrt{m}}.$$

So

$$P(X\left(\tilde{I}\right)-X\left({\tilde{I}}_j\right)\ge 0,\tilde{I}\in {\mathbb{K}}_0)\le P(\frac{Z\left(\tilde{I}\right)}{2h\left(0\right)\sqrt{m}}-\frac{Z\left({\tilde{I}}_j\right)}{2h\left(0\right)\sqrt{m}}\ge {\mu }_j\sqrt{\mid {\tilde{I}}_j\mid }-{\mu }_j+\frac{\zeta \left({\tilde{I}}_j\right)}{\sqrt{m}}-\frac{\zeta \left(\tilde{I}\right)}{\sqrt{m}})\le P(Z\left(\tilde{I}\right)-Z\left({\tilde{I}}_j\right)\ge \sqrt{2(1+∊∕2)\text{log}n}-\sqrt{\text{log}n}∕m)+{\mathit{Cn}}^{-C}\le P(N(0,2)\ge \sqrt{2(1+C)\text{log}n})+{\mathit{Cn}}^{-C},$$

where the second inequality is because

$${\mu }_j\sqrt{\mid {\tilde{I}}_j\mid }-{\mu }_j\ge \sqrt{\mid {\tilde{I}}_j\mid }\sqrt{1-\frac{∊}{2(1+∊)}}$$

by conditions (21), (15) and the choice of m, and

$$P(\zeta \left({\tilde{I}}_j\right)-\zeta \left(\tilde{I}\right)<-\frac{\sqrt{\text{log}n}}{m})\le {\mathit{Cn}}^{-C}$$ (46)

by (31). Therefore, (44) follows.

For (45), since $\tilde{I}\cap {\tilde{I}}_j\ne \varnothing$, we can write

$$X\left(\tilde{I}\right)-X\left(I\right)={\mathit{LR}}_1+{\mathit{LR}}_2+{\mathit{LR}}_3,$$

$${\mathit{LR}}_1=(\frac{1}{\sqrt{\mid \tilde{I}\mid }}-\frac{1}{\mid {\tilde{I}}_j\mid })\sum _{k\in \tilde{I}\cap {\tilde{I}}_j}{X}_k=(\frac{1}{\sqrt{\mid \tilde{I}\mid }}-\frac{1}{\mid {\tilde{I}}_j\mid })\left({\mu }_j\mid \tilde{I}\cap {\tilde{I}}_j\mid +\frac{{\Sigma }_{k\in \tilde{I}\cap {\tilde{I}}_j}{Z}_k}{2h\left(0\right)\sqrt{m}}+\frac{{\Sigma }_{k\in \tilde{I}\cap {\tilde{I}}_j}{\zeta }_k}{\sqrt{m}}\right),$$

$${\mathit{LR}}_2=\frac{1}{\sqrt{\mid \tilde{I}\mid }}\sum _{k\in \tilde{I}\backslash \tilde{I}\cap {\tilde{I}}_j}{X}_k\le \frac{1}{\sqrt{\mid \tilde{I}\mid }}\left({\mu }_j+\frac{{\Sigma }_{k\in \tilde{I}\backslash \tilde{I}\cap {\tilde{I}}_j}{Z}_k}{2h\left(0\right)\sqrt{m}}+\frac{{\Sigma }_{k\in \tilde{I}\backslash \tilde{I}\cap {\tilde{I}}_j}{\zeta }_k}{\sqrt{m}}\right)$$

$${\mathit{LR}}_3=\frac{1}{\sqrt{\mid {\tilde{I}}_j\mid }}\sum _{k\in {\tilde{I}}_j\backslash \tilde{I}\cap {\tilde{I}}_j}{X}_k=\sqrt{\mid {\tilde{I}}_j\mid }\left(-{\mu }_j\mid {\tilde{I}}_j\backslash \tilde{I}\cap {\tilde{I}}_j\mid -\frac{{\Sigma }_{k\in {\tilde{I}}_j\backslash \tilde{I}\cap {\tilde{I}}_j}{Z}_k}{2h\left(0\right)\sqrt{m}}-\frac{{\Sigma }_{k\in {\tilde{I}}_j\backslash \tilde{I}\cap {\tilde{I}}_j}{\zeta }_k}{\sqrt{m}}\right)$$

Note that LR₁, LR₂ and LR₃ are independent, and

$$(\frac{1}{\sqrt{\mid \tilde{I}\mid }}-\frac{1}{\sqrt{\mid {\tilde{I}}_j\mid }})\frac{{\Sigma }_{k\in \tilde{I}\cap {\tilde{I}}_j}{Z}_k}{2h\left(0\right)\sqrt{m}}+\frac{1}{\sqrt{\mid \tilde{I}\mid }}\frac{{\Sigma }_{k\in \tilde{I}\backslash \tilde{I}\cap \tilde{I}}{Z}_k}{2h\left(0\right)\sqrt{m}}-\frac{1}{\sqrt{\mid {\tilde{I}}_j\mid }}\frac{{\Sigma }_{k\in {\tilde{I}}_j\backslash \tilde{I}\cap {\tilde{I}}_j}{Z}_k}{2h\left(0\right)\sqrt{m}}~\frac{1}{\sqrt{m}}N(0,\tau )$$

for some τ > 0. On the other hand, $D(\tilde{I},{\tilde{I}}_j)\ge C{\delta }_n$ implies

$$(\frac{\mid \tilde{I}\cap {\tilde{I}}_j\mid }{\sqrt{\mid \tilde{I}\mid }}-\sqrt{\mid {\tilde{I}}_j\mid }){\mu }_j<-C{\delta }_n\sqrt{\mid {\tilde{I}}_j\mid }{\mu }_j.$$

Combing above with (46) we have

$$P(X\left(\tilde{I}\right)-X\left({\tilde{I}}_j\right)\ge 0,\tilde{I}\in {\mathbb{K}}_1)\le P(N(0,\tau )\ge C{\delta }_n{\mu }_j\sqrt{\mid {\tilde{I}}_j\mid }-\frac{\sqrt{\text{log}n}}{m})+{\mathit{Cn}}^{-C}.$$

Given (15) and the choice of m, (45) follows for δn satisfying $\sqrt{\text{log}q+\text{log}(\stackrel{‒}{s}∕m)+\text{log}(L∕m)}∕\sqrt{\text{log}}⪡{\delta }_n⪡1$