Generalized localization model of relaxation in glass-forming liquids

Abstract

Glassy solidification is characterized by two essential phenomena: localization of the solidifying material’s constituent particles and a precipitous increase in its structural relaxation time τ. Determining how these two phenomena relate is key to understanding glass formation. Leporini and coworkers have recently argued that τ universally depends on a localization length-scale <u²> (the Debye-Waller factor) in a way that depends only upon the value of <u²> at the glass transition. Here we find that this ‘universal’ model does not accurately describe τ in several simulated and experimental glass-forming materials. We develop a new localization model of solidification, building upon the classical Hall-Wolynes and free volume models of glass formation, that accurately relates τ to <u²> in all systems considered. This new relationship is based on a consideration of the the anisotropic nature of particle localization. The model also indicates the presence of a particle delocalization transition at high temperatures associated with the onset of glass formation.

Introduction

When glasses,∰ crystals, and gels solidify, their constituent particles become localized; ie., they cease to freely explore space. In glass-forming liquids, a rapid increase in the structural relaxation time and viscosity accompanies this localization transition. These two facts raise a fundamental question: how does the extent of particle localization relate to the structural relaxation time of glass-forming liquids?

Two types of activated transport model have typically been employed to answer this question. In the ‘elastic models’ of activated transport, barriers to transport are assumed to relate to high frequency (picosecond to nanosecond) elastic properties of the material¹. In the ‘free volume models’ of activated transport, on the other hand, barriers to relaxation are related to the amount of free volume accessible to individual particles in the system. Below, we review the predictions of each class of model.

In our discussion of these models, we focus on the Debye-Waller factor 〈u²〉 as a measure of localization because it is directly measurable via neutron², Mossbauer³, and x-ray⁴ scattering, and more recently by time-resolved Stokes Shift measurements⁵. Physically, 〈u²〉 reflects the average rattle length-scale of a particle in the cage of its neighbors.

The ‘elastic’ activated transport models for relaxation assume that relaxation occurs through the escape of particles from local potential wells with an activation energy that increases in proportion to the local ‘stiffness’ of the material^1,6–8. An influential model in this class was developed by Hall and Wolynes, who worked from a density functional theory to arrive at a simple model of relaxation in glass forming liquids. This mean field model specifically suggests that particles in low-temperature glasses are localized in effectively harmonic wells, providing a relationship between particle displacement, energy of activation, and thermal energy. On this basis, Hall and Wolynes relate the structural relaxation time τ to 〈u²〉 by⁷

$$\tau ={\tau }_0\text{exp}[{u_0}^2/\langle u^2\rangle ],$$ (1)

where τ₀ is a constant prefactor, as in ordinary theories of activated transport, and u₀² is interpreted as a critical displacement required for delocalization (‘cage escape’).

Equation (1) was first examined computationally by Starr et. al, who found it to reasonably describe relaxation in several simulated polymeric glass-forming materials over a limited temperature range^9,10. This approach has been more recently extended by Leporini and coworkers, who modified it by assuming a Gaussian distribution of u₀ as a way of modeling the known nanoscale heterogeneity of glasses^11–13, leading to the form

$$\tau ={\tau }_0\text{exp}[a^2/2\langle u^2\rangle +{\sigma }^2/2{\langle u^2\rangle }^2],$$ (2)

where a² is the mean value of u₀² and σ² is its variance. Leporini and coworkers argue that this modification results in a universal form for τ as a function of 〈u²〉 that applies to all glass-forming materials^14–18. We examine this model below and do not find it to be universal. Indeed, the fact that the fast beta relaxation rate (which is directly related to 〈u²〉 ¹⁹) and alpha relaxation rate can vary inversely²⁰ makes any fixed universal relationship between τ and 〈u²〉 unlikely. An additional parameter would seem to be required to capture this relationship.

An alternate approach relating relaxation to localization is offered by the classical free volume theory of τ, which relates relaxation time to free volume through a simple exponential relationship²¹:

$$\tau ={\tau }_0\text{exp}[v_0/v_f],$$ (3)

where v_f is the ‘free volume’. Various measures of free volume have been proposed, but it is frequently conceived of as the space accessible to a particle center within the ‘cage’ of its neighbors²². This free volume definition can be related to the collision frequency in hard sphere systems, fundamentally linking dynamics to thermodynamics^22–25. However, this free volume is not directly measurable in experiments. A direct comparison of the free volume-based approach with equations (1) and (2) thus requires equation (3) to be recast in terms of 〈u²〉.

Scaling Theory

Simple dimensional consistency suggests⁹ that free volume should scale with the Debye-Waller factor as v_f ∝ 〈u²〉^3/2, and Starr et al. have found this proportionality to approximately hold for a simulated coarse-grained polymeric glass-former (FENE model)⁹. This scaling argument implies that equation (3) can alternatively be written as

$$\tau ={\tau }_0\text{exp}\left[{({u_0}^2/\langle u^2\rangle )}^{3/2}\right].$$ (4)

However, in arriving at equation (4), we implicitly assumed the free volume shape to be compact and did not consider that this shape might change with temperature. In contrast, work by Rahman²⁶ and others has emphasized that local free volume is anisotropic and that this anisotropy is correlated with particle motions^27–29. Rahman specifically argued that particle localization can be described by motion in a ‘tunnel’ comprised of neighboring particles. This ‘tunnel model’ is consistent with more recent results demonstrating the presence of one-dimensional, ‘string-like’ collective rearrangements of particles^27,30.

The scaling relation between free volume and 〈u²〉 for Rahman’s ‘tunnel’ differs considerably from that for a simple spherical model of free volume. The volume v_f of a tube scales linearly with length L, while 〈u²〉 ~ L². Thus, if the free volume takes the form of tubes with temperature-dependent length, free volume should scale with 〈u²〉 as v_f ~ 〈u²〉^1/2. In contrast, for particle localization in spherically shaped cavities of radius R, v_f ~ R³ and 〈u²〉 ~ R². It follows that, for spherically symmetric free volume, v_f ~ 〈u²〉^3/2, consistent with the naïve free volume theory discussed above.

More generally, particles may be localized within cages that are neither spherical nor cylindrical, but which have anisotropic shapes that vary with temperature. This suggests a more general scaling relationship of v_f ~ 〈u²〉^α/2. Combining this expression with the basic free volume theory statement of equation (3) suggests the expression

$$\tau ={\tau }_0\text{exp}\left[{({u_0}^2/\langle u^2\rangle )}^{\alpha /2}\right],$$ (5)

which we refer to as the localization model for relaxation.

We now consider a scaling theory relating free volume to the Debye-Waller factor for a slightly more general model of anisotropic free volume: an ellipsoidal local free volume. We begin by analytically determining 〈u²〉 for this case. For any local free volume shape, 〈u²〉 is equivalent to the mean distance between two uncorrelated points within the free volume, given by

$$\langle u^2\rangle =\frac{{\displaystyle ∰{\displaystyle ∰DdVd{V}^{\text{'}}}}}{{\displaystyle ∰{\displaystyle ∰dVd{V}^{\text{'}}}}},$$ (6)

where distance D is given by D = [(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²] in Cartesian coordinates. Introducing reduced variables x̂ = x/L_x, ŷ = y/L_y, and ẑ = z/L_z, the equation for an ellipsoid centered at the origin becomes x̂² + ŷ² + ẑ² = 1. Casting equation (6) and the distance formula in these reduced Cartesian cordinates yields dimensionless (albeit complicated) limits of integration, and performing the integration then gives remarkably simple result

$$\langle u^2\rangle =\frac{2}{5}\left({L_x}^2+{L_y}^2+{L_z}^2\right),$$ (7)

which reduces to the well-known result for the sphere when all three characteristic length-scales are equal.

In order to cast the free volume theory of glass formation in terms of 〈u²〉 rather than free volume v_f, it would appear that we need an equation for v_f in terms of 〈u²〉. However, v_f is not a direct function of 〈u²〉 in real systems. Rather v_f and 〈u²〉 each vary with temperature, so that dv_f/d〈u²〉 is well approximated not by ∂v_f/∂〈u²〉 but rather by (∂v_f/∂T)/(∂〈u²〉/∂T). Proceeding now requires some assumption about the temperature dependence of the three characteristic lengthscales L_x, L_y, and L_z, and we choose power law relations,

$$L_x=a{T}^x,L_y=b{T}^y,L_z=c{T}^z$$ (8)

as a reasonably general form. We later test this assumption and find it to be excellent for the simulated glass-forming systems examined in the following sections. Since the free volume of an ellipsoid is given by v_f = 4L_xL_yL_z/3, it follows that

$$\frac{\partial v_f/\partial T}{\partial \langle u^2\rangle /\partial T}=\frac{5v_f(x+y+z)}{4(x{L_x}^2+y{L_y}^2+z{L_z}^2)}.$$ (9)

This form leads to v_f = 〈u²〉^α/2, consistent with equation (5), with

$$\alpha =\left(1+\frac{x+y}{z}\right)f(T)$$ (10)

and

$$f(T)=\frac{1+\frac{a}{c}{T}^{2(x-z)}+\frac{b}{c}{T}^{2(y-z)}}{1+\frac{a}{c}\frac{x}{z}{T}^{2(x-z)}+\frac{b}{c}\frac{y}{z}{T}^{2(y-z)}}.$$ (11)

Equation (10) yields reasonable limits in the cases of single dimensional free volume growth with temperature (x >> y ~ z), for which α → 1, and perfectly isotropic growth (x = y = z and a = b = c), for which α → 3. These cases correspond correctly to the scaling for a tube and a cylinder, described above. However, a more physically reasonably situation is that the three growth rates are not equal but are of the same order. In this case, f(T) → 1 to leading order in the low tempreature limit, so that

$$\alpha \cong \left(1+\frac{x+y}{z}\right)$$ (12)

where we have used the convention that x ≥ y ≥ z. In this case, α ranges from a minimum value of 3 for perfectly isotropic free volume growth with temperature to higher values reflecting increasingly anisotropic growth of free volume.

As discussed in the results section below, the three growth rates are indeed found to be of the same order in our simulated systems. Given the scaling nature of this argument, with the expectation of qualitative predictions only, we focus on equation (5) with α scaling as suggested by equation (12) in further discussion, and we accordingly interpret α as reflecting the anisotropy of local free volume growth with temperature. We begin in the following sections by demonstrating equation (5) to be remarkably successful in describing relaxation-time data in diverse systems.

Methodology

Experiments

Three small-molecule glass formers are examined in this study: sorbitol, propylene glycol, and glycerol. Sorbitol and propylene glycol were purchased from Sigma Chemical Company and used as received without further purification. All data for glycerol are obtained for the literature³¹.

Debye-Waller factor data for propylene glycol and glycerol were obtained via time-of-flight measurements performed at the Disk Chopper Spectrometer³² (DCS) installed at the NIST Center for Neutron Research (NCNR). For all of the neutron scattering experiments, samples were transferred in a helium glovebox to an annular-geometry aluminum sample cell, sealed with an indium O-ring, and mounted on a closed-cycle helium refrigerator. Sample thickness was chosen for about 10% total scattering to minimize multiple scattering effects. The DCS spectra were acquired using an incident-neutron wavelength of λ=4.0 Å with momentum transfer Q, range of 0.1–2.0 Å⁻¹ and an energy resolution of approximately 200 µeV. All the samples were also measured at 30 K, where dynamics is expected to be purely elastic. These scattering functions were used to normalize the data and also as the instrumental resolution. The DAVE software package was used for data reduction and the standard Fourier Transform Toolkit was used to transform the measured scattering function S(Q,ω) into intermediate scattering function S(Q,t), from which the nonergodicity factor h at approximately 1 ps can be directly obtained. Debye-Waller factor <u²> values at 1 ps are then calculated from the nonergodicity factor via 〈u²〉 = −6ln(h)/q². For all the glass formers, <u²> values were calculated from h at q=1.4A⁻¹, which corresponds to the first peak in the static structure factor.

Simulations

The simulated systems include a coarse-grained polymeric glass-former with harmonic bonds with and without the addition of an antiplasticizer additive. Each of these simulated systems has previously been studied and is well characterized in the literature^{9,19,20,33–35}.

The pure polymer simulated systems examined in this study consists of 50 coarse-grained polymer chains. Each chain contains 32 beads, with nonbonded interactions being given by a 6–12 Lennard-Jones potential with diameter σ = 1 and energy constant ε = 1. Bonded beads interact via a stiff harmonic potential with force constant 2000 ε/σ. The antiplasticized polymer simulation adds to the above system 674 antiplasticizer particles, comprising about 5% by mass or 30% by mole. Each antiplasticizer particle is a monomeric 6–12 Lennard-Jones bead with diameter σ = ½. Interactions between chain monomers and antiplasticizer particles are characterized by σ = ¾, and for all interaction types ε = 1. Furthermore, for both pure and antiplasticized systems, nonbonded interactions are cut off at a distance of 2.5, and potentials are shifted such that they go to zero at this cutoff.

Simulations were performed with the LAMMPS molecular dynamics simulation package using a RESPA timestepping scheme. Nose-Hoover thermo- and baro-stats were employed, as implemented in LAMMPS. Temperature and pressure damping parameters were both 2 τ, where τ is the LJ unit of time. The RESPA timestep for LJ interactions was 0.01 τ for the pure polymer and 0.004 τ for the antiplasticized polymer. In each case, the time step for bonded interactions was one quarter that for nonbonded interactions.

The equilibration scheme for these systems has been described in detail elsewhere¹⁹. In short, it employs a slow quench of the system from high temperature in an NPT ensemble, followed by a long NPT equilibration at each temperature, followed by rescaling to the average density and a final brief equilibration in the NVT ensemble. Production runs are then performed from these configurations in the NVT ensemble.

Results

Comparison with data

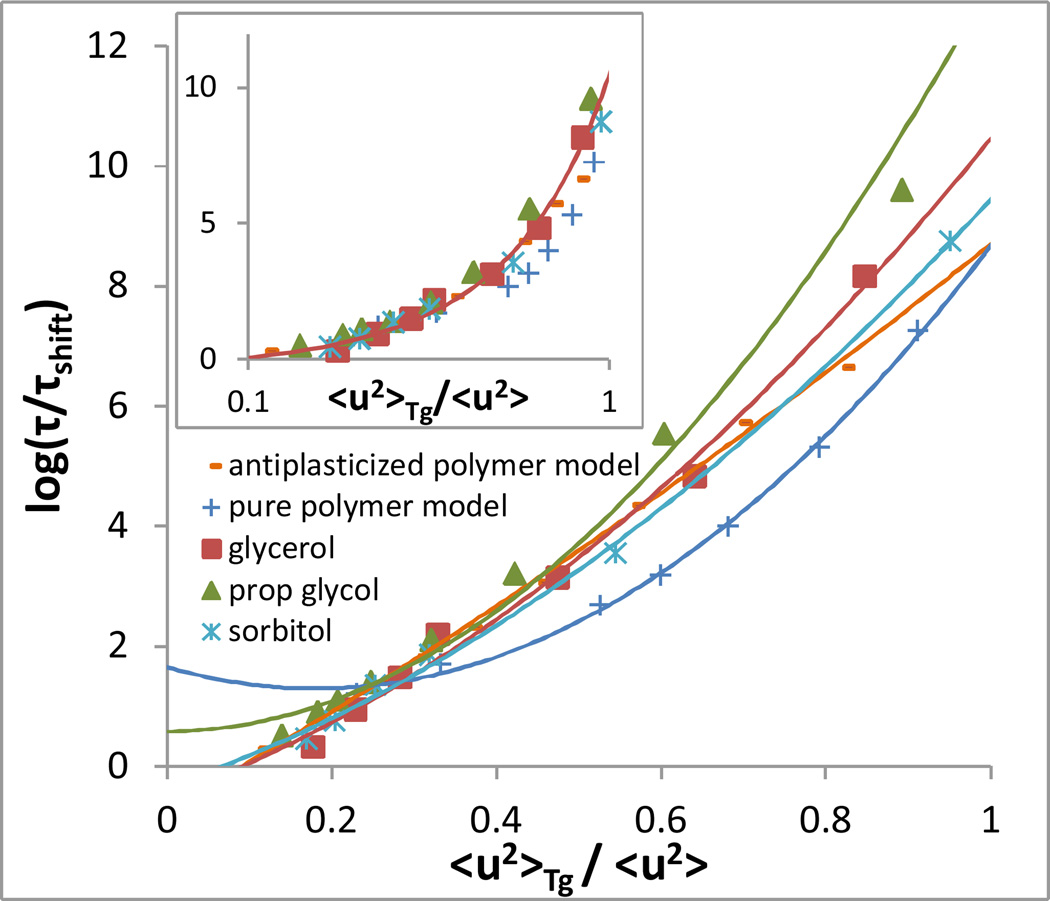
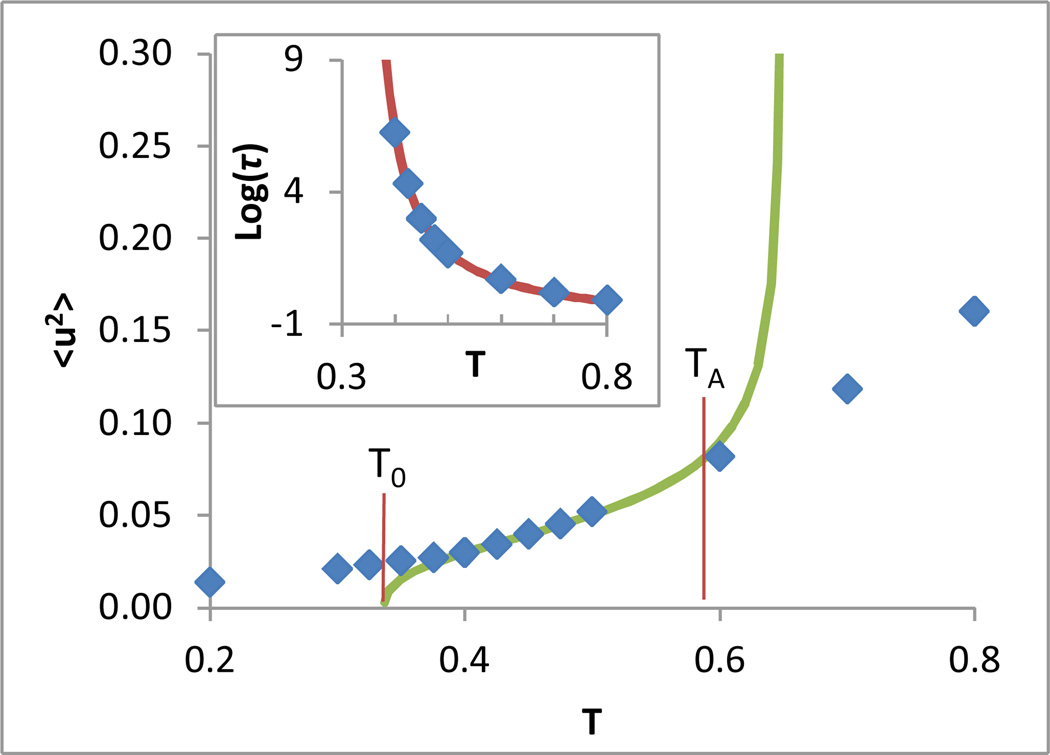
We now examine the effectiveness of equation (5) in comparison to earlier activated transport models in the context of several experimental and simulated systems. Figure 1 depicts a fit of data for the above systems to the ‘universal’ form given by Leporini et. al. Universality of this model minimally requires that an appropriate rescaling of τ_α for each system collapse the data to a single quadratic curve when log(τ_α) is plotted versus 〈u²〉_Tg/〈u²〉. As shown in the inset of Figure 1, plotting the log of relaxation time data for our systems vs log(〈u²〉_Tg/〈u²〉), as in the recent series of papers of Leporini and coworkers, gives the impression of a universal collapse. However, a plot of the same data on a linear abscissa, shown in Figure 1, reveals that the data do not follow a single ‘universal’ quadratic curve but rather conform to a range of quadratic forms. Moreover, there is no clear physical meaning of the fitting parameters describing these forms; for example, in the case of the pure model polymer the best fit to the mean square ‘escape distance’ parameter u₀² is unphysically negative.

Figure 1.

Log relaxation time vs inverse Debye-Waller factor scaled by its value at T_g for the systems described in the text. The inset shows the same data plotted with a logarithmic x-axis, as in papers by Leporini and coworkers^7–9. An arbitrary renormalization of relaxation time has been manually applied to each system to yield the best possible collapse, in the high temperature range, following the approach of Leporini and coworkers. This shift is equivalent to varying the value of τ₀ in any of the models described in the text. Curves represent quadratic fits of the form given by Leporini et. al.

Equation (1) (the Hall-Wolynes model) also does not well describe the data, as it predicts straight lines for the curves in this plot. However, we note that a linear fit is sufficient for all systems in the high temperature range of the data, explaining both the earlier success of the Hall-Wolynes form for a limited (high) temperature range and the apparent collapse of the data via the Leporini form when plotted on a log-log plot, which emphasizes the high temperature range of data.

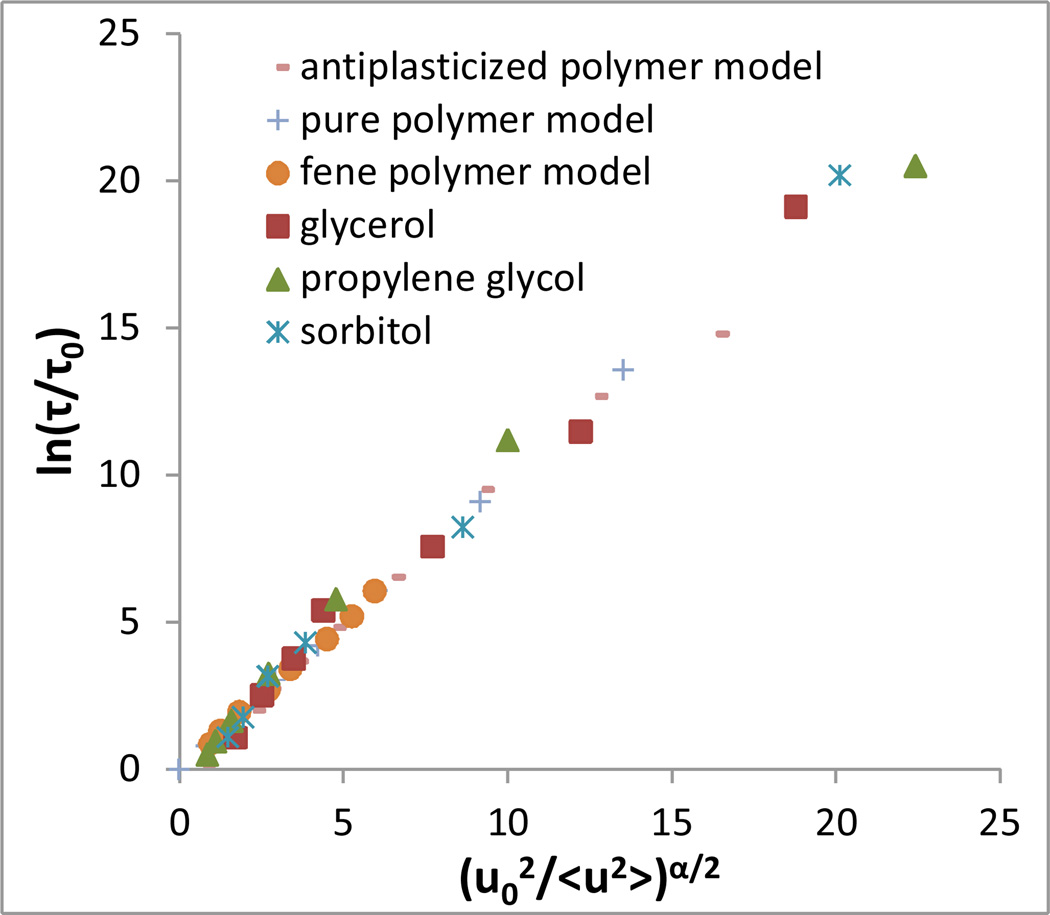
In contrast, we find that the new form given by equation (5) describes the relationship between τ and <u²> for all systems that we have considered. As shown by Figure 2, linearizing the data in accordance with this form yields an almost perfect collapse of all systems to a single master curve. The parameters describing these fits are shown in Table 1.

Figure 2.

Linear collapse of relaxation time vs Debye-Waller factor data via equation (5) for experimental and simulated systems depicted in Figure 1. Also included is course-grained polymer data provided from reference 9, where the bonded force constant involves a nonlinear rather than harmonic spring.

Table 1.

Parameters for fits of equation (5) to data for systems examined in this paper.

	τ0	u02	α
Glycerol	22.4 ps	3.26 A	3.07
Propylene glycol	97.6 ps	1.41 A	4.13
Sorbitol	17.1 ps	1.11 A	3.03
Pure harmonic polymer	2.30 τ	0.0761	5.56
Antiplasticized harmonic polymer	1.65 τ	0.122	3.09
FENE polymer	1.67 τ	0.139	3.09

Quantification of free volume ‘shape’ in simulations

In order to determine whether the apparent success of this model reflect underlying physics or merely a foruitious fitting form, we compare the scaling prediction of equation (12) for α with the values obtained from the above fits to data from the pure and antiplasticized simulated polymer systems, remembering that, because the proportionality constant in that expression depends on the precise shape of the free volume, only prediction of qualitative trends in the value of α can be reasonably expected. Estimating the value of α via equation (12) requires that one quantify the temperature dependence of the shape of local free volume, in terms of the three characteristic lengthscales L_x, L_y, and L_z.

How can one quantify the shape of free volume? In Rahman’s consideration of this problem, he focused on the anisotropy of the Voronoi cells defined about each particle²⁶. Since our focus is on 〈u²〉 as a measure of localization, it is natural to consider the anisotropy of the trajectories of the particles within their local cages. The radius of gyration tensor R_ij is commonly used to quantify the shape of polymers in solution³⁶, and we adopt this quantity to describe the shape of our particle trajectories. This tensor is given by

$$R_{ij}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{r}_m^i{r}_n^i,}$$ (13)

where N is the number of points in the trajectory and $r_m^i$ and $r_n^i$ are the m^th and n^th component of the vector from the trajectory centroid to the i^th point in the trajectory.

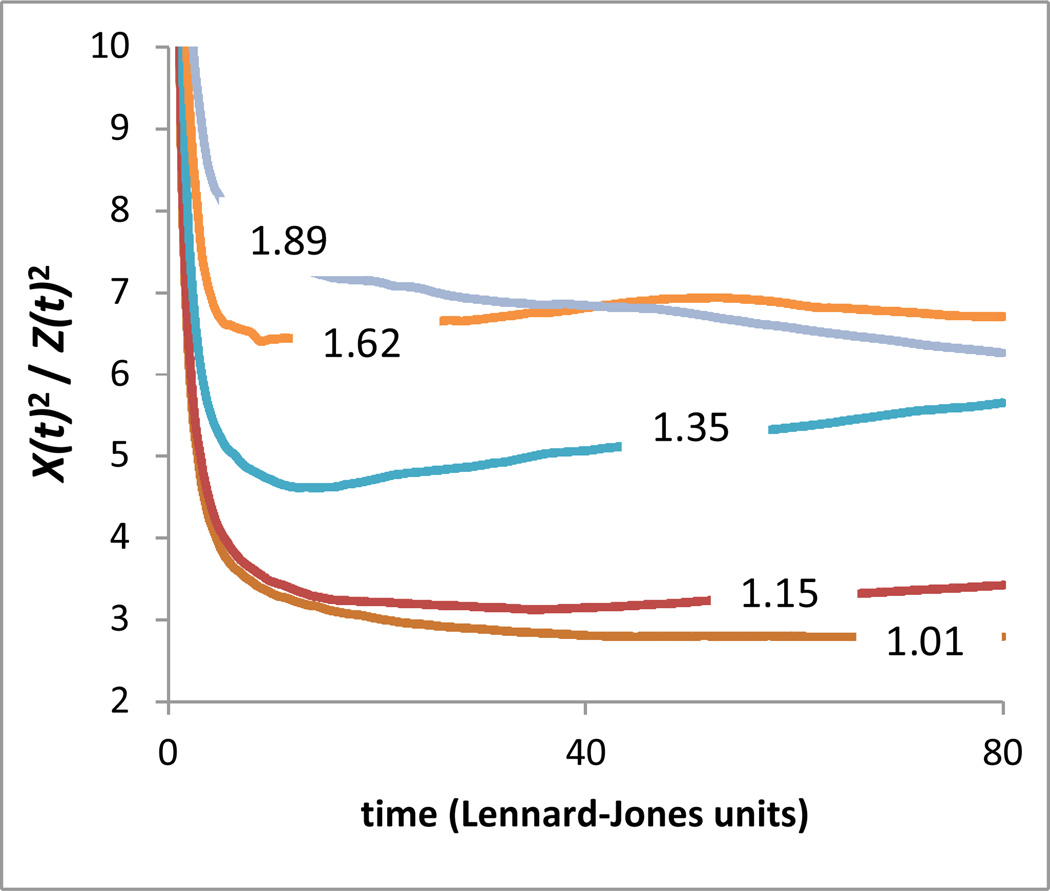
The eigenvalues of R_ij provide three length-scales X²(t), Y²(t), and Z²(t), that are generally functions of the duration t of the trajectory considered. A measure of the average trajectory anisotropy as a function of time is given by the ratio of the ensemble average of the largest to smallest lengthscales 〈X²(t)〉/〈Z²(t)〉 At very short, inertial times, this ratio must go to infinity, reflecting the linear nature of inertial motion. At long times, it is expected to converge to a fixed value of 11.7 associated with diffusive motion³⁶, or in polymeric systems to some smaller constant value associated with monomeric subdiffusion. At some intermediate ‘cage time’ t_c, the particle trajectories will have, on average, most fully explored the particles’ local free volume without escaping the cage of their neighbors to freely diffuse. Unless this cage is extremely anisotropic (more so even than diffusive motion), this time should correspond to a local minimum in the value of 〈X²(t)〉/〈Z²(t)〉. As shown in Figure 3, this minimum indeed emerges in our simulations below the onset temperature T_A of glass formation, at T = 0.6 in Lennard Jones units in the case of the pure polymer. Accordingly, we identify the values of X(t), Y(t), and Z(t) at this time as the characteristic lengthscales L_x, L_y, and L_z that characterize the local free volume in the scaling theory above. At temperatures near and below T_g, this minimum moves to long times. Although these times are well within the timescale of our simulations, calculation of the gyration tensor at longer times becomes very computationally expensive, and since the minimum is evidently broad and shallow at these temperatures, we use the values of the length-scales at the longest calculated time as a reasonable approximation of the value at the minimum.

Figure 3.

Ratio of largest to smallest eigenvalues of gyration tensor for pure simulated polymer system as a function of time. The number on each curve specifies T/T_g for that curve.

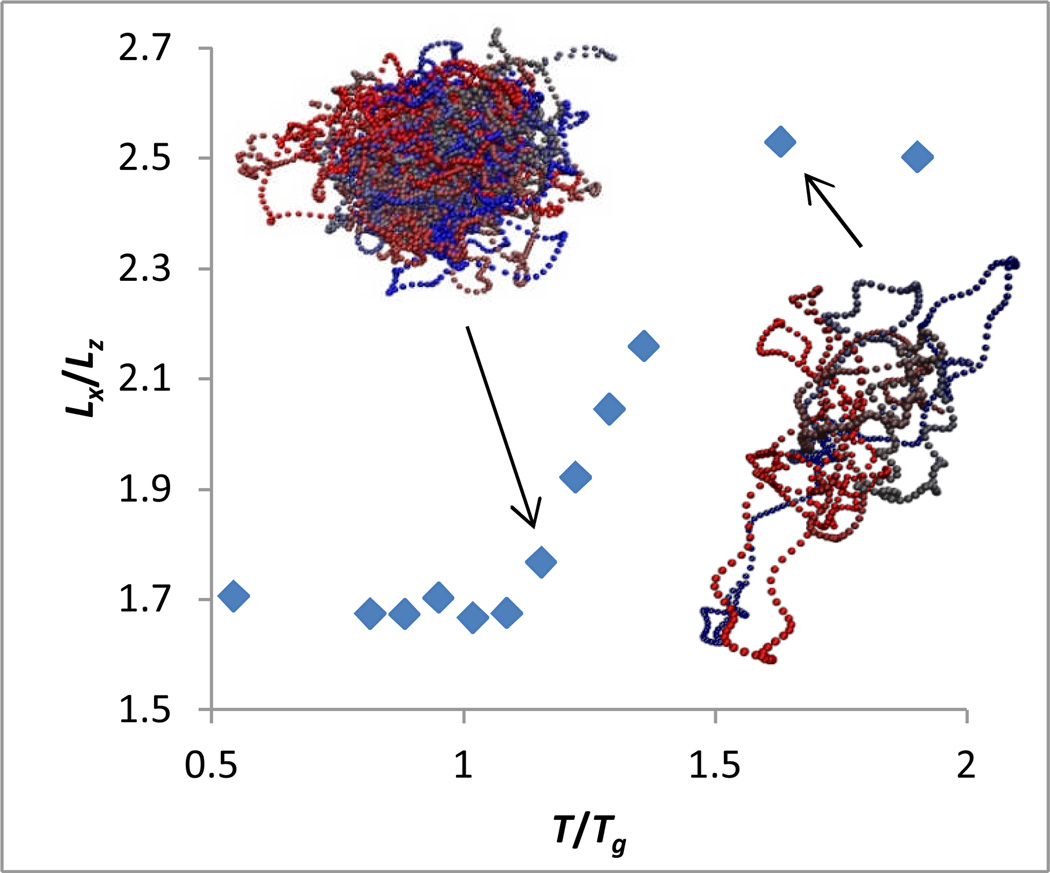
We now examine the free volume anisotropy in our pure and antiplasticized model polymer systems via calculation of the mean value of L_x, L_y, and L_z as a function of temperature. These three length-scales provide an ellipsoidal description of the free volume, and their relative magnitudes characterize the free volume anisotropy. As shown in Figure 4 for the pure polymer, the free volume anisotropy L_x/L_z exhibits considerable temperature dependence in the glass formation regime, with reducing anisotropy as the system is cooled towards T_g. This trend is qualitatively consistent with observations of concentration dependent anisotropy in a glass-forming material³⁷. Furthermore, we find that the temperature dependencies of L_x, L_y, and L_z in the glass-formation region reasonably conform to power laws, as assumed in the above scaling argument, with exponents x, y, and z, respectively, shown in Table 1.

Figure 4.

Plot of anisotropy of particle in-cage trajectories as a function of temperature, with sample trajectories. The duration of each trajectory is equal to the caging time t_c described in the supplementary material.

Because the proportionality constant in equation (12) depends on the precise shape of the free volume, this expression can only be expected to provide qualitative trends in the value of α. In order to test the validity of the anisotropic free volume model at this qualitative level, we apply equation (12) to the fits of x, y and z described above for the pure and antiplasticized simulated polymer systems. The resulting predictions are in good qualitative agreement with the trend of reduced α in the antiplasticized polymer relative to the pure polymer (In the limit of low T equation (12) predicts that α = 4.3 for the pure system vs 3.9 for the antiplasticized system), providing support for the physical underpinnings of this model.

Consistency with the VFT relation

The localization model relating τ to 〈u²〉 holds over the same general temperature range for which the Vogel-Fulcher-Tammann (VFT) equation describes the temperature dependence of τ for many glass-forming materials:

$$\tau ={\tau }_{0,\mathit{\text{VFT}}}\text{exp}\left(D\frac{T_0}{T-T_0}\right).$$ (14)

where T₀ is an extrapolated divergence temperature of the relaxation time, τ_0,VFT is an extrapolated high temperature relaxation time, and D is related to the fragility (or temperature-breadth) of the glass transition. This form also accurately describes our data, as shown in the inset of Figure 5 for the pure polymer model (and in the literature for the experimental systems²⁸). It is then reasonable to ask whether the localization model is consistent with the VFT equation and, if so, whether this consistency yields any further insights into the physical meaning of the other parameters in the localization model.

Figure 5.

Temperature dependence of 〈u²〉 for the pure polymer simulation. Points are simulation data and the solid curve is the model fit of equation (15). Inset shows fit of VFT equation to relaxation data from the same system.

Consistency between the VFT expression and equation (5) requires that the temperature dependence of 〈u²〉 is given by

$$\langle u^2\rangle ={u_0}^2{\left[\text{ln}\frac{{\tau }_{0,\mathit{\text{VFT}}}}{{\tau }_0}+D\frac{T_0}{T-T_0}\right]}^{-2/a}.$$ (15)

As one might expect, equation (15) requires that 〈u²〉 goes to zero as T approaches T₀, consistent with the extrapolated divergence in the relaxation time at this temperature. However this equation also predicts a divergence in 〈u²〉, at a “delocalization temperature” T_D (see Figure 5),

$$T_D=T_0\left(\raisebox{1ex}{$1+D$}\!\left/ \!\raisebox{-1ex}{$\text{ln}\frac{{\tau }_0}{{\tau }_{0,\mathit{\text{VFT}}}}$}\right.\right),$$ (16)

which is the high temperature counterpart of T₀. Together, T₀ and T_D demarcate a well-defined onset and end of the congested fluid regime in terms of particle localization.

The glass transition temperature T_g is somewhat above T₀ and corresponds to a condition where the particles are sufficiently localized for dynamics to become effectively arrested and where solid-like behavior first emerges. This condition can be estimated roughly by a Lindemann condition³⁸ as in crystals. Correspondingly, we can define a temperature T_s where localization first becomes appreciable enough to noticeably affect particle dynamics. In particular, we define T_s as the point below which the mean particle oscillation is insufficient to escape its cage; i.e., 〈u²〉 = u₀². This condition leads to an explicit expression for T_s:

$$T_s=T_0\left[1+{\left(\frac{T_0}{T_D-T_0}+\frac{1}{D}\right)}^{-1}\right].$$ (17)

Both T_s and T_D are roughly compatible with the onset temperature T_A of glass formation⁸ where deviation from Arrhenius relaxation behavior first becomes apparent. The onset condition u₀²/〈u²〉 = 1 for fluid congestion may thus be interpreted as a high-temperature counterpart of the Lindemann condition³⁸. This type of condition for incipient solidification was previously introduced by Laviolette and Stillinger³⁹ and we accordingly refer to it as the ‘Stillinger condition’ for the onset of the ‘congested’ fluid state.

Conclusions

We have described a new ‘localization model’ for the relaxation of glass-forming materials. This model accurately describes relaxation data for a variety of simulated and experimental glass formers, suggesting that it may provide a universal relationship between localization length-scale and relaxation time. The exact quantitative form of this relationship depends on the nature of the glass former under consideration: a parameter α reflects the nature of the inter- and intra-molecular forces and their effects on the temperature dependence of the local packing anisotropy; parameters u₀² and τ₀ reflect the onset temperature T_A (and thus the fragility or temperature breadth²⁰) of glass formation.

Since previous work has established that the Debye-Waller factor is directly connected to the fast beta relaxation time¹⁹, this model also implicitly relates the structural relaxation time to the fast (picosecond timescale) beta relaxation time. Given that the fast beta relaxation time represents the elementary structural relaxation process in glass-forming liquids, and also has been directly implicated in controlling processes such as transport and chemical degradation in glassy matrices⁴⁰, a relationship between fast and slow relaxation processes is of immense practical value. Furthermore, earlier proposed relations between the Debye-Waller factor and structural relaxation time have been employed in an attempt to estimate diffusion rates from fast-dynamics scattering data⁴¹, and use of the localization model should greatly improve such estimations. This will be especially useful in estimating relaxation times and diffusion rates in molecular simulations of glass-forming materials, where direct calculation of these quantities at low temperature is often prevented by prohibitively large computational time requirements.

Given the close parallels between glass formation in molecular liquids and jamming in colloids and granular media, it seems likely that the localization model describes relaxation behavior in those systems as well. Since the motion of particles in colloids can be experimentally tracked, these systems would provide an excellent setting for testing the physical underpinnings of this model by correlating direct experimental measurements of free volume shape with relaxation behavior. Validation of this model in such systems could provide substantial new insight into the physics of jamming and glass formation.

The localization model emphasizes the existence of a congested fluid regime having a definite beginning and end. The high temperature onset of this regime is demarcated by a ‘Stillinger onset condition’, while the low temperature end is demarcated by the classical Lindemann criterion for melting. Associated with each condition is an extrapolated divergence – of relaxation time at T₀ in the case of the Lindemann criterion and of localization length-scale at T_D in the case of the Stillinger condition.

The apparent universality of equation (5) implies that the free energy of activation of structural relaxation in strongly interacting fluids obeys a general limit theorem associated with particle localization. A limit theorem is also known to govern the free energy of localized polymer chains⁴². Strikingly, that limit theorem takes the same functional form as equation (5), where the free energy of chain localization in that model corresponds to the activation energy of transport in the present model. The correspondence is natural if one identifies the particle trajectories depicted in Figure 4 with the polymer chain conformations. This parallel strongly implies that the essential features of localization are highly universal, and we suggest that the broad success of the localization model reflects this universality.

Table 2.

Parameters for power-law fits to characteristic length-scales of local free volume.

	Prefactor	Exponent
Lx,pure	0.644	2.14
Ly,pure	0.270	1.54
Lz,pure	0.150	1.12
Lx,anti	0.834	2.06
Ly,anti	0.309	1.57
Lz,anti	0.165	1.26