Abstract
It has long been suggested that transitive reasoning relies on spatial representations in the posterior parietal cortex (PPC). Previous neuroimaging studies, however, have always focused on linear arguments, such as “John is taller than Tom, Tom is taller than Chris, therefore John is taller than Chris.” Using functional magnetic resonance imaging (fMRI), we demonstrate here that verbal representations contribute to transitive reasoning when it involves set-inclusion relations (e.g., “All Tulips are Flowers, All Flowers are Plants, therefore All Tulips are Plants”). In the present study, such arguments were found to engage verbal processing regions of the left inferior frontal gyrus (IFG) and left PPC that were identified in an independent localizer task. Specifically, activity in these verbal regions increased as the number of relations increased in set-inclusion arguments. Importantly, this effect was specific to set-inclusion arguments because left IFG and left PPC were not differentially engaged when the number of relations increased in linear arguments. Instead, such an increase was linked to decreased activity in a spatial processing region of the right PPC that was identified in an independent localizer task. Therefore, both verbal and spatial representations can underlie transitive reasoning, but their engagement depends upon the structure of the argument.
Keywords: fMRI, linear relation, set-inclusion relation, transitive reasoning
Introduction
Making inferences about transitive relations is one of the most common forms of human thinking. For instance, when told that “John is taller than Tom and Tom is taller than Chris,” one can easily conclude that “John is taller than Chris.” Transitive reasoning is considered a fundamental element of cognitive development (Piaget 1928; Bryant and Trabasso 1971; Wright 2000) and may provide the foundation for many other important abilities. For example, transitive reasoning may be critical for understanding dominance hierarchies in social groups (Paz et al. 2004; Grosenick et al. 2007), navigating in a spatial environment (Byrne and Johnson-Laird 1989; Goel et al. 2004), or learning mathematical concepts such as ordinality and class inclusion (Bryant and Kopytynska 1976; Newstead et al. 1985; Kallio 1988; Rabinowitz and Howe 1994). Yet, the cognitive and neural bases of transitive reasoning remain poorly understood.
It has been proposed that transitive reasoning involves the construction of an integrated spatial representation of the premises in working memory (Goodwin and Johnson-Laird 2005). For instance, when faced with the argument John is taller than Tom and Tom is taller than Chris, reasoners would construct a mental model of the form “John–Tom–Chris.” The conclusion “John is taller than Chris” would be inferred from the mental scanning of this spatial representation. Some evidence for this claim comes from the observation that linear transitive orderings such as the one above are characterized by a “distance effect.” That is, when participants are presented with several premises (e.g., “A is taller than B; B is taller than C; C in taller than D; D is taller than E; E is taller than F”), they experience more difficulty in evaluating a conclusion involving a pair of relatively close items (e.g., “B is taller than D”) than a conclusion involving a more distant pair (e.g., “B is taller than E”) (Potts 1972, 1974; Trabasso et al. 1975; Prado et al. 2008). Such a behavioral distance effect supports the idea that transitive items are arranged along a spatial mental line (A–B–C–D–E–F): close items (BD) are less easily distinguishable than far items (BE) along this line. Consistent with a link between transitive reasoning and spatial processing, linear transitive orderings are also associated with a “neural” distance effect (i.e., increased activity as distance between items decreases) in a brain region typically associated with spatial processing, that is, the posterior parietal cortex (PPC) (Hinton et al. 2010; Prado, Noveck, et al. 2010).
It is unclear, however, whether such an integrated spatial representation underlies all forms of transitive reasoning or is specific to linear transitive orderings. Indeed, transitive reasoning is not restricted to linear relations. For example, many researchers have emphasized that the universal quantifier “all” also allows for transitive inferences (Griggs 1976; Griggs and Osterman 1980; Nguyen and Revlin 1993; Barrouillet 1996; Favrel and Barrouillet 2000). This property explains how reasoners can infer statements such as “All Tulips are Plants” from the premises “All Tulips are Flowers” and “All Flowers are Plants.” Such transitive problems have been termed “set-inclusion” problems in the behavioral literature (Because the universal quantifier all defines categorical propositions, set-inclusion problems can also be referred to as “categorical” problems [Goel 2007; Reverberi et al. 2010]. However, the term categorical may also refer to problems that contain other quantifiers, such as “some” and “no.” For example, the argument “No As are Bs, Some Cs are As, therefore Some Cs are not Bs” may also be considered categorical [Hurley 2003]. These sorts of arguments have a structure much less similar to traditional linear transitive problems than set-inclusion arguments and are typically not referred to as transitive problems in the reasoning literature. The present study is only concerned with transitive reasoning. Therefore, it focuses on arguments containing exclusively the quantifier all, as those have been considered transitive in behavioral research [Nguyen and Revlin 1993; Barrouillet 1996; Favrel and Barrouillet 2000].). Unlike linear orderings, set-inclusion problems are typically not associated with a distance effect. In fact, when participants evaluate a set-inclusion problem with several premises (e.g., “All As are Bs; All Bs are Cs; All Cs are Ds; All Ds are Es; All Es are Fs”), they can experience more difficulty in evaluating a conclusion involving a pair of relatively distant items (e.g., “All Bs are Es”) than a conclusion involving a close pair (e.g., “All Bs are Ds”) (i.e., a “reverse” distance effect) (Griggs 1976; Griggs and Osterman 1980; Carlson et al. 1992; Barrouillet 1996; Favrel and Barrouillet 2000). The fact that a behavioral distance effect is typically not observed in set-inclusion problems suggests that participants might not integrate the premises of set-inclusion arguments into a unified spatial representation (as they might do for linear problems) (Griggs 1976; Griggs and Osterman 1980; Carlson et al. 1992). As suggested by Favrel and Barrouillet (2000), this might be because set-inclusion orderings involve items that represent sets of objects rather than single elements. Such sets might be relatively difficult to map onto a single analogical dimension (e.g., size, age, etc.), and reasoners might thus hold propositional representations of set-inclusion premises in verbal rather than spatial working memory. This view is broadly consistent with several theories suggesting that reasoning calls upon verbal rules of inference that link propositional representations of the premises (Rips 1994; Braine and O'Brien 1998). Importantly, this account is able to explain the reverse distance effect in set-inclusion problems: the more premises there are to consider, the more verbal rules there are to apply and the more difficult the problem. It also predicts that, contrary to what is observed for linear arguments, activity in verbal brain regions should increase with the number of premises being integrated (i.e., a reverse neural distance effect should be observed in verbal regions). Overall, this account posits that the neural bases of transitive reasoning might be heterogeneous and depend upon the type of argument considered (i.e., set-inclusion vs. linear).
To date, no studies have investigated whether increasing the number of premises of set-inclusion arguments is associated with enhanced activity in verbal brain regions. This lack of evidence leaves the behavioral reverse distance effect open to other interpretations. For example, some have argued that the effect might stem from the step-by-step integration of “spatial” (rather than verbal) representations of the premises (Favrel and Barrouillet 2000). According to this account, intermediate conclusions would be drawn based on isolated spatial representations of pairs of premises. For instance, the premises “All As are Bs” and “All Bs are Cs” could be integrated in a temporary spatial model representing the statement “All As are Cs.” This temporary representation could subsequently be integrated with the premise “All Cs are Ds” to infer that “All As are Ds.” This hypothesis also accounts for the behavioral reverse distance effect: the more premises that need to be integrated, the more spatial representations need to be constructed and the longer the response time. However, it does not predict that activity in verbal brain regions should increase with the number of premises being integrated. Instead, it predicts a reverse neural distance effect in brain regions supporting spatial processing. In sum, this interpretation raises the possibility that set-inclusion and linear arguments rely on the same type of spatial representations, despite being associated with different behavioral signatures.
Given the lack of consensus regarding the type of representations that may underlie set-inclusion arguments, we used functional magnetic resonance imaging (fMRI) to investigate the role of verbal and spatial brain regions in transitive reasoning with set-inclusion and linear arguments. A key and novel aspect of our study is that 2 localizer tasks were used to identify regions of interest (ROIs) involved in verbal and spatial processing on a subject-by-subject basis. Participants were then asked to evaluate set-inclusion and linear arguments containing 3 premises. The number of premises that were necessary to assess the validity of the conclusion was systematically varied (see Table 1). In some arguments (hereafter referred to as 2-premise arguments), only 2 of the 3 premises needed to be integrated to evaluate the conclusion. In other arguments (hereafter referred to as 3-premise arguments), integrating all 3 premises was necessary to evaluate the conclusion. If set-inclusion and linear arguments do not rely on the same type of representations, one should observe a dissociation between their neural correlates. Specifically, there should be more activity for 3- than 2-premise set-inclusion arguments (i.e., a reverse neural distance effect) in verbal ROIs, whereas there should be more activity for 2- than 3-premise linear arguments (i.e., a neural distance effect) in spatial ROIs (Hinton et al. 2010; Prado, Noveck, et al. 2010). However, if set-inclusion and linear arguments both rely on spatial representations, one should not observe a reverse neural distance effect for set-inclusion arguments in verbal ROIs. Instead, a reverse neural distance effect for set-inclusion arguments and a distance effect for linear arguments should be observed in the same spatial ROIs.
Table 1.
Sample problems used in the critical conditions of the linear and set-inclusion reasoning tasks
| Linear | Set-Inclusion | |
|---|---|---|
| 2-Premise problem | Ken is smaller than Ace | All gofs are old |
| Ace is smaller than Rob | All old things are pink | |
| Rob is smaller than Doc | Ken is a gof | |
| Ken is smaller than Rob | Ken is old | |
| 3-Premise problem | Ken is smaller than Ace | All gofs are old |
| Ace is smaller than Rob | All old things are pink | |
| Rob is smaller than Doc | Ken is a gof | |
| Ken is smaller than Doc | Ken is pink |
Note: The conclusion of each argument is underlined.
Materials and Methods
Participants
Thirty-eight healthy adults from the Chicago community participated in the study. All were right-handed native English speakers and had no reported history of neurological or psychiatric disorders. Some participants had fMRI data sets that were compromised by technical issues (i.e, poor whole-brain coverage and issues with the stimulus delivery system, n = 2), excessive head movement (i.e., greater than 4 mm, n = 4), and unacceptably low behavioral performance (i.e., lower than 60% accuracy on the critical reasoning trials, n = 2). The remaining participants (n = 30, 11 males) were aged between 22 and 30 years (mean age: 26 years). All participants gave written informed consent and were compensated $20 an hour for their time. Experimental procedures were approved by the Northwestern University Institutional Review Board.
Reasoning Tasks
Participants evaluated 2 types of transitive reasoning problems in the scanner: set-inclusion and linear orderings.
In the set-inclusion reasoning task, each problem described a series of implication relationships among 3 classes (e.g., All gofs are old, All old things are pink), such that the first class (e.g., gofs) was included in the second class (e.g., old things) and the second class was included in the third class (e.g., pink things). The third sentence in each problem stated that an imaginary character belonged to the first class (e.g., Ken is a gof) (see Table 1, right column). The first class was characterized by a one-syllable name that was different in each problem (e.g., gofs, trabs, nasps, progs, mabs, blons, zods, etc.). The second and third classes were described by the following adjectives: tall, short, big, small, old, young, fast, slow, brown, red, black, blue, green, white, pink. Critically, although all arguments had 3 premises, they varied regarding the number of premises that needed to be considered to evaluate the conclusion. In the 2-premise condition (9 arguments with a true conclusion and 3 with a false conclusion), only 2 premises were necessary to answer the problem (see Table 1, upper right cell) (Our behavioral and fMRI analyses of the reasoning tasks exclusively focused on valid trials. Therefore, we included in the design more valid than invalid arguments in order to maximize the number of trials that contributed to such analyses. We acknowledge that such an unbalanced ratio of valid/invalid arguments might seem unrepresentative of real-world problems. However, it is important to note that this ratio was kept constant across critical conditions (2-premise problems, 3-premise problems) and reasoning tasks (set-inclusion, linear). Therefore, none of our results related to differences between 2- and 3-premise problems in set-inclusion and linear tasks can be explained by an unbalanced ratio of valid/invalid problems.). In the 3-premise condition (9 arguments with a true conclusion and 3 with a false conclusion), the 3 premises were necessary to evaluate the conclusion (see Table 1, lower right cell). In other words, both 2-premise and 3-premise problems involved the exact same 3 premises, for example, “All gofs are old, All old things are pink, Ken is a gof.” However, evaluating the conclusion of a 2-premise problem (e.g., “Ken is old”) only required reasoners to integrate the first and the third premise (i.e., “All gofs are old” and “Ken is a gof”), whereas evaluating the conclusion of a 3-premise problem (e.g., “Ken is pink”) required them to integrate the first, the second, and the third premise altogether (i.e., “All gofs are old, All old things are pink, and Ken is a gof”). Note that this design ensured that reasoners were required to use the third premise in both 2- and 3-premise problems. Therefore, although the first 2 premises differed from the third premise in terms of sentence structure (the first 2 premises are universal, whereas the third one is particular), participants did not have to switch between different sentence structures to a greater extent in 3- than 2-premises problems (i.e, they always had to use at least one universal premise and exactly one particular premise). To discourage participants from using shortcut strategies and developing expectations during the task, we also included a number of filler trials in which the conclusion included a negation (“All babs are slow, All slow things are blue, Joe is not slow, therefore Joe is not a bab”) (5 arguments with a true conclusion and 5 arguments with a false conclusion) or was indeterminate (e.g., “All mods are pink, All pink things are tall, Jon is pink, therefore Jon is a mod”) (2 arguments). Five trials were presented in the practice session. Different sets of stimuli were used in the practice and in the scanning sessions.
In the linear reasoning task, each problem described the linear relationships between 4 imaginary characters (each of whom was characterized with a one-syllable name whose first letter was unique) (see Table 1, left column). Six different prepositions were used in the task (“taller, shorter, bigger, smaller, older, younger, faster, slower”), but only a single preposition was used throughout a given argument. As for set-inclusion problems, all linear problems had 3 premises but varied regarding the number of premises that needed to be considered to evaluate the conclusion (i.e., 2- vs. 3-premise arguments). 2-Premise problems (9 arguments with a true conclusion and 3 with a false conclusion) only required participants to integrate 2 premises to evaluate the conclusion (see Table 1, upper left cell). 3-Premise problems, however, required participants to integrate all 3 premises to evaluate the conclusion (see Table 1, lower left cell). We also included a number of filler trials in which the conclusion included a negation (e.g., “Bee is younger than Ted, Ted is younger than Rae, Rae is younger than Jon, therefore Jon is not younger than Bee”) (5 arguments with a true conclusion and 5 arguments with a false conclusion) or was indeterminate (e.g., “Moe is younger than Liz, Ben is younger than Liz, Liz is younger than Gus, therefore Moe is younger than Ben”) (2 arguments). Five trials were presented in the practice session. Different sets of stimuli were used in the practice and in the scanning sessions.
Importantly, the design of the above tasks made it possible to measure the effect of varying one parameter critical to reasoning (i.e., the number of premises needed to evaluate the conclusion) while keeping constant potentially confounding factors such as semantic content of the premises or superficial structure of the problems. Such a parametric design allowed us to not only investigate the effects of varying the number of premises in set-inclusion and linear problems separately but to also directly compare the size of these effects in both verbal and spatial ROIs.
Localizer Tasks
Two independent localizer tasks were used to identify the brain regions involved in spatial and verbal processing on a subject-by-subject basis. Both tasks have been described elsewhere in full detail (Prado, Mutreja, et al. 2011) but are explained briefly below.
To localize the brain regions involved in verbal processing, we used a word rhyming task. In each trial of this task, participants were asked to decide whether 2 visually presented words rhymed or not. Orthography and phonology were manipulated independently in the task. That is, the 2 words could have similar orthography and similar phonology (e.g., dime–lime; 12 trials), similar orthography but different phonology (e.g., pint–mint; 12 trials), different orthography but similar phonology (e.g., jazz–has; 12 trials), or different orthography and different phonology (e.g., press–list; 12 trials).
To localize the brain regions involved in spatial processing, we used a numerosity comparison task. In each trial of this task, participants were asked to decide which of 2 visually presented dot arrays were composed of the larger number of dots. The numerical comparison involved a 1:3 ratio (i.e., 12 dots vs. 36 dots; 24 trials), a 1:2 ratio (i.e., 18 dots vs. 36 dots; 24 trials), or a 2:3 ratio (i.e., 24 dots vs. 36 dots; 24 trials).
For each task, 12 trials of each condition were presented in the practice session. Different sets of stimuli were used in the practice and in the scanning sessions.
Experimental Procedure
Stimulus timing was identical in both transitive reasoning tasks. In each trial, 3 premises and a conclusion appeared on the screen one at a time (first premise at 0 s, second at 2 s, third at 4 s, and conclusion at 6 s). The participants were instructed to evaluate the validity of the conclusion as soon as they could by pressing 1 of 2 response keys. The trial ended with either the participant’s response or 8 s after the presentation of the conclusion if the participant failed to respond. Each trial was directly followed by a period of visual fixation (ranging from 2600 to 3400 ms) during which no response could be made.
For both localizer tasks, a trial started with the presentation of a first stimulus (dot array or word, depending on the task) for 800 ms, followed by a blank screen for 200 ms. A second stimulus (dot array or word, depending on the task) was then presented for 800 ms, followed by a red fixation square indicating the need to make a response during a subsequent interval ranging from 2800 to 3600 ms.
Additionally, we included 18 null trials in each reasoning task and 24 null trials in each localizer task. The structure of these null trials was identical in all tasks. Specifically, a blue square was presented for 1800 ms, and participants were asked to press a key when the blue square turned red (the red square was presented for a variable interval ranging from 2800 to 3600 ms). These null trials were included in order to improve estimation and removal of overlapping responses from adjacent trials in the stimulus sequence (Dale 1999). They also provided a low-level baseline against which the conditions of interest could be compared, while controlling for motor activity related to button presses.
Each task (except the rhyming task) was decomposed into 2 functional runs. The rhyming task was administered in one single run. The order of trial presentation within each run was optimized for estimation efficiency using optseq2 (http://surfer.nmr.mgh.harvard.edu/optseq/) (Dale 1999). Task order was fully counterbalanced across participants. Behavioral responses were recorded using an MR-compatible keypad placed below the right hand. Visual stimuli were generated using E-prime software (Psychology Software Tools, Pittsburgh, PA) and projected onto a translucent screen that was viewed by the participants through a mirror attached to the head coil.
Data Acquisition
Images were collected using a Siemens 3-T TIM Trio MRI scanner (Siemens Healthcare, Erlangen, Germany) at Northwestern University’s Center for Advanced Magnetic Resonance Imaging. The fMRI blood oxygenation level dependent signal was measured with a susceptibility weighted single-shot echo planar imaging sequence. The following parameters were used: time echo (TE) = 20 ms, flip angle = 80°, matrix size = 128 × 120, field of view = 220 × 206.25 mm, slice thickness = 3 mm (0.48 mm gap), number of slices = 32, time repetition (TR) = 2000 ms.
Before functional image acquisition, a high resolution T1-weighted 3D structural image was acquired for each subject (TR = 1570 ms, TE = 3.36 ms, matrix size = 256 × 256, field of view = 240 mm, slice thickness = 1 mm, number of slices = 160).
fMRI Data Analysis
Preprocessing
Data analysis was performed using SPM8 (Statistical Parametric Mapping) (www.fil.ion.ucl.ac.uk/spm). The first 6 images of each run were discarded to allow for T1 equilibration effects. The remaining functional images were corrected for slice acquisition delays, spatially realigned to the first image of the first run to correct for head movements, and spatially smoothed with a cubic Gaussian filter (8-mm full width at half-maximum). Prior normalizing images with SPM8, we used the ArtRepair software (Mazaika et al. 2009) (http://cibsr.stanford.edu/tools/ArtRepair/ArtRepair.htm) to 1) suppress residual fluctuations due to large head motion and 2) identify volumes with significant artifact and outliers relative to the global mean signal (2% from the global mean). Volumes showing rapid scan-to-scan movements of greater than 3 mm were excluded via interpolation of the 2 nearest nonrepaired volumes. Interpolated volumes were then partially deweighted when first-level models were calculated on the repaired images (Mazaika et al. 2007). No participant had more than 2% of the total number of volumes replaced in a single run. Finally, all functional volumes were normalized into standard stereotaxic space using the Montreal Neurological Institute (MNI) template.
Processing
Event-related statistical analysis was performed according to the general linear model (Josephs et al. 1997). In both reasoning tasks, activation was modeled as epochs with onsets time locked to the presentation of the conclusion and with duration matched to the trial response time. Additionally, the 3 premises of each problem were modeled as events of no interest. In both localizer tasks, activation was modeled as 2-s epochs with onsets time locked to the presentation of the first stimulus. Similarly, activity associated with null trials was modeled as 2-s epochs with onsets time locked to the presentation of the blue square in all 4 tasks. For both transitive reasoning tasks, although problems with true and false conclusions were included in the model, only nonfiller problems with a true conclusion were considered of interest in the behavioral and fMRI analyses. All epochs were convolved with a canonical hemodynamic response function. The time series data were high-pass filtered (1/128 Hz), and serial correlations were corrected using an autoregressive AR (1) model.
ROI Analyses
ROIs were defined using the group-constrained subject-specific method implemented in the spm_ss toolbox (http://www.nitrc.org/projects/spm_ss). This method, described in detail elsewhere (Fedorenko et al. 2010), allows one to automatically identify subject-specific activation sites associated with functional localizer tasks. It involved the following 4 steps. First, localizer contrasts aimed at identifying regions involved in spatial and verbal processing were calculated for each individual. Specifically, whole-brain activity resulting from comparing dot arrays was contrasted to null trials (in the numerosity comparison task) to generate the spatial localizer contrast, whereas whole-brain activity resulting from reading words was contrasted to null trials (in the rhyming task) to generate the verbal localizer contrast. Each individual contrast map was thresholded with a height threshold of P < 0.005 (uncorrected). Second, these individual maps were overlaid on top of one another to generate a probabilistic overlap map displaying, for each voxel, the number of subjects who showed a significant effect in the localizer contrast. Third, a watershed algorithm was used to automatically divide the probabilistic map into ROIs by identifying clusters surrounding points of high overlap. Fourth, the individual localizer maps were intersected with each ROI. In other words, only those voxels that were significantly activated (P < 0.005 voxelwise) at the subject level in the localizer tasks were included in each individual ROI. Finally, neural activity associated with 2- and 3-premise reasoning problems was contrasted to activity associated with null trials and extracted from each set of subject-specific voxels activated in the localizer contrasts. Specifically, we extracted from each ROI the beta values corresponding to the following contrasts: 2-premise set-inclusion problems versus null trials, 3-premise set-inclusion problems versus null trials, 2-premise linear problems versus null trials, 3-premise linear problems versus null trials. These beta values were then averaged across subjects in each ROI. To correct for multiple comparisons, P values were adjusted using the false discovery rate (FDR) method (Benjamini and Hochberg 1995). In each ROI, we tested whether 1) 3-premise set-inclusion problems were associated with greater activity than 2-premise set-inclusion problems and 2) 2-premise linear problems were associated with greater activity than 3-premise linear problems. Therefore, such comparisons were evaluated using one-tailed FDR adjusted P values (referred to as q values).
Left Rostrolateral Prefrontal Cortex
Recent studies have proposed that the left rostrolateral prefrontal cortex (RLPFC) plays a central role in deductive reasoning (Monti et al. 2007, 2009). Because this region could not be localized by our localizer tasks, we used a voxelwise small volume correction approach to investigate its role in our transitive reasoning tasks. Specifically, we created a mask of the left RLPFC, based on previously published coordinates. This mask included all voxels within a 10 mm radius sphere centered on the average of the 2 sets of coordinates (x = −36, y = 56, z = 8 and x = −32, y = 60, z = 4) reported in Monti et al. (2007). Therefore, the mask was centered on coordinates x = −34, y = 58, z = 6. A Monte–Carlo simulation conducted with the “AlphaSim” program (http://www.afni.nimh.nih.gov/afni/docpdf/alphasim.pdf) determined that a height threshold of P < 0.01 with an extent threshold of 4 voxels would reduce the probability of false positives to P < 0.01 inside the left RLPFC volume.
Error Trials Do Not Appear to Have Driven the Present Findings
To ensure that the same number of problems would be included in the analyses of the set-inclusion and linear tasks, both correct and incorrect trials from each critical condition (valid 2- and 3-premise set-inclusion and linear problems) were incorporated in the fMRI analyses. Incorrect trials are unlikely to have affected the analyses of set-inclusion problems because performance in this task was near ceiling, and no difference in accuracy was observed between 2- and 3-premise set-inclusion problems. However, because accuracy was lower for 2- than 3-premise linear problems, it remains possible that any difference (or lack of) in fMRI activity between 2- and 3-premise linear problems might result from the greater number of error trials in the 2-premise condition. To test this hypothesis, we investigated whether our findings varied with the difference in accuracy between 2- and 3-premise linear problems across participants. In other words, we correlated the difference in accuracy between 2- and 3-premise linear problems with the difference in fMRI activity between these conditions in each ROI across all subjects. We did not find any such correlations in our data (all Rs < 0.2, all Ps > 0.2). In sum, our findings do not appear to have been driven by the greater number of error trials in 2- than 3-premise linear problems.
Results
Behavioral Results
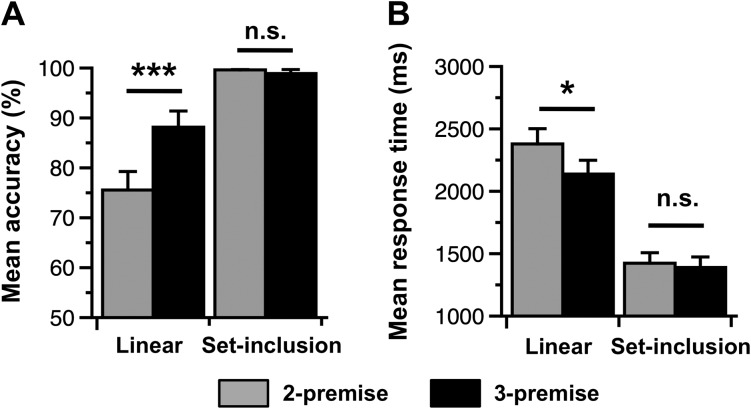
We first tested whether set-inclusion and linear problems were associated with different behavioral effects. Accuracy was submitted to a within-subject analysis of variance (ANOVA) with the factors number of premises (2-premise vs. 3-premise) and problem type (set-inclusion vs. linear) (see Fig. 1A). This analysis revealed a significant interaction between number of premises and problem type (F1,29 = 21.31, P < 0.0001). Specifically, 3-premise linear problems were evaluated more accurately than 2-premise problems (88.1% vs. 75.6%, t29 = 4.07, P = 0.0002 one tailed), whereas no difference was observed between 3-premise and 2-premise set-inclusion problems (98.9% vs. 99.6%, t29 = 1, P = 0.16 one tailed). That is, we observed a distance effect in linear problems and no distance effect in set-inclusion problems. The ANOVA also revealed a main effect of problem type, indicating that set-inclusion problems were evaluated more accurately than linear problems (99% vs. 82%, F1,29 = 33.43, P < 0.00001).
Figure 1.
Behavioral results. (A) 2-Premise linear problems were evaluated less accurately than 3-premise linear problems, whereas no difference was observed between 2- and 3-premise set-inclusion problems. (B) 2-Premise linear problems were evaluated slower than 3-premise linear problems, whereas no difference was observed between 2- and 3-premise set-inclusion problems. *q < 0.05; ***q < 0.001; n.s., not significant.
An analogous ANOVA on response time indicated a tendency for an interaction between number of premises and problem type (F1,29 = 2.91, P = 0.09), such that 3-premise linear problems were evaluated faster than 2-premise problems (2138 vs. 2379 ms, t29 = 2.30, P = 0.01 one tailed), whereas no such difference was observed for set-inclusion problems (1424 vs. 1389 ms, t29 = 0.69, P = 0.24 one tailed) (see Fig. 1B). There was also a main effect of problem type, indicating that set-inclusion problems were evaluated faster than linear problems (1406 vs. 2259 ms, F1,29 = 59, P < 0.000001).
Therefore, we did not find that set-inclusion problems were associated with a reverse behavioral distance effect (3-premise associated with poorer performance than 2-premise problems), as suggested by previous studies (Griggs 1976; Griggs and Osterman 1980; Favrel and Barrouillet 2000). One possible explanation for this lack of difference is that participants performed near ceiling level in both the 2-premise and the 3-premise conditions of the set-inclusion task (over 98% correct). Nonetheless, consistent with previous studies (Potts 1972, 1974; Favrel and Barrouillet 2000; Prado et al. 2008), our behavioral results demonstrate that transitive arguments involving linear orderings are associated with a significant distance effect.
Imaging Results
ROIs Definition
Using a watershed algorithm to automatically segment the functional localizer maps (see Materials and Methods), we identified 2 ROIs in the verbal task and 1 ROI in the spatial task in which a majority of our subjects (>15) showed reliable activation in the localizer tasks (see Fig. 2). In the verbal task, the anterior ROI was located in the left inferior frontal gyrus (IFG) (MNI coordinates: x = −48, y = 9, z = 30; BA 44/9) and the posterior ROI was in the left PPC (MNI coordinates: x = −26, y = −60, z = 53; BA 7). In the spatial task, this ROI was located in the right PPC (MNI coordinates: x = 23, y = −66, z = 50; BA 7). As detailed in the Materials and Methods, subject-specific activation sites in the localizer tasks were identified in these ROIs.
Figure 2.
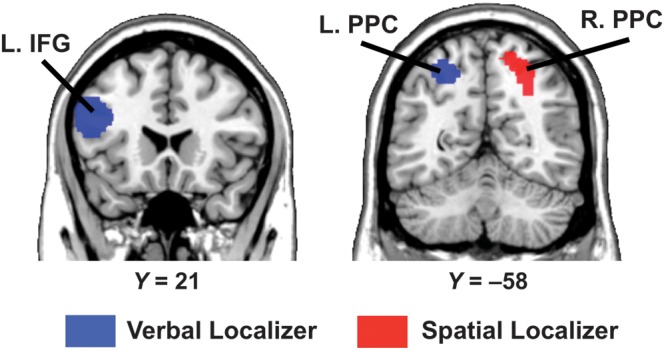
Location of the spatial and verbal ROIs identified using the spatial and verbal localizer tasks. The spatial ROI (red) was localized in the right posterior parietal cortex (R. PPC). The verbal ROIs (blue) were localized in the left inferior frontal gyrus (L. IFG) and left posterior parietal cortex (L. PPC). ROIs are overlaid on coronal slices of the MNI-normalized anatomical brain.
ROIs Results
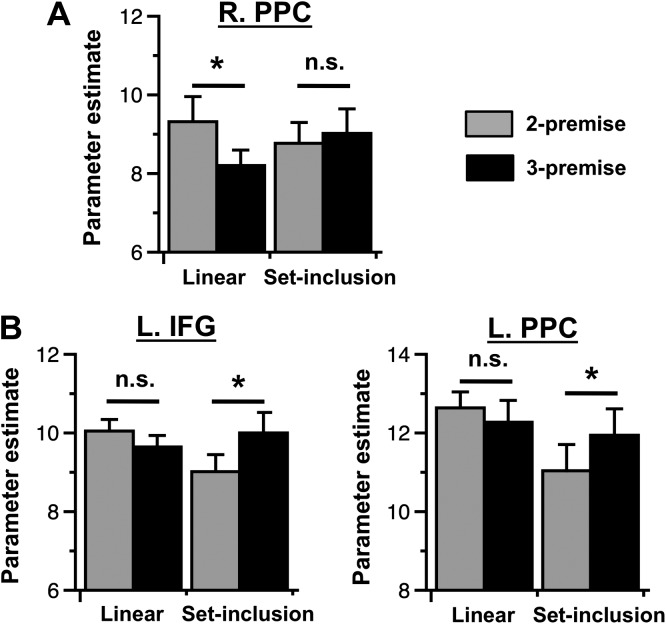
We then investigated the neural activity associated with set-inclusion and linear orderings in the verbal and spatial ROIs. In both verbal ROIs, we found more activity for 3- than 2-premise set-inclusion problems (i.e., a reverse neural distance effect) (left IFG: q = 0.036; left PPC: q = 0.036) (see Fig. 3B). These results support the claim that set-inclusion orderings involve the step-by-step integration of propositional representations of the premises (Griggs 1976; Griggs and Osterman 1980; Carlson et al. 1992). In contrast, we found no evidence for a neural distance effect associated with linear problem in these regions. That is, in neither of these verbal ROIs were 2-premise linear problems associated with greater activity than 3-premise problems (left IFG: q = 0.097; left PPC: q = 0.167). Consistent with the pattern reported above, there was a significant interaction between problem type (set-inclusion vs. linear) and number of premises (2-premise vs. 3-premise) (left IFG: q = 0.031; left PPC: q = 0.038) in both verbal ROIs (left IFG and left PPC) (see Fig. 3B).
Figure 3.
ROIs results. (A) In the right posterior parietal cortex (R. PPC) identified in the spatial localizer task, 2-premise linear problems were associated with greater activity than 3-premise linear problems, whereas no difference was observed between 2- and 3-premise set-inclusion problems. (B) In the left inferior frontal gyrus (L. IFG) and left posterior parietal cortex (L. PPC) identified in the verbal localizer task, 3-premise set-inclusion problems were associated with greater activity than 2-premise set-inclusion problems, whereas no difference was observed between 3- and 2-premise linear problems. *q < 0.05; n.s., not significant.
In the spatial ROI, there was significantly greater activity for 2- than 3-premise linear problems (q = 0.038). In other words, there was a neural distance effect for linear orderings. This effect mirrors the behavioral distance effect observed with linear orderings (lower accuracy for 2-premise than 3-premise problems) and replicates previous findings (Hinton et al. 2010; Prado, Noveck, et al. 2010). In contrast, we found no evidence for a reverse neural distance effect associated with set-inclusion problems in this region. Indeed, 3-premise set-inclusion problems were not associated with more activity than 2-premise problems (q = 0.396). In other words, we did not observe a neural distance effect for set-inclusion orderings in the spatial ROI. Consistent with the pattern reported above, there was a tendency toward a significant interaction between problem type (set-inclusion vs. linear) and number of premises (2-premise vs. 3-premise) in the spatial ROI (right PPC) (q = 0.099) (see Fig. 3A).
Left RLPFC Results
Monti and colleagues have recently proposed that even though the left IFG and PPC may be involved in reasoning, a core region of deduction is located in the left RLPFC (Monti et al. 2007, 2009). Because the left RLPFC has been found to support the integration of multiple relations in a variety of tasks (Christoff et al. 2001; Ramnani and Owen 2004), this region may underlie the crucial operation of premise integration in reasoning. This account predicts that an increase in the number of relations (or premises) to consider in a problem would be associated with enhanced RLPFC activation. We thus applied a small volume correction to the left RLPFC in order to examine the influence of the number of premises in our reasoning tasks (see Materials and Methods). We found that 3-premise set-inclusion problems were associated with greater activity in the left RLPFC than 2-premise problems (x = −26, y = 52, z = 10) (t > 2.46, P < 0.01, small volume corrected) (see Fig. 4B). Therefore, increasing the number of premises of set-inclusion arguments was associated with enhanced left RLPFC activity. In contrast, 3-premise linear problems were not associated with greater left RLPFC activity than 2-premise problems. Instead, we found greater activity for 2-premise linear problems than 3-premise linear problems (x = −34, y = 56, z = −2) (t > 2.46, P < 0.01, small volume corrected) (see Fig. 4A). Consistent with the pattern described above, there was a significant interaction between number of premises (2-premise, 3-premise) and problem type (linear, set-ordering) in the left RLPFC (x = −26, y = 52, z = 10) (t > 2.46, P < 0.01, small volume corrected) (see Fig. 4C).
Figure 4.
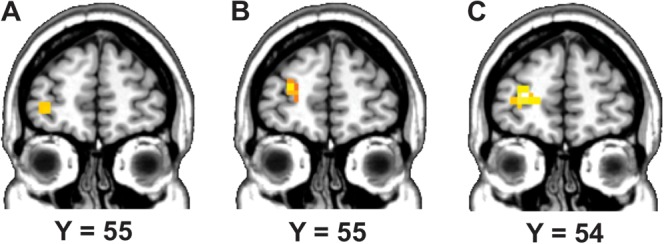
Small volume correction analysis in the left RLPFC. (A) Voxels significantly more activated in 2- than 3-premise linear problems. (B) Voxels significantly more activated in 3- than 2-premise set-inclusion problems. (C) Voxels showing a significant interaction between number of premises (2-premise, 3-premise) and problem type (linear, set-inclusion).
Discussion
Prior neuroimaging studies generally support the idea that transitive reasoning relies on a spatial representation of the problem premises (Goel and Dolan 2001; Acuna et al. 2002; Prado, Noveck, et al. 2010; Prado, Chadha, et al. 2011). Such studies, however, have focused exclusively on linear transitive orderings, such as “John is taller than Tom, Tom is taller than Chris, therefore John is taller than Chris.” In the present fMRI study, we demonstrate that transitive reasoning can also rely on verbal representations when set-inclusion relations (e.g., “All Tulips are Flowers, All Flowers are Plants, therefore All Tulips are Plants”) are involved. Much like other reasoning tasks (Prado, Van der Henst, et al. 2010; Prado, Chadha, et al. 2011), the type of representations that underlie transitive reasoning might depend upon the type of logical argument considered (e.g., linear vs. set-inclusion).
Set-Inclusion Orderings Rely on Verbal Representations
Behavioral studies investigating set-inclusion orderings have found that conclusions involving pairs of relatively distant items are typically more difficult to evaluate than conclusions involving closer pairs (Griggs 1976; Griggs and Osterman 1980; Carlson et al. 1992; Barrouillet 1996; Favrel and Barrouillet 2000). It has thus been suggested that solving set-inclusion problems might involve the step-by-step coordination of isolated verbal representations of the premises. Consistent with this proposal, we found that 3-premise set-inclusion problems were associated with greater activity than 2-premise problems in 2 brain regions (i.e., the left IFG and the left PPC) that were localized by a verbal processing (i.e., word rhyming) task. This was the case despite the fact that accuracy in the set-inclusion task was near ceiling and thus did not differ between 2- and 3-premise problems. This effect was also specific to set-inclusion problems, as no difference between 3- and 2-premise linear problems was observed in any of the brain regions identified by the verbal localizer task. Taken together, these results demonstrate that, even in the absence of a significant behavioral difference, increasing the number of premises of transitive reasoning problems is related to increased activity in verbal brain regions when those problems involve set-inclusion, but not linear, relations.
The verbal localizer task required participants to make phonological judgments based on words that were presented sequentially. Such a task clearly includes a verbal working memory component (i.e., the first word has to be held in verbal working memory in order to make the rhyming judgment). Consistent with this observation, neuroimaging studies indicate that both of the regions activated in the rhyming task (i.e., the left IFG and left PPC) are critical nodes of the verbal working memory network (Chein et al. 2003). For example, left PPC and left IFG have been implicated in the storage and subvocal rehearsal of phonological information, respectively (Chein et al. 2003; Jonides et al. 2005; Smith et al. 1998). Both regions are active when serial order has to be maintained in verbal working memory (Wager and Smith 2003; Majerus et al. 2006; Van Opstal et al. 2009). Overall, these findings are consistent with the claim that the premises of set-inclusion arguments are 1) stored as isolated propositional representations and 2) coordinated in a step-by-step manner to derive conclusions (Favrel and Barrouillet 2000). Such a step-by-step coordination has been widely thought to rely on formal rules of inference akin to rules of syntax or grammar in natural language (Rips 1994; Braine and O'Brien 1998). Although our study cannot directly provide evidence for this claim, it is interesting to note that the left IFG (specifically BA 44) is thought to be critical for rule-based grammar processing in natural language (Dapretto and Bookheimer 1999; Grodzinsky and Friederici 2006; Grodzinsky and Santi 2008). This region may thus also underlie rule-based processing in reasoning (Reverberi et al. 2007, 2010; Prado, Van Der Henst, et al. 2010; Prado, Chadha, et al. 2011). As suggested by Hagoort (2005), the systematic involvement of the left IFG in tasks requiring syntactic processing may also indicate a more general role for this region in linking subordinate linguistic representations into superordinate structures. In our experiment, it is possible that premises of set-inclusion arguments are stored as verbal representations in the left PPC, consistent with the role of this region in verbal working memory (Ravizza et al. 2004). The left IFG might be necessary to retrieve these isolated propositional representations and combine them in a step-by-step manner. In any case, our study reveals that set-inclusion orderings are supported by verbal mechanisms, whereas linear orderings are not.
Why would some forms of transitive reasoning (i.e., set-inclusion arguments) rely on verbal representations but not other forms (i.e., linear arguments)? As suggested by several researchers, it is possible that different kinds of processes underlie reasoning, depending on the type of argument processed (Mani and Johnson-Laird 1982; Prado, Van Der Henst, et al. 2010; Reverberi et al. 2010; Prado, Chadha, et al. 2011). For example, Mani and Johnson-Laird (1982) have argued that the initial stage of understanding a reasoning problem always involves a verbal (or propositional) representation of the premises. This propositional representation might then serve as the basis for constructing a spatial mental model (structurally similar to the content of the problem), and reasoners can then discard the initial propositional representation. Mani and Johnson-Laird (1982) further suggested that, in some cases, reasoners may not construct spatial mental models and only rely on propositional representations. One such case is when several mental models are compatible with a reasoning problem. Interestingly, linear arguments such as those used in the current study are only compatible with one single mental model (e.g., Ken–Ace–Rob–Doc for the problem in the left column of Table 1). However, set-inclusion problems are ambiguous because each universal premise is compatible with 2 different mental models. For example, the premise “All gofs are old” can be represented by a model in which “every” old thing is a gof (the set gofs is equivalent to the set old things) or by a model in which “only some” old things are gofs (the set gofs is included in but smaller than the set old things) (Favrel and Barrouillet 2000). Because they are compatible with several mental models, set-inclusion relations might thus be more easily represented verbally than spatially.
More generally, the idea that arguments involving categorical relations (such as those involving the preposition all but also some or no) rely on verbal representations is consistent with prior neuroimaging findings. For example, in an early study by Goel et al. (2000), categorical syllogisms were found to engage the left IFG (BA 44/45) irrespective of their semantic content. More recently, Reverberi et al. (2010) demonstrated that the left IFG (BA 44/45) is activated during both the encoding and the integration of categorical premises. In fact, activation of the left IFG during studies investigating categorical reasoning appears to be highly consistent across studies, as shown by a recent quantitative meta-analysis of the literature (Prado, Chadha, et al. 2011). None of the previous studies, however, have formally identified the brain regions involved in verbal processing in the left IFG. By doing so and showing that these regions are engaged in a transitive reasoning task involving categorical relations (i.e., set-inclusions), our study confirms and extends earlier findings regarding the link between categorical reasoning and verbal processing.
Linear Orderings Rely on Spatial Representations
Although no difference between 3- and 2-premise linear problems was observed in verbal regions, we found that fMRI activity in a region of the right PPC involved in visuospatial processing was inversely related to the number of relevant premises of linear arguments. In other words, fMRI activity was greater for 2- than 3-premise linear problems in this region, a finding that mirrors the behavioral distance effect observed in this task (i.e., error rates and response times (RT) were also greater for 2- than 3-premise linear problems). This finding replicates the results from 2 previous studies that have also demonstrated a neural distance effect (i.e., an increase of activity as the distance between transitive items decreases) in the PPC in linear transitive reasoning tasks (Hinton et al. 2010; Prado, Noveck, et al. 2010). The behavioral and neural distance effects in linear orderings support the idea that the premises of linear transitive arguments are integrated into a unified spatial representation. Along this representation, close items (e.g., items in the conclusion of 2-premise problems) are less easily distinguishable than relatively distant items (e.g., items in the conclusion of 3-premise problems) and are thus associated with increased activity in regions supporting spatial processing and decreased performance. More generally, these results are consistent with a recent meta-analysis showing that neuroimaging studies have consistently associated linear transitive reasoning with activity in the right PPC (Prado, Chadha, et al. 2011). This type of activity has often been interpreted in the literature as reflecting an increase in visuospatial demands (Goel and Dolan 2001; Prado, Chadha, et al. 2011). However, our study is the first reasoning study to use an independent task to localize, on a subject-by-subject basis, the brain system involved in visuospatial processing in the PPC. By showing that this brain system underlies the distance effect associated with linear transitive arguments, our study demonstrates a strong link between linear transitive orderings and visuospatial processing.
It is interesting to note that we did not observe any difference between 2- and 3-premise set-inclusion problems in the right PPC. This null finding could suggest that, unlike linear orderings, set-inclusion orderings might not make use of spatial representations. However, such a lack of effect is difficult to interpret because behavioral performance was near ceiling in the set-inclusion task, and we did not observe any difference between 3- and 2-premise problems in terms of either accuracy or RT. Therefore, we cannot rule out the possibility that a difference between 2- and 3-premise set-inclusion problems might have been observed in the right PPC had the behavioral manipulation been effective. Indeed, some researchers have suggested that the reverse behavioral distance effect typically observed with set-inclusion tasks might reflect the step-by-step integration of spatial representations of the premises (see Introduction) (Favrel and Barrouillet 2000). In contrast to this view, the present study demonstrates that set-inclusion problems are associated with a reverse neural distance effect in “verbal” brain regions, thus supporting the idea that those sorts of problems rely on verbal representations. However, future studies might test whether such problems might also be associated with a reverse neural distance effect in spatial regions when a behavioral effect is observed, therefore supporting the idea that set-inclusion problems might involve both verbal and spatial representations.
The Role of the Left RLPFC in Transitive Reasoning
In line with the current findings, a large body of neuroimaging evidence suggests that the left IFG and the bilateral PPC are generally involved in deductive reasoning (Goel 2007; Prado, Chadha, et al. 2011). In a series of recent studies, however, Monti and colleagues have proposed that another brain region, the left RLPFC, may implement the “core operations of deduction” (Monti et al. 2007, p. 1010). Studies have found that this region is central to the integration of visuospatial (Kallio 1988; Christoff et al. 2001) and semantic relations (Bunge et al. 2005; Wendelken et al. 2008). The left RLPFC might thus also be central to the integration of logical relations (i.e., premises) in deductive reasoning. This hypothesis predicts that an increase in the number of relations to integrate would be associated with increased activity in the left RLPFC. We found mixed support for this prediction. On the one hand, an increase in the number of premises of set-inclusion arguments was associated with enhanced activity in the left RLPFC (i.e., a reverse neural distance effect). This finding appears to be consistent with the idea that the left RLPFC supports relational integration in deductive reasoning. On the other hand, we also found that this effect was specific to set-inclusion problems, as 3-premise linear problems were not associated with more activity than 2-premise problems. In fact, 3-premise linear problems were related to less activity than 2-premise problems in the left RLPFC, mirroring the findings from the right PPC. These results suggest that whereas relational integration might explain left RLPFC activity in arguments involving set-inclusion (Rodriguez-Moreno and Hirsch 2009) or conditional (Monti et al. 2007, 2009) relations, this account is unlikely to explain the pattern of activity observed for linear problems. Rather such a pattern is consistent with the idea that left RLPFC activity might also reflect cognitive difficulty in the linear task (Christoff et al. 2001; van den Heuvel et al. 2003). The question of the role of the left RLPFC in deductive reasoning should be explored in future studies.
Conclusion
In summary, our study replicates the finding that transitive arguments involving linear relations make use of parietal mechanisms supporting spatial processing rather than left frontoparietal brain regions involved in verbal processing (Hinton et al. 2010; Prado, Noveck, et al. 2010). Critically, however, we also provide novel evidence that this finding depends upon the type of logical relation embedded in the transitive problem. Indeed, we demonstrate that transitive arguments relying on set-inclusion relations engage regions of the left IFG and left PPC involved in verbal processing. More generally, our study is consistent with the idea that the neural bases of deductive reasoning are fractionated and task dependent (Goel 2007; Prado, Chadha, et al. 2011). Although our findings reveal that the type of logical relation contained in a transitive argument is an important factor, there are likely others. For example, the ability to reason transitively about familiar spatial relations (e.g., Spain is south of England) has been shown to depend upon the integrity of regions involved in verbal processing, whereas these regions are not critical when the relations are not unfamiliar (e.g., Children are seated to the right of adults) (Vartanian et al. 2009). Therefore, together with the type of logical relation, the semantic content of an argument might also determine whether verbal processing mechanisms are involved in transitive reasoning.
Funding
National Institute of Child Health and Human Development (grant number HD059177) to J.R.B.
Acknowledgments
The authors would like to thank the anonymous reviewers for helpful comments on the manuscript. Conflict of Interest : None declared.
References
- Acuna B, Eliassen J, Donoghue J, Sanes J. Frontal and parietal lobe activation during transitive inference in humans. Cereb Cortex. 2002;12:1312–1321. doi: 10.1093/cercor/12.12.1312. [DOI] [PubMed] [Google Scholar]
- Barrouillet P. Transitive inferences from set inclusion relations and working memory. J Exp Psychol Learn Mem Cogn. 1996;6:1408–1422. [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc Ser B. 1995;57:289–300. [Google Scholar]
- Braine M, O'Brien D. Mental logic. Mahwah (NJ): Lawrence Erlbaum; 1998. [Google Scholar]
- Bryant P, Kopytynska H. Spontaneous measurement by young children. Nature. 1976;260:773.. [Google Scholar]
- Bryant PE, Trabasso T. Transitive inferences and memory in young children. Nature. 1971;232:456–458. doi: 10.1038/232456a0. [DOI] [PubMed] [Google Scholar]
- Bunge S, Wendelken C, Badre D, Wagner A. Analogical reasoning and prefrontal cortex: evidence for separable retrieval and integration mechanisms. Cereb Cortex. 2005;15:239–249. doi: 10.1093/cercor/bhh126. [DOI] [PubMed] [Google Scholar]
- Byrne RM, Johnson-Laird PN. Spatial reasoning. J Mem and Lang. 1989;28:564–575. [Google Scholar]
- Carlson RA, Lundy DH, Yaure RG. Syllogistic inference chains in meaningful text. Am J Psychol. 1992;105:75–99. [Google Scholar]
- Chein JM, Ravizza SM, Fiez JA. Using neuroimaging to evaluate models of working memory and their implications for language processing. J Neurolinguist. 2003;16:315–339. [Google Scholar]
- Christoff K, Prabhakaran V, Dorfman J, Zhao Z, Kroger JK, Holyoak KJ, Gabrieli JD. Rostrolateral prefrontal cortex involvement in relational integration during reasoning. Neuroimage. 2001;14:1136–1149. doi: 10.1006/nimg.2001.0922. [DOI] [PubMed] [Google Scholar]
- Dale AM. Optimal experimental design for event-related fMRI. Hum Brain Mapp. 1999;8:109–114. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<109::AID-HBM7>3.0.CO;2-W. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dapretto M, Bookheimer SY. Form and content: dissociating syntax and semantics in sentence comprehension. Neuron. 1999;24:427–432. doi: 10.1016/s0896-6273(00)80855-7. [DOI] [PubMed] [Google Scholar]
- Favrel J, Barrouillet P. On the relation between representations constructed from text comprehension and transitive inference production. J Exp Psychol Learn Mem Cogn. 2000;26:187–203. doi: 10.1037//0278-7393.26.1.187. [DOI] [PubMed] [Google Scholar]
- Fedorenko E, Hsieh PJ, Nieto-Castanon A, Whitfield-Gabrieli S, Kanwisher N. New method for fMRI investigations of language: defining ROIs functionally in individual subjects. J Neurophysiol. 2010;104:1177–1194. doi: 10.1152/jn.00032.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goel V. Anatomy of deductive reasoning. Trends Cogn Sci. 2007;11:435–441. doi: 10.1016/j.tics.2007.09.003. [DOI] [PubMed] [Google Scholar]
- Goel V, Buchel C, Frith C, Dolan RJ. Dissociation of mechanisms underlying syllogistic reasoning. Neuroimage. 2000;12:504–514. doi: 10.1006/nimg.2000.0636. [DOI] [PubMed] [Google Scholar]
- Goel V, Dolan RJ. Functional neuroanatomy of three-term relational reasoning. Neuropsychologia. 2001;39:901–909. doi: 10.1016/s0028-3932(01)00024-0. [DOI] [PubMed] [Google Scholar]
- Goel V, Makale M, Grafman J. The hippocampal system mediates logical reasoning about familiar spatial environments. J Cogn Neurosci. 2004;16:654–664. doi: 10.1162/089892904323057362. [DOI] [PubMed] [Google Scholar]
- Goodwin GP, Johnson-Laird PN. Reasoning about relations. Psychol Rev. 2005;112:468–493. doi: 10.1037/0033-295X.112.2.468. [DOI] [PubMed] [Google Scholar]
- Griggs R. Logical processing of set inclusion relations in meaningful text. Mem Cogn. 1976;4:730–740. doi: 10.3758/BF03213241. [DOI] [PubMed] [Google Scholar]
- Griggs R, Osterman L. Processing artificial set inclusion relations. J Exp Psychol Hum Learn Mem. 1980;6:39–52. [Google Scholar]
- Grodzinsky Y, Friederici AD. Neuroimaging of syntax and syntactic processing. Curr Opin Neurobiol. 2006;16:240–246. doi: 10.1016/j.conb.2006.03.007. [DOI] [PubMed] [Google Scholar]
- Grodzinsky Y, Santi A. The battle for Broca's region. Trends Cogn Sci. 2008;12:474–480. doi: 10.1016/j.tics.2008.09.001. [DOI] [PubMed] [Google Scholar]
- Grosenick L, Clement TS, Fernald RD. Fish can infer social rank by observation alone. Nature. 2007;445:429–432. doi: 10.1038/nature05511. [DOI] [PubMed] [Google Scholar]
- Hagoort P. On Broca, brain, and binding: a new framework. Trends Cogn Sci. 2005;9:416–423. doi: 10.1016/j.tics.2005.07.004. [DOI] [PubMed] [Google Scholar]
- Hinton EC, Dymond S, von Hecker U, Evans CJ. Neural correlates of relational reasoning and the symbolic distance effect: involvement of parietal cortex. Neuroscience. 2010;168:138–148. doi: 10.1016/j.neuroscience.2010.03.052. [DOI] [PubMed] [Google Scholar]
- Hurley PJ. A concise introduction to logic. 8th ed. Belmont (CA): Wadsworth; 2003. [Google Scholar]
- Jonides J, Lacey SC, Nee DE. Processes of working memory in mind and brain. Curr Dir Psychol Sci. 2005;14:2–5. [Google Scholar]
- Josephs O, Turner R, Friston K. Event-related fMRI. Hum Brain Mapp. 1997;5:1–7. doi: 10.1002/(SICI)1097-0193(1997)5:4<243::AID-HBM7>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- Kallio K. Developmental difference in the comprehension of simple and compound comparative relations. Child Dev. 1988;59:397–410. [Google Scholar]
- Majerus S, Poncelet M, Van der Linden M, Albouy G, Salmon E, Sterpenich V, Vandewalle G, Collette F, Maquet P. The left intraparietal sulcus and verbal short-term memory: focus of attention or serial order? Neuroimage. 2006;32:880–891. doi: 10.1016/j.neuroimage.2006.03.048. [DOI] [PubMed] [Google Scholar]
- Mani K, Johnson-Laird PN. The mental representation of spatial descriptions. Mem Cogn. 1982;10:181–187. doi: 10.3758/bf03209220. [DOI] [PubMed] [Google Scholar]
- Mazaika P, Hoeft F, Glover G, Reiss A. 2009. Methods and software for fMRI analysis for clinical subjects. The Organization of Human Brain Mapping, 15th Annual Meeting; 2009 Jun 18–23; San Francisco, CA. Minneapolis (MN): The Organization of Human Brain Mapping. [Google Scholar]
- Mazaika P, Whitfield Gabrieli S, Reiss A. 2007. Artifact repair for fMRI data from high motion clinical subjects. The Organization of Human Brain Mapping, 13th Annual Meeting; 2007 Jun 10–14; Florence, Italy. Minneapolis (MN): The Organization of Human Brain Mapping. [Google Scholar]
- Monti MM, Osherson DN, Martinez MJ, Parsons LM. Functional neuroanatomy of deductive inference: a language-independent distributed network. Neuroimage. 2007;37:1005–1016. doi: 10.1016/j.neuroimage.2007.04.069. [DOI] [PubMed] [Google Scholar]
- Monti MM, Parsons LM, Osherson DN. The boundaries of language and thought in deductive inference. Proc Natl Acad Sci U S A. 2009;106:12554–12559. doi: 10.1073/pnas.0902422106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newstead S, Keeble S, Manktelow K. Children’s performance on set inclusion and linear ordering relationships. Bull Psychon Soc. 1985;23:105–108. [Google Scholar]
- Nguyen DB, Revlin R. Transitive inferences from narrative relations. J Exp Psychol Learn Mem Cogn. 1993;19:1197–1210. [Google Scholar]
- Paz YMCG, Bond AB, Kamil AC, Balda RP. Pinyon jays use transitive inference to predict social dominance. Nature. 2004;430:778–781. doi: 10.1038/nature02723. [DOI] [PubMed] [Google Scholar]
- Piaget J. Judgement and reasoning in the child. London: Routledge Chapman & Hall; 1928. [Google Scholar]
- Potts G. Information processing strategies used in the encoding of linear ordering. J Verbal Learn Verbal Behav. 1972;11:727–740. [Google Scholar]
- Potts G. Storing and retrieving information about ordered relationship. J Exp Psychol Gen. 1974;103:431–439. [Google Scholar]
- Prado J, Chadha A, Booth JR. The brain network for deductive reasoning: a quantitative meta-analysis of 28 neuroimaging studies. J Cogn Neurosci. 2011;23:3483–3497. doi: 10.1162/jocn_a_00063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prado J, Mutreja R, Zhang H, Mehta R, Desroches AS, Minas JE, Booth JR. Distinct representations of subtraction and multiplication in the neural systems for numerosity and language. Hum Brain Mapp. 2011;32:1932–1947. doi: 10.1002/hbm.21159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prado J, Noveck IA, Van Der Henst JB. Overlapping and distinct neural representations of numbers and verbal transitive series. Cereb Cortex. 2010;20:720–729. doi: 10.1093/cercor/bhp137. [DOI] [PubMed] [Google Scholar]
- Prado J, Van der Henst J-B, Noveck IA. Spatial associations in relational reasoning: evidence for a SNARC-like effect. Q J Exp Psychol (Colchester) 2008;61:1143–1150. doi: 10.1080/17470210801954777. [DOI] [PubMed] [Google Scholar]
- Prado J, Van Der Henst JB, Noveck IA. Recomposing a fragmented literature: how conditional and relational arguments engage different neural systems for deductive reasoning. Neuroimage. 2010;51:1213–1221. doi: 10.1016/j.neuroimage.2010.03.026. [DOI] [PubMed] [Google Scholar]
- Rabinowitz FM, Howe ML. Development of the middle concept. J Exp Child Psychol. 1994;57:418–448. doi: 10.1006/jecp.1994.1020. [DOI] [PubMed] [Google Scholar]
- Ramnani N, Owen AM. Anterior prefrontal cortex: insights into function from anatomy and neuroimaging. Nat Rev Neurosci. 2004;5:184–194. doi: 10.1038/nrn1343. [DOI] [PubMed] [Google Scholar]
- Ravizza SM, Delgado MR, Chein JM, Becker JT, Fiez JA. Functional dissociations within the inferior parietal cortex in verbal working memory. Neuroimage. 2004;22:562–573. doi: 10.1016/j.neuroimage.2004.01.039. [DOI] [PubMed] [Google Scholar]
- Reverberi C, Cherubini P, Frackowiak RSJ, Caltagirone C, Paulesu E, Macaluso E. Conditional and syllogistic deductive tasks dissociate functionally during premise integration. Hum Brain Mapp. 2010;31:1430–1445. doi: 10.1002/hbm.20947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reverberi C, Cherubini P, Rapisarda A, Rigamonti E, Caltagirone C, Frackowiak RSJ, Macaluso E, Paulesu E. Neural basis of generation of conclusions in elementary deduction. Neuroimage. 2007;38:752–762. doi: 10.1016/j.neuroimage.2007.07.060. [DOI] [PubMed] [Google Scholar]
- Rips L. The psychology of Proof. Cambridge (MA): MIT Press; 1994. [Google Scholar]
- Rodriguez-Moreno D, Hirsch J. The dynamics of deductive reasoning: an fMRI investigation. Neuropsychologia. 2009;47:949–961. doi: 10.1016/j.neuropsychologia.2008.08.030. [DOI] [PubMed] [Google Scholar]
- Smith EE, Jonides J, Marshuetz C, Koeppe RA. Components of verbal working memory: evidence from neuroimaging. Proc Natl Acad Sci U S A. 1998;95:876–882. doi: 10.1073/pnas.95.3.876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trabasso T, Riley CA, Wilson EG. The representation of linear order and spatial strategies in reasoning: a developmental study. In: Falmagne R, editor. Reasoning: representation and process. Hillsdale (NJ): Erlbaum; 1975. pp. 201–229. [Google Scholar]
- van den Heuvel OA, Groenewegen HJ, Barkhof F, Lazeron RH, van Dyck R, Veltman DJ. Frontostriatal system in planning complexity: a parametric functional magnetic resonance version of Tower of London task. Neuroimage. 2003;18:367–374. doi: 10.1016/s1053-8119(02)00010-1. [DOI] [PubMed] [Google Scholar]
- Van Opstal F, Fias W, Peigneux P, Verguts T. The neural representation of extensively trained ordered sequences. Neuroimage. 2009;47:367–375. doi: 10.1016/j.neuroimage.2009.04.035. [DOI] [PubMed] [Google Scholar]
- Vartanian O, Goel V, Tierney M, Huey ED, Grafman J. Frontotemporal dementia selectively impairs transitive reasoning about familiar spatial environments. Neuropsychology. 2009;23:619–626. doi: 10.1037/a0015810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wager TD, Smith EE. Neuroimaging studies of working memory: a meta-analysis. Cogn Affect Behav Neurosci. 2003;3:255–274. doi: 10.3758/cabn.3.4.255. [DOI] [PubMed] [Google Scholar]
- Wendelken C, Nakhabenko D, Donohue S, Carter C, Bunge S. “Brain is to thought as stomach is to??”: investigating the role of rostrolateral prefrontal cortex in relational reasoning. J Cogn Neurosci. 2008;20:682–693. doi: 10.1162/jocn.2008.20055. [DOI] [PubMed] [Google Scholar]
- Wright B. Reconceptualizing the transitive inference ability: a framework for existing and future research. Dev Rev. 2000;21:375–422. [Google Scholar]