Modulation of Conduction Velocity by Nonmyocytes in the Low Coupling Regime

Abstract

This paper explores the conditions under which nonmyocytes, when electrically coupled to myocytes, act as a passive load during the depolarization phase. Using theoretical arguments and numerical simulations in a tissue incorporating fibroblasts, the passive load approximation is shown to be accurate at low coupling conductances (< 2 nS). In this case, the effect on conduction velocity can be expressed as a function of the elevation in resting potential and the coupling only.

I. Introduction

There are several physiological scenarios in which the electrical interactions between cardiac myocytes and nonmyocytes are important. First, fibroblasts are more numerous than myocytes in the heart and under certain diseased states, can locally proliferate and possibly couple to the myocytes, affecting electrical activity [1]–[3]. Second, the presence of fibroblasts in ischemic or scarred regions represents a possible target for cell therapy to restore normal electrical conduction [4]. Finally, the use of autologous nonmyocytes such as myoblasts or mesenchymal stem cells has been proposed to restore cardiac structure and function [5]. Recent studies have suggested that the success of this cell therapy was affected by the quality of myocyte-nonmyocyte electrical interactions [6]. Because the electrical activity in one cell type can affect the behavior of the other it is critical to understand the mechanism of the potential interactions.

While nonexcitable, these nonmyocytes are not passive. However, when the time constant of nonmyocyte activation is larger than the rising time of the action potential, nonmyocytes are expected to act as a passive load during the depolarization process. Because the electrical activity of a myocyte-nonmyocyte pair is driven by the myocyte action potential [1], this time constant is expected to also depend on the coupling resistance. This paper describes in terms of coupling and nonmyocyte properties the conditions under which general nonmyocytes act as a passive load. The consequences on conduction velocity (CV) are explored in a tissue model incorporating recent detailed fibroblast models [7], [8], reproducing a setup in which the effect on CV has been demonstrated in vitro [3]. The simulations reveal the range of coupling conductances for which passive load approximation is valid and explain how the CV change with coupling is not always monotonic.

II. Methods

A. Mathematical Formulation

The monodomain propagation equations for a homogeneous mixture of two cell types can be formulated in a way similar to the bidomain model:

$${\beta }_m{c}_m\frac{\partial V_m}{\partial t}=\nabla \cdot {\sigma }_m\nabla V_m-{\beta }_m{c}_m{I}_{\text{ion},m}(V_m,q_m)-g_c(V_m-V_f)$$ (1)

$${\beta }_f{c}_f\frac{\partial V_f}{\partial t}=\nabla \cdot {\sigma }_f\nabla V_f-{\beta }_f{c}_f{I}_{\text{ion},f}(V_f,q_f)-g_c(V_f-V_m).$$ (2)

The indices m and f stand for myocyte and nonmyocyte (fibroblast) respectively. The surface-to-volume ratio (in cm⁻¹) is denoted by β, the membrane capacitance per unit area (μF/cm²) by c, the tissue conductance (mS/cm) by σ, the ionic current density (pA/pF) by I_ion,, the membrane state variables by q, and the myocyte-nonmyocyte coupling density per unit volume (mS/cm³) by g_c.

The coupling strength g_c can be expressed as a function of experimentally relevant microstructure parameters by considering that the discrete coupling conductance G_c (in nS) between one myocyte and one nonmyocyte spreads out over a discretization volume (Vol) associated with a nonmyocyte. For a nonmyocyte of capacitance C_f (in pF), this volume is identified as C_f/(β_fc_f), i.e., the capacitance divided by the capacitance per unit volume, leading to the formula

$$g_c=\frac{G_c}{Vol}=\frac{G_c{\beta }_f{c}_f}{C_f}.$$ (3)

The factor β_fc_f (in μF/cm³) can be interpreted as the nonmyocyte density and the capacitance C_f as a measure of nonmyocyte size.

B. Low Coupling Approximation

Experimental recordings [9] and numerical simulations [7], [8], [10], [11] have shown that the nonmyocyte membrane potential V_f varies slowly during the upstroke phase of the myocyte, unless the myocyte-nonmyocyte coupling is strong. Under the hypothesis V_f (t) = V̅_f = constant, Eq. (1) becomes equivalent to the monodomain propagation equation

$${\beta }_m{c}_m\frac{\partial V_m}{\partial t}=\nabla \cdot {\sigma }_m\nabla V_m-{\beta }_m{c}_m{I}_{\text{ion},mf}(V_m,{\overline{V}}_f,q_m)$$ (4)

for a modified membrane model incorporating the additional load due to the nonmyocyte and whose ionic current is given by I_ion,mf = I_ion,m + g_load(V_m − V̅_f), where the load conductance g_load (nS/pF) reads

$$g_{\text{load}}=\frac{g_c}{{\beta }_m{c}_m}=\frac{{\beta }_f{c}_f}{{\beta }_m{c}_m}\cdot \frac{G_c}{C_f}.$$ (5)

The effect of nonmyocyte coupling on CV is now fully characterized by two parameters: the resting potential V̅_f and the coupling g_load (which combines information about nonmyocyte size, capacitance, density and coupling). Since more reliable experimental measurements are available for the myocyte resting potential [3], V̅_f was computed as a function of the steady-state value of V_m, assumed to be known and denoted by V̅_m. This relation, expressing that I_ion,mf vanishes at steady state, reads:

$${\overline{V}}_f={\overline{V}}_m+\frac{I_{\text{ion},m}({\overline{V}}_m,q_{\infty }({\overline{V}}_m))}{g_{\text{load}}},$$ (6)

where q_∞(V̅_m) means the steady-state values for the gating variables and ionic concentrations at clamped potential V̅_m [12]. Note that under the low coupling approximation, the CV depends on the nonmyocyte membrane kinetics only through its loading effect and its impact on the myocyte resting potential.

C. Theoretical Justification of the Approximation

The range of coupling conductance over which the approximation holds can be estimated in the absence of nonmyocyte-nonmyocyte coupling (σ_f = 0) by linearizing the nonmyocyte current-voltage relationship around its resting potential. Assuming that I_ion,f(V_f) = g_f (V_f − E_f), where g_f is the membrane conductance (nS/pF) and E_f is the reversal potential (mV), the differential equation (2), with σ_f = 0, can be written in integral form

$$V_f(t)=V_f(0)\text{ exp }(-\frac{t}{{\tau }_f})+{\displaystyle {\int }_0^t\mathrm{d}t\prime (g_f{E}_f+\frac{g_c}{{\beta }_f{c}_f}{V}_m(t-t\prime ))\text{ exp }(-\frac{t\prime }{{\tau }_f})},$$ (7)

where the time constant τ_f (in ms) is defined as

$${\tau }_f=\frac{1}{g_f+{{\displaystyle ({\beta }_f{c}_f)}}^{-1}{g}_c}.$$ (8)

If the system is at steady state at t = 0, i.e., if V_f(t) = V_f(0) and V_m(t) = V_m(0) is a solution to Eq. (7), then

$$V_f(t)=V_f(0)+\frac{G_c}{C_f}{\int }_0^{t}dt\prime (V_m(t-t\prime )-V_m(0))\text{ exp }(-\frac{t\prime }{{\tau }_f}).$$ (9)

As a result, the membrane potential of the nonmyocyte is a filtered version of the myocyte membrane potential with a filtering window of length τ_f. The nonmyocyte membrane potential V_f remains approximately constant during the upstroke phase (whose duration is denoted by τ_up) provided that τ_f ≫ τ_up. The limit case τ_f = τ_up arises when $g_c={\beta }_f{c}_f({{\displaystyle \tau }}_{\text{up}}^{-1}-g_f)$. The cell activation process usually take about τ_up = 2 ms and, in fibroblasts, ${{\displaystyle g}}_f^{-1}$ is of the order of 20 ms [13]. The approximation is therefore valid as long as the coupling is smaller than 0.45 nS/pF, which, for a fibroblast with a capacitance of 4.5 pF [8], [13], corresponds to a coupling conductance G_c of ≈2 nS. This value lies within the midrange of the conductances measured experimentally in myocyte-fibroblast cell pairs (0.31 to 8 nS [2]).

D. Numerical Simulations

Equations (1)–(2) were solved numerically using a finite differences discretization (100 elements of 100 μm) and explicit Euler time integration (time step: 5 μs). The parameters were: c_m = c_f = 1 μF/cm², σ_m = 0.84 mS/cm, σ_f = 0 to 0.84 mS/cm, β_m = 2000 cm⁻¹, and β_f was set to 500, 1000 and 1500 cm⁻¹. The coupling g_c was computed from Eq. (3) with C_f = 4.5 pF and G_c varying from 0.03 to 5 nS. The myocyte membrane kinetics was described by the Pandit et al. model [14] and that of the nonmyocyte by the MacCannell et al. [7] or the Sachse et al. [8] fibroblast models. The initial condition was set to the steady state obtained by computing the time-independent solution to the system (1)–(2) through a root-finding procedure [12], [15]. A wavefront propagation was initiated by injecting a stimulus current (150 μA/cm² for 1 ms) in the first myocyte of the cable. CV was computed by linear regression of the activation times (defined using a threshold at −40 mV) of all the cells between #20 and #80. In order to test the low coupling approximation, every simulation was repeated using the same initial condition, but with the nonmyocyte membrane potentials V_f being fixed to their initial value during the activation process.

Equation (4) was discretized and solved the same way as Eqs (1)–(2), and the same values for the parameters were used. Simulations were run and CV were reported for g_load ranging from 0.001 to 1 nS/pF. As initial condition, V_m was set to values ranging from the myocyte intrinsic resting potential to −70 mV. The nonmyocyte resting potential V̅_f was computed according to Eq. (6) to ensure that the tissue is at steady state. In order to provide insight into the model dependence of myocyte-nonmyocyte interactions, similar simulations were performed using the Ramirez et al. myocyte model [16].

III. RESULTS

A. Validation of the Low Coupling Regime Approximation

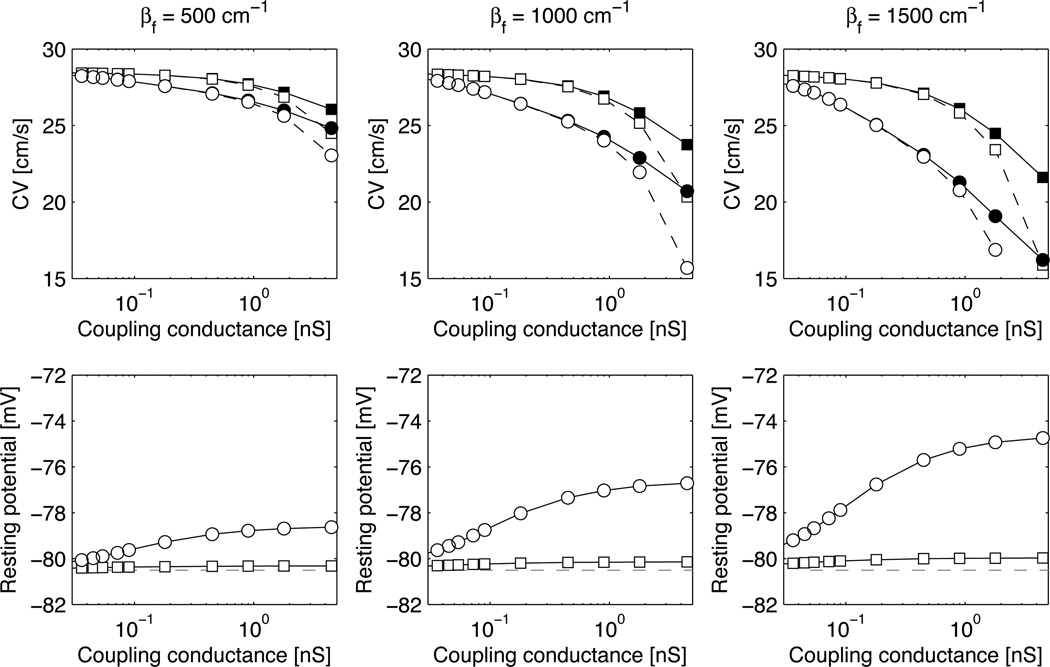
Figure 1 shows the modulation of CV due to coupling with nonmyocytes for three different nonmyocyte densities and two nonmyocyte membrane models (MacCannell et al., circles; Sachse et al., squares) in the absence of nonmyocyte-nonmyocyte coupling (σ_f = 0). At low coupling, the CVs obtained with V_f fixed to its initial value (open symbols) matched well those taking into account the nonmyocyte dynamics (filled symbols). For G_c < 1 nS, the relative error in CV was <0.4% for β_f = 500 cm⁻¹, <1% for β_f = 1000 cm⁻¹ and <2.5% for β_f = 1500 cm⁻¹. Note, however, that these results validating the low coupling approximation still make use of the complete information about the nonmyocyte membrane kinetics for determining the steady state of the coupled system myocyte-nonmyocyte. The steady-state myocyte membrane potential is displayed on the bottom panels of Fig. 1 as a function of the coupling conductance.

Figure 1.

Conduction velocity (CV) and myocyte resting potential as a function of the myocyte-nonmyocyte coupling conductance G_c. Circles and squares correspond to the MacCannell et al. and the Sachse et al. nonmyocyte membrane kinetics respectively. Open symbols represent simulations with clamped nonmyocyte potential and filled symbols represent simulations with time-dependent nonmyocyte potential. In the bottom panels, the horizontal dashed line is placed at the resting potential of an isolated myocyte (Pandit et al. model).

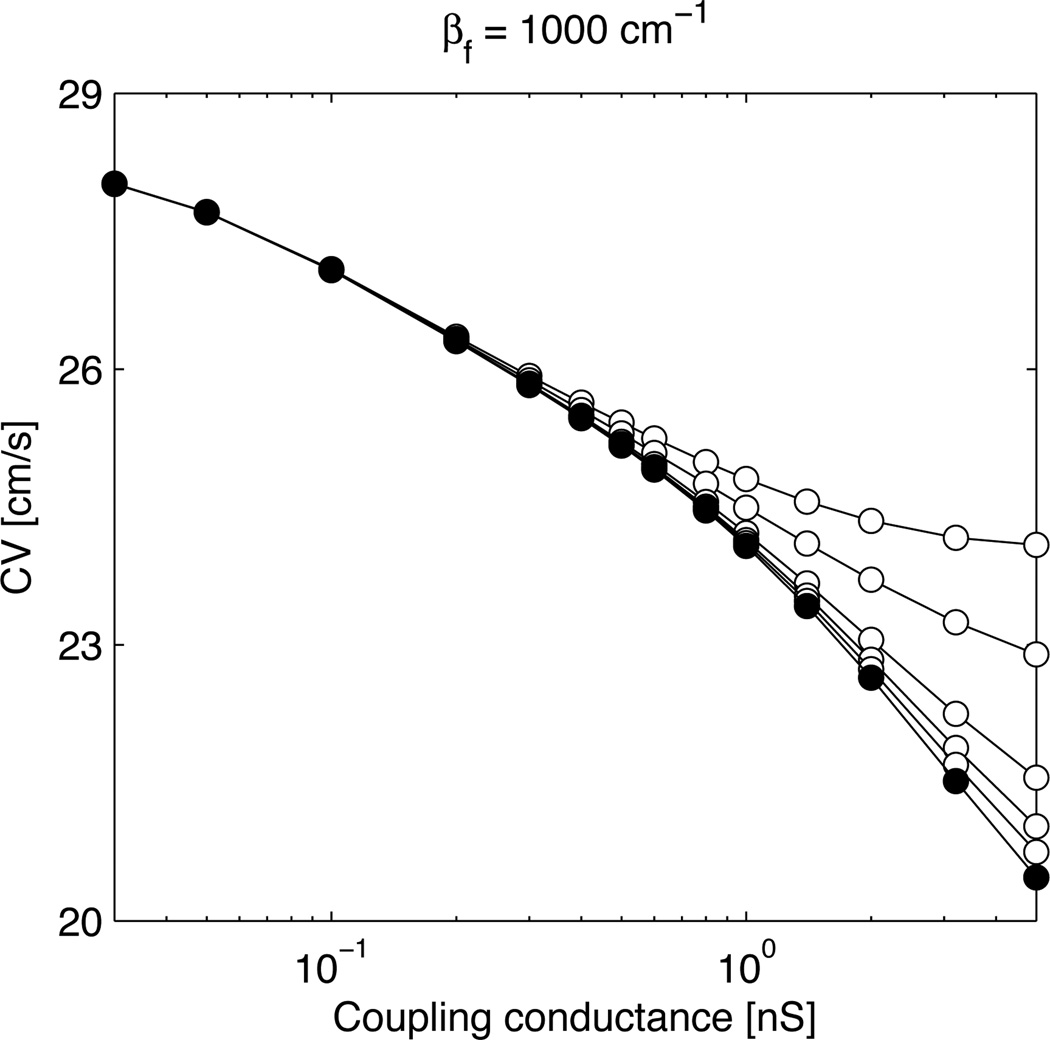
The effect of introducing nonmyocyte-nonmyocyte coupling is illustrated in Fig. 2. When σ_f is increased, conduction is enhanced because the layer of nonmyocytes contributes to impulse propagation through the myocyte-nonmyocyte-myocyte pathway. The effect is however small at low myocyte-nonmyocyte coupling and reasonable values of σ_f. In fact, for σ_f to be equal to σ_m (upper curve), nonmyocyte-nonmyocyte discrete coupling conductances would need to be much larger (about 10–20 times if the myocyte capacitance is 100 pF) than the myocyte-myocyte ones because nonmyocytes are smaller here (C_f = 4.5 pF). On the other hand, increasing the size of the nonmyocytes (for example by setting C_f = 45 pF) is equivalent to decreasing G_c because the effect on CV depends only on g_c [see Eq. (3)]. Therefore, in the low coupling regime (G_c < 2 nS), nonmyocyte-nonmyocyte coupling does not significantly affect impulse propagation in the configuration considered here when its strength (in nS) is at most that of the myocyte-myocyte coupling.

Figure 2.

Conduction velocity (CV) as a function of the myocyte-nonmyocyte coupling conductance G_c with β_f = 1000 cm⁻¹ and C_f = 4.5 pF and using the MacCannell et al. nonmyocyte model. The nonmyocyte-nonmyocyte conductivity σ_f is equal to 0 (filled circles), 0.05, 0.1, 0.2, 0.5 and 0.84 mS/cm (open circles, from bottom to top).

B. Effect of Load on the Conduction Velocity

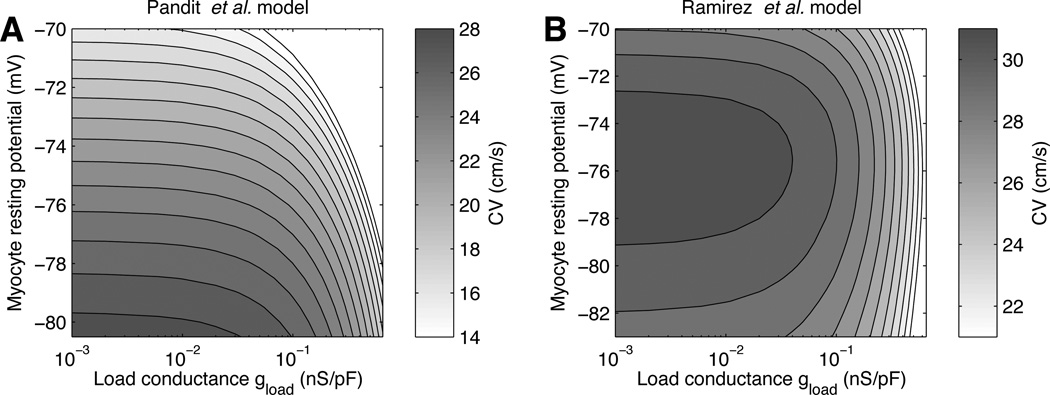
Figure 3 shows the CV predicted by the low coupling approximation [Eq. (4)], as a function of the load conductance g_load and the steady-state myocyte potential V̅_m. This display separates the effect of elevating the resting potential from the effect of increasing the coupling or nonmyocyte density. Comparison between Figs. 3A and 3B illustrates the model-dependence of the loading effect of nonmyocytes. With the Pandit et al. model (Fig. 3A), the CV decreases monotonically for both an elevation of the resting potential and an increase of load conductance. In contrast, with the Ramirez et al. model (Fig. 3B), the CV has a biphasic dependence on the resting potential at fixed load conductance, in a way consistent with the biphasic CV–fibroblast density relation reported by Miragoli et al. [3].

Figure 3.

Conduction velocity (CV) for different myocyte resting potentials V_m and load conductances g_load, as computed using the Pandit et al. (A) and the Ramirez et al. (B) myocyte membrane models. The vertical axis ranges from the myocyte intrinsic resting potential to −70 mV. The step size between isolines is 1 cm/s.

IV. DISCUSSION AND CONCLUSION

In the low coupling regime, the influence of coupling to nonmyocytes on CV does not directly depend on a detailed description of the nonmyocyte membrane kinetics and is determined by only two parameters: the elevation of the myocyte resting potential and the load conductance g_load [Eq. (5)]. The latter encapsulates quantitative data about nonmyocyte size, capacitance, density and coupling, demonstrating the intuitive idea that fewer, but larger nonmyocytes with larger coupling conductance per nonmyocyte would lead to the same effect. Another condition for a general nonmyocyte to act as a passive load at low coupling is that the time constant of the nonmyocyte membrane has to be larger than the rising time of the action potential, because ${\tau }_f<{{\displaystyle g}}_f^{-1}$ [Eq. (8)]. This condition (g_f < 0.5 nS/pF at rest) is verified for a wide variety of nonmyocytes [1], [7], [13].

The passive load approximation also revealed different responses of myocyte models (in terms of variations in CV) to an increase in load (Fig. 3). This response depends on the myocyte intrinsic resting potential and sodium kinetics, and may be either monotonic or biphasic. The diagrams in Fig. 3 provide a simple and direct way to predict how much structural changes (nonmyocytes size, density and coupling) are needed to significantly affect the CV. This remarkable simplicity, however, does not extend to repolarization, which was previously found to depend on both the myocyte and the nonmyocyte membrane kinetics [7], [8], [10].

The configuration studied in this paper is relevant to cell culture models covered by a layer of nonmyocytes. Another clinically relevant configuration involves the intermingling of myocytes and nonmyocytes. Propagation across a myocyte-fibroblast-myocyte bridge, however, may require very large myocyte-nonmyocyte coupling. In a computer model, Sachse et al. found that propagation across a bridge did not occur in the low coupling regime (G_c < 2 nS) where the passive load model is valid, but did occur when the coupling was at least 20 nS.