Abstract
This paper explores the conditions under which nonmyocytes, when electrically coupled to myocytes, act as a passive load during the depolarization phase. Using theoretical arguments and numerical simulations in a tissue incorporating fibroblasts, the passive load approximation is shown to be accurate at low coupling conductances (< 2 nS). In this case, the effect on conduction velocity can be expressed as a function of the elevation in resting potential and the coupling only.
I. Introduction
There are several physiological scenarios in which the electrical interactions between cardiac myocytes and nonmyocytes are important. First, fibroblasts are more numerous than myocytes in the heart and under certain diseased states, can locally proliferate and possibly couple to the myocytes, affecting electrical activity [1]–[3]. Second, the presence of fibroblasts in ischemic or scarred regions represents a possible target for cell therapy to restore normal electrical conduction [4]. Finally, the use of autologous nonmyocytes such as myoblasts or mesenchymal stem cells has been proposed to restore cardiac structure and function [5]. Recent studies have suggested that the success of this cell therapy was affected by the quality of myocyte-nonmyocyte electrical interactions [6]. Because the electrical activity in one cell type can affect the behavior of the other it is critical to understand the mechanism of the potential interactions.
While nonexcitable, these nonmyocytes are not passive. However, when the time constant of nonmyocyte activation is larger than the rising time of the action potential, nonmyocytes are expected to act as a passive load during the depolarization process. Because the electrical activity of a myocyte-nonmyocyte pair is driven by the myocyte action potential [1], this time constant is expected to also depend on the coupling resistance. This paper describes in terms of coupling and nonmyocyte properties the conditions under which general nonmyocytes act as a passive load. The consequences on conduction velocity (CV) are explored in a tissue model incorporating recent detailed fibroblast models [7], [8], reproducing a setup in which the effect on CV has been demonstrated in vitro [3]. The simulations reveal the range of coupling conductances for which passive load approximation is valid and explain how the CV change with coupling is not always monotonic.
II. Methods
A. Mathematical Formulation
The monodomain propagation equations for a homogeneous mixture of two cell types can be formulated in a way similar to the bidomain model:
| (1) |
| (2) |
The indices m and f stand for myocyte and nonmyocyte (fibroblast) respectively. The surface-to-volume ratio (in cm−1) is denoted by β, the membrane capacitance per unit area (μF/cm2) by c, the tissue conductance (mS/cm) by σ, the ionic current density (pA/pF) by Iion,, the membrane state variables by q, and the myocyte-nonmyocyte coupling density per unit volume (mS/cm3) by gc.
The coupling strength gc can be expressed as a function of experimentally relevant microstructure parameters by considering that the discrete coupling conductance Gc (in nS) between one myocyte and one nonmyocyte spreads out over a discretization volume (Vol) associated with a nonmyocyte. For a nonmyocyte of capacitance Cf (in pF), this volume is identified as Cf/(βfcf), i.e., the capacitance divided by the capacitance per unit volume, leading to the formula
| (3) |
The factor βfcf (in μF/cm3) can be interpreted as the nonmyocyte density and the capacitance Cf as a measure of nonmyocyte size.
B. Low Coupling Approximation
Experimental recordings [9] and numerical simulations [7], [8], [10], [11] have shown that the nonmyocyte membrane potential Vf varies slowly during the upstroke phase of the myocyte, unless the myocyte-nonmyocyte coupling is strong. Under the hypothesis Vf (t) = V̅f = constant, Eq. (1) becomes equivalent to the monodomain propagation equation
| (4) |
for a modified membrane model incorporating the additional load due to the nonmyocyte and whose ionic current is given by Iion,mf = Iion,m + gload(Vm − V̅f), where the load conductance gload (nS/pF) reads
| (5) |
The effect of nonmyocyte coupling on CV is now fully characterized by two parameters: the resting potential V̅f and the coupling gload (which combines information about nonmyocyte size, capacitance, density and coupling). Since more reliable experimental measurements are available for the myocyte resting potential [3], V̅f was computed as a function of the steady-state value of Vm, assumed to be known and denoted by V̅m. This relation, expressing that Iion,mf vanishes at steady state, reads:
| (6) |
where q∞(V̅m) means the steady-state values for the gating variables and ionic concentrations at clamped potential V̅m [12]. Note that under the low coupling approximation, the CV depends on the nonmyocyte membrane kinetics only through its loading effect and its impact on the myocyte resting potential.
C. Theoretical Justification of the Approximation
The range of coupling conductance over which the approximation holds can be estimated in the absence of nonmyocyte-nonmyocyte coupling (σf = 0) by linearizing the nonmyocyte current-voltage relationship around its resting potential. Assuming that Iion,f(Vf) = gf (Vf − Ef), where gf is the membrane conductance (nS/pF) and Ef is the reversal potential (mV), the differential equation (2), with σf = 0, can be written in integral form
| (7) |
where the time constant τf (in ms) is defined as
| (8) |
If the system is at steady state at t = 0, i.e., if Vf(t) = Vf(0) and Vm(t) = Vm(0) is a solution to Eq. (7), then
| (9) |
As a result, the membrane potential of the nonmyocyte is a filtered version of the myocyte membrane potential with a filtering window of length τf. The nonmyocyte membrane potential Vf remains approximately constant during the upstroke phase (whose duration is denoted by τup) provided that τf ≫ τup. The limit case τf = τup arises when . The cell activation process usually take about τup = 2 ms and, in fibroblasts, is of the order of 20 ms [13]. The approximation is therefore valid as long as the coupling is smaller than 0.45 nS/pF, which, for a fibroblast with a capacitance of 4.5 pF [8], [13], corresponds to a coupling conductance Gc of ≈2 nS. This value lies within the midrange of the conductances measured experimentally in myocyte-fibroblast cell pairs (0.31 to 8 nS [2]).
D. Numerical Simulations
Equations (1)–(2) were solved numerically using a finite differences discretization (100 elements of 100 μm) and explicit Euler time integration (time step: 5 μs). The parameters were: cm = cf = 1 μF/cm2, σm = 0.84 mS/cm, σf = 0 to 0.84 mS/cm, βm = 2000 cm−1, and βf was set to 500, 1000 and 1500 cm−1. The coupling gc was computed from Eq. (3) with Cf = 4.5 pF and Gc varying from 0.03 to 5 nS. The myocyte membrane kinetics was described by the Pandit et al. model [14] and that of the nonmyocyte by the MacCannell et al. [7] or the Sachse et al. [8] fibroblast models. The initial condition was set to the steady state obtained by computing the time-independent solution to the system (1)–(2) through a root-finding procedure [12], [15]. A wavefront propagation was initiated by injecting a stimulus current (150 μA/cm2 for 1 ms) in the first myocyte of the cable. CV was computed by linear regression of the activation times (defined using a threshold at −40 mV) of all the cells between #20 and #80. In order to test the low coupling approximation, every simulation was repeated using the same initial condition, but with the nonmyocyte membrane potentials Vf being fixed to their initial value during the activation process.
Equation (4) was discretized and solved the same way as Eqs (1)–(2), and the same values for the parameters were used. Simulations were run and CV were reported for gload ranging from 0.001 to 1 nS/pF. As initial condition, Vm was set to values ranging from the myocyte intrinsic resting potential to −70 mV. The nonmyocyte resting potential V̅f was computed according to Eq. (6) to ensure that the tissue is at steady state. In order to provide insight into the model dependence of myocyte-nonmyocyte interactions, similar simulations were performed using the Ramirez et al. myocyte model [16].
III. RESULTS
A. Validation of the Low Coupling Regime Approximation
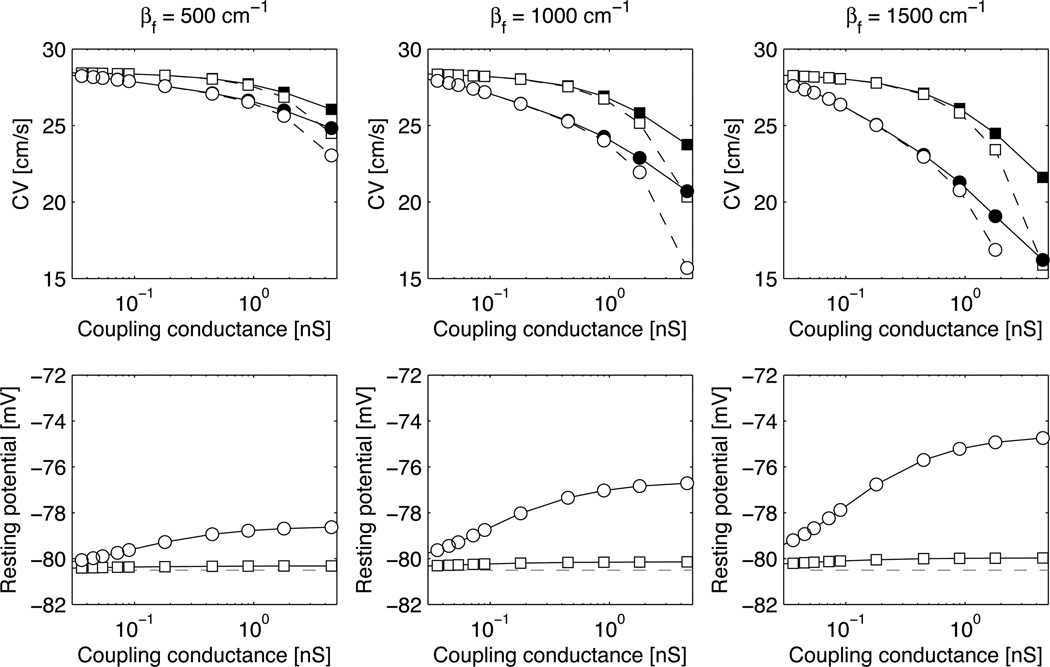
Figure 1 shows the modulation of CV due to coupling with nonmyocytes for three different nonmyocyte densities and two nonmyocyte membrane models (MacCannell et al., circles; Sachse et al., squares) in the absence of nonmyocyte-nonmyocyte coupling (σf = 0). At low coupling, the CVs obtained with Vf fixed to its initial value (open symbols) matched well those taking into account the nonmyocyte dynamics (filled symbols). For Gc < 1 nS, the relative error in CV was <0.4% for βf = 500 cm−1, <1% for βf = 1000 cm−1 and <2.5% for βf = 1500 cm−1. Note, however, that these results validating the low coupling approximation still make use of the complete information about the nonmyocyte membrane kinetics for determining the steady state of the coupled system myocyte-nonmyocyte. The steady-state myocyte membrane potential is displayed on the bottom panels of Fig. 1 as a function of the coupling conductance.
Figure 1.
Conduction velocity (CV) and myocyte resting potential as a function of the myocyte-nonmyocyte coupling conductance Gc. Circles and squares correspond to the MacCannell et al. and the Sachse et al. nonmyocyte membrane kinetics respectively. Open symbols represent simulations with clamped nonmyocyte potential and filled symbols represent simulations with time-dependent nonmyocyte potential. In the bottom panels, the horizontal dashed line is placed at the resting potential of an isolated myocyte (Pandit et al. model).
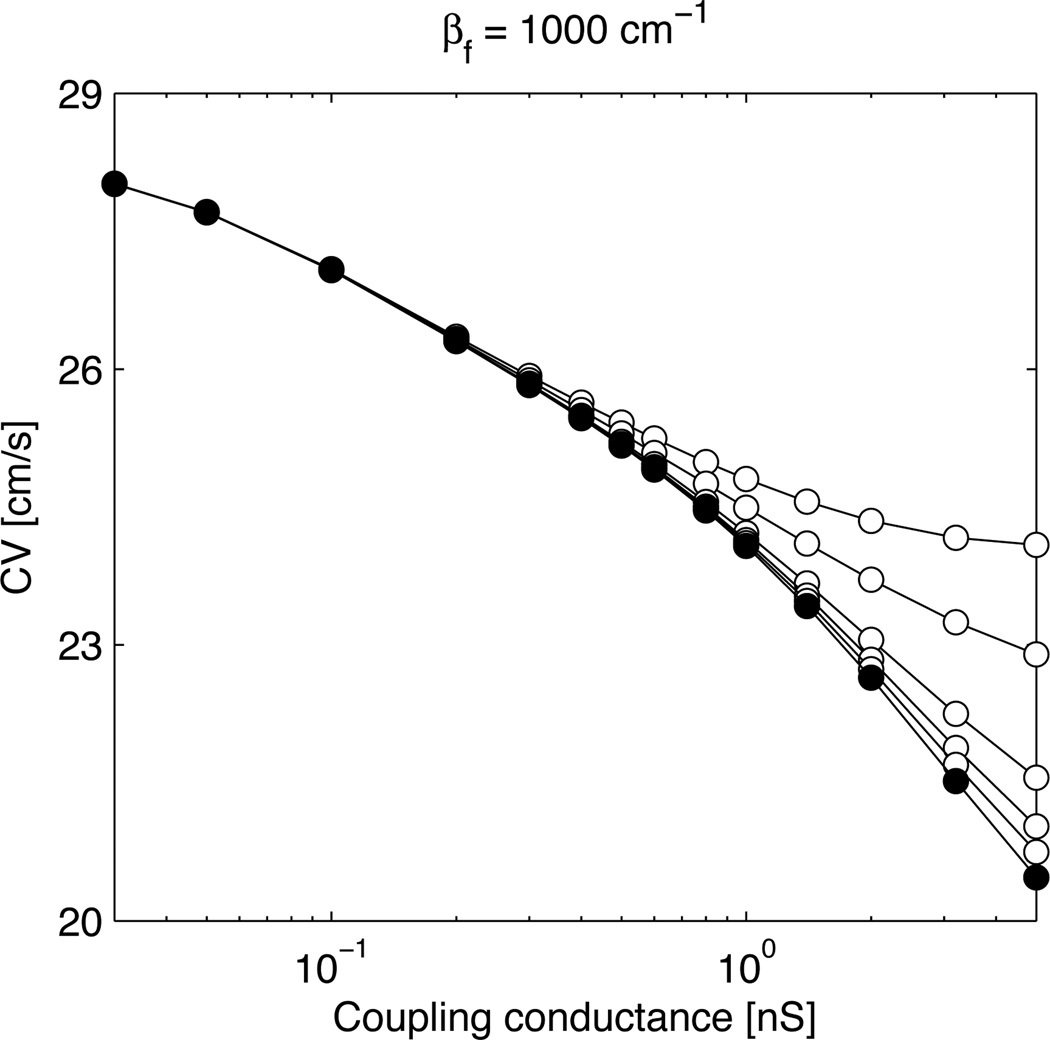
The effect of introducing nonmyocyte-nonmyocyte coupling is illustrated in Fig. 2. When σf is increased, conduction is enhanced because the layer of nonmyocytes contributes to impulse propagation through the myocyte-nonmyocyte-myocyte pathway. The effect is however small at low myocyte-nonmyocyte coupling and reasonable values of σf. In fact, for σf to be equal to σm (upper curve), nonmyocyte-nonmyocyte discrete coupling conductances would need to be much larger (about 10–20 times if the myocyte capacitance is 100 pF) than the myocyte-myocyte ones because nonmyocytes are smaller here (Cf = 4.5 pF). On the other hand, increasing the size of the nonmyocytes (for example by setting Cf = 45 pF) is equivalent to decreasing Gc because the effect on CV depends only on gc [see Eq. (3)]. Therefore, in the low coupling regime (Gc < 2 nS), nonmyocyte-nonmyocyte coupling does not significantly affect impulse propagation in the configuration considered here when its strength (in nS) is at most that of the myocyte-myocyte coupling.
Figure 2.
Conduction velocity (CV) as a function of the myocyte-nonmyocyte coupling conductance Gc with βf = 1000 cm−1 and Cf = 4.5 pF and using the MacCannell et al. nonmyocyte model. The nonmyocyte-nonmyocyte conductivity σf is equal to 0 (filled circles), 0.05, 0.1, 0.2, 0.5 and 0.84 mS/cm (open circles, from bottom to top).
B. Effect of Load on the Conduction Velocity
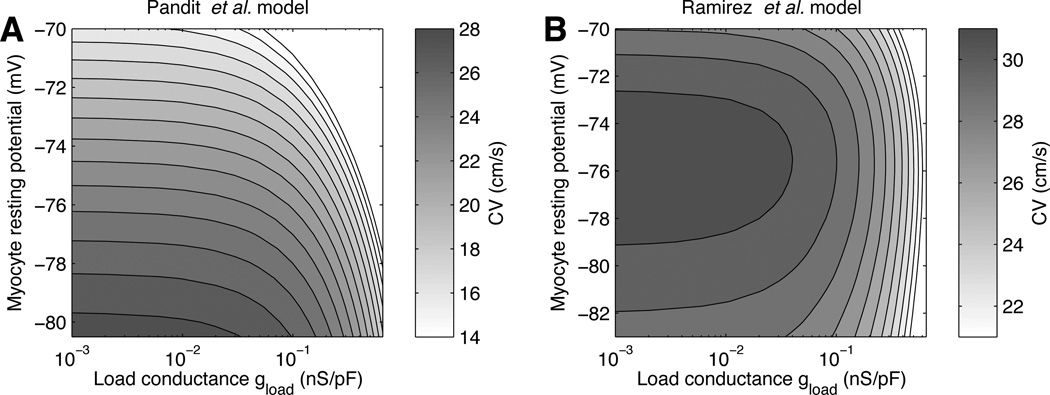
Figure 3 shows the CV predicted by the low coupling approximation [Eq. (4)], as a function of the load conductance gload and the steady-state myocyte potential V̅m. This display separates the effect of elevating the resting potential from the effect of increasing the coupling or nonmyocyte density. Comparison between Figs. 3A and 3B illustrates the model-dependence of the loading effect of nonmyocytes. With the Pandit et al. model (Fig. 3A), the CV decreases monotonically for both an elevation of the resting potential and an increase of load conductance. In contrast, with the Ramirez et al. model (Fig. 3B), the CV has a biphasic dependence on the resting potential at fixed load conductance, in a way consistent with the biphasic CV–fibroblast density relation reported by Miragoli et al. [3].
Figure 3.
Conduction velocity (CV) for different myocyte resting potentials Vm and load conductances gload, as computed using the Pandit et al. (A) and the Ramirez et al. (B) myocyte membrane models. The vertical axis ranges from the myocyte intrinsic resting potential to −70 mV. The step size between isolines is 1 cm/s.
IV. DISCUSSION AND CONCLUSION
In the low coupling regime, the influence of coupling to nonmyocytes on CV does not directly depend on a detailed description of the nonmyocyte membrane kinetics and is determined by only two parameters: the elevation of the myocyte resting potential and the load conductance gload [Eq. (5)]. The latter encapsulates quantitative data about nonmyocyte size, capacitance, density and coupling, demonstrating the intuitive idea that fewer, but larger nonmyocytes with larger coupling conductance per nonmyocyte would lead to the same effect. Another condition for a general nonmyocyte to act as a passive load at low coupling is that the time constant of the nonmyocyte membrane has to be larger than the rising time of the action potential, because [Eq. (8)]. This condition (gf < 0.5 nS/pF at rest) is verified for a wide variety of nonmyocytes [1], [7], [13].
The passive load approximation also revealed different responses of myocyte models (in terms of variations in CV) to an increase in load (Fig. 3). This response depends on the myocyte intrinsic resting potential and sodium kinetics, and may be either monotonic or biphasic. The diagrams in Fig. 3 provide a simple and direct way to predict how much structural changes (nonmyocytes size, density and coupling) are needed to significantly affect the CV. This remarkable simplicity, however, does not extend to repolarization, which was previously found to depend on both the myocyte and the nonmyocyte membrane kinetics [7], [8], [10].
The configuration studied in this paper is relevant to cell culture models covered by a layer of nonmyocytes. Another clinically relevant configuration involves the intermingling of myocytes and nonmyocytes. Propagation across a myocyte-fibroblast-myocyte bridge, however, may require very large myocyte-nonmyocyte coupling. In a computer model, Sachse et al. found that propagation across a bridge did not occur in the low coupling regime (Gc < 2 nS) where the passive load model is valid, but did occur when the coupling was at least 20 nS.
References
- 1.Kohl P, Camelliti P, Burton FL, Smith GL. Electrical coupling of fibroblasts and myocytes: relevance for cardiac propagation. J. Electrocardiol. 2005;vol. 38:45–50. doi: 10.1016/j.jelectrocard.2005.06.096. [DOI] [PubMed] [Google Scholar]
- 2.Rook MB, van Ginneken AC, de Jonge B, el Aoumari A, Gros D, Jongsma HJ. Differences in gap junction channels between cardiac myocytes, fibroblasts, and heterologous pairs. Am J Physiol. 1992;vol. 263(no. 5 Pt 1):C959–C977. doi: 10.1152/ajpcell.1992.263.5.C959. [DOI] [PubMed] [Google Scholar]
- 3.Miragoli M, Gaudesius G, Rohr S. Electrotonic modulation of cardiac impulse conduction by myofibroblasts. Circ Res. 2006;vol. 98(no. 6):801–810. doi: 10.1161/01.RES.0000214537.44195.a3. [DOI] [PubMed] [Google Scholar]
- 4.Kizana E, Ginn SL, Allen DG, Ross DL, Alexander IE. Fibroblasts can be genetically modified to produce excitable cells capable of electrical coupling. Circulation. 2005;vol. 111(no. 4):394–398. doi: 10.1161/01.CIR.0000153812.64956.EF. [DOI] [PubMed] [Google Scholar]
- 5.Rosenzweig A. Cardiac cell therapy–mixed results from mixed cells. N Engl J Med. 2006;vol. 355(no. 12):1274–1277. doi: 10.1056/NEJMe068172. [DOI] [PubMed] [Google Scholar]
- 6.Mills WR, Mal N, Kiedrowski MJ, Unger R, Forudi F, Popovic ZB, Penn MS, Laurita KR. Stem cell therapy enhances electrical viability in myocardial infarction. J Mol Cell Cardiol. 2007;vol. 42(no. 2):304–314. doi: 10.1016/j.yjmcc.2006.09.011. [DOI] [PubMed] [Google Scholar]
- 7.MacCannell KA, Bazzazi H, Chilton L, Shibukawa Y, Clark RB, Giles WR. A mathematical model of electrotonic interactions between ventricular myocytes and fibroblasts. Biophys J. 2007;vol. 92(no. 11):4121–4132. doi: 10.1529/biophysj.106.101410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sachse FB, Moreno AP, Abildskov JA. Electrophysiological modeling of fibroblasts and their interaction with myocytes. Ann Biomed Eng. 2008;vol. 36(no. 1):41–56. doi: 10.1007/s10439-007-9405-8. [DOI] [PubMed] [Google Scholar]
- 9.Kohl P, Kamkin AG, Kiseleva IS, Noble D. Mechanosensitive fibroblasts in the sino-atrial node region of rat heart: interaction with cardiomyocytes and possible role. Exp Physiol. 1994;vol. 79(no. 6):943–956. doi: 10.1113/expphysiol.1994.sp003819. [DOI] [PubMed] [Google Scholar]
- 10.Jacquemet V, Henriquez CS. Modelling cardiac fibroblasts: interactions with myocytes and their impact on impulse propagation. Europace. 2007;vol. 9(Suppl 6):vi29–vi37. doi: 10.1093/europace/eum207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jacquemet V, Henriquez CS. Loading effect of fibroblast-myocyte coupling on resting potential, impulse propagation and repolarization: Insights from a microstructure model. Am J Physiol Heart Circ Physiol. 2008;vol. 294(no. 5):H2040–H2052. doi: 10.1152/ajpheart.01298.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jacquemet V, Henriquez CS. An efficient technique for determining the steady-state membrane potential profile in tissues with multiple cell types. Computers in Cardiology. 2007;vol. 34:113–116. [Google Scholar]
- 13.Shibukawa Y, Chilton EL, MacCannell KA, Clark RB, Giles WR. K+ currents activated by depolarization in cardiac fibroblasts. Biophys J. 2005;vol. 88(no. 6):3924–3935. doi: 10.1529/biophysj.104.054429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pandit SV, Clark RB, Giles WR, Demir SS. A mathematical model of action potential heterogeneity in adult rat left ventricular myocytes. Biophys J. 2001;vol. 81(no. 6):3029–3051. doi: 10.1016/S0006-3495(01)75943-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jacquemet V. Steady-state solutions in mathematical models of atrial cell electrophysiology and their stability. Math Biosci. 2007;vol. 208(no. 1):241–269. doi: 10.1016/j.mbs.2006.10.007. [DOI] [PubMed] [Google Scholar]
- 16.Ramirez RJ, Nattel S, Courtemanche M. Mathematical analysis of canine atrial action potentials: rate, regional factors and electrical remodeling. Am J Physiol Heart Circ Physiol. 2000;vol. 279(no. 4):H1767–H1785. doi: 10.1152/ajpheart.2000.279.4.H1767. [DOI] [PubMed] [Google Scholar]