Nanoparticle location and material dependent dose enhancement in X-ray radiation therapy

Abstract

Nanoparticles of high atomic number (Z) materials can act as radiosensitizers to enhance radiation dose delivered to tumors. An analytical approach is used to calculate dose enhancements to tumor endothelial cells and their nuclei for a series of nanoparticles (bismuth, gold and platinum) located at different locations relative to nuclei by considering contributions from both photoelectrons and Auger electrons. The ratio of the dose delivered to cells with and without the nanoparticles is known as the dose enhancement factor (DEF). DEFs depend on material composition, size and location of nanoparticles with respect to the cell and the nucleus. Energy of irradiating X-ray beam affects X-ray absorption by nanoparticles and plays an important role in dose enhancements. For diagnostic X-ray sources, bismuth nanoparticles provide higher dose enhancements than gold and platinum nanoparticles for a given nanoparticle size, concentration and location. The highest DEFs are achieved for nanoparticles located closest to the nucleus where energy depositions from short range Auger electrons are maximum. With nanoparticles ranging in diameter between 2-400 nm, the dose enhancement increases with decrease in particle size. The results are useful in finding optimized conditions for nanoparticle enhanced X-ray radiation therapy of cancer.

1. Introduction

Radiotherapy aims to maximize radiation dose delivered to tumor with minimum damage to surrounding healthy tissues. The promising ability of gold nanoparticles as effective radiosensitizers for localized tumor dose enhancements have been extensively explored due to high X-ray absorption cross-section of gold compared to biological tissues.^1-8 Previous experiments with mice have shown significant increase in dose delivered to tissue volumes in presence of gold nanoparticles.⁹ Monte Carlo simulations have been performed extensively to investigate various parameters such as photon energy, particle size, concentration and location that govern radiosensitizing properties of gold nanoparticles.^10-14 A recent study also shows how geometry of nanoparticles affect X-ray dose enhancement.¹⁵ Other theoretical studies reveal that targeted gold nanoparticles can enhance dose to endothelial cells surrounding a tumor by over 200 times depending on their concentration and energy of the irradiating X-ray photons.¹⁶ Dose enhancement is often attributed to photoelectrons and Auger electrons generated from X-ray irradiated nanoparticles. Photoelectrons are highly energetic, have a long range (up to hundreds of microns) in surrounding water, and deposit a small fraction of their energy near the nanoparticle. On the other hand, Auger electrons have lower energy and shorter range (less than 1 μm), allowing most of the energy to be deposited close to the nanoparticle. Energy deposition by electrons will hydrolyze water molecules surrounding cells and their nuclei, producing free radicals that will induce DNA damage, eventually leading to cell death. Cell nucleus that contains DNA, is thus considered to be the most sensitive to radiation exposure.^17-19 Due to major contributions from short range Auger electrons, dose enhancement to nuclei is significantly different than that to entire cell. A recent theoretical study indicates that nucleus dose enhancement factor (nDEF) or the ratio of dose delivered to nucleus with and without gold nanoparticles can be as high as 73 for endothelial cell nuclei.²⁰ Experiments have also shown that gold nanoparticles can be internalized inside cancer cells, which makes nanoparticle location control a feasible choice for dose enhancement.²¹ In addition, although gold nanoparticles have been the prime choice for radiosensitizers due to their high biocompatibility, ease of conjugation to tumor targeting agents, and high X-ray absorption coefficients, nanoparticles of other heavy metals such as bismuth and platinum can also serve as promising alternatives to gold in radiotherapy.^22-27 However, there is no systemic investigation over potential benefits by controlling location and material composition of nanoparticles relative to cancer cells in X-ray radiation therapy.

We use an analytical approach developed by Ngwa et al.¹⁶ to derive radiosensitizing abilities of bismuth, gold and platinum nanoparticles at diagnostic X-ray conditions (50, 110 or 300 kVp). For each type of nanoparticles, doses delivered to endothelial cells and their nuclei are derived for particle sizes ranging between 2 to 400 nm in diameter, and concentrations ranging between 7-350 mg of nanoparticles per gram of tumor tissue. The contributions from both photoelectrons and Auger electrons are derived. Unlike previous studies, this work primarily focuses on dependence of dose enhancements on material composition and size, as well as location of nanoparticles using diagnostic X-ray sources (instead of using brachytherapy sources). In addition, the variation of nDEFs with respect to nanoparticle location has been discussed in context of photoelectron and Auger electron generation. Although Auger electron cross sections are derived from a previous Monte Carlo simulation due to lack of such data, the theoretical results from this investigation provide useful insights in choice of nanoparticles in terms of nanoparticle nature, size and targeting location to achieve maximum efficacy in nanoparticle enhanced X-ray radiation therapy of cancer.

2. Methods

A slab of tumor endothelial cells with dimensions of 2 μm (thickness) × 10 μm (length) × 10 μm (width) has been considered in the following simulations (Fig. 1).¹⁶ The radius of sphere with nanoparticle in center is equal to the range of emitted photoelectrons. Calculations are performed for spherical nanoparticles attached to the outer surface of the tumor endothelial cell. Nanoparticles of a wide range of diameters are used to establish a relation between nanoparticle size and dose enhancements. Concentration of nanoparticles is expressed in terms of mass of nanoparticles per unit mass of tumor tissue, and corresponds to values found in previous theoretical and experimental studies. An arbitrary dose D_w (2 Gy) is taken as the dose absorbed by the cell without nanoparticle, which is also the dose absorbed by water inside the cell. The photon flux or the number of photons per unit area of nanoparticle that corresponds to D_w is calculated using:

$${\mathrm{D}}_{\mathrm{w}}={\sum }_E\Phi E_p{(\frac{{\mathrm{\mu }}_{\mathit{en}}}{\rho })}_E$$ (1)

where Φ is photon flux (photon/cm²), E_p is energy per photon (J), and ${(\frac{{\mathrm{\mu }}_{\mathit{en}}}{\rho })}_E$ is mass absorption coefficient of water (cm²/g) at a given energy E. The number of photons (N_ph) incident on the nanoparticle is derived by multiplying photon flux with cross-sectional area of nanoparticle; N_ph = Φ×πr², where r is radius of nanoparticle. The probability P of photoelectric interaction of incident photons with nanoparticle is given by $P~{(\frac{{\mathrm{\mu }}_{\mathit{PE}}}{\rho })}_E{\mathrm{\rho }}_{\mathrm{NP}}{\mathrm{d}}_{\mathrm{NP}}$ where ${(\frac{{\mathrm{\mu }}_{\mathit{PE}}}{\rho })}_E$ is the photoelectric absorption coefficient of nanoparticle at an energy E, ρ_NP is density of nanoparticle, and ${\mathrm{d}}_{\mathrm{NP}}=\frac{4r}{3}$ is the average distance traversed by photons through a spherical nanoparticle. A 50 kVp X-ray photon has an average energy E ~29 keV. At E = 29 keV, ${(\frac{{\mathrm{\mu }}_{\mathit{PE}}}{\rho })}_{29\mathit{keV}}=32.74{\mathrm{cm}}^2/\mathrm{g}$ for bismuth resulting in P~8.54 × 10^-3 for ρ_Bi = 9.78 g/cm³ and r = 200 nm. Since the number of photoelectric interactions is equal to the number of emitted photoelectrons, the number of emitted photoelectrons per nanoparticle is derived from N_PE = N_ph × P.

Figure 1.

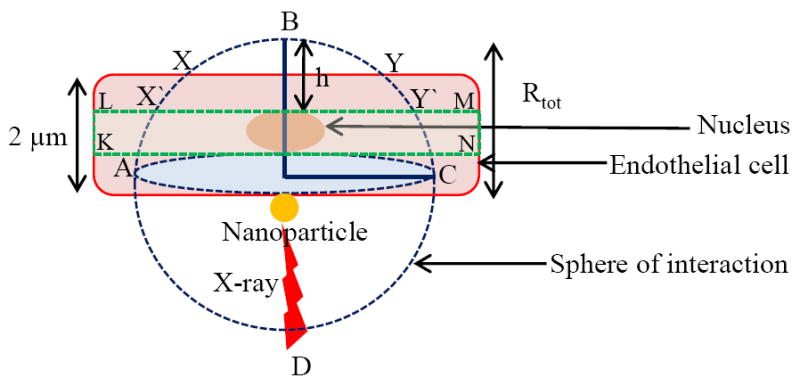
Slab model of endothelial cell lining a tumor.

The next step is to determine the number of nanoparticles that attach on cell surface at given nanoparticle concentrations. The total mass of nanoparticles mtotal in the entire volume of cell for a given concentration C (mg/g), is given by m_total= C×V_EC×ρ_EC, where V_EC (2×10^-10 cm³) and ρ_EC (1 g/cm³) are the volume and density of cell, respectively. The mass of nanoparticle is obtained as ${\mathrm{m}}_{\mathrm{NP}}=\frac{4}{3}\mathrm{\pi }{\mathrm{r}}^3{\mathrm{\rho }}_{\mathrm{NP}}$. Therefore, for any concentration C of nanoparticles, the number of nanoparticles that attach to cell is:

$${\mathrm{N}}_{\mathrm{NP}}=\frac{m_{\mathit{total}}}{m_{\mathit{NP}}}=\frac{{\mathit{CV}}_{\mathit{EC}}{\rho }_{\mathit{EC}}}{\frac{4}{3}\pi r^3{\rho }_{\mathit{NP}}}$$ (2)

The total number of emitted photoelectrons can now be calculated as N_PEtotal = N_PE × N_NP

To evaluate the range of emitted photoelectrons, the kinetic energy E_KE of emitted photoelectrons must be known, which is given by E_KE = E-E_edge, where E_edge is relevant photoelectric absorption edge of nanoparticle. The average L-edge of bismuth is 15 keV giving E_KE = 14 keV. As emitted photoelectrons interact with their surroundings, they will deposit kinetic energy in a sphere of interaction centered on the nanoparticle. The radius of interaction sphere defines the range R_tot of photoelectrons and is given by:

$${\mathrm{R}}_{\mathrm{tot}}=0.0431{(E_{\mathit{KE}}+0.367)}^{1.77}­0.007$$ (3)

At E_KE =14 keV, R_tot is 4.81 μm. For electron with kinetic energy between 20 eV to 20 MeV, Cole has derived an empirical relation²⁸ between electron energy loss $\frac{{\mathit{dE}}_{\mathit{KE}}}{\mathit{dx}}(\mathrm{keV}/\mathrm{\mu m})$ and range R_tot (μm):

$$\frac{{\mathit{dE}}_{\mathit{KE}}}{\mathit{dx}}=3.316{(R_{\mathit{tot}}-x+0.007)}^{-0.435}+0.0055{(R_{\mathit{tot}}-x)}^{0.33}$$ (4)

where x is the distance from photoelectron emission site. The total energy deposited by single photoelectron in cell volume is obtained by integrating differential energy loss from surface of nanoparticle (r) to maximum range (R_tot) of photoelectrons (Fig. 1):

$$E_{\mathit{EC}}={\int }_r^{R_{\mathit{tot}}}\frac{H_{\mathit{ABC}}-C_{\mathit{XBY}}}{S_{\mathit{ABCD}}}\times \frac{{\mathit{dE}}_{\mathit{KE}}}{\mathit{dx}}\mathrm{dx}$$ (5)

where, H_ABC = Area of hemisphere ABC = 2πR_tot², C_XBY = Area of hemispherical cap XBY = 2π(R_tot − t), S_ABCD = Surface area of entire sphere ABCD = 4πR_tot² and t is cell thickness. Assuming a homogenous distribution of nanoparticles, and dose deposited in the entire sphere of interaction, the total energy deposited to cell by photoelectrons can be derived by multiplying E_EC with the total number of emitted photoelectrons, i.e., E_ECtotal = E_EC ×N_PEtotal. This calculation does not take into account the hemispherical shell in the blood vessel and the spherical shell beyond the cell. Dose contributions from nanoparticles on the opposite side of blood vessel are relatively small and therefore have not been considered. The dose delivered to the entire cell by photoelectrons following nanoparticle and X-ray interactions is obtained by dividing energy deposited in cell by mass (volume×density) of cell: ${\mathrm{D}}_{\mathrm{NP}}(\mathrm{PE})=\frac{E_{\mathit{ECtotal}}}{V_{\mathit{EC}}\times {\rho }_{\mathit{EC}}}$. DEF due to photoelectrons is given by:

$$\mathrm{DEF}(\mathrm{Photoelectrons})=\frac{\mathit{Absorbed\; dose\; with\; nanoparticle}}{\mathit{Absorbed\; dose\; without\; nanoparticle}}=\frac{D_W+D_{\mathit{NP}}(\mathit{PE})}{D_W}$$ (6)

A DEF of 1.0 refers to 0% enhancement; while a DEF of 2.0 refers to 100% enhancement. For bismuth nanoparticles, at a concentration of 7 mg/g, DEF is 1.307, meaning that adding 7 mg of bismuth nanoparticles per gram of a tumor tissue increases X-ray dose by 65% when only the photoelectrons are considered for energy deposition. The calculations are repeated for a series of nanoparticle concentrations ranging from 7-350 mg/g, and radius ranging from 1-200 nm. DEFs due to photoelectrons are calculated for gold and platinum nanoparticles using the same approach.

In order to derive contribution from Auger electrons, Auger electron spectra obtained from Monte Carlo simulations for tumors loaded with gold nanoparticles at 7 mg/g and irradiated with a 50 kVp X-ray source is used.¹² The energy deposited by Auger electrons in the cell is determined as described for photoelectrons. Average number of Auger electrons generated per absorbed X-ray photon (at 7 mg/g nanoparticle concentration) is 0.56 as derived from the Auger spectra. The product of number of source photons and number of Auger electrons per source photon gives the total number of Auger electrons emitted. Number of Auger electrons per source photon at higher nanoparticle concentrations is obtained by scaling number of Auger electrons per source photon at 7 mg/g as described by Ngwa et al.¹⁶ For simplicity, the average number of Auger electrons per source photon generated from bismuth nanoparticles and platinum nanoparticles are also taken as 0.56 when irradiated by the same 50 kVp source. This is reasonable approximation assuming that the difference in Auger electron spectra of platinum (Z = 78), gold (Z = 79) and bismuth (Z = 83) is negligible due to their similar atomic numbers and therefore similar Auger yields when exposed to the same X-ray beam.

Both photoelectrons and Auger electrons can cause radiolysis of surrounding water, leading to formation of free radicals (mostly hydroxyl radicals). But free radical chain reaction can be terminated by scavengers such as lipids in cell membranes, or enzymes inside cell. It has been found that mean diffusion length of free radicals is in the range of 200 nm in presence of 10^-5 M scavengers in aqueous solution. Thus, to ensure maximum DNA damage caused by photoelectron and Auger electrons, it is necessary to position nanoparticles as close to nucleus as possible. The slab model, used to calculate dose enhancement to cell, is slightly adjusted to include a nucleus that occupies 10% of cell volume (Fig. 1).²⁰ The nucleus has a diameter of 0.5 μm and a thickness of 1.0 μm, and is located at the center of the 2 μm thick slab. The boundary conditions in equation (5) are adjusted to include only the dose deposited by electrons within 1 μm thick slab (KLMN) section containing the nucleus. Energy deposited within 1 μm thick slab section containing nucleus is calculated as:

$${\mathrm{E}}_{\mathrm{slab}}={\int }_r^{R_{\mathit{tot}}}\frac{H_{\mathit{ABC}}-C_{X^{\prime }B{Y}^{\prime }}}{S_{\mathit{ABCD}}}\times \frac{{\mathit{dE}}_{\mathit{KE}}}{\mathit{dx}}\mathrm{d}x-{\int }_r^{R_{\mathit{tot}}}\frac{H_{\mathit{ABC}}-C_{\mathit{ABC}}}{S_{\mathit{ABCD}}}\times \frac{{\mathit{dE}}_{\mathit{KE}}}{\mathit{dx}}\mathrm{d}x$$ (7)

For a centrally located nucleus inside a 2 μm slab C_X′BY′ = Area of spherical cap X′BY′ = 2πR_tot (R_tot − t + 0.5 μm) C_ABC = Area of spherical cap ABC = 2πR_tot(R_tot − t + 1.5 μm) with t = 2 μm being the cell thickness. Plugging in parameters for 1.9 nm bismuth nanoparticles gives E_slab=1.45 keV. The average dose deposited in the slab section containing the nucleus is given by:

$${\mathrm{D}}_{\mathrm{slab}}=\frac{{\mathit{Volume}}_{\mathit{nucleus}}}{{\mathit{Volume}}_{\mathit{slab}}}\times \frac{E_{\mathit{slab}}}{{\mathit{mass}}_{\mathit{nucleus}}}$$ (8)

The mass of nucleus is calculated from product of its volume and density (1.0 g/cm³). The nDEF is obtained as follows:

$$\mathrm{nDEF}=\frac{D_{\mathit{slab}}+D_W}{D_W}$$ (9)

where D_W = 2 Gy is arbitrary dose delivered to water surrounding the nucleus. Plugging in values yields nDEF = 1.02 for photoelectrons and 8.24 for Auger electrons at 7 mg/g concentration of 1.9 nm bismuth nanoparticles.

3. Results and Discussions

Fig. 2A shows variation of cellular DEF due to photoelectrons as a function of nanoparticle concentrations for 400 nm diameter bismuth, gold and platinum nanoparticles when irradiated by a 50 kVp source. For any given concentration, bismuth nanoparticles yield the highest dose enhancement while gold and platinum nanoparticles provide similar enhancements. This is in accordance with differences in X-ray absorption cross sections of bismuth, gold and platinum. At a concentration of 350 mg/g, bismuth nanoparticles provide 1.25 and 1.29 times higher dose enhancements than gold nanoparticles and platinum nanoparticles, respectively. Fig. 2B shows variation of dose enhancement due to Auger electrons with nanoparticle concentrations. Although, DEFs due to Auger electrons increase linearly with nanoparticle concentration, they are considerably higher than those from photoelectrons at the same concentration. This is attributed to the short range (less than 1 μm) of Auger electrons, which causes them to deposit most of their energies in the vicinity of the X-ray irradiated nanoparticle. As a result of the near particle energy deposition, dose contribution within several hundred nanometers from nanoparticle location is dominated by Auger electrons. Auger electrons from bismuth nanoparticles provide ~2 and 2.4 times higher enhancement than gold nanoparticles and platinum nanoparticles at 350 mg/g. Total dose enhancement factors are calculated by summing contributions from photoelectrons and Auger electrons. Table 1 summarizes total enhancement factors for three nanoparticle concentrations for three types of nanoparticles having a diameter of 400 nm.

Figure 2.

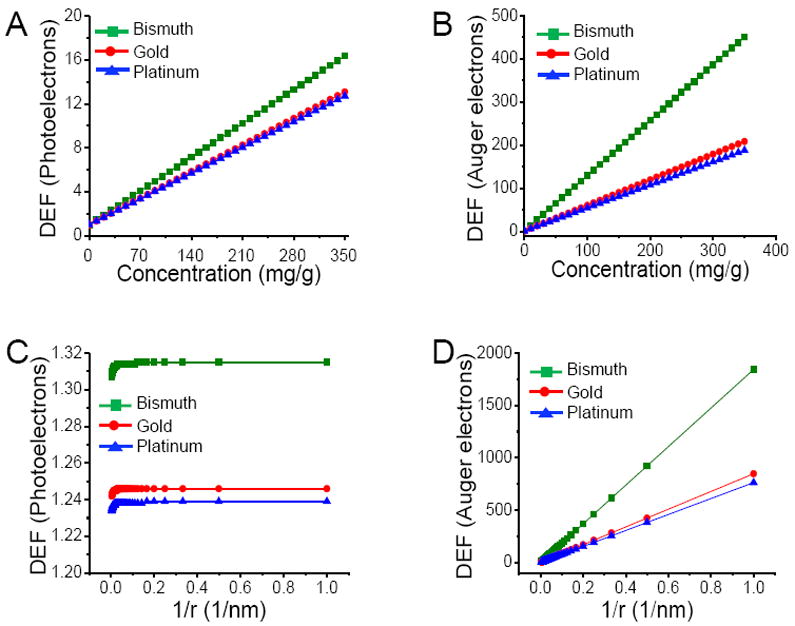
Endothelial cell dose enhancement factor (DEF) as a function of local nanoparticle concentration due to photoelectrons (A), Auger electrons (B) for 400 nm diameter nanoparticles irradiated by a 50 kVp external beam X-ray source; Endothelial cell dose enhancement factor (DEF) as a function of nanoparticle radius (r) due to photoelectrons (C), Auger electrons (D) for 7 mg of nanoparticles per gram of tumor irradiated by a 50 kVp external beam X-ray source.

Table 1.

Dose enhancements in endothelial cell due to photo/Auger electrons

Nanoparticle (400 nm)	DEF (Photoelectrons)			DEF (Auger electrons)			DEF (Total)
	7 mg/g	18 mg/g	350 mg/g	7 mg/g	18 mg/g	350 mg/g	7 mg/g	18 mg/g	350 mg/g
Bismuth	1.31	1.79	16.36	9.99	24.13	450.65	11.3	25.91	467.00
Gold	1.24	1.62	13.08	5.15	11.68	208.63	6.39	13.30	221.71
Platinum	1.23	1.60	12.73	4.74	10.62	188.01	5.97	12.22	200.71

Fig. 2C shows effect of nanoparticle size on dose enhancement due to photoelectrons alone at 7 mg/g for three different types of nanoparticles. Enhancement factor remains constant with increase in particle size from 2-400 nm. Fig. 2D shows enhancement factor due to Auger electrons decreases with increase in particle size. Following an ionizing event, photo or Auger electrons must escape nanoparticle before causing damage to surrounding cells; however, the percentage of electrons emitted from nanoparticle upon X-ray excitation strongly depends on particle size, with a majority of low energy and short range Auger electrons being absorbed more readily within nanoparticle of increasing size. Because more Auger electrons can escape from smaller nanoparticles, the overall energy deposited to surrounding cell is higher for smaller nanoparticles, resulting in higher dose enhancements.¹⁷ On the other hand, the percentage of energy escaping as photoelectrons and characteristic X-rays remains unchanged with increase in particle size, thereby, maintaining an almost constant dose enhancement.¹⁰ As shown in Fig. 2C and 2D, for any given size (and concentration), bismuth nanoparticles provide the maximum dose enhancement, while platinum nanoparticles have slightly lower DEFs than gold nanoparticles. The total enhancement including both Auger and photoelectrons with respect to particle size is calculated by summing the individual contributions from Auger and photoelectrons.

Fig. 3A and 3B show variations in nDEFs with nanoparticle concentrations for photoelectrons and Auger electrons, respectively, when irradiated by an external 50 kVp X-ray source. Since smaller nanoparticles have high Auger electron yield (due to low self-absorption), the nanoparticle diameter used to calculate nDEF is 1.9 nm instead of 400 nm in order to emphasize influence of Auger electrons. Bismuth nanoparticles provide the highest nDEFs for a given nanoparticle concentration, size and location. The total nDEFs can be obtained by adding nDEF values for photoelectrons and Auger electrons. Table 2 summarizes nDEFs due to photoelectrons and Auger electrons for a centrally located nucleus using three different concentrations with nanoparticle diameter of 1.9 nm.

Figure 3.

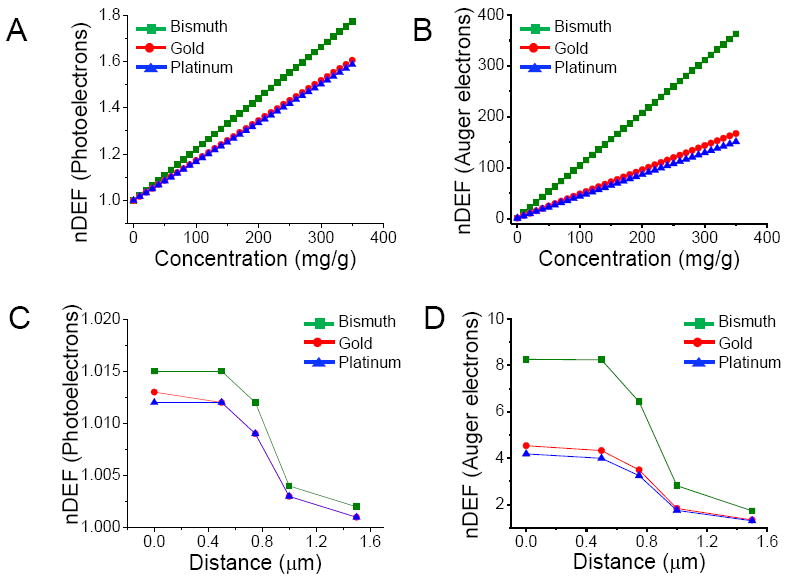
Nucleus dose enhancement factor (nDEF) as a function of local nanoparticle concentration due to photoelectrons (A), Auger electrons (B) for 1.9 nm diameter nanoparticles irradiated by a 50 kVp external beam X-ray source where the nucleus occupies 10% of the cellular volume; nDEF as a function of distance between the nanoparticle and nucleus, due photoelectrons (C), Auger electrons (D) for 1.9 nm diameter nanoparticles (at 7 mg/g) when irradiated by a 50 kVp external beam X-ray source where the nucleus occupies 10% of the cellular volume. Zero distance refers to the position when the nanoparticle is just inside the nucleus.

Table 2.

Dose enhancements in the nucleus of endothelial cell due to photo/Auger electrons

Nanoparticle (1.9 nm)	nDEF (Photoelectrons)			nDEF (Auger electrons)			nDEF (Total)
	7 mg/g	18 mg/g	350 mg/g	7 mg/g	18 mg/g	350 mg/g	7 mg/g	18 mg/g	350 mg/g
Bismuth	1.02	1.31	1.77	8.24	19.61	362.92	9.26	20.92	364.69
Gold	1.01	1.24	1.61	4.33	9.55	167.25	5.34	10.79	168.86
Platinum	1.01	1.23	1.59	4.00	8.70	150.75	5.01	10.29	152.34

The location dependent variation of nDEF is studied for photoelectrons and Auger electrons. The zero position is taken as the location where nanoparticle is closest to the nucleus or just inside the nucleus. Fig. 3C and 3D show how nDEF varies as the nanoparticle is moved away from the nucleus, with regards to the energy distributions from photoelectrons and Auger electrons, respectively. The concentration of nanoparticles is chosen to be 7 mg/g. The long-range photoelectrons deposit their energy relatively uniformly over the entire cell volume with nDEF remaining fairly constant as the nanoparticle is moved away from the nucleus. In contrast, short range Auger electrons deposit more energy closer to the nanoparticles; therefore, the highest nDEFs are achieved for nanoparticles that are located closest to the nucleus. Results summarized in Table 1 and 2, confirm that for any given nanoparticle concentration, size or location, bismuth nanoparticles offer significantly higher dose enhancements for both cell and nucleus compared to gold nanoparticles and platinum nanoparticles when irradiated with a typical low energy 50 kVp diagnostic X-ray source.

Fig. 4A-C shows how the cellular dose enhancements due to photoelectrons alone depend on energy of primary X-rays at different particle concentrations for bismuth, gold and platinum nanoparticles. For each type of particle, the diameter is taken at 400 nm. Fig. 4D shows the results obtained at nanoparticle concentration of 350 mg/g. In addition to 50 kVp source, two additional X-ray sources, 110 kVp (average energy ~40 keV)²⁹ and 300 kVp (average energy ~100 keV)¹⁰ are used to study the energy dependence of cellular dose enhancements. Our results are consistent with earlier studies¹⁰ that used Monte Carlo simulations and reveal a general trend of increasing dose enhancement with decreasing energy of X-ray sources for a given nanoparticle type. The k-edge energies of bismuth, gold and platinum are 91, 81 and 78 keV, respectively. The 50 kVp and 110 kVp sources have average energies below k-edge while 300 kVp source has an average energy above k-edge of particles. An abrupt increase in photoelectric absorption coefficients is observed only when the average energy of the primary X-ray photons matches k-edge energies or when a monochromatic X-ray source with the same energy as k-edge of nanoparticles is used. Low energy diagnostic X-ray sources are therefore ideal for nanoparticle enhanced therapeutic applications particularly for treatment of surface cancers. However, treating deeply buried cancers would still require high energy X-ray beams that can penetrate deeper inside the body.

Figure 4.

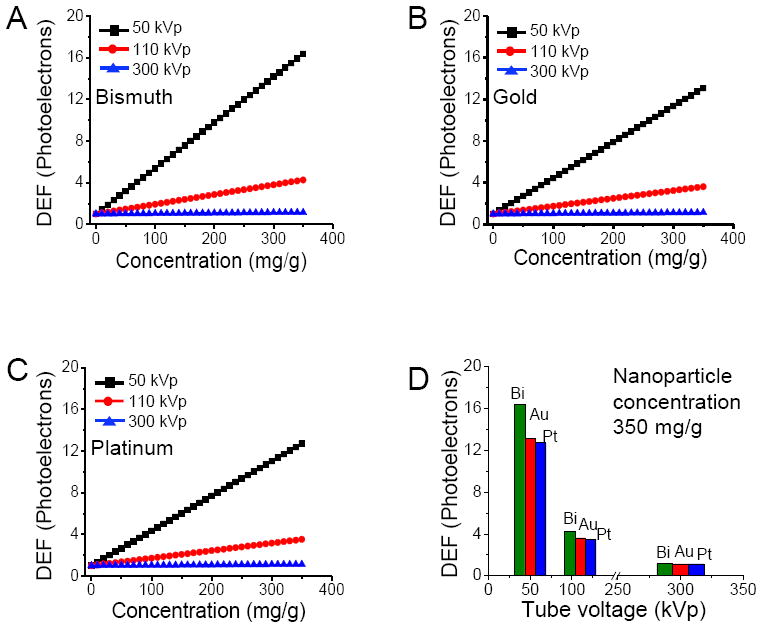
Endothelial cell dose enhancement factor (DEF) as a function of local nanoparticle concentration due to photoelectrons alone at different X-ray tube voltages for bismuth (A), platinum (B) and gold (C) nanoparticles; endothelial cell dose enhancement factor (DEF) due to photoelectrons alone for three different X-ray sources when the nanoparticle concentration is 350 mg/g(D).

4. Conclusion

In this work, an analytical approach is adopted to obtain does enhancements for tumor cells and their nuclei using bismuth, gold and platinum nanoparticles. Energy depositions from both photoelectrons and Auger electrons, generated by X-ray irradiation of nanoparticles have been considered. The dependence of dose enhancements on nanoparticle material composition, location, size, and concentration, as well as the energy of irradiating X-ray photons, are derived based on the mathematical model. Maximum dose enhancements are achieved in the case of bismuth nanoparticles; smaller nanoparticles coupled with low energy external beam X-ray sources can greatly enhance dose delivered to cell or nucleus with maximum enhancements being obtained for particles that are located closest to the nucleus. While, this study indicates the use of bismuth and platinum as a potential alternative to gold in nanoparticle aided radiation therapy of cancer, further studies are warranted to investigate X-ray induced DNA damage, toxicity and biocompatibility of these particles before the proposed method can be put into practical use.