Origin of Giant Ionic Currents in Carbon Nanotube Channels

Abstract

Fluid flow inside carbon nanotubes is remarkable: transport of water and gasses is nearly frictionless and the small channel size results in selective transport of ions. Very recently, devices have been fabricated in which one narrow single-walled carbon nanotube spans a barrier separating electrolyte reservoirs. Ion current through these devices is about two orders of magnitude larger than predicted from the bulk resistivity of the electrolyte. Electroosmosis can drive these large excess currents if the tube is both charged and transports anions or cations preferentially. By building a nanofluidic field-effect transistor with a gate electrode embedded in the fluid barrier, we show that the tube carries a negative charge and the excess current is carried by cations. The magnitude of the excess current, and its control by a gate electrode is correctly predicted by the Poisson-Nernst-Planck-Stokes equations.

New phenomena arise as fluid flows in channels that are small on the scale of a Debye length. Molecules and ions are transported selectively both as a consequence of the finite channel size and because of chemical and electrostatic interactions with the walls of the device.^1–4 Devices have been fabricated by cutting nanochannels into silica^{5, 6} and drilling nanopores into solid membranes.^{4, 7, 8} Flow of aqueous electrolytes inside carbon nanotubes is particularly interesting because of the prediction that it should be nearly frictionless,^9–11 a prediction born out by measurement of flow in well characterized membranes spanned by millions of carbon nanotubes.^{12, 13} We recently built devices in which just one single walled carbon nanotube (SWCNT) connects two fluid reservoirs.¹⁴ This device allowed measurement of the voltage-driven flow of electrolyte and molecules through individual tubes of a few microns in length. Ion currents through the SWCNTs were approximately two orders of magnitude larger than predicted using the classical formula for the resistance of a tube of fluid and the known resistivity of the electrolyte. Furthermore, these ion currents have a power-law dependence on electrolyte concentration (in the range of 1mM–1M) that is quite different from the concentration dependence observed in any other form of nanochannel. This behavior is probably limited to SWCNTs of nm-diameter and micron lengths, because current transport through much longer tubes (0.5 mm length) is dominated by protons.¹⁵

Electrophoretic ion mobilities are not enhanced inside SWCNTs,¹⁴ so electrophoretic flow cannot account for the large currents that were observed. If electrolyte in the SWCNT carries an excess charge of one sign, this can be transported selectively, resulting in nearly frictionless flow of water which drives very large electroosmotic currents. We have now tested these ideas using an ionic field effect transistor^16–20 in which an insulated gate controls the potential and charge of the SWCNT while the flow of ionic current between fluid reservoirs is measured. We modeled our results with solutions of the coupled Poisson, Nernst-Plank and Stokes (PNPS) equations.

RESULTS AND DISCUSSION

The construction of the ionic FET is shown in Figure 1. Long SWCNTs were grown from Co or Fe catalyst particles on an oxidized silicon substrate as described in Methods and the Supporting Information, S1.1. Index markers (Figure 1a) were fabricated to align subsequent lithographic steps with the axis of the SWCNTs. A 20–30nm thick SiO₂ layer is deposited on top of the SWCNTs as a dielectric for supporting the gold gate electrode. An optical image of the final device (taken through the PDMS microfluidic cover) is shown in Figure 1b. Figure 1c shows the overall device arrangement with the Ag/AgCl reference electrodes used as the source and drain electrodes in the fluid reservoirs. The length of the SWCNT connecting the reservoirs is typically 20 μm. Figure 1d shows a cross-section through the barrier. Further details of the device construction are given in Methods and Figure S1.

Figure 1.

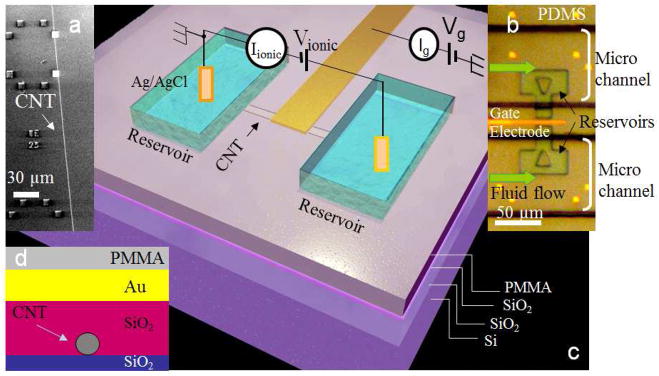
Device fabrication and measurement setup. (a) Scanning electron microscope image of a SWCNT on silicon oxide surface with gold alignment markers. The CNT is typically 1.7 nm in average outer diameter. (b) Optical microscope image of a device looking down into the PDMS microfluidic system that covers it. The scale bar is 50 Fm. (c) Schematic of the device and the electrical connections. A 10–30Fm long CNT connects two reservoirs with a 20–30 nm thick silicon oxide layer used as dielectric between the top gate (voltage V_g) and the CNT. A voltage (V_ionic) is applied across the two reservoirs using Ag/AgCl electrodes. Ionic current through the tube (I_ionic) and the gate charging current (I_g) are recorded. (d) Schematic cross-section through the barrier region.

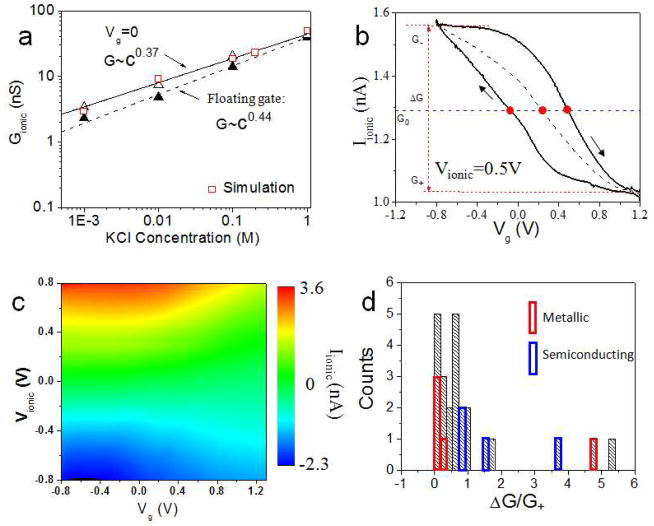
A critical step lies in opening SWCNTs using an oxygen plasma etch without damaging the insulating bridge that separates the fluid reservoirs. The use of a 20–30 Fm wide barrier (comparing with 2Fm wide barrier) has now pushed our yield of working devices to about 40%. We have described in supporting information and elsewhere the extensive control experiments used to eliminate the possibility that current is carried by a leak in the barrier rather than through the SWCNT.¹⁴ Now that we have made several hundred working devices, we have found that the simplest check on device quality is to measure the ionic current as a function of salt concentration (Figure 2a). A particular form of power law dependence of conductance, G, on salt concentration, c, G ~ c^b (where c > 0.1mM, b < 1) is unique to transport through SWCNTs. Other types of nanochannel (e.g., silicon based) often have an approximately constant conductance at low salt and the conductance become proportional to concentration at high salt (> 0.1M), giving rise to an opposite sign of curvature in the plots of conductance vs. salt concentration.^{14, 21} We have observed that b is sensitive to barrier materials and CNT electrical properties. A small range of b values (~0.3–0.4) is found for devices with PMMA barriers. The range is much bigger with SiO₂ barriers. Nonetheless, this form of power law is found only for ion transport through small diameter SWCNTs. It is, as we shall show, a consequence of electroosmtic flow in a very small channel. For the particular device used to generate the data shown in Figure 2b, b = 0.37 for the case of a grounded gate, and 0.44 for the floating gate, values well within the range measured for tubes without a gate.¹⁴ Since grounding the gate changes the electrical properties of the system, it implies that the floating gate carries a charge. The change of slope of this plot (Figure 2a) on grounding the gate electrode also indicates that the exponent, b, is probably affected by the total charge on SWCNT, as discussed in detail in S7.3 and S7.4. Also, this charge, Q, is a critical factor in determining the electroosmotic flow through the tube, and it can be found by fitting these conductance curves using solutions of the PNPS equations with different charges, as discussed in details in S7.3. An example of such a fit is shown by the red hollow squares in Figure 2a.

Figure 2.

SWCNT ionic-FET characteristics. (a) Concentration dependence of ionic conductance on salt concentration. Opened triangles are for a floating semiconducting tube, filled triangles are for a tube with the gate held at zero volts and the lines are fits to G_ionic ~c^b. The red squares are simulations in which the charge on the tube was adjusted to fit these data. (b) Ionic current vs. V_g at V_ionic= 0.5V for a semiconducting SWCNT with a V_g sweep rate of 80mV/s. The sweep direction is indicated by arrows. The black dashed line is the average of the sweep-up and sweep-down currents. The horizontal blue dashed line is the ionic current recorded when the gate is floating. The solid red circles label the points where the current through the gated device equals the current recorded with a floating gate. The definitions of the quantities G₊, G₋, ΔG(=G₋−G₊) are illustrated by the red dashed lines. (c) Heat map of the ionic current vs. V_ionic and V_g based on sweep-down curves. P-type transistor action is clearly displayed. (d) Histogram of the gating efficiency, ΔG/G₊, for all the measured devices for 1mM KCl solutions (pH=7). The gating voltage range is −0.5V to 0.8V on average. Bins outlined in red and blue indicate metallic and semiconducting CNT devices as measured independently using an electronic FET fabricated on the same tube. The datum pointed to by an arrow is an outlier that might be a consequence of a change in chirality of the SWCNT between the ionic and electronic FET devices.

Some typical ionic FET data are shown in Figures 2b and c. Figure 2b shows the dependence of the ionic current flowing between the Ag/AgCl source and drain electrodes on the bias applied to the gate electrode embedded in the barrier region. The response shows a significant hysteresis characteristic of the extrinsic charges that dominate SWCNT devices, but the ionic current is always reduced when the gate is swept to a positive bias (data for a number of devices is summarized in the supporting information, S2–S6). This reduction of ionic current on positive gating implies that the current is carried predominantly by cations (a situation that can be changed by using large cations, see Fig. S3). The dashed line shows the average of the sweep-up and sweep-down curves, and this average is always displaced to the right of V_g=0. That is to say, zero conductance occurs at a positive gate bias. The presence of a charge on the device was indicated by the change of the salt concentration dependence on grounding the gate (Figure 2a). The measured FET characteristic implies that this charge on the tube (and its immediate environment) is negative. This charge is most likely largely extrinsic, associated with the SiO₂/CNT interface, charge inside the barrier material close to the CNT and at the ends of the tubes, both on the barrier material and in the form of charged carboxylates on the ends of the SWCNTs. In the modeling (detailed in S7), we simplify what is possibly a complicated and extrinsic charge distribution on SWCNT by assigning a fixed total charge Q to the surface of the SWCNT. This is to be distinguished from the surface charge density σ_s, the two being connected by $Q=\underset{S}{\int }{\sigma }_{s}dS$. We allow the simulations to self-consistently adjust the surface distribution of charge on the tube as the gate bias and other parameters of the system are changed, as discussed in S7.3. The measured ion current as a function of both drain-source bias (vertical axis, V_ionic) and gate bias (horizontal axis, V_g) is shown in Figure 2c, where the magnitude of the ion current is shown by the color scale (blue is negative, red is positive - the raw data used to construct Fig. 2c are shown in Fig. S2). These data show “p-type FET” characteristics over a wide range of drain-source bias. The ion current is only partially gated, as is characteristic of ionic FETs,^{16, 17, 19} the ionic conductance falling to a lower limit, G₊, at the highest positive gate bias (G₊ is shown for a single value of V_ionic in Figure 2b). The fraction of conductance that can be switched is characterized by the “gating efficiency” ΔG/G₊ (where ΔG = G₋−G₊, see Figure 2b). A distribution of this parameter for 22 devices is shown in Figure 2d. Gating increases the ionic current many times in some devices (up to 5x) while other devices were barely gated.

One possible source of this variability of gating efficiency lies with the carbon nanotubes themselves. Metallic tubes might be expected to screen the gate field more effectively than semiconducting tubes,²² leading to a lower gating efficiency for devices made from metallic tubes. In order to test this effect, we have made a number of devices in which an electronic FET was fabricated at one end of the same SWCNT (Figure S1) used to make the ionic FETs. Thus, assuming that the tubes do not change their chirality over their length, we can use measurements of the electronic properties of the SWCNTs to determine whether a given ionic FET was made from a metallic or semiconducting tube.²³ Using this technique, we have outlined data from tubes identified as metallic in red and data from tubes identified as semiconducting as blue in Figure 2d. Clearly, gating is more effective in semiconducting tubes, as expected (the outlying point might be a consequence of a tube that changed chirality between the electronic FET and the ionic FET portions of the device). There is considerable spread in the characteristics of the semiconducting tubes, suggesting that external factors (such as variation in external surface charges) also contribute to the range of characteristics.

We turn now to the quantitative analysis of the FET response. Our simulations are based on the continuum approximation, assuming a micro-nano incompressible Newtonian fluid system in a steady flow, with small Knudsen and Reynolds numbers, with conservations of mass, energy, momentum and charge. Approximating the geometry with the an azimuthally symmetric system (illustrated in Figure S5) the problem is reduced to a two-dimensional set of the Poisson-Nernst-Planck and Stokes (PNPS) time-independent coupled partial differential equations (S1–S4), which we solve numerically, self-consistently, while achieving high accuracy and full convergence (Methods). The huge range of scales, from micron sized reservoirs and CNT lengths, to the ~ 2 nm diameter of the SWCNT channel poses significant numerical challenges. In particular, errors in the regions around the ends of the tubes are manifested in breakdown of the required conservation of the total currents through the device. We have overcome these problems with the use of an adaptive numerical mesh and a slight rounding the ends of the SWCNT, as described in detail in S7.2. These difficulties preclude modeling of a full sized system with a 20 μm long SWCNT. We have chosen not to compromise the small diameter of the nanotube (here d=2 nm), but rather to reduce the axial length of the tube to L=50 nm, keeping d/L≪1, with appropriate adaptations of other system dimensions as in Figure S5. Some tests of length effects are done using model SWCNTs with L of 200 nm and 500 nm (S7.3, S7.8). Detailed analysis is carried out only for the numerically most convenient 50 nm case. Scaling to longer tube lengths is not straightforward because of the variation of the electric fields through the tube length. A particularly large voltage drop close to the tube ends and large gradients of the excess charge concentrations cause strong mixing of various components of the electric current in that zone (electroosmotic, electrophoretic, diffusion), as discussed in detail in S7.6. The significance of the end effects decrease with the tube length, and our tube model of L=50 nm is not immune to these effects. However, this complication does not invalidate a key outcome of the simulation: the ratio of the electroosmotic conductance to the electrophoretic conductance is found to be >20 for L=50 nm, as discussed in detail S7.8, accounting for the very large conductances observed in the experiments. In the longer model tubes (S7.3, S7.8, Figures S10, S25, S26), the current is almost entirely electroosmotic in origin (the ratio of electroosmotic to electrophoretic conductance is >200:1 in 200 nm long tubes and > 3000:1 in 500 nm long tubes).

A perfect slip boundary condition, applied at the CNT inner surface²⁴, is responsible for large electroosmotic current through the tube.¹⁴ The molecular dynamics simulations (S7.7) show that the slip length on SWCNT inner surface is much larger (at least one order of magnitude) than the diameter (2 nm) of the SWCNT, for all charged CNT surfaces considered in this study, which validates use of the perfect slip boundary conditions at the inner surface of the model SWCNTs. The total negative charge, Q, assumed to be on the CNT surface, is a key parameter that has to be determined by fitting experimental data because it almost certainly arises from sources external to the tube. In case of V_g=0, our experimental measurements with both L=20 Fm (present) and L=2 Fm¹⁴ SWCNT show almost perfect linear dependence of conductance on salt concentration when plotted on a log-log scale, having the slope in range 0.3–0.4. Our calculations for various (much shorter) lengths of 50 nm and 200 nm (Figure S7) also show a similar dependence of G on c, where the slope and the quality of the power law fit depends on Q. Therefore, a reasonable hypothesis for determination of Q is that the G(c) for V_g=0 is in the form of the power law, G=A(L)c^b, where possible length effects are contained in the prefactor A(L), while the exponent b is independent of the tube length. The set of measured data in Fig. 2b, showing b=0.37 for V_g=0, is used as input in our fitting procedure. We discuss the inverse problem (S7.3) of finding Q by solving the PNPS equations for various c and Q, and finding the best fit of the hypothesized exponent b from the computed results with the experimental value of 0.37. The value of Q obtained this way is length dependent. Thus, Q=37.5e for L=50 nm (~0.003e per carbon atom), and Q=312.5e for L=200 nm (~0.006e per carbon atom), with b=0.37 in both cases (Figure S7). With Q determined, we have calculated the mean electroosmotic mobilities in the model CNTs, which are about 10⁻⁶ m²/Vs for L=50 nm and about 1×10⁻⁵m²/Vs for L=200 nm at c=0.1M (see details in S7.8). These values are about one (L=50 nm) or two orders (L=200 nm) higher than the electrophoretic mobility of potassium ion in bulk solution. The calculated mobilities are also comparable to the recent experimentally determined mobilities for potassium ions in one or a few SWCNTs¹⁵ and about 2 or 3 orders higher than the value measured in big modified MWCNTs²⁵ (where electrosmosis probably does not dominate).

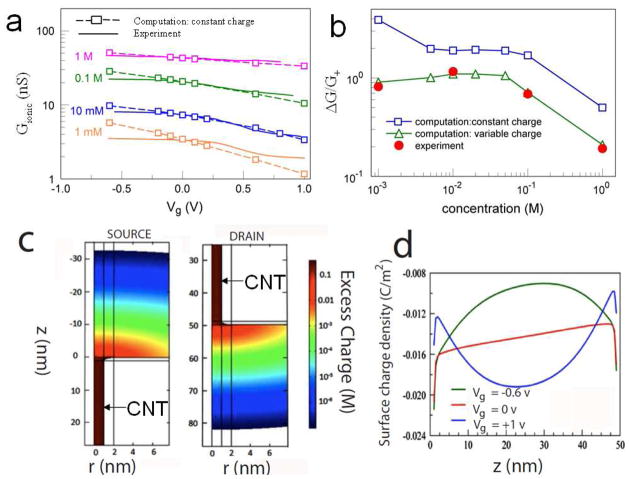
We have also simulated the G_ionic-V_g curves for various concentrations, obtaining solutions of the PNPS equations that are in general agreement with the experimental data. Figure 3a shows typical experimental data (sweep-down only) as solid lines. The general trend of G_ionic vs. V_g is fitted quite well using the constant charge Q deduced from the G_ionic vs. c curves in Figure 2a, and normalizing G at one c to the experimental conductance. A nearly perfect fit can be obtained by allowing Q to vary by a small amount with gate bias, to reflect polarization of the barrier material (Figure S11 in S7.4).

Figure 3.

Comparison between simulated and measured FET characteristics. (a) G_ionic vs. V_g at different KCl concentrations as marked. Lines are measured data (sweep down only). Squares are simulated conductances based on solution of the PNPS equations with constant charge. (b) Gating efficiency, ΔG/G₊, as a function of salt concentration. Blue squares and green triangles are predictions from solutions of the PNPS equations at constant charge and variable charge conditions respectively (lines serve as guides to the eye). Red filled circles are experimental data. (c) Spatial distribution of excess volume charge density (log(c₊ −c₋) in M units) in the reservoirs near the CNT mouths (only one side is shown here) for V_g=−0.6V at 10mM KCl. Distortions owing to the small size of the model reservoir (50 nm) are not significant because excess charges in the reservoirs fall more than three orders of magnitude at 10 nm away from the CNT mouths. (d) Axial distribution of the surface charge density along the CNT surface for different values of V_g. (V_g, −0.6V (green), 0V(red) and 1V(blue)). All the simulations in this study were carried out at 10x the experimental electric field to avoid numerical noise, but this is in a region where the current to voltage scaling is linear, so that the calculated conductances are unaffected.

The amount of gatable current (i.e., the gating efficiency, ΔG/G₊) varies non-montonically with salt concentration. The gate efficiency versus concentration, obtained both from the measured (filled symbols) and simulated data (hollow symbols) is shown at Figure 3b. In addition to values of the KCl concentrations in experiment, we have done calculations for additional concentrations (for 5, 20, 50 mM). Both constant and variable charge PNPS simulations reproduce well the shape of the measured gate efficiency curve for c > 5 mM including the plateau between 5 and 50 mM, while the curves diverge from each other at small concentrations (1mM). Further insight in the gating efficiency is given in S7.5, illustrating its dependence on c, based on just the electroosmotic currents. The difference of about factor 2 between the two curves in Figure 3b reflects the difference between the measured and calculated data in Figure 3a, which reaches a maximum at the ends of the range of V_g considered. This observation suggests possible strong sensitivity of the CNT charge to gate potential in low salt concentration conditions, as shown in Figure S11b.

Very large excess charge gradients (with correspondingly high electric fields) accumulate near the entrance and exit of the SWCNT as shown for the case of 10 mM electrolyte and a 50 nm long SWCNT in Figure 3c. The reservoir width in these simulations was also 50 nm, but the large charge gradients in the reservoirs are localized to within 10 nm of the tube entrances, confirming that the present reservoir size is good enough for describing the behavior of the real reservoirs. The excess charge accumulation within the tube is relatively constant and set mainly by the surface charge on the tube. This excess volume charge increases with electrolyte concentration and negative gate bias (Table S2). Electroosmotic current within the tube is driven by the axial field caused by the imbalance between the charge accumulation at the source and drain ends of the tube. Figure 3d shows the axial distribution of surface charge that gives rise to this driving field. The axial surface charge gradient along the tube is essentially constant at V_g = 0 (red line). The surface charge has a positive peak when V_g = −0.6V (green line) and is reduced when V_g = +1V (blue line - note the charge accumulation near the ends of the tube that balances the fields at the entrance and exit reservoirs near the mouths of the tube). The electric fields in the entrance and exit regions of the reservoirs are decreased as the bulk concentration of electrolyte approaches the concentration of excess ions inside the tube, with the consequence that much more of the applied bias is dropped in the form of an axial field inside the tube. The increased axial field gives rise to increased electroosmotic flow. However, as the internal field grows larger, it is less influenced by the gate field, whose magnitude is limited by the breakdown value of the dielectric layer. Thus, at low salt, the amount of current that can be gated increases with increased electroosmotic flow, but, above 10 mM salt the field inside the tube is too large to be affected significantly by the gate. This leads to the peak/plateau in gating efficiency shown in Figure 3b.

We turn finally to the origin of the charge on the SWCNT. We found that FET characteristics were strongly dependent on pH (Figure 4). The current through the SWCNTs is greatly reduced at pH 3 and is no longer gatable. The amount of gatable current is a maximum near pH 4, close to the pKa of the terminal carboxylates on the SWCNTs. These observations suggest that charged residues on the ends of the SWCNT (and possibly the surface of the reservoirs) contribute to the charge on the tube.

Figure 4.

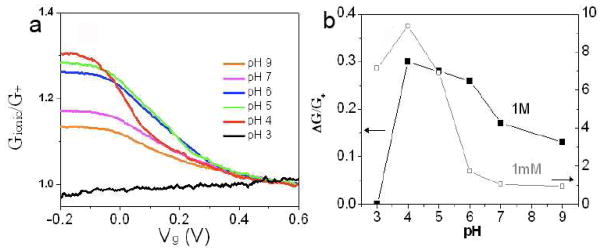
Tube charge is extrinsic and modulated by pH. (a) G_ionic/G₊ vs. V_g at different pH (sweep-down curves). (b) Gating efficiency ΔG/G₊ vs. pH in 1M (black) and 1mM KCl (gray, right axis).

In summary, we have successfully fabricated ionic FETs using individual SWCNTs. They display stable p-type ionic transistor characteristics, showing that the charge carriers are cations when a KCl electrolyte is used. Ion transport is turned off by the application of a positive gate bias, indicative of a negative charge on the channel. The characteristics of the devices are well-accounted for by simulations that show that the vast majority of the current is carried by electroosmosis, with only a small amount carried by electrophoretic and diffusion currents. The very large electroosmotic current arises from the nearly frictionless flow of water inside the SWCNTs, accounting for the giant ionic currents that flow through these devices. Devices based on a single SWCNT nanofluidic channel will probably offer new approaches for controlling the flow of biological molecules in nanochannels based on the charge sensitivity of the large electroosmotic flow.

METHODS

Experiments

High quality and well-separated SWCNTs, with an average outside diameter 1.7±0.6 nm, were grown on a 1000nm thick thermal silicon oxide (SiO₂) surface as described by Liu et al..¹⁴ Gold markers and large electrical pads were fabricated using optical lithography. Scanning electron microscope (SEM) images were used to locate the SWCNTs position relative to the markers (Figure 1a). After heating the chip at 400 °C in an argon flow for 1 hour to remove resist residue, a 20–30 nm thick layer of SiO₂ was deposited by e-beam evaporation onto the SWCNT (Figure 1d). This SiO₂ layer served as a high-impedance dielectric layer to prevent the electron transport between SWCNT and the top gate electrode. 3 Fm wide top-gate electrodes made of Cr (5 nm)/Au (40 nm) were fabricated by electron beam lithography (EBL). We then spun-on a 900 nm thick layer of polymethylmethacrylate (PMMA, A8) over the entire device structure, and reservoirs were formed along the path of a SWCNT using EBL aligned relative to the markers. Immediately before experiments, the thin SiO₂ layer in the reservoirs was etched away by a diluted buffered oxide etch (BOE) solution thereby exposing the portions of the SWCNTs in the reservoirs. These exposed regions were removed by oxygen plasma etching. Control devices, lacking SWCNTs, were placed on each chip so that we could check that the plasma etch caused no leakage paths across the barriers. Electrical measurements were carried out in a Faraday cage. Ionic current was measured using commercial Ag/AgCl electrodes (MF-2078, BAS, 2M KCl) and an Axopatch 200B amplifier (Molecular Devices, Inc., CA). A Keithley 2636A was employed to apply the gate voltage (V_g) and also to monitor the current (I_g) through the gate electrode. The range of gate voltage (V_g) was limited to avoid leakage as indicated by monitoring I_g. In addition to the use of control devices lacking SWCNTs on each chip, we also intentionally generated leakage current through the interface between the PDMS cover and PMMA barrier with longer oxygen plasma treatments to generate current via leakage paths. Such leaky devices showed no gating effects (Figure S3) and did not display the characteristic power law dependence of conductance on salt concetration.

Theory

The forms of the PNPS equations and the boundary conditions applied in the 2-dimensional, azimuthally symmetric system are presented in detail in the supporting information, S7. We solved these equations using a commercial finite element method multiphysics modeling software package, COMSOL.²⁶ The main challenge in the numerical simulation of the fluid dynamics of the system (Figure S5) is in the critical importance of the competition between large and small quantities, caused by huge differences in the reservoir characteristic size, L, and the CNT diameter, d=2 nm, d≪L. Huge gradients emerge from this geometry difference in quantities like charge densities and the electrical potential at the mouth regions of the CNT. These difficulties were somewhat relaxed by smoothing the corners in the mouth region of the CNT, but still requiring a fine numerical mesh, especially near the nanotube walls, near the tube entrance regions, near the electrodes and other walls. The mesh was refined iteratively until the total electric current in the inlet and exit reservoirs and in the tube matched to within three digits. Typically, the size of an axial numerical grid element was smaller than 0.1 nm in the entrance-exit regions of nanotube, while the minimum size of the numerical element in the radial direction in the interfacial region of the nanotube and electrolyte was less than 0.01 nm. The calculations showed the best stability with rectangular finite elements whose shape follows the geometry of the system for most of the computational domain. The total number of the finite numerical elements was 15,600.