Abstract
We examined how spatial smoothing affects the result of multivariate classification analysis using the linear support vector machine (SVM) for decoding columnar-level organization. It has been suggested that the effect of spatial smoothing on decoding performance is minor because smoothing operation is an invertible data transformation and such invertible transformation does not remove information in multivariate pattern. Our theoretical consideration, however, revealed that generalization score (performance for test samples unused during classifier training) was susceptible to non-uniform scaling of input data; SVM classifier became less sensitive to variability in shrunk dimension. This result indicates that spatial smoothing reduces sensitivity of SVM classifier to high spatial frequency pattern so that the effect of smoothing implies the amount of information distributed in spatial frequencies. We also examined the effect of smoothing in an fMRI experiment of decoding ocular dominance responses. The results of group statistic showed that large smoothing reduced decoding accuracies while the smoothing effect at individual subject were not the same for all subjects. These results suggest that spatial smoothing can have major effect on decoding performance and the informative pattern for columnar level decoding resides in higher frequencies on average across subjects while it may distribute multiple frequencies at individual subject level.
Keywords: multivoxel pattern analysis, support vector machine, informative spatial frequency, columnar-level decoding
1. Introduction
Multivoxel pattern analysis has been used to extract information contained in activation patterns of functional magnetic resonance imaging (fMRI). In particular, successful decoding of orientation column responses in the human primary visual cortex has been demonstrated using this method with a response pattern of 3-mm-sized voxels (Haynes and Rees, 2005; Kamitani and Tong, 2005). Whereas reliability of this analysis has been demonstrated, the fundamental mechanism of contrast formation allowing this decoding is still controversial (Boynton, 2005; Chaimow et al., 2011; Freeman et al., 2011; Gardner, 2010; Kamitani and Sawahata, 2010; Kriegeskorte et al., 2010; Op de Beeck, 2010a; Shmuel et al., 2010).
The effect of spatial smoothing on decoding performance is a concern for studies of decoding columnar-level organization with multivoxel pattern analysis. For the columnar level decoding, spatial smoothing has been thought to remove informative response variability across voxels and deteriorate decoding performance. Op de Beeck (2010a), however, demonstrated that classification accuracies for orientation selective responses stayed the same even with substantial smoothing (Gaussian kernel with 8 mm full-width-at-half-maximum [FWHM]) applied to multivoxel response patterns. In contrast, Swisher et al. (2010) demonstrated that the decoding information mostly resides in the high-frequency domain; decoding performance suffered from smoothing.
Furthermore, Kamitani and Sawahata (2010) implied that the smoothing effect could be irrelevant to informative spatial frequencies for decoding. They indicated that spatial smoothing with Gaussian kernel convolution is an invertible transformation, so that smoothing does not remove information for decoding. They also suggested that the smoothing effect for decoding accuracies depends on classification algorithm.
To resolve the controversy on the effect of smoothing, we investigated how Gaussian smoothing affects the decoding performance of multivariate classification analysis. Specifically we examined the changes in the generalization score (performance for test samples unused during classifier training) of the linear support vector machine (SVM) after smoothing. Op de Beeck (2010b) has suggested that spatial smoothing affects relative scaling of signals in different spatial frequencies. We further examine how the non-uniform scaling affects the generalization score of SVM by theoretical considerations.
This article consists of two parts. The first part consists of a theoretical assessment of the sensitivity of the linear SVM to smoothing operation on input data and a simulation to verify the smoothing effect expected by the theoretical consideration. In the second part, we performed a decoding analysis on fMRI data to evaluate empirically the effect of smoothing. In this experiment, responses of ocular dominance columns were decoded using the linear SVM.
2. The sensitivity of SVM generalization score to spatial smoothing
2.1. Theoretical inference
Spatial smoothing with a Gaussian kernel can be understood as an invertible transformation of data space (Kamitani and Sawahata, 2010). Here we consider the effect of the data transformation on the estimation of the classification boundary in multivariate classification analysis.
In a general form of a two-class linear classification, a classification function is represented as:
| (1) |
where y is the output of classifier, which is a column vector of outputs for each sample, X is the data matrix, in which each row corresponds to individual sample of multivariate data vector, w is the normal vector of the boundary, and b is a vector whose length corresponds to distance from the origin to the boundary. Since the b can be represented in X and w, this is omitted from the following equations. The classification label is provided as [−1, 1]; if yi > 0, xi is labeled as 1 otherwise it is labeled as −1 where yi and xi are the ith row components of y and X, respectively.
We represent a linear transformation of data as:
| (2) |
where Xt is the matrix of transformed data, Xo is the matrix of original data, and M is the transformation matrix. If M is invertible, a boundary giving exactly the same classification output for the transformed data as in the original data should exist. The normal vector of such boundary, which we represent as wot, is given by:
| (3) |
where wo is the normal vector of the boundary evaluated for the original data. From the Eqs. (1), (2), and (3), the outputs, yt with wot for the transformed data are the same as yo with wo for the original data:
| (4) |
The fact that equivalent outputs can be derived from the transformed data means that classifiers that optimize classification scores for given training samples are insensitive to invertible transformations of input data. Since the smoothing operator with Gaussian kernel can be expressed as an invertible transformation (Kamitani and Sawahata, 2010), spatial smoothing does not seem to affect the result of multivariate linear classification analysis.
However, in the decoding analysis, our interest is not in classification scores for the training samples themselves. When the number of samples is smaller than the number of data dimensionality, which is often the case in fMRI decoding analyses, arbitrarily high accuracies can be attained for the training samples because the number of parameters in the classifier is larger than the number of samples. In fMRI decoding analyses, the performance of the classifier should be evaluated with the results for test samples that are not used in the training, namely, using the generalization score.
Multivariate classification analysis that aims to optimize the generalization score can be sensitive to invertible transformation of input data. The SVM (Bishop, 2007; Cristianini and Shawe-Taylor, 2000; Vapnik, 1995) aims to maximize the generalization score by searching a boundary that maximizes margin between classes, which is represented as:
| (5) |
where tn is the class label ([−1,1]) and xn is the data vector for the nth sample. The margin and the optimal boundary for SVM can change after the data transformation if the transformation results in non-uniform scaling; scaling factors are different between axes, which is demonstrated in Fig. 1.
Figure 1.
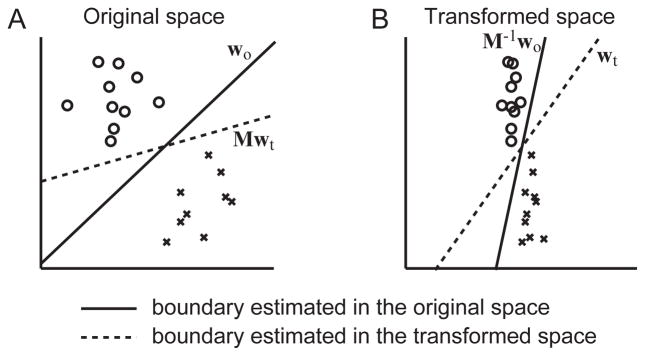
Schematic illustration for the effect of data transformation on boundary estimation of the linear SVM. A binary classification example for two-dimensional data with 20 samples (10 for each class) is shown in the original space (A) and in the transformed space (B). The solid line represents the boundary estimated in the original space and the dotted line represents the boundary estimated in the transformed space.
Fig. 1A shows the original data points, Xo, and Fig. 1B shows the transformed data points, Xt. The solid line in Fig. 1A is the boundary with the normal vector of wo, which is estimated for Xo with the linear SVM. This boundary was transformed into the data space of Fig. 1B using Eq. (3), which is shown by the solid line in Fig. 1B. While the solid-line boundaries in both Figs. 1A and 1B give the same classification results for the training samples as seen in Eq. (4), the boundary in the transformed space does not maximize the margin. The boundary that maximizes the margin for the transformed data is shown by the dotted line in Fig. 1B, which was estimated with the linear SVM for Xt. To compare the boundaries in the original space, the boundary with wt (dotted line in Fig. 1B) was transferred onto the original space (dotted line in Fig. 1A) using Eq. (3) in the reverse direction. As seen in Fig. 1A the boundary estimated for the transformed data (dotted line) is more parallel to the horizontal axis, which is shrunk with the transformation in Xt.
The discrepancy between the solid and dotted lines in Fig. 1 is due to the nonuniform scaling of the two dimensions. When transformation M includes non-uniform scaling, Xt and wot are scaled in opposite ways as seen in Eqs. (2) and (3) (M vs. M−1). Then the angle between Xt and wot becomes larger and their inner product becomes smaller. As a result, the margin (wTx in Eq. (5)) becomes smaller for the wot in the transformed space relative to wo in the original space. Note that the margin is defined in the direction of the normal vector of the boundary, so that the boundary maximizing the margin in the transformed space should be more parallel to the shrunk axis.
Although both boundaries output the same classification labels for the given training samples, generalization performance for unseen test samples can be changed substantially because the classification boundary estimated for the transformed data is less sensitive to variability on the shrunk dimension.
The Gaussian smoothing scales dimensions differently in the spatial frequency domain (Op de Beeck, 2010b); it shrinks data space more in high frequencies than low frequencies. While fMRI response patterns are represented by voxels, they can be transformed to frequency space using discrete Fourier transform, which is one of the linear orthogonal transformations that preserves angle of vectors in data space. Therefore, we can predict that spatial smoothing makes the decoding performance (generalization score) less sensitive to variability in high-frequency patterns and the effects of smoothing can indicate the relative amount of information in different frequencies. A simulation of pattern classification was carried out to confirm this prediction.
2.2. Verification of the theoretical inference by a simulation
We performed a simulation to examine the relationship between the effect of smoothing and informative frequency for pattern classification with the linear SVM. It should be noted that this simulation was not aimed to model an actual fMRI data, but to examine the effect of spatial smoothing on the linear SVM in a general pattern classification analysis.
2.2.1 Simulation procedures
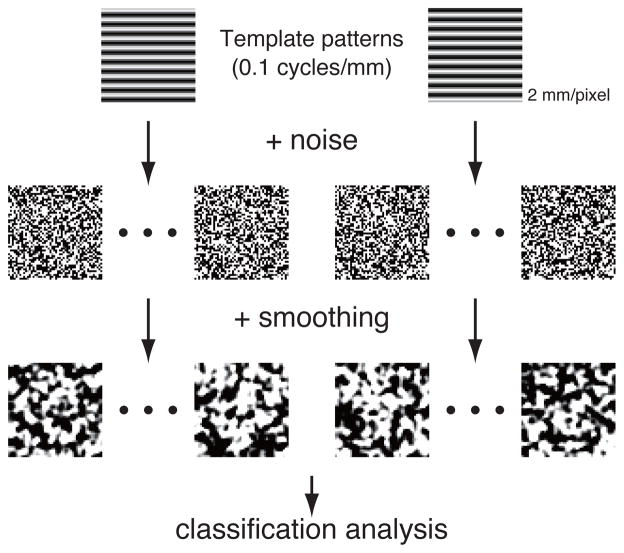
The overall procedures for the simulation are depicted in Fig. 2. The simulation was performed using MATLAB (The MathWorks, Natick, MA). Two template patterns were made with the same waveform of a sine function but their phases are different in half cycle. The pattern consists of 50 × 50 pixels with the frequency of the sine function at 0.1 cycles/mm where one pixel corresponds to 2 mm. From the two template patterns, 20 samples were constructed for each class by adding Gaussian noises at each pixel. Standard deviation of the noise is five times larger than the maximum amplitude of the sine function. For this data set, informative frequency was localized at 0.1 cycles/mm.
Figure 2.
Procedures of creating sample patterns in the simulation analysis
Spatial smoothing was applied for these sample patterns by convolving the Gaussian kernels of 2, 4, 6, 8, and 12 mm FWHM. Then the convolved patterns were subject to classification analysis using the linear SVM. The decoding performance was evaluated with generalization score using leave-one-out cross-validation (Bishop, 2007; Mitchell, 1997) with 100 repetitions of different random noise patterns.
2.2.2 Simulation results
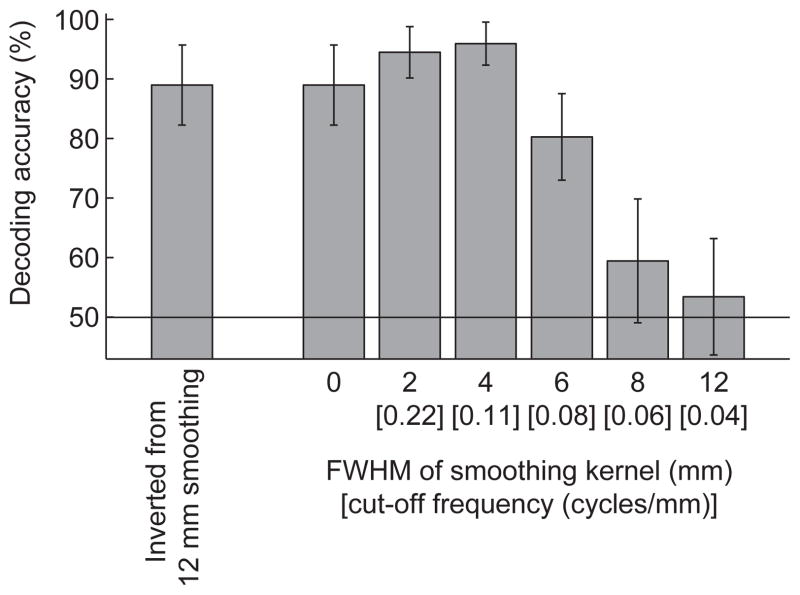
Fig. 3 shows the mean decoding accuracies and the standard deviations across 100 simulations. The best performance was obtained with smoothing by 4 mm FWHM Gaussian kernel. Further smoothing with larger kernels substantially reduced the decoding performance. Considering the cut-off frequencies of the Gaussian smoothing (at which the power of signals is halved by the filter), these results are consistent with the prediction that smoothing effect is systematically related to informative spatial frequency. As the information existed only at 0.1 cycles/mm, small smoothing up to 4 mm (cut-off frequency is 0.11 cycles/mm) was helpful to reduce high-frequency noise. Larger smoothing, in contrast, made the SVM classifier less sensitive to informative frequency, resulting in decreased decoding performance.
Figure 3.
The effect of smoothing on the decoding accuracy for the simulated patterns using the linear SVM. Average accuracy and standard deviations across 100 simulations with different random noise patterns are shown. The left most bar shows the decoding result for the patterns smoothed by 12-mm kernel, then inverted to the non-smoothed patterns.
To confirm that this performance reduction was not due to numerical loss in a smoothing calculation, we examined decoding performance for patterns that were smoothed with 12-mm kernel and then inverted to non-smoothed ones. If numerical loss in the filtering calculation was related to the performance reduction, this manipulation should induce large performance reduction. However, this operation did not affect the decoding accuracies (the left most bar in Fig. 3B), indicating that numerical loss in the calculation did not cause the performance reduction with large smoothing.
These results indicate that the effect of spatial smoothing on the generalization score reflects informative spatial frequencies contained in patterns if we use the linear SVM.
3. The effect of spatial smoothing on decoding ocular dominance responses
Next, we evaluated the effect of smoothing on decoding performance in an fMRI experiment. In the experiment, ocular dominance responses in the human visual cortex were measured using fMRI and decoded using multivoxel pattern analysis.
3.1. Materials and Methods
3.1.1. Experimental Procedures
Twelve subjects (22–35 years of age, 5 females) participated in this study and gave informed consent according to a protocol approved by the Institutional Review Board at the National Institutes of Health.
The visual stimulus was a radial checkerboard pattern, flashing at 6.7 Hz, back-projected onto a screen in the MRI bore, subtended 16.7° horizontally and 11.0° vertically in visual angle. The visibility of the stimulus for each eye was controlled through the LCD shutter goggles (PLATO Visual Occlusion Spectacles, Translucent Technologies Inc., Toronto, Canada) connected to a laptop computer by changing the opaqueness of the shutter goggles.
A slow event-related design was employed in the experiment; the stimulus duration was 1 s while the entire duration of each trial was 12 s (11 s rest) for five subjects (subjects A to E in Fig. 4) and 16 s (15 s rest) for the others. Two monocular stimulation conditions for measuring the ocular dominance responses, and another three (for subjects A to E) or five (for subjects F to L) conditions of binocular stimulations were presented. While all the conditions were modeled in the analysis, binocular conditions, which were employed for another decoding study, were not used for evaluating the smoothing effect in this study. A total of eight runs were performed for each subject with each condition presented four times per run. The order of conditions was randomized and was different for each run.
Figure 4.
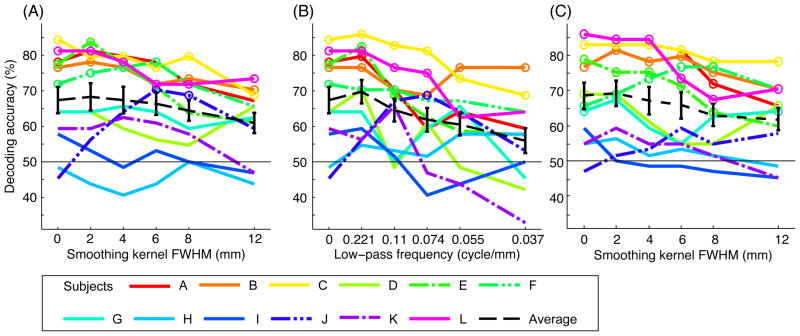
Smoothing and low-pass filtering effect on decoding accuracy. Ocular dominance decoding accuracies at each level of smoothing (A) and low-pass filtering (B) are shown for each subject. C shows decoding accuracies with vector normalization (the length of every input vector was normalized to 100) are shown. The dotted black lines with error bars show the average accuracies and standard errors across subjects. The circles indicate that decoding accuracy is significant (p < 0.05) by permutation test (5000 permutation) with Bonferroni correction (corrected for testing six times for different smoothing levels).
A fixation task was used to maintain subjects’ attention on the center of the stimulus. In every trial a small white fixation circle at the center of the stimulus was flashed green in random timing when the shutter was opened. Subjects were required to report the green flash as fast as they can by pressing a button.
3.1.2. MRI parameters
All imaging was performed on a 3T Signa MR scanner (GE Healthcare, Milwaukee, WI) with a 16-channel phased-array coil (NOVA Medical Inc., Wilmington, MA). The functional time series were obtained using single-shot gradient-recalled echo-planar imaging (EPI) pulse sequence with ASSET (Array Spatial Sensitivity Encoding Technique) acceleration factor = 2. The imaging parameters were TR = 250 ms, TE = 30 ms, FA = 35°, FOV = 192 × 192 mm, 96 × 96 matrix, 4 slices of 3 mm thickness with 0.3 mm gap, and voxel size of 2 × 2 × 3 mm. Slices were parallel to the calcarine sulcus and covered the calcarine region. The first 48 volumes before the first trial were excluded from the analysis.
For anatomical alignment, whole brain T1-weighted Magnetization Prepared Rapid Gradient Echo (MPRAGE) images were acquired for each subject with TR = 6 ms, TE = 2.736 ms, FA = 12°, and voxel size = 1 × 1 × 1 mm with ASSET acceleration factor = 2.
3.1.3. Image processing
All image processing was performed using AFNI software package (http://afni.nimh.nih.gov/) (Cox, 1996). Functional images were de-spiked, corrected for slice-acquisition timing, and realigned to the image volume closest to the anatomical scan. Signal values per voxel were scaled to percent signal change relative to the mean signal across the time-course of each run. Six levels of image smoothing were applied using Gaussian filters with 0 (no smoothing), 2, 4, 6, 8, and 12 mm FWHM. Smoothing operation was performed with 3dmerge program in AFNI. The smoothed data retained the same numerical precision as the original data (16-bit integer).
Anatomical region of interest (ROI) was defined in the calcarine gyrus using anatomical label from the TT_N27_EZ_ML mask based on the macrolabel maps of the Statistical Parametric Mapping Anatomy Toolbox (Eickhoff et al., 2005) provided with AFNI package. In order to transfer the anatomical mask to functional images, the template brain was transposed onto skull-stripped anatomical images and resampled to the resolution of the functional images.
3.1.4. Decoding analysis
The response of each voxel at each trial was estimated using the general linear model (GLM) analysis. Temporal responses for each trial were modeled as gamma functions using AFNI’s 3dDeconvolve program. The design matrix included response models for all trials, six motion parameters, and low frequency components modeled by the third order polynomial for each run. The t values of the model-fit for each trial of monocular stimulations were used as response estimates at each voxel. These values in ROI voxels were used as inputs for decoding analysis.
The SVM was used to decode ocular-dominance responses using the LIBSVM library (Chang and Lin, 2001) with the linear kernel and C parameter fixed to 1. Decoding performance (generalization score) was evaluated using the cross-validation procedure (Bishop, 2007; Mitchell, 1997): Responses in seven runs were used to train the classifier, and one run was used to test the decoding performance. Response estimations with the GLM analysis were performed independently for the training and the test data in each cross-validation fold. In this procedure, 56 training samples (7 runs × 8 trials per run) and 8 test samples were obtained in each validation fold. This estimation procedure was repeated 8 times for all possible training and test run combinations. Mean scores across cross-validations are reported in the results.
Statistical analyses of smoothing effects were performed with R statistical computing language and environment (R Core Team, 2012).
3.2. Results of fMRI experiment
Fig. 4A shows the decoding accuracies of ocular dominance decoding for each subject and the average scores across subjects (dotted line) at different levels of smoothing. The significance of decoding accuracy of individual subject at each smoothing was estimated by permutation test (Golland and Fischl, 2003) with 5000 random permutations of labels within each run. Significant accuracies (p < 0.05 with Bonferroni correction) were marked by circles in Fig. 4.
To compare the smoothing effect with the effect of clear-cut frequency filtering, Fig. 4B shows the decoding accuracies at different levels of low-pass Fourier filtering. Low-pass frequencies are approximately corresponded to the sizes of smoothing kernel. While the effect of clear-cut filtering was sharp compared to the smoothing, the same trend of the effect was observed in both cases.
The effect of smoothing was significant using the Friedman test (chi-squared(5) = 16.228, p = 0.006) (Demšar, 2006) for the average result. Post-hoc analysis using the Wilcoxon-Nemenyi-McDonald-Thompson test (Hollander and Wolfe, 1999) revealed significant difference between 0-mm and 12-mm smoothing (p = 0.035) and between 2-mm and 12-mm smoothing (p = 0.015).
While the smoothing decreased decoding accuracies in the average result, the smoothing effects at individual subject level were not always the same. For example, the effects in subject E and K (dashed lines in Fig. 4A) were larger than those in the other subjects; only for these subjects the effect of smoothing was significant (chi-squared(5) = 12.418, p = 0.030 for E and chi-squared(5) = 11.923, p = 0.036 for K). No significant effect of smoothing was observed for the other subjects. Although the effect was not significant, we also observed increased accuracy with smoothing (double-dashed lines in Fig. 4A) for subject F (up to 6 mm) and J (up to 6 mm).
To confirm these decoding accuracies and the smoothing effects were not due to response bias to one of the eyes, we performed the same analysis with normalized input vectors; the length of response vector for every trial was normalized to 100. Fig. 4C shows the results with the normalized input vectors. Even with this response vector normalization, we still observed similar effects of smoothing as in Fig. 4A: The effect of smoothing for the average result was significant (chi-squared(5) = 19.411, p = 0.002). Post-hoc analysis revealed significant difference between 0-mm and 12-mm smoothing (p = 0.042) and between 2-mm and 12-mm smoothing (p = 0.006). With individual subject analyses, significant effect was observed only for subject E (chi-squared(5) = 11.4198, p = 0.030) and subject L (chi-squared(5) = 14.390, p = 0.013).
4. Discussion
We showed that the effect of smoothing on the generalization score using linear SVM is related to the informative frequency for pattern classification. While spatial smoothing does not remove high frequency component, relative scaling of frequency component was sufficient to affect the generalization score of SVM classification analysis. Clear-cut low-pass filtering with Fourier filter (non-invertible operation) showed similar effect on the decoding accuracies with smoothing (Fig. 4). This result suggests that we could infer informative scale of neural organization from the result of smoothing effect on decoding accuracies (Brants et al., 2011).
In the ocular dominance decoding analysis, we observed large smoothing reduced decoding accuracies on average across twelve subjects. This result suggests that informative frequencies for the ocular dominance decoding resided in higher spatial frequencies. With individual subject analysis, however, significant decoding accuracies were observed even with the 12-mm smoothing for three of the subjects and the significant effect of smoothing was observed only for two of the subjects. This individual difference should not be ignored in the decoding analysis because many decoding analyses, especially for the early visual cortex, have been performed on individual subject basis. For instance, the previous decoding studies investigating informative frequencies (Freeman et al., 2011; Op de Beeck, 2010a; Swisher et al., 2010) were based on individual results of at most four subjects.
Regarding the individual variability of smoothing effects, Swisher et al. (2010) suggested that head motion can be one of the reasons to diminish the effect of smoothing. In the current experiment, one subject (subject B) had substantial head motion compared to the other subjects (Fig. S1 in the supplementary material). This subject showed less effect of smoothing, which was consistent with the discussion in Swisher et al. (2010). However, the subjects with less smoothing effect (e.g. subject C) did not necessarily exhibit significant head motion, so that the head motion was not the sole reason for the variability of smoothing effect.
Biased response to dominant eye (Haynes and Rees, 2005; Schwarzkopf et al., 2010) could also affect the smoothing effect. For a subject with strong eye dominance, smoothing could trivially improve decoding by spreading strong response bias in many voxels. The smoothing effect therefore could be irrelevant to informative frequencies. The results of decoding with response vector normalization (Fig. 4C), however, still showed similar effect of smoothing. This suggests that the response bias did not explain the variability of smoothing effects.
Although head motion and eye dominance did not explain all the variability of the smoothing effect, we still cannot exclude the possibility that the difference of individual noise was related to the smoothing effect. We, however, could at least say that informative pattern for decoding columnar-level organization did not reside only in a specific range of spatial frequencies for all the subjects. The results that significant decoding accuracies were observed at large smoothing level for some subjects indicate that decoding information could reside also in low spatial frequencies.
Variable smoothing effects seen at individual subject analyses might implicate the mechanism of contrast formation in decoding responses of columnar organization. It has been shown that the frequency of columnar width higher than the Nyquist frequency of the MRI data sampling cannot be aliased into voxel space (Chaimow et al., 2011; Kamitani and Tong, 2005). The decoding information, therefore, should come from another system representing the difference in response patterns of the columnar organization. The biased sampling for irregularly distributed columns (Boynton, 2005; Kamitani and Tong, 2005) has been proposed as one of the models for decoding contrast. If the irregularity induces organizations in multiple frequencies, this model could be consistent with the result of variable informative frequencies.
Freeman et al. (2011) indicated that not a columnar organization but a larger-scale map of orientation column (angular-position map) contributed to decoding. They showed that when the angular-position component was removed from the map, decoding accuracy was significantly reduced. They also showed an interesting effect of frequency filtering on decoding accuracy. Even though the angular-position map is a low spatial frequency pattern, they observed reducing effect of low-pass filtering on the decoding accuracies similar to the result of Swisher et al. (2010). This suggests that multiple spatial frequencies may have information for decoding even if the response is organized in large-scale map.
In our experiment, we used ocular dominance column instead of orientation column, so that the large-scale organization like the angular-position map would not affect the decoding. A low-frequency regular organization like an angular-position map has not been observed for ocular dominance column except in a region of periphery visual filed (Adams et al., 2007). We did not observe such biased response map in our result. The current results of smoothing effect, therefore, could suggest that variable frequencies could be informative even if the information is not derived from a large-scale map.
How the neural response of columnar organization creates a spatial pattern in multiple frequencies of BOLD response is still an open question. Irregular but stripped organization of ocular dominance column may form a pattern in multiple frequencies that can contribute to decoding. Vascular bias (downstream large vessel effects) was also proposed as a major source of contrast in low spatial frequencies (Gardner, 2010; Shmuel et al., 2010). Kriegeskorte et al. (2010) further suggested that blood flow may generate contrast in both small- and large-scale patterns. This model is consistent with the current results showing the variability of informative frequencies.
It should be noted that our investigation was focused on the linear SVM whereas the smoothing effect might be different in other classification analyses. The Fisher’s Linear Discriminant Analysis (LDA) (Bishop, 2007; Duda et al., 2000), for example, can be insensitive to non-uniform scaling because LDA normalizes the distance measured with covariance estimates so that the effect of scaling may be canceled. However, if we consider the generalization score, the LDA may also be affected by spatial smoothing. In fMRI decoding analysis, where the data dimensionality is very large compared to the number of samples, the estimate of the covariance matrix is not robust. In fact, the decoding performance of LDA using the sample covariance matrix was shown inadequate (Cox and Savoy, 2003). For robust covariance estimation and better decoding performance, LDA should be used with regularization technique such as the shrinkage method (Ledoit and Wolf, 2003; Schafer and Strimmer, 2005), which reduces the off-diagonal values in the covariance matrix. While regularization increased decoding performance (Kriegeskorte et al., 2006; Misaki et al., 2010), the effect of scaling cannot be cancelled out in covariance directions. As a result, smoothing could affect the decoding performance of LDA with shrinkage regularization.
In addition, we should note that our discussion has been focused on the multivariate classification analysis for columnar-level organization. Other multi-voxel pattern analyses like correlation analysis for pattern similarity can benefit from moderate smoothing (Chu, 2009; Etzel et al., 2011; LaConte et al., 2005), see also (de Brecht and Yamagishi, 2012). Furthermore, Etzel et al. (2011) showed interaction effect of spatial smoothing with temporal detrending of BOLD signal on the decoding accuracies.
Giving the dependency on analysis methods and possible interaction with other data processing, there is no simple rule to determine whether spatial smoothing can be beneficial in multivoxel pattern analysis. The current result that smoothing decreased decoding performance on average suggests that it might be safe to refrain from smoothing at least for ocular dominance decoding. However, if large noise or minimum information is present in high frequency patterns such as data with substantial head motion or in multi-subject analysis, smoothing may increase the decoding performance. For a usage of spatial smoothing in multivoxel pattern analysis, we should consider multiple factors that may affect the result, including data processing stream, multivariate analysis method, scale of neural organization, and possible individual difference.
Supplementary Material
Highlights.
We examine the effect of smoothing on multivoxel pattern analysis.
Non-uniform data scaling across dimensions changes results of SVM classification.
The effect of smoothing on SVM decoding was related to informative frequency.
Large smoothing reduced decoding accuracy on average across subjects.
The smoothing effect could be observed differently at individual subject.
Acknowledgments
This study was supported by the Intramural Research Program of the National Institutes of Health, National Institute of Mental Health (NIMH). This study utilized the high performance computational capabilities of the Biowulf Linux cluster at the National Institutes of Health, Bethesda, MD (http://biowulf.nih.gov). We thank the editorial assistance of Elizabeth J. Sherman and the NIH Fellows Editorial Board.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adams DL, Sincich LC, Horton JC. Complete pattern of ocular dominance columns in human primary visual cortex. J Neurosci. 2007;27:10391–403. doi: 10.1523/JNEUROSCI.2923-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop CM. Pattern Recognition and Machine Learning. Springer; New York: 2007. [Google Scholar]
- Boynton GM. Imaging orientation selectivity: decoding conscious perception in V1. Nature neuroscience. 2005;8:541–2. doi: 10.1038/nn0505-541. [DOI] [PubMed] [Google Scholar]
- Brants M, Baeck A, Wagemans J, de Beeck HP. Multiple scales of organization for object selectivity in ventral visual cortex. NeuroImage. 2011;56:1372–81. doi: 10.1016/j.neuroimage.2011.02.079. [DOI] [PubMed] [Google Scholar]
- Chaimow D, Yacoub E, Ugurbil K, Shmuel A. Modeling and analysis of mechanisms underlying fMRI-based decoding of information conveyed in cortical columns. NeuroImage. 2011;56:627–42. doi: 10.1016/j.neuroimage.2010.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C-C, Lin C-J. LIBSVM: a library for support vector machines. Software. 2001 available at http://www.csie.ntu.edu.tw/~cjlin/libsvm.
- Chu C-YC. Wellcome Trust Centre for Neuroimaging Institute of Neurology. University College London; 2009. Pattern recognition and machine learning for magnetic resonance images with kernel methods. [Google Scholar]
- Cox DD, Savoy RL. Functional magnetic resonance imaging (fMRI) “brain reading”: detecting and classifying distributed patterns of fMRI activity in human visual cortex. NeuroImage. 2003;19:261–70. doi: 10.1016/s1053-8119(03)00049-1. [DOI] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res. 1996;29:162–73. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Cristianini N, Shawe-Taylor J. An Introduction to Support Vector Machines and Other Kernel-based Learning Methods. Cambridge University Press; Cambridge, UK: 2000. [Google Scholar]
- de Brecht M, Yamagishi N. Combining sparseness and smoothness improves classification accuracy and interpretability. NeuroImage. 2012;60:1550–61. doi: 10.1016/j.neuroimage.2011.12.085. [DOI] [PubMed] [Google Scholar]
- Demšar J. Statistical Comparisons of Classifiers over Multiple Data Sets. Journal of Machine Learning Research. 2006;7:1–30. [Google Scholar]
- Duda RO, Hart P, Stork DG. Pattern Classification. 2. John Wiley and Sons; New York: 2000. [Google Scholar]
- Eickhoff SB, Stephan KE, Mohlberg H, Grefkes C, Fink GR, Amunts K, Zilles K. A new SPM toolbox for combining probabilistic cytoarchitectonic maps and functional imaging data. NeuroImage. 2005;25:1325–35. doi: 10.1016/j.neuroimage.2004.12.034. [DOI] [PubMed] [Google Scholar]
- Etzel JA, Valchev N, Keysers C. The impact of certain methodological choices on multivariate analysis of fMRI data with support vector machines. NeuroImage. 2011;54:1159–67. doi: 10.1016/j.neuroimage.2010.08.050. [DOI] [PubMed] [Google Scholar]
- Freeman J, Brouwer GJ, Heeger DJ, Merriam EP. Orientation decoding depends on maps, not columns. J Neurosci. 2011;31:4792–804. doi: 10.1523/JNEUROSCI.5160-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner JL. Is cortical vasculature functionally organized? NeuroImage. 2010;49:1953–6. doi: 10.1016/j.neuroimage.2009.07.004. [DOI] [PubMed] [Google Scholar]
- Golland P, Fischl B. Permutation tests for classification: towards statistical significance in image-based studies. Information processing in medical imaging. 2003:330–41. doi: 10.1007/978-3-540-45087-0_28. [DOI] [PubMed] [Google Scholar]
- Haynes J-D, Rees G. Predicting the orientation of invisible stimuli from activity in human primary visual cortex. Nature neuroscience. 2005;8:686–91. doi: 10.1038/nn1445. [DOI] [PubMed] [Google Scholar]
- Hollander M, Wolfe DA. Nonparametric Statistical Methods. 2. Wiley-Interscience; 1999. [Google Scholar]
- Kamitani Y, Sawahata Y. Spatial smoothing hurts localization but not information: Pitfalls for brain mappers. NeuroImage. 2010;49:1949–52. doi: 10.1016/j.neuroimage.2009.06.040. [DOI] [PubMed] [Google Scholar]
- Kamitani Y, Tong F. Decoding the visual and subjective contents of the human brain. Nat Neurosci. 2005;8:679–85. doi: 10.1038/nn1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Cusack R, Bandettini P. How does an fMRI voxel sample the neuronal activity pattern: Compact-kernel or complex spatiotemporal filter? NeuroImage. 2010;49:1965–76. doi: 10.1016/j.neuroimage.2009.09.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Goebel R, Bandettini P. Information-based functional brain mapping. Proc Natl Acad Sci U S A. 2006;103:3863–8. doi: 10.1073/pnas.0600244103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LaConte S, Strother S, Cherkassky V, Anderson J, Hu X. Support vector machines for temporal classification of block design fMRI data. NeuroImage. 2005;26:317–29. doi: 10.1016/j.neuroimage.2005.01.048. [DOI] [PubMed] [Google Scholar]
- Ledoit O, Wolf M. Improved estimation of the covariance matrix of stock returns with an application to portfolio selection. Journal of Empirical Finance. 2003;10:603–21. [Google Scholar]
- Misaki M, Kim Y, Bandettini PA, Kriegeskorte N. Comparison of multivariate classifiers and response normalizations for pattern-information fMRI. NeuroImage. 2010;53:103–18. doi: 10.1016/j.neuroimage.2010.05.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell T. Machine Learning. McGraw Hill; New York: 1997. [Google Scholar]
- Op de Beeck HP. Against hyperacuity in brain reading: Spatial smoothing does not hurt multivariate fMRI analyses? NeuroImage. 2010a;49:1943–8. doi: 10.1016/j.neuroimage.2009.02.047. [DOI] [PubMed] [Google Scholar]
- Op de Beeck HP. Probing the mysterious underpinnings of multi-voxel fMRI analyses. NeuroImage. 2010b doi: 10.1016/j.neuroimage.2009.12.072. In Press, Uncorrected Proof. [DOI] [PubMed] [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2012. URL http://www.R-project.org/ [Google Scholar]
- Schafer J, Strimmer K. A Shrinkage Approach to Large-Scale Covariance Matrix Estimation and Implications for Functional Genomics. Statistical Applications in Genetics and Molecular Biology. 2005;4:Article 32. doi: 10.2202/1544-6115.1175. [DOI] [PubMed] [Google Scholar]
- Schwarzkopf DS, Schindler A, Rees G. Knowing with Which Eye We See: Utrocular Discrimination and Eye-Specific Signals in Human Visual Cortex. PLoS ONE. 2010;5:e13775. doi: 10.1371/journal.pone.0013775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmuel A, Chaimow D, Raddatz G, Ugurbil K, Yacoub E. Mechanisms underlying decoding at 7 T: Ocular dominance columns, broad structures, and macroscopic blood vessels in V1 convey information on the stimulated eye. NeuroImage. 2010;49:1957–64. doi: 10.1016/j.neuroimage.2009.08.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swisher JD, Gatenby JC, Gore JC, Wolfe BA, Moon CH, Kim SG, Tong F. Multiscale pattern analysis of orientation-selective activity in the primary visual cortex. Journal of Neuroscience. 2010;30:325–30. doi: 10.1523/JNEUROSCI.4811-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vapnik V. The Nature of Statistical Learning Theory. Springer-Verlag; NY: 1995. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.