A novel biomechanical model assessing continuous orthodontic archwire activation

Abstract

Objective

The biomechanics of a continuous archwire inserted into multiple orthodontic brackets is poorly understood. The purpose of this research was to apply the birth-death technique to simulate insertion of an orthodontic wire and consequent transfer of forces to the dentition in an anatomically accurate model.

Methods

A digital model containing the maxillary dentition, periodontal ligament (PDL), and surrounding bone was constructed from human computerized tomography data. Virtual brackets were placed on four teeth (central and lateral incisors, canine and first premolar), and a steel archwire (0.019″ × 0.025″) with a 0.5 mm step bend to intrude the lateral incisor was virtually inserted into the bracket slots. Forces applied to the dentition and surrounding structures were simulated utilizing the birth-death technique.

Results

The goal of simulating a complete bracket-wire system on accurate anatomy including multiple teeth was achieved. Orthodontic force delivered by the wire-bracket interaction was: central incisor 19.1 N, lateral incisor 21.9 N, and canine 19.9 N. Loading the model with equivalent point forces showed a different stress distribution in the PDL.

Conclusions

The birth-death technique proved to be a useful biomechanical simulation method for placement of a continuous archwire in orthodontic brackets. The ability to view the stress distribution throughout proper anatomy and appliances advances understanding of orthodontic biomechanics.

INTRODUCTION

Despite the use of fixed appliances for over a hundred years, our understanding of orthodontic biomechanics is still limited. Prediction of the forces and moments transferred to the dentition by a continuous wire is generally limited to a 2D force diagram containing only 2–3 teeth without accurate anatomy (e.g., PDL and alveolar bone).¹ Free body diagrams assuming rigid body motion of archwires and teeth have been used to estimate forces and moments. Beyond this point, the system frequently becomes indeterminate.²

New advances in three-dimensional technology, such as computer aided design (CAD) and computerized tomography (CT) imaging, allow for a more accurate description of dental anatomy. While the associated force transfer through the dentition during orthodontic treatment frequently is statically indeterminate, these systems can be solved by incorporating the principles of solid mechanics. However, current finite element analysis (FEA) that could predict applied forces with a continuous archwire is rarely combined with 3D multiple tooth systems.

Several CAD/CAM-based appliance systems (Invisalign, Insignia, Incognito, and SureSmile) have already built computer models for appliance design purposes, but they do not focus on portraying forces produced by the appliances or transferring these forces to accurate anatomy. Huiskes et al,³ Lin et al⁴ and Cattaneo et al⁵ have reported that accurate anatomy of the patient-based models is important. In a study by Field et al,⁶ it was concluded that multiple teeth should be included in a model to allow the transfer of forces through both contact areas and interproximal tissues. Proper morphology of appliances and ligation methods are important as well to accurately predict responses in three planes of space.

Current simplified finite element modeling (FEM) often applies a point force to simulate orthodontic appliances rather than including the appliances. ^5–10 Kim et al,¹¹ Mo et al,¹² and Sung et al¹³ included brackets and wires to study the retraction of the anterior segment, however the teeth were bonded together at the contact points and at between the wire and the braces rather than individually ligated to the archwire with contact interfaces. These point force models did not recreate the unloading force that is expressed by orthodontic wires in clinic.

The present study proposes a new model which includes proper morphology of teeth, surrounding tissues, and appliances. It is unique in that it examines the behavior of an activated continuous archwire that includes individual ligation of each tooth in the model rather than an archwire that, for modeling purposes, is assumed to be indistinguishable from “brackets” (bonded interfaces) as in the point-force models. Much as fence posts secure fence rails, or railroad ties secure railroad tracks, this new model includes the brackets to secure the continuous archwire to allow teeth sliding and thus has been named the rail and brace (i.e. fence posts or railroad ties) model. Generating this more inclusive model will allow more accurate prediction and quantification of forces from appliances used in modern practice.

In order to simulate the effect of including the bracing structures (fence posts or railroad ties) in the model, a computer technique known as the “birth-death” technique (ANSYS, Inc. Canonsburg, PA) was utilized. It will be discussed in detail below, but in brief, refers to a two-step technique of initially ignoring one aspect of the model (by “killing” it via the “death” step) and then adding it back in (the “birth” step). This is necessary because in the virtual/computational world, unrealistic or impossible actions can occur such as the step bend passing right through a bracket as if not present. In this model, the bracket is initially “killed” in the “death” step when the archwire is activated. Forces that result from the bracket engaging the step bend of the archwire are ignored until the bracket is added back into the model via the “birth” step.

The purpose of this study was to simulate the activation of a step bend in an orthodontic archwire using a virtual, three-dimensional (3D) FEM with complete orthodontic appliances on four teeth. The specific aims were to place complete standard bracket-wire systems on accurate anatomy including multiple teeth, and to transfer and analyze forces throughout the dentition and surrounding structures by clinically realistic wire bends using the birth-death technique.

MATERIALS AND METHODS

A virtual maxilla, including cortical bone, trabecular bone, and sinuses, was constructed by sequentially stacking cone beam computerized tomography (CBCT) slices of a human dentate maxilla. In a similar manner, the dentition was built using micro-CT templates by identifying the pulp, dentin, and enamel on sequential slices. Periodontal ligament (PDL, 0.25 mm thick) and lamina dura (0.5 mm thick) were added around each tooth using Solidworks (Solidworks Corp., Concord, MA, USA). The models were merged together by Boolean operations. Fig 1A–B shows the details of the model.

Fig 1.

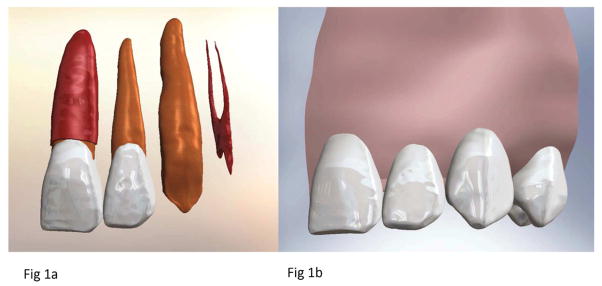
Final anatomy used for simulation. (A). Illustration of the different layers of tooth structure present in the model, including the complete left central incisor with PDL, the complete left lateral incisor without PDL, the left canine dentin, and the left first premolar pulp. (B). Complete model with all four teeth and supporting tissues, including cortical bone, trabecular bone and lamina dura.

3D CAD models of 0.022 inch slot, standard (0° tip, torque, and rotation) labial brackets on teeth #9, 10, 11, and 12 were constructed and placed so that the gingival base of each slot was on the same reference plane. The bases of the bracket pad were adjusted to ensure a smooth interface with the facial surface of the tooth. No cement layer was included because it was deemed to have little effect unless a stress sufficient to debond the bracket was achieved.

The lingual and occlusal walls of the brackets were used as reference planes to create a passive 0.019 × 0.025 inch stainless steel archwire in Solidworks (Fig 2A). Using the passive wire as a starting point, a 0.5 mm intrusion bend was formed at the lateral incisor position. Bends were placed over a 1.0 mm section of wire in the adjacent interproximal areas. Two 0.010 inch cylinders were added at either end of the slot opening to simulate passive stainless steel ligature wires that hold the archwire inside the bracket slot. The ligatures were placed to touch but not to overlap the archwire and were combined with each bracket to form one body. The complete CAD model was established using Solidworks software and the solid body information was saved in IGES format.

Fig 2.

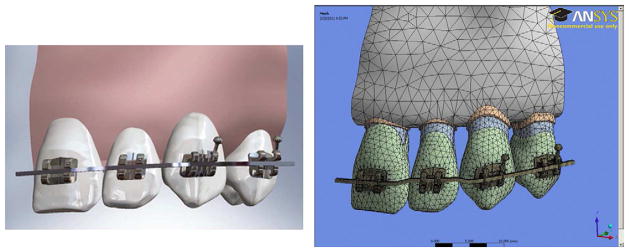
(A). Final 3D Solidworks model of 0.022″ slot, standard labial brackets and passive 0.019″ x 0.025″ archwire placed on four tooth maxillary model. (B). Model meshed in ANSYS.

Construction of the Finite Element Model

IGES geometry files were loaded into ANSYS 13.0 Workbench (Swanson Analysis Inc., Hutson, PA, USA). Using ANSYS Design Modeler, the individual solid bodies (e.g., bracket, ligature wire, enamel, dentin, pulp, PDL, lamina dura, trabecular and cortical bone) were merged into a multi-body part, allowing for conformal meshing of the model. Conformal meshing creates shared nodes at the interfaces, providing accurate modeling for bonded heterogeneous biological structures. The archwire was not merged into this multi-body part, allowing for frictionless contacts areas with non-conformal meshing and wire movement relative to the brackets. In addition, the interproximal contacts were also considered frictionless so the teeth were allowed to move relative to each other. All other interfaces were rigidly bonded using the penalty method. Proper material properties were assigned for enamel, dentin, pulp, PDL, cortical bone, trabecular bone, and stainless steel (Table 1^14–19), with the assumption that all materials were isotropic and linear elastic. The final model was meshed using the tetrahedral 10-node element, except for the swept hexahedral 8-node element in the archwire, and consisted of 238758 nodes and 147747 elements (Fig 2B). The model was fixed at the ends of the archwire and at the cortical and trabecular bone at the midline and distal to the first premolar.

Table 1.

Material Properties^14–19

	Poisson’s Ratio	Young’s Modulus (Pa)
Enamel	0.41	8.00E+10
Dentin	0.31	1.80E+10
Pulp	0.3	1.75E+08
PDL	0.3	1.75E+09
Cortical Bone	0.31	1.37E+10
Trabecular Bone	0.3	1.37E+09
Stainless Steel	0.3	2.00E+11

The static equilibrium equations were solved under the large displacement assumption. Deformation of the system was evaluated to confirm the validity of the solution.

The “Birth-Death” Technique

To simulate the insertion of an active archwire, a two-step computer technique called “Birth and Death” was utilized. Since the archwire with the 0.5 mm step bend initially overlaps the lateral incisor bracket, the first step involves displacing the wire into bracket slot. This requires intentionally ignoring the interaction between elements in the contact area involving the wire and bracket, known as a “kill” or “death” step. Displacement of the wire into the slot removes the overlap with the bracket and loads stored energy in the wire and adjacent teeth (Figure 3). Using this solution, the deactivated elements of the contact area were reactivated, known as an “alive” or “birth” step. Then, in this second step, the displacement of the wire was relaxed, loading the lateral incisor (Figure 4). This “Birth and Death” function allows elements to change status in contact areas at a later step in the simulation, which is required for insertion of active archwires.

Fig 3.

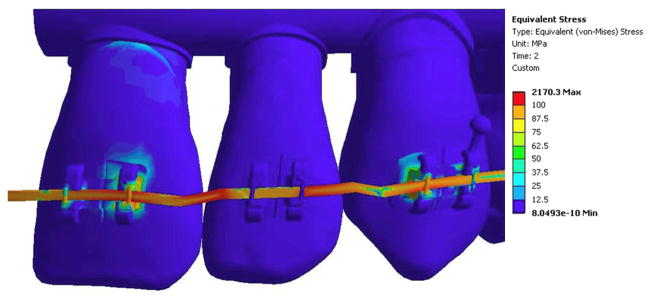
Equivalent (von-Mises) stress (MPa) at the end of the first step with the contact deactivated and the wire displaced into the bracket slot. High stress is seen in the central incisor and lateral brackets.

Fig 4.

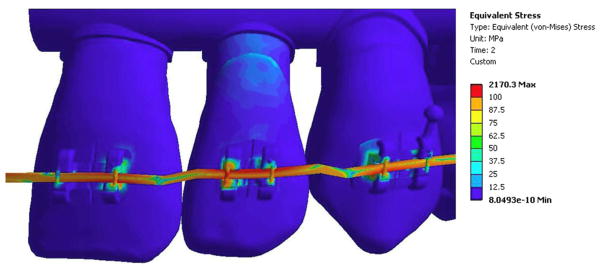
Final equivalent (von-Mises) stress (MPa) after reactivation of the contact elements and allowing the wire to load the lateral incisor.

Static structural solutions were converged at two steps (element kill and element birth) and results were generated for reaction forces, maximum and minimum principal elastic strain, equivalent elastic strain, maximum and minimum principal stress, equivalent (von-Mises) stress, and total deformation. Convergence of the solution was checked using the Newton-Raphson method.

To compare the birth-death technique with previously published point-force models, a second model was generated with identical anatomy. In this model, the archwire was removed and point forces were applied using the reaction forces calculated from the birth-death model. Stress distribution through the dentition and surrounding tissue was compared to the birth-death model.

RESULTS

The solution converged for both steps in the birth-death model. Before the contact area was activated in the lateral incisor bracket, displacement of the wire placed stress on the canine and central incisor brackets (Figure 3). Note the lateral incisor was not loaded in this step because the elements were deactivated. Additionally, more stress was seen in the central incisor bracket than the canine and premolar bracket, since the activation force was primarily placed on one bracket instead of evenly distributing to two brackets. Once the contact was reactivated, the stress increased in the lateral incisor bracket and decreased in the adjacent brackets (Figure 4). The final solution showed higher force levels (Table 2) in the lateral incisor bracket than the central incisor or canine brackets.

Table 2.

Bracket-Wire Reaction Force (N) During Birth-Death Technique.

	Central Incisor	Lateral Incisor	Canine
Step One	40.1	0	18.8
Step Two	19.1	21.9	19.9

Overall tooth displacement differed from the expected results using free body diagrams – intrusion and labial tipping of the lateral incisor; extrusion and lingual tipping of the central incisors and the canine. The lateral incisor was intruded and experienced labial tipping as the force was facial to the center of resistance (Figure 5A). Unexpectedly, a small distal displacement was also seen. The central incisor and canine both were slightly extruded and tipped 0.00085 mm and 0.000023 mm facially for the incisor and the canine, respectively, although slight lingual crown tipping would be expected since the force application is located facial to the center of resistance.

Fig 5.

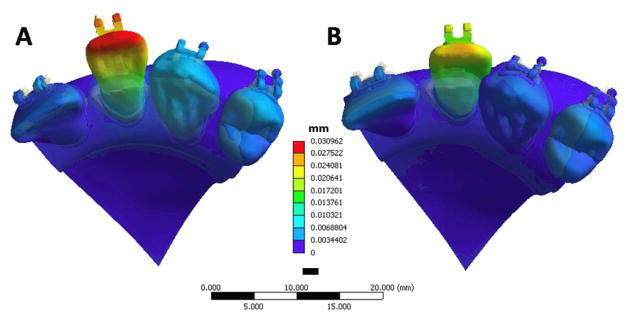
Converged solutions for displacement (mm) in the (A) birth-death model and (B) point-force model. The overall displacement is exaggerated 200 times to better visualize side effects.

The results from the point force simulation showed significant differences from the birth-death model. First of all, the overall displacement was 28% less in the point force simulation (Figure 5A & B). The central incisor, lateral incisor, and canine all displaced further facially in the birth-death model, possibly due to the wire lengthening because of flattening of the activated bend. In the point force model, the lateral incisor was also displaced slightly to the distal, possibly because the bracket was slightly distal to the center of resistance. However, the center of rotation of the lateral incisor was very different between the two models (Figure 6). When the birth-death technique was used to accurately model the bracket-wire interface, the center of rotation moved apically compared to the point force model.

Fig 6.

Center of rotation for the lateral incisor in the (A) birth-death model and (B) point-force model. The total displacement (mm) is displayed graphically, emphasized 200 times.

The stress distribution in surrounding bone was different between two models (Figure 7). The birth-death model showed compressive stress (1 MPa-2 MPa) uniformly distributed over the buccal cortical bone across all four teeth while the point force model revealed tensile stress in the buccal bone of the central incisor and the canine. Both models displayed compressive stress concentration on the buccal cortex of the lateral incisor with 19% higher levels for the birth-death model. The tensile stresses concentrated in the lingual alveolar crest of the lateral incisor were 40% greater in the birth-death model than the point force model. As a result, von Mises stresses were 47% greater for the birth-death model.

Fig 7.

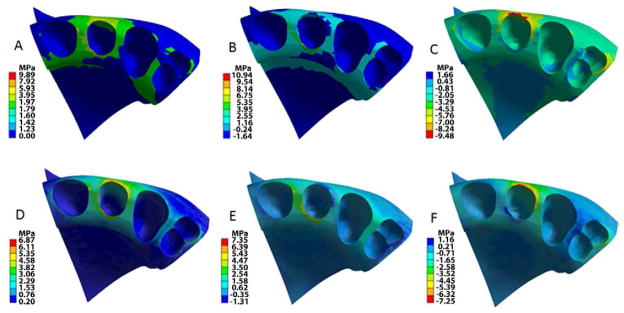
Stress (MPa) distribution in alveolar bone and tooth sockets; teeth, brackets, wire and PDL are hidden. The birth-death model (A, B, C) showed higher stress levels that that of the point force model. Equivalent (von Mises) stress: A and D; Tensile stress: B and E; Compressive stress: C and F.

DISCUSSION

Birth-Death Technique

In the clinic, a step bend provides intrusive force and hence intrusion to one or more teeth. Since the archwire is active, force is required to insert the archwire into the bracket slot. This creates stored elastic energy which is then released during unloading of the wire and tooth movement. Simulating this insertion and unloading using computer modeling can be challenging. A unique method that can accomplish these mechanics, the birth- death technique, has not been previously utilized in orthodontic biomechanical studies.

The present birth- death method combines placement of accurate CAD brackets on anatomically-correct computer models and manipulation of contact conditions, which allows the virtual placement of active archwires into bracket slots. Simulation of active archwires was not previously possible. This model allows for clinically-relevant examination of complications associated with intrusive bends. For example, unexpected tooth displacements were found including slight distal movement of the lateral and facial tipping of the central incisor and canine. Both compression and tension stresses were underestimated by the conventional point force model. Our model has advanced the field in finite element simulation of orthodontic biomechanics, profoundly increasing the complexity of computing contacts between teeth and within orthodontic appliances.

Often FE models do not include brackets or archwires. When appliances are not present, forces and moments are often applied at a point near an ideal bracket position to simulate the appliances.^5–10 Tanne et al¹⁰ examined the behavior of the PDL with a force applied at a single point on the buccal surface. Cattaneo et al constructed detailed FE models and used point-forces without including bracket-wire systems.^5,8,9 None of these previous models could predict unwanted tooth displacements with associated wire bending. While these studies help understand how the PDL is loaded, ultimately bracket-wire appliances must be included in order to understand the clinically-relevant interaction between multiple teeth and appliances.³ The birth and death technique provides the first reported method of achieving this goal.

Anatomic Accuracy

Finite element models require a balance of creating proper anatomic accuracy without requiring unrealistic computational CPU time to obtain a solution. Previous studies have used micro-CT scans with a voxel dimension of 37 micrometers and applied intensity segmentation to form a 3-D model using Mimics software and found that level of detail to be important.^5,8,9 The present study generated a model from high-quality micro-CT scans with a similar voxel size, but further refined the model to allow manipulation of the contact conditions.

In this study, lower stress was seen at the contact points between the teeth compared to the model with bonded teeth (Figure 8). In addition, higher levels of stress were transferred through the alveolar bone between adjacent teeth, which could potentially stimulate bone remodeling for orthodontic tooth movement. The bonded teeth model predicted stress concentration at contacts of the adjacent teeth consistent with Field et al⁶ who constructed a 3-D computer aided design (CAD) model of cortical bone, alveolar bone, enamel and dentin based on computed tomography images of an adult mandible. Field et al analyzed both a single tooth and a three tooth segment after the addition of brackets and wires. Their results showed limited crown displacements in the multiple-tooth model and more displacement in the single tooth model, showing that “adjacent teeth significantly alter stress distribution and their magnitudes.”⁶ Field et al concluded that the inclusion of multiple teeth in an FE model was found to transfer force at the interproximal contacts of adjacent teeth but also through the PDL and alveolar bone. In summary, the bonded teeth model underestimated the stress trajectory passing through the alveolar bone and could not accurately predict bone remodeling.

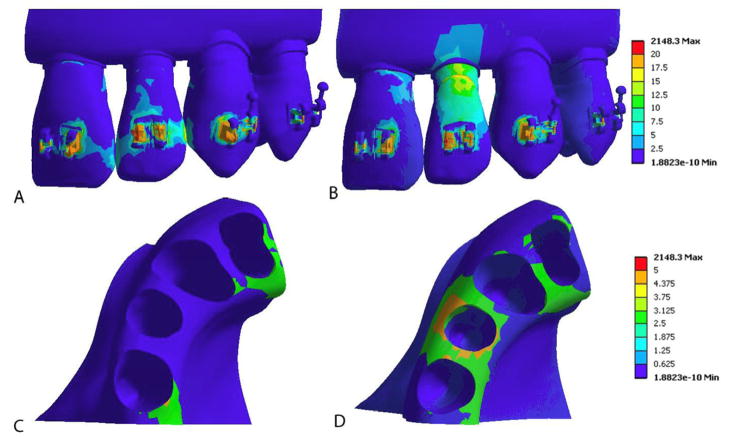
Fig 8.

Equivalent (von-Mises) stress (MPa) between the central and lateral incisor when the brackets are loaded. The orthodontic wire is hidden. A and C: All adjacent teeth were bonded at the contact areas. B and D: The adjacent teeth were simulated as frictionless contact. A and B reveal von Mises stress (MPa) on teeth; stress fringe values are shown on the right. C and D show von Mises stress (MPa) in alveolar bone; teeth are hidden.

Both these findings indicate that multiple teeth and inclusion of the archwire with the rail and brace structure are important when modeling orthodontic forces. Our findings were also supported by Cattaneo et al.⁵ However, previous studies rigidly bonded contacts together, while this study had a frictionless contact area. This led to a stress concentration at the alveolar crest as teeth were loaded.

In FE studies that do include appliances, contact points between teeth are often rigidly fixed which can affect the results depending on the tooth movements being studied. Examples include several recent studies that have used archwires and brackets in the FE models to examine en-masse retraction of anterior teeth into a first premolar extraction site. Kim et al¹¹ studied the length and position of the power-arm needed for parallel translation of anterior teeth. Sung et al examined the mini-implant position, anterior retraction hook position, and compensating curve.¹³ Mo et al studied the length of the retraction arm and degree of gable bend when using a C-implant as the exclusive source of anchorage in retraction of the anterior segment.¹² In each of these studies, the focus is on a segment of teeth bound at the contact points. The model in the present study looks closely at the interaction between the archwire and brackets, while individual teeth are not bound together at the contact points. Allowing both the teeth and the archwire freedom to move independently is important in simulating tooth response to the appliances.

Force Prediction

The force magnitudes (19.1 N – 21.9 N) that resulted from the 0.5 mm step bend of a 0.019×0.025 archwire appear too heavy to intrude the incisor according to the light force concept.²⁰ Nevertheless, the current prediction is within the reasonable range based on the simple beam theory (three-point bending). According to the theory, F = 48EIv/L³ where F is the point force at the middle of the beam, E is Young’s modulus of stainless steel, I is the moment of inertia, v is the vertical displacement (step bend depth), L is the beam span, and the “48” is the support constant²¹. The two three-point bend analogs are the 7 mm step bend span and the 15 mm interbracket distance between the central incisor and the canine, which predict forces of 79 N and 8 N, respectively. The present FE model predicting the forces of 19.1 N – 21.9 N are bounded within the theoretic values. The simple beam theory partially provides validity of the present model with frictionless contacts. On the contrary, a fix supported beam (binding between the wire and brackets), which has the support constant of 192, would predict higher force level compared to the present model. Perhaps, ligation effects and friction at the bracket-wire interface would increase the constant in the bending equation, which would increase the loads.

Clinically recorded archwire deformation perhaps could serve as the best validation for the present model. Although we did not have quantitative deformation data to validate the model, a clinical photo was taken to compare with the shape of wire deformation of the prediction (Figure 9). Qualitatively speaking, the shape of the intrusive bend was similar between the computer prediction and the clinical photo from a superimposition of the facial view. The matched archwire deformation partially supported the birth-death simulation, which warrants future clinical trials for the study of clinical biomechanics and computational biomechanics using 3D quantitative images.

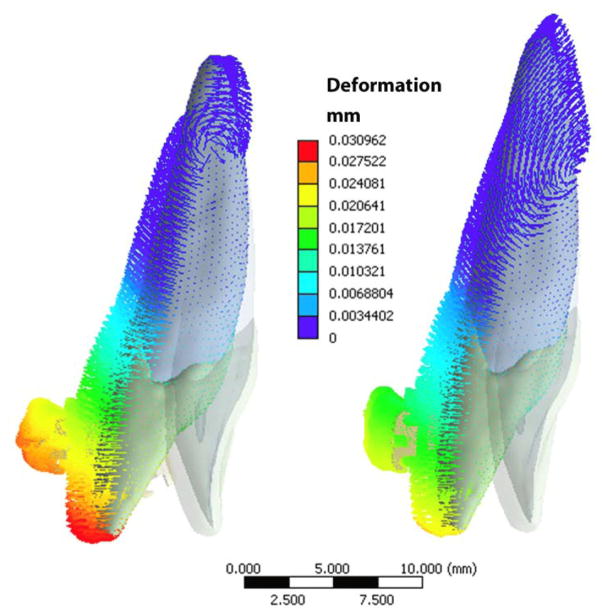
Fig 9.

Clinically recorded archwire deformation (the facial view photo) matches with the computer (Birth-Death model) predicted wire deformation (the colored mapped wire with blue brackets). Note each white scale interval (right) stands for 1mm. The color fringe on left represents the deformation (mm) map by computer prediction.

The predicted compressive stress values on the lamina dura (socket) of the lateral incisor ranged from 500 KPa to 2000 KPa with the associated high reactant force (20 N). Assuming one can use a smaller size archwire to reduce the intrusive force to 0.2N (20g), the stress should proportionally decrease to 5–20 KPa that was consistent with the stress value (4–13 KPa) for proper tooth movement previously reported by Iwasaki et al²². The peak von Mises stresses that were frequently used to predict failure of engineering materials were 9.28 MPa for the birth-death model and 6.28 MPa for the point force model located at the facial alveolar crest of the lateral incisor. Similarly, the magnitude of von Mises stress could drop to 0.9 MPa and 0.6 MPa as the less rigid archwire was used. It is unlikely that these stresses would cause microdamage to bone because the yield strength of cortical bone is around 100 MPa to 170 MPa²³.

Further manipulation of this model can advance understanding of orthodontic biomechanics used with various appliances. In addition, this study demonstrates the technological capability of modeling the anatomy of the alveolar dental complex and then viewing, in detail, the forces applied from and throughout the appliances. If coupled with the CAD/CAM design procedures used to make custom appliances (Invisalign, Insignia, Incognito, and SureSmile), perhaps a custom appliance can be designed to apply specified force levels to the teeth and ideal pressure to the PDL.

Limitations

The limitations of the present study include the frictionless assumption between the archwire and the bracket. Adding friction when modeling multiple teeth increases the complexity of the computation, which requires future investigations. The absence of friction (frictionless) may have underestimated the distal and mesial force on the intruded and adjacent teeth. The frictionless assumption partially eased the wire expansion effect that might be caused by the activated step bend with the fixed boundary condition at the both ends of the archwire. Nevertheless, our model already predicted distal displacement of the lateral incisor that could not be estimated by the conventional point force model. Such information is clinically important. Another limitation of our model is the linear elastic assumption of the PDL property. Brosh et al²⁴ found that 82% of the elastic behavior of PDL was regained in the first one minute while 6% of the viscous response occurred 30 minutes later. The present assumption allowed investigation of initial tooth loading, which accounts for the first minute of tooth movement with the PDL effect that cannot be simulated with the most recent laboratory simulator.²⁵ Recent reports indicate that mathematical modeling with rigorous assumptions may provide more accurate results approximating clinical situations than do laboratory tests.^26,27 Future expansion to a full arch and full dentition model would advance the field of orthodontic biomechanics.

CONCLUSION

The birth-death technique was used to create a new method to simulate the clinical effects of inserting an archwire in brackets to allow force transferred to the surrounding dental structures. We named this method the rail and brace model. It may be more valid than the point force model and should be considered for future investigation of computer simulations of orthodontic force application.