Critical closing pressure determined with a model of cerebrovascular impedance

Abstract

Critical closing pressure (CCP) is the arterial blood pressure (ABP) at which brain vessels collapse and cerebral blood flow (CBF) ceases. Using the concept of impedance to CBF, CCP can be expressed with brain-monitoring parameters: cerebral perfusion pressure (CPP), ABP, blood flow velocity (FV), and heart rate. The novel multiparameter method (CCPm) was compared with traditional transcranial Doppler (TCD) calculations of CCP (CCP1). Digital recordings of ABP, intracranial pressure (ICP), and TCD-based FV from previously published studies of 29 New Zealand White rabbits were reanalyzed. Overall, CCP1 and CCPm showed correlation across wide ranges of ABP, ICP, and PaCO2 (R=0.93, P<0.001). Three physiological perturbations were studied: increase in ICP (n=29) causing both CCP1 and CCPm to increase (P<0.001 for both); reduction of ABP (n=10) resulting in decrease of CCP1 (P=0.006) and CCPm (P=0.002); and controlled increase of PaCO2 (n=8) to hypercapnic levels, which decreased CCP1 and CCPm, albeit insignificantly (P=0.123 and P=0.306 respectively), caused by a spontaneous significant increase in ABP (P=0.025). Multiparameter mathematical model of critical closing pressure explains the relationship of CCP on brain-monitoring variables, allowing the estimation of CCP during cases such as hypercapnia-induced hyperemia, where traditional calculations, like CCP1, often reach negative non-physiological values.

Introduction

The first theoretical model, demonstrating that small vessels collapse when local blood pressure is reduced to a critical value, was developed by Burton in 1951.¹ Since then, zero-flow pressure or critical closing pressure (CCP) has been studied in various vascular beds and conditions.^{2, 3, 4}

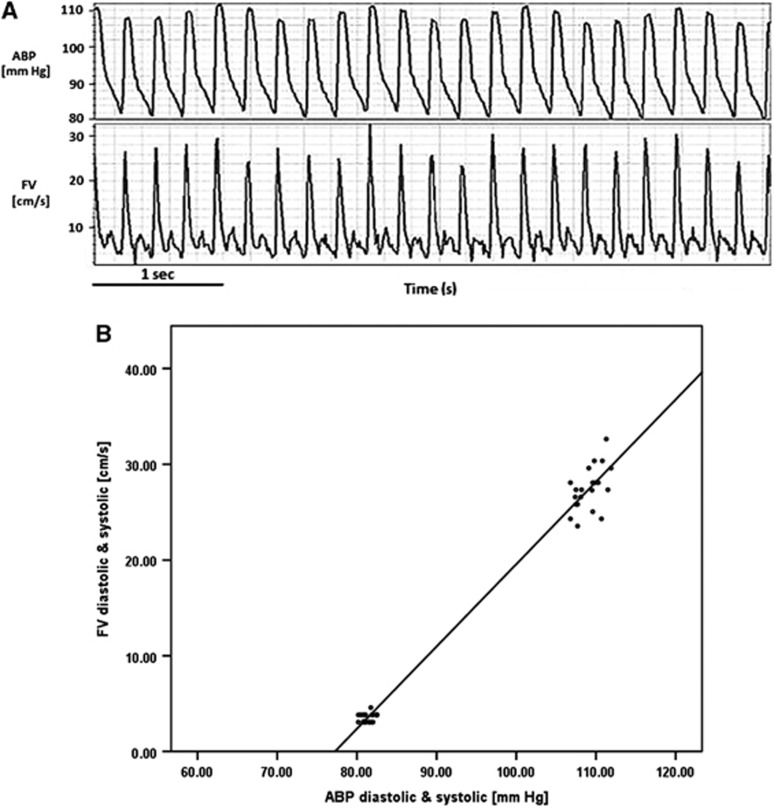
In the cerebral circulation, CCP has been determined by plotting the dynamic pressure-flow relationship between arterial blood pressure (ABP) and blood flow in the carotid artery under conditions of constant vasomotor tone.⁵ With the introduction of transcranial Doppler ultrasonography (TCD), CCP was assessed noninvasively by comparing the pulsatile waveforms of blood flow velocity (FV) and ABP.^{3, 4, 6} Using this technique, CCP may be estimated, for example, by the intercept point of a regression line between arterial systolic and diastolic pressure plotted along the x-axis and the systolic and diastolic values of blood FV plotted along the y-axis (Figures 1A and 1B).⁷ Other methods for calculating CCP have been proposed, all derived from the same assumption of a linear relationship between cerebral blood FV and ABP during one cardiac cycle. Linear regression between a single pulse of ABP and FV has been used.⁴ Alternatively, the fundamental harmonics of the pulse waveforms of ABP and FV can be used.^{6, 8} The limitation of all current methods is the possibility of obtaining negative values of CCP, which cannot be interpreted physiologically.^{9, 10}

Figure 1.

(A) Waveforms of arterial blood pressure (ABP) and flow velocity (FV). (B) Regression line between systolic and diastolic values of ABP and FV. The intercept point between the regression line and the x-axis signifies the pressure at which flow ceases (FV equal to zero) and is equivalent to Burton's critical closing pressure (CCP).

According to Burton's model, CCP is equal to the sum of intracranial pressure (ICP) and vascular wall tension (WT):^{1, 5} CCP=ICP+WT

Therefore, a reliable estimation of CCP from noninvasive TCD might be clinically useful in the effort to estimate changes in ICP noninvasively for patients at risk of intracranial hypertension. Alternatively, when ICP is known but the risk of pathological vasospasm or hyperemia is present, estimation of CCP may provide an estimator of cerebrovascular WT to direct therapies that modulate vascular tone.⁴ It has been further suggested that CCP is linked to metabolic regulation of blood flow in the brain.¹¹

In the past, mathematical modeling was helpful in explaining cerebral haemodynamics in various scenarios.^{12, 13, 14} For that purpose, experimental material has also been previously used, attempting to study the response of CCP to various physiological stimuli.¹⁵ It was found that changes in ICP and changes in vascular tone cause predictable changes in estimated CCP, with the exception of the occurrence of negative CCP in cases such as hypercarbia. For that reason, in order for CCP and WT to be established as clinically useful monitored parameters, a more reliable metric of CCP is required.

The model of cerebrovascular impedance has been used to describe the relationship between Pulsatility Index and CCP,¹⁶ where capacitance and resistance are in parallel such that the impedance to flow is considered as a function of heart rate. In the present study, we intended to use a cerebrovascular impedance,¹⁶ which is compatible with well-rehearsed models applicable to central and peripheral circulation.¹⁷ We applied an expression for TCD pulsatility index¹⁸ for calculating CCP as a function of cerebral perfusion pressure (CPP), ABP, Ra, cerebrovascular compliance (Ca), and heart rate. We compared this novel CCP calculation—termed as multiparameter mathematical model of critical closing pressure (CCPm)—with the traditional calculation of CCP^{6, 16} using our database of physiological recordings in rabbits under a wide range of conditions affecting cerebrovascular tone and ICP. Furthermore, we also associated the arterial WT with the cerebrovascular physiological parameters by creating its multiparameter mathematical descriptor (termed as WTm).

Materials and methods

Experimental procedure

All animal experiments in this study were carried out under UK Home Office license, permission from the Institutional Animal Care and Use Committee at Cambridge University, and in accordance with the standards set by the UK Animals Scientific Procedures Act of 1986. Recordings from 29 experiments of male New Zealand White rabbits (weighting from 2.7 to 3.7 kg) were performed^{15, 19, 20} including high-resolution sampling of ABP, ICP, and basilar artery FV. The experimental protocols have been described in detail^{19, 20, 21, 22} and are briefly recapitulated here.

Rabbits were produced using methods described previously.²² General anesthesia was induced using intravenous alphaxalone/alphadalone (Saffan, Pitman-Moore, Uxbridge, UK, 0.2 mL/kg) and maintained using 1±3% halothane at 1.5% in 3:1 nitrous oxide/oxygen. Rectal temperature was monitored and the animals placed on a padded warming blanket. A jugular vein was cannulated and a tracheostomy was performed. The rabbits were then given an intravenous infusion of pancuronium (pavulon, 0.5 mg/kg/hour) and ventilation was controlled. Halothane was maintained at 1.5%. One femoral artery was cannulated and the catheter advanced to lie high in the dorsal aorta. This catheter was used for blood pressure recording (GaelTec, Dunvegan, UK) and for regular sample collection for blood gas analysis. The animals were then supported in a Sphinx position using a purpose-built head frame with three-point skull fixation. A posterior frontal burr hole ∼7 mm diameter was made at the bregma to the left of the midline and an 8-MHz pulsed Doppler ultrasound probe (PcDop 842, SciMed, Bristol, UK) was positioned over the exposed dura and adjusted to obtain the best Doppler spectra from the basilar artery, before being clamped in position. A second burr hole of diameter ∼1.5 mm was made over the contralateral cerebral hemisphere close to the bregma, and a laser-Doppler probe of diameter 1 mm placed epidurally (Moor Instruments, Axbridge, Devon, UK). A third burr hole, ∼1.5 mm in diameter, was made for the insertion of an intraparenchymal microsensor to measure ICP (Codman and Shurtleff, Raynham, MA, USA, inserted intraparenchymally). Lumbar laminectomy was performed and a catheter was inserted into the lumbar subarachnoid space, sealed with cyanoacrylate to perform lumbar infusion of Hartmann's solution.

After recovery from surgery and stabilization of ABP, temperature and arterial blood gas tensions, recordings of ABP, ICP, and basilar artery FV were used to establish baseline before experimental maneuvers. Laser Doppler was not used in the signal analysis and statistical evaluation as it was not appropriate for the purpose of estimation of CCP. Three experimental maneuvers were studied in combination, including (1) lumbar infusion to induce intracranial hypertension (all 29 subjects), (2) sympathetic blockade to induce hypotension (n=10), and (3) modulation of minute ventilation to induce hypercapnia or hypocapnia (n=8).

Intracranial hypertension (all 29 rabbits)

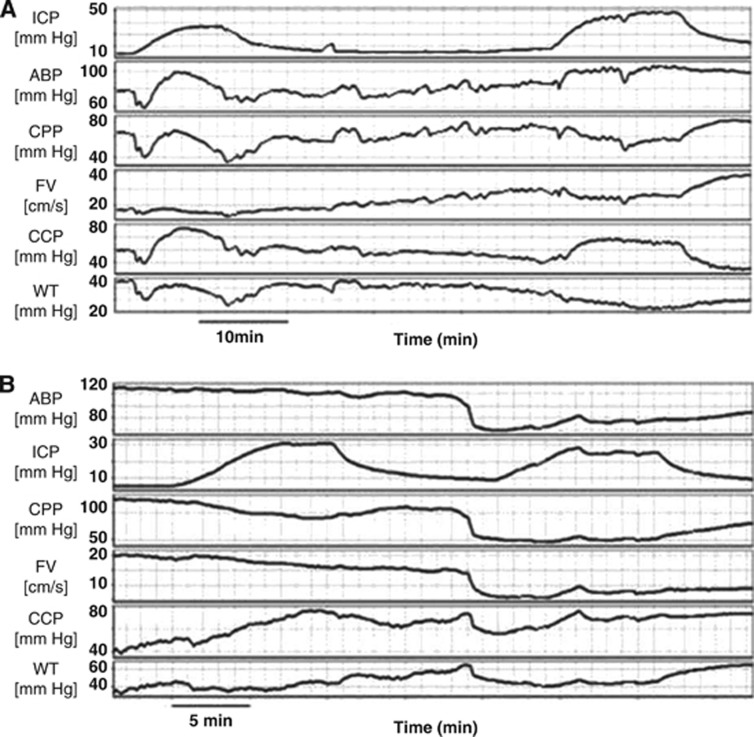
Figure 2A. In all rabbits (under various conditions of ABP and PaCO₂), ICP was increased by infusion of Hartmann's solution into the lumbar subarachnoid space at a rate of 0.15 mL/minute producing gradual rise in ICP to 20–30 mm Hg and return to baseline after cessation of the infusion.

Figure 2.

(A) Intracranial hypertension owing to infusion of normal saline into the lumbar subarachnoid space at a rate of 0.15 mL/minute and the corresponding waveforms of arterial blood pressure (ABP), cerebral perfusion pressure (CPP), flow velocity (FV), critical closing pressure (CCP), and wall tension (WT). (B) Trimetaphan induced arterial hypotension and the corresponding waveforms of intracranial pressure (ICP), CPP, FV, CCP, and wall tension (WT). In both figures, CCP has been calculated with the first harmonic model of critical closing pressure (CCP1). Gaps left after artifacts removal have been interpolated graphically.

Arterial hypotension (n=10)

Figure 2B. Arterial hypotension was induced by administration of the short-acting ganglion blocking drug trimetaphan (Arfonad, Roche, Welwyn, UK) at a dose of 0.5 mg/kg intravenously When necessary, additional doses of trimetaphan were administered to maintain the desired ABP level. Cerebral haemodynamic parameters were compared at normal ICP and normocapnic levels of PaCO₂. Furthermore, infusion of normal saline into the subarachnoid spaces, as described above, was performed both at baseline and hypotension.

Controlled changes in PaCO2 (n=8)

The ventilator tidal volume was adjusted to change the arterial PaCO₂ (confirmed by blood-gas analysis) to either hypocapnia or hypercapnia. Parameters were compared at baseline ICP and ABP. Infusion of saline, as described above, was repeated at different stable PaCO₂ levels.

In total, 145 maneuvers (different levels of ICP, ABP, and PaCO₂) were identified in these 29 experiments. The estimates of CCP and WT from each maneuver were pooled for comparison under conditions of mixed CPPs and PaCO₂ levels.

Data acquisition and analysis

ABP, ICP, and basilar artery FV were converted into digital samples using an analog-to-digital converter fitted into an IBM-compatible personal computer.¹² Sampling frequency was set to 50 Hz. The recorded signals were then analyzed using our own software for clinical data processing (ICM+ http://www.neurosurg.cam.ac.uk/icmplus).

The amplitudes of the fundamental harmonics of ABP and FV (A1 and F1) were derived using 10-second discrete Fourier transformations. Heart rate was calculated using spectral position of the peak associated with the first harmonic of ABP. Mean values of ABP, ICP, FV, and CPP were calculated in ICM+ by averaging values in a 10-second time window.

Values of these parameters were time averaged from baseline values and stable periods of each of the listed physiological maneuvers.

Calculation of CCP and WT

Traditional calculation of CCP (termed as CCP1) was calculated using the formula proposed by Michel:¹⁶

where A1 and F1 are amplitudes of the fundamental harmonics of ABP and FV, respectively.

WT was calculated using Dewey's model⁵ as: WT1=CCP1−ICP.

Modeling CCPm is expressed by equation (B). Details of this mathematical analysis are given in Appendix.

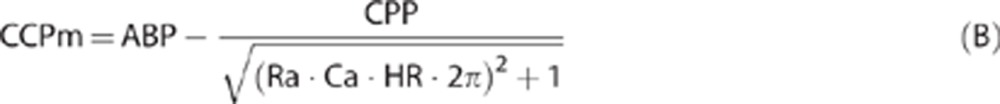where CPP=ABP–ICP, Ra is cerebrovascular resistance, Ca is compliance of cerebral arterial bed, and HR is heart rate (beat/second). Although Ra and Ca cannot be measured directly, they can be estimated using TCD blood FV and ABP and CPP waveforms according to algorithm presented in Appendix and also given in refs 23,24,25.

Modeling WTm was calculated using Dewey's equation:⁵ WTm=CCPm−ICP.

Statistical analysis

Statistical analysis of the data was conducted with IBM SPSS Statistics 20 package (Armonk, NY, USA). The analysis included comparison of changes in the group of data of ABP, ICP, CPP, CCP1, CCPm, WT1, and WTm after intracranial hypertension, arterial hypotension, and PaCO₂ change (from low, below 40 mm Hg, to high, above 40 mm Hg PaCO₂). Normal distribution was established with the Shapiro-Wilk test and T-tests were used to examine the significance of each sample comparison. The level of significance was set at 0.05. Bland–Altman method was used to determine the agreement between CCPm and CCP1.

Results

Correlation between CCPm and CCP1

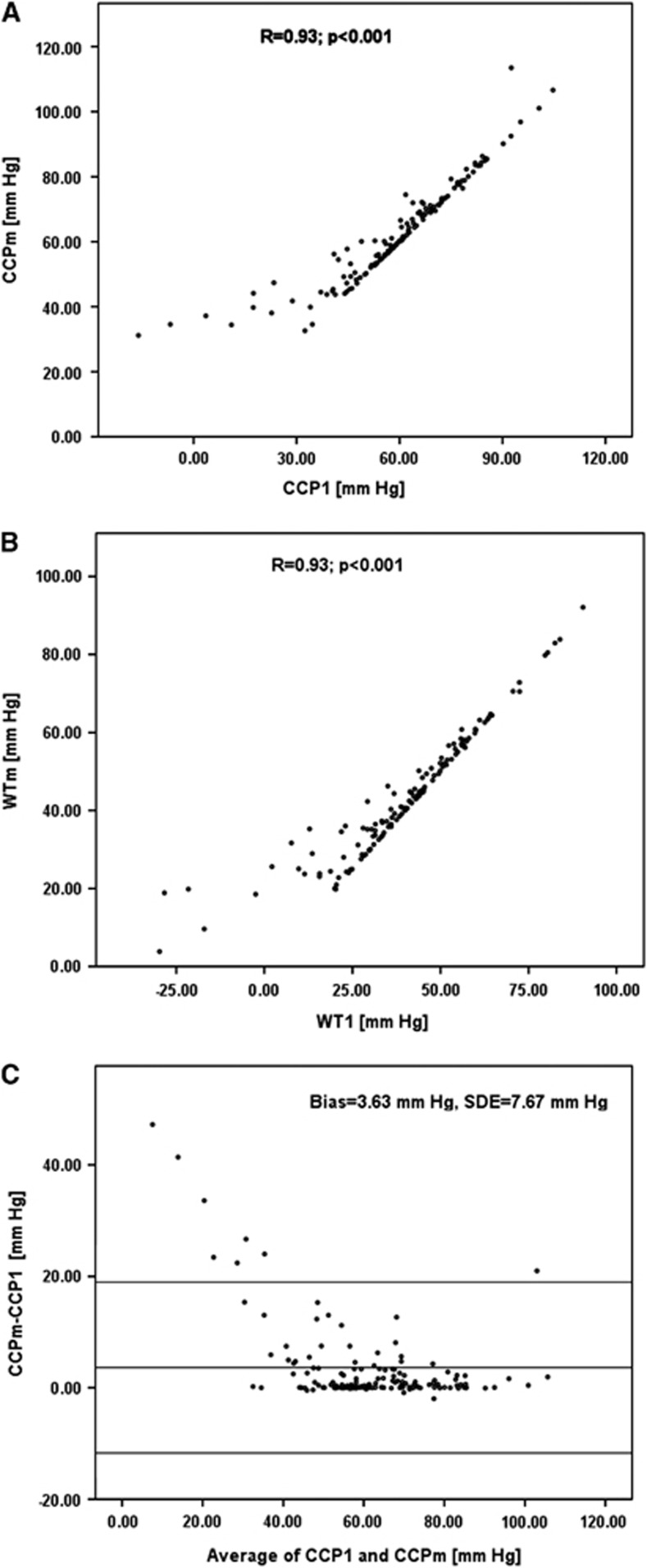
Overall, there was a strong correlation between CCPm and CCP1 when data from all the maneuvers were pooled (N=145), reaching a Pearson correlation coefficient: R=0.93 (Figure 3A). The same high correlation was observed between values of WT WTm and WT1 (Figure 3B).

Figure 3.

(A) Correlation between first harmonic model of critical closing pressure (CCP1) and multiparameter mathematical model CCPm. (B) Correlation between first harmonic wall tension model (WT1) and multiparameter mathematical model WTm. (C) Bland–Altman plot for comparing difference between CCPm and CCP1 to average value of CCP1 and CCPm. Note that after the physiological threshold of 40 mm Hg the difference is becoming minimal.

When specific phenomena were analyzed, there was a good correlation between changes in CCP1 and CCPm: during intracranial hypertension (R=0.93, P<0.0001; N=29), arterial hypotension (R=0.98, P<0.0001; N=10), as well as increases in PaCO₂(R=0.81, P=0.0148; N=8).

Bland–Altman plot (Figure 3C) demonstrates the overall agreement between CCPm and CCP1 (bias=3.63 mm Hg, standard deviation of error (SDE)=7.67 mm Hg). When CCP1 was below 40 mm Hg, the agreement deteriorated significantly as compared with values above 40 mm Hg (mean difference of 21.11±15.10 and 2.65±4.25 mm Hg; P=0.001 for values of CCP <40 mm Hg and >40 mm Hg, respectively).

Intracranial hypertension

The effect of changes in measured and calculated parameters during lumbar infusion is summarized in Table 1. Intracranial pressure increased during infusion on average by a margin of 24.53 mm Hg (P<0.001), causing a significant increase in CCP1 (P<0.001) by 27.15%, and CCPm (P<0.001) by 20.83%. Owing to vasodilation compensating for decreasing CPP, both WT1 and WTm decreased by 22.74% and 24.81%, respectively (P<0.001 in both cases). Overall, as CCP equals the sum of ICP and WT, it can be seen in both CCP calculations that an increase in ICP has a more pronounced effect, resulting in an increase in CCP, in contrast to WT that decreased.

Table 1. Mean values and s.d.'s of measured and calculated variables during experimental maneuvers.

	Intracranial hypertension (N=29)			Arterial hypotension (N=10)			Changes in PaCO2(N=8)
	Baseline ICP	High ICP	P-value	Baseline ABP	Low ABP	P-value	<40 mm Hg	>40 mm Hg	P-value
ICP (mm Hg)	9.17±5.31	33.70±12.40	<0.001	8.21±6.94	10.7±5.07	0.026	9.36±4.93	13.64±4.80	0.123 (NS)
ABP (mm Hg)	92.47±17.50	93.73±19.62	0.523 (NS)	101.47±21.58	68.09±19.75	<0.001	88.17±11.59	103.65±11.88	0.025
CPP (mm Hg)	83.30±16.31	60.02±16.43	<0.001	93.26±18.93	57.39±20.61	<0.001	81.05±15.27	95.22±11.74	0.050
FV (cm/second)	19.00±7.71	15.87±8.05	<0.001	21.29±5.45	12.15±3.01	0.001	12.15±7.78	21.11±7.46	0.010
CCP1 (mm Hg)	53.36±21.44	67.85±16.08	<0.001	65.34±17.05	56.17±14.09	0.006	58.92±16.05	54.92±16.67	0.161 (NS)
CCPm (mm Hg)	58.75±14.57	70.99±14.57	<0.001	67.71±16.84	56.03±13.85	0.002	59.19±11.96	59.15±10.13	0.889 (NS)
CCPm–CCP1 (mm Hg)	5.56±9.78	3.25±5.40	0.048	2.58±1.73	5.34±17.25	0.176	0.74±5.16	4.83±7.51	0.017
WT1 (mm Hg)	44.19±21.75	34.14±15.56	<0.001	57.13±16.89	45.47±15.14	<0.001	48.14±16.88	40.42±16.49	0.123 (NS)
WTm (mm Hg)	49.58±14.36	37.28±12.23	<0.001	59.50±16.17	45.33±14.80	<0.001	48.41±13.33	48.21±9.76	0.306 (NS)

Abbreviations: ICP, intracranial pressure; ABP, arterial blood pressure; CPP, cerebral perfusion pressure; FV, flow velocity; CCP1, first harmonic model of critical closing pressure; CCPm, multiparameter mathematical model of critical closing pressure; WT1, first harmonic model of wall tension; WTm, multiparameter mathematical model of wall tension.

Arterial hypotension

Table 1 summarizes the results of changes in measured and calculated parameters during induced arterial hypotension. There was a decrease in ABP (P<0.001) by 33.38 mm Hg on average (a decrease of 31.9%) causing a significant decrease in CCP1 (P=0.006) by 14.03% and this proved to be also the case for CCPm (P=0.002 with a decrease of 17.25%). Owing to vasodilation compensating for decreasing ABP, both WT1 and WTm decreased by 20.41% and 23.81%, respectively (P<0.001 for both), being the reason for respective decreases in both CCP calculations.

Change in PaCO₂ levels

Table 1 summarizes the results of changes in measured and calculated parameters during PaCO₂ manipulation. As CO₂ is a known vasodilator, increase of 52.21% in PaCO₂ levels from normocapnia (PaCO₂=28.25±4.74 mm Hg) to hypercapnia (PaCO₂=43.00±13.07 mm Hg) (P=0.001) lead to vasodilation (thereby reducing Ra) causing an increase in FV (P=0.01) by 73.74%. Contrarily, ABP increased simultaneously (P=0.025) by 17.56% subsequently causing an increase in CPP (P=0.05) by 17.48%. During this maneuver, the PaCO₂ change and ABP change have opposing effects on vascular tone, with increased PaCO₂ inducing vasodilation and increased ABP inducing vasoconstriction. Thus, WT being affected by this dual (opposite) effect of PaCO₂ did not change significantly in either WT1 (P=0.123) or WTm (P=0.306). Critical closing pressure change is the sum of WT and ICP changes, and CCP did not show consistent change with either method (CCP1 (P=0.161), CCPm (P=0.889)).

Negative CCP

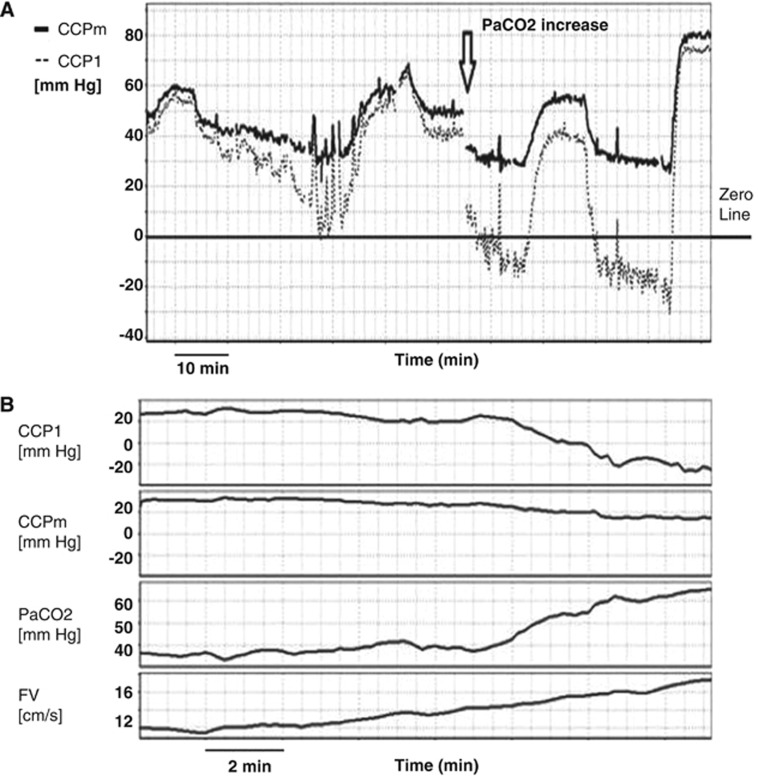
The drawback of traditional methods for calculation of zero-flow pressure is the appearance of non-physiological negative values of CCP. Below-zero CCP values using Michel's formula are demonstrated in our material when PaCO₂ is high leading to an increase in mean FV. This effect is illustrated in Figure 4A when, after introduction of profound hypercapnia, CCP1 becomes negative. In Figure 4B, similar effect of negative CCP1 is illustrated by gradual increase in PaCO₂. However, when CCP is calculated using the formula derived from the cerebrovascular impedance, there are no negative values (see Appendix).

Figure 4.

(A) Comparison of first harmonic model of critical closing pressure (CCP1) and multiparameter mathematical model (CCPm) in the maneuver of increase in PaCO₂ (after 13:10). At high PaCO₂, CCP1 decreased to non-physiological negative values, while CCPm stayed positive. (B) Example of gradually increasing PaCO₂ leading to increase of flow velocity (FV), and decrease in both CCP1 and CCPm. Negative values of CCP1 can be seen whereas CCPm stays positive.

Wall tension

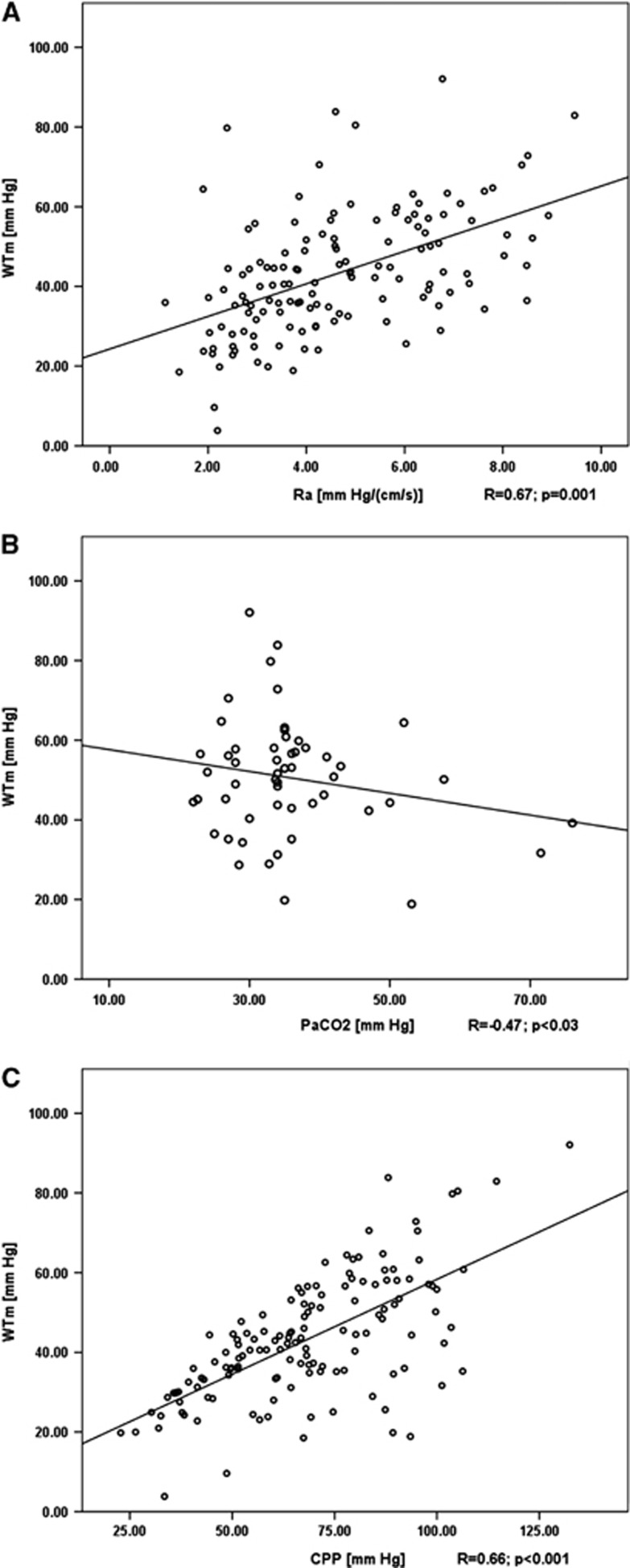
Pooling all 145 maneuvers shows that WTm is strongly correlated with WT1 values (R=0.93; Figure 3B). The advantage of WTm is the absence of negative values that can be seen in WT1, which are not interpretable. At that time, WTm remained positive, proving the potential of the model. As WTm and WT1 are highly correlated and thus similar, we used WTm to prove the significantly positive correlation of WT with Ra (R=0.67, P=0.001) at baseline ICP, ABP, and PaCO₂ (Figure 5A). Even if maneuvers with PaCO₂ tended to alter ABP (Table1), overall relationship between PaCO₂ and WTm was significant (R=−0.47; P<0.03) at baseline ICP and ABP (Figure 5B).

Figure 5.

(A) Multiparameter mathematical model of wall tension (WTm) is used to demonstrate that wall tension is significantly correlated to cerebrovascular resistance (Ra) (P<0.001) at baseline levels of intracranial pressure (ICP), arterial blood pressure (ABP), and PaCO₂ (normocapnia). (B) Modeled wall tension is significantly correlated to PaCO₂ at baseline ICP and ABP. (C) Relationship between modeled vessel's wall tension and cerebral perfusion pressure cerebral perfusion pressure (CPP) (P=0.001).

Multiple regression of WTm versus PaCO₂, ICP, and ABP gives a significant model (R²=0.60; P<0.0001; at baseline values of ICP, ABP, and PaCO₂, N=29):

Discussion

We have designed a mathematical model of the cerebrovascular zero-flow pressure (see Appendix). The introduction of parameters describing the cerebral circulation aids the understanding of factors influencing the dynamics of CCP. The presented model showed good agreement with established methods of calculating CCP. This has been achieved despite mathematical formulas A and B are not being convergent, even if substantial simplifications are used. Divergence between ‘traditional' and ‘modeled' CCP can be seen only when ‘traditional' CCP achieves non-physiologically low (or negative) values. The model allows for estimation of vessel WT using recognized determinants of cerebral vasculature. By calculating CCP, we can identify the ABP at which brain vessels collapse and cerebral blood flow (CBF) ceases. In a neurointensive care environment, a measurement of CCP for a patient would provide the threshold for the patient's ABP, below which irreversible brain ischemia may be developed. It may be useful in care of patients after traumatic brain injury or stroke.

Negative CCP

The values of CCPm showed good agreement with CCP1 in the majority of cases. However, significant discrepancies between the methods were seen when CCP1 (equation A) demonstrated low and negative values.^{9, 10} The existence of negative CCP1 values has been previously described during hyperemia, vasospasm, or with artificially elevated diastolic FV.^{9, 10, 27} However, at present, there is no physiologically relevant interpretation for these findings and they are commonly viewed as methodological limitations. In the presented model, providing physiological values of Ra, Ca, ABP, and CPP are considered; CCPm cannot be negative (equation B).²³ Therefore, using the described model, zero-flow pressure can be estimated even in cases when CCP1 would be negative being more relevant to actual clinical reality.

Linking model to cerebrovascular time constant: TAU

The presented mathematical modeling approach gives a theoretical explanation of brain zero-flow pressure by taking into account changes in primary variables describing cerebral hemodynamics and cardiac function. When reduced to the Dewey's equation,⁵ CCP can be expressed as a sum of ICP and WT, which in turn is proportional to CPP multiplied by a nonlinear function of the cerebrovascular time constant TAU (the product of Ra and Ca) and heart rate (see Appendix). The relationship between vessel WT and CPP (Figure 5C) represents vasomotor reactions, i.e., vasodilatation and vasoconstriction that occur as responses to blood pressure fluctuations.^{26, 28} However, it needs to be noted that the formula describing WT is complex. Part of equation (8) in brackets (see Appendix) describes a nonlinear, monotonically increasing function of TAU*HR, which starts from zero when TAU*HR is zero and converging to 1 when TAU*HR increases to infinity. In experimental animals, the previously described values of change from around 1.2 to 6 across similar physiological maneuvers.²³ Therefore, expected values of vessel WT may fluctuate from 0% to as much as 80% of CPP.

Previously, the interplay between Ra and cerebral arterial compliance, i.e., TAU, has been described in various clinical as well as experimental conditions.^{23, 24, 26} These findings aid in the interpretation of the observed CCP changes. In healthy subjects, it was described that TAU decreased during hypercapnia,^{23, 29} suggesting a decrease in WT (providing no change in CPP was present) and correspondingly to CCP owing to vasodilatation. Similarly, TAU was shown to decrease in carotid artery stenosis, where distal vasodilatation is present,²⁴ suggesting again a compensatory decrease in WT and CCP. This finding was amplified when bilateral carotid artery stenosis was present and TAU decreased even further. During a decrease in CPP, both as a result of arterial hypotension as well as intracranial hypertension, TAU was shown to increase.²³ But in these cases, the concomitant decrease in CPP was of a greater magnitude and dynamic than the factor including TAU (equation 8), therefore a decrease in WT is observed. This is in keeping with the expected autoregulatory vasodilatation, which is observed with decreased CPP.²⁸

PaCO₂ affects both CCP and arterial pressure

The observed changes in CCPm and WTm during intracranial hypertension and arterial hypotension are not different from those previously described.^{20, 22} CCPm was found to increase with increasing ICP, while it decreased with a decrease in ABP.²² However, in contrast to previous studies^{20, 22} during transition from hypocapnia/normocapnia to hypercapnia, we did not observe significant changes in CCPm and WTm. This finding is counterintuitive, as hypercapnia is known to lead to vasodilatation and a decrease in both WT and CCP.¹⁵ However, in the described animal experiment during a rise in PaCO₂, two phenomena can be observed simultaneously. First, owing to vasodilatory role of CO₂ the vessels dilate leading to decrease in active vasomotor tone (Figure 5B). However, during hypercapnia, we have also observed a significant rise in ABP (Table 1). This phenomenon, which is not commonly shown in humans' studies, has been previously described in this set of animal experiments.^{15, 21} Presumably, the observed hypertension triggers an autoregulatory response and induces vasoconstriction, therefore, increasing the active vasomotor tone. The net effect of the two stimuli (hypercapnia and hypertension) is an insignificant change in CCPm and WTm (which has a tendency to decrease). In the same maneuver, traditionally calculated WT1 and CCP1 do not change significantly as well and are well correlated to the modeled indices.

Linear multiple regression model for WTm

The linear multiple regression model between WTm, PaCO2, ICP, and ABP illustrates significant and independent influence of all factors on WTm. It decreases with hypercapnia, and decreases with increasing difference between ABP and ICP (i.e., CPP). It truly supports the definition of CPP as the difference of ABP and ICP,^{5, 15} suggesting that greater emphasis should be put on change in ICP than change in ABP (coefficients in the model are not equal, suggesting that ICP has a stronger influence on WTm than ABP).³⁰

Limitations

The retrospective nature of the study is a limiting factor. However, although these experimental data have been published previously,^{15, 19, 20, 21, 22} the authors are of the opinion that multiple use of experimental material to conduct mathematical modeling studies is scientifically sound and ethically justifiable as it reduces the need for new animals to be killed in compliance with the 3Rs principles of replacement, reduction, and refinement (http://www.nc3rs.org.uk/). Furthermore, the set of experiments that was performed in our laboratory was intended to be used for purposes of in-depth study of cerebral hemodynamics. The parameters deemed important were all taken into consideration and controlled for, and we do not envisage any changes that would be necessary if we would like to run the experimental protocol again.

The disadvantage of the modeling approach used for calculating CCP (CCPm) is that it cannot be readily performed noninvasively, as measurement of ICP is required. Although it would be useful to adjust the existing equation (equation B) to incorporate only ABP, it is recognized that CPP is a more accurate estimate of the transmural pressure gradient and therefore is more relevant to changes in vasomotor tone.

The use of femoral artery ABP instead of actual blood pressure in the brain could be considered as a limitation of the study. However, peripheral ABP was used in both models in comparison, therefore not affecting the actual aim of this study.

It was possible that in some animals extracranial section of the basilar artery was insonated. Theoretically, measuring blood FV with TCD in an artery that is confined inside the skull would give more accurate results, in a sense of measuring exact blood flow inside the brain. However, in this model both cranial and lumbar spaces are treated as one craniospinal system. Infusion of mock CSF into lumbar space clearly interacts with pulsatility of blood FV in the basilar artery. This proves that both lumbar and cranial spaces are well coupled in our model. Moreover, insonation of the basilar artery was achieved at minimal possible depth, i.e., close to the point where the artery branches to PCAs.

Unfortunately, at the time of performing experiments, arterial hypertension was not studied, as we could not find hypertensive drug, suitable for small animals, really not crossing blood–brain barrier. It is very likely that above upper limit of autoregulation, the linear relationship between WTm and CPP (as in Figure 5C) becomes distorted. This range of CPPs is not covered by values obtained from our recordings.

Arterial hypotension was studied with one method only. Trimetaphan is supposed to affect vascular tone purely by decreasing mean arterial pressure. This surely affects all variables in equation B, which are accounted for in our previous study.²³ In the same study,²³ comparison of trimetaphan to bleeding was done and no qualitative difference was revealed.

Retrospective character of the recording seems to be really not a serious limitation. The data have been acquired in rely 1990 by HKR (Physiologist) and MC (Brain Physicist) in the same laboratory in Cambridge, in uniform manner previously described in multiple scientific publications.^{15, 19, 20, 31}

In our opinion, it was rather unlikely that manipulations might interfere with each other. After each of the manipulation was completed, there was some time given in order for all the physiological parameters to stabilize to their previous unaffected level. Infusions for intracranial hypertension, for example, were separated by a range from 10 minutes up to 1 hour. In cases of arterial hypotension, two infusions for increasing ICP were separated by 10 minutes, including the inducing of trimetaphan in between. The only interference that we saw was of a significantly increased blood pressure after a PaCO2 challenge, resulting in insignificant changes in both CCP and WT as has been mentioned earlier.

Conclusion

CCP can be estimated using a complex mathematical model taking into account physiological parameters such as CPP, ABP, cerebrovascular time constant, and heart rate. The modeling approach allows in-depth understanding of how CCP and WT react to physiological maneuvers and its translation to clinical conditions. Contrary to noninvasively calculated CCP, the proposed methodology disallows negative values, improving the physiological interpretation of this parameter.

Appendix

In the model, arterial compliance and resistance are set in parallel, giving an impedance spectrum across the frequencies of the cardiac cycle (Figure 6).

Figure 6.

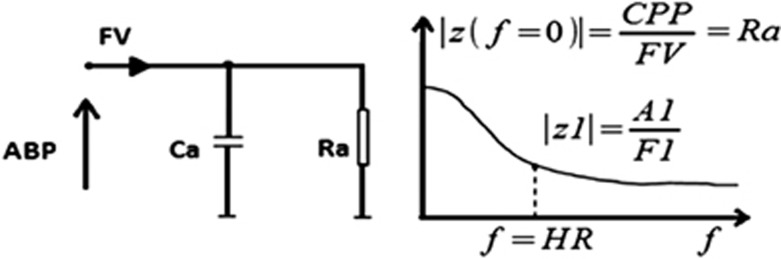
Input circuit of electrical model of the cerebrovascular bed and diagram demonstrating the resulting modulus of impedance |z(f)| where f stands for frequency in Hz. Ca, cerebrovascular compliance; Ra, cerebrovascular resistance; CPP, mean cerebral perfusion pressure; FV, mean flow velocity; A1 and F1, first harmonics' amplitudes of arterial blood pressure (ABP) and FV, respectively; HR, frequency (beats/second).

Modulus of impedance is defined as a function of circular frequency:^{17, 18}

where ω symbolizes circular frequency (ω=2π*frequency), Ra is cerebrovascular resistance, and Ca is compliance of cerebral arterial bed.

Using this model, the amplitude of the fundamental harmonic of basilar flow velocity (F1) can be expressed as a function of cerebrovascular impedance:

where |Z(f_HR)|is the modulus of cerebrovascular impedance at heart rate frequency (f_HR).

The mean value of basilar flow velocity (FV) can be expressed using the same model at a theoretical heart rate of zero. In this steady state, cerebral blood flow acts as a direct current, arterial compliance is saturated, and impedance at heart rate zero (|Z(0)|) is a function of arteriolar resistance (Ra) alone.

In formula (2), pulsation of CPP (i.e., ABP-ICP) should be formally used instead of A1. However, the use of A1 is justified because the pulsation of ICP is much lower than the pulsation of ABP (average proportion 1:25).

Combination of equations (1), (2), (3) derives a formula for CCP that accounts for ABP, ICP, Ra, Ca, and HR:

The product of Ra and Ca can be interpreted as a cerebrovascular time constant (TAU^{23, 26}). Changes in TAU as previously described^{15, 25, 29} may be helpful in interpreting changes in critical closing pressure or cerebral wall tension. To calculate CCPm in this way, it is necessary to estimate both Ra and Ca, which can be done using ABP, ICP, and basilar flow velocity with the following equations:²⁵

and

In both equations, Sa represents the cross-sectional area of the insonated vessel inside which there is blood flow. CaBV1 is the amplitude of the fundamental harmonic of cerebral arterial blood volume (CaBV) and is derived by using a 10-second discrete Fourier transformation of CaBV's time series. Changes of pulsatile CaBV can be approximated by sampling instant and average values of arterial flow velocity:²⁶

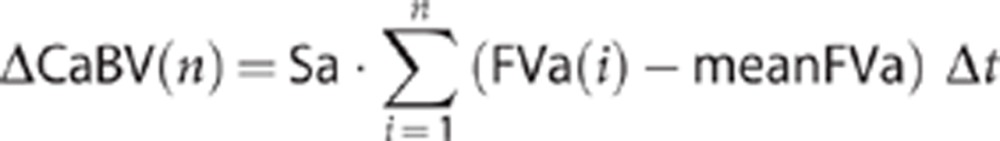where n is the number of the samples and Δt is the time interval between two consecutive samples. Instant (sampled) arterial blood flow velocity is represented by FVa(i), while meanFVa represents the corresponding average value.

The actual diameter of the insonated vessel is unknown and that leads to difficulties in calculating the cross-sectional area of the vessel. However, TAU is the product of Ra and Ca, so the remaining unknown value Sa is cancelled:²³

Using concept of TAU, equation (B) becomes:

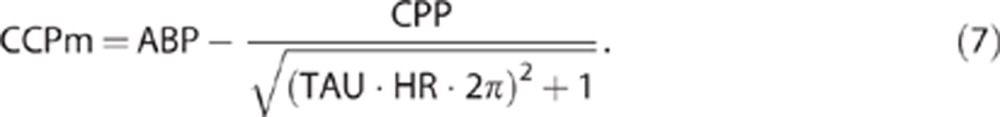Wall tension was calculated with the same procedure as before by using Dewey's model:⁵ WTm=CCPm−ICP or using the TAU concept as stated previously for CCPm:

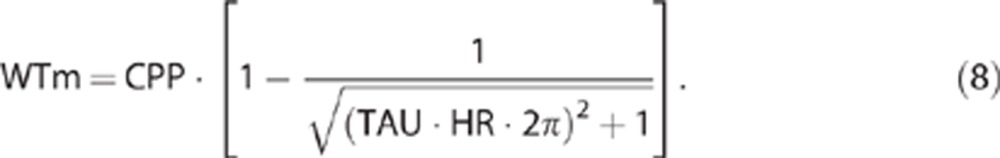ICM+ is licensed by the Cambridge Enterprise Ltd.(Cambridge, UK, www.neurosurg.cam.ac.uk/icmplus). PS and MC have financial interest in a fraction of the licensing fee.