Quantum Chemical Calculations of Amide-¹⁵N Chemical Shift Anisotropy Tensors for a Membrane-Bound Cytochrome b₅

Abstract

There is considerable interest in determining amide-¹⁵N chemical shift anisotropy (CSA) tensors from biomolecules and understanding their variation for structural and dynamics studies using solution and solid-state NMR spectroscopy and also by quantum chemical calculations. Due to the difficulties associated with the measurement of CSA tensors from membrane proteins, NMR-based structural studies heavily relied on the CSA tensors determined from model systems, typically single crystals of model peptides. In the present study, the principal components of backbone amide-¹⁵N CSA tensor have been determined using density functional theory for a 16.7-kDa membrane-bound paramagnetic heme containing protein, cytochrome b₅ (cytb₅). All the calculations were performed by taking residues within 5Å distance from the backbone amide-¹⁵N nucleus of interest. The calculated amide-¹⁵N CSA spans agree less well with our solution NMR data determined for an effective internuclear distance r_N-H = 1.023 Å and a constant angle β = 18° that the least shielded component (δ₁₁) makes with the N-H bond. The variation of amide-¹⁵N CSA span obtained using quantum chemical calculations is found to be smaller than that obtained from solution NMR measurements, whereas the trends of the variations are found to be in close agreement. We believe that the results reported in this study will be useful in studying the structure and dynamics of membrane proteins and heme-containing proteins, and also membrane-bound protein-protein complexes such as cytochromes-b5-P450.

INTRODUCTION

NMR has become an obvious choice to study the structure and dynamics of ground and excited states of biomolecules in solution and solid-state.^1–4 While increasing number of atomic-level 3D structures of proteins are commonly solved using multidimensional NMR spectroscopy, recent studies have demonstrated the importance of the very basic NMR parameter – chemical shift – for high-throughput structural studies.^5–7 In addition, chemical shift tensor that reveals the local electronic environment surrounding nucleus⁸ has emerged as one of the most important module that is widely used for better interpretation of structure^{5–7, 9–13} and dynamics^14–18 of biomolecules. CSAs are in fact essential to study aligned samples such as proteins and peptides embedded in lipid bilayers or bicelles using solid-state NMR spectroscopy.¹⁹ Although previous studies have shown that CSA tensors can be measured directly from well-behaved water-soluble proteins, extension to membrane proteins remains a major challenge.^20–23 In fact, structural studies of membrane proteins using solid-state NMR techniques heavily rely on the CSA tensors determined from model peptides. However, the CSA tensors of a given nucleus can depend on the nature of the environment. For example, ¹⁵N chemical shift highly depends on the electrostatic interaction.^{24, 25} Therefore, there is considerable interest in determining CSA parameters directly from membrane-bound proteins. To this end, in this study, we report amide-¹⁵N CSA tensors from a membrane-bound cytochrome-b₅ (cytb₅) determined using quantum chemical calculations and compare them with CSA values determined from experimental measurements to understand their variation in detail. Because of the above-mentioned importance of the chemical shift parameters, a plethora of studies focused on the development of approaches to measure them accurately. Computer programs have been developed to accurately predict chemical shift tensors for biomolecules,^{11, 26–29} which are increasingly used to determine their secondary and tertiary structures.^{5, 9, 30–32} A number of experimental methods have been developed for the determination of anisotropic component of the chemical shift tensor both in solids and solution. Due to fast change in the orientation of molecules in solution, the anisotropic interactions are averaged out resulting in a lack of information about individual components of chemical shift anisotropy (CSA) tensors from the frequency of NMR peaks. Relaxation experiments are mostly used for the determination of CSA tensors from solution NMR studies.^{18, 20, 22, 23, 33–36} In solids, where the motion of the molecules is restricted, CSA tensors can be determined by several methods such as static NMR measurements from single crystals,^{37, 38} static powder pattern,^39–42 magic angle spinning,^43–48 two-dimensional separated-local-field (SLF) experiments^{49, 50} and recoupling methods^{51, 52} from polycrystalline sample. However, a study on the variation of CSA tensors obtained through NMR experiments alone is not sufficient to completely characterize a system, it requires the use of quantum chemical calculations as an alternative. The accurate and precise determination of CSA tensors is essential for better interpretation of experimental results. Recent advancements in high performance computing resources have enabled efficient and accurate chemical shift tensor calculations for a variety of biomolecules. Quantum chemical calculations using semiemperical, ab initio Hartree-Fock theory or density functional theory (DFT) have been routinely used for the determination of chemical shift tensors^{8, 53–65} in a range of compounds and the accuracy of the outcome is exclusively dependent on the level of theory used.^66–70

Automated fragmentation quantum mechanics combined with molecular mechanics (AF-QM/MM) is also being used for precise determination of isotropic as well as anisotropic components of chemical shift tensors from biomolecules.^71–74 Reports on amide-¹⁵N CSA tensors for large biomolecules are relatively less in comparison to ¹H and ¹³C CSA as they are very sensitive to backbone torsion angles/secondary structure, amino acid sequence, inter and intra molecular hydrogen bonding interactions, intra-residue angle, chemical nature of side chain, electrostatic interactions and solvent effect.^{60, 61, 75–80} Hence, their determination with higher accuracy and precision becomes a daunting task. Many attempts have been made in past for the determination of both isotropic as well anisotropic components of amide-¹⁵N chemical shifts of biomolecules using quantum chemical calculation.^{25, 54, 81, 82} A theoretical study by Poon et al.,²⁴ provided a methodical analysis of how the amide-¹⁵N CSA tensors vary in different peptides. Several computational methods were developed by Cai et al.,⁸³ that included most of the important effects influencing amide-¹⁵N CSA values for helical residues of protein G. In another study, a disagreement of computed principal components of ¹⁵N CSA tensors with experimental data in beta-sheet and turn residues of protein G was assessed.⁸⁴ In a recent work AF-QM/MM method was used for the computation of CSA tensors where the variation of the anisotropies matched well with solid-state NMR results in comparison to solution NMR measurements.⁷³

COMPUTATIONAL METHODS

In this study, quantum chemical calculations of backbone amide-¹⁵N chemical shift tensors for cytb₅ were performed using Gaussian 03⁸⁵ program. Gauge-including atomic orbital (GIAO) method^86–89 in combination with density functional theory using Becke-Lee-Yang-Parr (B3LYP) exchange-correlation functional was employed.⁹⁰ In the calculations, a higher basis function 6-311+G(2d,p) and a relatively lower basis function 6-31G(d,p) basis function⁹¹ were used for nitrogens and all other remaining atoms, respectively, to reduce the computational time. The atomic coordinates were taken directly from the NMR structure of membrane-bound cytb₅ without any further optimization.⁹² The cytb₅ structure incorporated in membrane employed in our calculation was derived from CYANA⁹³ using constraints obtained from NOESY and backbone assignment data.⁹² This was followed by HADDOCK (High Ambiguity Driven biomolecular DOCKing)^{94, 95} simulations to dock the heme in the NMR structure of cytb₅ calculated using CYANA. The distance restraints for docking heme were essentially taken from previously reported cytb₅ structure (PDB code 1DO9)⁹⁶ where pseudocontact shifts were employed as one of the constraints for solving the structure of ferric microsomal rabbit cytb₅. Details of the structure of full-length membrane-bound ferric cytb₅ will be reported elsewhere. A previous quantum chemical calculation study on short peptides showed that amide-¹⁵N CSA can be accurately determined by considering all atoms and charges within about 5Å distance from the ¹⁵N of interest.²⁴ Similarly, the calculations in the present study were performed by taking all the residues of cytb₅ within a 5Å distance from the atom of interest (amide-¹⁵N). Chemical shielding constants obtained from calculations were converted to chemical shift frequency values by calculating the difference from the isotropic chemical shift value of liquid ammonia (δ = 244.6 ppm at 25°C) using the relation,⁹⁷ δ_ii = 244.6 - σ_ii. Here, δ_ii and σ_ii represent the principal components of the chemical shift tensor and the chemical shielding constant in ppm, respectively. The three principal components of the chemical shift tensor follow the usual convention δ₁₁ ≥ δ₂₂ ≥ δ₃₃.

RESULTS AND DISCUSSION

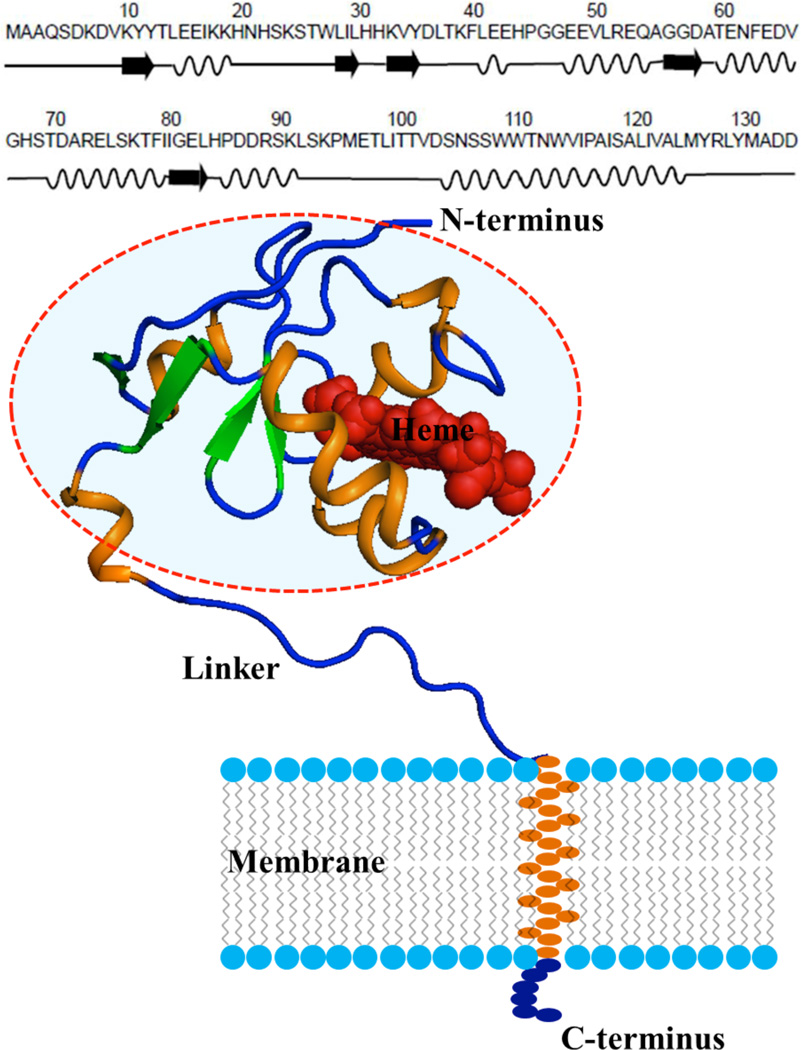
Cytb₅ is a 16.7-kDa (134 amino acid residues) electron transfer protein present in eukaryotic organisms. It contains a water-soluble domain (M1-K91) with a paramagnetic heme unit in the N-terminal region, a transmembrane helical domain (S105-L125) in the C-terminal region, and an unstructured 14-residue long linker region (L92-D104) which connects the transmembrane and soluble domains.^{98, 99} The different structural elements of the membrane-bound cytb₅ along with its amino acid sequence are shown in Figure 1.

Figure 1. Structure of different regions along with amino acid sequence of a membrane-bound protein cytochrome-b₅.

Quantum chemical calculations of amide-¹⁵N chemical shift tensors were carried out for amino acid residues in the circled region by taking a molecular fragment within 5Å distance from the residue of interest while for the residues in the linker region the calculation was performed by including the entire linker chain (S90-D104).

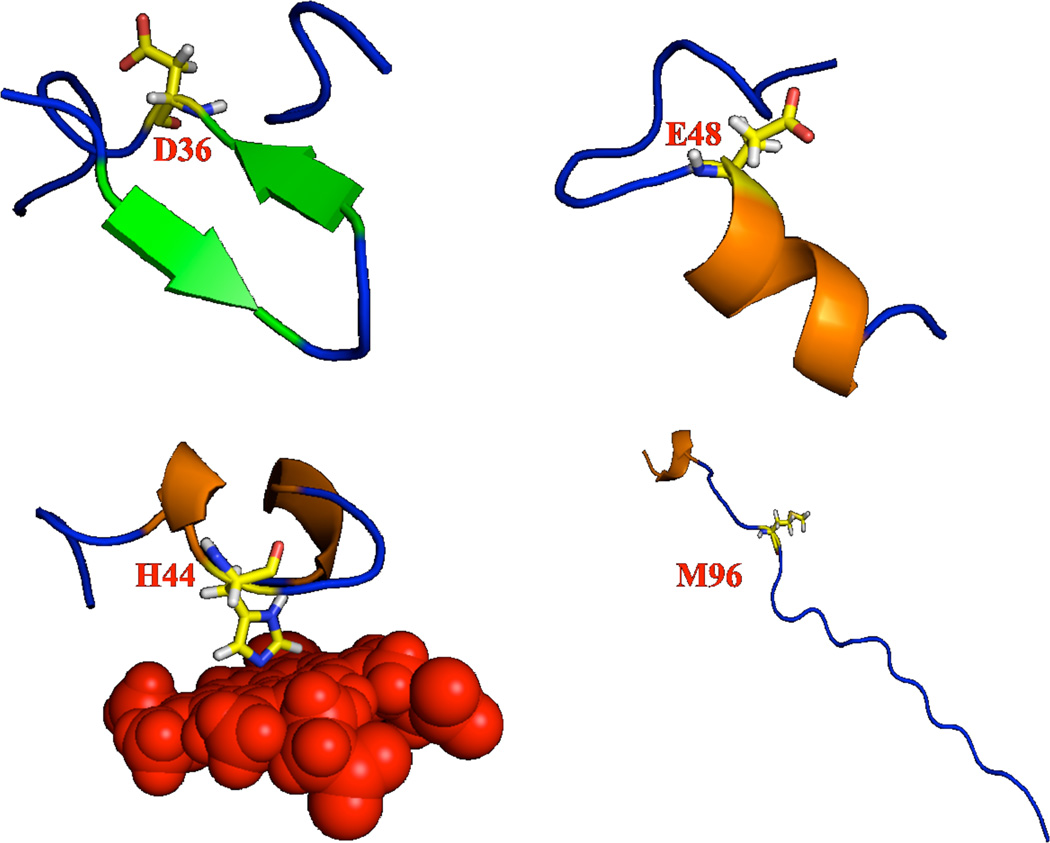
In a recent study fragment based calculations using adjustable density matrix assembler (ADMA) approach was implemented for the prediction of isotropic chemical shifts to a higher accuracy based on the level of theory, proper selection of basis set used and the size of the molecular fragment considered for the calculation.⁵⁷ Other studies^{27, 83} recommended the inclusion of 7–9 residues in the calculation for residues in an alpha-helix, which is to avoid terminal artifacts due to a lack of interacting H-bonded partners and a change in the dipole moment of the helix. Therefore, to calculate accurate amide-¹⁵N chemical shift tensor values and to keep the computational time at an optimum, in this study we have carried out calculations by considering at least 5–6 residues on either side of the ¹⁵N nucleus of interest, in addition to including all residues present within 5 Å distance from the ¹⁵N atom, irrespective of the secondary structure (whether it belongs to alpha-helix, beta-sheet or turn). Representative regions surrounding a few selected residues (D36, E48, H44 and M96) of cytb₅ used in the calculations are shown in Figure 2. Since none of the residues of the soluble domain are located within 5 Å distance from the linker region residues, the amide-¹⁵N CSA calculations were performed by taking the complete linker region along with the end residues from the soluble domain of the protein in order to avoid any terminal artifacts as shown in Figure 2.

Figure 2.

Representations of atoms within 5Å distance from a few selected residues (D36, E48, H44 and M96) of cytb₅ included in the quantum chemical calculation of amide-¹⁵N CSA using Gaussian-03.

Comparison of calculated and experimental backbone amide-¹⁵N isotropic chemical shift values of cytb₅

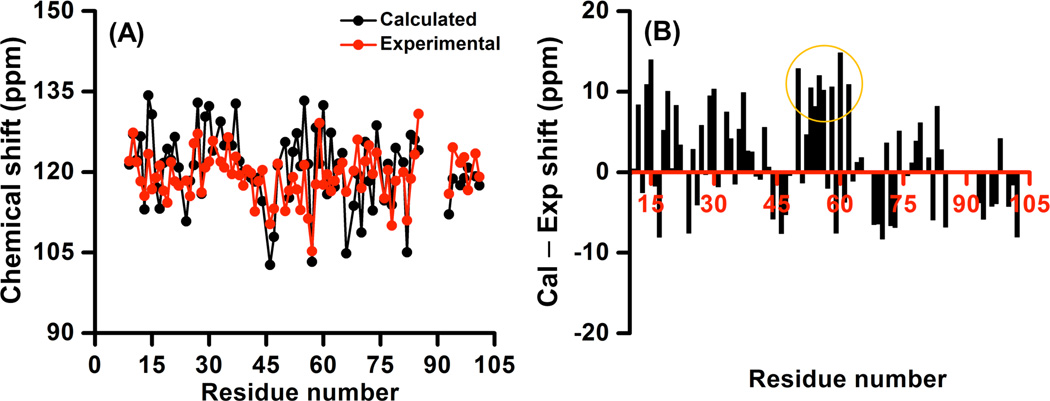
Amide-¹⁵N isotropic chemical shift values of amino acid residues of cytb₅ were calculated from the computational method as described above. The calculated values are compared with the experimentally determined values in Figure 3A; refer to Table S1 in the Supporting Information for the chemical shift values. The range of calculated isotropic chemical shift values is slightly larger (102.7–134.3 ppm) than the range of experimentally determined values (105.3–130.8 ppm),³⁵ which is still smaller than the range reported for Tfb1/p53 complex in a recent work.⁵⁶ Interestingly, in another report⁵⁷ it was shown that the use of 6-311g(d) basis set coupled with B3LYP functional produced larger deviations in comparison to experimental results. However, in the present study, the use of larger basis set 6-311+g(2d,p) on ¹⁵N is shown to reduce the variation when compared to the experimental data. This result shows that the addition of diffused and polarized functions in the calculation could improve the agreement between calculated and experimental data. It is worth mentioning that although the use of a larger basis set leads to a better agreement with experimental data, the required computational time was found to be longer.

Figure 3. Amide-¹⁵N isotropic chemical shifts of cytochrome-b₅.

Comparison of (A) and difference between (B) calculated and experimental values of amide-¹⁵N isotropic chemical shift against the residue number of cytb₅.

The difference between the calculated and experimental chemical shift values lies within a range of ±15 ppm (Figure 3B). In fact, for most residues, the difference is less than ±10 ppm, which is similar to discrepancies reported from other computational studies on globular proteins in the literature.^{72, 84} The calculation performed in this study was in gas phase and does not include any solvent effects and motional averaging. The omission of these effects in the calculation could contribute to the observed discrepancies between calculated and experimental chemical shift values obtained from solution NMR measurements.^{56, 68, 69, 74, 100–102} In a previous study a difference of ~5 ppm in experimentally measured isotropic chemical shift values was reported between oxidized and reduced state of cytb₅.¹⁰³ Therefore, the interaction of amide nitrogen with the paramagnetic center of the heme unit could also contribute to the discrepancy. One of the possible reasons for a large difference of ~9–15 ppm between calculated and experimental chemical shift values for V50, E53, Q54, A55, G56, D58, A59, T60 and N62 (circled residues in Figure 3B) located in close proximity to the heme unit of cytb₅ could also be due to this interaction. We thought the inclusion of the heme unit in the calculation could further improve the agreement between calculated and experimental values as the interaction of amide nitrogen with paramagnetic center is now taken into account. However, even the inclusion of the heme unit in calculations for V50, E53, Q54 and N62, as it lies within 5Å distance from amide-¹⁵N of interest, did not improve the agreement between calculated and experimental data. This suggests that the interaction of amide nitrogens of these residues with the low-spin paramagnetic center (Fe (III)) of the heme unit is not fully taken into account in our calculations possibly due to limitations of the DFT method used for the metal ion. It is also possible that the interaction between the paramagnetic center and amide nitrogens could extend beyond the 5Å distance from the ¹⁵N of interest. Longer computational time requirement prevented further calculations using a higher basis function on the metal ion along with the inclusion of large number of atoms.

Variation of calculated principal components with the inclusion of atoms beyond 5Å distance from amide-¹⁵N

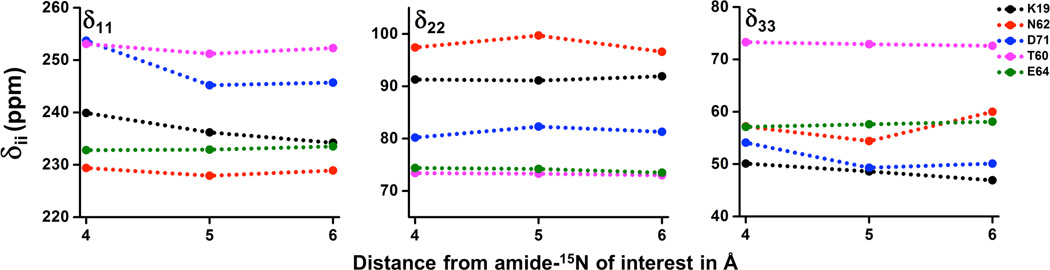
Previous studies have shown that the calculated ¹⁵N CSA values highly depend on the size of the molecular portion considered in the calculation.^{24, 27} Portions of the molecule considered for calculations in this study are depicted in Figure 2. To examine the accuracy of CSA values calculated by taking residues within 5Å distance from the chosen residue, we also carried out calculations by taking residues within 4Å and 6Å distances for a few selected residues (K19, T60, N62, E64 and D71) of cytb₅. The calculated values for these residues are plotted in Figure 4 and also listed in Table S1 in the Supporting Information along with their isotropic chemical shift constant, CSA values and span. It can be seen from Figure 4 that the variations in the calculated δ₁₁, δ₂₂ and δ₃₃ values are small when the distance is changed from 4 Å to 5 Å and become constant afterwards; an exception of residue N62 that shows slightly a higher variation for δ₂₂ and δ₃₃ in comparison to other residues at a larger distance. However, this variation can be significant for residues close to heme depending on the inclusion of heme in the calculation. We chose the residue D71 to demonstrate this point. The heme unit was absent when we considered residues within 4Å distance from D71 while it was present when 5Å or a larger distance was used. Calculated values for the least (δ₁₁) and most (δ₃₃) shielded components are decreased by ~8.5 and ~5.0 ppm, respectively, with ~7.0 ppm change in the CSA span. This variation could be attributed to the ring current effect from the aromatic porphyrin ring of the heme unit. Calculations were also performed for N62 and D71 by considering residues within a distance of 8Å (refer to Table S1 in the Supporting Information for amide-¹⁵N CSA values). A substantial change in δ₃₃ value was observed when increasing the distance from 6 to 8Å for these residues. It should be mentioned that the increase in the radius from 6Å to 8Å obviously increased the number of atoms included in the calculation; this was computationally demanding and it might have contributed errors in the calculation due to a superposition of extensive number of mixed basis sets used in the calculation.

Figure 4. Variation of principal components of CSA tensor with the size of molecular fragment considered in the calculation.

The three principal components (δ₁₁, δ₂₂ and δ₃₃) of CSA are plotted against the radial distance from backbone amide-¹⁵N for residues K19, N62, D71, T60 and E64 of cytb₅.

Variation of principal components of amide-¹⁵N CSA with isotropic chemical shift

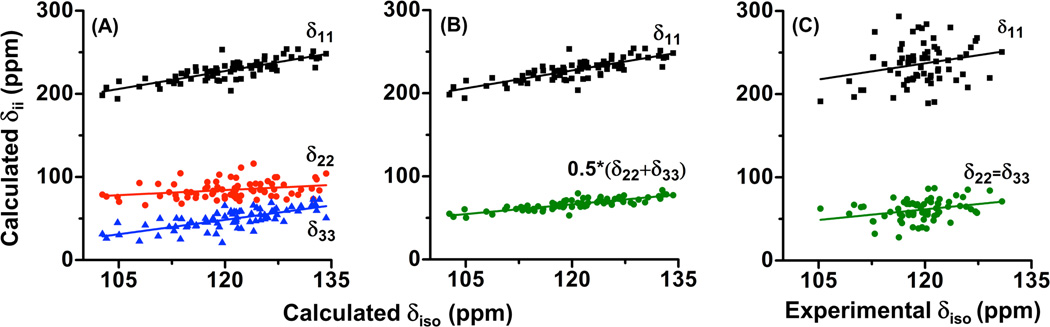
The variation of the principal component values with the isotropic chemical shift (δ_iso) values is represented in Figure 5. The best-fit lines correspond to δ₁₁ =1.43δ_iso + 55.25, δ₂₂ = 0.41δ_iso + 35.20 and δ₃₃ = 1.16δ_iso - 90.45 and are shown in Figure 5A. It is evident from Figure 5A that the least (δ₁₁) and the most shielded (δ₃₃) components of the amide-¹⁵N CSA tensor vary significantly while δ₂₂ shows a minor variation when plotted against the isotropic chemical shift.

Figure 5. Principal components of amide-¹⁵N CSA tensor vs isotropic chemical shift.

Panel A shows the variation of all the three principal components (δ₁₁, δ₂₂ and δ₃₃) of CSA tensors determined computationally while in panel B the variation of δ₁₁ and the average of other two components (δ₂₂ and δ₃₃) with isotropic chemical shift is shown. Panel C represents the variation of principal components of CSA tensors with isotropic chemical shift measured experimentally under the assumption of an axially symmetric tensor (δ₂₂ = δ₃₃).

Nitrogen-15 CSA were experimentally determined under the assumption of an axially symmetric tensor i.e., δ₂₂ = δ₃₃. Therefore, to compare the variation of principal component values obtained from calculations with the experimentally determined values (refer to Figure 5C), an average (δ_ave) of δ₂₂ and δ₃₃ were plotted along with δ₁₁ against the isotropic chemical shift in Figure 5B. The two best-fitted lines having linear correlations with the isotropic chemical shift correspond to δ₁₁ = 1.43δ_iso + 55.25 and δ_ave = 0.78δ_iso - 27.63 (Figure 5B), while the experimental best-fitted lines have linear correlations as δ₁₁ = 1.29δ_iso + 81.55 and δ₂₂ = δ₃₃ = 0.85δ_iso - 40.77 (Figure 5C). The slope values reported in Figure 5 suggest that the variations of the calculated (Figure 5B) and experimental (Figure 5C) principal component values with the increasing isotropic chemical shift are nearly similar. However, it is important to note here that the computationally obtained principal components show a narrow distribution (Figure 5B) as compared to the experimentally determined values (Figure 5C). One of the possible reasons for a large spread of ¹⁵N CSA components determined from CSA-dipolar cross-relaxation experiments using solution NMR method have been ascribed to the inclusion of a correction due to the effects of rapid internal motion.^{104, 105} These effects were not included in our calculations in the present study; whereas we expect that inclusion of these effects could result in a better agreement with experimentally measured principal components of amide-¹⁵N CSA.

Variation of principal components of amide-¹⁵N CSA tensors in secondary structural elements of cytb₅

The average value of calculated backbone amide-¹⁵N CSA defined as Δδ = δ₁₁ – 0.5 × (δ₂₂+δ₃₃) for cytb₅, 162.2 ppm, is slightly less than the experimental value of 171.7 ppm.³⁵ Nevertheless, these values fall within the range of amide-¹⁵N CSA values previously reported for biomolecules from solid-state NMR, solution NMR and quantum chemical studies.^{16, 20–22, 33, 39, 40, 53, 82, 84, 106–114} The backbone amide-¹⁵N CSA is sensitive to various factors such as intramolecular hydrogen bonding and side chain chemistry. As a result ¹⁵N CSAs of residues located in different structural elements of the protein can show a variation. In order to understand the amide-¹⁵N CSA dependence on the secondary structure of the protein, we calculated amide-¹⁵N CSAs for residues in alpha helices, beta sheets and turns of cytb₅. The mean ¹⁵N CSA value is found to be similar for residues in the alpha-helix (165.2 ppm) and the beta-sheet (165.4 ppm) while it is smaller (156.5 ppm) in the turn regions. Lower mean ¹⁵N CSA value for residues in turns can be attributed to the flexibility due to lack of H-bonding interactions. The observed trend in this study is similar to an earlier report on protein G from density functional calculations⁸⁴, while CSA measurements on GB3, cytb₅ from solution NMR^{35, 115} and GB1 from solid-state NMR⁴⁷ experiments showed higher mean amide-¹⁵N CSA values for residues in alpha-helix in comparison to beta-sheet residues.

The dependence of principal components of the CSA tensor on the secondary structure of the protein can be evaluated based on their average values obtained from calculations. Average values of δ₁₁, δ₂₂ and δ₃₃ are 231.4, 81.2, 51.3 ppm for residues in alpha helices, 232.8, 88.0, 47.7 ppm for residues in beta sheets and 224.4, 85.1, 50.7 ppm for residues in a turn, respectively. The turn residues are more shielded (~5–6 ppm) along the Z-direction (or along the direction of the least shielded component) of the chemical shift tensor in comparison to helical and beta-sheet residues. The least shielded component δ₁₁ is very close to the direction of the hydrogen bond (N-H---O=C) in alpha-helix and beta-sheet²⁵ and therefore it is more deshielded than that determined for the turn residues which lack such H-bonds. A substantial deviation from the axial symmetry, defined by asymmetry parameter, η = (δ₂₂ - δ₃₃)/(δ₁₁ - δ_iso) was found for the secondary structure elements of cytb₅. This value is found to be slightly smaller (0.28) for helical residues than that for the beta sheet (0.35) and turn (0.33) residues which fall within the range reported in the literature.^{7, 82, 115}

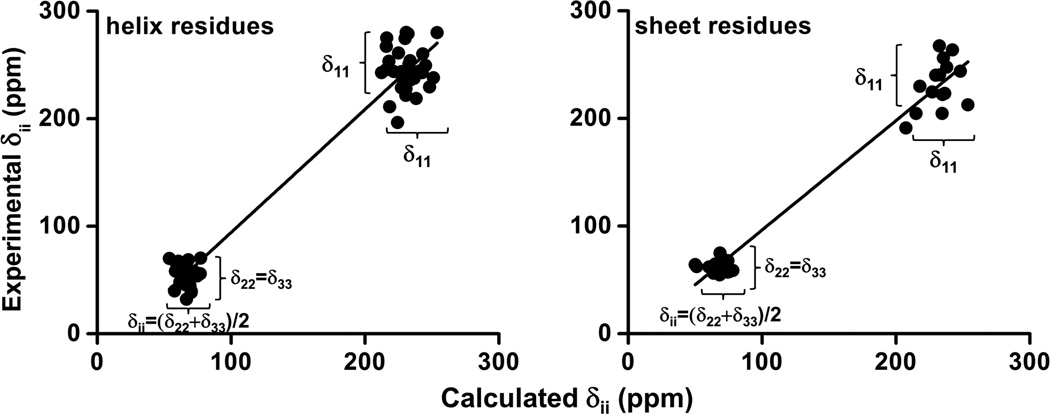
The individual principal components of the calculated amide-¹⁵N CSA tensor for alpha-helix and beta-sheet residues of cytb₅ were compared with experimental data obtained from solution NMR experiments (Table S3 in the Supporting Information). It is evident from Figure 6 that the principal components of amide-¹⁵N CSA tensor for alpha-helix and beta-sheet residues are in good agreement with the experimental values with a correlation coefficient of 0.98. The correlation lines have slopes of 1.14±0.03 and 1.01±0.04 for alpha-helix and beta-sheet residues, respectively. These results are in accord with reported values in the literature.⁸⁴

Figure 6. Linear regression plots between the calculated principal components of amide-¹⁵N CSA tensors and the corresponding experimental components for alpha-helix and sheet residues.

Linear correlation curves between calculated and experimental amide-¹⁵N CSA tensor components for alpha-helix (left) and beta-sheet (right) residues of cytb₅. The parameters obtained from the regression lines are: slope = 1.14±0.03 (helix) and 1.01±0.04 (beta-sheet), and the Pearson’s coefficient (r), for residues both in helix and beta-sheet is 0.98.

Variation of backbone amide-¹⁵N CSA tensors in individual alpha helices and beta sheets of cytb₅

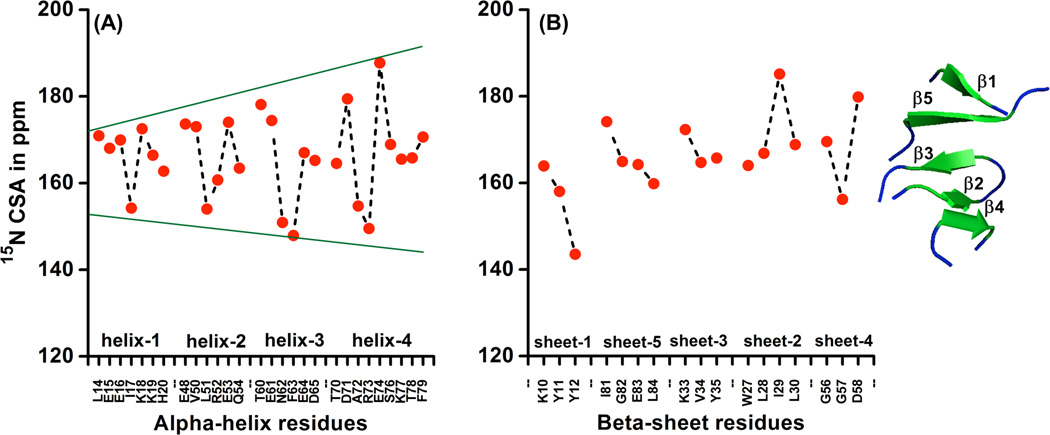
Amide-¹⁵N CSA values for residues in different alpha helices and beta sheets of cytb₅ were calculated as explained earlier and the results are shown in Figure 7. The trend of CSA variation is almost similar for residues located in alpha helices (Figure 7A). Similarly, residues in beta-sheet conformation also have a definite trend of amide-¹⁵N CSA variation (Figure 7B). The β1/β5 and β2/β4 arranged in parallel to each other have opposite trend with a large variation while β3 which is flanked between β2 and β5 shows a narrow variation of amide-¹⁵N CSA. This uniform trend of variation of backbone amide-¹⁵N CSA suggests a uniform characteristic of the ¹⁵N nuclei in amide backbone of alpha helices and beta sheets wherein the residues are experiencing direct and indirect H-bonding interactions and also validates the CSA dependence on the backbone torsion angles. The calculated mean values of amide-¹⁵N CSA in individual beta-sheet show a significant variation (152.0, 171.2, 167.6, 168.5, 165.8 ppm for β1, β2, β3, β4 and β5, respectively) in contrast to values in individual alpha helices (166.7, 166.4, 163.9 and 167.0 ppm for four alpha helices shown in Figure 7A). This observation is in agreement with an earlier DFT report on protein G.⁸⁴ The observed behavior may be because of H-bonding patterns in individual alpha helices and beta sheets. Residues belonging to the same helix (or residues adjacent to each other) participate in H-bonding whereas in a beta-sheet residues of different strands participate in H-bonding. This results in far more extended beta-sheet conformations in comparison to alpha-helix conformations; as a consequence residues in a beta-sheet are also dependent on the conformations of the other strand and therefore show larger variations in the calculated mean values of amide-¹⁵N CSA. It is also important to note that the variation for alpha-helix residues increases with a decreasing distance of the ¹⁵N of interest from the heme unit as shown in Figure 7A. Residues belonging to the first alpha-helix (L14-H20) are at a larger distance from heme and hence show a narrow distribution of CSA. The residues belonging to second (E48-Q54), third (T60-D65) and fourth (T70-F79) helices are located either above or below the plane of heme; as a consequence, the orientation of these residues must be a function of the position of the plane of the heme unit and therefore could result in a larger distribution of CSA as shown in Figure 7A.

Figure 7. Variation of backbone amide-¹⁵N CSA for different alpha-helix and beta sheet residues.

Panel A shows a variation of backbone amide-¹⁵N CSA obtained from quantum chemical calculations for residues present in different alpha-helices based on their closeness to the heme unit of cytb₅. Residues of first alpha-helix (L14-H20) are situated at larger distance while second (E48-Q54), third (T60-D65) and fourth (T70-F79) alpha-helix residues are located above or below the plane of heme unit of cytb₅.

Comparison of experimental and calculated spans of amide-¹⁵N CSA

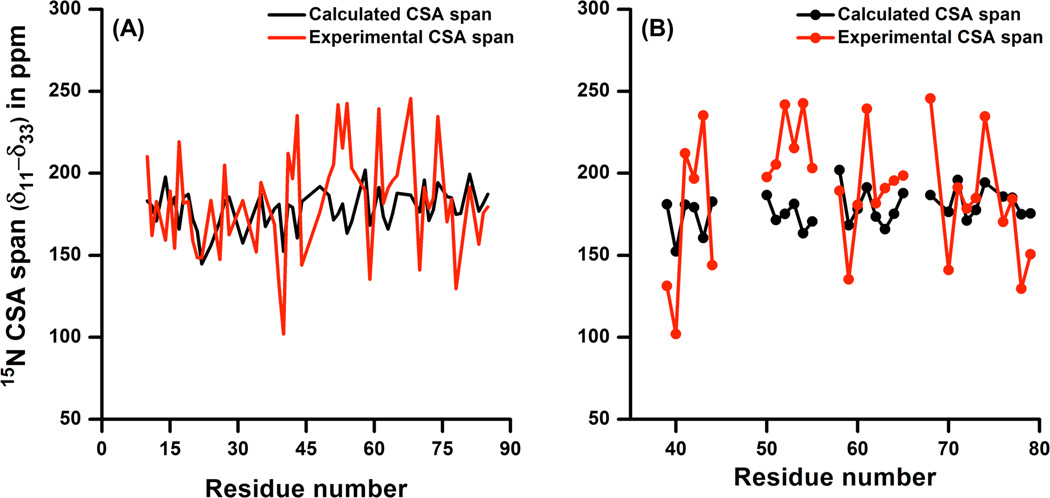
The calculated CSA span which represents the difference between least shielded and most shielded components of CSA tensor given by the relation Ω = δ₁₁ - δ₃₃ (Table S2 in the Supporting Information) is compared with experimentally determined CSA span for values cytb₅.³⁵ The experimental CSA spans for backbone amide residues were obtained by assuming axially symmetric CSA tensors and considering an effective internuclear distance r_N-H = 1.023 Å and a constant angle (β = 18°) between δ₁₁ and the N-H bond. As shown in Figure 8A, the variation in the calculated spans is smaller than the experimentally measured span values. One of the recent reports using an automated fragmentation quantum mechanics/molecular mechanics (AF-QM/MM) method for ¹⁵N CSA determination from water-soluble GB1 and GB3 proteins also validates this aspect.^{73 15}N CSA obtained from solution NMR studies were found to show a larger variability as compared to solid-state and quantum mechanical/molecular mechanical calculations. This is attributed to the fact that the solution NMR approach applies a correction for the effects of small amplitude internal motion which can alter N-H bond length (by ~ 10–15%),^{21, 106, 116, 117} while solid-state NMR utilizes the motionally averaged CSA and N-H dipolar couplings.³³ In addition, the use of fixed values for the N-H distance and angle β could contribute to the variations of ¹⁵N CSA obtained from a solution NMR study. It was also experimentally observed that the residues near the heme unit of cytb₅ exhibited a slightly larger variation in the amide-¹⁵N CSA span as compared to earlier reports on water-soluble proteins. To understand the variation more closely through quantum chemical calculations we carried out an investigation based on the calculated CSA span for the residues near heme. An expanded region of Figure 8A depicting residues near the heme unit (residues 39 to 79) is shown in Figure 8B. It can be seen that the trend in the variation of calculated amide-¹⁵N CSA span for these residues is almost similar to our experimental data with few exceptions. Calculated amide-¹⁵N CSA span for residues near the heme unit such as F40, L41, E42, E43, H44, L51, R52, E53, Q54, A55, A59, E61, F63, E64, H68, T70, E74, S76, T78 and F79 show a difference in amide-¹⁵N CSA span greater than 15 ppm when compared to experimental data. Out of these residues the calculations were performed only for H44, L51, E53, Q54, A59, F63, H68, A72, R73, S76 and F79 with the inclusion of the heme unit as it lies within 5Å distance from these residues. It is clear that the inclusion of the heme unit in the calculation didn’t improve the comparison with the experimental data, which could be due to the limitation of the level of theory applied in the DFT calculations as explained earlier.

Figure 8. A comparison of experimental and theoretical backbone amide-¹⁵N CSA spans determined from solution NMR and Gaussian calculations.

Panel A shows a comparison between computed and experimentally measured backbone amide-¹⁵N CSA span. Panel B is the expansion of the region from panel A for residues 39 to 79, which are in close in proximity to the heme of cytb₅.

CONCLUSIONS

In summary, we have determined backbone amide-¹⁵N CSA tensors for a heme-containing membrane-bound protein, cytb₅, using DFT calculations. We believe that these CSA parameters can be utilized in the structural and dynamic studies of proteins using solid-state and solution NMR techniques; there is no need to rely on the CSA tensors determined from model peptides. The calculated CSA provides further insight into the experimentally measured CSA values. The variation in computed CSA shows a narrow distribution as compared to the experimentally measured data. However, the overall trend in the variation of CSA spans obtained by the two different approaches is in close agreement for most regions of the protein. It is important to note here that the calculations were performed on a rigid single molecule in gas phase that did not include motional averaging, rapid fluctuations of NH bond length and solvent effects. Omission of these effects could also result in discrepancies in the outcome and hence it becomes vital to incorporate these effects in calculation in the future studies. Our results suggest that the effect of the paramagnetic center is not fully taken into account possibly due to the limitation of theory employed in this study to avoid a long computational time. However, it is worthwhile to determine the effect of the metal ion in such paramagnetic systems to improve the accuracy of the calculated CSA values. It is of great importance to perform such calculations and solution or solid-state NMR experiments to determine CSA tensors from intrinsic membrane proteins such as G-protein coupled receptors. Such studies would enable the use of CSAs – instead of isotropic chemical shifts – to study protein-protein and protein-ligand interactions, which will provide insights into the function of the protein and could aid in the design of drugs/compounds to alter the function of the protein.