Unobserved heterogeneity can confound the effect of education on mortality

Abstract

Two opposing hypotheses were proposed to explain the lifecourse pattern in the effect of education on mortality: “cumulative advantage,” where the education effect becomes stronger with age, and “age-as-leveler,” where the effect becomes weaker in old age. Most empirical studies bring evidence for the latter hypothesis but the observed convergence of mortality patterns could be an artifact of selective mortality due to unobserved heterogeneity. A simulation shows that unobserved heterogeneity can bias the estimated effect of education downward so that the cohort-average effect of education decreases in old age regardless of the shape of the underlying subject-specific trajectory.

Does the effect of education on mortality increase with age or does it attenuate in old age? The increasing pattern is consistent with a theoretical perspective referred to as “cumulative advantage,” which suggests that socioeconomic inequalities in health increase with age. The opposing “age-as-leveler” pattern describes converging mortality hazards in old age and is better supported by empirical observations.

Vaupel (1979, 1985a, 1985b) showed that unmeasured heterogeneity in a cohort biases the shape of the cohort mortality hazard. Heckman and Singer (1984) and Trussell and Rodríguez (1990) described how heterogeneity systematically biases estimates of structural parameters in survival models. Social epidemiological literature on determinants of mortality has not, however, considered the extent to which unobserved heterogeneity can affect the estimates of covariates such as education on mortality.

A simple simulation will show the possible role of unmeasured heterogeneity on the effect of education on mortality across age: age-specific effects of education can increase for every individual but decrease for the cohort as a whole. This finding lends indirect support to the “cumulative advantage” hypothesis and highlights how unobserved heterogeneity can distort inferences about subject-specific processes from population-average estimates (Vaupel and Carey, 1993).

Review of the literature

Under the “age-as-leveler” hypothesis, the effect of education on health and mortality declines among the elderly (House et al., 1990, 1994). The weaker effect in old age is hypothesized to be caused by two main factors. First, government support to the elderly in the form of Social Security payments and Medicare is believed to counteract the socioeconomic inequalities growing during adulthood. Second, biological frailty in later life is assumed to level socioeconomic differences in health (House et al., 1994; Markides and Black, 1996).

The explanations for the narrowing economic and health care inequalities, however, have not been demonstrated empirically. Social Security has not reduced socioeconomic differentials among the elderly (Easterlin et al., 1993) and Medicare has not diminished socioeconomic differences in health care access (Crystal et al., 2000).

Under the alternative hypothesis, referred to as “cumulative advantage,” the effect of education on health increases with age whereby the socioeconomic disadvantages and advantages cumulate gradually to produce an increasingly diverse cohort (Dannefer, 2003; O’Rand, 2001). Mediators of the education-health association include income and wealth, health behaviors such as smoking, and psychosocial stress. Crystal and Shea (1990), Easterlin et al. (1993), and O’Rand (1996) described the gradual growth of income inequality in adulthood and old age: the effects of Social Security and other government support to the elderly are outpaced by private income and wealth accumulation. The detrimental effects of risky health behaviors such as smoking accumulate over time (Ferraro and Kelley-Moore, 2003). A consistent higher exposure and vulnerability to chronic stress has significant deleterious health consequences (Lynch and George, 2002; McEwen, 1998; Turner et al., 1995). All these mediators are strongly socially stratified and may explain the widening health differentials within cohorts.

The “cumulative advantage” perspective has counterparts in various social science disciplines because as cohorts age, they tend to show increasing heterogeneity with respect to many characteristics (O’Rand, 1996). This perspective has been successfully employed in lifecourse studies for questions ranging from the faster health declines of disadvantaged minority adults (Ferraro and Farmer, 1996), differentials in children’s academic skills which increase with age (Scarborough and Parker, 2003), growing wage inequalities (Bernhardt et al., 2001), to the Matthew effect which describes the diverging trajectories of academic careers (Merton and Zuckerman, 1968).

While the “cumulative advantage” hypothesis is theoretically well-founded and resonates in social sciences, most health research has supported the “age-as-leveler” hypothesis (Ferraro and Kelley-Moore, 2003). Kitagawa and Hauser (1973) found that the differentials of mortality with respect to education were considerably smaller for people 65+ compared to younger adults. Using the National Longitudinal Mortality Study, others found a similar pattern of smaller mortality differentials in older age (Backlund, Sorlie, and Johnson, 1996; Elo and Preston, 1996; Preston and Elo, 1995; Sorlie, Backlund, and Keller, 1995). Using different data, House and colleagues (1990, 1994), Christenson and Johnson (1995), Feldman et al. (1989), Kunst and Mackenbach (1994), Mustard et al. (1997), and Zajacova (2006) also found smaller effects of education on mortality in old age in U.S. and Europe.

In contrast, little empirical support has been found for the “cumulative advantage”” perspective. Ross and Wu (1996) explored how educational attainment affects changes in health over the course of one year and found that adults with less education evidenced steeper declines in health than the better educated. Unfortunately, Ross and Wu did not attempt to reconcile their findings with the literature, and they did not explain the observed divergence. Lynch (2003) employed hierarchical models to analyze mortality rates among adults and concluded that mortality selection and cohort effects could explain the observed convergence of mortality hazards by education in old age. His analysis suggested that at the individual level the effect of education on health increases during the lifecourse. A similar conclusion was reached by Lauderdale (2001) who used indirect estimation with census data and found that the effect of education on survival becomes stronger with age.

The missing link: unobserved heterogeneity

Vaupel and Yashin (1985b) proposed that unmeasured heterogeneity be considered when theoretical predictions conflict with observed lifecourse patterns. Such inconsistency occurs here. Our contention is that the observed convergence of mortality hazards by education in old age may be an artifact of unobserved heterogeneity in risks of mortality.

Heckman and Singer (1984), and Trussell and Richards (1985) showed that failing to adjust for cohort heterogeneity in hazard models may severely bias estimates of structural effects in survival models. Moreover, unlike in linear regression, in hazard models the bias occurs even when the omitted sources of variation are uncorrelated with the predictors included in the model (Rodríguez, 1994).

To what extent does unmeasured heterogeneity bias the estimates of the effect of education on mortality in hazard models? We show that given a set of plausible assumptions and parameters, an underlying individual-level “cumulative-advantage” lifecourse process can be observed as the opposite “age-as-leveler” pattern of converging cohort death rates at the oldest ages.

Simulation

Suppose we measure the mortality risks for a cohort comprised of two groups of individuals, one with a low educational attainment and another with a high educational attainment. The population-average mortality risk at age x for the low education group is denoted by μ̄_l(x) and the risk for the high education group is μ̄_h(x). The horizontal bars describe any population-average factor. The population-average effect of low education on mortality at age x, β̄(x), is the ratio of these two mortality hazards:

$$\overline{\beta }(x)=\frac{{\overline{\mu }}_l(x)}{{\overline{\mu }}_h(x)}.$$ (1)

The subject-specific effect of education is defined correspondingly as the ratio of age-specific mortality hazards. The effect β(x) is specified as multiplicative on the baseline high-education mortality hazard at age x:

$${\mu }_l(x)=\beta (x){\mu }_h(x).$$ (2)

The central question is to what degree does β̄(x) represent the subject-specific effect β(x) when additional heterogeneity in the cohort mortality risk, also referred to as frailty, is not accounted for. Frailty, denoted by z, is defined as multiplicative on the baseline mortality hazard and assumed to remain constant across individuals’ lives. An individual whose frailty z = 1 is referred to as the standard individual.

We simulate a cohort with two levels of educational attainment, and follow its mortality process from age 25 to 100. We specify three parameters:

1. the subject-specific effect of low education relative to high education on the mortality risk at age x, β(x);

2. the initial distribution of frailty f(x) in each education group, as a gamma distribution with a mean of 1;

3. the mortality hazard function for the standard individual in the high education group, μ_h(x).

The simulation requires an additional parameter, denoted by π, which specifies the proportion of the cohort assigned to the high-education group at the start of the simulation. This parameter is needed to calculate the cohort survival schedule in order to find a set of plausible values for the baseline mortality function.

Using Eq. (2), we calculate the mortality hazard function for the standard individual in the low education group μ_l(x). From these two standard-individual hazard functions and the distribution of frailty f (z), we calculate the cohort-average mortality hazard functions for both education groups, μ̄_h(x) and μ̄_l(x), using identities developed by Vaupel et al. (1979; 1985a; 1985b) and summarized in Appendix A. The ratio of the two functions equals the population-average definition for the effect of education β̄(x), which we can then compare to the predetermined subject-specific effect β(x).

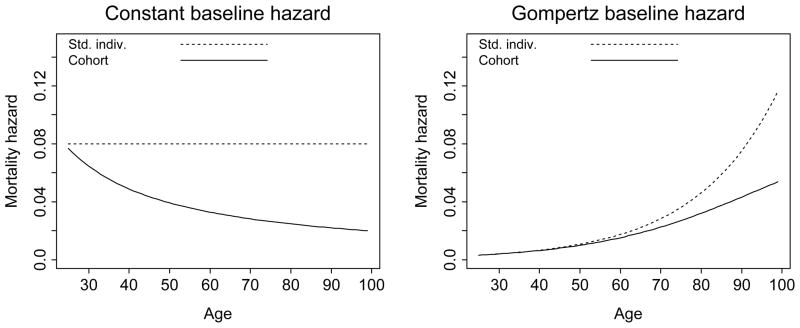
The mean frailty in each education group at the start of the simulation equals the standard individual’s frailty (z̄(0) = 1) and the average mortality hazard function in each group equals the respective standard individual’s hazard function. As the cohort ages, individuals at higher frailty levels die at a faster rate than individuals with a lower frailty. This mortality selection causes the cohort-average hazard to increase more slowly than the individual hazards. Appendix A describes the process more formally and Figure 3 shows two examples of the subject-specific and average-hazard rates in frailty-heterogeneous cohorts.

Figure 3.

Subject-specific and population-average mortality hazard functions for two hypothetical cohorts with heterogeneous frailty. The plots highlight the divergence between the standard-individual hazard μ(x) and the corresponding cohort hazard function μ̄(x). In both examples, the frailty at the start of simulation is gamma-distributed with k=2. In the first plot, the standard-individual hazard function is constant across age at μ(x) = μ = 0.08. In the second plot, μ(x) is a Gompertz function with parameters b = 0.003 and c = 1.05.

The mortality selection process occurs more rapidly in the low education group compared to the high education group. This is because the rate of mortality selection is proportional to the standard-individual hazard rate, which is higher in the low education group. The difference in the rates of mortality selection between the two groups causes μ̄_l(x) to converge to μ̄_h(x). Because the cohort effect of education β̄(x) is determined by the ratio of these two hazard functions, it will gradually decline with age. The goal here is to explore the amount of convergence given a set of plausible parameter values.

The simulation covers ages 25 to 100 so x = 0 represents the starting age of 25. We proceed conditionally on survival to 25 and assume that the assignment to one of the two education levels is completed at that age. Individuals remain at their respective levels of education and frailty throughout life. The distributions of education and frailty in the cohort are not correlated, that is, the distribution of frailty f(z) is the same in both education groups at the start of the simulation. This is an important assumption: in regression models, estimates of the effects associated with predictors are unbiased when the residual is uncorrelated with the predictors. In survival models, the orthogonality assumption does not guarantee unbiased estimates.

Parameter values

For the baseline hazard μ_h(x) we sought a functional form that, when combined with the other model parameters, would yield a cohort mortality hazard function μ̄(x) which is comparable to the schedule in the actual U.S. population. The U.S. survival data are based on the 2002 U.S. life table (Arias, 2004). We used the inversion formula Eq. (18) presented in Rodríguez (1994) to calculate the standard-individual hazard functions for each education group from the U.S. data. From these standard-individual hazard rates we calculated the cohort mortality hazard μ̄(x) and compared it with the U.S. data. The calculations are described in Appendix C. The first plot in Figure 1 shows that the simulated cohort hazard function matches the data well. The second plot shows the corresponding standard-individual hazard rates in the high education and the low education groups.

Figure 1.

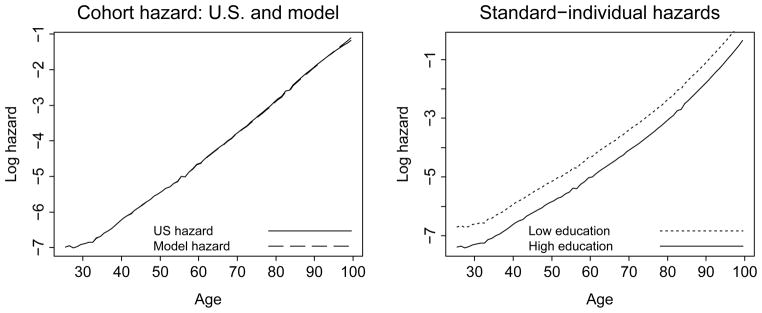
The U.S. and simulated cohort hazard functions and the simulated standard-individual hazard 0.4 functions. The first plot shows mortality hazard functions for the 2002 U.S. population at ages 22.5, 23.5, …, 99.5 and the schedule for the simulated cohort, μ̄(x). The second plot shows the hazard functions for simulated standard individuals in the high and low education groups, μ_h(x) and μ_l(x).

The second component of the simulation is β(x). We examine three lifecourse trajectories of the effect β(x) on mortality:

1. a constant effect of education across age;

2. a decreasing effect (corresponding to the “age-as-leveler” pattern);

3. an increasing effect (corresponding to the “cumulative advantage” pattern).

Sorlie, Backlund, and Keller (1995) found that men under 12 years of schooling had mortality risks 1.9 times as high as men with 12 or more years of schooling. Young men with the least education (0–4 years) had mortality risks 3.2 times as high as men with graduate degrees. Elo and Preston’s (1996) results suggested a mortality risk for the low education group 1.7–1.8 times as high as that for the high education group. Feldman et al. (1989) found that among middle-aged men, the mortality risk was twice as high among men with 0–7 years of education, and 1.6 times as high among men with 8–11 years, as compared to their counterparts with a higher educational attainment.

We consider a comparable set of values for β(x). For the constant trajectory, β = 1.5 and 2. For the increasing and decreasing trajectories, we use linear functions β(x) = β₀ + β₁x with an average value of 2. For the increasing trajectory, β₀=1.5 and β₁=1/75. For the decreasing trajectory, β₀=2.5 and β₁=−1/75.

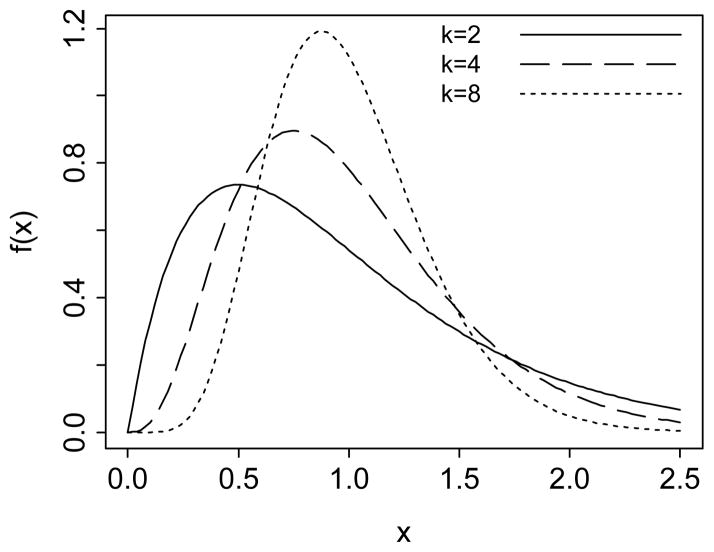
The third component is the distribution of frailty at the start of the simulation f(z), specified as a gamma distribution with mean one and shape parameter k, which is the inverse of the variance. Values of k between 2 and 8 were considered by Vaupel et al. (1979) as plausible for describing the mortality process of human populations. Horiuchi and Coale (1982) suggested k = 4 as optimal for human aging, while others considered a higher variability of frailty. Manton, Stallard and Vaupel (1981) and Manton and Stallard (1981) proposed k in the range of 0.6–3.9. We consider more conservative values of k = 2, 4, and 8. Figure 2 shows gamma distributions with a mean of 1 and these three values of the parameter k.

Figure 2.

Gamma density functions where the mean equals 1 and the shape parameter k = 2, 4, and 8. These three densities are used to describe the distributions of frailty in each education group at the start of the simulation.

Results

Table 1 presents the population-average effect of education on mortality β̄(x) for a constant β = 1.5 and 2 and three values of the frailty parameter k: 2, 4, and 8. For instance, when β=1.5 and k=2, the cohort-average effect of education is 50% higher mortality for the less educated at age 25, but only 23% higher mortality at the oldest ages.

Table 1.

Cohort-average effect of education β̄(x) corresponding to a constant subject-specific effect β =1.5 and 2 and three levels of heterogeneity. The baseline hazard function is calculated from the 2002 U.S. life table.

	Age 25	Age 50	Age 75	Age 90
β=1.5
k=2	1.5	1.49	1.41	1.23
k=4	1.5	1.49	1.45	1.31
k=8	1.5	1.50	1.47	1.39
β=2
k=2	2.0	1.97	1.77	1.42
k=4	2.0	1.98	1.87	1.59
k=8	2.0	1.99	1.93	1.74

The more heterogeneity there is in the cohort, as determined by a smaller k, the greater is the disparity between the subject-specific effect β and the population-average effect of education β̄(x). The level of β also influences the disparity because a higher β causes the mortality selection to occur at a faster rate.

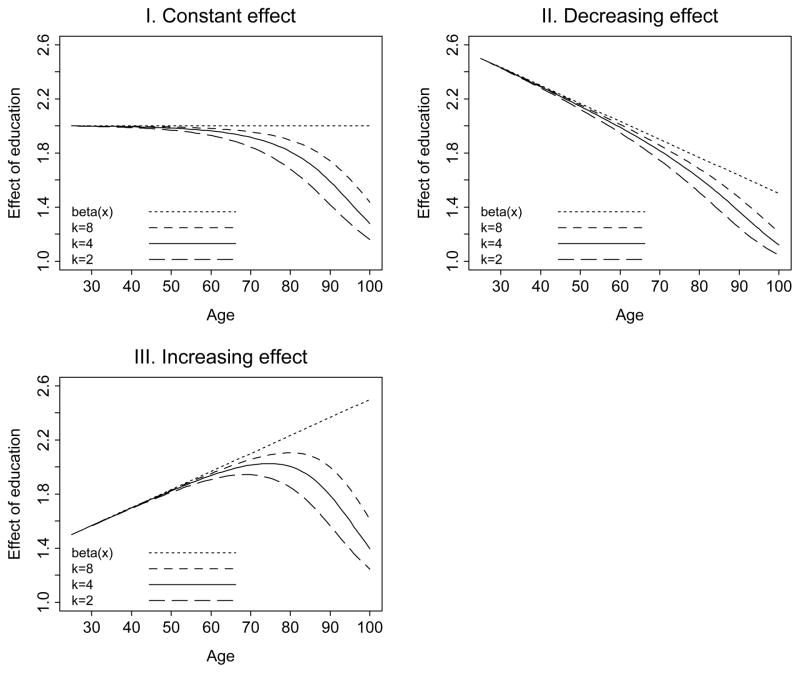
Figure 4 displays the trajectories of β̄(x), juxtaposed against three underlying subject-specific education effect functions: constant, decreasing, and increasing, for different levels of the frailty parameter k: 2, 4, and 8. The first plot shows results for a constant β =2. Throughout young adulthood and middle age, the baseline mortality hazard is fairly low, so there is little mortality selection affecting the cohort. The subject-specific and population-average effects β and β̄(x) are virtually indistinguishable. Later, an increased rate of mortality hazard—and mortality selection—causes the two effects to diverge so that the cohort effect of low education on the mortality hazard declines from 2 in early adulthood to 1.16–1.43 in old age, depending on the amount of residual heterogeneity in the cohort.

Figure 4.

Trajectories of the subject-specific β(x) and population-average β̄(x) effect of education. The three plots show the results for constant, decreasing (“age-as-leveler”), and increasing (“cumulative advantage”) subject-specific effects. The average values of β(x) across age equals 2 in all three plots.

The second plot of Figure 4 depicts a decreasing β(x) function, which corresponds to the “age-as-leveler” hypothesis. The difference between the subject-specific and cohort function is sizeable; at the oldest ages where the subject-specific effect of education is β = 1.5, the cohort-average effect is in the range of 1.05–1.21, depending on the amount of heterogeneity. However, the cohort lifecourse pattern, like the subject-specific trajectory, declines with age.

The third plot of Figure 4 shows a “cumulative advantage” pattern for β(x) increasing with age. The cohort-average trajectory is different: it is not linear but grows through middle age and decreases at older ages. Throughout most of adulthood, the subject-specific and population-average effects are close to one another. For example, at age 50 and k = 4, the subject-specific and population-average effects of education are 1.83 and 1.82, respectively. At the oldest ages, however, while the subject-specific effect increases to 2.5, the population-average effect declines sharply to only 1.24–1.61, depending on the parameter k.

The nonlinear population-average trajectories of the effect of education apparent in the third plot are similar to the lifecourse shape observed by House et al. (1990, 1994). While these authors considered this shape as inherent, we suggest that it may be an artifact of mortality selection due to unobserved heterogeneity.

Conclusion

Literature on the lifecourse pattern of the relationship between education and mortality is marked by a disparity. On one hand, a persuasive cumulative advantage hypothesis suggests that the effect of education on mortality increases with age. This hypothesis offers a coherent explanation for the “fanning out” mechanism and also resonates with lifecourse theories on various cohort characteristics in other social science disciplines (Becker, 1975; Dannefer, 2003; Merton and Zuckerman, 1968; O’Rand, 1996). On the other hand, empirical evidence tends to support the opposite age-as-leveler perspective, according to which mortality hazard rates for groups with different levels of educational attainment converge as the effect of education weakens in old age (Adler et al., 1993; Kitagawa and Houser, 1973; Sorlie, Backlund, and Keller, 1995).

We explored how unobserved heterogeneity could explain the disparity between theory and data. We simulated a frailty-heterogeneous cohort with various trajectories of subject-specific effects of education on mortality. We used mathematical relationships due to Vaupel et al. (1979, 1985a, 1985b) to calculate and compare corresponding population-average trajectories of the effect of education. Given a set of plausible assumptions and parameter values, we find that unobserved heterogeneity can cause a convergence of mortality hazard rates between high and low education groups in old age. This convergence, corresponding to the age-as-leveler hypothesis, can be observed at old ages regardless of how the underlying subject-specific effect of education changes with age—whether the trajectory is constant, decreasing, or increasing. Even a moderate amount of residual heterogeneity in the cohort causes the “cumulative advantage” lifecourse pattern to appear as the opposite, converging “age-as-leveler” pattern in old age.

The study has several limitations. Our conclusions are based on a simple model which fails to capture the complexity of the mortality process in a real cohort. The results are constrained by the assumptions underlying the model structure and by the values chosen for the model parameters. For example, we assume frailty to be gamma-distributed. While this is perhaps the most frequently used distribution, alternative specifications can be employed as well, such as an inverse Gaussian. For the model parameters, we use estimates from the literature. However, they are unobservable so we cannot be certain of how well they represent the values in the actual population.

Survival models accounting for residual heterogeneity are employed in medical science and epidemiology but little in social science. Frailty models can now be estimated in various statistical software applications; for instance, Stata has powerful facilities for fitting parametric and semi-parametric survival models with gamma or inverse Gaussian-distributed heterogeneity. Other programs such as aML provide more flexibility in specifying the baseline hazard, with linear splines and mixture distributions. S-plus incorporates frailty even in proportional hazard models and Stata will likely offer a comparable routine soon. Gutierrez (2002) discusses survival models with frailty and their implementation in Stata. Examples of empirical studies with frailty include Keiding et al.’s (1997) estimation of the effects of several predictors on survival after an operation for malignant melanoma or Vaida and Xu’s (2000) study of the effect of experimental drug treatment on time to death from lung cancer.

However, the essential identification problem remains. For single-spell data, one must make assumptions about the shape of the distribution of unobserved heterogeneity or the shape of the underlying mortality hazard (Heckman and Singer, 1984). A survival model without covariates cannot distinguish between unobserved heterogeneity and the shape of the subject-specific mortality hazard. A model with covariates such as education cannot distinguish between heterogeneity and changes in the effect of the predictor over time. Two converging hazards could result from a weakening effect of a predictor across age or faster mortality selection due to heterogeneity in the higher risk groups. These two explanations, which are equally consistent with empirical observations, cannot be distinguished from single spell data.

An alternative approach to incorporating unobserved heterogeneity is the multivariate survival model (Andersen et al., 1997; Rodríguez, 1994). These models are suitable for multiple observations of an event, using either sibling or twin data, or multiple occurrence of an event for an individual. These models rely on the strong assumption that multiple occurrences have the same frailty, which solves the identification problem. Excellent examples include Guo’s (1993) classic study of factors affecting childhood mortality in Guatemala using sibling data, Gutierrez’ (2002) analysis of infection recurrence, or Andersen et al.’s (1997) cogent discussion of shared-frailty models.

There is no simple strategy to address the problem of heterogeneity in the mortality experience of a cohort. Our simulation provided indirect support for the cumulative advantage theory by showing that the converging age-as-leveler pattern of the effect of education on mortality can be an artifact of unobserved heterogeneity in the cohort. Unobserved heterogeneity should be considered in research on socioeconomic determinants of health in the life course.

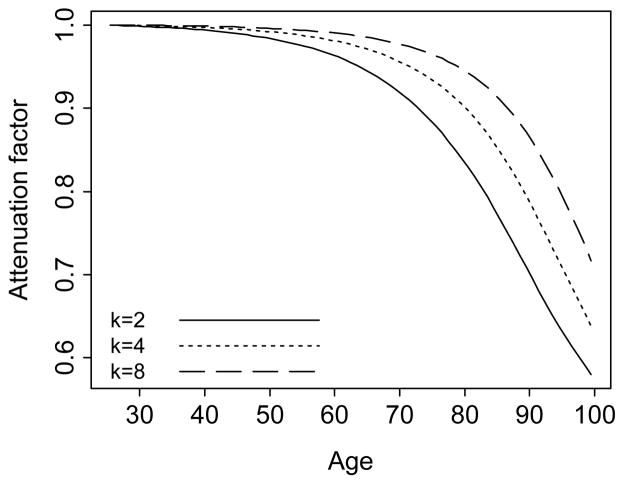
Figure 5.

The attenuation function, Eq. (15). The function determines the relationship between β(x) and β̄(x). The three trajectories correspond to a constant subject-specific effect β = 2, the gamma parameter k = 2, 4, and 8, and the baseline mortality hazard calculated from the 2002 U.S. life table.

Appendix A: The Mortality Process in a Cohort with Heterogeneous Frailty

We review basic identities describing the survival and mortality schedules of a cohort with heterogeneous frailty. A comprehensive discussion is in Vaupel et al. (1979, 1985a, 1985b) and Hougaard (1995).

The mortality process can be described by three interrelated functions: the survival function S(x), the mortality hazard μ(x), and the cumulative hazard H(x). The survival curve S(x) represents the probability of surviving to age x. It is a strictly decreasing function, reflecting the gradual dying out of a cohort. The mortality hazard is defined as the instantaneous death rate at age x, and calculated as

$$\mu (x)=-\frac{\mathit{d}lnS(x)}{dx}.$$ (3)

The cumulative mortality hazard at age x is

$$H(x)={\int }_{t=0}^x\mu (t)dt.$$ (4)

In Eqs. (3) and (4), age is the only predictor of mortality and all individuals of a given age are implicitly assumed to have the same hazard μ(x). The assumption of cohort homogeneity is implausible (Manton, Stallard, and Vaupel, 1981). Many research efforts in health analysis focus on identifying factors affecting individuals’ mortality risks: sex, race, income, or education (Trussell and Rodríguez, 1990). The residual part of the variation in the likelihood of dying comprises all unobserved genetic and nongenetic variability. This mixture of factors is called frailty and denoted by z.

Frailty z is described by a random variable defining an individual’s mortality risk as possibly different from other individuals’ mortality risks. An individual with a frailty level z=1 is called a standard individual, with the mortality hazard denoted by μ(x, 1) or μ(x) for parsimony. Frailty is defined as multiplicative on the baseline hazard:

$$\mu (x,z)=z\mu (x).$$ (5)

From definition (4), frailty is also multiplicative on the cumulative hazard:

$$H(x,z)={\int }_{t=0}^x\mu (t,z)dt={\int }_{t=0}^{x}z\mu (t)dt=z{\int }_{t=0}^x\mu (t)dt=zH(x).$$ (6)

The survival function for an individual at frailty level z is determined as

$$S(x,z)=e^{-H(x,z)}=e^{-zH(x)}=S{(x)}^z.$$ (7)

Frailty is usually assumed constant within individuals throughout the lifecourse—an individual at any given frailty level at birth remains at that level throughout life. For example, an individual with a frailty level z=2 has twice as high a mortality risk at any age, compared to the standard individual.

Eq. (5), (6), and (7) describe the subject-specific mortality and survival functions in a frailty-heterogeneous cohort. However, these trajectories are unobservable; for any individual, the only observed value is the age at death. The ages at death for all individuals in a cohort can be used to find the average mortality rate for a cohort at age x, denoted μ̄(x). The cohort mortality rate is the mean mortality rate for survivors at each frailty level z:

$$\overline{\mu }(x)=\frac{{\int }_z\mu (x,z)f(x,z)dz}{{\int }_{z}f(x,z)dz},$$ (8)

where f(x, z) denotes the distribution of frailty in the cohort at age x. Using Eq. (5), we write μ(x, z) in the numerator as zμ(x). Then

$${\int }_{z}z\mu (x)f(x,z)dz=\mu (x){\int }_{z}zf(x,z)dz,$$ (9)

where the integral ∫_z zf (x, z)dz represents the mean value of z at age x, z̄(x). From the definition of frailty as a proper random variable, the p.d.f. in the denominator integrates to one: ∫_z f (x, z)dz = 1. Hence,

$$\overline{\mu }(x)=\mu (x)\overline{z}(x).$$ (10)

According to this identity, referred to as the fundamental theorem of heterogeneity, the average mortality hazard for a cohort at age x is the product of the standard individual’s mortality hazard μ(x) times the average frailty of survivors in the cohort z̄(x).

Eq. (10) contains an identification problem. The left-hand side of Eq. (10), μ̄(x), represents the population-average mortality rate. On the right hand side of Eq. (10), there are two unobserved functions: the mortality hazard function for the standard individual and the average level of frailty in the cohort at age x. In order to determine these two unobserved quantities from the one available function, we impose a particular distribution of frailty z.

A gamma distribution for frailty was shown to be an analytically tractable choice for the study of mortality selection processes (Manton, Stallard, and Vaupel, 1981; Scheike and Jensen, 1997; Zahl, 1997). A random variable z is gamma-distributed if its probability density function is

$$f(z\mid \lambda ,k)=\frac{{\lambda }^k}{\mathrm{\Gamma }(k)}{z}^{k-1}{e}^{-\lambda z}\text{for}z\ge 0,$$ (11)

with mean $\overline{z}=\frac{k}{\lambda }$ and variance ${\sigma }_z^2=\frac{k}{{\lambda }^2}$.

Gamma distributions take different shapes with respect to the share parameter k. Without loss of generality for calculating the effects of heterogeneity on the mortality process, we set the mean frailty at the start of the simulation z̄(0) = 1 by constraining the scale parameter λ to be equal to the shape parameter k (Vaupel, Manton, and Stallard, 1979). This constraint also simplifies the initial variance to ${\sigma }_z^2(0)=1/k$. Figure 2 shows such gamma probability density functions, with k = 2, 4, and 8, the values used in the simulation. When k = 2, the distribution is positively skewed. As the parameter k increases, the distribution becomes similar to a Gaussian one. As k → ∞, the variance of the distribution approaches zero, describing a homogeneous cohort.

Vaupel et al. (1979) showed that when the frailty at the origin is gamma-distributed with a mean of 1, the frailty of the survivors to age x is also gamma-distributed, with parameters (k +H(x), k). Two equalities for the mean frailty in the cohort z̄ at age x hold:

$$\overline{z}(x)=\frac{k}{k+H(x)}$$ (12)

and

$$\overline{z}(x)=\overline{S}{(x)}^{1/k}.$$ (13)

Eq. (12), together with the fundamental theorem of heterogeneity (10), show how the population-average mortality hazard μ̄(x) depends on the baseline hazard and the gamma parameter k:

$$\overline{\mu }(x)=\mu (x)\frac{k}{k+H(x)}.$$ (14)

Eq. (13) can be used to find the average cohort survival curve. Figure 3 shows two examples of the divergence of the cohort mortality trajectories μ̄(x) from the mortality schedules of the standard individuals μ(x). Frailty z is gamma-distributed in both examples, and the subject-specific mortality hazard rates are constant in age and Gompertz, respectively.

Appendix B: The Relationship Between the Subject-Specific and the Population-Average Effects of Education β(x) and β̄(x)

β̄(x) is calculated as the ratio of the average mortality hazard rates in the low to high education groups – see Eq. (1). From the theorem of heterogeneity (10) and the definition of the subject-specific effect of education in Eq. (2), we get

$$\overline{\beta }(x)=\frac{{\overline{\mu }}_l(x)}{{\overline{\mu }}_h(x)}=\frac{{\mu }_1(x){\overline{z}}_l(x)}{{\mu }_h(x){\overline{z}}_h(x)}=\frac{\beta (x){\mu }_h(x){\overline{z}}_l(x)}{{\mu }_h(x){\overline{z}}_h(x)}=\beta (x)\frac{{\overline{z}}_l(x)}{{\overline{z}}_h(x)}.$$ (15)

The ratio z̄_l(x)/z̄_h(x) is referred to as the attenuation ratio (Rodríguez, 1994). It quantifies the dependence of the population-average effect of education on the average frailty levels in the two education groups across age. At the start of the simulation, the average frailty in each education group is z̄_l(x) = z̄_h(x) = 1 by design, so the population-average and subject-specific effects of education are the same. As the cohort ages, the mortality selection process occurs more rapidly in the low education group, and the average frailty in that group declines faster than in the high education group. As a result, the attenuation ratio decreases and the population-average effect of education β̄(x) becomes gradually smaller relative to the underlying subject-specific effect β(x).

Using Eq. (12), we express the attenuation ratio with model parameters k and H(x):

$$\overline{\beta }(x)=\beta (x)\frac{k+H_h(x)}{k+H_l(x)}.$$ (16)

Eq. (16) is valid for any function β(x), and for examples when β(x) is linear we refer to Figure 4. Of particular interest is the case when β(x) increases monotonically and tends to a limit greater than 1 or tends to infinity. Then β̄(x) may be decreasing for large x. When β(x) is a constant function β₀ > 1, Eq. (16) is expressed as

$$\overline{\beta }(x)=\frac{k+H_h(x)}{(k/{\beta }_0)+H_h(x)}.$$ (17)

A simple calculation shows that β̄(x) = β₀ for x = 0 and tends monotonically to 1 as x tends to infinity.

Appendix C: Calculating the Baseline Hazard Rate μh(x)

We selected the baseline hazard rate μ_h(x) so that, with the other model parameters, the simulated cohort mortality function μ̄(x) approximates the U.S. population schedule based on the 2002 U.S. life table (Arias, 2004). From the survival data at ages 25–100, we calculated the U.S. mortality rates at ages 25.5, 26.5,…, 99.5, using Eq. (3). We set the additional parameters for the simulated cohort to β = 2, k = 4, and the proportion of the cohort comprising the high education group at the start of the simulation π = 0.5.

To calculate the standard-individual hazard function μ(x) from the observed population-average hazard, we assumed a gamma-distributed frailty and used the inversion formula (Rodríguez, 1994):

$$\mu (x)=\overline{\mu }(x)e^{\overline{H}(x)/k^{\ast }},$$ (18)

where k^* denotes the shape parameter for the distribution of heterogeneity in the cohort.

We account for observed (two levels of educational achievement) and unobserved (frailty) heterogeneity. The total variance of heterogeneity in the cohort had to be larger than the variance of unobserved heterogeneity in each education group, or k^* < k. We found that for k = 4 and β = 2, k^* = 3 provided a good fit to the data. The subject-specific hazard rate μ(x) calculated from Eq. (18) was multiplied by 2/3 to obtain the baseline standard-individual hazard rate for the high education group μ_h(x), and by 4/3 for the low education baseline rate μ_l(x). These two functions are shown in the second plot in Figure 1.

We calculated the simulated cohort survival curve z̄(x) and the mortality rate μ̄(x) from these two standard-individual hazard rates, in order to compare them with the 2002 U.S. data. The cohort survival function is a function of the survival schedule in each education group and the initial proportion of the groups in the cohort:

$$S(x)=\pi {\overline{S}}_h(x)+(1-\pi ){\overline{S}}_l(x),$$ (19)

or

$$\overline{S}(x)=\frac{1}{2}({\overline{S}}_h(x)+{\overline{S}}_l(x))$$ (20)

when π = 0.5. Expressed in terms of the parameter k and the standard individuals’ cumulative hazard rates H_h(x) and H_l(x),

$$\overline{S}(x)=\frac{1}{2}\left[{\left(\frac{k}{k+H_h(x)}\right)}^k+{\left(\frac{k}{k+H_l(x)}\right)}^k\right].$$ (21)

H_h(x) and H_l(x) were approximated by summing up the respective hazard rates μ_h(x) and μ_l(x). Finally, from the simulated cohort survival function z̄(x) we calculated the cohort hazard rate μ̄(x) using Eq. (3). Figure 1 shows the close match between the U.S. mortality rate and the simulated cohort schedule.