Abstract
The limitation of using low electron doses in non-destructive cryo-electron tomography of biological specimens can be partially offset via averaging of aligned and structurally homogeneous subsets present in tomograms. This type of sub-volume averaging is especially challenging when multiple species are present. Here, we tackle the problem of conformational separation and alignment with a “collaborative” approach designed to reduce the effect of the “curse of dimensionality” encountered in standard pair-wise comparisons. Our new approach is based on using the nuclear norm as a collaborative similarity measure for alignment of sub-volumes, and by exploiting the presence of symmetry early in the processing. We provide a strict validation of this method by analyzing mixtures of intact simian immunodeficiency viruses SIV mac239 and SIV CP-MAC. Electron microscopic images of these two virus preparations are indistinguishable except for subtle differences in conformation of the envelope glycoproteins displayed on the surface of each virus particle. By using the nuclear norm-based, collaborative alignment method presented here, we demonstrate that the genetic identity of each virus particle present in the mixture can be assigned based solely on the structural information derived from single envelope glycoproteins displayed on the virus surface.
Keywords: Collaborative, averaging, alignment, classification, 3D reconstruction, cryo-tomography, HIV envelope glycoproteins, nuclear norm, clustering, conformational separation, model bias
INTRODUCTION
Cryo-electron tomography is a widely used 3D imaging technique for the analysis and visualization of macromolecular complexes in their native cellular context (Milne and Subramaniam, 2009). Because cryo-electron tomography is carried out at low electron doses to minimize radiation damage during data collection, the signal-to-noise ratios in the images is typically very low, making it challenging to interpret structural features in tomograms. In order to obtain improved density maps of macromolecular complexes, state-of-the-art averaging methods in the literature rely on a proper alignment and averaging of many subvolumes, each containing the feature of interest (Frank, 2006; Bartesaghi et al., 2008; Wu et al., 2009; Zhu et al., 2006); Bartesaghi and Subramaniam, 2009. Thus, for the analysis of subvolumes that contain a discrete or continuous spread of conformations and variable stoichiometry of the components, it is critical to be able both to align and discriminate among different (heterogeneous) noisy subvolumes prior to averaging. The alignment and classification of cryo-electron tomographic data is further complicated by the presence of the so-called missing-wedge – typically composed of 30% or more of all frequencies in a wedge-shaped region in the Fourier domain that are not sampled due to geometrical limitations of the range of angle that can be sampled by the specimen holder in the microscope (McIntosh et al., 2005). The missing-wedge results in anisotropic distortion and lower spatial resolution in a direction parallel to that of the incident beam (Foerster et al., 2008). Unless properly treated, these missing-wedge effects may arbitrarily bias the alignment and classification leading to erroneous results.
One solution to eliminate the detrimental effect of the missing-wedge in subvolume averaging is to constrain the similarity measure between two tomograms only to those frequencies where the signal is sampled in both tomograms (introduced first in (Frangakis et al., 2002) and adopted by many others (Schmid et al., 2006; Foerster et al., 2008; Liu et al., 2008). This already provides a significant improvement in the alignment between two tomograms. However, it still lacks consistency for tomogram classification/separation. This follows from the fact that different frequency-overlap regions may carry different information and signal intensity values. In order to construct a similarity measure that is invariant to these signal intensity differences, one needs to properly equalize/normalize them. Unfortunately, such normalization cannot be attained by the constrained-correlation, since it is applied on subtomograms that contain noise with unknown and frequency-dependent signal-to-noise ratios (SNR; such normalization is also challenging due to the presence of the missing wedge itself). This may result in significantly different correlation values even between pairs of equal structures (as a function of their frequency-overlap dependent SNR). As a result, the conformational separation/classification is prone to be biased by the missing wedge locations of tomograms. In this work we circumvent this frequency-overlap inconsistency by imposing symmetry which, effectively, helps to complete the missing data needed for the conformational separation.
A variety of alignment and classification approaches have been recently proposed, based typically on the assumption that all subvolumes are somehow pre-aligned to their respective reference frames (Heumann et al., 2011), or adopting very powerful iterative Joint Alignment-Classification (JAC) techniques widely used also in single particle electron microscopy (Frank, 2006; Wu et al., 2009; Foerster et al., 2008; Winkler et al., 2009; and many others). The main idea of these types of approaches can be briefly formulated as an expectation-maximization type of problem where, given a data distribution, the alignment is refined with respect to cluster centroids, followed by refinement of the clusters using the updated alignment. This is the paradigm in the standard K-means for example.
However, all of these methods are limited by the special challenges of dealing with low SNR images that are modulated by the missing-wedge of data collection. One key limitation is a phenomenon referred to as the “curse of dimensionality” which captures the idea that the concept of distance, needed both for alignment and classification in such methods, becomes less accurate when increasing the number of noisy data dimensions. Methods such as principal component analysis can partially alleviate the effects of the curse of dimensionality, but may also arbitrarily discard information that can be critical for alignment and classification, since there is in general no basis to presume that information critical to describing individual structures lies in the low dimensional subspace that captures most of the energy of the aggregate dataset. This is a significant problem in cryo-electron tomography, since there are as many low-SNR dimensions as the number of voxels in the subvolumes, which are of the order of thousands. For a single distribution and lp norms in high dimensions , where and xm are entries of x ) the proportional distance between farthest-points and closest-points vanishes (Beyer et al., 1999). This concentration effect of this distance measure is known to be one aspect of this curse of dimensionality, which occurs in a broad range of data distributions and distance measures (Donoho, 2000; Houle et al., 2010). Therefore, extra care has to be taken when dealing with pair-wise distances that are commonly applied for aligning subvolumes to class centroids, as well as in other blocks of JAC techniques.
Despite the general success of the joint alignment and classification methods currently used for aligning and distinguishing distinct sub-populations in tomographic volumes (Bartesaghi and Subramaniam, 2009; Frank et al. 2012; Liu et al., 2008; White et al., 2010; Foerster et al., 2008; Yu and Frangakis, 2011), the accuracy of alignment remains a major bottleneck, especially as the data gets more complex and heterogeneous, including the presence of moderately populated classes. Averaging in the absence of accurate alignment can, and frequently does lower resolution of the final 3D maps.
In this manuscript we propose a new collaborative alignment method to address the above-mentioned challenges. We propose to replace classical similarity measures based on pair-wise distances between two particles, or a particle and a class average, by a one-to-many collaborative similarity function measured between a particle and a group of particles. This approach was inspired by an observation that a matrix composed of aligned particles has a lower complexity (lower rank) as compared to a matrix composed of unaligned particles. Therefore, one can align particles by minimizing their corresponding matrix complexity. The proposed collaborative scheme allows to harnesses contributions of all particles collaboratively for the alignment of every individual particle, as opposed to current state-of-the art approaches that are based on pair-wise comparisons.
Our new method is validated with the problem of separation and reconstruction of SIV Env complexes in a mixture of viruses expressing either the closed conformation alone (SIV MAC239) or the open conformation alone (SIV CP-MAC). This task is particularly difficult since the mixture includes the presence of a very moderately populated class (with an approximate occupancy ratio of 1:10), a challenge that has not been addressed before. In our proposed pipeline we apply the nuclear norm as a collaborative similarity measure for alignment, which is the convex surrogate of the rank of the matrix composed of all available heterogeneous sub-tomograms, thereby retaining all data details essential for the alignment which may be lost when resorting to the use of dimensionality reduction or class averages. We also properly impose 3-fold symmetry early in the alignment procedure, which allows us to complete missing wedge information and, thus, avoid errors in the classification stage of the algorithm.
METHODS
Strategy of using nuclear norm as a collaborative reference frame
The concept of alignment, as often considered in the literature, implies the selection of some canonical reference frame and a similarity measure that determines optimal alignment parameters for each sampled sub-tomogram. As discussed before, the concept of pairwise distances as used in other approaches (Bartesaghi et al., 2008; Foerster et al., 2008; Winkler et al., 2009; Stoelken et al., 2011; Yu and Frangakis, 2011; Heumann et al., 2011) is problematic due to the curse of dimensionality. A commonly adopted remedy to the curse of dimensionality is dimensionality reduction via signal subspace estimation methods such as principal component analysis (Liu, 2008). This task in itself is nontrivial since the distinction between relevant and irrelevant attributes (and dimensions) is not always clear (Houle et al., 2010). The problem is aggravated even more in low SNR conditions, where noise can arbitrarily skew the resulting subspace estimation (Kuybeda et al., 2007).
In order to address these problems, we propose a novel collaborative alignment framework in which the reference frame is defined by all data vectors simultaneously, without resorting to single reference samples such as cluster-centroids. The proposed collaborative alignment framework is greatly inspired by the framework recently introduced in (Vedaldi et al., 2008) and (Peng et al., 2010), which was designed for robustly aligning linearly correlated heterogeneous images as a part of batch image preprocessing for compression, pattern recognition and data mining tasks. In this work we extended this approach to 3D and to work on Cryo-EM data.
Consider we are given ζ completely aligned and identical d -dimensional data elements (subtomograms) v1,…, vζ ordered in a vector form and normalized to have a unit l2-norm. (We will always use this unit-norm normalization of the feature vectors in the sequel, unless explicitly stated otherwise). Then, the matrix obtained by stacking all the vectors column-wise,
| (1) |
should have a rank of one. When the subtomograms are not perfectly aligned, the rank of V grows. Therefore, aligning all data vectors is equivalent to reducing the rank of V back to one. The same argument works when the data is composed of mdifferent non-homologic shape classes, m ≤ ζ. When the subtomograms are aligned, the rank of V is equal to m, which grows when the alignment is altered. This observation provides us with a collaborative reference frame for the alignment procedure, i.e., the optimal alignment parameters are those that minimize the rank of V.
While this approach is conceptually clear, it is not practically tractable. One major difficulty is that rank minimization is an NP-hard problem (Candes and Recht, 2009). Another problem is, that in the presence of noise and/or continuous structural differences, V is not necessarily a rank m matrix, even for perfectly (class) aligned subtomograms. Fortunately, there is an alternative to the rank function that addresses both problems above, and under certain general conditions, is equivalent to the rank optimization task. This minimizes the sum of singular values of V called nuclear norm (Recht et al., 2011),
| (2) |
Where σi(V) denotes the i-th largest singular value of V.
Whereas the rank functions count the number of nonvanishing singular values, the nuclear norm sums their values, and is a convex function that can be efficiently optimized via convex programming methods e.g., (Candes and Recht, 2009; Candes et al., 2011; Lin et al., 2010; Peng et al., 2010). Minimizing the nuclear norm-based objective function is also very effective for combined alignment and sparse noise recovery of linearly correlated images. Since the nuclear norm is equivalent to the l1-norm of the matrix singular values, there is a strong relationship between l1 minimization methods, widely used to recover signals in the compressed sensing and sparse modeling literature (Bruckstein et al., 2009; Candes and Wakin, 2008), and the nuclear norm minimization methods. Intuitively, by facilitating sparsity of the singular values, one helps to reduce the effective rank of the matrix.
We illustrate the utility of nuclear norm minimization with an example from tomograms of SIVmac239 viruses (Figure 1a, b). Starting from n = 190 SIV spikes that were automatically selected, the resulting m1×m2×m3 = 99×99×99 subtomograms were first aligned coarsely in the direction normal to the virus membrane, which we designate as the z-axis. These subtomograms, denoted as , were projected onto the z-axis, producing
| (3) |
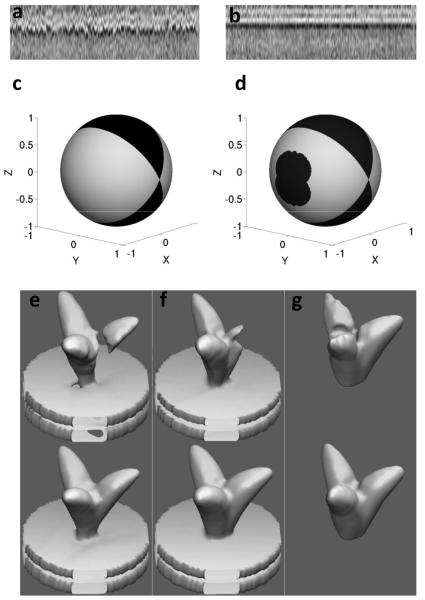
where r is the estimated spike radius (20 pixels). The resulting matrix P, composed of pi(z) ordered column-wise and normalized to a unity l2-norm, is shown in Figure 1a. The bright horizontal band corresponds to the location of the virus membrane, which now becomes visible due to the averaging. In Figure 1b we show the result of the nuclear norm minimization obtained with the algorithm described in greater detail the next subsection. In other words, the columns of P are transformed (translated/rotated) in order to minimize the overall nuclear norm of the resulting matrix and the “particles” are aligned in a collaborative fashion. As it can be clearly seen, all projection vectors were aligned by translations in the z-axis, revealing the (biologically correct) lipid bilayer structure of the membrane. The nuclear norm of the corresponding matrix P decreased from 39.51 to 33.45 as a result of the optimization of the alignment.
FIGURE 1.
Collaborative alignment and missing wedge effects. (a) Subtomograms of SIV spikes projected onto the z-axis and stacked columnwise (each column represents one such subtomogram); (b) the resulting matrix after applying z-axis translations that minimize the nuclear norm; (c) and (d) represent missing-wedge-related information (dark regions) in terms of Euler angles on a sphere. (c) missing-wedge frequency orientations in the Fourier domain; (d) spike orientations in the spatial domain that do not allow a perfect recovery via 3-fold symmetry imposition; (e), (f) and (g) show trimeric phantom shapes before (top) and after the symmetrization recovery (bottom) for shape directions (1,0,0) - x-pole, (e) (0,1,0) - y-pole, (f) (0,0,1) - z-pole (g).
RESULTS AND DISCUSSION
A. Nuclear-norm based alignment
We now introduce an algorithm for nuclear-norm based alignment (NNA), which will be used to estimate all the transformation parameters in the proposed joint alignment and classification scheme. Initially, all spikes have random orientations and translations corresponding to p = 6 rigid body transformation parameters. In the Algorithm 1 below, we present a greedy procedure (efficiently implemented in GPU) that iteratively updates one transformation parameter λ ( x-axis translation for example), denoted by τi,λ, 1 ≤ λ ≤ p, for each of the data subtomograms vi, 1 ≤ i ≤ ζ, respectively. We discretize the domain of possible τi,λ increments into l intervals on a grid denoted as (l depends on λ). Then, we apply all possible l transformations (see definition in Algorithm 1 below), each one corresponding to an interval for the λ-th parameter, 1 ≤ t ≤ ζ , and select the one that minimizes the nuclear norm of the resulting data matrix V .
Algorithm 1.
Greedy update of transformation parameters τi,λ, i =1,…,n
| INPUT: . | normalized data vectors, transformations, and transformation search domain |
|
| 1. | For each i =1,…,ζ do | run through all volumes |
| 3. | sample the search domain of a transformation parameter τi,λ |
|
| 2. | apply l resulting transformations on a volume vi |
|
| 3. | select parameter vector index that minimizes the nuclear norm |
|
| 4. | update transformation | |
| 5. | end | |
For example, in the case of x-axis translations update, the grid can be selected such that the region of interest of x translations, e.g., [−5, 5], is logarithmically sampled. Multi-parameter updates can be similarly performed by constructing multidimensional grids. The logarithmic scheme provides a finer transformation parameters sampling around their current value (see Step 2 of Algorithm 1 above). I.e., small parameter adjustments have denser sampling intervals than large ones. This is why particles that select to move closer to where there are at a given iteration, have a finer selection of potential positions as opposed to particles that select to move farther. At the same time, subtomograms that are far from the convergence select to move farther and, therefore, they receive a coarser update. Their position will be further refined in the following iterations as they converge to a (local) minimum. We experimentally observed that this scheme significantly reduces the number of nuclear norm evaluations in each iteration, with a negligible (if any) increase in the total number of iterations. The nuclear norm evaluations can be sped-up via incremental SVD updates of the matrix (the hat symbol stands for the current update, while the non-hat vectors represent the values from the previous iterations),
| (4) |
Since in each evaluation of the nuclear norm, a single column , is changed, one has
| (5) |
Since the eigenvalues of the symmetric matrix VTV are equal to squares of the singular values of V, the above equation implies that the nuclear norm of , can be obtained from the singular values of V via two rank-one updates of VT V. Fortunately, there is an efficient O(ζ2) algorithm for the rank-one update of the eigen-decomposition of a real symmetrical matrix (Bunch et al., 1978). This provides a significant computational improvement compared to O(ζ3)operations needed for calculating the SVD from scratch. Moreover, this algorithm can be highly parallelized allowing a very fast implementation on GPU platforms. The total number of two-rank updates in Step 3 of Algorithm 1 is l + 1 - one for removing the contribution of vi from the eigen-decomposition of VTV, and l updates by vi,p, for each of the possible p values in the discretized interval. Algorithm 1 is iteratively applied, using different spatial windows (defining different volumes v around the region of interest), tuned to each parameter τλ, and exploiting the virus spike structure.
We have also empirically found that the following normalization of the columns further stabilizes and expedites the algorithm:
| (6) |
Where denotes a matrix composed of the vectors stacked column-wise. In other words, before examining the new matrx , we bring all other columns to have their corresponding nuclear norm equal to one, which is equal to . Before proceeding further, we note a key concept, which is the nuclear norm, when properly normalized, can be used to define a new collaborative distance between sets of vectors. These vectors properly normalized are simply stacked as columns of a joint matrix, and the nuclear norm is computed.
B. Missing-wedge and 3-fold symmetry
We now experimentally assess the effects of the missing-wedge on shapes such as those seen in trimeric envelope glycoprotein spikes. The traditional geometry for data collection in cryo-electron tomography does not allow collection of tilted images with angles greater than ~70°; about a third of the data space is therefore not accessible. According to the Radon Projection Theorem, the nonsampled angular region, when projected in the Fourier space, is composed of planes normal to the electron beam generating a wedge-shaped segment that contains no information, e.g., a missing-wedge. In Figure 1c we show Euler angles on a sphere that represent frequency components that are missing (dark region). The lack of frequency information due to the missing-wedge may have detrimental effects on the alignment process, unless properly treated, since all subtomograms might tend to align according to the missing-wedge orientation, which is typically random.
The presence of 3-fold rotational symmetry, commonly found in envelope glycoprotein structures, can, however, be exploited in order to alleviate the missing-wedge problem (Winkler, 2007). Let denote the Fourier transform of a subtomogram v, and let denote the rotation operator of the subtomogram v by an angle α around the symmetry axis (which is assumed to be z in our analysis). Let also Ω(v) be an indicator function, being 1 for the frequencies at which the data of v is available in the Fourier space, and 0 otherwise. Then, the missing data can be (partially) completed via
| (7) |
where , are n rotated versions of v, by applying spike symmetry angles ( n = 3 in the case of HIV/SIV and Influenza for example), and is the Fourier transform of the resulting subtomogram. In this formula, we complete the missing information using the frequency data that become available due to the shape rotations. Frequencies with more than one value available are averaged, allowing for additional noise reduction. Unrecoverable frequencies, which correspond to zeros both in the nominator and denominator of the fraction in (7), are substituted by zeros.
We note that use of 3-fold symmetry of course does not guarantee that all the missing information will be recovered. In Figure 1 d we show Euler angles on a sphere representing spike orientations (in the coordinate system of the microscope) that allow a perfect reconstruction of the missing-wedge (bright regions), via (7) and orientations that do not allow such perfect reconstruction (dark regions). As expected, spikes with the z-axis oriented in directions that belong to the missing-wedge region cannot be recovered applying the rotational symmetry around z-axis. There are, however, other regions located on the sphere sides that are also not fully recoverable. However, the main point here is that a large portion of possible spike orientations is in the perfectly recoverable region. This implies that the data study can be restricted to perfectly recoverable spike orientations on the virion, without significantly sacrificing the total number of spikes available for the analysis. Moreover, many spike orientations that belong to dark regions of Figure 1d, still allow a fair, though non-perfect, reconstruction. In Figure 1e-g we show a trimeric phantom shape before (top) and after the recovery (bottom) for z-axis directions of (1, 0, 0), (0, 1, 0) and (0, 1, 0) in the microscope coordinate system, respectively. These directions come from the x-pole, y-pole and z-pole of the spike orientations sphere (Figure 1d), respectively. The spike corresponding to the y-pole, (Figure 1f), allows for a perfect reconstruction, the bottom shape of (Figure 1f) is equal to the original one used in this experiment.
The spike corresponding to the x-pole (Figure 1e) is in the middle of the unrecoverable region on the sphere sides. Although it corresponds to the worst-case of the side region spikes, it still retains the basic original phantom shape characteristics albeit with a slight thinning of the stalk connecting the spike to the membrane. This is an encouraging observation because it suggests that even the “dark” region of the sphere can be used for structural analysis.
C. Missing-wedge and alignment
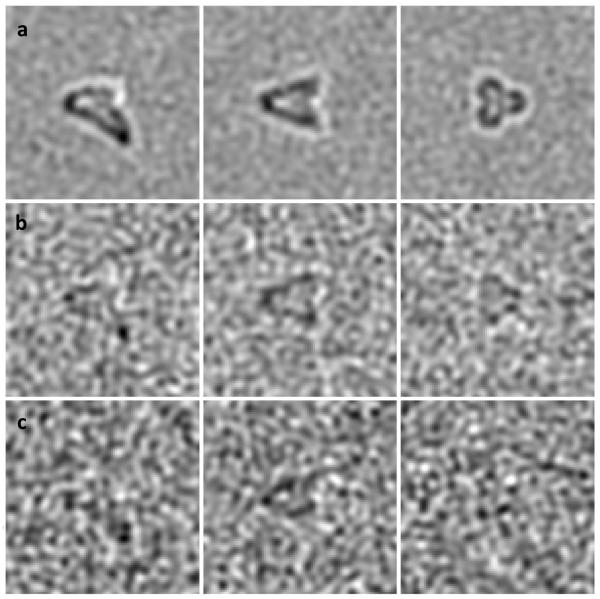
We have just discussed how missing-wedge data may be recovered via the 3-fold symmetry imposition. This is an ideal-case scenario which assumes that all structures are well-aligned with respect to their symmetry axis. Unfortunately, most often, the symmetry axis is not known in advance and, therefore, a straightforward 3-fold symmetry imposition prior to alignment and classification is not always possible. As an example, we show an off-centered phantom in Figure 2a, which, after applying missing wedge (Figure 2b), looks as shown in Figure 2c. Figure 2d shows the resulting shape after imposing the 3-fold symmetry. As clearly seen from the figure, the symmetrized shape looks centered and distorted. Although it can still be good enough for estimating rotations around the z-axis, the xy-plane translations are completely lost. In the following subsections we describe two approaches that allow exploiting the 3-fold symmetry throughout the alignment and classification process even when the symmetry axis is not known.
FIGURE 2.
Imposing 3-fold symmetry on off-centered phantoms. (a) original off-centered phantom; (b) missing wedge in the Fourier domain; (c) phantom shape after applying missing wedge; (d) the resulting shape after imposing the 3-fold symmetry.
Membrane-based approach
In the presence of cellular membrane, the symmetry axis location and orientation can be coarsely estimated by recording normal direction to the membrane during the particle pickup process. This helps using the aforementioned missing wedge completion strategy for estimating some transformation parameters like z-axis rotation in the presence of errors in symmetry axis location. The resulting symmetrized shape, as shown in the example above, does not recover the original shape. Nevertheless, the 3-fold symmetry completion will have a number of important properties: First, it centers the shape on the z-axis, second, by definition, it restores the 3-fold symmetry, which carries information about the original shape rotation angle; furthermore, it corresponds to an improved SNR in the particle being aligned. Although th e obtained shapes will look different depending on the particular error in the xy-plane offset, we experimentally found that they still can be very useful for the z-axis rotation estimation. Moreover, as xy translation estimates are progressively improved when the alignment algorithm advances in iterations (which will be further discussed in below), one obtains a progressive improvement of the 3-fold-restored shapes used for z-axis rotation estimation using this strategy.
Membrane-free approach
Unfortunately, not all translation/rotation types can benefit from the 3-fold symmetry completion strategy. Thus, for example, translations in the xy-plane are lost if one uses the 3-fold symmetry imposition. The same applies to rotations around x and y axes. Moreover, the coarse symmetry axis estimation is also not always known as not all datasets have an ancillary knowledge about the symmetry axis available (like membrane, or preferred particle orientations, for instance). Nevertheless, the symmetry can still be exploited in the NNA algorithm even in these cases by applying the following trick: The relation in Step 3. of Algorithm 1 can be replaced by:
| (8) |
vector descriptors of each shape vk are augmented via the following construct:
| (9) |
where , are versions of v rotated around z-axis, as defined in (7), and stacked one above the other. Initially, z-axis is not assumed to be equal to the symmetry axis. The vector vi,t, (which is being aligned) is augmented differently - by duplication:
| (10) |
This way, the nuclear norm in equation (9) allows to measure similarity between vi - the structure being aligned, and all rotated versions of reference structures vk,1 ≤ k ≤ ζ, k ≠ i.
In the absence of the missing wedge, the resulting cost function will be minimized when all vectors are aligned and their symmetry axis is oriented along the z-axis. This allows for a simultaneous alignment of the particles and the symmetry axis determination. When the missing wedge is present, the concept of comparing particles to all rotated versions of other particles helps to alleviate its detrimental effect. As a result, the alignment is expected to be guided by the existing signal and not by the missing wedge. Here, again one obtains an improvement in SNR due to redundancy of symmetrical signal components present in the data.
Both approaches above allow alignment in the presence of missing wedge, and they both have their advantages and drawbacks. The first method has a better SNR performance, as symmetry redundancies are used both ways - for constructing particle being aligned, as well as in reference particles. However, it is limited to estimating z-axis rotations only and it assumes a coarse prior knowledge of symmetry axis. The second method is applicable in a more general framework – for estimating all transformation parameters with no prior knowledge about the symmetry axis, but it uses symmetry redundancy in reference particles only, which makes it less robust to noise.
D. Combining NNA with a classification algorithm
In subsections above, we explained how we align one subtomogram with respected to a group or class of other subtomograms. Here, we elaborate on how these groups are selected in the alignment through classification strategy as described in Algorithm 2 below. The goal of this strategy is to avoid biasing of misclassified vectors in early stages of the algorithm towards presumably wrong structures dominating their classes. This phenomenon is also commonly referred to as “model bias” which is known to be very detrimental in conformational separation problems (Frank et al., 2012).
Algorithm 2.
Combined NNA and classification algorithm (NNAC)
| INPUT: τ - transformation parameters matrix, C- a set of classes | ||
| 1. | For each c ∈ C do | |
| 2. | update transformations with respect to each class |
|
| 3. | calculate class centroids | |
| 4. | end | |
| 5. | for each vector select best fitting class | |
| 6. | update each vector transformation | |
In Algorithm 2 we assume that we are given a set C of classes, where each class is represented by a group of vector indices obtained via a clustering algorithm. In order to avoid the model bias, we let each vector to be aligned with respect to each class c∈C (Step 2), obtaining the corresponding set of optimal transformations τc, for all subtomograms via NNA procedure explained above. Then, for each subtomogram vi,i = 1,...,n, the transformation parameter τc,i is selected (Steps 5,6) such that maximizes a similarity measure π(τc,i○ Vi, Vc) between the transformed vector τc,i ○ vi and the corresponding class centroid vc calculated in Step 3. We propose to use a l2-normalized cross-correlation similarity measure to define π(·,·). This scheme allows all subtomograms to select a reference class for the alignment irrespectively of their classification label and, therefore, helps avoiding their entrapment by a wrong class in early iterations, when the alignment is still not good enough to produce reliable classification results.
E. High-level joint alignment through classification iterations
We now describe the proposed high-level iterations of the joint alignment through classification (JAC) procedure.
Algorithm 3.
Joint Alignment through Classification Algorithm
| INPUT: τ -initial transformation parameters matrix, q - number of iterations | ||
| 1. | initialize all data in a single class | |
| 2. | Repeat q times | |
| 3. | τ ← NNAC(Tz, τ, C) | align z-translations |
| 4. | τ ← NNAC(Rxy, τ, C) | align xy rotations |
| 5. | τ ← NNAC(Rz, τ, C) | align z rotations |
| 6. | τ ← NNAC(Txy, τ, C) | align xy translations |
| 7. | C ← K-means(V) | recluster data |
| 8. | end | |
In Algorithm 3, we start the first iteration by aligning all data volumes versus one reference cluster composed of all data vectors (Step 1). In Steps 3-7 of th e proposed algorithm we progressively improve the transformation parameters in the following order: z-axis translations Tz, xy- off plane rotations Rxy, rotations around z-axis Rz xy-plane translations Txy .1 Thus, for example, by NNAC(Txy,τ ,C) we denote a successive application of the Algorithm 2, initialized at τ (transformation parameters matrix) a predefined number of iterations, or until no further significant change in the xy translations is observed. Then we cluster the data into a set C of clusters (Step 2) via an off-the-shelf clustering algorithm like K-means. The number of classes is selected such that the minimum class size is large enough to allow a good structure reconstruction via volume averaging. In our experiments we used minimum class size of 100 volumes2. These clusters will be used as references in further iterations. The JAC procedure is performed q times, where a significant improvement is typically observed even after 3-5 iterations. In our simulations, we used q = 10 . This concludes the presentation of the proposed collaborative alignment procedure. Next, we briefly describe how the alignment results are used to obtain clusters that permit detection of different conformations that are present in the data.
F. Hierarchical clustering
Once all the tomographic sub-volumes are aligned in a collaborative manner, they can be averaged together to obtain a density map with higher SNR. When dealing with heterogeneous conformations where more than one conformation is present simultaneously, it is necessary to separate the sub-volumes into homogeneous clusters before averaging. In addition to real structural variation, a significant fraction of the sub-volumes could also be composed of noise that is unrelated to biologically meaningful data. To address these challenges, we use a semisupervised hierarchical clustering approach, in which an agglomerative bottom-up hierarchical clustering is obtained via recursively merging pairs of clusters that have mutually maximal cross-correlations between their corresponding centroids (remember that by now, all the subtomograms have been properly aligned). Subsequently, clusters at any hierarchical level that can be unambiguously assigned to represent noise are separated after manual inspection. We note that every step in the collaborative alignment process itself is fully automated; the separation of “junk” in the data is done after the processing is complete.
G. SNR estimation
In this section we present a method to evaluate the SNR of each data volume. We use this for designing simulated experiments that closely mimic real data conditions, as well as for pruning content-free volumes that may be present as contaminants in the data set.
Let v = vp + vn be a noisy shape vector, where vp is a pure signal component and vn is the noise component; and let be the mean shape of the cluster that contains , as obtained following the proposed alignment and hierarchical clustering technique described in the previous subsections. Then is an estimate of the pure structure vp, which we further normalize to have unit norm, . Since the dimension of the data is high, leading to the noise estimation . Therefore,
| (11) |
Note how we have derived a collaborative way of estimating the SNR of a particle, since the cluster average is obtained from the proposed collaborative alignment and hierarchical clustering procedures. We have experimentally observed that the estimated SNR values are robust to small errors in the alignment parameters. Therefore, one can start estimating SNR values before the alignment algorithm converges. This fact can be used for pruning empty sub-tomograms that, presumably, contain only noise, and therefore are expected to have very low or even negative SNR values.
H. Validation with phantom shapes and with experimental data
We now present results of applying the proposed approach starting first with phantoms, and then testing it with experimentally obtained data. In order to assess how the proposed approach deals with mixtures of phantoms that mimic closed conformation (SIV MAC239) and open conformation (SIV CP-MAC) present in different proportions in the real-data experiment described below, we used a mixture of 100 closed and 400 open phantoms in 99×99×99 subvolumes with 4.1Å pixel size (see left and right top corner shapes in Figure 3, respectively). The SNR was defined as a quotient of signal and noise variance, , and the noise was added similarly to the protocol proposed in (Foerster et al., 2008):
White Gaussian noise with a variance was added to each simulated subtomogram.
The Fourier transformed subtomograms were multiplied by CTF function (approximated for 200 kV acceleration voltage and a defocus of 2.5 μm) and by MTF function of the CCD (approximated to be Gaussian shaped and amounted at 0.2 intensity at half Nyquist frequency).
Another portion of noise with variance was added to achieve the targeted SNR.
Each subtomogram was low-pass filtered to approximately(14Å )−1.
Missing wedges of random orientations, with parameters borrowed from experimentally obtained real-data images, were applied to the simulated subtomograms.
FIGURE 3.
Hierarchical clustering of phantom shapes for SNR = 0.005, following the procedure introduced in this work. Original phantom shapes are in the top left and right corners. Each node contains a density isosurface of the mean shape of the corresponding cluster in the hierarchy. The numbers in blue in each node indicate the number of open and closed shapes that belong to the cluster, respectively. The table then presents the true positive ratio which is equal to proportions of correctly identified spikes of each class for SNR = 0.2, 0.1, 0.01, 0.005, respectively. The highlighted row corresponds to the hierarchy tree (with SNR = 0. 005) shown above the table.
The phantoms were then uniformly and randomly rotated by applying random 3D rotations; and translated with translations in the range [−5,5] in all xyz directions. In the middle of Figure 3 we show the hierarchical clustering of phantoms obtained for SNR = 0.005 using the membrane-free alignment approach (see Section D). Each node in the tree contains a density isosurface for the mean shape of the corresponding cluster. At the bottom of each node we show its corresponding sequential number and the number of subtomograms that came, respectively, from the phantom with the closed and open shapes. As observed from the root node 0, which contains contributions from both shapes, it is easy to miss the presence of open phantoms in the mixture, unless a proper classification/clustering is applied following the alignment. The first classification level shows separation into two groups that already allow identification of the two phantom shapes. At the bottom of Figure 3 we present statistics corresponding to experiments with SNR = 0.2, 0.1, 0.01, 0.005. Each column contains the proportion of correctly assigned particles to the corresponding class. Particles that belong to uninterpretable clusters, like the cluster labeled 2:34 in the figure, were assigned to the “Undetermined” class. As expected, the class assignment performance deteriorates as SNR values decrease. It can be also observed that correctly assigned particle averages exhibit a strikingly good match to the original phantoms, which is an encouraging observation that could be helpful in interpreting real-data results for which ground truth information is not available. In Figure 4 we show xz, yz and xy-plane slices of a simulated noisy phantom for SNR of 0.1 (a), 0.01 (b) and 0.005 (c), respectively. The main goal of the proposed approach is to perform confor mational separation, a procedure whose performance highly depends on user experience regarding what model and/or parameters should be chosen for particular data properties. This is why a direct back-to-back comparison with the existing state-of-the-art methods is a very challenging task. Alternatively, as a stringent test of the success of the proposed collaborative algorithm, we carried out an experiment in which viruses expressing either the closed conformation alone (SIV mac239) or the open conformation alone (SIV CP-MAC) were mixed together (White et al., 2010; White et al., 2011).
FIGURE 4.
Slicing simulated phantom at xz plane yz and xy-plane (from left to right) corresponding to SNR levels of 0.1 (a), 0.01 (b) and 0.005 (c).
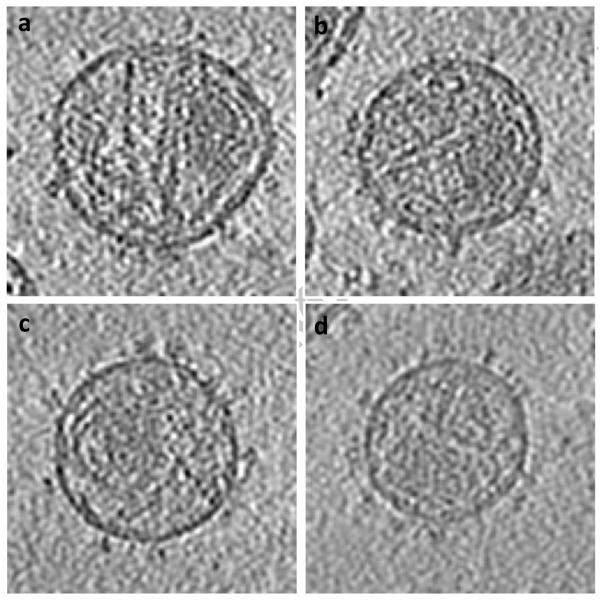
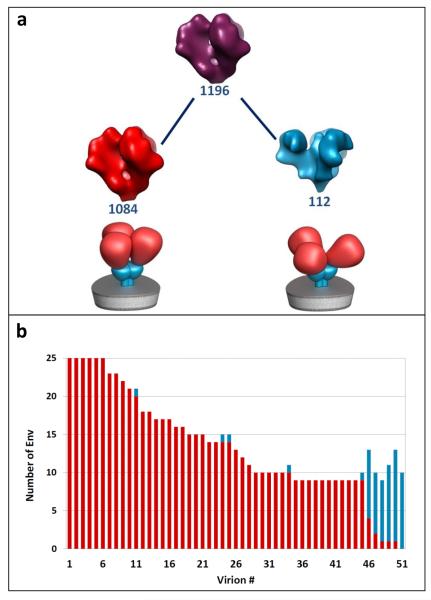
Data was collected using a Tecnai G2 Polara transmission electron microscope (FEI Company, Hillsboro, OR) operated at 200 kV, and equipped with an energy filter and 2K × 2K post-energy filter CCD (Gatan, Pleasantown, CA). Tilt series were acquired over a ± 60° angular range at 2° tilt intervals to yield 61 projections per series. Each projection image in the series was acquired at a nominal magnification of 34,000x (effective 4.1Å pixel size at the specimen plane) with an average underfocus value of 2.5 m, and a dose of 1-2 e/Å2 . About 1200 envelope glycoprotein spike subtomograms were segmented from virion surfaces without applying denoising or binning and had final dimensions of 99×99×99 voxels. Each subtomogram was low-pass filtered with a cutoff at 16Å resolution. A cylindrical window with a radius of 80Å and a height of 160Å was used for the alignment, whereas a height of 120Å was used for the particle classification.3 The two types of viruses cannot be distinguished by visual appearance (see Figure 5 where tomographic slices of different virions are shown), and in any given field of view there are an unknown number of viruses of each kind. It is essential, therefore, that the outcome of the proposed analysis provides not only the 3D structures of the component conformations present in the mixture as a whole, but also allow reliable mapping of each of the subvolumes to one of two types of viruses present. The latter criterion is a particularly stringent test because all of the envelope glycoprotein spikes in a single virus are structurally homogeneous by virtue of the amino acid sequences of the respective envelope glycoprotein spikes. Since there are numerous spikes on each virus, the success of the conformational separation can therefore be quantitated by measuring the consistency with which the spikes assigned to each virus. As illustrated in the hierarchical classification tree (Figure 6a) and the mapping to individual virions (Figure 6b), the collaborative alignment accurately retrieves the two distinct conformations present in the mixture. Schematic representations of two well-defined structures representing native trimeric Env in the closed conformation (SIV MAC 239) and open conformation (CP-MAC) are below the corresponding classes. In Figure 6b, we plot a bar for each virion that contributes its spikes to left and right nodes of the first hierarchical level following the root node in Figure 6a. Bar heights represent the number of spikes detected on the corresponding virions, whereas SIV MAC 239 and SIV CP-MAC portions are marked in red and cyan, respectively.
FIGURE 5.
Tomogram slices of individual virions; (a) and (b) contain majority of spikes identified as SIVmac239; (c) and (d) contain majority of spikes identified as SIV CP-MAC.
FIGURE 6.
(a) Hierarchical separation of SIV MAC 239 and SIV CP-MAC following the collaborative alignment procedure introduced in this paper. Schematic representations of two well-defined structures representing native trimeric Env in the closed conformation (SIV MAC 239) and open conformation (CP-MAC) are shown below the corresponding classes. Each node contains a density isosurface of the mean shape of the corresponding cluster in the hierarchy. The numbers in blue in each node indicate the number of shapes that belong to the cluster, respectively. (b) Virion separation bar-plot corresponding to left and right nodes of the first level in the hierarchy. For each virion, we plot a bar with height equal to the number of spikes detected on the virion. SIV MAC 239 and SIV CP-MAC portions are marked in red and cyan, respectively.
The accuracy with which the spikes are mapped back to the individual virions allows for a reliable discrimination of the originating virions, thus enabling to distinguish viruses in a mixture that represent chemically distinct populations, but are individually indistinguishable at the level of a single tomogram. Using this procedure, we identify SIV MAC 239 virions as those that have most (more than 50%) of their spikes (marked by red), and vice versa for SIV CP-MAC. Keeping this definition in mind, the proportions of incorrectly classified subvolumes of SIV MAC 239 and SIV CP-MAC virions are 2% and 12%, respectively.
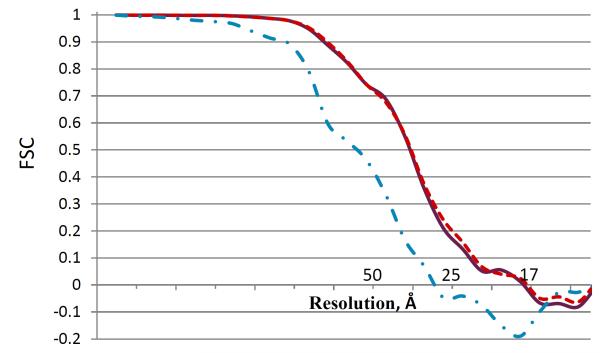
In Figure 7 we show Fourier shell correlation plots for the root shape (purple solid line), which is a mixture of both conformations present in the data, and two shapes of the first hierarchical level corresponding to SIV MAC 239 (red dashed line) and SIV CP-MAC (cyan dot-dashed line). Please refer to Figure 6 for the shape hierarchy description. As observed, there is no significant difference between the mixed shape resolution (purple solid line) and the dominant conformation shape resolution (red dashed line), where both correspond to about 25Å FSC resolution. This observation is reasonable because of low (~1:10) occupancy ratio of the rare class versus the dominant class in the mixture, which renders the “mixed” and “pure” average shape resolutions to be very similar. On the other hand, the unmixed rare-class average shape exhibits a slightly inferior resolution curve of about 30Å (cyan dot-dashed line), probably, because it is composed of a lower number of 112 subvolumes.
FIGURE 7.
Fourier shell correlation (FSC) plots of the root shape (purple solid line), which is a mixture of both conformations present in the data, and two shapes of the first hierarchical level corresponding to SIV MAC 239 (red dashed line) and SIV CP-MAC (cyan dot-dashed line). See Figure 6 for the shape hierarchy description.
Although FSC is a widely used quality-control measure in the TEM literature, its use is fraught with challenges in our case. The actual value depends considerably on numerous incidental parameters such as the way the mask is applied, and the use of a higher number of subvolumes in the average could artificially boost the resolution by correlation of noise in the images along with the signal. Earlier studies have in fact shown precisely this trend (see for example Borgnia, Shi, Zhang and Milne J. Struct. Biol. 2004) that fewer particles with lower phase residual can produce visually better maps than when more particles are used, even though the nominal resolution is higher with more particles. The focus of our work is the discrimination of closely related conformations, and the design of our experiment is such that the emphasis is on discriminating between conformations that look distinct even when the maps are filtered to 50 Å resolution.
I. Algorithm Complexity and Implementation Details
Prior to algorithm optimization, the proposed scheme scales as O(N3 + N4) operations per iteration, where N is the number of particles in the largest cluster. The first N 3 term stems from SVD calculation of the matrix composed of all particles in the cluster. The next N4 term stems from successive updates of each particle transformation in this cluster, which entails an SVD update per particle. By using the incremental SVD update scheme (Equation (5)), one reduces the update complexity to O(N3)(O(N2) per SVD update per particle in the cluster). The use of GPU allows reducing the complexity of SVD updates to O(N) per particle by performing the computation of N singular values in parallel.4. I.e., the optimized complexity of the proposed algorithm is O(N3 + N2), which can be further reduced to O(NM + M3) by reducing the data dimensionality to a fixed number M ≈ 1000 (that may be determined by the number of concurrent threads available in the GPU). This is the complexity of the proposed collaborative data-processing approach, which is higher compared to the state-of-the-art methods based on pair-wise comparisons between particles and cluster average, which scale as O(N), i.e., one update with respect to a cluster centroid per particle.
The algorithm was coded in MATLAB 2011b with the Parallel Toolbox that allows a concurrent use of 12 cores for computationally intense CPU operations (like particle transformations and symmetrization). We also use the Parallel Toolbox for performing incremental SVD updates in GPU via engaging NVIDIA CUDA kernels programmed in C++. The computational time of the real-data experiment above was about 48 hours on a single 2.5GHz CPU Linux machine with 72 GB RAM and 2 NVIDIA C2050 GPU cards. The GPU part in the current implementation takes about 10% of the total time and allows for a speed up of more than 10 times versus (parallelized) CPU implementation of the incremental SVD updates. The algorithm can be further optimized using Matlab mex-files and GPU kernels more extensively.
CONCLUSION
We have presented a comprehensive platform for carrying out subvolume alignment and classification in cryo-electron tomography via collaborative alignment of the component subvolumes in a way that maximizes the accuracy of alignment, and performs over strategies that combine the alignment and classification steps, in particular for heterogeneous data. We show that it can be successfully used for separating closely related, yet distinct conformations of viral envelope glycoprotein spikes present in mixtures, and that the alignment procedures can be executed with a high level of automation. There are, however, challenges like relaxing symmetry requirement and dealing with a broader class of shapes like globular proteins, which are the subject of further research.
ACKNOWLEDGEMENT
This work was jointly supported by funds from the National Library of Medicine and the Center for Cancer Research at the National Cancer Institute, NIH, Bethesda, MD. We thank Steven Fellini, Susan Chacko and colleagues for support with our use of the high-performance computational capabilities of the Biowulf Linux cluster at NIH, Bethesda, MD (http://biowulf.nih.gov).
Footnotes
This order is rather arbitrary. Other orders with multiparameter combination searches are also possible. Combined multiparameter searches facilitate the algorithm robustness to local minima on the expense of increased computational complexity.
This size was selected for robustness in this experiment, however in smaller datasets, we observed that the proposed method was able to detect classes as small as 40 subtomograms.
The 160Å height allows inclusion of the upper-membrane layer in the alignment, whereas by using 120Å height, we exclude the membrane from the analysis.
We perform dimensionality reduction of the matrix if N exceeds the number of concurrent threads per GPU cure, which is equal to 960 in our GPU implementation.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Bartesaghi A, Subramaniam S. Membrane protein structure determination using cryo-electron tomography and 3D image averaging. Curr. Opin. Struct. Biol. 2009;19:402–407. doi: 10.1016/j.sbi.2009.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartesaghi A, Sprechmann P, Liu J, Randall G, Sapiro G, et al. Classification and 3D averaging with missing wedge correction in biological electron tomography. J. Struct. Biol. 2008;162:436–450. doi: 10.1016/j.jsb.2008.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beyer KS, Goldstein J, Ramakrishnan R, Shaft U. When Is “Nearest Neighbor” Meaningful? In Int. Conf. on Database Theory. 1999:217–235. [Google Scholar]
- Bruckstein AM, Donoho DL, Elad M. From Sparse Solutions of Systems of Equations to Sparse Modeling of Signals and Images. SIAM Rev. 2009;51:34–81. [Google Scholar]
- Bunch JR, Nielsen CP, Sorensen DC. Rank-one modification of the symmetric eigenproblem. Numer. Math. 1978;31:31–48. [Google Scholar]
- Candes EJ, Recht B. Exact matrix completion via convex optimization. Found. Comp. Math. 2009;9:717–772. [Google Scholar]
- Candes EJ, Wakin MB. An Introduction To Compressive Sampling. IEEE Signal Process. Mag. 2008;25:21–30. [Google Scholar]
- Candes EJ, Li X, Ma Y, Wright J. Robust principal component analysis? J. Acm. 2011;58:1–37. [Google Scholar]
- Donoho DL. High-dimensional data analysis: The curses and blessings of dimensionality. AMS Math Challenges Lecture. 2000:1–32. [Google Scholar]
- Foerster F, Pruggnaller S, Seybert A, Frangakis AS. Classification of cryo-electron subtomograms using constrained correlation. J. Struct. Biol. 2008;161:276–286. doi: 10.1016/j.jsb.2007.07.006. [DOI] [PubMed] [Google Scholar]
- Frank GA, Bartesaghi A, Kuybeda O, Mario JB, White TA, et al. Cryo-electron tomography of trimeric SIV and HIV-1 envelope glycoproteins: Computational separation of conformational heterogeneity in mixed populations. J Struct. Biol. 2012 doi: 10.1016/j.jsb.2012.01.004. In Press, Accepted Manuscript. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank J. Three-Dimensional Electron Microscopy of Macromolecular Assemblies: Visualization of Biological Molecules in their Native State. Oxford University Press; US: 2006. [Google Scholar]
- Frangakis AS, Bohm J, Forster F, Nickell S, Nicastro D, et al. Identification of macromolecular complexes in cryoelectron tomograms of phantom cells. Nat. Acad. Sci. Proc. 2002;99(22):14153–14158. doi: 10.1073/pnas.172520299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heumann JM, Hoenger A, Mastronarde DN. Clustering and Variance Maps For Cryo-electron Tomography Using Wedge-Masked Differences. J Struct. Biol. 2011 doi: 10.1016/j.jsb.2011.05.011. In Press, Accepted Manuscript. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houle M, Kriegel HP, Kroeger P, Schubert E, Zimek A. Can shared-neighbor distances defeat the curse of dimensionality? Scientific and Statistical Database Management. 2010;6187:482–500. [Google Scholar]
- Kuybeda O, Malah D, Barzohar M. Rank estimation and redundancy reduction of high-dimensional noisy signals with preservation of rare vectors. IEEE Trans. Signal Process. 2007;55:5579–5592. [Google Scholar]
- Lin Z, Chen M, Wu L, Ma Y. The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices. 2010. Arxiv Preprint arXiv:1009.5055.
- Liu H. Computational Methods of Feature Selection. Chapman & Hall/CRC; Boca Raton: 2008. [Google Scholar]
- Liu J, Bartesaghi A, Borgnia MJ, Sapiro G, Subramaniam S. Molecular architecture of native HIV-1 gp120 trimers. Nature. 2008;455:109–113. doi: 10.1038/nature07159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh R, Nicastro D, Mastronarde D. New views of cells in 3D: an introduction to electron tomography. Trends Cell Biol. 2005;15:43–51. doi: 10.1016/j.tcb.2004.11.009. [DOI] [PubMed] [Google Scholar]
- Milne JLS, Subramaniam S. Cryo-electron tomography of bacteria: progress, challenges and future prospects. Nature Rev. Microbiol. 2009;7:666–675. doi: 10.1038/nrmicro2183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Y, Ganesh A, Wright J, Xu W, Ma Y. RASL: Robust alignment by sparse and low-rank decomposition for linearly correlated images. IEEE Trans. Pattern. Anal. Mach. Intell. 2011 Dec 28; doi: 10.1109/TPAMI.2011.282. [Epub ahead of press] [DOI] [PubMed] [Google Scholar]
- Recht B, Xu W, Hassibi B. Null space conditions and thresholds for rank minimization. Math. Program. 2011;127:175–202. [Google Scholar]
- Schmid MF, Paredes AM, Khant HA, Soyer F, Aldrich HC, et al. Structure of Halothiobacillus neapolitanus carboxysomes by cryo-electron tomography. J. Mol. Biol. 2006;364:526–535. doi: 10.1016/j.jmb.2006.09.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheres SH, Melero R, Valle M, Carazo JM. Averaging of Electron Subtomograms and Random Conical Tilt Reconstructions through Likelihood Optimization. Structure. 2009;vol 17(issue 12):1563–1572. doi: 10.1016/j.str.2009.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoelken M, Beck F, Haller T, Hegerl R, Gutsche I, et al. Maximum likelihood based classification of electron tomographic data. J. Struct. Biol. 2011;173:77–85. doi: 10.1016/j.jsb.2010.08.005. [DOI] [PubMed] [Google Scholar]
- Vedaldi A, Guidi G, Soatto S. Joint data alignment up to (lossy) transformations. Conf. CVPR. 2008;2008:1–8. [Google Scholar]
- Walz J, Typke D, Nitsch M, Koster AJ, Hegerl R, et al. Electron Tomography of Single Ice-Embedded Macromolecules: Three-Dimensional Alignment and Classification. J. Struct. Biol. 1997;120:387–395. doi: 10.1006/jsbi.1997.3934. [DOI] [PubMed] [Google Scholar]
- White TA, Bartesaghi A, Borgnia MJ, Meyerson JR, de la Cruz, et al. Molecular Architectures of Trimeric SIV and HIV-1 Envelope Glycoproteins on Intact Viruses: Strain-Dependent Variation in Quaternary Structure. PLoS Pathog. 2010;6:e1001249. doi: 10.1371/journal.ppat.1001249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White TA, Bartesaghi A, Borgnia MJ, de la Cruz MJV, Nandwani R, et al. Three-Dimensional Structures of Soluble CD4-Bound States of Trimeric Simian Immunodeficiency Virus Envelope Glycoproteins Determined by Using Cryo-Electron Tomography. J. Virol. 2011;85(23):12114–12123. doi: 10.1128/JVI.05297-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler H. 3D reconstruction and processing of volumetric data in cryo-electron tomography. J. Struct. Biol. 2007;157:126–137. doi: 10.1016/j.jsb.2006.07.014. [DOI] [PubMed] [Google Scholar]
- Winkler H, Zhu P, Liu J, Ye F, Roux KH, Taylor KA. Tomographic subvolume alignment and subvolume classification applied to myosin V and SIV envelope spikes. J. Struct. Biol. 2009;165:64–77. doi: 10.1016/j.jsb.2008.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu S, Liu J, Reedy MC, Winkler H, Reedy MK, et al. Methods for identifying and averaging variable molecular conformations in tomograms of actively contracting insect flight muscle. J. Struct. Biol. 2009;168:485–502. doi: 10.1016/j.jsb.2009.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Z, Frangakis AS. Classification of electron subtomograms with neural networks and its application to template-matching. J. Struct. Biol. 2011;174:494–504. doi: 10.1016/j.jsb.2011.02.009. [DOI] [PubMed] [Google Scholar]
- Xu M, Beck M, Alber F. High-throughput subtomogram alignment and classification by Fourier space constrained fast volumetric matching. J. Struct. Biol. 2012 Mar 7; doi: 10.1016/j.jsb.2012.02.014. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu P, Liu J, Bess J, Chertova E, Lifson JD, et al. Distribution and three-dimensional structure of AIDS virus envelope spikes. Nature. 2006;441:847–852. doi: 10.1038/nature04817. [DOI] [PubMed] [Google Scholar]