Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Feb 6;3:1218. doi: 10.1038/srep01218

Microscopic mechanism of protein cryopreservation in an aqueous solution with trehalose

Dario Corradini 1,a, Elena G Strekalova 1,3, H Eugene Stanley 1, Paola Gallo 2
PMCID: PMC3565168  PMID: 23390573

Abstract

In order to investigate the cryoprotective mechanism of trehalose on proteins, we use molecular dynamics computer simulations to study the microscopic dynamics of water upon cooling in an aqueous solution of lysozyme and trehalose. We find that the presence of trehalose causes global retardation of the dynamics of water. Comparing aqueous solutions of lysozyme with/without trehalose, we observe that the dynamics of water in the hydration layers close to the protein is dramatically slower when trehalose is present in the system. We also analyze the structure of water and trehalose around the lysozyme and find that the trehalose molecules form a cage surrounding the protein that contains very slow water molecules. We conclude that the transient cage of trehalose molecules that entraps and slows the water molecules prevents the crystallisation of protein hydration water upon cooling.

The preservation of the structural and functional integrity of biomolecules under different thermodynamic conditions is a key topic in current biophysical research1,2,3. One current research problem is how to best preserve proteins, tissues, seeds, organs, and food at low temperatures2. The low temperature technology has recently made substantial progress. One example is the ability to preserve at low temperature ovarian tissue from women about to become infertile due to cancer treatment. This has contributed to the success of the orthotopic reimplantation of the tissue leading to the birth of the first human baby after this procedure4,5.

Biomolecules are damaged by water crystallisation, but ice formation can be inhibited through the use of cryoprotectant solutions. Dimethyl sulfoxide (DMSO) is an effective cryoprotectant but its biocompatibility is limited. Thus often carbohydrates are the compounds of choice to prepare cryoprotectant solutions. In a number of different pharmaceutical, food industry, and biomedical applications, biomolecules are immersed in glassy matrices prepared using sugar, in order to achieve their long-term preservation. Among sugars, trehalose, a naturally occurring disaccharide of glucose, has an extraordinary ability to preserve biomolecules3,6,7,8,9,10. Different organisms naturally produce trehalose when exposed to such external stresses as dehydration or large temperature changes11. Trehalose is also able to stabilise living cells when they are subjected to freezing temperatures12,13.

Although the properties of aqueous solutions of trehalose have been extensively investigated13,14,15,16,17,18,19,20,21,22,23,24,25,26, our understanding of the microscopic mechanism by which trehalose—and sugar in general—is able to protect against freezing is incomplete. Understanding the microscopic dynamics of biomolecular aqueous solutions of carbohydrates is essential if we are to construct effective cryoprotectant solutions.

In both simulations and experiments on aqueous solutions of trehalose, a destructuring effect on the water network was observed3,14,15,16,17. Using Raman scattering experiments, Branca et al.16 found that trehalose protects against crystallisation when the temperature decreases because it deconstructs the tetrahedral hydrogen bond network of water and inhibits the appearance of ice-forming hydrogen bond configurations. Trehalose affects not only the structure of water but also the dynamics. When trehalose is present, the dynamics of water slows dramatically17,18,19,20,21,22,23. Computational18,23 and experimental studies17,20,22 reveal that trehalose is able to introduce an additional, slower, relaxation process in the dynamics of water due to its hydration layer.

Because the interaction between proteins and water crucially influences protein structure, dynamics, and functionality27,28,29,30, understanding the interplay between water, trehalose, and proteins is necessary if we are to understand the cryoprotectant nature of trehalose. Several hypotheses have been presented to explain the effectiveness of trehalose in preserving proteins. In the water replacement scenario, first proposed by Crowe et al.31,32, hydration water molecules are replaced by trehalose molecules that hydrogen-bond to biomolecules. The vitrification (or mechanical entrapment) scenario, first hypothesised by Green and Angell33, assumes that the mobility of the biomolecule is inhibited because of the vitrification upon cooling of the entire trehalose-water solution. Belton and Gil34 proposed a water entrapment scenario. Their Raman scattering results indicated the possible formation of a cage of trehalose molecules, able to contain slow water, around the protein. This allows to maintain a high level of hydration and to smooth the motions of the protein that would lead to denaturation upon cooling. Using computer simulations Fedorov et al.35 recently hypothesised a broken glass scenario in which the mobility of the protein is reduced by the formation of trehalose non-uniform patches interacting with the protein.

In this paper we present a molecular dynamics (MD) computer simulation study of a system composed of the globular protein lysozyme immersed in a solution of trehalose and water. The amount of trehalose involved corresponds to a concentration φ = 40 wt% on a protein-free basis, approximately 1.33 mol/l. Experiments have shown that solutions with trehalose concentration greater than 1 mol/l are particularly effective in preserving biomolecules36. Previous computational studies have also shown that the relative effect of trehalose on water dynamics becomes markedly noticeable at the φ = 40 wt% threshold concentration19,37. Although many contributions from experimental31,34,38,39,40 and computational studies8,35,37,38 have addressed the properties of lysozyme-trehalose-water ternary systems under different conditions and using different techniques, we still do not have a complete picture.

We first focus on the dynamics of water. Using the simulation trajectories recorded at atmospheric pressure and at T = 300 K, T = 280 K, and T = 260 K, we calculate the Fourier transform in the (q, t) space of the density-density self correlation function known as the self intermediate scattering function (SISF) Fs(q, t). From this quantity we extract the relaxation times. The correlation function F obtained from the entire system is compared to the same function computed when either the first or the first and second hydration layers around the trehalose are excluded. We then compute the SISF inside hydration layers close to protein and compare the results to a “trehalose-free” solution of water and lysozyme. We find that when trehalose is present in the system, a dramatic slowing down of water in the hydration layers around the lysozyme occurs. We also investigate the structure of water and trehalose around the centre of mass (COM) of the protein and their coordination numbers. The study of the structure shows that a cage of trehalose molecules forms around the protein.

Results

Dynamics of water

In liquids at ambient temperature the SISF exhibits an initial Gaussian decay followed by an exponential decay from which the relaxation time of the system can be extracted. When a liquid is cooled so rapidly it avoids crystallisation (is supercooled), it approaches the glass transition temperature. Following glass transition theory the liquids show, upon supercooling, a two-step relaxation behaviour. After a short ballistic regime, the SISF reaches a plateau corresponding to the molecules rattling inside the transient cage formed by neighbour molecules that have slowed down because of the supercooling. On longer time scales, the SISF decays following a stretched exponential relaxation, the “α relaxation”, during which the cage relaxes. Computer simulations on the SPC/E model41,42 show that in supercooled bulk water the SISF can be fit to the equation

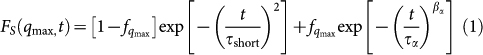graphic file with name srep01218-m1.jpg

where qmax = 2.25 Å−1 at the peak of the oxygen-oxygen structure factor. The Gaussian term describes the first relaxation process of the particle trapped in the cage formed by its neighbours and its relaxation time is τshort. The second term refers to the α relaxation. It has the form of a stretched exponential, also known as the Kohlrausch-Williams-Watts (KWW) function, typical of glass formers, and the associated relaxation time is τα. The coefficient fq is the Debye-Waller factor and it is related to the cage radius.

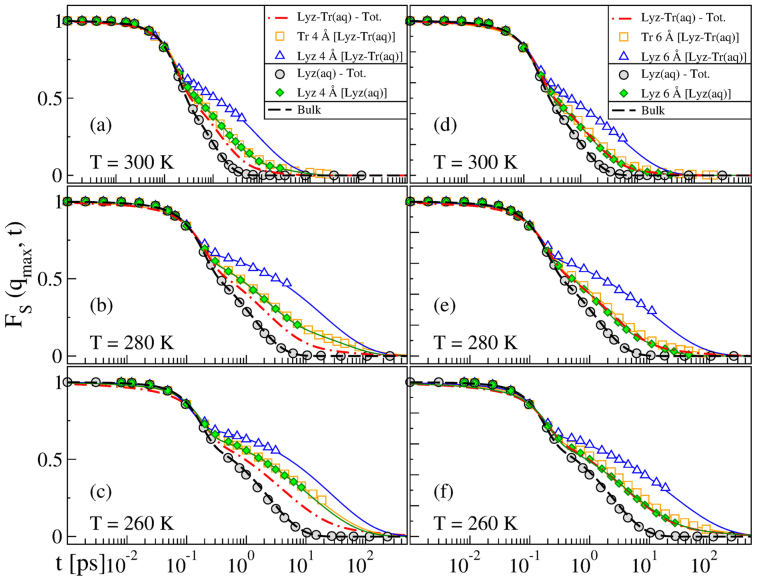
Figure 1 shows the FS(qmax, t) for the bulk and for the lysozyme-trehalose aqueous solution, “Lyz-Tr(aq)”, at the three temperatures studied, T = 300 K, T = 280 K, and T = 260 K. We note that the SISF of the Lyz-Tr(aq) system always decays on a longer time scale with respect to the bulk at the corresponding temperature and shows glassy features already at ambient temperature. Besides, for water in Lyz-Tr(aq), already at ambient temperature, the correlation function F shows not only the two-step relaxation behaviour but also an additional tail at long times. Due to this tail a fit of the SISF for the Lyz-Tr(aq) system can be obtained only adding to the two terms of Eq. 1 a slower relaxation in the form of an additional stretched exponential term:

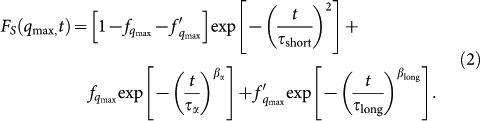graphic file with name srep01218-m2.jpg

This functional form was first proposed by Magno and Gallo18 for aqueous solutions of water and disaccharides. The additional term was ascribed to the slower relaxation due to water in the hydration shell of the sugars and it is characterised by a relaxation time τlong longer than the α relaxation time.

Figure 1. Self intermediate scattering function (SISF) of water in Lyz-Tr(aq) and bulk water.

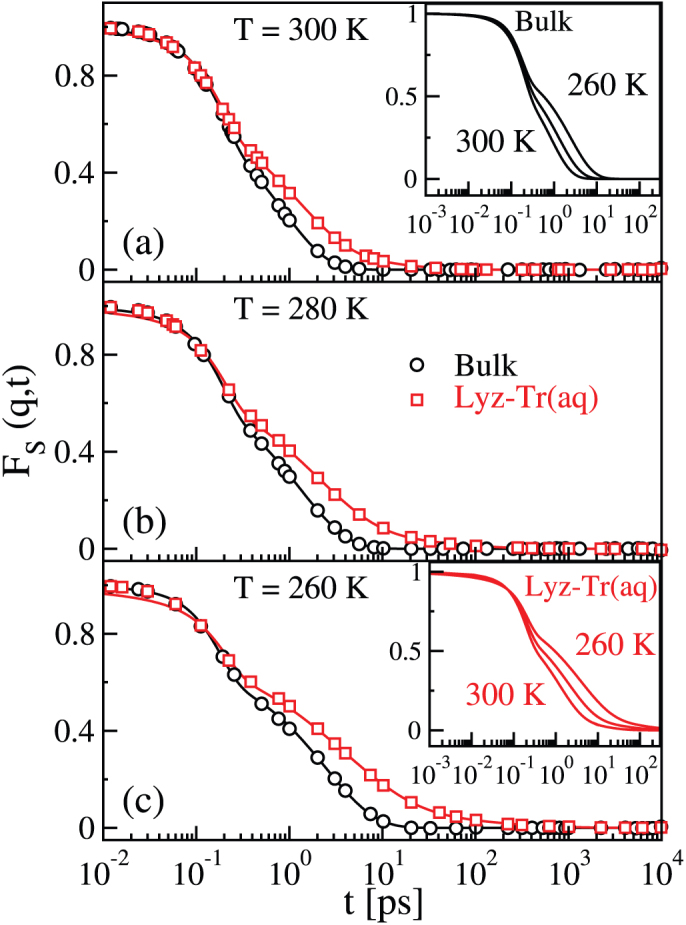
Figure 1

Open in a new tab

The SISF of the oxygen atoms of water FS(qmax,t), with qmax = 2.25 Å−1 at peak of the oxygen–oxygen structure factor, is shown for water in the lysozyme–trehalose mixture, “Lyz-Tr(aq)” (red squares) and for bulk water, “Bulk” (black circles) at (a) T = 300 K, (b) T = 280 K and (c) T = 260 K. Black lines are fits to Eq. 1, red lines are fits to Eq. 2. The tails of the correlation function FS(qmax, t) found for water in the Lyz-Tr(aq) indicate the presence of an additional slower relaxation time with respect to Bulk. Insets: for temperatures T = 300 K, 280 K and 260 K, (top) the fits to Eq. 1 show the change of the FS(qmax, t) with temperature for Bulk (black lines); (bottom) the fits to Eq. 2 show the change of FS(qmax,t) with temperature for water in the Lyz-Tr(aq) (red lines).

Figure 1 also shows how the SISF of bulk water fits Eq. 1 and the SISF of Lyz-Tr(aq) fits Eq. 2. Note that both fits are excellent. The insets show the temperature dependence of the fits of SISF of bulk water to Eq. 1 and of Lyz-Tr(aq) to Eq. 2. Upon supercooling the difference between the SISF of bulk water and of Lyz-Tr(aq) becomes sharper as the stretching of the α and long relaxations in the Lyz-Tr(aq) system become more pronounced. Supplementary Table S1 online provides the fitting parameters of the SISF FS(qmax, t) to Eqs. 1 and 2 in the cases shown in Fig. 1.

Figure 2 shows the temperature dependence of the fit parameters of the SISF curves shown in Fig. 1. We plot the parameters τα and βα of Eq. 1 for bulk water and the parameters τα, βα, and τlong and βlong of Eq. 2 for water in Lyz-Tr(aq). In both bulk water and Lyz-Tr(aq) the α-relaxation time τα increases with decreasing temperature with a power law behaviour. Such behaviour is in agreement with the mode coupling theory (MCT)43 of the glass transition, which predicts a temperature behaviour τα = (T – Tc)-γ for the α-relaxation time. From the fits shown in Fig. 2 we find Tc = 202.8 K and γ = 2.05 for bulk water and Tc = 205.3 K and γ = 2.12 for water in the Lyz-Tr(aq) system. Similar values have been previously found in aqueous mixtures of sugars18.

Figure 2. Temperature dependence of the relaxation times and stretching parameters in Lyz-Tr(aq) and bulk water.

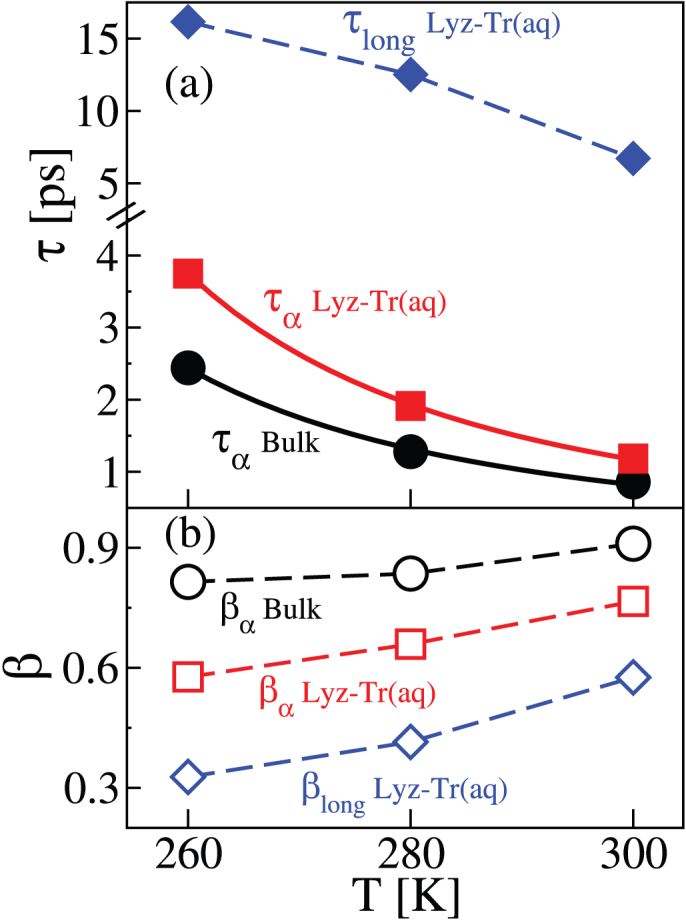
Figure 2

Open in a new tab

The relaxation times and stretching parameters have been extracted from the fits of the SISF to Eq. 2 for water in the lysozyme–trehalose mixture, “Lyz-Tr(aq)”, and from the fits of the SISF to Eq. 1, for bulk water, “Bulk”. (a) For bulk, only the α-relaxation is present with the corresponding relaxation time 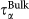Inline graphic (black solid circles) while water in Lyz-Tr(aq) displays both α-relaxation, 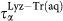Inline graphic (red solid squares) and a long relaxation 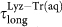Inline graphic (blue solid diamonds). Continuous lines are fits to the MCT power law (see text). (b) Corresponding β stretching parameters 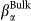Inline graphic for Bulk (black empty circles) and 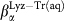Inline graphic (red empty squares) and 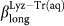Inline graphic (blue empty diamonds) for water in Lyz-Tr(aq).

As the temperature decreases the long relaxation time τlong exhibits an increase that is approximately linear. At all temperatures τlong is four to six times larger than τα. This indicates that water in contact with the biomolecules possesses an additional relaxation time, much larger than that caused by the cage formed by the neighbour water molecules (α relaxation). Note that light scattering experiments on trehalose aqueous mixtures20, supported by MD simulations23, find a “retardation factor” τlong/τα of approximately 6.0 at T = 308 K. Our results are in good agreement with this finding, in fact we find a retardation factor of 5.7 at T = 300 K. When we look at the relaxation times we find 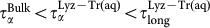Inline graphic; the reverse is true for the stretching parameters β for which 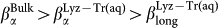Inline graphic, at all temperatures. This indicates a progressively increasing departure from the exponential relaxation going from the α relaxation in the bulk to the long relaxation in Lyz-Tr(aq). In all cases the temperature dependence of the stretching parameters is approximately linear in the range of temperatures investigated.

Water close to hydrophilic confining surfaces such as silica recovers a bulk-like behaviour when the layers closest to the surface are excluded44,45,46. In those systems, the perturbation due to the surface usually extends from 3 to 6 Å. We have observed in our system a total SISF that shows already a diversification of relaxation times indicating a similar behaviour for biological water. To better characterise it we now study in the following the dynamics of water in our mixture by calculating the SISF that comes from excluding water molecules in the hydration shells of trehalose.

Note that the number of water molecules surrounding the trehalose molecules in our system is much larger than the number of water molecules surrounding the lysozyme. In fact in our system only one lysozyme is present as opposed to 491 trehalose molecules so that in the SISF of Fig. 1 the contribution coming from water around the lysozyme is not statistically relevant. In fact, when only water in the first hydration shell of the lysozyme is excluded from the computation of the FS(qmax, t), we find a behaviour very similar to the case with no exclusions (see Supplementary Figure S1 online).

We define the first hydration shell (I) around the trehalose as that composed of water molecules hydrogen-bonded to the trehalose. We use a geometrical criterion to define whether a hydrogen bond exists. A hydrogen bond exists if the donor (D) – acceptor (A) distance is less than 3.4 Å, and if the D-H-A angle is larger than 120°. This criterion has been widely employed in defining the formation of hydrogen bonds from simulation trajectories in aqueous solutions of carbohydrates14,15,38,47. To define water that belongs to the first two shells (II) around trehalose we take into account only distance: water is said to be within the second hydration shell of trehalose if the OW-OT distance is less than 5.8 Å, where OW indicates a water oxygen and OT a trehalose oxygen. We choose this distance by looking at the second minimum of the OW-OT radial distribution function (RDF). The definition of these two shells is reminiscent of that used for water close to hydrophilic silica surfaces44,45,46.

In Fig. 3 we compare at all three temperatures investigated, the results for the FS(qmax, t) calculated excluding the first shell around the trehalose (I*, where * indicates exclusion) and the first two shells around the trehalose (II*) in the Lyz-Tr(aq) with the FS(qmax, t) calculated for the Lyz-Tr(aq) with no exclusions and with the FS(qmax, t) calculated for bulk water. These last two SISF were already shown in Fig. 1. We see that when we exclude the first and then also the second layer around the trehalose, the SISF of the Lyz-Tr(aq) solution progressively approaches the bulk behaviour.

Figure 3. SISF of water with progressive exclusion of the hydration layers around trehalose.

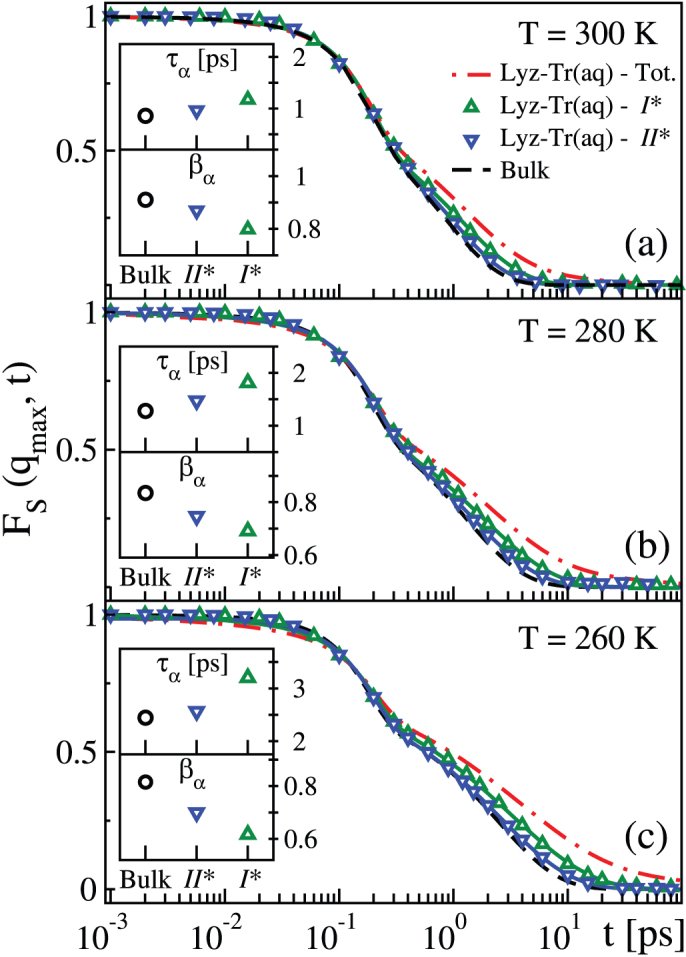
Figure 3

Open in a new tab

FS(qmax,t), of the oxygen atoms of water with progressive exclusion of first hydration layer, “Lyz-Tr(aq) – I*” (green triangles up), and the first two hydration layers. “Lyz-Tr(aq) – II*” (blue triangles down), around trehalose in the Lyz-Tr(aq) system, at (a) T = 300 K, (b) T = 280 K and (c) T = 260 K. Solid lines are fits to Eq. 1 for Lyz-Tr(aq) – I* (green) and Lyz-Tr(aq) – II* (blue). The fits of the FS(qmax, t) for bulk water, “Bulk” (black dashed lines) and for water in the Lyz-Tr(aq) with no exclusions, “Lyz-Tr(aq) – Tot.” (red dot-dashed lines) are also replotted from Fig. 1 for comparison. The behaviour of the FS(qmax, t) progressively approaches the bulk behaviour when the layers around the sugar trehalose are excluded, with the disappearance of the long time relaxation. Insets: (top) α-relaxation time τα for bulk water and for water in Lyz-Tr(aq) excluding the first, I*, and the first two, II*, hydration shells around trehalose; (bottom) βα stretching parameters for bulk water and for water in Lyz-Tr(aq) excluding the first, I*, and the first two, II*, hydration shells around trehalose.

The insets in Fig. 3 compare the relaxation times τα and the stretching exponent βα extracted from the fits in the different cases. When the first shell of trehalose is excluded, the FS(qmax, t) recovers a one-relaxation (beyond the initial Gaussian term) behaviour and it can be fit to Eq. 1 showing that the slow relaxation comes from water molecules hydrogen bonded to the trehalose. However after the exclusion of these water molecules the dynamic behaviour of water remains significantly slower than in bulk water. In fact 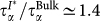Inline graphic at all temperatures. When two hydration shells around the trehalose are excluded, the behaviour of the FS(qmax, t) approaches that of bulk water, although a residual slowing down can also be seen, i.e., 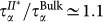Inline graphic. The relaxation time τα and the stretching parameter βα approach bulk values when the shells around trehalose are progressively excluded.

These results indicate that in our Lyz-Tr(aq) the additional long relaxation time is primarily caused by the water molecules bonding to the trehalose. A global slowing down of the dynamics of water nevertheless remains evident when the first hydration shell is excluded. Even when the first two shells around trehalose are excluded, there is still a residual global slowing down, with water dynamics being approximately 10% slower than in bulk water. Supplementary Table S1 online provides the fitting parameters of the SISF FS(qmax, t) to Eqs. 1 and 2 in the cases shown in Fig. 3.

To focus on the effect that trehalose has on the protein, we study the dynamics of water close to the surface of the lysozyme in our Lyz-Tr(aq) system and in a system without trehalose—“Lyz(aq)”—and we compare it with the dynamics of water close to the surface of the trehalose molecules.

Figure 4 shows the FS(qmax, t) calculated for water in the vicinity of trehalose and lysozyme in our Lyz-Tr(aq) and Lyz(aq) system. In order to have sufficient data to calculate the SISF for water in the shells close to lysozyme and trehalose molecules we now consider water oxygen atoms located ≤ 4 Å and ≤ 6 Å from every trehalose or lysozyme atom (see also Refs. 48 or 49). We compare the results obtained from the system containing trehalose and lysozyme, Lyz-Tr(aq) with the ones obtained from the system containing lysozyme only, Lyz(aq).

Figure 4. SISF of water inside the hydration layers of lysozyme and trehalose.

Figure 4

Open in a new tab

FS(qmax, t) of the oxygen atoms of water calculated inside the hydration layers close to the lysozyme and trehalose, at (a, d) T = 300 K, (b,e) T = 280 K and (c,f) T = 260 K. (a,b,c) The left side panels show the SISF for water within 4 Å from the atoms of trehalose, “Tr 4 Å [Lyz-Tr(aq)]” (empty orange squares), lysozyme, “Lyz 4 Å [Lyz-Tr(aq)]” (empty blue triangles) and lysozyme when no trehalose is present, “Lyz 4 Å [Lyz(aq)]” (filled green diamonds). (d,e,f) The right side panels show the SISF of water within 6 Å from the same molecules, with analogous labelling. In both cases the results are compared with the average behaviour in the lysozyme-trehalose system, “Lyz-Tr(aq) – Tot.” (red dot-dashed line from Fig. 1), the system without trehalose, “Lyz(aq)” (filled grey circles) and with bulk water, “Bulk” (black dashed line from Fig. 1). Lines are fits to Eq. 1 or Eq. 2 (see text).

We show in Fig. 4 that water in contact with the trehalose or with the lysozyme and at both distances considered (4 Å and 6 Å) exhibits a slow relaxation behaviour. Note that water ≤ 4 Å and ≤ 6 Å from the lysozyme decays much more slowly in the Lyz-Tr(aq) system than in the Lyz(aq) system.

The SISF computed ≤ 4 Å from the lysozyme in the Lyz(aq) system is very similar to the SISF ≤ 4 Å from the trehalose in Lyz-Tr(aq), and the SISF computed ≤ 6 Å from the lysozyme in the Lyz(aq) system to the SISF computed considering water ≤ 6 Å from the trehalose in Lyz-Tr(aq) (which is also similar to the average SISF of the Lyz-Tr(aq) system).

We also fit the curves to extract the relaxation times and the related stretching parameters. Because of the slow decay rate for this particular SISF and of the limited size of the shells, we were not always able to determine whether a slower second relaxation was present. Thus we used either Eq. 1 or Eq. 2, depending on the particular SISF. Supplementary Table S2 online provides the fitting parameters of the SISF FS(qmax, t) to Eqs. 1 and 2 in the various cases shown in Fig. 4.

This analysis shows that water in contact with lysozyme in the Lyz(aq) system has a dynamic behaviour similar to water in contact with trehalose in the Lyz-Tr(aq) system, while water in contact with lysozyme in the Lyz-Tr(aq) system is much slower. For example, water ≤ 6 Å from the surface of the lysozyme in Lyz-Tr(aq) is approximately 4 times slower than when no trehalose is present at T = 300 K and it becomes approximately 6 times slower at T = 260 K.

Note that when trehalose is present in the system, water in contact with lysozyme slows and crystallisation is more easily avoided. Following our analysis of structure reported in the following section, we will comment further on the origin of this slow dynamic behaviour close to lysozyme. Recent experimental results on the dynamics of water in lysozyme solutions50 were interpreted in terms of two relaxation processes, the second caused by water in the hydration shell of lysozyme. Note that the slower relaxation of the lysozyme hydration water in the presence of trehalose agrees with recent experimental and simulation results38 on the lysozyme-water hydrogen bond dynamics in lysozyme and trehalose glassy matrices.

Structure

In considering the structure of water and trehalose molecules around the protein we first examine the RDF of water around the lysozyme in both the Lyz-Tr(aq) and Lyz(aq) systems. We then examine the density profile of trehalose around the protein in the Lyz-Tr(aq) system.

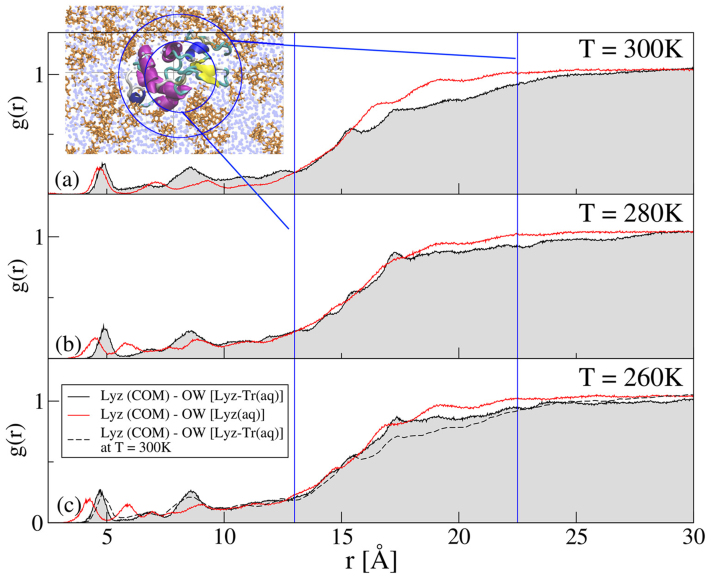
Note that geometrically the lysozyme, a globular protein, has an ellipsoidal shape with major/minor axes of approximately 45 × 26 × 26 Å51. With this in mind, we examine the RDF of the the oxygen atoms of water molecules, around the COM of the lysozyme at T = 300 K, T = 280 K, and T = 260 K. In order to study the structure in the region proximal to the lysozyme and for the sake of comparison, we consider the two distances that approximately correspond to the semi-axes of the protein r = 13 Å and r = 22.5 Å and one larger distance r = 30 Å.

Figure 5 shows the lysozyme-water, “Lyz (COM)-OW”, RDFs for T = 300 K, T = 280 K, and T = 260 K. The results for Lyz-Tr(aq) system are compared with those of the Lyz(aq) system. Note that in both cases some water molecules penetrate deep inside the ellipsoidal region defined by the lysozyme. The RDFs begin to increase at the minor semi-axes distance r = 13 Å and reach an approximately stable value near the major semi-axis distance r = 22.5 Å. Overall in Lyz-Tr(aq) the shape of the RDFs remains similar at the three temperatures, but the water content between the two semi-axes distances increases when the temperature decreases [see Fig. 5(c)]. When compared to the Lyz(aq) system the RDFs of water around the lysozyme show a more corrugated behaviour and a reduction of the height, especially in the region between the two semi-axes distances.

Figure 5. Radial distribution functions (RDFs) of water around the lysozyme.

Figure 5

Open in a new tab

RDFs of water around the COM of the lysozyme in the Lyz-Tr(aq) system (black lines with gray shading to baseline) and in the Lyz(aq) system (red lines). We present the results at all three investigated temperatures (a) T = 300 K, (b) T = 280 K and (c) T = 260 K. The RDF at T = 300 K for Lyz-Tr(aq) is reported in the bottom panel for comparison (dashed line). The blue vertical lines mark the minor and major semi-axes (13 Å and 22.5 Å) of the approximately elliptical shape of the lysozyme. Inset: pictorial representation of a 20 Å × 60 Å × 85 Å cut of the simulation box of the Lyz-Tr(aq) mixture. The lysozyme is represented by a cartoon highlighting of the secondary structure, trehalose molecules by orange bond sticks and water molecules by the blue spheres. The blue circles have radii corresponding to the minor and major semi-axes of lysozyme.

To quantify the number of water molecules close to the lysozyme surface we calculate the coordination numbers by integrating the RDFs. Table 1 shows the lysozyme-water coordination numbers in both Lyz-Tr(aq) and Lyz(aq) systems. We also show in the same Table the lysozyme-trehalose coordination numbers of the Lyz-Tr(aq) system. In the latter case the COM of the trehalose is considered. In order to compare the same regions also for the trehalose we consider here r = 15 Å, slightly larger than the protein minor semi-axes distance, r = 22.5 Å, the protein major semi-axis distance, and r = 30 Å. From the coordination number values of water, nOW, we can see that the number of water molecules at the considered distances always increases with decreasing temperature. Looking at the coordination number of trehalose nTr we observe that the number of trehalose molecules at r = 15 Å is very small, approximately 2, but already approximately 30 molecules of trehalose can be found at the protein major semi-axis distance.

Table 1. Coordination numbers of water and trehalose around the lysozyme. Coordination numbers of water molecules, nOW, and of trehalose molecules, nTr, around the COM of the lysozyme at r = 15 Å, r = 22.5 Å and r = 30 Å for all simulated temperatures. The values of the coordination numbers of water around the COM of the lysozyme in the “trehalose-free” system, nOW [Lyz(aq)], are also reported for comparison.

  nOW nTr nOW
T(K) [Lyz (aq)] [Lyz (aq)] [Lyz aq)]
r = 15 Å
300 65.0 ± 1.7 1.59 ± 0.19 73.8 ± 0.5
280 66.5 ± 1.5 1.68 ± 0.18 90.1 ± 0.8
260 66.8 ± 0.4 1.959 ± 0.042 93.3 ± 0.7
r = 22.5 Å
300 635.1 ± 6.4 33.55 ± 0.94 1026.8 ± 0.6
280 702.0 ± 4.2 27.66 ± 0.25 1042.1 ± 0.9
260 717.4 ± 4.3 27.67 ± 0.54 1057.6 ± 0.6
r = 30 Å
300 2144 ± 12 87.25 ± 0.97 3159.9 ± 0.7
280 2220 ± 16 83.5 ± 1.2 3230.9 ± 0.7
260 2225 ± 13 85.49 ± 0.87 3257.8 ± 0.9
Open in a new tab

When we compare the coordination numbers of water nOW in the Lyz-Tr(aq) and in the Lyz(aq) systems, we see that the presence of the trehalose in the vicinity of the lysozyme lowers the number of water molecules in the Lyz-Tr(aq) system. Note also that fluctuations caused by the motion of trehalose molecules increase the error estimate for this system. The coordination numbers indicate that when the temperature is lowered the trehalose rearranges while a layer of water always hydrates the lysozyme.

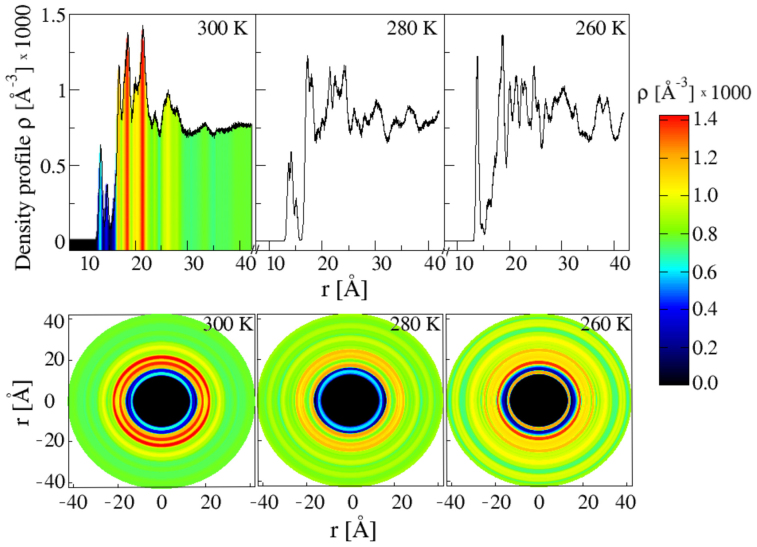
To better characterise the distribution of trehalose molecules around the lysozyme, we calculate the trehalose density profile and from that we extract the density heat map. Figure 6 shows the trehalose density profiles and the corresponding 2D projection of the density colour heat maps at all the temperatures investigated.

Figure 6. Density profile of trehalose molecules around the lysozyme and colour heat maps.

Figure 6

Open in a new tab

(Top panels) Density profile of the COM of trehalose molecules around the COM of the lysozyme at (left) T = 300 K, (middle) T = 280 K and (right) T = 260 K. The density profile is obtained dividing the number of trehalose molecules found between r and r + Δr by the volume of the corresponding spherical shell 4π[(r + Δr)3 − r3]/3, with Δr = 0.02 Å. (Bottom panels) Colour heat map (see scale on the right side) of the 2D projections of the density profile of trehalose molecules around the lysozyme. As an example the density profile at T = 300 K in the top left corner is coloured using the same scale.

The density maps clearly show that there is a region close to the protein where the density of trehalose is higher than average, signalling the formation of a transient cage of trehalose molecules around the protein. At T = 300 K we clearly see an excess density of trehalose in the region from ≈ 17 Å to ≈ 30 Å (with the lysozyme COM in the centre). At T = 280 K we see an excess density of trehalose from ≈ 17 Å to ≈ 25 Å. At T = 260 K the density of trehalose is high very close the lysozyme and up to ≈ 30 Å. At greater distances areas of higher and lower density alternate. The excess density of trehalose near the lysozyme is important because it signals a molecular crowding near the protein that slows the water dynamics and thus inhibits the crystal formation.

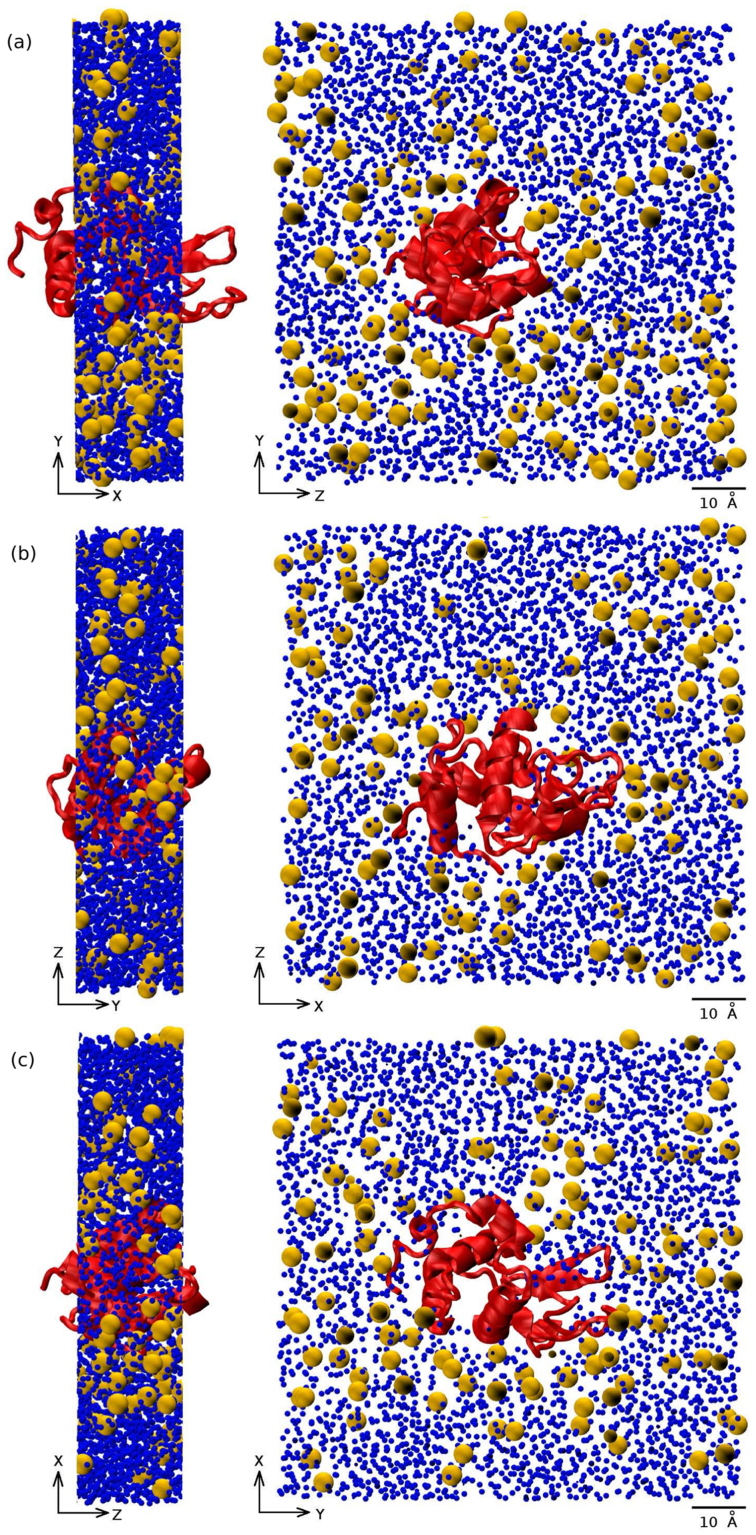
Finally, Fig. 7 shows snapshots of 20 Å cuts of the system along the x, y, and z directions and their projections on the y-z, z-x, and x-y planes, respectively. The snapshots are taken at T = 300 K but the picture remains similar at lower temperatures. We can clearly see that an approximate shell of trehalose molecules surrounds the lysozyme.

Figure 7. Snapshots of the Lyz-Tr(aq) system.

Figure 7

Open in a new tab

Snapshots of the Lyz-Tr(aq) system at T = 300 K obtained performing 20 Å thick cuts (a) along the x axis with its y–z projection; (b) along the y axis with its z – x projection; (c) along the z axis with its x – y projection. The lysozyme is represented by the red ribbon, trehalose by the yellow spheres and water by the blue spheres.

The results for the structure of water and trehalose around the protein indicate the existence of a layer of water packed between the lysozyme and an approximate shell of trehalose molecules. Dynamically, water molecules in the layer between the trehalose cage and the lysozyme are slower than in bulk water. This layer contains many water molecules that are in the lysozyme hydration shell and thus have a slow dynamic behaviour (see Fig. 4).

Discussion

For all temperatures the dynamics of water is significantly slower in the Lyz-Tr(aq) than in bulk water (Fig. 1). In particular, in the Lyz-Tr(aq) system the SISF FS(qmax, t) shows two different relaxation times, τα and τlong. The retardation factor 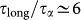Inline graphic (Fig. 2) is compatible with experimental and computational results for solutions of trehalose20,23. This lends support to the vitrification hypothesis in that the appearance of a very slow, glass-like dynamics for water could inhibit the protein molecular motions and thus help preserve protein conformations.

Water residing in the first shell of trehalose (Fig. 3) is the major contributor to the slowing of the dynamics. When this water is excluded from the computation of the Fs(qmax, t), a one-relaxation behaviour is recovered, albeit much slower than in bulk water. When the second shell of trehalose is also excluded, the behaviour of the SISF approaches the behaviour of bulk water, with a residual slowing down. Thus, as previously observed17,18,20,22,23, trehalose introduces a further relaxation time in the dynamics of water.

Studying the SISF for water molecules residing close the lysozyme in the Lyz-Tr(aq) (Fig. 4), we see that this dynamic behaviour is extremely slow, much more so than in water close to the lysozyme when no trehalose is present. Thus the presence of trehalose induces a major general slowing down but the strongest effect is for water close to the lysozyme.

The study of the structure around the protein (Figs. 5, 6, and 7) suggests a picture in which a cage of trehalose molecules containing hydration water is formed around the lysozyme. Note that, when the temperature decreases, the amount of slow water close to the protein increases (Table 1).

We now further test the hypothesis that the formation of a cage of trehalose molecules induces the presence of slow water close to the lysozyme. Figure 8 shows the SISF computed for water within a sphere of 30 Å from the centre of geometry (COG) of the lysozyme, or from outside this sphere, at the three temperatures investigated. We select the distance 30 Å after examining the density maps of the trehalose molecules around the lysozyme shown in Fig. 6. Although there are changes with temperature in the density profile, we use 30 Å at all temperatures for the sake of comparison. We compare the results with those of the Lyz(aq) system, and find that in Lyz-Tr(aq) water contained within the 30 Å distance from the lysozyme COG is slower than the average of Lyz-Tr(aq) and dramatically slower than in the same region in the Lyz(aq) system. In both cases, water outside the 30 Å region exhibits a behaviour that is slightly faster than that of the average SISF of the corresponding system. Thus the presence of trehalose causes the formation of a region around the lysozyme in which water is much slower than average, and this is consistent with previous dynamic and structural results. In the case of the lysozyme-trehalose system the points have been fit to Eq. 2, while in the case of lysozyme only to Eq. 1. The list of the parameters of the fits is presented in the Supplementary Table S3 online.

Figure 8. SISF of water in/out a spherical region around the lysozyme.

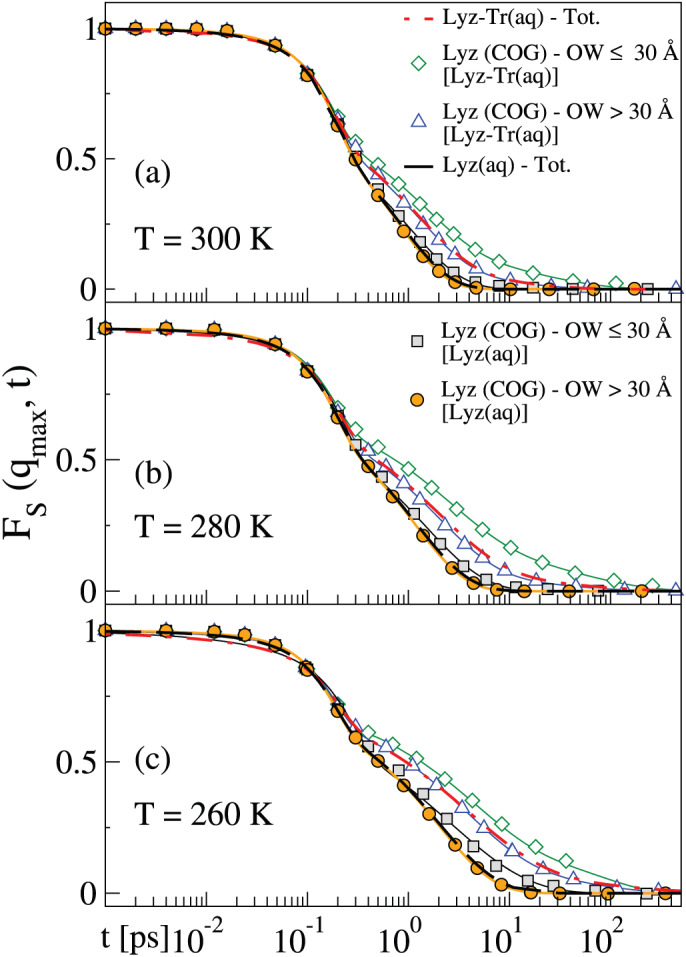
Figure 8

Open in a new tab

FS(qmax, t) of the oxygen atoms of water calculated within a sphere of 30 Å radius from the COG of the lysozyme, “Lyz COG–OW ≤ 30 Å [Lyz-Tr(aq)]” (green empty diamonds), and outside this sphere, “Lyz COG–OW > 30 Å [Lyz-Tr(aq)]” (blue empty triangles) at (a)T = 300 K, (b) T = 280 K and (c) T = 260 K. The same quantities are shown for the system without trehalose, “Lyz COG–OW ≤ 30 Å [Lyz(aq)]” (grey solid squares) and “Lyz COG–OW > 30 Å [Lyz(aq)]” (orange solid circles). The results are compared with the average behaviour of the SISF in the trehalose–lysozyme system, “Lyz-Tr(aq) – Tot.” (red dot-dashed line replotted from Fig. 1) and in the system with lysozyme only, “Lyz(aq)– Tot. ” (black solid line). Lines are fits to Eq. 1 or Eq. 2 (see text).

Globally, our results point to the water entrapment scenario in which very slow water is packed between the protein and a cage of trehalose molecules. Note that Lins et al.8 indicated the formation of a cage of trehalose molecules around the lysozyme containing a thin layer of water, in MD simulations performed at a lower trehalose molarity than ours. They studied a 0.5 M trehalose aqueous mixture with lysozyme using a different force-field, at ambient conditions and on a shorter time scale than ours. Together with the formation of the cage of trehalose molecules, we note that the presence of trehalose introduces a glass-like behaviour into the water dynamics. This would seem to indicate that the water entrapment and vitrification scenarios are not mutually exclusive. Note that some trehalose molecules move very close to the lysozyme, with a possible substitution of water in some hydration sites around the protein as hypothesised by the water replacement scenario. To determine whether the water replacement or broken glass hypotheses are relevant here, we would need to analyse trehalose-lysozyme interactions in detail52. This would be an interesting focus for future work. In order to determine whether different scenarios take place at different concentrations of trehalose, another possible future project would be to study to what extent our results are trehalose-concentration dependent.

It will also be interesting to compare the mechanism of cryopreservation of trehalose to that of other antifreezing molecules. Many living organisms, particularly those living at high latitudes (e.g. the Arctic char fish), are able to produce antifreeze proteins which inhibit the growth of ice formations and lower the freezing temperature of biological fluids53. For example the spruce budworm protein allows this insect to resist at temperatures down to −30°C54. Recently a non-protein antifreeze compund has been also discovered in the form of a sugar linked to a fatty acid component55. This is for example exploited by the alaskan beetle, able to tolerate temperatures down to −60°C.

In summary, using MD simulations, we study the dynamic and structural features of a aqueous mixture of lysozyme and trehalose with a trehalose concentration φ = 40 wt%. We carry out our investigation at atmospheric pressure and at three temperatures, T = 300 K, T = 280 K, and T = 260 K. We investigate the dynamics of water by studying the SISF Fs(qmax, t), first looking at the whole system and then progressively excluding hydration layers close to trehalose molecules and the lysozyme. We also investigate the relaxation behaviour of the SISF calculated within the hydration shells of the sugar and of the protein. Finally we examine the structural properties by studying the distribution of water and trehalose molecules around the COM of the lysozyme. The results point to a water entrapment scenario in which very slow water is trapped between the protein and a layer of trehalose molecules. This water keeps the protein hydrated and inhibits crystallisation. We also observe an overall slowing down of the water dynamics, which also inhibits crystallisation.

Methods

We perform MD all-atom simulations on the hen-egg lysozyme protein immersed in a mixture of water and α, α-trehalose. The system contains one lysozyme protein, 491 trehalose molecules and 13982 water molecules. The charges on the lysozyme residues are neutralised adding 8 Cl− counterions. The ratio of trehalose to water molecules 1 : 28.5 corresponds to a weight percentage φ = 40 wt% (the protein and ions are not considered), with the trehalose molarity being approximately 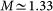Inline graphic mol/l.

The geometrical structure of the lysozyme is obtained from crystallographic experimental data56 (Protein Data Bank entry 193L). We take the bonded and non-bonded interactions parameters for the lysozyme and for trehalose from the CHARMM force-field for proteins57,58 and for sugars59,60, respectively. The water solvent is modelled using the SPC/E potential61.

We obtain the initial configuration of the system by placing the lysozyme at the centre of the cubic simulation box and distributing the other molecules at random positions. After an energy minimisation run, we equilibrate the system for 4 ns with the positions of the protein atoms restrained, after which the starting configuration is produced. We study the system at three temperatures: T = 300 K, T = 280 K, and T = 260 K. At all temperatures we equilibrate the system for 10 ns before executing the production run for another 10 ns (20 ns for the structure). We analyse the dynamics in the hydration shells using further 1 ns production runs with a high frequency of coordinates storage (every 0.1 ps).

The temperature is progressively lowered starting from the final configurations of the higher temperature runs. The pressure is kept fixed at 1 atm. We control temperature and pressure using weak coupling algorithms62. At all temperatures the average density of the system is 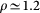Inline graphic g/cm3.

The equations of motion are integrated using the Verlet leap-frog algorithm and a time step of 1 fs. Periodic boundary conditions are applied. The cut-off radius for non-bonded Lennard-Jones short ranged interactions is set at 10 Å, and we use the particle-mesh Ewald (PME) method to deal with the electrostatics. The package GROMACS 4.5.363 is used to carry out the simulations.

For the sake of comparison, we also perform simulations at all temperatures on a “trehalose-free” system composed of the protein lysozyme immersed in 13982 SPC/E water molecules and 8 Cl− counterions, with simulation conditions identical to those of the complete system. In the “trehalose-free” system, the average density is 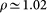Inline graphic g/cm3. We also conduct simulations on bulk water on a sample of 500 SPC/E water molecules, with simulation conditions identical to the complete system, where applicable.

We study the dynamics of water by calculating from the trajectories of our simulations the SISF of water oxygen atoms, FS(q, t). The SISF is defined by

graphic file with name srep01218-m3.jpg

where N denotes the number of atoms, q the transfer momentum, and ri(t) the position of atom i at time t.

The brackets Inline graphic indicate the average overall time origins. The correlation function F is calculated for |q| = qmax = 2.25 Å−1 at the peak of the oxygen-oxygen structure factor.

Author Contributions

All authors contributed equally to this work.

Supplementary Material

Supplementary Information

Supplementary Information

srep01218-s1.pdf (214.4KB, pdf)

Acknowledgments

DC, EGS, and HES thank the NSF chemistry Division for support (Grants CHE-1213217, CHE-0911389, and CHE-0908218). PG gratefully acknowledges the computational support reveived by the INFN RM3-GRID at Roma Tre University.

References

  1. Franks F. (Ed.), Biophysics and Biochemistry at Low Temperatures (Cambridge University Press. Cambridge, 1985). [Google Scholar]
  2. Arora N., Singh K., Garg T. & Bilandi A. A review on the cryopreservation technology and cryoprotectant. J. Pharm. Res. 5, 2087–2090 (2012). [Google Scholar]
  3. Jain N. K. & Roy I. Effect of trehalose on protein structure. Prot. Sci. 18, 24–36 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Donnez J. et al. Livebirth after orthotopic transplantation of cryopreserved ovarian tissue. Lancet 364, 1405–1410 (2004). [DOI] [PubMed] [Google Scholar]
  5. Donnez J. et al. Children born after autotransplantation of cryopreserved ovarian tissue. A review of 13 live births. Ann. Med. 43, 437–450 (2011). [DOI] [PubMed] [Google Scholar]
  6. Crowe J. H., Crowe L. M. & Jackson S. A. Preservation of structural and functional activity in lyophilized sarcoplasmic reticulum. Arch. Biochem. Biophys. 220, 477–484 (1983). [DOI] [PubMed] [Google Scholar]
  7. Lee S. L., Hafeman A. E., Debenedetti P. G., Pethica B. A. & Moore D. J. Solid-state stabilization of α-chymotrypsion and catalase with carbohydrates. Ind. Eng. Chem. Res. 45, 5134–5147 (2006). [Google Scholar]
  8. Lins R. D., Pereira C. S. & Hünenberger P. H. Trehalose-protein interaction in aqueous solution. PROTEINS: Structure, Function and Bioinformatics 55, 177–186 (2004). [DOI] [PubMed] [Google Scholar]
  9. Cordone L. et al. Internal dynamics and protein–matrix coupling in trehalose-coated proteins. BBA-Proteins and Proteomics 1749, 252–281 (2005). [DOI] [PubMed] [Google Scholar]
  10. Magazù S., Migliardo F. & Ramirez-Cuesta A. J. Inelastic neutron scattering study on bioprotectant systems. J. R. Soc. Interface 2, 527–532 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Crowe J. H. et al. The trehalose myth revisited: Introduction to a symposium on stabilization of cells in the dry state. Cryobiology 43, 89–105 (2001). [DOI] [PubMed] [Google Scholar]
  12. Robinson C. H. Cold adaptation in arctic and antarctic fungi. New Phytol. 151, 341–353 (2011). [Google Scholar]
  13. Wang G. M. & Haymet A. D. J. Trehalose and other sugar solutions at low temperature: Modulated differential scanning calorimetry (MDSC). J. Phys. Chem. B 102, 5341–5347 (1998). [Google Scholar]
  14. Lee S. L., Debenedetti P. G. & Errington J. R. A computational study of hydration, solution structure, and dynamics in dilute carbohydrate solutions. J. Chem. Phys. 122, 204511 (2005). [DOI] [PubMed] [Google Scholar]
  15. Lerbret A., Bordat P., Affouard F., Descamps M. & Migliardo F. How homogeneous are the trehalose, maltose, and sucrose water solutions? An insight from molecular dynamics simulations. J. Phys. Chem. B 109, 11046–11057 (2005). [DOI] [PubMed] [Google Scholar]
  16. Branca C., Magazù S., Maisano G. & Migliard P. Anomalous cryoprotective effectiveness of trehalose: Raman scattering evidences. J. Chem. Phys. 111, 281–287 (1999). [Google Scholar]
  17. Malsam J. & Aksan A. Hydrogen bonding and kinetic/thermodynamic transitions of aqueous trehalose solutions at cryogenic temperatures. J. Phys. Chem. B 113, 6792–6799 (2009). [DOI] [PubMed] [Google Scholar]
  18. Magno A. & Gallo P. Understanding the mechanism of bioprotection: A comparative study of aqueous solutions of trehalose and maltose upon supercooling. J. Phys. Chem. Lett. 2, 977–982 (2011). [Google Scholar]
  19. Bordat P., Lerbret A., Demaret J.-P., Affouard F. & Descamps M. Comparative study of trehalose, sucrose and maltose in water solutions by molecular modelling. Europhys. Lett. 65, 41–47 (2004). [Google Scholar]
  20. Paolantoni M. et al. Light scattering spectra of water in trehalose aqueous solutions: Evidence for two different solvent relaxation processes. J. Phys. Chem. B 113, 7874–7878 (2009). [DOI] [PubMed] [Google Scholar]
  21. Lerbret A. et al. Slowing down of water dynamics in disaccharide aqueous solutions. J. Non-Cryst. Solids 357, 695–699 (2011). [Google Scholar]
  22. Gallina M. E. et al. Rotational dynamics of trehalose in aqueous solutions studied by depolarized light scattering. J. Chem. Phys. 132, 214508 (2010). [DOI] [PubMed] [Google Scholar]
  23. Lupi L., Comez L., Paolantoni M., Fioretto D. & Ladanyi B. M. Dynamics of biological water: Insights from molecular modeling of light scattering in aqueous trehalose solutions. J. Phys. Chem. B 116, 7499–7508 (2012). [DOI] [PubMed] [Google Scholar]
  24. Roberts C. J. & Franks F. Crystalline and amorphous phases in the binary system water-β-β-trehalose. J. Chem. Soc., Faraday Trans. 92, 1337–1343 (1996). [Google Scholar]
  25. Pagnotta S. E., Alegría A. & Colmenero J. Dynamical behaviour of highly concentrated trehalose water solutions: a dielectric spectroscopy study. Phys. Chem. Chem. Phys. 14, 2991–2996 (2012). [DOI] [PubMed] [Google Scholar]
  26. Pagnotta S. E., McLain S. E., Soper A. K., Ricci M. A. & Bruni F. Water and trehalose: How much do they interact with each other? J. Phys. Chem. B 114, 4904–4908 (2010). [DOI] [PubMed] [Google Scholar]
  27. Ball P. Water as an active constituent in cell biology. Chem. Rev. 108, 74–108 (2008). [DOI] [PubMed] [Google Scholar]
  28. Teeter M. M. Water-protein interactions: Theory and experiment. Annu. Rev. Biophys. Biophys. Chem. 20, 577–600 (1991). [DOI] [PubMed] [Google Scholar]
  29. Gregory R. B. (Ed.) Protein-Solvent Interactions (Marcel Dekker Inc. New York, 1995). [Google Scholar]
  30. Bizzarri A. R. & Cannistraro S. Molecular dynamics of water at the protein-solvent interface. J. Phys. Chem. B 106, 6617–6633 (2002). [Google Scholar]
  31. Crowe J. H., Crowe L. M. & Chapman D. Preservation of membranes in anhydrobiotic organisms: The role of trehalose. Science 223, 701–703 (1984). [DOI] [PubMed] [Google Scholar]
  32. Carpenter J. F. & Crowe J. H. An infrared spectroscopic study of the interactions of carbohydrates with dried proteins. Biochemistry 28, 3916–3922 (1989). [DOI] [PubMed] [Google Scholar]
  33. Green J. L. & Angell C. A. Phase relations and vitrification in saccharide-water solutions and the trehalose anomaly. J. Phys. Chem. 93, 2880–2882 (1989). [Google Scholar]
  34. Belton P. S. & Gil A. M. IR and Raman spectroscopic studies of the interaction of trehalose with hen egg white lysozyme. Biopolymers 34, 957–961 (1994). [DOI] [PubMed] [Google Scholar]
  35. Fedorov M. V., Goodman J. M., Nerukh D. & Schumm S. Self-assembly of trehalose molecules on a lysozyme surface: the broken glass hypothesis. Phys. Chem. Chem. Phys. 13, 2294–2299 (2011). [DOI] [PubMed] [Google Scholar]
  36. Sola-Penna M. & Meyer-Fernandes J. R. Stabilization against thermal inactivation promoted by sugars on enzyme sturcture and function: Why is trehalose more effective than other sugars? Arch. Biochem. Biophys. 360, 10–14 (1998). [DOI] [PubMed] [Google Scholar]
  37. Lerbret et al. How do trehalose, maltose, and sucrose influence some structural and dynamical properties of lysozyme? Insight from molecular dynamics simulations. J. Phys. Chem. B 111, 9410–9420 (2007). [DOI] [PubMed] [Google Scholar]
  38. Lerbret et al. How strongly does trehalose interact with lysozyme in the solid state? Insights from molecular dynamics simulation and inelastic neutron scattering. J. Phys. Chem. B 116, 11103–11116 (2012). [DOI] [PubMed] [Google Scholar]
  39. Magazù S., Migliardo F., Benedetto A., Mondelli C. & Gonzalez M. A. Thermal behaviour of hydrated lysozyme in the presence of sucrose and trehalose by EINS. J. Non-Cryst. Solids 357, 664–670 (2011). [Google Scholar]
  40. Bellavia G., Giuffrida S., Cottone G., Cupane A., & Cordone L. Protein thermal denaturation and matrix glass transition in different protein–trehalose–water systems. J. Phys. Chem. B 115, 6340–6346 (2011). [DOI] [PubMed] [Google Scholar]
  41. Gallo P., Sciortino F., Tartaglia P. & Chen S.-H. Slow dynamics of water molecules in supercooled states. Phys. Rev. Lett. 76, 2730–2733 (1996). [DOI] [PubMed] [Google Scholar]
  42. Sciortino F., Gallo P., Tartaglia P. & Chen S.-H. Supercooled water and the kinetic glass transtion. Phys. Rev. E 54, 6331–6343 (1996). [DOI] [PubMed] [Google Scholar]
  43. Götze W. Complex Dynamics of Glass-Forming Liquids: A Mode Coupling Theory (Oxford University Press. New York, 2009). [Google Scholar]
  44. Gallo P., Rovere M. & Spohr E. Supercooled confined water and the mode coupling crossover temperature. Phys. Rev. Lett. 85, 4317–4320 (2000). [DOI] [PubMed] [Google Scholar]
  45. Gallo P., Rovere M. & Spohr E. Glass transition and layering effects in confined water. A computer simulation study. J. Chem. Phys. 113, 11324–11335 (2000). [Google Scholar]
  46. Gallo P., Rovere M. & Chen S.-H. Dynamic crossover in supercooled confined water: Understanding bulk properties through confinement. J. Phys. Chem. Lett. 1, 729–733 (2010). [Google Scholar]
  47. Dirama T. E., Carri G. A. & Sokolov A. P. Role of hydrogen bonds in the fast dynamics of binary glasses of trehalose and glycerol: A molecular dynamics simulation study. J. Chem. Phys. 122, 114505 (2005). [DOI] [PubMed] [Google Scholar]
  48. Rocchi C., Bizzarri A. R. & Cannistraro S. Water residence times around copper plastocyanin: a molecular dynamics simulation approach. Chem. Phys. 241, 261–276 (1997). [Google Scholar]
  49. Rocchi C., Bizzarri A. R. & Cannistraro S. Water dynamical anomalies evidenced by molecular-dynamics simulations at the solvent-protein interface. Phys. Rev. E 57, 3315–3325 (1998). [Google Scholar]
  50. Perticaroli et al. Broadband depolarized light scattering study of diluted protein aqueous solutions. J. Phys. Chem. B 114, 8262–8269 (2010). [DOI] [PubMed] [Google Scholar]
  51. Sanders L. K. et al. Structure and stability of self-assembled actin-lysozyme complexes in salty water. Phys. Rev. Lett. 95, 108302 (2005). [DOI] [PubMed] [Google Scholar]
  52. Dirama T. E., Curtis J. E., Carry G. A. & Sokolov A. P. Coupling between lysozyme and trehalose dynamics: Microscopic insights from molecular-dynamics simulations. J. Chem. Phys. 124, 034901 (2006). [DOI] [PubMed] [Google Scholar]
  53. Fletcher G. L. Hew C. L. & Davies P. L. Antifreeze Proteins of Teleost Fishes. Annu. Rev. Physiol. 63, 359–390 (2001). [DOI] [PubMed] [Google Scholar]
  54. Graether S. P. et al. β-helix struture and ice binding properties of a hyperactive antifreeze protein from an insect. Nature 406, 325–328 (2000) [DOI] [PubMed] [Google Scholar]
  55. Walters Jr K. R., Serianni A. S., Sformo T., Barnes B. M. & Duman J. G. A nonprotein thermal hysteresis–producing xylomannan antifreeze in the freeze-tolerant Alaskan-tolerant Alaskan-beetle Upis ceramboides. Proc. Natl. Acad. Sci. USA 106, 20210–20215 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Vaney M. C., Maignan S., Riès-Kaut M. & Ducriux A. High-resolution structure (1.33 Å) of a HEW lysozyme tetragonal crystal grown in the APCF apparatus. Data and structural comparison with a crystal grown under microgravity from SpaceHab-01 mission. Acta Crystallogr. Sect. D 52, 505–517 (1996). [DOI] [PubMed] [Google Scholar]
  57. MacKerell Jr A. D., Feig M. & Brooks C. L. III. Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 25, 1400–1415 (2004). [DOI] [PubMed] [Google Scholar]
  58. MacKerell Jr A. D. et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 102, 3586–3616 (1998). [DOI] [PubMed] [Google Scholar]
  59. Guvench O. et al. Additive empirical force field for hexopyranose monosaccharides. J. Comput. Chem. 29, 2543–2564 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Guvench O., Hatcher E., Venable R. M., Pastor R. W. & MacKerell Jr A. D. CHARMM additive all-atom force field for glycosidic linkages between hexopyranoses. J. Chem. Theory Comput. 5, 2553–2370 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Berendsen H. J. C., Grigera J. R. & Straatsma T. P. The missing term in effective pair potentials. J. Phys. Chem. 91. 6269–6271 (1987). [Google Scholar]
  62. Berendsen H. J. C., Postma J. P. M., van Gunsteren W. F., DiNola A. & Haak J. R., Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81, 3684–3690 (1984). [Google Scholar]
  63. Hess B. Kutzner C., van der Spoel D. & Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comp. 4, 435–447 (2008). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep01218-s1.pdf (214.4KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES