Parallel Mapping Approaches for GNUMAP

Abstract

Mapping short next-generation reads to reference genomes is an important element in SNP calling and expression studies. A major limitation to large-scale whole-genome mapping is the large memory requirements for the algorithm and the long run-time necessary for accurate studies. Several parallel implementations have been performed to distribute memory on different processors and to equally share the processing requirements. These approaches are compared with respect to their memory footprint, load balancing, and accuracy. When using MPI with multi-threading, linear speedup can be achieved for up to 256 processors.

1 Introduction

Over the past 30 years, Sanger-type sequencing (Sanger et al., 1977) has been the standard technique for DNA sequencing. This approach has enabled, among other things, the sequencing of the first complete human genome sequence (Consortium, 2004). However, recent developments in sequencing technologies have led to a second generation of sequencing approaches, from Illumina/Solexa, ABI/SOLiD, 454/Roche, Helicos, which currently produce gigabases sequence information during each instrument run.

Next generation sequencing technologies promise to revolutionize the field of biomedical research by producing large volumes of sequence data for a reasonable price. However, the size of the datasets generated are much larger and the diverse nature of the dataset produced novel statistical and computational challenges that must be overcome. One very important problem facing researchers today is the identification and characterization of single nucleotide polymorphisms (SNPs). Researchers are often interested in identifying SNPs that vary between one individual a reference genome, or in comparing the sequence composition of two individuals, strains or species at homologous or orthologous regions. Researchers are most often interested in associating these SNPs with disease or important phenotypes of interest, so the accurate identification of these SNPs is extremely important.

When identifying SNPs, short reads from 35-100 base pairs in length must be mapped to their best position in the human genome. See Figure 1 for an example mapping. A rigorous probabilistic approach to mapping repeat regions and reads with lower quality scores can result in a significantly larger number of mapped reads. This can often lead to the identification of regions of interest on the genome that otherwise would have been overlooked —for example, mapping to the large number of repetitive genomic elements in mammalian genomes. This approach requires the algorithm to have the entire genome in memory so that a read can be proportionally mapped to all matching sites. This approach requires more memory and processing time but results in a more accurate mapping (Clement et al., 2010). The following section presents a detailed overview of the GNUMAP algorithm so that later descriptions of the parallelization will make sense.

Figure 1.

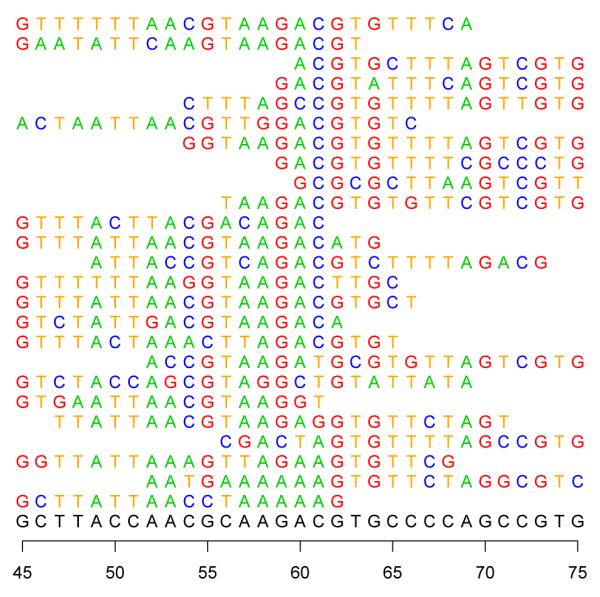
A cartoon representation of the sequence mapping process. Each of these 25 sequences were mapped to the reference genome, shown on the bottom. Notice the SNP at position 56, where reads have a “T” instead of a “C”

2 Algorithmic details

Many mapping algorithms discard reads from repeat regions and do not utilize quality scores once the base has been “called.” GNUMAP provides a probabilistic approach that utilizes this additional information to provide more accurate results from fewer costly sequencing runs. Accurately mapping reads to repetitive genomic elements is essential if next-generation sequencing is to be used to draw valid biological conclusions. For example, a ChIP-seq experiment attempts to accurately identify small DNA regions interacting with a protein of interest. Binding motifs often appear in or near the repeat regions van Helden (2004); Park et al. (2002) that are ignored by some mapping algorithms. Other applications such as transcription mapping, alternative splicing analysis, and miRNA identification may also suffer from inaccuracies if repeat regions are ignored.

Several programs (RMAP (Smith et al., 2008), SeqMap (Jiang and Wong, 2008), and ELAND) have attempted to significantly speed up this mapping process through creating a hash map to efficiently map reads to the genome. Reads are broken into short, 9–15 base pair segments and assigned a numerical value in the hash map according to their sequence. The genome is then scanned and the hashing function is used to find corresponding locations for the genomic sequences in the read hash table. The reads at these locations are then aligned with the genome until either a match is found or the alignment is deemed too insignificant to continue.

The GNUMAP algorithm effectively incorporates the base uncertainty of the reads into mapping analysis using a Probabilistic Needleman-Wunsch algorithm. The Probabilistic Needleman-Wunsch was developed to improve upon the common dynamic programming algorithm used for sequence alignment to accurately use reads with lower confidence values.

Care must be taken to develop an algorithm that can accurately map millions of reads to the genome in a reasonable amount of time. In the GNUMAP algorithm, the genome is first hashed and then stored in a lookup table rather than hashing the reads. This allows reads to be accounted for in all of the duplicate genome sites. Next, the reads are efficiently stored as a position-weight matrix so that quality scores can be used when aligning the read with genomic data. A Needleman-Wunsch alignment algorithm is modified to use these matrices to score and probabilistically align a read with the reference genome. Figure 2 is a flowchart which shows the major steps of the algorithm.

Figure 2.

A flow-chart of the GNUMAP algorithm. First, the algorithm will incrementally find a k-mer piece in the consensus Solexa read. This k-mer is used as an index into the hash table, producing a list of positions in the genome with the exact k-mer sequence. These locations are expanded to align the same l nucleotides from the read to the genomic location. If the alignment score passes the user-defined threshold, the location is considered a hit, and recorded on the genome for future output.

Step 1: Hashing and Storing the Genome

Hashing a large portion of the data allows for quick data retrieval while still maintaining a reasonable amount of memory use. GNUMAP creates a hash table from the genome instead of the reads, allowing for the computation of a probabilistic scoring scheme.

The entire genome is hashed based upon either a user-supplied hash size or the default hash size of nine. A larger hash size will tolerate fewer mismatches. For example, in a 30bp read, a hash size of 9bp will guarantee that the read is matched to every possible location while still allowing for three mismatches. Larger hashes will require more memory, but will also reduce the search space. The amount of memory, B, required based on the number of bases in the genome, s, and the mer-size of the hash, k, can be computed as follows:

$$B=4\ast (4^k+s).$$ (1)

For example, for a genome (s) of 200,000bp and a mer-size (k) of 9, the total memory used (B) will be 4 * (4⁹ + 200,000) ≈ 2Mb of RAM.

Step 2: Processing the Reads

One of the novel approaches implemented by GNUMAP lies in the data structure used for storing the reads. Instead of storing the reads as simple sequences, or even sequences with an attached probability as in the FASTQ format, each sequence is stored as a position-weight matrix (PWM) (see Table 1 for an example).

Table 1.

DP Matrix for Probabilistic Needleman-Wunsch.

j	0	1	2	3	4	5
PWM	A	0.059	0.000	0.172	0.271	0.300
	C	0.108	0.320	0.136	0.209	0.330
	G	0.305	0.317	0.317	0.164	0.045
	T	0.526	0.578	0.375	0.356	0.325
NW		T	T	T	T	C
	0	−2	−4	−6	−8	−10
T	−2	0.052	−1.948	−3.948	−5.948	−7.984
T	−4	−1.844	0.208	−1.792	−3.792	−5.792
C	−6	−3.844	−1.792	−0.520	−2.448	−4.448
A	−8	−5.844	−3.792	−2.374	−0.978	−2.978
C	−10	−7.984	−5.792	−4.131	−2.774	−1.318

Aligning the genomic sequence TTCAC and read TTTTC, with the optimal alignment shown in bold. Also notice the PWM for the sequence, with several fairly ambiguous positions (especially the final position, probably representing a C, even though the probabilities for the C and T are nearly equal).

Raw data from the Solexa/Illumina platform are obtained as either an intensity file or a probability file. From either of these files, it is possible to compute a likelihood score for any nucleotide of any position on any given read. There will often be a lack of distinction between the most probable and another base, such as the ambiguity between G and T seen in position 3 of the PWM in Table 1. Since each read is stored in memory as a position-weight matrix, the information included in each base call allows for the correct mapping of a given sequence. Converting these bases to a single probability score will result in the loss of information.

Step 3: Score Individual Matches

In order to match the reads to the reference genome, the reads are first subjected to a quality filter, removing reads with too many unknown bases. In order to pass GNUMAP’s quality filter, a sequence (stored as a position-weight matrix) must be able to obtain a positive score when aligned with its own consensus sequence (the sequence created from using only the most probable bases). Using this method, very few reads are discarded by the quality filter (usually only removing reads identified by the Solexa pipeline as having an intensity of zero at each base).

A sliding window of size k is used to create a hash value which can be used to find matching positions in the reference genome. The matching genomic sequence is then aligned to the read using the probabilistic Needleman-Wunsch algorithm (see Table 1).

The probabilistic Needleman-Wunsch score (PNWScore) for read r and genomic sequence S at position i, j in the dynamic programming matrix NW can be calculated as:

$${\mathit{NW}}_{i,j}=\text{max}\{\begin{array}{c}{\mathit{NW}}_{i-1,j-1}+{\Sigma }_{k\in A,C,G,T}{\mathit{PWM}}_{k,j}\ast {\text{cost}}_{k,S_i}\hfill \\ {\mathit{NW}}_{i-1,j}+\text{gapcost}\hfill \\ {\mathit{NW}}_{i,j-1}+\text{gapcost}\hfill \end{array}\phantom{\}}$$ (2)

given that cost_k,j is the cost of aligning the character at position r_j with the character k. For example, using the PWM in Table 1, the calculation of the score for position 3,3 in the dynamic programming matrix would be:

$$\text{max}\{\begin{array}{c}0.208+0.172\ast -1+0.136\ast 1+0.317\ast -1+0.375\ast -1\hfill \\ -1.792+-2\hfill \\ -1.792+-2\hfill \end{array}\phantom{\}}$$ (3)

(For this example, a match yields a cost of 1, a mismatch yields a cost of −1, and the cost for a gap is -2. This results in a cost of −0.520 which is stored at position 3,3 in the dynamic programming matrix NW .

Step 4: Processing Scores

Once the read has been scored against all plausible matches in the genome, a proportional share of this read will be added to all the matching genomic locations . In order to compute the hit score at a position in the reference genome, a posterior probability for each read is computed. For a read r, the algorithm first finds the n most plausible match locations on the genome, M₁…M_n. These matches are scored using the probabilistic Needleman-Wunch algorithm, to obtain the scores Q₁…Q_n. The value added to the genome G for each read, r, obtained from each significant match location M_j, signified by G_Mj, will then be

$$G_{M_j}=\frac{Q_{M_j}}{n_{M_j}{Q}_{M_j}+{\Sigma }_{k\ne j}^n{n}_{M_k}{Q}_{M_k}},$$ (4)

where n_Mk is the number of times the sequence located at position M_k appears in the genome.

When using this scoring method, the total score for each sequence at a particular site in the genome is weighted by its number of occurrences in the genome. If a given sequence occurs frequently, the value added to a particular matching site in the final output is down-weighted, removing the bias that would occur if the match was added to all repetitive regions in the genome. If, however, there are the same number of duplicate reads as the number of times the sequence is duplicated in the genome then a whole read will be added to each of the duplicate locations in the final output.

This scoring technique requires the hashing and storing of the genome instead of the set of reads. Because the score for a given read is not only calculated from its alignment score but also by the number of occurrences of similar regions in the genome, the genome must be scanned for each read to fairly allocate the read across all matching sites.

Step 5: Create Output

After all the reads have been matched and scored on the genome, two output files are created. The first file is in SAM format and identifies the highest scoring match for each read. The second file contains the genome in .SGR or .SGREX (SGR-EXtended) format providing a genome-wide base-pair resolution overview of the mapping results, which can be viewed in the UCSC Genome Browser or Affymetrix’s Integrated Genome Browser.

3 Methods

In this section, two terms are used to identify different architectures. A thread refers to a lightweight process spawned within an instantiation of GNUMAP. A node executes a stand-alone instance of GNUMAP that has no shared memory with other instances.

3.1 Multi-Threading on a Single Machine

All threads on a node access structures such as the seed index table and Genome, so a single copy of these data structures is kept in shared memory. When using multiple threads on a single node, GNUMAP employs a master-slave paradigm to efficiently handle a large number of reads. Each thread is assigned a constant number of reads from the sequence files. As a given thread finishes its current workload, it obtains additional reads from the sequence file until they have all been mapped. When matching genomic locations are found, the thread will access a shared Genome object to store this information, and save the read for later writing. Periodically, a master thread will write this information to a file in SAM format.

Each step requires a certain amount of data sharing.

1. In the first step, care must be taken to avoid race conditions in accessing read data. One thread reads the data from the file, and all other threads use a semaphore to gain access to this shared memory. This sequential component of the algorithm can limit the total speedup of the algorithm, but when each thread is assigned a large enough number of reads, this overhead is minimal.

2. In the second step of the computation, there is a race condition if two threads write to the same location in the Genome object at the same time. If each read is assumed to come from an equally-likely random location in the genome, in theory there would not need to be any control structures surrounding Genome writes. However, DNA from many next-generation sequencing experiments originate from only a few genomic locations, weakening this assumption. Moreover, as the genomic coverage in a specific location grows higher, there is a greater chance for multiple threads to be scoring reads at the same location. For these reasons, each write to the genome is surrounded by a locking mutex. Since the critical section for assigning a read score to the genome is small, threads do not spend a significant time waiting for Genome availability.

3. Two different output types are produced by GNUMAP: an SGR or SGREX (SGR-EXtended) file, providing a genome-wide base-pair resolution overview of the mapping results (such as SNP locations or regions with many matches), and a SAM file reporting matching locations for each read. The second step of this computation described above applies to creating the SGR file, and the third to the SAM file, in this manner. After positive matches are found, each thread stores information about this match to a global list. Periodically during the mapping process, a single thread will print this information to an output file. (This is also critical when using MPI to reduce the memory footprint, which will be explained in Section 3.3.) This provides another location that requires locking accesses, but once again, when handling large numbers of reads, the waiting time is negligible.

3.2 Employing MPI With Multi-Threading

When the entire Genome fits into the memory on a single node, a simplistic MPI approach can further take advantage of independence to significantly reduce the time of computation.¹

With multi-threading enabled on a single machine, it is relatively simple to use MPI to split the work even further. GNUMAP uses the open source OpenMPI library to perform many of the more complicated method calls, including starting individual processes and syncing information across nodes. In a similar manner to that taken by multi-threading on a single machine, the reads are split among nodes and mapped independently. In order to reduce the number of times synchronization must occur among nodes, each sequence file is split into equal portions, and the unique machine number assigned by OpenMPI is used to determine which section of the file should be mapped. In this manner, each node independently writes SAM records to a separate file, and no extra communication costs are needed until the end. At the end of the mapping process, each node performs a global sum on the Genome object, which is then printed out by a single node (along with any sort of additional analyses) to a single file.

3.3 Employing MPI to Reduce the Memory Footprint

The statistical rigor employed by GNUMAP limits the mechanisms that can be used to reduce the memory footprint. Each character in the genome can feasibly reduced to 4 bits (four different nucleotides plus an ambiguity character), decreasing the memory requirement by half, and smart memory allocation can reduce the size of the k-mer lookup table to a reasonable size (around 12GB). Other algorithms have created structures that significantly reduce this memory footprint; however, nothing can be done to compress the Genome object. To obtain full accuracy, the posterior likelihood score for reads are mapped to the genome is added to the corresponding location. This requires at least single floating point precision, which is 4 bytes that cannot be compressed. Two methods to avoid this are either increasing the number of positions stored at a given memory cell (“binning”), or post-processing the reads in such a way that only a portion of the genome is in memory at a time. Distributing memory across MPI nodes can also reduce the memory footprint.

• Binning Internally, GNUMAP creates five floating point arrays to represent the four nucleotides—A, C, G, and T—and one ambiguity character. Determining locations that are different from the reference genome requires knowing what characters existed in the sequence data set at that location. If these are binned, then a sequence of A’s, C’s, G’s, and T’s would appear all as one nucleotide. In addition, GNUMAP uses a pairwise-Hidden Markov Model (pair-HMM) to determine the probability of each nucleotide matching to a specific location and being represented by a distinct character. Binning locations from these scores would discard the information obtained from a pair-HMM, resulting in an inability to call SNPs.

• Post-Processing Post-processing the reads requires only a portion of the genome to be in memory at a time, but this also has issues. GNUMAP’s probabilistic algorithm assigns a score to all locations a given read could match. Repetitive genomic regions and reads with very similar alignment scores all need to be added to the genome, requiring many entries for a single read. Taking shortcuts to find an approximate answer would decrease the accuracy. Accuracy is one of the major motivating factors behind the creation of GNUMAP, so this option is also undesirable.

• Memory Distribution A third alternative, used by GNUMAP, is to spread the memory across multiple nodes. Using MPI to spread portions of the genome across different nodes solves the problem of high memory requirements, but incurs additional costs of communication. This occurs because nodes must communicate to find the total number of matching locations for a given read, a requirement for calculating the posterior alignment score of a given read.

GNUMAP uses the following large-memory algorithm for memory distribution (refer to Figure 3 for labels):

• Step 1 The MASTER_Node reads the genome and assigns each SLAVE_Node its portion of the Genome.

• Step 2 Each SLAVE_Node hashes and stores its portion of the Genome, allocating memory as if it were only mapping to this single piece of the Genome.

• Step 3 In a step-by-step fashion, each SLAVE_Node performs the mapping of k reads (a subset of all those in a given run).

  • Step 3.1 Each SLAVE_Node divides the k reads among its Threads, and performs the Multi-Threading on a Single Machine as described in Section 3.1. The numerator for the final score for a read is the alignment score at that location divided by the number of times it appeared in the genome. The denominator is computed by summing together the alignment scores across all the “good” matching locations. (See Clement et al. (2010) for a further description.) The denominator is saved in the Read Denominator array and the highest matching score in the Top Read Score array.
  • Step 3.2 Each SLAVE_Node performs an MPI_REDUCE_ALL with a SUM on the Read Denominator for k reads.
  • Step 3.3 Each SLAVE_Node performs an MPI_REDUCE_ALL with a MAX on the Top Read Score for k reads.
  • Step 3.4 Each SLAVE_Node uses the Read Denominator to obtain the posterior score, and writes the SAM output to a unique file for each read which is equal to the value in Top Read Score.

• Step 4 Each SLAVE_Node performs any needed genomic analysis (such as SNP identification), and prints the Genome to separate sgr or sgrex file, thus reducing the need for a semaphore.

Figure 3.

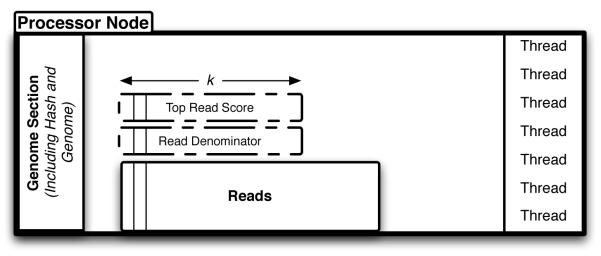
Pictoral representation of a single node of an MPI large-memory run. k reads are processed at a time, storing the needed information in the Read Denominator and Top Read Score arrays. Individual nodes will communicate information at synchronization points.

4 Results

In order to evaluate performance, a subset of a 32,000,000 read Illumina lane (short-read archive number NA20828, found at http://trace.ncbi.nlm.nih.gov/Traces/sra/sra.cgi?cmd=viewer&m=data&s=viewer&run=ERR005645) was mapped to the human genome. It is difficult to plot results for different parallelization approaches due to the different problem sizes that are needed to expose parallel artifacts. A comparison of these different problem sizes was performed by plotting a relative speedup for each algorithm. For the Multiple Processors algorithm, all threads run on a single 32-processor node. The Multiple Nodes and Large Memory experiments run on up to 32 nodes with 8 processors each for a total of 256 processors.

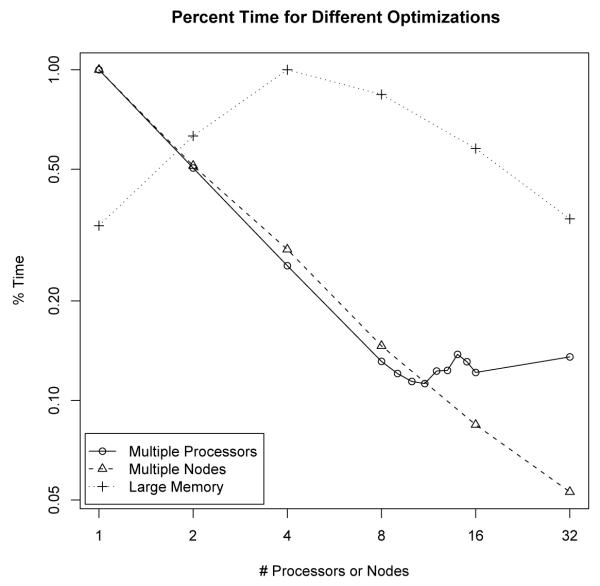
Figure 4 plots the relative percentage of time for different number of processors instead of the absolute time in order to compare the efficiency of all approaches fairly. Using Multiple Processors on a single node results in linear speedup as long as 8 or fewer processors are used. Beyond this, the synchronization costs overwhelm the parallel benefits. When spreading the memory across Multiple Nodes, nearly linear speedup can be achieved even with 32 nodes (256 processors). The Large Memory approach appears to take longer as additional processors are used. This is due to an increased number of computations that are performed when the algorithm is parallelized. With more than 4 nodes, the number of computations is approximately constant and the algorithm achieves nearly linear speedup.

Figure 4.

Plots for the relative speedups for different optimizations. Note that each axis is logged, so a straight line would show optimal speedup. Splitting the reads across multiple nodes achieves linear speedup. Splitting the memory across multiple nodes can obtain nearly log-linear speedup. Because of the high cost of thread synchronization, linear speedup is not possible beyond 8 threads.

4.1 Multi-Threading on a Single Machine

To determine the cost of synchronizing multiple threads, we ran a test data set on a shared-memory machine with 32 processors². Figure 4 shows an almost-perfectly linear speedup until GNUMAP tries to use more than 8 threads, after which the completion time does not decrease significantly. In this particular example, a single compute node using 8 threads mapped 600k reads to human chromosome 1 in 564 seconds. The time for 10 threads was 478 seconds.

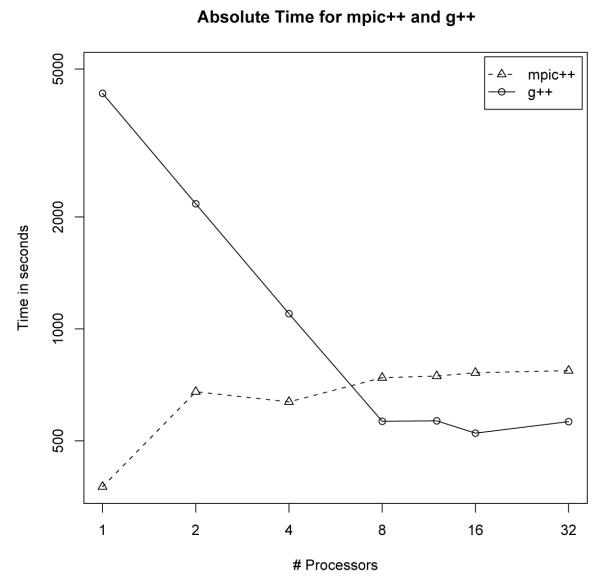
These results can only be obtained when using the GNU g++ compiler. When compiling with the mpic++ compiler, using multiple threads in fact takes longer than a single thread. This is likely due to MPI communication libraries that prevent multiple threads from executing simultaneously. In Figure 5, the mpic++ experiments were performed with a smaller problem size in order to diagnose the speedup limitation. This is why they appear to take a shorter amount of time.

Figure 5.

Comparison between mpic++ and g++. mpic++ does not allow more than one thread to be used, taking much longer if it does.

4.2 MPI With Multi-Threading

Because of the minimal number of synchronizations required when spreading the reads across multiple nodes, approximately linear speedup can be seen with even 32 nodes (see Figure 6). For each of these runs, 1.2M sequences were aligned to the entire human genome. This took just under an hour on only one node, and only 178 seconds on 32 nodes (256 processors)³. Clearly, when the memory and hardware are available, this is the preferred option.

Figure 6.

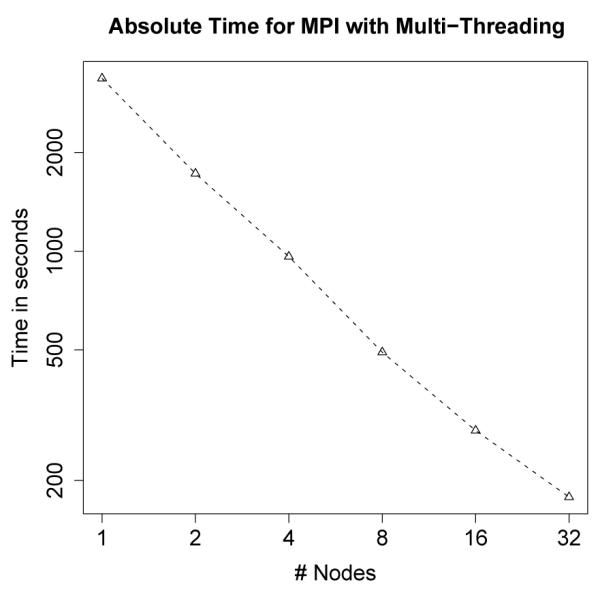
Absolute time for MPI with Multi-Threading. Linear speedup is achieved even with 32 nodes (256 processors).

4.2.1 Memory Requirements

With the default settings, GNUMAP requires 56 GB of RAM to map any number of sequences to the human genome. To perform SNP comparison, this increases to 100GB of RAM. Since many machines do not have this much memory, spreading the program across different nodes provides an obvious alternative.

4.3 MPI to Reduce the Memory Footprint

Some installations may not have enough memory for the entire genome to fit on a single node. Although the speedup shown in Figure 7 does not appear advantageous, it may be the only option for small-memory machines. Execution time increases between 1 and 4 nodes due to an increased number of computations. Internally, GNUMAP uses a hash map with shorter sequences as a key to find possible mapping locations. When a given hash key contains too many matches, this key is labelled as uninformative. (On the human genome, there are over one million occurrences of the character “a” repeated ten times.) Setting a limit for the size of a hash entry that is uninformative can greatly reduce the number of computations performed. When the genome is split into multiple pieces, the number of elements at each hash location is naturally reduced, thus limiting the number of uninformative hash entries. This increases the total number of computations performed since there are fewer eliminated entries. While it may take longer, the resulting computation is more accurate.

Figure 7.

Absolute time for MPI with Reduced Memory Footprint. After 4 nodes are used, approximately linear speedup occurs.

After 4 nodes are used, the number of uninformative hash entries stabilizes, and the speedup is approximately linear. This approach may be the only way for calling SNPs on small-memory nodes.

The biggest cost for this type of optimization is in the synchronization after each portion of reads. We looked at load balancing with fewer synchronizations. Even with a large grain size where millions of reads are processed before a synchronization event, there is always one machine with a larger proportion of difficult reads to map that becomes the bottleneck of the computation. Future work will try to identify a way to load balance more correctly to alleviate this problem.

5 Conclusions

Mapping short next-generation reads to reference genomes is an important element in SNP calling and expression studies. A major limitation to large-scale whole-genome mapping is the large memory requirements for the algorithm and the long run-time necessary for accurate studies. Several parallel implementations have been performed to distribute memory on different processors and to equally share the processing requirements. These approaches are compared with respect to their memory footprint, load balancing, and accuracy.

When using multiple threads (pthreads) on a shared memory machine, linear speedup can be achieved until more than 8 threads are used. After this time, the mutual exclusion costs overwhelm the benefits of more processors.

This approach can be combined with distributed-memory parallelization using MPI and pthreads. In this case, machines with a sufficient amount of memory can achieve linear speedup. When calling SNPs, 100GB of memory is required, with 56GB required for a normal mapping.

If large memory machines are not available, the genome can be divided among multiple processors to reduce the memory footprint. Although more computations are required for up to 32 processors (4 nodes), linear speedup can be achieved with greater accuracy for up to 256 processors (32 nodes).

This research has shown that the mapping problem can be effectively parallelized in several different environments without reducing accuracy. Future work will focus on reducing the memory requirements and load balancing.