On the role of lateral stabilization during early patterning in the pancreas

Abstract

The cell fate decision of multi-potent pancreatic progenitor cells between the exocrine and endocrine lineages is regulated by Notch signalling, mediated by cell–cell interactions. However, canonical models of Notch-mediated lateral inhibition cannot explain the scattered spatial distribution of endocrine cells and the cell-type ratio in the developing pancreas. Based on evidence from acinar-to-islet cell transdifferentiation in vitro, we propose that lateral stabilization, i.e. positive feedback between adjacent progenitor cells, acts in parallel with lateral inhibition to regulate pattern formation in the pancreas. A simple mathematical model of transcriptional regulation and cell–cell interaction reveals the existence of multi-stability of spatial patterns whose simultaneous occurrence causes scattering of endocrine cells in the presence of noise. The scattering pattern allows for control of the endocrine-to-exocrine cell-type ratio by modulation of lateral stabilization strength. These theoretical results suggest a previously unrecognized role for lateral stabilization in lineage specification, spatial patterning and cell-type ratio control in organ development.

1. Introduction

The pancreas is a complex organ consisting of two functionally distinct tissue compartments [1]. Exocrine acinar cells make up approximately 95–99% of cells in the pancreas, and produce digestive enzymes that are released into the intestine. Cells organized in the islets of Langerhans are endocrine and are vital in the regulation of glucose homeostasis throughout the body by releasing hormones, such as insulin and glucagon, into the blood. Both cell types are known to arise from a common pool of multi-potent pancreatic precursors [2–4]. However, despite the identification of key transcription factors and intercellular signalling pathways, the mechanisms underlying the cell fate decision between these lineages remain unclear. In particular, the low endocrine-to-exocrine cell ratio and the scattered spatial distribution of early endocrine cells are poorly understood. Elucidation of these mechanisms may have important consequences for the development of therapeutic cell reprogramming and cell-replacement therapies [5].

Over the last decade, great progress has been made in revealing the transcriptional regulation of murine pancreatic development, and the endocrine compartment in particular [6,7]. Several transcription factors that are crucial for the cell fate decision between the exocrine and endocrine lineages have been identified (see [6–8]). Transgenic studies have identified neurogenin-3 (Ngn3) as a pro-endocrine factor which is required to induce endocrine cell fates, since its overexpression results in massive conversion into endocrine cells at the expense of the exocrine compartment [9,10] and loss of Ngn3 causes depletion of endocrine cells [11]. Pancreas-specific transcription factor 1 subunit alpha (Ptf1a) has been shown to be crucial for exocrine specification, as mice deficient in this transcription factor form normal endocrine cells but lack an exocrine pancreas [12–14].

Endocrine cells appear as individual cells or in small clusters scattered over the central pancreatic epithelium [10,11,15,16] with a low ratio of endocrine to exocrine cells, up to 1 : 50 in the developing pancreas, depending on the specific developmental stage. Investigation of intercellular signalling during pancreatic development (reviewed in [7,17]) suggests that local cell–cell communication, rather than long-range morphogen gradients, is important in lineage specification. In particular, it has been convincingly demonstrated that Notch signalling regulates the cell fate decision between exocrine and endocrine lineages. A series of transgenic studies has shown that loss of genes in this pathway (Dll1, Rbp-jκ, Hes1) causes precocious endocrine differentiation and loss of exocrine cells, similar to Ngn3 misexpression [9,17–22]. This suggests that the exocrine–endocrine cell fate decision is controlled by contact-mediated lateral inhibition in which pro-endocrine cells inhibit endocrine specification of their neighbouring cells, forcing them into an exocrine fate [22].

Yet, the spatial distribution of endocrine cells within the early pancreatic epithelium is not well explained by models of lateral inhibition [17]. Lateral inhibition alone causes the formation of fine-grained regular patterns, as observed in neural tissue and bristle patterns [23–25], instead of the irregular scattered distribution of endocrine cells in the developing pancreas. Moreover, the predicted cell-type ratio of 1:3 or 1:6 for lateral inhibition [26] does not agree with the observed endocrine to exocrine ratio in the pancreas. These inconsistencies suggest that additional mechanisms are involved in the control of pancreatic cell fate.

An important clue can be found in studies of acinar-to-islet cell transdifferentiation in vitro, in which the endocrine-to-exocrine cell fate decision is recapitulated. In these experiments, adult acinar cells spontaneously de-differentiate to pancreatic progenitor-like cells upon dissociation of the tissue [27–30]. This suggests that maintenance of acinar cell fate crucially depends on a continuous signal provided by contacts between acinar cells [31]. Indeed, recent evidence has shown that the de-differentiation depends on the disruption of cadherin-mediated cell adhesion [32]. Similarly, inhibition of Mist1 is reported to cause de-differentiation as a result of disruption of gap junction intercellular communication [33]. Thus, cells of the exocrine pancreas appear to mutually stabilize their cell fate through physical contacts, in a mechanism that may be called lateral stabilization.

In this study, we propose that lateral stabilization provides positive feedback between pro-exocrine factors in adjacent progenitor cells and acts together with lateral inhibition in the regulation of lineage specification during early development of the pancreas. A simple mathematical model is constructed to capture the feedback mechanisms among pancreatic progenitor cells. Our analysis shows that the relative timing of the two feedback loops regulates the cell fate decision and tissue patterning in the central part of the developing pancreas. Specifically, our results show that the combination of lateral inhibition and lateral stabilization can explain the particular scattered spatial distribution of endocrine cells and provides a means to regulate endocrine and exocrine cell-type ratios in the pancreas.

2. Material and methods

Interactions between transcription factor genes control cell fates by constraining the possible patterns of gene expression. Similarly, interactions between cells control patterning of a tissue through cell–cell signalling. The dynamics of gene–gene and cell–cell interactions can be modelled and analysed in terms of differential equations. Whereas analysis of models of gene regulatory networks can reveal the existence of stable attractors that represent cellular phenotypes [34–36], models of intercellular signalling, mediated by diffusive or membrane-bound ligands, can reveal pattern formation abilities in developing tissues [26,37,38]. In this study, the coupling between both modules, gene–gene interactions and cell–cell interactions, is analysed mathematically to reveal the dynamics and attractors of gene expression and spatial patterning of endocrine cells in the pancreas.

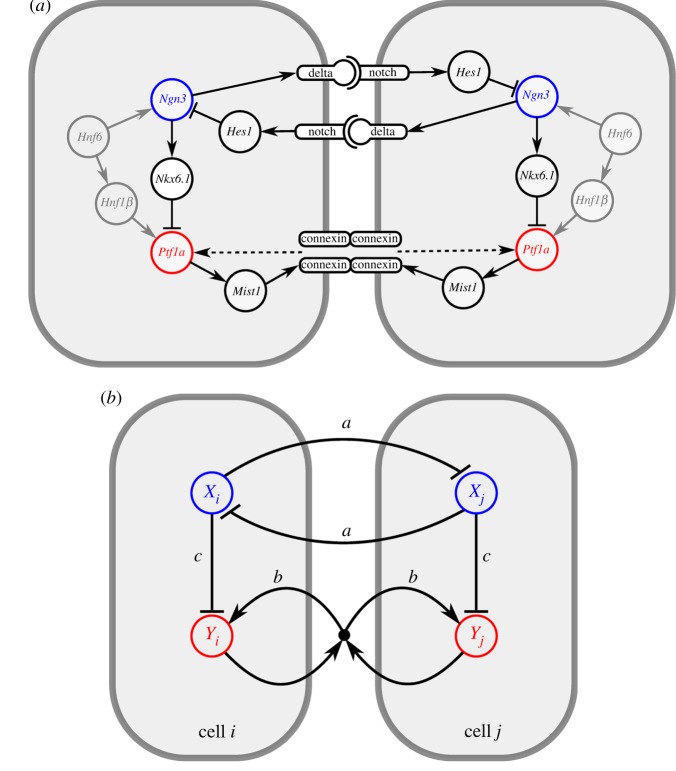
The state of a cell is specified by two variables, X and Y, that represent the expression levels of fate-determining transcription factors. X represents a pro-endocrine transcription factor that is involved in lateral inhibition. Among the various pro-endocrine factors that have been described (Nkx6.1, NeuroD, Ngn3) [6], only Ngn3 is known to be actively involved in Notch signalling. Ngn3 activates the expression of Delta-like1 (Dll1) [9] and is suppressed by Hes1 upon Notch receptor activation [18] (figure 1a). Therefore, we interpret X as the expression level of the transcription factor Ngn3 while Y represents a factor that is expressed in both progenitor and exocrine cells, but inhibited in cells that commit to the endocrine lineage. Therefore, Y is interpreted as the transcription factor Ptf1a because this is the only factor with that specific expression profile and is known to be necessary and sufficient to induce the exocrine cell fate [12,14].

Figure 1.

Interactions between transcription factors and signalling pathways. (a) Known regulatory interactions involved in the exocrine–endocrine cell fate decision in the pancreas, including contact-mediated signalling (see main text for details and references). Receptor–ligand binding in the Notch signalling pathway induces lateral inhibition. Formation of gap junctions represents one possible pathway for lateral stabilization (dashed arrow). (b) Interactions in the two-variable model in which cells i and j are coupled by lateral inhibition and lateral stabilization (see main text for details). Parameters a, b and c represent the interaction strengths. (Online version in colour.)

We assume a weak external activation, θ, for both X and Y. This is based on evidence that Ngn3 is activated by Hnf6 [39], and Ptf1a is activated by Hnf1β [40], which is itself regulated by Hfn6 [41]. For the sake of simplicity, the external activation is assumed to be constant during the developmental stage.

Cells in our model interact with adjacent cells through two cell–cell signalling mechanisms: lateral inhibition and lateral stabilization. The factor X in each cell mediates lateral inhibition of surrounding cells: the rate of production of X is downregulated by expression of this factor in neighbouring cells. This mechanistically captures the well-established pathway that expression of Ngn3 upregulates the Notch ligand Dll1 which, when bound to Notch receptors on adjacent cells, activates the expression of Hes1 which represses Ngn3 in these adjacent cells [9,18,20,42].

Factor Y is involved in lateral stabilization, which provides a positive feedback loop between Y-expressing neighbouring cells. The rate of production of Y is upregulated by simultaneous expression of Y in neighbouring cells. Although the molecular details of a lateral stabilization pathway are unclear, such conditional activation is in principle consistent with both cadherin/β-catenin signalling [32] and gap junctional communication via expression of Mist1 and connexin, which are downstream targets of Ptf1a [33]. In both cases, the expression of gene products in the form of homotypic transmembrane molecules is required in all participating cells to allow intercellular signalling. Mathematically, this is captured by a multiplication such that Y⁻ (non-expressing) cells neither contribute nor benefit from stabilization.

Despite many observations that endocrine markers (e.g. Isl1) and Ptf1a are mutually exclusive [43], the underlying regulatory mechanisms remain unclear. One proposal states that Nkx6.1, a pro-endocrine factor downstream of Ngn3 [44,45], antagonizes the expression of Ptf1a [46]. Independent of the precise molecular pathway, we can assume that pro-endocrine factors suppress the expression of Ptf1a, leading to the restriction of the latter factor to the exocrine compartment. Accordingly, X inhibits Y in a cell-autonomous fashion in our model.

At a later stage during development of the pancreas, Hnf6 and Ngn3 become downregulated and are not expressed in the adult pancreas. Because our primary interest lies in the lineage specification prior to this stage, we can neglect this downregulation. This considerably simplifies the model formulation and analysis, but implies that the common endocrine marker Ngn3 cannot be used to indicate commitment to the endocrine lineage. Instead, the absence of Ptf1a (i.e. Y) expression will be used to mark endocrine cells, as supported by single-cell transcript analysis [43].

In this fashion, the details of the molecular pathways (figure 1a) have been reduced to a core regulatory interaction network (figure 1b), which has been formalized in terms of stochastic ordinary differential equations using Hill kinetics as follows (table 1):

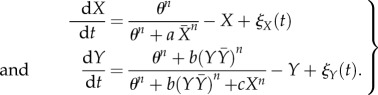2.1

Table 1. Overview of variables, parameters and observables of the mathematical model (equation (2.1)).

	symbol	description	value
variables	X	expression of pro-endocrine transcription factor Ngn3	0 (initial)
	Y	expression of transcription factor Ptf1a	0 (initial)
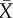		average Ngn3 expression in neighbouring cells	0 (initial)
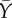		average Ptf1a expression in neighbouring cells	0 (initial)
parameters	a	strength of lateral inhibition	1
	b	strength of lateral stabilization	20
	c	strength of intracellular inhibition	1
	θ	external activation	0.1
	n	Hill coefficient	4
	ηx	amplitude of Gaussian white noise on X	10−4
	ηy	amplitude of Gaussian white noise on Y	0
observables	τx	time until symmetry break in X
	τy	time until super-induction of Y
	ε	ratio of endocrine cells

Both transcription factors X and Y are activated by θ, which is chosen to be small relative to the parameters of cell–cell interaction. The parameter a represents the strength of lateral inhibition by neighbouring cells, b denotes the strength of lateral stabilization and c models the strength of cell-autonomous inhibition of Y by X. To focus on the impact of lateral stabilization, the model is scaled such that external activation θ is weak compared with the interaction terms and the parameters a and c have been set to unity. In this way, the strength of lateral stabilization b can be treated as a control parameter. Both factors are subjected to non-regulated first-order degradation, such that expression levels are between 0 (not expressed) and 1 (fully expressed). The terms 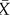and 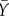denote the average expression of X and Y in neighbouring cells. The additive stochastic terms ξ(t) are random variables with a Gaussian white noise distribution N(0,η) with mean 0 and amplitude η. The Hill coefficient n is chosen to achieve nonlinear step-like behaviour (n = 4). Production of X is inhibited by the expression of X in neighbouring cells, 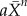, independent of its own activation. In contrast, cell-autonomous activity of Y is required for an increase in production of Y by the lateral stabilization term, 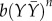. Thus, this cell–cell interaction acts to stabilize a pre-existing expression.

Pattern formation abilities are determined by the topology of the network, rather than the precise kinetic parameters [36, 47]. Thus, for the purpose of this study, the molecular details of the regulatory pathways can be lumped into activatory or inhibitory interactions without altering the qualitative behaviour of the system.

This qualitative treatment allows us to work with a small enough number of variables and parameters to gain insight into the spatio-temporal dynamics by mathematical analysis. Although the various patterning solutions reported below are independent of our particular choice of parameters (table 1), they do depend on the Hill coefficient n > 2 to induce the required bistability in X.

Concerning initial conditions, it is known that expression of Ngn3 and Ptf1a is initiated at around the same time in the developing pancreas. Both factors are, directly or indirectly, induced by the same upstream transcription factor Hnf6 and are both first detected around E9 in mice [13]. Therefore, we consider the simultaneous initiation of X and Y ((X,Y) = (0,0) at t = 0) by external activation at rate θ. We assume a symmetric activation of both factors (θ_X = θ_Y) for reasons of clarity, but unequal activation (θ_X ≠ θ_Y) results in the same qualitative behaviour. The numerical simulations presented below use this zero initial condition.

Morphogenetic events, such as proliferation, cell motility and branching, are excluded from the model. Lineage tracing experiments have shown that the majority of cells are committed to the exocrine or endocrine compartments around E10, before the onset of major morphogenetic events [2,48]. In the relevant developmental stage, the pancreatic epithelium can thus roughly be approximated by a fixed two-dimensional lattice of densely packed hexagonal cells.

Analysis and numerical simulation were performed using GRIND (phase plane analysis) [49], XPPAUT (bifurcation analysis) [50] and our modelling environment Morpheus (lattice simulations) [51]. Numerical integration was performed using the Runge–Kutta (RK4) method with time-step size dt = 0.02. A similar combination of numerical simulations with bifurcation analysis has previously been proved to facilitate the fundamental and mechanistic understanding of self-organizing behaviours from cellular decision-making to bursting oscillations [52–54]. The deterministic model of the cell couplet is available in SBML format in the electronic supplementary material and has been submitted to the biomodels database (http://www.ebi.ac.uk/biomodels; BioModels ID: MODEL1211010000). The lattice model is included as an example in the Morpheus software (http://imc.zih.tu-dresden.de/wiki/morpheus).

3. Results and discussion

To investigate the pattern formation properties, the model was computed on a lattice under varying conditions of cell–cell signalling. The results in figure 2 demonstrate that various spatial patterns can arise under different combinations of cell–cell interaction parameters.

Figure 2.

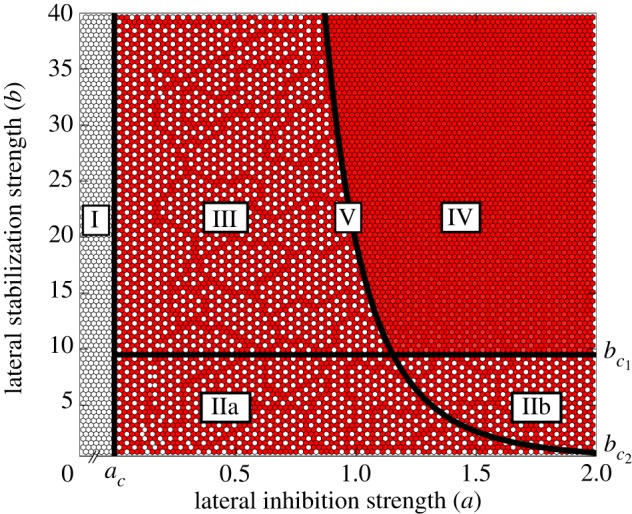
Classification of different spatial pattern domains under varying strengths of lateral inhibition a and lateral stabilization b. Colour (dark/white) indicates (high/low) expression of Y. The Roman numerals (I–V) denote different patterning domains. Solid lines indicate phase transitions with critical values a_c, 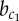and 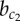that are found by means of bifurcation analysis. Parameters as in table 1; a and b as indicated on axes. (Online version in colour.)

3.1. Precocious endocrine specification

Domain I in figure 2 shows the absence of exocrine cells under conditions of weak or no lateral inhibition, a < a_c where a_c = θⁿ , independent of the strength of lateral stabilization b. This is in line with seminal loss-of-function studies showing that a deficiency in Notch signalling pathway members causes precocious endocrine differentiation and absence of Ptf1a expression [9,18]. In the context of the model, the reasons behind this phenotype are straightforward. In the absence of lateral inhibition, expression of X is uninhibited and exhibits simple saturated growth. Owing to intracellular antagonization of X on Y, the upregulation of the pro-exocrine factor is always slower, independent of the strength of lateral stabilization. Therefore, the fast uninhibited expression of X results in (i) fast commitment to the endocrine lineages and (ii) absence of exocrine cells owing to the inhibition of Y.

3.2. Chequerboard patterning

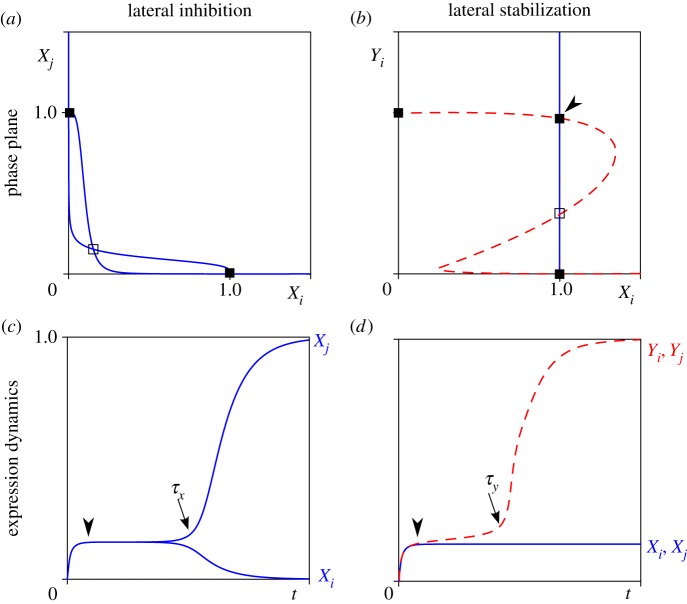
Over a wide range of parameters, the system organizes itself into a regular well-spaced, chequerboard-like pattern (figure 2). This spatial distribution is expected for models of lateral inhibition [24,26] and is known to arise as a result of Notch signalling during neurogenesis in Drosophila as well as in vertebrates [55,56]. It is instructive to consider the dynamics of X in a system of only two cells i and j for which the phase plane is depicted in figure 3a,b. This shows the coexistence of an unstable steady state where X_i = X_j and two stable steady states where X_i ≠ X_j. From the zero initial condition, the dynamics of expression displays a rapid initial evolution towards the unstable equilibrium (arrowhead in figure 3c). This represents the expression of X in the undecided progenitor state, the level of which inversely depends on the strength of lateral inhibition a. Subsequently, perturbations around this symmetric unstable state self-amplify and result in the divergence into opposite states of expression. The timing of the break in symmetry, τ_x (arrow in figure 3c), depends on the amplitude of noise η, because, on average, critical perturbations arise earlier under increased levels of stochasticity. In a two-dimensional array of cells, lateral inhibition causes alternating expression states to be established [26] following the propagation of the breaking of symmetry. Defects in regularity can occur at the boundary of those domains owing to off-register initial symmetry breaks in distant cells.

Figure 3.

Analysis of cell–cell interaction mechanisms in a system of two cells i and j. Phase plane analysis (a,b) and time plots of gene expression dynamics (c,d). (a) Nullclines of X (where dX/dt = 0) under lateral inhibition. One symmetric unstable steady state (open box) and two asymmetric stable steady states (filled boxes) coexist. (b) Nullclines of X_i (solid line) and Y_i (dashed line) under lateral stabilization where Y_j = 1. One unstable steady state (open box) and three stable steady states (filled boxes) exist. Arrowhead indicates a ‘new’ steady state dependent on lateral stabilization. (c) Symmetry breaking in X expression. After induction, a transient of intermediate expression at the symmetric unstable steady state (arrowhead) is followed by symmetry breaking (arrow, at t = τ_X) into one X⁺ and one X⁻ cell. (d) Biphasic growth of Y in the deterministic system (η = 0 to exclude symmetry breaking of X). After induction, expression of Y remains at a plateau level (arrowhead) followed by super-induction (arrow, at t = τ_Y) through lateral stabilization. Parameter values as in table 1. (Online version in colour.)

In all domains where chequerboard patterning occurs (IIa, IIb and III), the expression of Y is ‘enslaved’ through the antagonization by X. In domain II(a and b), the strengthening effect of lateral stabilization is too weak to counteract intracellular inhibition by X. The reasons for the same type of patterning in domain III are more subtle and are discussed below.

3.3. Biphasic growth through lateral stabilization

A homogeneous pattern of cells expressing the pro-exocrine Y factor is observed in domain IV (figure 2). That is, when both intercellular signalling mechanisms are strong, an absence of endocrine cells is observed. Under these conditions, the positive feedback between Y-expressing cells is strong enough to escape antagonization by X. Indeed, the phase portrait given in figure 3b shows the existence of stable attractors where Y is highly expressed, independent of X.

Interestingly, the dynamics of Y towards this expression state shows biphasic growth in which phases of growth are separated by a transient plateau (arrowhead in figure 3d). Upon initial activation, there is initial growth up to a level where it is approximately balanced by suppression by X, which is itself expressed at intermediate levels. At this stage, both cells have moderate expression of Y and mutually promote each other's expression of Y through positive feedback. If this feedback is strong enough, it accelerates expression and initiates the second growth phase. The timing of the super-induction at t = τ_y (figure 3d), and whether it occurs at all, depends on the strength of the stabilizing coupling between cells (b).

Intriguingly, the prediction of biphasic growth is in line with the expression pattern of Ptf1a during pancreatic development. While this factor is maintained at low expression levels at the progenitor stage, Ptf1a expression is superinduced in cells initiating acinar cell differentiation [57].

The fact that strong lateral inhibition is necessary for ubiquitous exocrine specification seems counterintuitive, since lateral inhibition is responsible for the establishment of heterogeneous chequerboard patterning. However, as mentioned, the strength of lateral inhibition a determines the level of intermediate expression in the uncommitted progenitor state and thereby the inhibition of Y. Accordingly, weak lateral inhibition leads to high expression levels of X in the progenitor state, and therefore inactivates the lateral stabilization mechanism of exocrine specification, resulting in a reduction of exocrine cells (domain III).

3.4. Multi-stability of patterns

To investigate how the stability of different patterning solutions changes under the influence of model parameters, we performed a bifurcation analysis on a reduced system of two cells. Figure 4a shows a bifurcation diagram where the strength of lateral stabilization b is varied, while keeping lateral inhibition strength constant, a = 1. Comparing with figure 2, we observe that the system passes through three qualitatively different domains (Ia, III, IV) and two spatial patterning solutions: a chequerboard and a ‘homogeneous’ pattern. Whereas in the chequerboard pattern the endocrine and exocrine cell fates are found in an alternating pattern, only exocrine Y⁺ cells exist in the ‘homogeneous’ pattern, despite small differences in Y expression. Two critical values 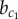and 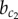are identified that determine the transition between domains. Below 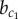, the only stable pattern is the chequerboard solution (Y_i + Y_j = 1). Indeed, the chequerboard solution is stable for all b. Between the critical values 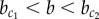, a stable homogeneous solution of high Y expression coexists, but this cannot be reached from zero initial conditions. This is because the expression at the plateau is stable for Y but not for X (in red in figure 4). Thus, expression of Y rests at an intermediate level and ‘waits’ until the symmetry in X expression is broken, after which the dynamics of Y becomes enslaved by X (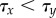, figure 5a). Conversely, for 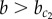, the stable state at plateau-level expression does not exist. Instead of resting at intermediate levels, Y expression continually grows as a result of lateral stabilization. This causes super-induction of Y before the symmetry of X is broken and, thus, a homogeneous exocrine pattern emerges (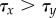, figure 5b).

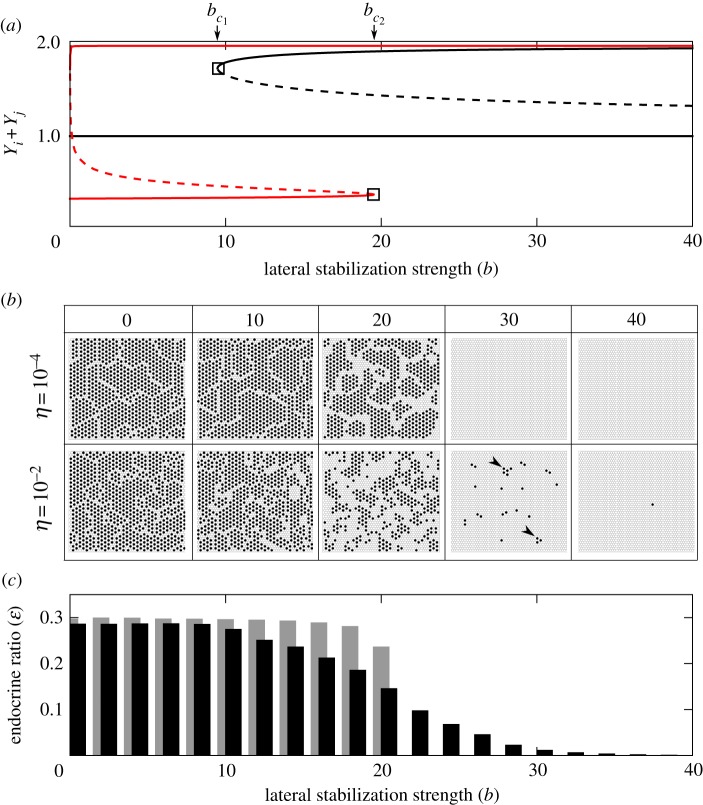
Figure 4.

Scattering and cell-type ratio control by lateral stabilization. (a) Bifurcation diagram showing the steady states of Y expression of a two-cell system. Two saddle–node bifurcations are found at that explain the phase transitions in figure 2. The four-variable system is projected onto a one-dimensional scale using the sum of Y expression in the couplet (Y_i + Y_j ). Dashed lines indicate unstable states; solid lines indicate stable states. Black lines represent globally stable states; thick lines represent states in which Y is stable but X is unstable. (b) Spatial patterns of endocrine (black) and exocrine (white) cells in a lattice simulation at different strengths of lateral stabilization b and under two conditions of noise η. Under higher noise levels, scattering is observed at the phase transition (see domain V in figure 2). Arrowheads indicate small clusters of chequerboard pattern. (c) Cell-type ratio of endocrine cells ɛ as a function of lateral stabilization strength b. Grey (η = 10⁻⁴)/black (η = 10⁻²) indicate noise levels. (Online version in colour.)

Figure 5.

Relative timing of cell fate decisions depends on lateral stabilization b and controls patterning. (a) For , symmetry breaking of X precedes super-induction of Y (), resulting in chequerboard patterning (b = 15). (b) In contrast, for 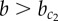, super-induction of Y precedes symmetry breaking of X (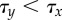) and results in ubiquitous exocrine cell fates (b = 35). (Online version in colour.)

These results demonstrate that (i) the model exhibits multi-stability of the patterning solution for a wide range of parameters (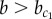) and (ii) under initial conditions relevant for development, the deterministic model switches from a heterogeneous (chequerboard) to a homogeneously exocrine pattern when lateral stabilization strength exceeds the critical value 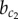. This switch in spatial patterning is driven by the relative timing between lateral inhibition and lateral stabilization mechanisms.

3.5. Noise controls timing of the cell fate decision

Next, we studied the effect of noise on this transition. Because the timing of the cell fate decision owing to lateral inhibition, τ_x, depends on the amplitude of noise η, an increase in stochastic fluctuations will trigger a faster emergence of X⁺ and X⁻ cells. In contrast, the mechanism of lateral stabilization is, by itself, insensitive to stochasticity, and in fact acts to homogenize noisy expression [38]. Autonomously, the time τ_y required for the lateral stabilization feedback loop to exceed a critical threshold value depends only on its strength b. Yet, when coupled to the lateral inhibition module upstream, stochasticity will also affect lateral stabilization. When, for a particular noise amplitude, the time to break symmetry in X decreases below the time required for lateral stabilization, i.e. τ_x¡τ_y, the dynamics of Y becomes enslaved to X. Consequently, less exocrine and more endocrine cells arise, thus increasing the endocrine cell ratio (see the electronic supplementary material, S1).

Under noisy conditions, a chequerboard pattern may arise, even in the case 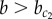, if a fluctuation happens to lead to a fast symmetry break of X which enslaves the dynamics of Y. Conversely, a homogeneous Y⁺ solution may emerge for 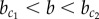if, by chance, the divergence of X is delayed, which allows the super-induction of Y by stabilization. Thus, the discontinuous phase transition at 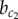becomes continuous in the presence of noise because of its modulation of the timing in expression dynamics.

Many sources of cellular noise exist that may affect cell fate decisions. In addition to noise in gene expression, e.g. owing to transcriptional bursts, there are stochastic factors influencing signal transduction as well as fluctuations of local cell–cell contacts. To investigate the effects of different sources of noise, we systematically explored different noise terms in the ODE model. The results show that pre-existing cell-to-cell variability or noise on signalling have qualitatively identical effects to gene expression noise (see the electronic supplementary material, S1). Interestingly, however, irregularities in local cell–cell contacts can have the opposite effect if contacts between non-neighbouring cells occur. In this case, slower symmetry breaking and a reduction in the endocrine cell ratio is observed (see the electronic supplementary material, S1), in line with observations of pattern refinement via filopodia in Drosophila [58]. Thus, both molecular- and cell-level sources of variability are important in control of the timing of cell fate decisions and the regulation of cell-type ratios. Note that the same does not hold for the phase transition at 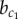, which is independent of X and therefore insensitive to noise.

3.6. Scattering of endocrine cells under noise

To investigate the effect of stochasticity on patterning, simulations were performed on a lattice of cells. Figure 4b shows that under low noise levels (η = 10⁻⁴), as expected, a chequerboard pattern of pro-endocrine cells is observed for 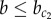, whereas a homogeneous exocrine pattern is established for 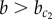. In contrast, under higher noise amplitude (η = 10⁻²), a continuous transition appears for 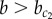that is characterized by the concomitant appearance of the two multi-stable patterns in the same tissue. In other words, noise expands the region in parameter space where chequerboard and homogeneous exocrine patterning may occur side by side (domain V in figure 2).

Above the critical value 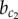, we observe the emergence of a scattered distribution of endocrine Y⁻ cells amidst a majority of exocrine Y⁺ cells. The particular scattering pattern predicted by our model is characterized by the presence of isolated or small clusters of endocrine cells, consisting of local patches of a chequerboard pattern (arrowheads in figure 4b, b = 30). Although no detailed study on the spatial distribution of endocrine cells during pancreas development has been conducted to our knowledge, the observed pattern is in agreement with the numerous reports on a scattered distribution in which endocrine cells were found as individual cells or small clusters in the pancreatic epithelium [9–11,15,18].

In the model, the formation of these clusters involves a competition between two wave fronts. Once an early X⁺ cell arises by chance, it initiates the propagation of the chequerboard pattern by inhibition of X in neighbouring cells. While inhibiting X in adjacent cells, these become Y⁺ and in turn initiate the propagation of a second wave by stabilization of Y in their neighbours. When the wave of lateral stabilization propagates faster than the wave of lateral inhibition, the chequerboard pattern halts at a particular size (see the electronic supplementary material, S2). Thus, the model predicts the propagation of inductive signals through homeogenetic induction, in which a differentiated cell causes the differentiation of nearby progenitor cells. To date, no evidence of homeogenetic signals exists for the developing pancreas. However, novel dynamic imaging studies may provide a more detailed insight into the spatio-temporal progression of signals and the precise spatial distribution of endocrine cells.

3.7. Lateral stabilization modulates cell-type ratios

An interesting consequence of these dynamics is that it allows the regulation of cell-type ratios in the pancreas, even in the absence of proliferation. Owing to noise in expression, endocrine-to-exocrine cell-type ratios can be modulated between the ratios expected for chequerboard patterning by lateral inhibition (1:3) and the homogeneous exocrine solution (0:1) (figure 4c). For a particular set of parameters, the locations where clusters of endocrine cells appear are chosen randomly but the ratio of cells that commit to the endocrine and exocrine lineages is determined by the parameters and can thus be predicted. From this model, it follows that downregulation of the strength of lateral stabilization will dramatically increase the endocrine-to-exocrine cell-type ratio.

Although proliferation is clearly important in the regulation of pancreatic cell-type ratios during development, several experimental studies are in agreement with this finding. For instance, it was found that a conditional knock-out of β-catenin downregulates Ptf1a, which results in a striking paucity of exocrine acinar cells while preserving the endocrine compartment [59,60]. Conversely, overexpression of β-catenin around E12.5 leads to an increased exocrine cell mass, with only minimal changes to the endocrine cell count [61]. Although β-catenin is a key player in Wnt signalling as well as in cadherin-mediated cell–cell contact, and it remains unclear which role is decisive in the context of cell-type ratio control [60], it is tempting to assume its participation in lateral stabilization of Ptf1a through cell–cell contacts takes part in the regulation of cell-type ratios in the pancreas.

3.8. Related mechanisms

It should be noted that the proposed coupling between lateral inhibition and lateral stabilization is not the only mechanism that can produce scattering patterns. In particular, models using an activator–inhibitor mechanism that include a long-range inhibitor produced by cells entering one lineage can generate scattered distributions, even without Notch-mediated lateral inhibition [62]. However, although the mesenchyme surrounding the early pancreas emits diffusive inhibitory signals [63,64], no evidence exists to suggest that such signals are produced within the primitive pancreatic epithelium itself. In contrast, there is accumulating evidence that short-range contact-mediated signals are crucial for lineage regulation in the pancreas [21,32,33], and the role of Notch signalling is already well established [9,18,65].

The mechanism of lateral stabilization proposed in this study is closely related to other inductive mechanisms. Similar to lateral stabilization, the community effect is an inductive mechanism that results in the homogenization of cell fates [38, 66]. However, it is typically associated with diffusive signalling among large groups of cells [67], whereas the contact-mediated mechanism of lateral stabilization only requires small groups of cells. Moreover, the community effect operates by receptor–ligand binding [68], whereas lateral stabilization assumes homodimerization of membrane-bound proteins. This implies that, for lateral stabilization to take place, all participating cells must already be alike in their expression of this particular protein. In this sense, lateral stabilization also bears similarity to the homeogenetic induction mechanism introduced by Mangold & Spemann [69] in which differentiated cells induce surrounding undifferentiated cells to commit to the same lineage. Although the presence of differentiated cells is not required for lateral stabilization because interaction between progenitor cells themselves can lead to uniform induction (if 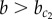), their presence would set out a wave of induction which eventually homogenizes cell fates in the tissue (even if 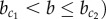. In fact, this predicted wave propagation effect can be used to experimentally test the lateral stabilization mechanism using grafting of adult exocrine (Ptf1a⁺) cells within a population of pancreatic progenitor cells.

4. Conclusion

Despite indisputable evidence that Notch signalling is important in the regulation of the cell fate decision between the endocrine and exocrine lineages [9,18], it is still controversial whether it acts through lateral inhibition or an alternative mechanism, such as suppressive maintenance [65,70–72]. Yet, none of the theories proposed to date is able to explain the observed scattered distribution of endocrine cells in the pancreatic epithelium [17]. Interestingly, recent evidence from transdifferentiation studies suggests the existence of an additional mechanism that stabilizes the fate of pancreatic exocrine cells by a positive feedback loop mediated by cell–cell contacts. In this study, we have shown that the coupling between lateral inhibition and lateral stabilization may control early lineage specification and patterning in the pancreas. We have constructed and analysed a minimal mathematical model combining these contact-mediated signalling mechanisms, and showed that its behaviour agrees with recent transgenic loss- and gain-of-function experiments: abrogation of lateral inhibition leads to precocious commitment to the endocrine lineage; lateral stabilization causes biphasic expression of pro-exocrine factors; and cell-type ratios can be modulated by up/downregulation of the strength of lateral stabilization. Moreover, the coupling of the two feedback mechanisms causes a multi-stability of spatial patterning solutions that, in the presence of noise, generates a scattered distribution of endocrine cells, as observed in the central part of the pancreatic epithelium. Our analysis shows that the scattering pattern arises as a side-effect of noise on the relative timing of the two feedback mechanisms. This enables two qualitatively different patterns to appear concomitantly and persist side by side. The scattering pattern predicted by our model is characterized by the presence of small clusters of endocrine cells in local chequerboard-like patches, rather than a uniform random distribution. Although it remains unclear whether pro-endocrine Ngn3⁺ cells actually appear as clusters within the primitive pancreatic epithelium, it is known that they rapidly aggregate after their delamination from the epithelium. It may thus be speculated that the specification of endocrine cells in a clustered fashion serves as a pre-pattern to expedite the formation of aggregates that eventually form the islets of Langerhans.

Unlike for lateral inhibition, the molecular pathways underlying lateral stabilization remain unknown. Yet, based on the mathematical conditions under which the multistability occurs, receptor–ligand interactions can be excluded. Rather, our model predicts that lateral stabilization depends on homotypic binding of membrane-bound proteins. Recent studies offer several possible candidates. For instance, Minami et al. [32] demonstrated that disruption of cadherin-mediated cell–cell adhesion is required for the induction of de-differentiation of adult acinar cells in vitro. This suggests that cadherins may be involved in stabilizing exocrine factors and maintaining acinar cell fate. Another, potentially complementary, possibility is that gap junctional communication mediates acinar cell fate stability. This is supported by experimental evidence that inhibition of Mist1 activity, a key regulator of gap junctional communication in exocrine cells and downstream target of Ptf1a, also causes the de-differentiation of acinar cells [33,73].

Independent of the precise molecular realization, the fact that both the inhibitory and stabilizing mechanisms of contact-mediated induction have been reported for a wide range of tissues suggests that the model and results presented here for the pancreas may also be applicable to other developing tissues.