Finger pad friction and its role in grip and touch

Abstract

Many aspects of both grip function and tactile perception depend on complex frictional interactions occurring in the contact zone of the finger pad, which is the subject of the current review. While it is well established that friction plays a crucial role in grip function, its exact contribution for discriminatory touch involving the sliding of a finger pad is more elusive. For texture discrimination, it is clear that vibrotaction plays an important role in the discriminatory mechanisms. Among other factors, friction impacts the nature of the vibrations generated by the relative movement of the fingertip skin against a probed object. Friction also has a major influence on the perceived tactile pleasantness of a surface. The contact mechanics of a finger pad is governed by the fingerprint ridges and the sweat that is exuded from pores located on these ridges. Counterintuitively, the coefficient of friction can increase by an order of magnitude in a period of tens of seconds when in contact with an impermeably smooth surface, such as glass. In contrast, the value will decrease for a porous surface, such as paper. The increase in friction is attributed to an occlusion mechanism and can be described by first-order kinetics. Surprisingly, the sensitivity of the coefficient of friction to the normal load and sliding velocity is comparatively of second order, yet these dependencies provide the main basis of theoretical models which, to-date, largely ignore the time evolution of the frictional dynamics. One well-known effect on taction is the possibility of inducing stick–slip if the friction decreases with increasing sliding velocity. Moreover, the initial slip of a finger pad occurs by the propagation of an annulus of failure from the perimeter of the contact zone and this phenomenon could be important in tactile perception and grip function.

1. Introduction

Grasping an object between the pads of the thumb and the index finger is the prototype grip used for precision-handling studies. Precision grip must be controlled in order to achieve the optimal minimum force necessary to prevent the slip of an object. In perceptual tasks such as surface discrimination, the normal loading must be modulated to provoke a controlled slip. The precise control of finger pressure derives from the responses of strain-sensitive cutaneous mechanoreceptors at the tips of the digits, as well as from motor control systems that sense muscle length and power based on sensory input from both cutaneous and muscle mechanoreceptors [1,2]. The dynamic tactile signals from the cutaneous mechanoreceptors reliably encode various aspects of contact events around which most object manipulation tasks are organized [3,4]. In 1984, Westling & Johansson [5] published the results of an ingenious paradigm to study the control of grip force during the grasping and lifting of objects. They reported that the normal component of the grip force is influenced by three important factors: (i) the weight of the object, (ii) the friction between the object and the skin, and (iii) the safety margin set by the individual based on prior experience. Moreover, data from studies involving healthy participants with experimentally induced sensory deficits and from patients with sensory loss, because of peripheral nerve damage or central brain lesions, clearly demonstrate the central role of somatosensory feedback for dexterous manipulation. Several methods have been used to transiently interrupt sensory information from the hands of healthy subjects: the use of gloves [6], cooling with sprays or gels [7] and injections of local anaesthetics [8,9]. An almost invariable effect of these manipulations was an increase in the grip force applied against the grasped object. One logical primary reason for the increases in the motor output is a strategic response of the nervous system to ensure against slippage of the object despite a deficit of sensory information. Excessive grip forces have also been observed for the paretic hands of both children with hemiplegic cerebral palsy [10] and stroke patients [11], and also for patients with strong compression of the median nerve [12]. The excessive grip forces were generally attributed to the perturbed feedback of sensory information.

Tactile exploration involves the movement of a finger pad across a counter body, typically at smaller normal loads than those used in grip. The subjective assessment of the roughness of fine but not coarse textures is greatly enhanced by sliding [13]. This was considered as evidence for the duplex theory of texture perception, which was originally proposed by Katz [14]. He argued that coarse textures involve spatial coding as a result of the response of the low-threshold cutaneous mechanoreceptors in the finger pad while fine texture perception relies on a temporal coding, which has been termed vibrotaction. Essentially, the movement of the finger pad over such surfaces causes vibrations that have been measured directly by proximity sensing [15]. A similar mechanism applies to indirect touch in which a probe is moved across a surface causing vibrations to be propagated along the probe to the fingers [16,17]. These studies suggest that the friction of the finger pad may not play a primary role in assessing the surface roughness. However, the analysis of oscillations in the frictional force has shown that there is some correlation with roughness [18], and that the oscillation amplitude depends on both the orientation of the fingerprint ridges and any load dependence of the coefficient of friction [19,20]. Moreover, lubrication can reduce the perceived magnitude of the roughness [18,21].

In texture perception, the frictional and normal forces are adjusted optimally in a way that depends on the topography of the surface [22], which supports the contention that friction is a significant factor in tactile appraisal. Data from such active touch studies on rough surfaces, which involve the subject stroking the surface rather than by an imposed sliding of the surface against the finger pad (passive touch), are difficult to interpret because of this tendency to optimize the friction by changing the normal load in a way that is probably governed by pleasantness. There is not compelling evidence to support a feedback mechanism based on pleasantness. However, Skedung et al. [23] found that, for test papers having different roughnesses, the subjects reduced the normal force as the coefficient of friction increased. Correlations with perceived roughness have been found with both the measured roughness and the coefficient of friction, which is further evidence of the importance of friction [24].

The ranking of roughness is a relatively restricted attribute of a tactile response and is an example of discriminatory touch. For example, Gwosdow et al. [25] investigated the influence of perspiration on fabrics and found that the resulting increase in skin friction enhanced the perception of roughness. The increase in friction correlated with a reduction in comfort, which is arguably more important. Gerhardt et al. [26] also observed an increase in the friction of skin against fabrics as a function of increasing epidermal moisture. They pointed out the relevance of this work on textiles to skin damage such as blisters, abrasion and decubitus ulcers. Similar types of damage can result from sports activities that involve, for example, sliding contacts with equipment, grass or artificial playing surfaces.

Simultaneous measurements of vibration and friction would establish whether tribological interactions play a significant role in modifying the vibratory response, which is currently regarded as the primary sensory cue in assessing fine surface texture. However, it is clear from a recent work [27] that subjects are capable of ranking friction quite accurately. It was found that the Weber index for the coefficient of friction of a glass surface is 0.18. That is, subjects could distinguish a difference of about an 18 per cent reduction in the coefficient of friction, which was achieved by increasing the amplitude of ultrasonic vibrations applied to the glass; this method of reducing the friction is well established in metal forming, for example [28]. These results are consistent with earlier work by Smith & Scott [29], who showed that subjects can scale the friction of smooth surfaces, for which vibrotaction is not applicable.

Thus, it is reasonable to conclude that friction is a significant factor in discriminatory touch. It is also an important factor in affective and hedonic touch, and in associated emotional attributes such as pleasantness and comfort. Although affective touch is commonly connected with the unmyelinated mechanoreceptive afferents that innervate hairy skin (the C tactile or CT-afferent system) [30], it is clearly an important aspect in the context of the finger pads where such afferents are not thought to exist. It is also obvious that a lubricated surface is felt quite differently to one that is unlubricated even if the presence of a lubricant, owing to sensory compensation mechanisms, has a minor effect on the discrimination of the roughness. On the other hand, in the case of relatively smooth surfaces, friction must be a major source of sensory information. For example, Guest et al. [31] investigated the sensory attributes of a wide range of lubricants on a slightly textured polypropylene (PP) sheet and found that there were correlations between the measured friction and sensory dimensions such as watery. Even for unlubricated surfaces, the perception of dryness for a wide range of materials was found to increase as the friction decreased [32]. It has also been observed for dry surfaces that unpleasant tactile sensations increased with the extent of stick–slip motion [33].

Nakano et al. [34] simulated the application of cosmetic foundations by measuring the sliding friction between silicone elastomer surfaces in the presence of such products. They processed the data using artificial neural networks and were able to predict the emotional tactile comfort with relatively high accuracy based on the frictional data. However, despite such observations and that intuitively it might be expected that friction is a major factor in touch, attempts to objectively deconvolve the unique role of friction have proved to be difficult. For example, in one study, the human tactile evaluation of a range of surfaces was dominated by the rough/smooth and soft/hard dimensions with the stick/slippery dimension being ranked as a much weaker contribution [35]. More recently, Chen et al. [36] explored a wider range of dimensions and only a strong correlation between the coefficient of friction and the wet/dry dimension was observed. The interactions between the various dimensions, e.g. with the surface topography, will have a considerable effect on the friction, which is one complicating factor that was clearly recognized in this study and others [37]. Another is the sensitivity of the coefficient of friction to variables such as normal load, sliding velocity and occlusion, which will be discussed in the current review. As a further indication of the role of friction, virtual reality studies have shown that subjects can readily identify complex textured surfaces on the basis of vibrations alone [38]. While both low- and high-frequency components of the finger–surface interaction were due to friction, subjective reports indicated that absence of the low-frequency components in the simulation, i.e. the absence of net friction, decreased the level of realism.

The detection of slip on the surface of the skin and sudden changes in the load force during object manipulation have been attributed to the fast-adapting low-threshold mechanoreceptors [39–41]. The extremely high densities of these units in the fingertips, together with their small receptive fields, certainly provide a high spatial acuity to the fingertips [3]. The early adjustment to a new frictional condition, which may appear soon after the object is initially touched (approx. 0.1–0.2 s), depends on the vigorous responses of the mechanoreceptors during the initial phase of lifting an object [39]. In order to prevent slip, the grip/load force ratio must exceed a minimal value determined by the coefficient of friction between the skin and the object, i.e. the critical ratio at which slips occurs will increase with the slipperiness of the object. Moreover, the responsiveness of especially the fast-adapting units to localized slips, which are not accompanied by acceleration events, suggests that they are also sensitive to other aspects of the mechanical changes reported by Johansson & Westling [39]. These include ‘local redistributions of the strain/stress pattern of the field related to the sliding of the surface structure over the skin’ [39, p. 151]. These authors also note that ‘one important factor contributing to the low frequency of localised slip responses actually observed … might have been the spotty appearance of the slip zones’ that portends widespread slip.

In seminal work, Phillips & Johnson [42] applied a simple analytical model to estimate the compressive strains that were developed at the locations of the slow-adapting mechanoreceptors as a result of a grating being indented into a finger pad. Linear expressions were derived in order to relate these values to the discharge rates of the afferents. This concept of neuromechanical coupling has since been adopted by a number of researchers using more complex finite-element models of the finger pad, e.g. Maeno et al. [43] and Shao et al. [44] or closed-form solutions [45]. Such work should lead to a more quantitative understanding of tactile perception and grip function based on the principles of contact mechanics and the critical neurophysiological factors. However, the formulation of the stress boundary conditions to prescribe the frictional interactions in such models is simplistic compared with the actual behaviour of the finger pads. An aim of the current paper is to critically review the current knowledge about the friction of the finger pad. This will provide a basis for developing more realistic stress boundary conditions in order to improved simulations of touch and grip and, hence, more accurately predict the response of the low-threshold mechanoreceptors located just beneath the skin surface.

The fingerprint ridges and the large number density of sweat pores that are located in the ridges [46,47] are the main physiological characteristics that explain the tribological complexity of a finger pad (figure 1). In particular, the continuous eccrine sweat secretion causes an accumulation of moisture at the sliding interface for a finger pad in an enduring contact with an extended impermeable surface. This phenomenon is termed occlusion in the present paper. The dominant mechanism is the reduction in the evaporation of the secreted sweat because of the large decrease in the free surface area when such a contact is made. The kinetics of occlusion will be reviewed as will be the influence of the nature of the countersurface and the addition of excess water, when the contact is defined as being in the wet state. The contact mechanics of the finger pad, which is dominated by the fingerprint ridges, will be considered in terms of the influence of the load dependence of the contact area and friction. The mechanoreceptors respond to dynamic as well as static perturbations. Consequently, the evolution of a finger pad contact, when subjected to tangential loading, will be discussed in addition to the changes in the friction that occur when the sliding velocity is varied.

Figure 1.

A microstructural cross-section of a human finger pad (middle finger) obtained using Optical Coherence Tomography (Spectral Radar OCT – OCP930SR, ex Thorlabs). Typical fingerprint height and spacing are shown with four (spiral) sweat ducts (filled circles) and a drop of sweat (open circle) emerging from a pore on a ridge surface. The sweat ducts are visible within the stratum corneum layer which is relatively dark. The thickness of the stratum corneum is estimated to be approximately 300 µm. This is based on the difference of 400 µm in the optical depth between the light skin surface and the upper boundary of the intermediate light layer, which is the remainder of the epidermis [48,49], and using an assumed value of the refractive index for skin of 1.4. The inset photograph shows the same skin region from above, bounded top and bottom by the edges of the OCT contact probe. (Online version in colour.)

2. Contact area

Friction can be described by the two-term model that assumes an additive decomposition of an adhesion and a deformation term [50]. The deformation component is mainly important for the sliding or rolling of hard lubricated probes on planar softer materials such as elastomers, i.e. polymers at temperatures that are greater than their glass transition value [51,52]. It arises from mechanical hysteresis (e.g. viscoelasticity) during the deformation of a subsurface region at the front of a contact and the subsequent inelastic recovery. A characteristic of this mechanism is that the velocity sensitivity arises from that of the bulk deformation behaviour of the substrate. However, it has been shown that this contribution is negligible for unlubricated skin on the basis of measurements on the inner forearm [53].

Invariably the friction of organic polymers in the glassy [54] and also the rubbery states [55] may be described by the adhesion mechanism with the frictional force, F, being given by the following expression:

2.1

where τ is the interfacial shear strength and A is the real area of contact. The parameter τ arises from the energy dissipated by the rupture of intermolecular junctions formed intermittently at the sliding interface and the coupled viscoelastic deformation in a thin subsurface layer adjacent to this interface. For glassy organic polymers τ increases linearly with the mean contact pressure, p, thus [56]

2.2

where τ₀ is the intrinsic value of τ at zero contact pressure, α a pressure coefficient and p is given by W/A, where W is the applied normal force. The relationship between the contact area and the normal force for a sphere in contact with a flat surface may be written in the following form:

2.3

where the areal load index, m, is unity when at least one of the contacting bodies is surface topographically rough [57]. That is, the real area of contact is linearly proportional to the applied normal load. For a contact between a smooth sphere of radius, R, and a smooth flat solid, with one of the contacting bodies being rigid, equation (2.3) corresponds to the Hertz equation [58] such that m = 2/3:

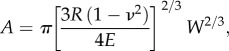2.4

where E and ν are Young's modulus and Poisson's ratio of the deformable body, respectively. The advantage of this form is that it can be applied to a spherically tipped rigid probe and a planar area of skin or to the finger pad and a rigid planar surface. This assumes that the finger pad may be approximated by the cap of an elastic sphere or an elliptical cap with R = (R′R″)^1/2 such that R′ and R″ are the major and minor radii of curvature.

It is difficult to accurately measure the real area of contact for any system not involving perfectly smooth surfaces except for very compliant materials such as elastomers, for which it is usually assumed that the asperities are compressed to form an intimate interface. In the case of the finger pad, it is common to measure two parameters to characterize the contact area. The gross value, A_gross, is defined as the total area contained within the overall contact boundary, including non-contacting regions such as the valleys between the fingerprint ridges. The apparent contact area of the fingerprint ridges, A_ridge, ignores the potential influence of any topographical features on the surfaces of the ridges, viz. A_gross > A_ridge ≥ A. Skin is complicated by having a layered structure so that the bulk deformation depends mainly on the underlying tissue with a Young's modulus that is considerably less than that of the outermost epidermal layer, viz. the stratum corneum. Thus, it has been found that the indentation of a rigid spherical probe on the forearm may be described by the Hertz equation in a way that is not strongly affected by the hydration behaviour of the skin [59]. However, the contact area for dry skin calculated from the Hertzian form of equation (2.4) would be significantly greater than the real area of contact because of the surface topography.

In the nominal dry state under ambient conditions, the surface layers of stratum corneum behave as a typical glassy organic hydrophilic polymer, e.g. nylon and keratin [53], provided that there has been no occlusion. A characteristic of such polymers is that invariably the friction increases with the absorption of moisture and, hence, with increasing relative humidity [60], despite a reduction in the value of τ [61]. This is because plasticization by the moisture causes a reduction in Young's modulus. If the configuration involves a smooth sphere sliding on a smooth flat surface, there will be an increase in A that may be calculated using equation (2.4). In addition, if either of the sliding bodies is surface topographically rough, the softening of the asperities may also lead to an increase in A under an applied normal load since the roughness in the dry state prevents an intimate contact being formed.

The plasticization mechanism leads to an increase in the friction by a factor of two for nylon, from the dry to the saturated wet states [60], whereas the comparable increase for the inner forearm is about an order of magnitude [53]. The enormous increase for the forearm was attributed to the extreme sensitivity of the elastic modulus of stratum corneum to moisture that leads to a large increase in the contact area due to the flattening of the asperities under an applied normal force. A large increase in the friction in the wet state has also been observed for the finger pad. It was argued that this was associated with an increase in A towards A_ridge as a result of fingerprint ridge asperity plasticization [62].

The elastic modulus of stratum corneum decreases by about three orders of magnitude from the dry to the wet state [63]. This corresponds to a glass–rubber transition since the Young's modulus of stratum corneum in the wet state is comparable with that of an elastomer. Consequently, the tribological properties are similar in terms of the relatively large values of the coefficient of friction compared with glassy organic polymers. Similarly, as described in §4 and §5, also in terms of the initiation of slip and the velocity dependence of the coefficient of friction. Another important similarity is that both materials are hydrophobic; the advancing contact angles with water are about 100° for both stratum corneum [64,65] and elastomers [66]. The common use of elastomers as artificial skin materials may be attributed to these similarities with the properties of skin.

It has been commonly observed that the coefficient of friction of the finger pad can increase with decreasing normal load for the relatively small normal loads associated with taction. For example, André et al. [67] observed that this was the case for normal loads of less than 3.5 N. It is possible to account for such observations by considering equations (2.1), (2.2) and (2.4), which provide a relationship between the frictional and normal forces:

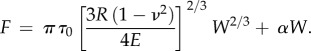2.5

It has been shown that equation (2.5) may be approximated by the following expression [68]:

2.6

where n is termed the frictional load index and k₂ is a load-dependent coefficient of friction, μ, thus

2.7

For such contacts, it has been shown that 2/3 ≤ n ≤ 1 [68] but by inspection of equation (2.5) it is evident that this is the case since the friction depends on two terms involving W having indices of 2/3 and unity, with the actual value depending on the relative magnitudes of the coefficients of the two terms.

The above approach has been applied to frictional data for the skin of the inner forearm using smooth rigid spherical probes and flooded with water [53]. Since water plasticizes skin, which leads to an intimate contact for such probes, it is reasonable to assume that equation (2.5) for the Hertzian case is then valid. For the inner forearm, the values of τ₀, α, k₂ and n are given in table 1 for both glass and PP probes. The frictional load indices are in the expected range and the values of τ₀ are similar for both probes. It was speculated that the smaller value of α for the glass probe could have been associated with a pressure-dependent ultrathin layer of water molecules formed on the glass surface. As has been pointed out, wet stratum corneum is in a rubbery state; however, the load index for elastomers is 2/3 [55]. This suggests that the interfacial shear stress for elastomers is independent of the contact pressure, which has been confirmed by the direct measurement of the distribution of shear stresses for the sliding contact of an elastomer and a rigid spherical probe [69]. The pressure dependence for glassy polymers arises from a free volume mechanism. The transition to the rubbery state causes an increase in the free volume but, because Poisson's ratios of elastomers approach 0.5, they are considered to be incompressible, i.e. the bulk modulus is very much greater than the tensile value.

Table 1.

The interfacial shear strength, τ₀, and the pressure coefficient, α, of wet forearm skin for glass and PP spherical contacts, obtained for the best fits of equation (2.2) to shear strength and pressure data derived from experimental friction force data as a function of normal load using equations (2.1) and (2.4). The power-law parameters k₂ and n are derived from τ₀ and α by approximating equation (2.5) using equation (2.6) [53].

	glass, R = 0.008 m	glass, R = 0.021 m	PP, R = 0.020 m
τ0 (kPa)	4.8 ± 0.4	4.8 ± 0.4	6.1 ± 0.6
α	0.8 ± 0.1	0.8 ± 0.1	2.0 ± 0.1
k2 (N1−n)	1.1	1.4	2.7
n	0.85	0.80	0.85

For dry skin, it was observed in the above work on the inner forearm [53] that the load index is unity. Consequently, Amontons' law of friction applies such that the coefficient of friction is independent of the normal force. This is because of the pronounced surface topography of forearm skin that forms an extended multiple asperity contact in the unplasticized state. That the coefficient of friction is a constant equal to (k₁τ₀ + α) may be shown from equations (2.1)–(2.3) with m = 1.

The deformation behaviour of the finger pad is more complex than that of the inner forearm. For compression against a rigid flat plate, Derler et al. [70] found that A_gross increased by only a small extent for increasing normal loads greater than 1 N. Similarly, Childs & Henson [71] reported that the transition to an approximately constant value of A_gross occurred in the range 1–2 N. A load of about 2 N seems to typically characterize the upper bound of the deformation limit due to the underlying tissue being compressed against the distal phalanx of the finger. That is, at high normal forces a finger pad would behave as an extended multiple asperity contact with m = 1 in equation (2.3) and it would be expected that n = 1 in equation (2.6). Tomlinson et al. [72] found that this was the case, albeit with a small negative intercept on the normal load axis in some cases. In general, such an intercept may be ascribed to the pull-off or adhesive force, W_A, by a generalization of equation (2.6) [55]:

2.8

That is, the adhesive force effectively augments the applied normal force. In practice, it is difficult to distinguish the fit of equation (2.8) with n = 1, W_A > 0 and W_A = 0, n ≠ 1 unless accurate data are available at small normal loads. This is evident with the data of Tomlinson et al. [72] even at small normal loads, but it is clear that virtually all of their data correspond to a small value of the adhesive force.

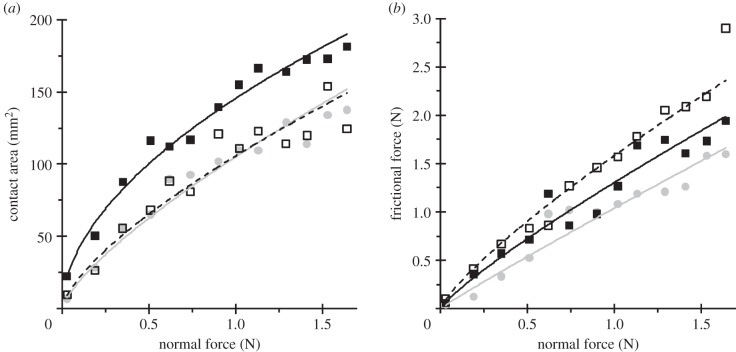
The relatively large normal force range of greater than 2 N is generally relevant to grip but precision grip and tactile exploration invariably occur at smaller forces. Warman & Ennos [73] measured A_ridge and the friction of the finger pad in this smaller force range (0–1.7 N) as shown in figure 2; these measurements were carried out with ink so that it is reasonable to presume that the fingerprint ridges were fully plasticized, i.e. A_ridge = A. They found that A_ridge increased with the load to a power in the range 0.68–0.95, depending on the finger. The value would be 0.67 on the basis of equation (2.4) if it is assumed that the finger pad approximates to a Hertzian contact and that A_ridge scales linearly with A_gross. They also observed that the ratio of A_ridge to A_gross was approximately 70 per cent. However, in more recent work using an optical method, it was reported that this ratio was about 30 per cent for a normal force of 1 N and that A_ridge increased with load according to the Hertz equation but A_gross was associated with a smaller index of 0.52 [74]. Despite the approximate applicability of the Hertz equation, Warman & Ennos [73] found that the load indices for different fingers were generally in the range expected from equation (2.5). Their data for the dynamic frictional force as a function of the normal load are also shown in figure 2 and the deviation from linearity is evident.

Figure 2.

The relationship between (a) the contact area and (b) the dynamic frictional force of individual finger pads as a function of the applied normal force, for three different fingers held flat against an acrylic sheet. Index finger, filled black squares; middle finger, filled grey circles and thumb, unfilled black squares. The lines in (a) and (b) are the best fits to equations (2.3) and (2.6), respectively. Index finger, black line; middle finger, grey line; and thumb, dashed line. The data are taken from fig. 2 in the study of Warman & Ennos [73].

Like Adams et al. [53], Warman & Ennos [73] also argued that Wolfram's [75] suggestion that the friction of skin could be described by a pressure independent coefficient of friction is incorrect since it predicts a load index of two-thirds, i.e. equation (2.5) with α = 0. On the basis of their friction data they computed values of τ₀ and α that were similar to those obtained for the inner forearm [53]. As mentioned above, a common complicating feature is that if the data are sparse, particularly at small normal forces, or if there are significant errors in the data, it is difficult to distinguish between equations (2.8) and (2.6) in terms of the quality of the fit. Tomlinson et al. [76] argued that this problem applied to some of the published data of the friction of the finger pad.

3. Occlusion

Smith & Scott [29] measured the coefficient of friction of a finger pad against a range of surfaces using a repetitive unidirectional stroking procedure. It was found that the values increased with the number of strokes; in one example it increased from 0.36 to 0.79 after seven strokes. They concluded that it was the result of increased sweat secretion, which possibly was triggered mechanically by the stroking action although they stated that physiological evidence was not available to support this contention. Occlusion is an alternative mechanism. The importance of sweat in determining the friction of the finger pad has been observed in a number of studies. Smith et al. [77] described the results of applying scopolamine patches to subjects in order to suppress palmar sweating by blocking the muscarinic receptors of the eccrine sweat glands. On the basis of grip experiments it was found that, for some of the surfaces examined, there was an increase in the peak and static grip forces, which was interpreted as a response to an increase in the slipperiness of the skin. Johansson & Westling [78] carried out precision manipulation studies and observed that the friction of the hand was reduced significantly after washing and drying, which was considered to arise from the removal of accumulated moisture.

More systematic studies were carried out by André et al. [67], who reported values of the coefficient of friction measured during grip studies as a function of the moisture content at the skin surface of a finger pad using a device that had been developed previously [79]. The subjects exhibited moisture levels that ranged from dry to very wet and it was found that there was a maximum value of the coefficient of friction at intermediate moisture levels. Subsequently, it was observed that the measured moisture values either increased, remained unchanged or decreased after prolonged contact depending on the inherent wetness exhibited by the subject at the initial contact [80]. They argued that this was evidence for a natural mechanism, which resulted in an optimal moisture content for achieving a maximum friction between the finger pad and an object. An example for one subject is shown in figure 3. The measured grip forces as a function of the moisture level for all subjects are given in figure 4. The majority of the trials resulted in moisture values that were in the range required to minimize the grip force by maximizing the coefficient of friction, which corresponded to a moisture level of 7.75 arbitrary units. Moreover, it is clear that the grip force increases for levels of the moisture outside of this optimal range.

Figure 3.

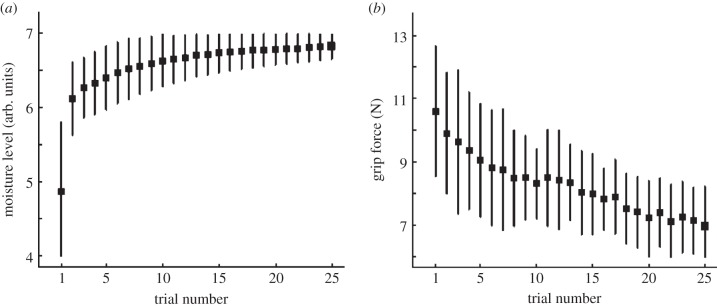
(a) Moisture levels and (b) static grip forces for the finger pad of a single subject as a function of sequential grip and release procedures on a manipulandum defined in terms of a trial number. The points are the mean values obtained from 20 blocks of trials, and the associated bars represent±1 s.d. The subject (S2) was judged to have dry skin and the data demonstrate that the sequential contact in this case results in an increase in the moisture level with a corresponding reduction in the grip force required to stabilize the position of the manipulandum. Adapted from André et al. [80].

Figure 4.

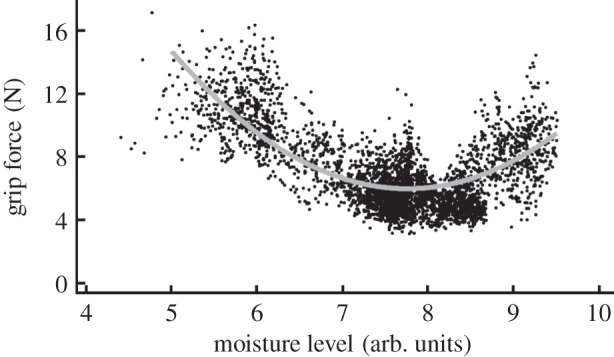
The static grip force as a function of moisture level for the finger pads of eight subjects each involving 20 blocks of 25 trials of the type described in figure 3, which is for one of the subjects. The line is the best fit to the data and exhibits a minimum at approximately 7.75 arbitrary units corresponding to the optimal moisture level for grip. Adapted from André et al. [80].

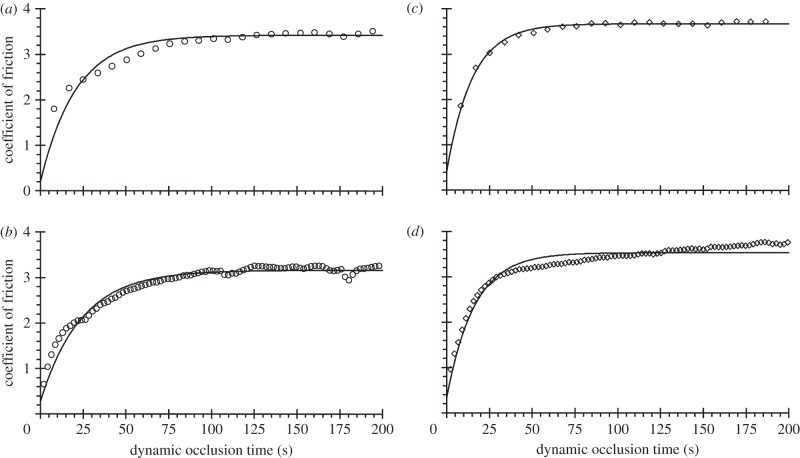
Pasumarty et al. [62] measured the friction of a finger pad as a function of the contact time for a range of surfaces. This included smooth glass and PP as examples of hydrophilic and hydrophobic surfaces, respectively. Typical data at sliding velocities of 6 and 24 mm s⁻¹ are shown in figure 5, which were measured for continuous sliding in a reciprocating manner. The lines are the best fit to the following relationship for the coefficient of friction, μ, as a function of time, t:

3.1

where μ₀ and μ_∞ are the initial and steady-state values of the coefficient of friction. The parameter λ is a characteristic time that was relatively independent of the sliding velocity. It has mean values of about 23 and 16 s for glass and PP in the velocity range 3–24 mm s⁻¹. The corresponding mean values of μ₀ are 0.23 and 0.37 and for μ_∞ they are 3.1 and 3.6. Equation (3.1) was derived on the basis that the coefficient of friction is proportional to the quantity of moisture at the sliding interface and that the excretion of sweat can be described by first-order kinetics. This was consistent with the moisture level measured instrumentally as a function of time, which could also be described by an analogous relationship with a characteristic time of about 16 s. In summary, there is strong evidence that the increase in friction is due to an occlusive mechanism in which the rate of sweat excretion is not influenced by sliding. This is because there was not a systematic trend in the characteristic times associated with the coefficients of friction when the sliding velocities were varied. Moreover, similar data were obtained when a finger pad was held statically in contact for various time periods before measuring the friction. It is possible that there is some active mechanism of sweat secretion associated with the contact pressure, which may also have some neurophysiological basis, but experimental evidence does not currently exist to support this contention.

Figure 5.

The dynamic coefficient of friction (W = 0.2 N) as a function of the dynamic occlusion time corresponding to sliding speeds of (a) V = 6 mm s⁻¹ and (b) V = 24 mm s⁻¹ for glass, (c) V = 6 mm s⁻¹ and (d) V = 24 mm s⁻¹ for PP. Best-fit curves to equation (3.1) are shown. Adapted from Pasumarty et al. [62].

The above work shows that the coefficient of friction of a finger pad in an occluded contact increases by about an order of magnitude over tens of seconds. The increase is comparable to that observed for the inner forearm when water is introduced in the contact region [53]. The latter work was carried out using spherical probes with sliding distances of many contact diameters so that it was not possible to determine the influence of occlusion in the dry state. It is reasonable to assume that the plasticization mechanism for the wet state also applies in the case of the finger pad in the occluded state. When a contact in the forearm study was allowed to dry from the wet state, it was found that the coefficient of friction increased to a maximum value before decreasing to that for the dry state [53]. When excess water was added to a fully occluded finger pad contact, the coefficient of friction was reduced by a factor of about 3, as shown in figure 6 [62]. This is analogous to the results reported by André et al. [80], who showed that the coefficient of friction decreased when the moisture level was greater than the optimal value as described above. Similar data have been reported by Tomlinson et al. [81], who also observed a maximum in the coefficient of friction for intermediate levels of moisture in the contact region.

Figure 6.

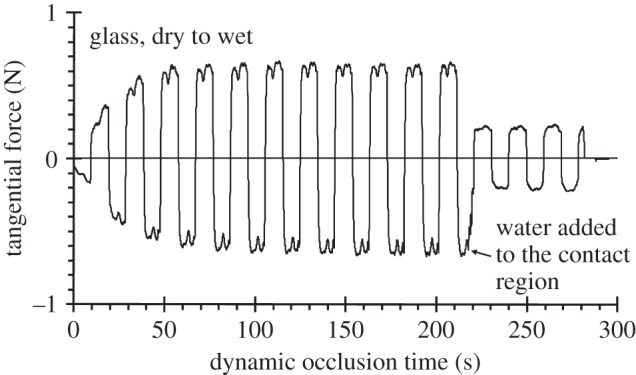
Tangential force data for a dry finger pad sliding against optically smooth glass as a function of the dynamic occlusion time, followed by the addition of water in the contact (W = 0.2 N and V = 6 mm s⁻¹ ). Adapted from Pasumarty et al. [62].

Thus, the fully occluded state for a finger pad must correspond approximately to the maximum possible coefficient of friction, although the actual value will depend on the subject. This suggests that there is some mechanism that limits the maximum accumulated level of moisture in the contact region to a value that is less than in the wet state. The simplest mechanism could involve the hydrostatic pressure developed in the sweat pores being effectively blocked by contact with the countersurface. Evaporation and two-dimensional Darcy flow of water vapour through the valleys of the fingerprint ridges could also contribute. Finally, it is possible that excess moisture could be deposited on the counter body by leakage flows. This is known to occur for elastomers/glass contacts under certain conditions; the residual films with thicknesses of less than 600 nm were not visible to the naked eye [82].

Since the coefficient of friction of the finger pad in the fully occluded state is comparable to the maximum value observed when forearm skin is allowed to dry, it suggests that the mechanism involved is similar. Adams et al. [53] argued that the behaviour of the forearm is analogous to that of nylon in a sphere/flat configuration, which also shows such a maximum in the friction [83]. Nylon is plasticized by moisture so that the steady-state friction in the wet state is greater than that in the dry state since the real area of contact increases more than the interfacial shear stress is reduced as discussed in §2. When the surface of nylon was allowed to dry, there was an initial further increase in the friction because the interfacial shear strength increased while the contact area was unchanged. The contact area is controlled by the deformation characteristics of a subsurface region with a length scale of the order of the contact radius while the corresponding length scale for the interfacial shear strength is of the order of nm. Thus, the diffusion time associated with drying will be much shorter for the interfacial layer, which results in the initial increase in the interfacial shear strength without a significant reduction in the real area of contact. Both forearm and finger pad skin are somewhat different since the thickness of the stratum corneum may be less than the nominal contact radius and it is topographically much rougher than the nylon studied. Consequently, it was argued by Adams et al. [53] that the increase in contact area arose from the plasticization of the surface asperities, which also have a length scale that is large compared with that governing the interfacial shear strength.

It has also been proposed that the increase of the friction in the presence of moisture is due to capillary forces [33]. It was explained in §2 that the friction depends on the sum of the applied and adhesive forces (see equation (2.8)). The capillary forces arise from the surface tension and the reduced Laplace pressure in a liquid junction having a concave meniscus [84]. For poorly wetted surfaces, such as skin, the large contact angle may result in a convex meniscus with the Laplace pressure being positive so that this component of the capillary forces could be repulsive. For some systems not involving skin, it has been shown that the capillary forces can make a major contribution to the measured friction [85]. However, this is only the case if they are of a similar order to the applied normal forces. The adhesive force for wet forearm skin, which was measured using a spherical steel probe of radius 6.35 mm in direct pull-off experiments, is only about 5 mN [86], which is a small fraction of the normal forces that are typically applied in tactile exploration. Correspondingly small values were also obtained by extrapolation of the measured frictional force to a zero applied force [53]. However, these data were for a dry forearm and consequently any adhesion could only arise from molecular interactions rather than capillary forces. Tomlinson et al. [81] recently analysed friction data for the finger pad following immersion in water and could not unequivocally estimate the role of capillary bridges. Their analysis was based on a model developed by Persson [87] for a hard rough surface in contact with a more deformable body, who considered individual asperity contacts with condensed liquid bridges. Thus, currently, there is not evidence to support the contention that the capillary forces are a significant factor in increasing the friction of skin except possibly at small applied normal forces.

The smaller value of the friction of forearm skin in the wet state compared with the partially dried or damp state was attributed by Adams et al. [53] to the formation of a boundary film of water on the counter body. This was again based on the study of nylon friction by Cohen & Tabor [83], who showed that the friction in the wet state was increased by initially subjecting the contact to a normal force for an extended period, which would be consistent with disrupting a bound water film. More recently, the formation of water films has been measured directly in elastomer/glass contacts by Deleau et al. [82] and, as discussed in §2, elastomers are a useful model material for moisture plasticized skin. At low sliding velocities (less than 10 mm s⁻¹), it was found that water caused a reduction in the friction by about a factor of two. The surface mean roughness of the elastomer was 1 µm and the contact area of the asperities was unaffected by the presence of water; the reduction in friction was considered to arise from an attenuation of the autoadhesion. It is well established that such interactions are attenuated by wetting [85] and they were large for the elastomer studied by Deleau et al. [82] compared with skin. Elastomers are also different from skin because they are not plasticized by water and hence the friction does not increase in the wet state. However, these results show that sliding can operate in a boundary regime (i.e. a solid–solid interaction regime where the term ‘solid’ may include a thin molecular layer of bound water molecules) at low sliding velocities; this is important in the context of the velocity dependence of the friction (see §5). More importantly, in the current context, this may provide an alternative explanation for the reduction in skin friction in the wet compared with the fully occluded or damp states. That the adhesive forces for skin are small in terms of the pull-off values is common for topographically rough surfaces because the stored elastic strains in the asperities effectively act to create elastic repulsive forces [88]. However, adhesive interactions must operate when the asperities are deformed under an applied normal force in order to account for the friction. It is possible that these interfacial shear interactions are attenuated by the presence of moisture, which could also be the case for the elastomer/glass contacts since the contact area was unaffected by the presence of water. This will be discussed further in §5 where a fracture mechanics treatment is considered. Adhesive pull-off involves mode I fracture (tensile crack propagation), whereas sliding involves mixed-mode II and III fracture corresponding to a combination of in-plane and out-of-plane shear fracture [89].

Skedung et al. [90] observed that the friction of paper decreases as a function of sliding time as shown in figure 7. It was ascribed to the deposition of a lubricating layer of lipid from the surface of the skin although Gee et al. [91] had proposed that similar data could be explained by the absorption in the paper of secreted sweat. This is consistent with the data being described by equation (3.1); the best fit is also shown in figure 7. Paper is an example of a rough surface and Skedung et al. [90] found that the friction decreased with increasing surface roughness as shown in figure 8. Pasumarty et al. [62] measured the influence of occlusion on the friction of rough glass and reported that the steady-state value of the coefficient of friction decreased to approximately one-third of that for smooth glass. This is a result of the smaller real area of contact for the rough compared with the smooth glass. Dinç et al. [33] found that the friction of the finger pad decreases with increasing roughness of the countersurface but they believed that this was due to a reduction in the capillary forces. It is an unlikely explanation since the normal forces were in the range 0.1–20 N, which is very much greater than those arising by a capillary mechanism as discussed above. In summary, the occlusive frictional behaviour of paper could arise from a combination of competing factors possibly involving the permeability and topography of the paper, and lubrication by moisture and lipids. The behaviour of porous surfaces is in marked contrast to those that are impermeable and will contribute to the considerable different feel and grip of materials such as paper and glass. However, permeable surfaces tend not to be smooth so that any comparisons would have to account for any differences in surface topography.

Figure 7.

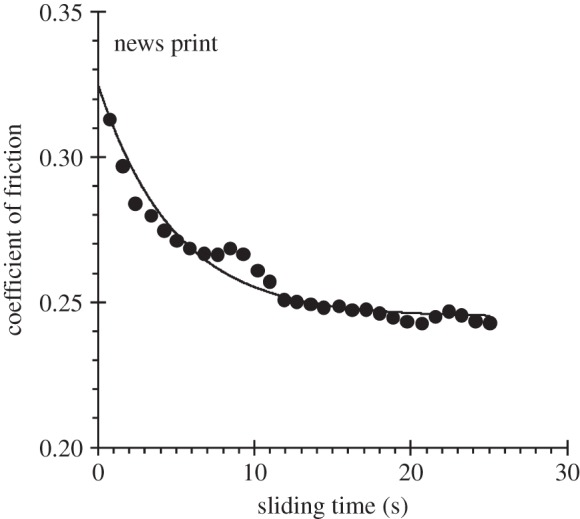
Typical dynamic coefficient of friction data for a finger pad sliding on news print as a function of time; the line is the best fit to equation (3.1). The data are taken from fig. 2 in the study of Skedung et al. [90].

Figure 8.

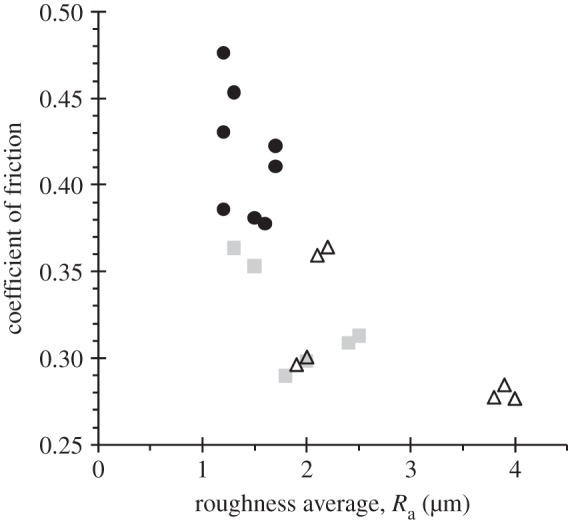
The dynamic coefficient of friction for different types of paper as a function of surface roughness. Uncoated: unfilled black triangles; coated mechanical: filled grey squares; and woodfree-coated: filled black circles. The data are taken from fig. 6 in the study of Skedung et al. [90].

4. Evolution of slip in the contact region

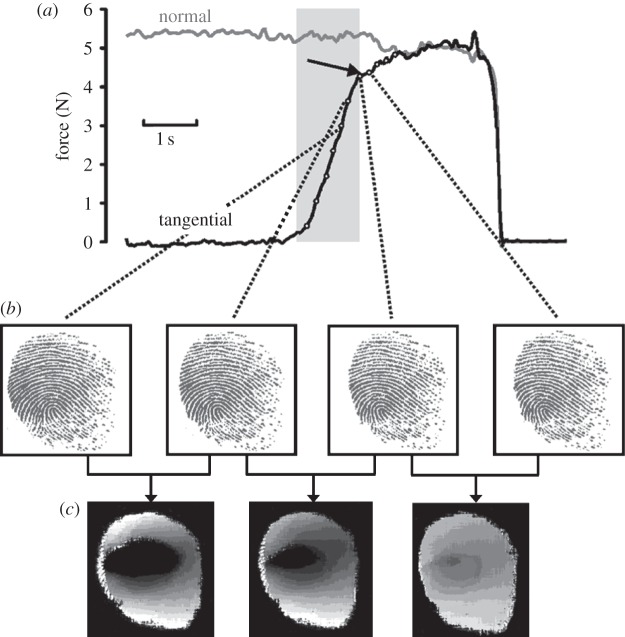
The evolution of slip is extremely important in both tactile perception and grip (see §1). In particular, it has been shown that increments in the grip force when holding an object stationary against gravity are triggered by incipient slips [5]. For small tangential stresses, relative slip does not occur and the effectiveness of the human mechanoreceptor tactile system to estimate the magnitude and direction of such stresses has been demonstrated in a number of studies [92–94]. At some critical tangential stress, Westling & Johansson [40] first reported that localized slip occurred at the periphery of the contact zone before the onset for sustained sliding. André et al. [95] employed an optical technique to measure the contact region of a finger pad in the static state and with increasing tangential force for normal loads of approximately 0.5 and 5 N, which is particularly relevant to tactile exploration and grip, respectively. Some typical images are shown in figure 9. As the tangential force, F, is increased, the stick area in the centre of contact region gradually decreases in size until gross sliding occurs when F = μW. The data are shown in figure 10 in terms of the stick ratio, φ, as a function of the tangential force where φ = C/A_gross and C is the gross contact area in the no slip region. It was observed that A_gross is approximately independent of F, although in some cases there was a small reduction when the contact was first loaded tangentially. Similar trends were reported by Tada et al. [96]. In addition, Terekhov & Hayward [97] showed that, frequently, the decreasing stick area apparently vanished at some critical tangential load rather than decreasing to zero before gross sliding occurred. They proposed that this phenomenon was mathematically consistent with the condition that the coefficient of dynamic friction is smaller than the static value.

Figure 9.

(a) Typical data for the time evolution of the normal and tangential forces involving a finger pad in contact with optically smooth glass, (b) associated image frames and (c) derived optical flow images. During the tangential preloading period (grey box in (a)), the tangential force increases until gross slip occurs (black arrow in (a)). Frames were selected during the preloading phase and compared with obtain the optical flow images. The apparent contact area is not correlated with the tangential force. The stick area within the contact (black areas in (c)) decreases with increasing tangential force and tends to zero with the initiation of gross slip. Adapted from André et al. [95].

Figure 10.

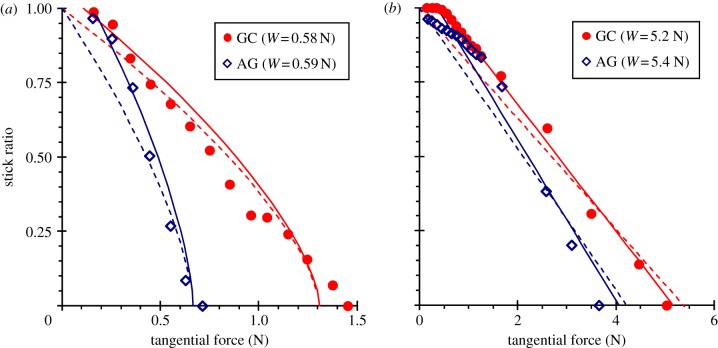
The stick ratio as a function of the tangential force for two subjects with very different hydration levels (filled circles, GC wettest; unfilled diamonds, AG driest) and for two target normal forces: (a) 0.5 N and (b) 5 N. Each point corresponds to the mean of five trials for a given subject and normal force. The dashed and full lines are best fits to equations (4.3) and (4.4) and equations (4.7) and (4.8) for (a) and (b), respectively, using the values of the parameters given in table 2. The data are taken from fig. 6 in the study of André et al. [95]. (Online version in colour.)

The formation of a slip annulus in a Hertzian contact that increases in size with increasing tangential force until the onset of gross slip was analysed independently by Cattaneo [98] and Mindlin [99]. As discussed in §2, at relatively small loads (less than 1 N) the contact between a finger pad and a planar surface may be approximated by a Hertzian contact between a sphere and a planar surface, which corresponds to a circular contact region of radius, a. Within the contact region, the Hertzian normal pressure distribution is parabolic with a maximum value in the centre (equal to 1.5p) that decreases to zero at the edges. Cattaneo and Mindlin assumed a coulombic slip boundary condition (τ = μp), which leads to the following axi-symmetric distribution of tractional stresses for the Hertzian normal pressure distribution when slip occurs:

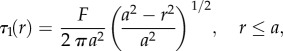4.1

where r is the radial coordinate with an origin in the centre of the contact. This distribution satisfies the stress boundary condition and the axi-symmetric form results in an annular slip region of constant width with F < μW. In order to satisfy the condition that the subsurface displacements relative to the interface are constant, it was necessary to superimpose a second stress distribution:

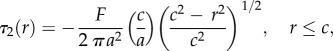4.2

where c is the radius of the no slip region. Integrating the stress distribution, τ₁(r)+τ₂(r), between 0 and a leads to the following expression for the tangential force:

4.3

Tada et al. [96] employed this relationship for data from finger pads but found that it generally underestimated the experimental data. Figure 10a shows the best fits to the low normal force data reported by André et al. [95], which demonstrates that equation (4.3) provides a first-order description of the trends for these datasets. The best-fit values of μ for the data corresponding to W = 0.6 N are given in table 2. In this case, the best fit was done on the basis of minimizing the maximum squared error for the data with φ < 0.5. The values are greater for GC than AG, which is consistent with the expected trend for the relative moisture levels as discussed in §3.

Table 2.

The parameters obtained for the best fit of equations (4.3) and (4.4) to the data shown in figure 10a for W ≈ 0.6 N, and of equations (4.7) and (4.8) to the data shown in figure 10b for W ≈ 5 N.

subject	W (N)	μ	τ0 (kPa)	α
AG	0.59	1.1	4.0	0.9
GC	0.58	2.3	2.3	2.1
AG	5.4	0.8	5.6	0.7
GC	5.2	1.0	5.6	0.9

The data of both Tada et al. [96] and André et al. [95] suggest that there is a threshold value of the tangential force required for a reduction in the stick ratio. One possible explanation is that the stress boundary condition given by equation (2.2) would be more appropriate than the simple coulombic condition, provided account is taken of the reduction in the contact area due to the topography of the finger pad. Tüzün & Walton [100] have derived an upper bound solution for the tangential force, F_U, that leads to the prediction of a threshold value, which may be written in the following form for a finger pad:

4.4

where such that A_gross/A approximately 3.3 according to Soneda & Nakano [74]. The upper bound was obtained by the addition of the constant term, to the Cattaneo and Mindlin stress distribution. It is useful to note that equation (2.2) may be written as

4.5

Thus, α → μ at high loads so that equation (4.4) tends to the solution given by equation (4.3) in this limit.

The best fits of equation (4.4) to the data of André et al. [95] for W = 0.6 N are also shown in figure 10a; they were weighted such as to minimize the maximum squared error for data in the range 0.5 < φ < 0.75. The figure demonstrates that the threshold tangential force required for the initiation of partial slip is captured by this model. The best-fit parameters are given in table 2 and are of similar order to those given in table 1 for the inner forearm in the wet state. The value of τ₀ for the subject GC is about a factor of two smaller than that for AG. This is consistent with GC being classed as moist since it would be expected that the interfacial shear stress would be reduced by the more extensive plasticization at a relatively greater moisture content. For example, the values of τ₀ for glassy (unplasticized) organic polymers are about three orders of magnitude greater [101] than those determined here for the finger pad. This demonstrates the considerable effect of plasticization by moisture on the finger print ridges. As discussed previously, moisture-induced plasticization occurs primarily by a free volume mechanism although, in the case of skin, there could be a contribution from a bond scission mechanism involving the dissociation of hydrogen bonds. The former mechanism refers to the increase in free volume caused by disruption of the packing of polymer chains, while the latter refers to the dissociation of polymer–polymer hydrogen bonds. Either mechanism will increase the mobility of the polymer chains and contribute to the reduction in τ₀. Since it is a free volume in polymeric systems that leads to the pressure sensitivity of the mechanical properties, the larger value of the pressure coefficient of the interfacial shear strength, α, for GC could be rationalized on this basis.

The Hertz equation assumes mechanical isotropy and homogeneity. Wang & Hayward [102] found that Young's modulus of the finger pad was typically 3.61 and 1.54 MPa in the directions parallel and orthogonal to the fingerprint ridges. Such anisotropy could influence the shape of the contact region but the effect seems to be second order compared with deviations from a perfectly ellipsoidal cap geometry of the finger pad. The Hertz equation neglects the influence of adhesive forces, in which case more complex theories are involved [103] although they do not account for the distortion of the circular contact area to one that is elliptical as has been observed for elastomers [104].

As discussed in §2, there are deviations from Hertzian deformation of a finger pad at loads greater than approximately 1 N. Hence the selection of a parabolic normal pressure distribution may not be appropriate for the data published by André et al. [95] at approximately 5 N where A_gross would be expected to be independent of the normal load. The normal pressure distribution obtained experimentally for a finger pad depends critically on its orientation and the load applied. Moreover, such distributions are difficult to measure with sufficient spatial resolution to determine whether their functional form is load-dependent [105–108]. However, there is some evidence for a flatter than Hertz distribution in the results measured for a normal load of 4 N by Johansson & Flanagan [107], and in the theoretical distributions obtained for a compressed thin elastic layer when the thickness of the layer is much less than the contact area [109]. Since this will also be the case for the finger pad at large loads, there is some justification for selecting a uniform pressure distribution for the slip analysis. Here, the frictional force associated with the slip region would be given by

4.6

Since τ′ = μW/A_gross, equation (4.6) can be written in the following form:

4.7

An analogous upper bound solution to equation (4.4) may be obtained by assuming that the intrinsic interfacial stress acts only in the stick region, thus:

4.8

In both cases, the stick ratios decrease linearly with the tangential force. The best fits of equations (4.7) and (4.8) to the results of André et al. [95] are shown in figure 10b and the upper bound solution appears to be most consistent with these data; the values of τ₀ and α as well as μ are given in table 2. It should be noted that similar values (within 20%) are obtained if the data are analysed using equations (4.3) and (4.4), which indicates that the analysis is relatively insensitive to the exact functional form of the normal pressure distribution. The values for AG are similar within experimental error to those obtained at the smaller normal load but it is not the case for GC. This probably reflects the experimental difficulties of working with real subjects. Inevitably there will be variations in the extent of sweat secretion at different times and moreover it was not possible to control the occlusion time in these experiments. Nevertheless, the approach does provide some useful insights into the mechanisms involved.

Initially at small applied tangential loads, André et al. [95] observed in some cases that there was a small reduction in the gross area of contact before a slip annulus was initiated. Presumably this involves a peeling mechanism. In the above analyses, only data corresponding to a constant value of the gross contact area were considered.

5. Influence of sliding velocity

The sliding velocity range that is most relevant to tactile exploration is about 10–200 mm s⁻¹ [31,110]. As in the case of the normal force during tactile exploration, it might be expected that the velocity is a variable that is controlled by a subject at an intermediate range of values; the factors involved would include comfort and an optimization of the time to make a tactile assessment. Bensmaïa & Hollins [15] investigated the influence of the sliding velocity on vibrotaction particularly in the context of measuring the intensity and frequency of the induced vibrations in tactile perception. However, there have been only a few systematic studies of the effect of this variable on the friction of the finger pad [111]. Dinç et al. [33] carried out measurements at three sliding velocities of 6, 20 and 60 mm s⁻¹. They found that the coefficient of friction typically decreased with increasing velocity in this range for both smooth and rough polymeric surfaces. Pasumarty et al. [62] carried out more detailed studies. Figure 11 shows their data for smooth glass and PP surfaces in the occluded and wet states; as described in §3 the values are less in the wet compared with the fully occluded state. It appears that the coefficients of friction exhibit a maximum in approximately the velocity range for tactile exploration. There is some evidence that the wet friction of the inner forearm also exhibits a maximum in a similar velocity range [59].

Figure 11.

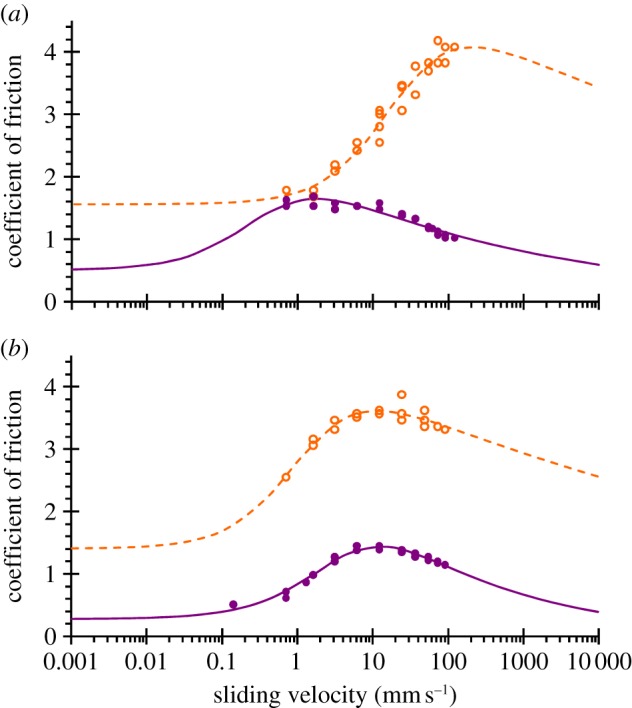
The dynamic coefficient of friction (W = 0.2 N) for a finger pad as a function of sliding velocity for (a) an optically smooth glass surface, and (b) a smooth PP surface. The steady-state dry values of the coefficient of friction, μ_∞: unfilled circles and the wet values of the coefficient of friction, μ_w: filled circles. The lines are the best fits to equation (5.4) using the parameter values given in table 3. The data are taken from figs 18 and 19 in the study of Pasumarty et al. [62]. (Online version in colour.)

As described in §2, the energy dissipation associated with the adhesion mechanism of friction is primarily the result of viscoelastic deformation. More specifically the interfacial shear strength depends on molecular relaxation mechanisms and may be related to the viscoelastic loss spectrum. Consequently, maxima in the frictional force occur for polymeric materials at characteristic sliding velocities and temperatures [112]; the activity of a plasticizer has an equivalent effect to temperature on molecular mobility. A number of approaches for the development of models to describe the adhesion mechanism of friction for glassy organic polymers, elastomers and thin organic films such as SAMs (self-assembled monolayers) have been adopted. As mentioned in §3, sliding friction may be usefully considered as mixed-mode interfacial fracture. In such processes, the fracture energy also arises from local deformation at the crack tip caused by the transmission of stress from the interface. The relative interfacial and bulk contributions in friction models are a critical factor in developing the underlying principles.

The evidence from the friction of elastomer/glass contacts at low sliding velocities suggests that under these conditions solid–solid contacts could prevail for the finger pad in the fully occluded and wet states (see §3). However, a critical complexity for skin is that it is not possible to discount the possibility of the role of water films on the basis of the available experimental evidence. For elastomer/glass contacts, it has been observed that thin water films (approx. 200 nm) are progressively developed at asperity contacts as the sliding velocity is increased from 10 to 100 mm s⁻¹ [82]. In this mixed lubrication regime, the friction decreased with increasing velocity, thus providing evidence that this is a possible mechanism for the smaller friction of a wet finger pad compared with that in the fully occluded state. However, the coefficients of friction for the finger pad even in the wet state are greater than 1 at the highest velocities studied (figure 11). This is not consistent with effective mixed lubrication, which refers to regime in which small domains of the sliding surfaces are separated by fluid films. Such lubrication and, possibly a hydrodynamic regime in which the sliding surfaces are completely separated by water, will almost certainly apply at sufficiently high sliding velocities. The data in figure 11 may be compared with those obtained with hydrogels for which a maximum in the friction is also observed at intermediate velocities [113]. This was believed to correspond to a boundary regime and an increase in the friction at greater velocities was considered to be the result of hydrodynamic lubrication.

On the basis of the above arguments, the analysis of the data in figure 11 will be considered in terms of a boundary regime. An Eyring model has been applied to glassy polymers [101]. This is a thermally activated description of plastic flow with stress activation volumes of approximately 0.5 nm³ that correspond to the size of the region in the unit shear process. The model could be fitted to the data to account for the increase in the interfacial shear stress at the smaller values of the velocity but it would not account for the maximum in the friction at intermediate sliding velocities. This phenomenon is characteristic of elastomers and, as has been discussed in §2, such materials are a useful model of skin. Some models of the dry friction of elastomers consider only interfacial processes. For example, Pasumarty et al. [62] interpreted the velocity dependence of the friction of the finger pad by applying a stochastic approach proposed by Schallamach [114] for elastomers that was based on the concept that reversible bonds involving molecular chains at the sliding interface continuously form and dissociate.

The stochastic model predicts frictionless slip at low and high velocities because the energy dissipation is only ascribed to interfacial processes. This limitation is eliminated by considering a fracture mechanics description of sliding friction, which has been developed for elastomers and which accounts for viscoelastic losses at the crack tip [115]. It was formulated for rough surfaces but it could be applied to those that are smooth. The model is based on an expression for the fracture energy associated with adhesion of a viscoelastic contact [116]:

5.1

where V is the sliding velocity, T the absolute temperature and G_Ic the critical mode I fracture energy so that this expression was assumed to be applicable to shear fracture. The parameter Δγ is the work of the adhesion, which may be approximated by a decreasing function of the sliding velocity [117]:

5.2

where Δγ₀ is the thermodynamic work of adhesion corresponding to V = 0, V^⊗ = V/V_s such that V_s = ℓ/ξ_j where ℓ is a characteristic length (see below) and ξ_j is a junction formation time.

The second term in equation (5.1) is an increasing function of the sliding velocity arising from viscoelastic dissipation:

5.3

where E_∞/E₀ is the ratio of the glassy and rubbery moduli (approximately 100) and V_e is a characteristic velocity associated with viscoelastic relaxation. The final expression for the coefficient of friction can be written in the following form:

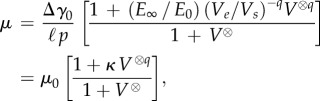5.4

where q is a material parameter (0 ≤ q ≤ 1), μ₀ = Δγ₀/ℓp and κ = (E_∞/E₀)(V_e/V_s)^−q. Momozono et al. [115] obtained close agreement with published data for a range of polymers including elastomers. However, Vorvolakos & Chaudhury [118] argued that their data for elastomers sliding on smooth surfaces could be adequately described by the stochastic model without the need to invoke viscoelastic losses. They suggested that the finite values observed for an elastomer sliding on polystyrene could arise from surface diffusion that would be too slow at high velocities so that only the stochastic process would operate.

The above approach is based on the global energy change due to fracture and so ignores the details of the slip process, which is complex since the surfaces remain in contact unlike a tensile fracture. Attempts have been made to develop microscopic models but inevitably more parameters are introduced that are difficult to measure directly. For example, Persson & Volokitin [119] proposed that small stress domains adjacent to the sliding interface exist. It was argued that the onset of microslip of a domain occurred at a critical depinning stress, which is governed by thermal fluctuations. By considering the viscoelasticity of the domains it was possible to account for the maxima in the velocity dependant frictional stress.

As discussed in §3, the adhesive force for a finger pad in a sliding contact is negligibly small compared with the range of applied normal forces considered in the current work. This arises from the stored elastic strains in the asperities on the surfaces of the fingerprint ridges and will result in the value of G_Ic in equation (5.1) also being insignificantly small. However, equation (5.4) may be applied to analyse the friction of a finger pad in the occluded or wet states because under an applied load the asperities are deformed so that intimate contact regions are developed as explained in §3. Thus, although it would not be possible to measure the value of Δγ₀ by pull-off measurements, as in the case of smooth elastomer contacts, there will be an effective shear adhesive interaction in sliding a topographically rough surface such as a finger pad, which of course is the basis of the adhesion mechanism of friction. The main source of error in applying such models is the limited range of sliding velocities that are possible in practice. In the case of the work published by Pasumarty et al. [62] for a finger pad sliding on PP in the occluded state and glass in the wet state, there is insufficient data at low sliding velocities to fit an accurate value of μ₀. For glass in the occluded state, the friction data have not been measured at sufficiently high velocities to identify a peak and thus it is not possible to accurately fit a value of q. Consequently, here reasonable estimates of these parameters were made in order to obtain the best fits of the data in figure 11 to equation (5.4). The regression fits are shown in figure 11; the corresponding values of the parameters μ₀, κ, q and Vs are given in table 3 together with the standard errors. It is not possible to comment on the validity of the values of these parameters based on independent measurements since pull-off data cannot be obtained as explained previously. However, it is reasonable that similar values of q are obtained for the dry occluded and wet cases since q is a material parameter. In addition, the values are less than the upper limit of unity; for comparison the typical value for elastomers is 0.4 [115].

Table 3.

The parameters obtained for the best fit of equation (5.4) to the data shown in figure 11. The values given in parentheses are the standard errors for the fitted parameters obtained by nonlinear regression. Parameter values given without standard errors were kept constant during the fitting procedure.

	μ0	κ	q	Vs (mm/s)
PP (dry, occluded)	1.4	3.1 (± 0.1)	0.94 (± 0.02)	1.2 (± 0.2)
PP (wet)	0.28 (± 0.05)	8.6 (± 1)	0.77 (± 0.04)	4.7 (± 1)
glass (dry, occluded)	1.6 (± 0.1)	3.2 (± 0.2)	0.94	22 (± 4)
glass (wet)	0.50	4.7 (± 0.2)	0.86 (± 0.02)	0.39 (± 0.1)

For V → 0, μ → μ₀ and in this asymptotic limit, it is possible to calculate a value of ℓ if a reasonable value of Δγ₀ is assumed, which was taken to be 35 mJ m⁻² [65]. The contact area (A_ridge = A) of the fingerprint ridges for the normal force of 0.2 N was estimated to be 0.3 cm², which leads to a contact pressure of approximately 22 kPa. On this basis, the values of ℓ for PP are about 1 and 6 µm in the dry occluded and wet states, and for glass they are about 1 and 3 µm in the dry occluded and wet states. However, Momozono et al. [115] argued that this parameter should be of the order of the molecular chain lengths for elastomers (approx. 10 nm). In terms of a fracture mechanics analysis, the length scale ℓ corresponds to the critical crack opening displacement, which is a measure of the crack tip bluntness induced during crack propagation. The mode I values are actually quite large being approximately 100 µm for glassy polymers and approximately 2000 µm for rat's skin [120]. There are no comparable experimental data for modes II and III, although it is normally assumed that they negligibly small compared with the mode I values since they do not nominally involve crack opening. In fact this topic is not understood but clearly the shear modes values should be finite otherwise the stresses at the crack tip would be singular. That the values determined here are two orders of magnitude greater than those expected for elastomers may be reflect the much greater deformability of plasticized skin. The smaller values of μ₀ for the wet compared with the dry occluded state would also be consistent with this interpretation if it resulted in a more plasticized state.

In summary, the friction of the finger pad in the occluded or wet states has a maximum value in a velocity range that is typical of that employed during tactile appraisal. Although the ability of subjects to discriminate velocities is relatively poor for smooth dry surfaces sliding against the finger pad [121], it would be of interest to examine the discriminative ability in the occluded and wet states at different velocities to determine if an improved magnitude estimation is possible based on the differences in friction. Currently, the role of the sliding velocity in touch is not well understood. However, as discussed below, it is an important variable for understanding the mechanisms of friction and it is a critical factor in intermittent motion.

It is possible to fit various theoretical models to frictional data as a function of the sliding velocity but the quality of the fit will not provide an unequivocal delineation of the models unless the fitting parameters can be determined independently. Moreover, it is essential to obtain data over a wider range of velocities in order to obtain more accurate values of the fitting parameters. However, there are practical limitations with in vivo measurements but data at lower velocities would discriminate the stochastic from the fracture mechanics model since the friction tends to zero and a finite value, respectively, for these models. Both models predict that the friction tends to zero at high velocities but it is possible that fluid lubrication could develop in the wet cases so that the models would not be applicable in this regime. Moreover, in the dry state at higher velocities than those studied by Pasumarty et al. [62], it is possible that there could be a significant increase in the contact temperature. The influence of temperature on the friction of human skin has not been studied systematically, but it is likely to be complicated by the effects on the rate of sweat secretion and its evaporation. However, it has been found that the characteristic occlusion times are similar for stainless steel, PP and glass, which have different thermal diffusivities, and this suggests that temperature is not an important parameter at least for small variations from body temperature [62].

It has been mentioned in §1 that stick–slip is associated with an unpleasant feel [33]. Stick–slip occurs when the friction decreases with increasing velocity provided that the system is not subcritically damped. Thus, in the case of the data reported by Pasumarty et al. [62] for smooth surfaces, stick–slip was observed for sliding velocities corresponding to those that were greater than those at the maximum value of the coefficient of friction, viz. glass in the wet state and PP in the wet and occluded states. They also observed that roughened glass resulted in stick–slip even in the occluded state albeit at a small amplitude, which could suggest that the motion involves relaxational oscillation. This is sinusoidal lateral motion of the whole finger pad whereas, as also discussed in §1, for rough surfaces, normal vibrations associated with the periodicity of the surface topography are important in tactile assessment. The corresponding role of relaxational oscillations has yet to be elucidated.

6. Conclusions

Although the frictional behaviour of a finger pad is extremely complex, it may be understood using theoretical models derived for conventional organic polymers. The main factors that contribute to the complexity are the unusual contact mechanics associated with the fingerprint ridges and the relatively large number of sweat glands under these ridges. In the dry state, a finger pad has a coefficient of friction that is comparable to glassy polymers. However, with sustained sliding on a smooth impermeable countersurface, the secretion of moisture from the sweat glands causes the fingerprint ridges to be highly plasticized so that the surface asperities become considerably more deformable and there is a large increase in the real area of contact at these ridges. This causes the coefficient of friction to increase by about an order of magnitude to values comparable with elastomers, which can also exhibit contact areas close to the nominal values due to the deformability of the surface asperities. Such behaviour is consistent with the adhesion model of friction that relates the frictional force to the product of the real area of contact and the interfacial shear strength. If excess water is added to a fully occluded finger pad contact, there is a reduction in the friction. For non-glabrous regions of the skin, such as the inner forearm, that have sparsely populated sweat glands, significant occlusion is absent but a similar maximum in the friction may be induced in wet contacts after a critical drying period. For a porous surface such as paper, there is a slight decrease in the friction of a finger pad with increasing dwell time and this may be attributed mainly to the absorption of the secreted sweat.

At normal loads that are generally applied in tactile exploration (less than 2 N), there is considerable evidence that the coefficient of friction of a finger pad sliding on a smooth countersurface decreases with increasing normal load. This is a characteristic of smooth sphere-on-flat or crossed-cylinder contacts and, consequently, it is an unexpected feature given the pronounced surface topography of a finger pad. It has been argued that an alternative explanation is that the data could be fitted within experimental uncertainty to a load independent coefficient of friction and an adhesion term. However, direct measurements of the adhesive force suggest that adhesion is relatively small compared with the typical forces usually applied in both taction and grip. Consequently, the contact mechanics of a finger pad requires further study in order to fully rationalize the observed frictional data.

The onset of slip for a finger pad occurs by the growth of an annulus of failure that is initiated at the perimeter of the contact region. This is commonly observed for elastomers rather than glassy polymers because the mixed-mode crack propagation involved is relatively stable for elastomers and therefore can be more readily observed. However, the theory developed for elastomers involving a simple coulombic boundary condition does not adequately describe the data for a finger pad. Unlike elastomers, skin exhibits a pressure-dependent frictional boundary condition that leads to a satisfactory description when the theory is modified to take this into account. In addition, at the relatively large normal loads employed in grip, there is some uncertainty about the exact distribution function for the contact pressure. However, it appears that the model is relatively insensitive to this function since both a parabolic (Hertz) and uniform function lead to similar values of the interfacial shear parameters.

The maximum in the coefficient of friction with increasing velocity for a dry occluded and wet finger pad is consistent with the behaviour of elastomers. It is possible to partly rationalize the results using stochastic models of molecular pinning and unpinning but they lead to the possibly unreasonable prediction of negligible coefficients of friction at low velocities. Models based on viscoelastic fracture mechanics are not subject to this limitation. However, this approach is difficult to validate without direct measurements of the parameters in the models. It is possible that the reduction in the friction at the larger sliding velocities could be ascribed to the partial formation of thin water films on the surfaces of the fingerprint ridges. This could be confirmed if it were possible to measure the thickness of such films directly.

The current paper has attempted to provide a coherent understanding of the friction of the finger pad that should assist in the interpretation of the response of the cutaneous mechanoreceptors and the development of computer simulations of touch and grip with neuromechanical coupling. For example, Srinivasan et al. [41] investigated the mechanoreceptive afferent response to smooth and rough surfaces. For smooth surfaces, directional sliding is encoded by the slowly adapting mechanoreceptors as a result of the tangential stretching of the skin, which depends on the complex behaviour of the friction involving such factors as occlusion and the sliding velocity. Interestingly, in the absence of intermittent motion, they found that it is not possible to perceive whether or not slip occurs, which required topographical features of a minimum critical size to activate the rapidly adapting mechanoreceptors. However, Johansson & Westling [39] observed that the onset of localized slip in the periphery of the contact zone was encoded by fast-adapting units and the physics of these slip events can be described quantitatively using the models described in the current paper. More work is required to fully understand the relative importance of stick–slip, relaxational oscillation and vibrations in the tactile evaluation of surfaces, particular with respect to affective touch.

Finally, in addition to the importance of the tribological properties of the finger pads in understanding the influence on tactile perception and grip function, there are relevant applications in robotics and prosthetics. Robots will play an increasingly important role, for example, as industrial tools in manufacturing and for assisting the disabled and elderly to lead independent lives. However, the precise coordination of the senses of vision and touch limits the current haptic performance of industrial and personal robots in carrying out manipulative tasks of the complexity that we take for granted. Novel polymeric materials for robotic and prosthetic hands that more closely mimic the tribological properties of the finger pads could greatly enhance current tactile and grip function.