An automated approach for three-dimensional quantification of fibrillar structures in optically cleared soft biological tissues

Abstract

We present a novel approach allowing for a simple, fast and automated morphological analysis of three-dimensional image stacks (z-stacks) featuring fibrillar structures from optically cleared soft biological tissues. Five non-atherosclerotic tissue samples from human abdominal aortas were used to outline the multi-purpose methodology, applicable to various tissue types. It yields a three-dimensional orientational distribution of relative amplitudes, representing the original collagen fibre morphology, identifies regions of isotropy where no preferred fibre orientations are observed and determines structural parameters throughout anisotropic regions for the analysis and numerical modelling of biomechanical quantities such as stress and strain. Our method combines optical tissue clearing with second-harmonic generation imaging, Fourier-based image analysis and maximum-likelihood estimation for distribution fitting. With a new sample preparation method for arteries, we present, for the first time to our knowledge, a continuous three-dimensional distribution of collagen fibres throughout the entire thickness of the aortic wall, revealing novel structural and organizational insights into the three arterial layers.

1. Introduction

The importance of fibrillar collagen in arterial tissue has long been known [1,2]. It is not only mechanically the most important tissue constituent [3,4], but research indicates that it also plays an important role in arterial disease and degeneration [5,6] as well as in the healing of dissecting aortic aneurysms [7], which makes the evaluation of morphological collagen data within arterial walls essential for an improved understanding of vascular health and mechanics. The architecture of the arterial wall, however, represents a major experimental challenge: first, its thickness up to approximately 1.4 mm [8] of non-transparent material limits the application of optical techniques to assess the orientation of fibrillar collagen; second, the specific detection of collagen in the three layers of the aortic wall typically requires labelling techniques such as the use of antibodies that are not feasible in thick tissues; third, because the orientation of the fibrillar collagen in the arterial wall responds to the internal blood pressure, any preparation of arterial wall samples for subsequent analysis requires preservation of in vivo conditions to obtain reliable information about the orientation of fibrillar collagen.

The use of optical clearing for enhanced visualization of morphological structures in whole organs or thick tissue structures has seen a renewed interest of late. Often, optical clearing is based on refractive index matching of various scatterers (e.g. collagen) and the ground matrix of soft tissue (e.g. interstitial fluid), by replacing water in the tissue with a fluid of a similar index of refraction as that of the proteins [9–11]. Measurements based on spectroscopy techniques, polarization or optical coherence microscopy as well as nonlinear imaging techniques such as two-photon fluorescence and second-harmonic generation (SHG) yield more valuable, otherwise virtually inaccessible information when performed on cleared (versus uncleared) soft biological tissue [12]. Multi-photon microscopy (MPM) is especially suited for three-dimensional visualization [13–15] owing to its optical sectioning capability using sequential automated slicing (z-stacks) [16]. In combination with optically cleared tissue, there is no more need for manual slicing to obtain images of whole organs or thick tissue structures and furthermore leaves the tissue whole for traditional histological investigations.

At the same time, numerical modelling based on continuum mechanical frameworks has developed into a powerful tool for hypothesis testing and verification of theoretical frameworks against experimental and clinical observations [17–22]. Despite the broad range of tissues studied through computational analyses (e.g. arteries, cartilage, heart, cornea, etc.), numerical models share the commonality of requiring physiologically determined material and/or structural parameters that can usually be obtained from biomechanical experiments [23], clinical data [24] or can be extracted from images [25].

Such an analysis, however, requires the integration of various tasks from different disciplines such as tissue preparation and imaging techniques, image analysis as well as numerical modelling. In this study, we aim to overcome these limitations by developing a novel, simple, fast and automated method consisting of combining well-established techniques and expertise from different fields for the purpose of extracting and quantifying three-dimensional morphological data from optically cleared whole tissues.

Specifically, we combine tissue clearing using a solution of benzyl alcohol to benzyl benzoate (BABB) [26,27] with SHG imaging of fibrillar collagen [28,29], Fourier-based image analysis for characterizing collagen organization [30–32] and maximum-likelihood estimation (MLE) for distribution fitting of three-dimensional-orientational datasets [33]. First, our method yields the three-dimensional distribution of amplitudes (1° resolution), representing the orientations of fibrillar collagen extracted from a z-stack; second, it identifies isotropic regions in the tissue where no preferred fibre orientations are observed; third, it identifies regions of anisotropy characterized by two structural parameters: one describing the preferred (or principal) orientation of the fibres (denoted μ), and the other describing the degree of fibre alignment (or concentration) about that preferred orientation (denoted b). Both structural parameters can be used directly in numerical modelling codes using fibre-reinforced constitutive laws [3,20,34].

In general, our method is suited to analyse images containing (straightened) fibrillar structures independent of the type of tissue or material. In this work, we use non-atherosclerotic human abdominal aortic tissue samples to explain our approach and additionally introduce a new sample preparation method that allows for the fixation of whole blood vessels approximating in vivo geometries (by considering axial pre-stretches and in vivo blood pressures [8,35]). Using our method, we are able to present, for the first time to our knowledge, a continuous three-dimensional distribution (1° resolution) of collagen fibre orientations throughout the entire thickness of the human abdominal aortic wall with a thickness of approximately 1 mm.

2. Material and methods

2.1. Tissue preparation and fixation

Five human abdominal aortas without atherosclerotic changes of type IV or higher [36] (age in years and gender (m/f): 53 m, 64 m, 65 f, 65 f, 77 m) were harvested within 24 h of death. All samples were cleaned from the surrounding tissue, and anatomic landmarks (such as branching of the common iliac arteries) were used to ensure consistent sample locations for all five vessels. To reconstruct the in vivo stress/strain state of the abdominal aortas, we developed a custom-made device that enabled us to mount the intact aortic tube, stretch it axially and simultaneously pressurize it. The axial stretch was controlled through a video extensometer, the pressure was automatically monitored and kept constant through a high precision pressure reducer (control range: 5.0–200.0 ± 0.1 kPa). The mounting device was encased in a pneumatic glass basin filled with 4 per cent paraformaldehyde (PFA), where the pre-stretched and pressurized vessel was kept for 12 h for a sufficient fixation. All vessels were pre-stretched 12 per cent in the axial direction based on the lower bound of in vivo values reported [37], and pressurized at the average systolic arterial pressure (SAP) of 130 mmHg. After chemical fixation, the newly stiff vessel was removed from the mounting device for subsequent optical clearing.

2.2. Optical clearing

The vessels were rinsed with phosphate-buffered saline (pH 7.4) to wash off excess PFA, and dehydrated using a graded ethanol series with each step lasting 45 min, according to the following protocol: 50 per cent, 70 per cent, twice at 95 per cent and twice at 100 per cent. For optical clearing, we used a solution of 1 : 2 BABB. Each vessel was initially submerged into a solution of 1 : 1 ethanol : BABB for 4 h before submerging them into a 100 per cent BABB solution where they remained to clear for at least 12 h before imaging. All steps involved in the tissue preparation, fixation and optical clearing were performed at room temperature.

2.3. Histology

Cleared aortic specimens were embedded in paraffin and sectioned at 5 µm. The resulting cross sections were then stained with picrosirius red (PSR) to highlight fibrillar collagen and Elastica Van Gieson (EVG) to highlight elastin. All images were acquired with a Nikon 80i microscope in combination with Nikon NIS-Elements F software. Magnification was set to 600×. Images from the PSR-stained sections were acquired using appropriate polarizing optics.

2.4. Nonlinear optical imaging

SHG imaging of collagen was performed using an imaging set-up consisting of a picosecond laser source and an optical parametric oscillator (OPO; picoEmerald; APE, Germany; HighQ Laser, Austria) integrated into a Leica SP5 confocal microscope (Leica Microsystems, Inc., Austria). To induce SHG of collagen, the OPO was tuned to 880 nm. Detection of backscattered second-harmonic signal was achieved using a BP 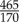emission filter and with a non-descanned detector in epi-mode. Image acquisition was performed using a Leica HCX IRAPO L 25 × 0.95 water objective with a working distance of 2.5 mm for deep tissue imaging; z-stacks (three-dimensional image stacks) of the cleared aorta specimens were acquired using 0.62 × 0.62 × 1 µm sampling (x–y–z). Image processing of z-stacks (three-dimensional Gaussian filtering) and subsequent volume-rendering were performed using Amira visualization software (Visage Imaging, Inc.).

2.5. Data analysis

2.5.1. Fibre orientation assessment

To extract collagen fibre orientations from two-dimensional images, we used a Fourier-based image analysis method in combination with wedge filtering [25]. Towards this end, we applied a window using a raised cosine function to reduce the grey-scale values to 0 at the image periphery, which could otherwise cause frequency-domain effects in subsequent steps. Next, we applied a fast Fourier transformation (FFT) to the windowed grey-scale image, represented by a distribution function f, where f(x, y) denotes its value at point (x, y). The Fourier transform (FT) of f is a function denoted F = ℱ(f), where its value at point (u, v) can be written as [ℱ(f)](u, v) = F(u, v). After performing a coordinate shift, which transforms the lowest spatial frequency to the origin, we calculated the power spectrum P by multiplying the FT with its complex conjugate, namely

2.1

The fibre directions are now discriminated by spatial frequency and orientation. To extract them from the power spectrum, we used wedge-shaped orientation filters [30]. By means of summation of every P(u, v) within individual 1° wedges, we obtained a discrete distribution of relative amplitudes I(Φ) (in %) as a function of the corresponding fibre angle Φ. Finally, the angular distribution was shifted back by 90° to adjust for the shift owing to the FT. This procedure was performed for all n images in a z-stack, yielding a three-dimensional dataset per z-stack containing I(Φ) of every image. The angles Φ and amplitudes I for individual images n were stored in the x-, y- and z-directions of the dataset, respectively; Φ = 0° and Φ = 90° correspond to the horizontal and vertical axes of the images, as well as to the circumferential and axial directions of the vessel, respectively.

2.5.2. Determination of anisotropy

In order to perform meaningful distribution fitting, we first distinguish between anisotropic and isotropic angular fibre distributions (the latter is not subjected to subsequent distribution fitting). Towards this end, we first smoothed the amplitudes of the original three-dimensional dataset using moving average filters in the z- and then in the x-direction with a span range of 17° and 33°, respectively. To ensure that our choice for both span ranges was robust, we performed a perturbation analysis. Note that a robust choice implies that the outcome regarding isotropy or anisotropy was not affected by small perturbations (approx. ± 5°) of either span range. To check for isotropy of a given distribution we made use of the fact that the cumulative distribution function (CDF) F(Φ) of an isotropic distribution is a straight line. Therefore, we calculated the CDF of every (now smoothed) angular distribution in the three-dimensional dataset, according to

2.2

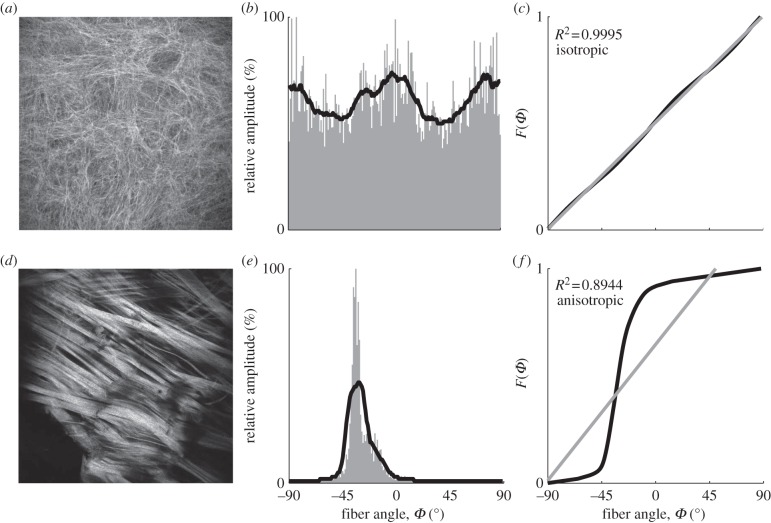
where −90° ≤ x ≤ 89°, fitted it with a first-order polynomial and determined the corresponding R² value as a measure of the goodness of fit. If the resulting R² value was above a threshold of 0.998, then the distribution was considered isotropic, otherwise anisotropic. We determined the appropriate threshold value by running a perturbation analysis for a broad range of potential thresholds. The most suited threshold value was identified based on where the results (isotropy or anisotropy) would correspond well to the fibre morphology visible in the original images. An illustrative example is shown in figure 1.

Figure 1.

Schematic of steps to distinguish between images showing an isotropic versus anisotropic fibre distribution. Two cases, one classified as isotropic (a–c) and another one classified as anisotropic (d–f) are shown. All images were acquired using second-harmonic generation imaging. The distribution of relative amplitudes (grey bars, second column) was determined through Fourier-based image analysis and subsequently smoothed using a moving average filter (solid black curves). From the smoothed distribution, the cumulative distribution function F(Φ) was calculated (third column, black curves), fitted with a first-order polynomial (grey curves), and the corresponding R² value was determined. If R² was above a threshold level of 0.998, then the distribution was considered to be isotropic, otherwise anisotropic.

2.5.3. Distribution fitting

To fit the anisotropic distributions using MLE, we first needed to determine the number of major peaks (fibre families) for every distribution I(Φ) in a three-dimensional dataset and second, the approximate locations Φ of those peaks used as starting parameters for subsequent MLE fitting. To that end, we first smoothed the amplitudes of the original (unsmoothed) three-dimensional dataset using moving average filters in the z- and then in the x-direction with a span range of 7° for both directions. Next, we used a standard peak detection algorithm, based on the alternating signs of the derivatives, to identify local maxima or minima in the smoothed angular distribution, yielding the locations of the major peaks. Subsequently, amplitude offsets were removed by subtracting the smallest amplitude value from every I(Φ). Depending on the number of peaks m (which was either one or two per image), each distribution was then fitted with either one or a mixture of two π-periodic von Mises distributions [25,34,38], given by

2.3

The fitting parameters are the concentration parameter b_i, determining the shape of the von Mises distribution (increased b_i-values correspond to narrower (more anisotropic) distributions), and the location parameter μ_i, describing the preferred (or principal) fibre orientation. Normalization is not necessary, because ρ(Φ) was used only to determine the fitting parameters [39]; I₀(b_i) denotes the modified Bessel function of the first kind of order zero, namely

2.4

with i = 1,2.

3. Results

The orientations of collagen fibres in a z-stack are represented by the three-dimensional distribution of the corresponding amplitudes with 1° resolution. By fitting this distribution using MLE and π-periodic von Mises distributions (either one or a mixture of two in the case of two fibre families), our method identifies specific regions of isotropy within the tissue and characterizes anisotropic regions by determining both structural parameters b and μ.

3.1. Optical clearing and histology

Figure 2 illustrates the effect of optical clearing using a solution of BABB; a segment of a human abdominal aorta before and after clearing is shown in the top row, left and right panel, respectively. Note the translucent nature of the cleared vessel, also visible by the lighter shadow under the same lighting conditions. To ensure that the clearing procedure did not negatively affect the microscopic structure of collagen fibres, we performed additional investigations on histological sections. Representative PSR and EVG stained cross sections are shown in figure 2b, left and right panel, respectively. Both revealed that collagen (bright red under polarized light) and elastin (black in the EVG-stained section) are consistent with observations one can expect from standard formalin-fixed, paraffin-embedded tissue samples.

Figure 2.

Effect of optical clearing using BABB. (a) Left and right panels show a segment of a human abdominal aorta before and after optical clearing, respectively. Note the translucent appearance of the cleared vessel, also visible by the lighter shadow under the same lighting conditions. (b) Both cross-section images were obtained from optically cleared tissues and stained subsequently with picrosirius red for visualizing collagen (left; collagen appears bright red under dark-field polarized light) and Elastica Van Gieson as a general stain (right; elastic fibres and nuclei appear black, collagen stains pink, muscle and cytoplasm stains light brown/yellowish). The appearances of both images are consistent with photographs of standard formalin fixed tissue samples.

3.2. Three-dimensional visualization

The left panel in figure 3 shows a volume-rendered radial projection (circumferential/radial plane; x–z) of an image stack (z-stack), featuring collagen fibres throughout the thickness of the aortic wall. In-plane volume-rendered projections (circumferential/axial plane; x–y) of regions from the intima, media and adventitia are highlighted individually in the smaller panels I, II and III, respectively; the horizontal and vertical sides of panels I–III correspond to the circumferential (x) and axial (y) axes of the vessel. Note the different fibre morphologies between the three arterial layers: in the adventitia (panel I), the fibres were generally organized in thick fibre bundles, oriented mostly diagonally (with high variations) between the major axes; in the media (panel II), the fibres were organized closer to the circumferential direction of the vessel but still showed two preferred fibre orientations; in the intima (panel III), we observed both regions of preferred fibre orientations as well as regions of increasingly isotropic fibre morphologies. The continuous changes in fibre morphology throughout the entire wall thickness are shown in the electronic supplementary material, movie S1.

Figure 3.

Volume-rendering of optical sections through an entire aortic wall acquired using second-harmonic generation imaging. The left panel shows a radial projection (circumferential/radial plane; x–z) highlighting fibrillar collagen throughout the thickness of a human abdominal aortic wall (age: 65 years, gender: f). The three smaller panels on the right are in-plane projections (circumferential/axial plane; x–y) from regions inside the adventitia (I), media (II) and intima (III), indicated by the red boxes in the left panel. Note the marked differences in collagen fibre morphology between the three arterial layers. Generally, the adventitia displayed characteristic fibre bundles, often organized as two counter-rotating fibre families oriented mostly between the major vessel axes; in the media, the fibre bundles changed into one fibre family, organized in a layered structure with alternating orientations closer to the circumferential direction. The intima of this vessel was characterized by a mostly isotropic organization of collagen fibres, whereas intimas of other vessels also displayed anisotropic fibre morphologies.

3.3. Continuous three-dimensional fibre orientations

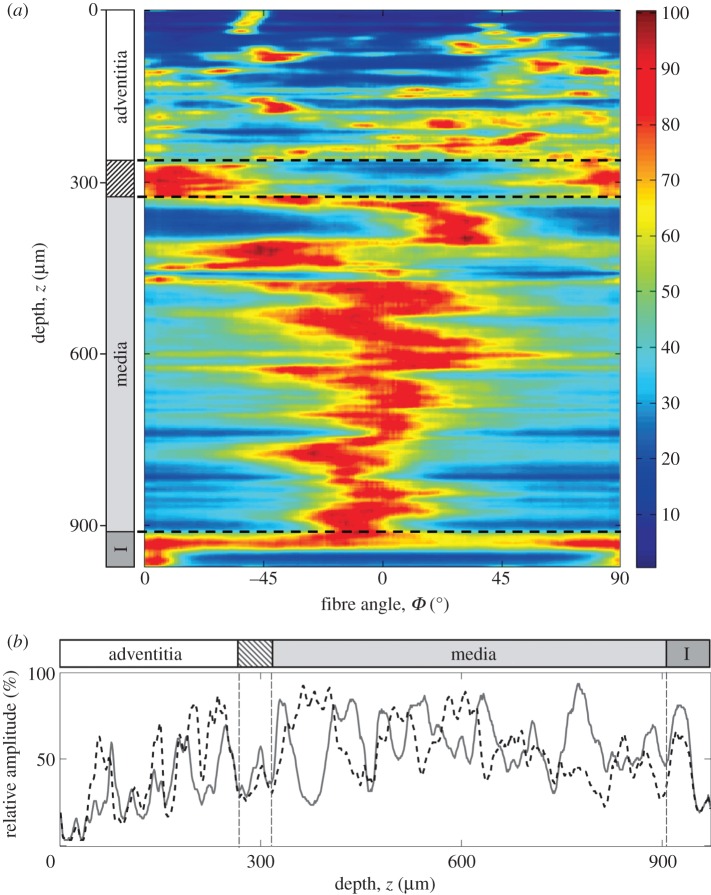
Figure 4a is a representation of the three-dimensional collagen fibre orientations with a 1° resolution throughout the entire thickness of the aortic wall (obtained from the z-stack shown in figure 3); Φ = 0° and 90° denote the circumferential and axial directions of the vessel, respectively. The colours denote relative changes in amplitudes ranging from dark blue (0%) to dark red (100%). Therefore, orientations of preferred (or principal) fibre directions (or fibre families) appear red, whereas blue corresponds to orientations with only few to no fibres present. The dashed lines indicate the transition regions between the arterial layers. In the adventitia, we observed highly aligned fibre orientations (note the relatively large dark blue areas between red regions of preferred orientations) with often two counter-rotating fibre families present, generally oriented between the major vessel axes. The adventitia is followed by a marked transition layer (indicated by the striped box on the left), characterized by a change in appearance of the collagen fibres. The thick fibre bundles visible in the adventitia could not be observed anymore and the preferred orientations of the fibres became axial (approx. 90°). Subsequently comes the media that displayed a layered structure of alternating preferential fibre orientations (layers of single fibre families with alternating orientations) closer to the circumferential direction, located around Φ ∼ ±20°. Next, the intima of this vessel was characterized by an isotropic fibre morphology that at regions closest to the lumen changed into preferred fibre orientations in the axial direction.

Figure 4.

Representation of the three-dimensional collagen fibre orientations throughout the entire thickness of a human abdominal aortic wall (age: 65 years, gender: f). (a) The angles Φ = 0° and 90° denote the circumferential and axial directions of the vessel respectively, the colours correspond to relative amplitudes ranging from dark blue (0%) to dark red (100%). Orientations of preferred fibre directions appear red, whereas blue regions represent orientations with a low fibre density. The striped box on the left indicates the transition layer between the adventitia and the media; I, intima. (b) Changes of relative amplitudes as a function of depth at two representative locations. The dashed black curve corresponds to amplitudes at Φ =+27°, the grey curve at Φ =−27° (0°= circumferential). A similar behaviour of both curves in the adventitia turns into an alternating pattern in the media, indicating a change in the structural organization of collagen fibres between the two layers; from two fibre families in the adventitia to one fibre family with alternating orientations in the media.

We emphasize that we observed strong biological variabilities in fibre orientations among the intimas of different aortas, while some showed isotropic as well as anisotropic regions with preferential orientations in various directions (depending on the sample it could be, e.g. two fibre families oriented axially and circumferentially), others displayed only anisotropic or only isotropic morphologies (table 1). A representative example that highlights these changes in morphology throughout the entire thickness of the wall is given in figure 4b, where the relative amplitudes at the locations Φ =+27° (dashed black curve) and Φ =−27° (grey curve) as a function of depth z are plotted. In the adventitia, the shapes of both amplitude curves tend to overlap, suggesting that two fibre families lie within the same imaging plane (circumferential/axial plane; x–y) which was confirmed by individual MPM images of the adventitia revealing the presence of two fibre families. In the media, on the other hand, the similar behaviour of both curves clearly changes into an alternating pattern, characteristic for a layered fibre family structure with alternating orientations (figure 4a).

Table 1.

Data from intimas of the five vessels showing high biological variabilities. (Summarized for each intima is the intima thickness (in %) compared with the entire wall, the percentage of anisotropic regions within the intima and the observed number of fibre families.)

intima no.	intima thickness (%)	anisotropic regions (%)	no. fibre families
1	3.6	100	2
2	5.6	60	1
3	17.2	68.6	2
4	20.2	0	—
5	34.1	0	—

Changes in collagen fibre morphology and its corresponding angular distributions throughout the wall thickness can be viewed in the electronic supplementary material, movie S2.

3.4. Parameter determination for numerical modelling

A representative example of fitting the fibre orientations extracted from a single MPM image (taken from the media) using MLE with one π-periodic von Mises distribution is shown in figure 5 including corresponding R² and p-values as a measure for the goodness of fit. From the fit, we obtained the location parameter μ =−22.7° describing the principal fibre orientation of the distribution as well as the concentration parameter b = 1.44, which determines the shape of the von Mises distribution. Both μ and b were calculated for every image in the z-stack, yielding the continuous behaviour of both parameters throughout the thickness of the entire wall, as shown in figure 6. Note that regions with no data points correspond to regions with isotropic fibre distributions.

Figure 5.

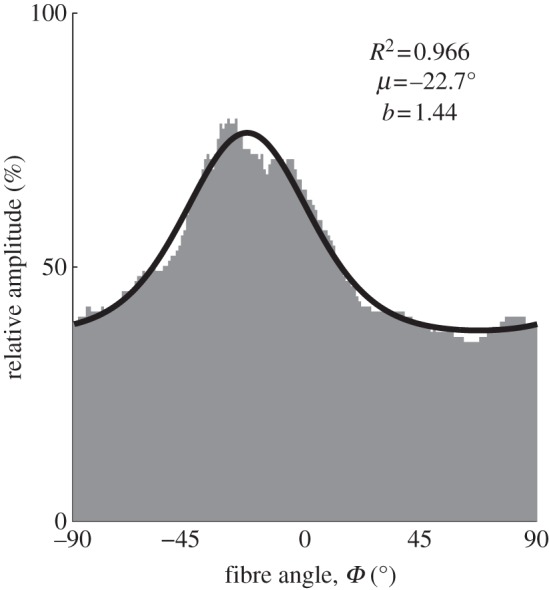
Angular distribution of relative amplitudes fitted with a π-periodic von Mises distribution. The distribution was extracted from a single MPM image taken from the media featuring one fibre family (corresponding to the location at 634 µm in figure 4a). The angles Φ = 0° and 90° denote the circumferential and axial directions of the vessel, respectively. From the fit, we extracted the location parameter μ describing the preferred (or principal) fibre orientation and the concentration parameter b as a measure of the degree of fibre alignment about μ. An increase in b corresponds to a narrower (more anisotropic) distribution.

Figure 6.

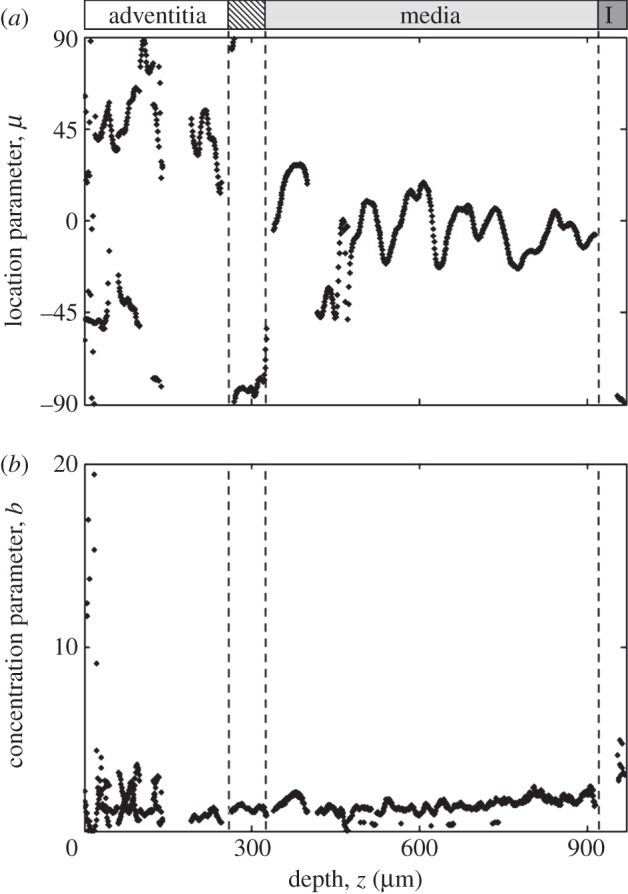
Changes in preferred fibre orientations and fibre alignment throughout the entire thickness of the aortic wall. (a) In the adventitia, often two counter rotating principal fibre directions were observed, whereas the media were characterized by alternating principal directions, oriented closer to the circumferential direction of the vessel. In the intima (I) only regions closest to the lumen showed anisotropic fibre alignment in the axial direction (∼±90°), oriented along the direction of blood flow. (b) The concentration parameter b quantifies the degree of fibre alignment about the preferred fibre orientation μ (figure 5), therefore, describing its degree of anisotropy. Increasing b values correspond to a narrower (more aligned) distribution. Generally, in the adventitia increased values of b were found compared to the media. Note that values of approximately b > 4 typically came from images containing a few highly aligned fibre bundles.

The results in figure 6a, highlight that in the adventitia often two counter rotating fibre families were observed oriented at around Φ ∼ ±45°, whereas in the media, only one fibre family with alternating orientations closer to the circumferential direction (Φ ∼ ±20°) was present. In the transition layer between the adventitia and the media, a preferred axial fibre orientation was observed. The intima of this vessel consisted largely of isotropic regions, which changed into one fibre family oriented in the axial direction closest to the lumen. The concentration parameter b showed relatively small variations throughout the media (figure 6b) and was generally slightly higher in the adventitia (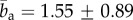, mean ± s.d.) compared with the media (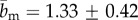), indicating that the observed collagen fibre distributions were more aligned (more anisotropic) in the adventitia. The very high values for b at the beginning of the adventitia (b > 5) correspond to images containing only a few highly aligned thick collagen fibre bundles, as can be seen in figure 3 (panel I), and were omitted in the calculation of 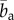. In the intima, close to the lumen, we observed an increased fibre alignment ().

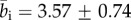4. Discussion

Based on established tools from different research fields, we are introducing a new method, which allows for a simple, fast and automated structural analysis of collagenous tissues or whole organs that have been optically cleared and imaged using nonlinear microscopy. Our method yields a three-dimensional orientational distribution accurately representing the morphology of fibrillar tissue structures, and it additionally extracts structural parameters that can be used in numerical models for soft biological tissues. We used tissue samples from human abdominal aortas to outline the method and in the course of this study we presented novel results pertaining to the structure of aortic walls.

To approximate the in vivo condition of the vessel as closely as possible, we developed a custom-made device allowing us to mount and chemically fixate (using formalin) the intact segment (tube) of the abdominal aorta as a whole, and subsequently apply a physiologically axial pre-stretch (approx. 12% [37]) and simultaneously pressurize it at constant SAP of 130 mmHg. The influence and importance of pressurization and axial pre-stretches upon fibre morphology has been previously reported [8,35,40,41] and is not only a prerequisite for mimicking in vivo states of the vessel, but also leads to (mostly) straightened collagen fibres necessary for a correct determination of fibre angles. Furthermore, our new sample preparation method allows for future studies of the influence of arterial blood pressure on collagen fibre orientations or investigations of microstructural recruitment variables for collagen [42].

Optical clearing using BABB leads to an increase in MPM penetration depth from approximately 120 µm (in the uncleared sample) to more than 1 mm, enabling us to image the entire thickness of the vessel wall without physically damaging the tissue [12]. Histological investigations using standard tissue stains (PSR and VVG) confirmed that the microstructural tissue components (collagen and elastin) were still intact after optical clearing (figure 2). A comparison of fibre distributions before and after clearing showed that the microscopical orientations were not affected by the clearing process.

Using SHG imaging, we can show, for the first time to our knowledge, a complete three-dimensional visualization of collagen fibres throughout the entire wall thickness of a human abdominal aorta (see figure 3 and the electronic supplementary material, movies S1 and S2). Visually, we observed some basic similarities between the five vessels we investigated: the adventitias showed characteristic fibre bundles, often organized as two counter-rotating fibre families, mostly oriented between the major vessel axes (figure 3, panel I); next came a transition layer leading to the media in which the marked organization into fibre bundles disappeared; the media generally displayed one fibre family organized in a layered structure with two alternating preferential orientations; the observed morphologies among these five intimas varied greatly, some displayed isotropic and anisotropic regions with preferential fibre orientations while others appeared completely isotropic or anisotropic. An overview is provided in table 1. Owing to the limited number of samples and the observed variabilities general statements seem here inadequate. Future studies on a larger number of vessels are required to obtain sufficient data for a meaningful, statistical, inter-subject analysis of the intimas.

For example, the intima of the vessel in figure 3 consisted of isotropic orientations adjacent to the media that became anisotropic close to the lumen, oriented along the direction of the blood flow (figures 4a and 6a). These observations are consistent with previously reported mean values for the three arterial layers [8], where two fibre families were observed in the adventitia and media and several fibre families as well as isotropic distributions were found in the intimas. Instead of having to rely on mean values for each layer, our new method provides the required three-dimensional spatial depth resolution to show in detail how the fibre families are organized within each layer.

To extract the fibre orientations from images, we used Fourier power spectrum analysis in combination with wedge filtering [25,30–32]. First, it is the rotational property; second, the addition theorem and third the shift theorem of the FT that ensure that the fibre orientations visible in an image are correctly represented by the distribution of relative amplitudes in Fourier space.

A statistical analysis of the CDFs, calculated from amplitude distributions, was used as an objective measure to identify regions of isotropy and anisotropy in the tissue. Note that anisotropic regions are characterized by a preferred direction of fibre orientations versus isotropic regions that show arbitrary fibre orientations. For distribution fitting of anisotropic regions, we used either one or (in the case of two preferred fibre orientations) a mixture of two von Mises distributions from which we determined μ, describing the principal fibre orientation and b, a measure for the fibre alignment about μ (figure 5). Our choice for using a von Mises distribution was based on well-established modelling frameworks of arterial tissues [25,34,38,43,44], in which b can be used to calculate dispersion parameters which, together with μ, can be directly used in the numerical modelling or finite element analyses, even in commercial codes such as Abaqus (SIMULIA, Providence, RI). The decision to perform distribution fitting through MLE instead of a simple least-squares method was motivated by its independence of bin size and the potential pitfalls arising from the normality-, constant variance- and independent-errors assumptions [45]. Using our method, we present for the first time to our knowledge, the (continuous) values of both modelling parameters μ and b throughout the thickness of the human aortic wall (figure 6).

The three-dimensional quantification of fibre orientations (figure 4a) confirmed our visual impression that the collagen fibres in the adventitia were oriented more axially and showed higher anisotropy (note the dark blue regions between preferred orientations) compared with the media, where they were oriented closer to the circumferential direction and the fibre alignment was less pronounced (note the light blue to turquoise regions indicating some presence of fibres in all directions). By analysing the behaviour of relative amplitudes throughout the entire thickness of the aortic wall, we were able to identify depth-resolved changes in the structural organization of the collagen fibre families (figure 4b). For the first time to our knowledge, we present continuous quantitative data showing the presence of two counter rotating fibre families in the adventitia (lying within axial-circumferential planes), while only one fibre family with alternating orientations between sequential axial-circumferential planes was found in the media. The results for the location parameter μ in figure 6a, further highlighted the alternating nature of the preferred fibre orientations in the media, and the more fluctuating orientations in the adventitia, which was found to be characteristic of all five vessels, and corresponds well with previously reported differences in the qualitative mechanical stress–stretch response of abdominal aortas [41] and carotid arteries [46]. To validate our data, several z-stacks from nearby positions were acquired and analysed for each sample. Statistical analysis showed that differences in the neighbouring regions of the same sample were low and the reported morphologies were indeed representative for each vessel. For example, statistical comparisons (t-tests) among four z-stacks obtained from different positions of the vessel shown in figure 2 yielded no significant differences (p < 0.05) for the concentration parameters b throughout the media.

Compared with previous studies of collagen organization in human arteries [35,40,47], our method is non-destructive, yields continuous data throughout the entire thickness of soft biological tissues, therefore, allowing for investigations of specific locations inside the tissue (e.g. transition regions between the three arterial layers). Owing to the automated nature of our method, it is not subject to limitations such as human measurement bias or fair sampling (both pose a risk when, e.g. measuring collagen fibre angles using polarized light [8]).

With an ultimate tensile strength in the range of 50–100 MPa [48], collagen fibres are responsible for the strength and load resistance of the arterial wall. Therefore, understanding their microscopic structure and changing morphologies throughout the three layers of the wall is key in the analysis of mechanical quantities such as stress and strain, both of which are used as a basis for numerical modelling of growth and remodelling processes [49].