Glide performance and aerodynamics of non-equilibrium glides in northern flying squirrels (Glaucomys sabrinus)

Abstract

Gliding is an efficient form of travel found in every major group of terrestrial vertebrates. Gliding is often modelled in equilibrium, where aerodynamic forces exactly balance body weight resulting in constant velocity. Although the equilibrium model is relevant for long-distance gliding, such as soaring by birds, it may not be realistic for shorter distances between trees. To understand the aerodynamics of inter-tree gliding, we used direct observation and mathematical modelling. We used videography (60–125 fps) to track and reconstruct the three-dimensional trajectories of northern flying squirrels (Glaucomys sabrinus) in nature. From their trajectories, we calculated velocities, aerodynamic forces and force coefficients. We determined that flying squirrels do not glide at equilibrium, and instead demonstrate continuously changing velocities, forces and force coefficients, and generate more lift than needed to balance body weight. We compared observed glide performance with mathematical simulations that use constant force coefficients, a characteristic of equilibrium glides. Simulations with varying force coefficients, such as those of live squirrels, demonstrated better whole-glide performance compared with the theoretical equilibrium state. Using results from both the observed glides and the simulation, we describe the mechanics and execution of inter-tree glides, and then discuss how gliding behaviour may relate to the evolution of flapping flight.

1. Introduction

Gliding is the simplest form of animal flight; with no flapping motion to generate thrust, an animal simply trades height for horizontal movement. Gliding has evolved numerous times in terrestrial vertebrates. Among extant taxa, gliding has evolved independently twice in amphibians, at least three times in reptiles and six times in mammals, and potentially many more times in extinct lineages [1]. In an evolutionary context, gliding is of particular interest because of its possible role as a precursor to flapping flight. Many discussions concerning gliding to flapping transitions, however, are based on relatively simple, abstract aerodynamic models of gliding that incorporate rather limited physical detail from gliding animals. To present more rigorous arguments about the plausibility of a gliding to flapping transition, we require a more in-depth understanding of the behaviour, mechanics and aerodynamics of living gliders.

1.1. Equilibrium gliding

Most aerodynamic models used to describe the evolution of powered, flapping flyers from gliding ancestors assume that animals glide at equilibrium for most or all of the glide [2–4]. Equilibrium gliding is a specific form of gliding, in which lift and drag sum to a resultant force that is equal in magnitude and opposite in direction to the glider's weight, producing a linear glide path at constant velocity (figure 1). Because aerodynamic force changes as a function of velocity, one particular speed, the equilibrium velocity, is required for a given wing shape and orientation to generate a force that exactly balances body weight. Additionally, a specific glide angle is required to exactly balance the horizontal components of aerodynamic force, so that speed remains constant throughout the glide. Given adequate time and height, a passive glider will eventually reach equilibrium, in the same way that a falling object will eventually reach terminal velocity. A common example of equilibrium gliding is travel between thermals or updrafts in soaring birds, which typically occurs over relatively long distances. However, for arboreal gliders, the distance between trees is relatively short compared with soaring, and these short distances might not provide sufficient time and height for them to reach equilibrium.

Figure 1.

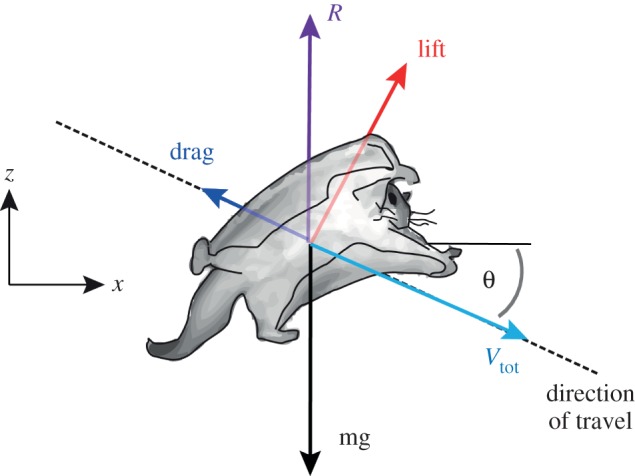
Schematic of an animal gliding at equilibrium. The light blue arrow indicates net velocity and the other arrows represent forces. As a gliding animal moves though the environment, it generates a lift force, L, perpendicular to the direction of travel, and a drag force, D, opposite to the direction of travel. These two sum to produce the resultant aerodynamic force, R, which, in general, acts in opposition to the animal's weight, mg. For equilibrium glides, R points in the vertical direction (z), and its magnitude is exactly equal to body weight (mg). The glide angle, θ, is the angle between the direction of the travel and horizontal (x). (Online version in colour.)

If there is an equilibrium phase when animals glide between trees, there must nonetheless be a non-equilibrium phase at the beginning of glides, as the beginning of a glide is influenced by the dynamics of the launch [5]. Additionally, some gliders may perform manoeuvres to decrease velocity and reduce impact force at landing. Because the distance between a launch and landing point might range from only a few to tens of metres, a substantial portion, or even the entire glide, may be dominated by the aerodynamics associated with launch and landing [6–9].

A few studies have analysed whole glides in enough detail to determine whether the requirements of equilibrium conditions are met in nature. While 48 per cent of gliding lizards (Genus: Draco) approached a constant velocity by the middle or end of glides [8], in gliding snakes (Genus: Chrysopelea), only a single instance of constant velocity gliding was observed in 237 trials [7]. In colugos (Genus: Galeopterus), a few instances of equilibrium have been observed during glides measured with accelerometers, although the proportion was not reported [9]. In the studies of gliding reptiles, equilibrium gliding was more common in individuals and species with lower wing loading, probably because more time is required for heavier or more highly loaded animals to accelerate to equilibrium velocity [2,5]. Recorded wing loadings in lizards have ranged from 9 to 23 N m⁻² [8], and values as high as 31 N m⁻² have been reported in flying snakes [7], but values for mammalian gliders are typically substantially higher, between 38 and 143 N m⁻² [10]. Given that most mammalian gliders travel an average of 15–30 m in a single glide, depending on the species [9–12], they may not have sufficient time or distance to achieve equilibrium conditions.

1.2. Glide mechanics

Many studies of mammalian gliding have recorded launch and landing points, and in some cases, glide duration, but those descriptors do not address time-resolved changes during glides [10–18]. Measurements of launch and landing provide information about whole-glide performance, such as glide ratio (GR), the ratio of the horizontal and vertical distances between the launch and landing points, and average glide velocity (AGV), the total glide distance divided by glide duration, which can be useful in an ecological context. However, time-resolved trajectories are required to determine if forces and velocities change during a glide and to resolve the detailed mechanics of glide execution.

There are good reasons to expect that at least some mammalian gliders have the ability to control their glide trajectory. Based on anatomy alone, we expect that gliders have considerable ability to change wing shape and orientation to oncoming flow, thereby modulating aerodynamic force coefficients and consequently force generation. Mammalian gliders can change the shape of their wings in a variety of ways, including: flexing and extending the elbow, knee, shoulder and hip; contracting and relaxing the intrinsic wing membrane muscles to control camber and area; and changing the angle of the leading edge membrane. In practice, in flying squirrels and sugar gliders, aerodynamic force coefficients vary among glides with differing body orientations and limb postures, implying active control of aerodynamic force coefficients [19,20]. Given this ability to modulate wing shape, mammalian gliders are theoretically capable of continuously varying aerodynamic force coefficients, and need not adhere to equilibrium requirements of constant forces and force coefficients.

In this study, we examine whole-glide performance and time-resolved aerodynamics of the northern flying squirrel (Glaucomys sabrinus), a representative gliding mammal, in its natural habitat. We ask: do these animals exhibit equilibrium gliding conditions, and if not, are equilibrium conditions physically possible in their natural setting? We develop an aerodynamic gliding model based on relevant parameters of squirrel glides, and compare whole-glide performance and specific execution of the natural glides with the model. Finally, we discuss how these findings may relate to the evolution of flapping flyers from a gliding ancestor.

2. Material and methods

2.1. Study site and video recording

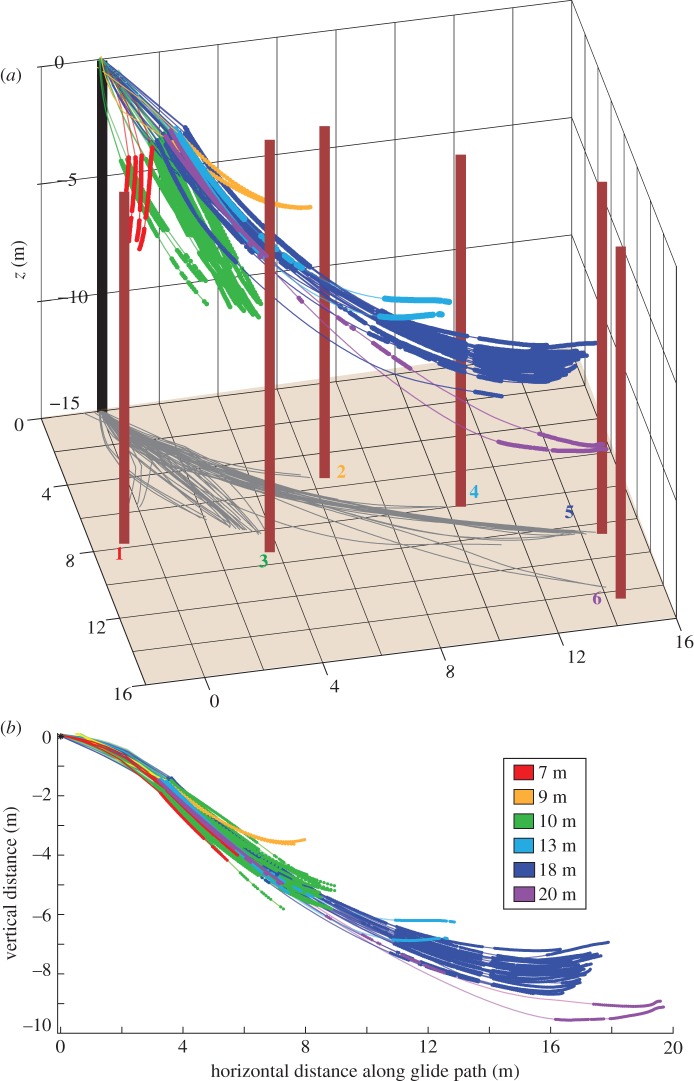
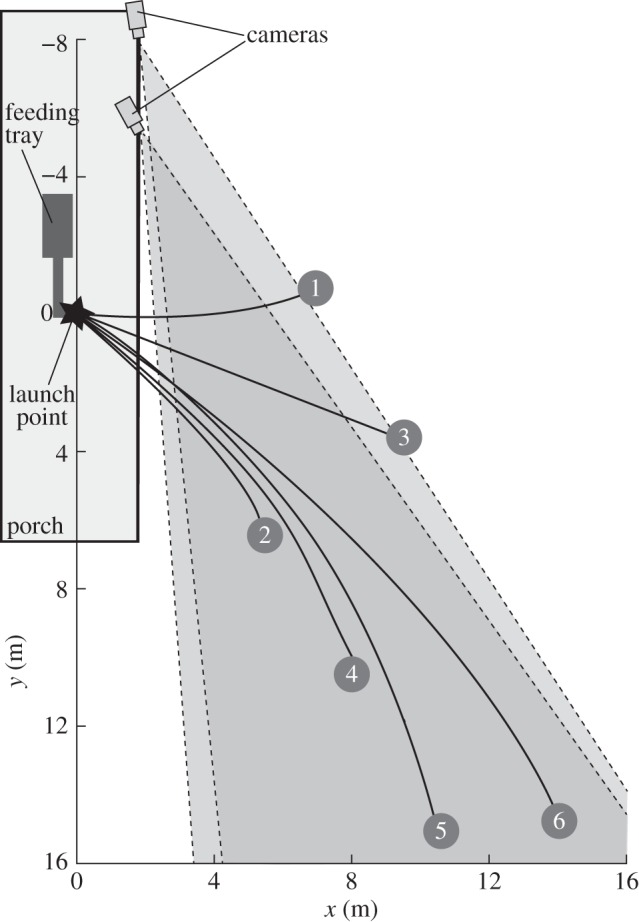
The study was conducted near Fort Fairfield Maine, USA, (46.7° N, 67.8° W) in November 2006. A feeding tray and platform were hung on the porch of a building (figure 3). Wild northern flying squirrels (G. sabrinus [21]) would arrive, visit the feeder, then jump from the platform and glide down a forested hillside before landing on trunks of trees some distance below. Glides were recorded with two synchronized high-speed video cameras, with a resolution of 480 × 420 pixels (Redlake PCI-1000, Redlake Systems, San Diego, CA, USA). The cameras were positioned approximately 4 m apart. The glide paths were illuminated using lights on the porch and two large halogen lamps on the hillside below. A total of 59 glides were recorded, seven at a frame rate of 60 Hz and 52 at 125 Hz. Video sequences ranged in duration from 0.40 to 2.48 s (50–310 frames or time-steps), covering glide distances ranging from 7 to 20 m. Because we did not handle or mark animals, we cannot assign specific individuals to specific glides, but the glides were performed by at least six individuals, the most we saw at the feeding tray at one time.

Figure 3.

(a) Three-dimensional perspective view of trajectories of 56 glides from a common launch point to six landing trees, 7–20 m from the launch. Thick line segments indicate where squirrels were visible in both camera views, thin lines where trajectories were interpolated. Grey lines show the horizontal projection of the glide paths upon the ground. The coloured numbers correspond to the tree numbers in table 1. (b) Common projection of all glide paths with direction of travel aligned to the graph's horizontal axis. Legend shows the horizontal distance between the launch point and the landing tree.

2.2. Calibration

To determine a squirrel's glide trajectory from its positions in the two camera views, we used the direct linear transformation (DLT) method [22,23]. The volume of interest was approximately 20 × 15 × 12 m, and was calibrated using 10 markers with known locations on the sides of trees within the volume of interest. The spatial coordinates of the markers relative to the launch point were determined by measuring the distance from each marker to each of three reference points using a laser tape measure, and then triangulating the markers' three-dimensional positions. The position of the launch point relative to the calibrated space was also recorded, but was not within the camera field of view.

2.3. Data processing

In each video frame, the approximate geometric centre of the squirrel was digitized using a custom-written program in MATLAB (MathWorks, Inc., Natick, MA, USA) to record its two-dimensional position in each frame. Because trees sometimes obstructed camera views and cast shadows on some parts of the glide path, gaps occurred in the trajectories when the animals were not visible. Data in the gaps were interpolated by fitting a fourth-order polynomial to the existing points for the entire glide in the two-dimensional data from each camera, then evaluating the polynomial in the gap regions. The two-dimensional data were smoothed by fitting a second-order polynomial to the data from a window of points surrounding a single time-step, and evaluating the polynomial at that time-step. For the middle of the glides the window was 22 time-steps before and after, for a total window size of 45. Near the beginning and end of the glides where there were fewer than 22 time-steps between the central frame and the edge of the data, the polynomial was fit to fewer time-steps, with a minimum window of 23 time-steps. The smoothed data from each camera were reconstructed into three-dimensional coordinates using DLT. For each glide, the reference axes were rotated and translated so that the horizontal axis (x) followed the glide's projection onto the ground and the vertical axis (z) pointed vertically up, with the launch point set at the origin.

2.4. Estimation of launch velocity

The launch site was not in the calibrated space of the two high-speed cameras, hence to estimate launch characteristics, a single 480 × 320 pixel 125 Hz camera (Fastec TroubleShooter, Fastec Imaging, San Diego, CA, USA) was positioned under the launch platform. We only recorded five launches that corresponded to the 18 m glides. For each trial, the position of the base of the squirrel's tail was digitized in the frame when the squirrel's hindlimbs left the platform, and in the last frame, when the base of the tail was visible. We estimated the squirrel's length to be 0.169 m based on literature [24], and calibrated the camera image using this value. Velocity was calculated as the difference in distance divided by the difference in time between the two frames. Although this method is rather crude in several respects, it provides a reasonable approximation of launch velocity that can be effectively used in our glide simulations (see below).

2.5. Calculating performance measures for all glides

Velocity and acceleration were calculated independently for the x and z directions by fitting a second-order polynomial to the 30 time-steps surrounding a given time-step and determining the derivatives from the polynomial coefficients. The process was repeated for all time-steps of position data to calculate velocity, and again for velocity data to calculate acceleration. We chose a large interrogation window because we were interested in trends in velocity and acceleration over the whole glide, rather than in minor stabilizing movements. At the ends of the trajectory, a half window was used. Total velocity (V_tot) was calculated as the vector sum of the horizontal (V_x) and vertical (V_z) velocities. We attempted several different methods for smoothing and calculating derivatives and selected this method because it produced the best balance between accuracy and smoothness.

2.6. Calculating the aerodynamic parameters of the long glides

To examine glide aerodynamics in greater detail, we selected the 23 glides that ended at one particular tree, Tree 5, 18 m from the launch point (see §3). We chose this subset of glides because the glide distance was one of the longest, providing more opportunity for animals to reach equilibrium velocity, and because we obtained a large sample of glides at this distance. We calculated several aerodynamic parameters:

Glide angle, θ, the angle between the horizontal and the net velocity vector (figure 1), was calculated at each time-step as

2.1

where V_z is the vertical velocity and V_x is the horizontal velocity.

Lift (L) is defined as the aerodynamic force perpendicular to the direction of travel, and drag (D) is defined as the aerodynamic force opposing the direction of travel (figure 1). Because we were not able to weigh the animals, we report aerodynamic forces in units of body weight by dividing all accelerations by the acceleration due to gravity (g = 9.81 m s⁻²), which is mathematically equivalent to dividing the force by body weight. Normalized lift and drag were calculated as

2.2

and

2.3

where m is body mass, a_x and a_z are the horizontal and vertical accelerations, respectively, and θ is the glide angle.

The equivalent lift coefficient, C_L, and equivalent drag coefficient, C_D, were calculated as

2.4

and

2.5

where V_tot is total velocity, ρ is air density (1.204 kg m⁻³), and S is the surface area of the body. To use equations (2.4) and (2.5), we calculated lift and drag forces by multiplying the lift and drag accelerations by a body mass value of 92.7 g, the mean body mass reported for a population of G. sabrinus located less than 200 km from our study site [11]. To estimate surface area, we used this body mass and mean published wing loading value for G. sabrinus of 59 N m⁻² [10] to arrive at a surface area of 154 cm². Because we use the same values for body mass and wing area for all glides and individuals, these force coefficients are ‘equivalent coefficients’, similar conceptually to the idea of ‘equivalent flat plate area’ [25]. Changes in the wing area will manifest as changes in the force coefficients. Thus, the absolute magnitudes of the force coefficients should be treated with caution, although the overall trends during the glide are nevertheless realistic and the lift-to-drag ratio (L/D) will not be affected by changes in wing area. If squirrel body mass is changed from our reference value of 92.7 g by 1 s.d., 13.5 g [11], the value of C_L is altered by only 15 per cent.

Kinetic energy (E_K), potential energy (E_P) and total energy (E_T) were normalized using body mass in a fashion similar to that for the estimates of lift and drag, and were thus calculated as

2.6

2.7

and

2.8

where h is the height of the glide above an arbitrarily chosen reference height. For calculating potential energy, the relative initial height was 10 m, approximately the largest change in height observed across all trials.

2.7. Estimating errors

Because the cameras were located near the launch point (figure 2), the error in position owing to digitizing was greater towards the end of the glide, and that error magnifies with each derivative computed from position data [26]. To estimate this error, we performed a sensitivity analysis. First, we digitized a single long glide trial seven times, each time by a different person. For each axis of each camera, we determined a mean trajectory, and the standard deviation from that mean. Next, at each time-step, we perturbed the mean position by adding values drawn randomly from a normal distribution defined by the measured standard deviation. Next, the trial was subjected to the same smoothing, three-dimensional reconstruction, and analysis procedures described previously. This process was repeated 100 times for the exemplar trial to determine the magnitude of uncertainty over the entire glide. Using each of these perturbed trials, we calculated the 95% CIs for position, velocity, acceleration and force coefficients.

Figure 2.

Schematic of experimental set-up. Top view. The encircled numbers represent landing trees and the solid line represents approximate glide path.

2.8. Simulating an equilibrium glide

We constructed a mathematical model to simulate glides based on a prescribed set of force coefficients. The simulations were used to: (i) predict the glide mechanics for the first few metres of the glides, (ii) determine if and when glides using constant force coefficients would achieve equilibrium conditions, and (iii) provide a constant force coefficient basis for comparing whole-glide performance with observed glides.

The mathematical model calculated horizontal and vertical velocity and position for a sequence of time-steps by integrating Newton's second law of motion (equations (2.9)–(2.12)), using a fourth-order Runge–Kutta solver (MATLAB ODE-45 function):

2.9

2.10

2.11

and

2.12

where a_x(t), a_z(t), v_x(t), v_z(t), represent the acceleration and velocity in the x- and z-directions. At every time-step, F_x and F_z were determined by calculating lift and drag from the prescribed aerodynamic force coefficients, C_L and C_D (equations (2.4) and (2.5)), and then rotating those forces onto the x- and z-axes (equations (2.2) and (2.3)). Estimates of body mass and wing surface area were the same as for the observed glides (see §2.6).

We validated the simulation by: (i) computing the mean trajectory from the 23 observed 18 m glides, calculating the C_L and C_D corresponding to that trajectory, simulating a trajectory using those force coefficients, and (ii) comparing the simulated trajectory with the mean observed trajectory.

We used the simulation to estimate the velocity at the launch and the force coefficients used during the first few metres of the glide, which occurred outside the camera view. We selected reasonable values for an initial guess of velocity (v_x(t = 0), v_z(t = 0)) and an initial guess of force coefficients for the first 3 m. A third-order polynomial was then used to smoothly transition the force coefficients, as a function of distance, from their initial values to the values experimentally obtained from squirrels' behaviour once within the camera field of view. These initial values for v_x, v_z, C_L and C_D, were systematically varied using MATLAB's optimization toolbox (fminsearch function), minimizing the difference between the simulated and observed glides in both position and velocity across the length of the glide. We refer to the simulation derived using these optimal launch values as the ‘best-matched simulation’. The ‘best-match’ launch velocity was then compared with the values determined directly from the launch camera (see §2.4).

A glider flying with constant force coefficients will eventually achieve equilibrium given sufficient time, height, and distance to travel. To determine whether flying squirrels could reach equilibrium within their observed glide range, we used our numerical model to simulate glides using a range of biologically relevant force coefficients. We selected C_L and C_D pairs at regular intervals across the full range of coefficients from the observed glides and the best-matched simulation, and generated simulations where the coefficients were held constant. From these simulations we determined the distance and height at which the animal would have reached equilibrium, defined as the position at which the total velocity remains within 5.0 per cent of the equilibrium velocity.

We calculated GR and AGV for the simulations for comparison with the observed 18 m glides. GR was calculated as 18 m divided by the height lost at 18 m. AGV was calculated as the mean velocity over the first 18 m of travel.

3. Results

3.1. Glide performance

We recorded 58 glides to six different trees (table 1 and figure 3). No trial displayed equilibrium, time-independent, conditions at any point during the glide. All glides showed acceleration in the vertical and/or horizontal directions throughout the observed portion of the glide (figure 4). In addition to displaying non-zero accelerations and, therefore, unbalanced forces, the magnitudes of those accelerations changed continuously over the course of the glides.

Table 1.

Summary of characteristics of glides to six observed landing trees. Distance to tree is the horizontal distance between launch and tree estimated to the nearest metre. Glide ratio (GR) was measured from the last observed position in both camera views. Values are given as mean and 1 s.d. or maximum and minimum values when n = 2.

	tree 1	tree 2	tree 3	tree 4	tree 5	tree 6
number of glides to tree	4	2	25	2	23	2
distance to tree (m)	7	9	10	13	18	20
change in height (m)	3.9 ± 0.2	3.5, 3.6	5.2 ± 0.3	6.3, 6.8	7.6 ± 0.5	8.9, 9.1
GR	1.4 ± 0.1	2.1, 2.3	1.6 ± 0.1	1.9, 2.1	2.4 ± 0.2	2.2, 2.2

Figure 4.

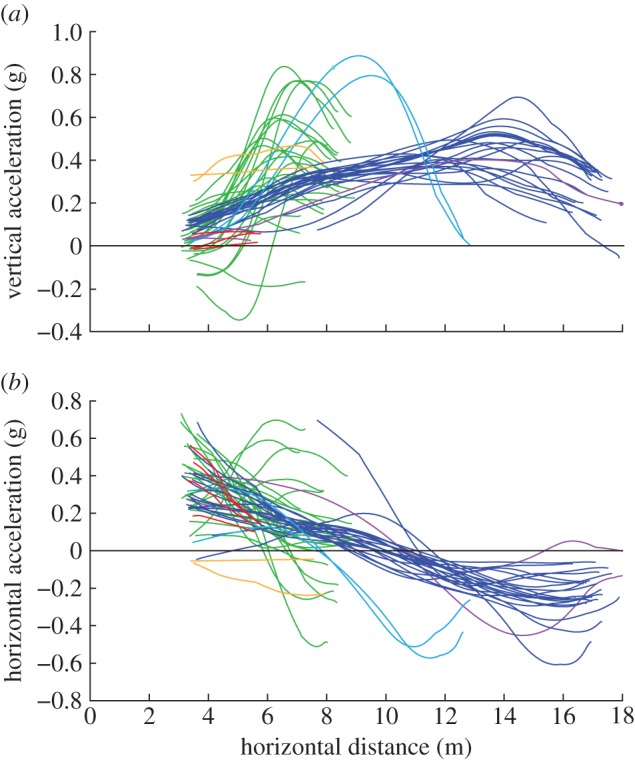
(a) Net vertical acceleration in multiples of gravity for all glides longer than 7 m. Values are mostly positive, indicating that aerodynamic forces exceed animals' weight. (b) Net horizontal acceleration in multiples of gravity for all but one glide. All glides display non-zero acceleration in at least one axis at every point along the trajectory.

3.2. Characteristics of 18 m glides

The 18 m glides, to Tree 5, showed a consistent pattern of velocity, acceleration, glide angle, force, force coefficients, kinetic energy and potential energy, all changing continuously over the course of each glide (figure 5). In these glides, squirrels had positive vertical acceleration, illustrated by a transition from a large negative vertical velocity (fast downward motion) when they first entered the calibrated volume, to a moderate positive vertical velocity (slow upward motion) near the end of the glide (figure 5a). In the horizontal direction, the gliders accelerated from the launch point for the first 10 m and then decelerated gently until landing (figure 5b). Total speed increased until 6 m from the launch, decreased slowly until 10 m from the launch point, then decreased rapidly until landing. The AGV was 7.2 m s⁻¹. The glide angle when first observed was very steep, approximately 45°, and then it continuously became more shallow until the glide angle transitioned from negative to positive, and the squirrel was gaining altitude when it landed on the tree (figure 5c).

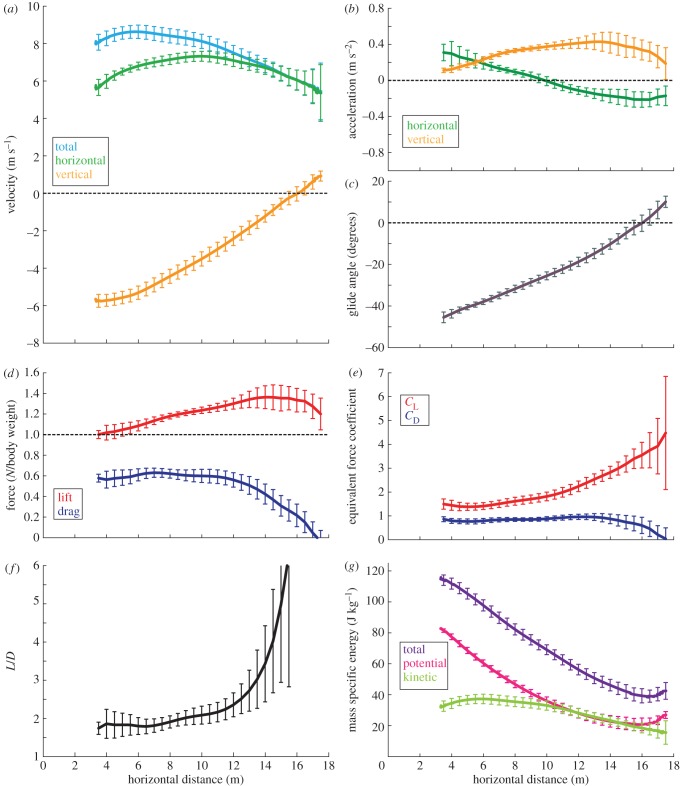
Figure 5.

Aerodynamic characteristics of 18 m glides. Lines represent the pooled average for 23 glides, with error bars extending one standard deviation above and below the mean. Measurement error is given in table 2 and in the electronic supplementary material. (a) Velocity, (b) acceleration, (c) glide angle, (d) normalized aerodynamic force, (e) equivalent force coefficients, (f) lift-to-drag ratio and (g) energy. (Online version in colour.)

Normalized lift exceeded one body weight for the entire observed portion of the glides, peaking around 3 m from the landing tree (figure 5d). The non-dimensional lift coefficient, C_L, was 1.4 when the squirrel entered the camera view and increased continuously, even during the last 3 m of the glide. At landing, C_L had increased approximately 300 per cent from its initial observed value (figure 5e).

In contrast, normalized drag remained relatively constant until 12 m from the launch point, then decreased until the end of the glide. The non-dimensional drag coefficient, C_D, started at 0.78, and increased very slightly (25% over 10 m), and then decreased towards zero at the end of the glide (figure 5e). In some trials the C_D fell below zero at the end of the glide. However, it is highly unlikely that this reflects physical reality and the negative portion falls well within the range of uncertainty, 0.25, for C_D. L/D started with a value of approximately 1.5, and slowly increased before rising sharply at around 12 m from the launch point.

Total energy decreased over the course of all glides as potential energy declined with descent; kinetic energy remained approximately constant. At the very end of the glide, there was a tendency in a few trials towards a slight increase in total energy; however, it is also highly unlikely that this reflects physical reality because to increase total energy the squirrel would have to gain energy through a sudden updraft, flapping or similar means. Again, the magnitude of this increase falls within the measurement uncertainty. The rate of loss in total energy was approximately constant, but showed slightly higher rates of energy loss early in the glides, and lower rates of loss during the last half of the glides.

Error estimates in each of the kinematic and aerodynamic parameters were highest at the ends of the glide. The 95% CIs based upon digitizing error are given in table 2.

Table 2.

Confidence intervals (95%) of glide parameters based on error analysis for beginning and end of observed portion of 18 m glide. Mean parameters provided in figure 5.

	beginning		end
	vertical	horizontal	vertical	horizontal
position (cm)	0.55	1.54	5.2	17
velocity (m s−1)	0.017	0.15	0.15	0.46
acceleration (m s−2)	0.04	0.44	0.37	1.12
force coefficient	0.09 (CL)	0.02 (CD)	0.56 (CL)	0.27 (CD)

3.3. Launch velocity

Mean launch velocity, estimated from the launch point camera, for the five launches was 5.4 m s⁻¹, with a range of 3.3–8.4 m s⁻¹ and a standard deviation of 1.0 m s⁻¹.

3.4. Glide simulations

Launch conditions that generate a trajectory best matching observed glides are a horizontal velocity of 5.37 m s⁻¹, which was within 0.1 m s⁻¹ or 2 per cent of the mean observed launch velocity, and small force coefficients (C_L = 0.01, C_D = 0.05) held constant for the first 3 m (figure 6).

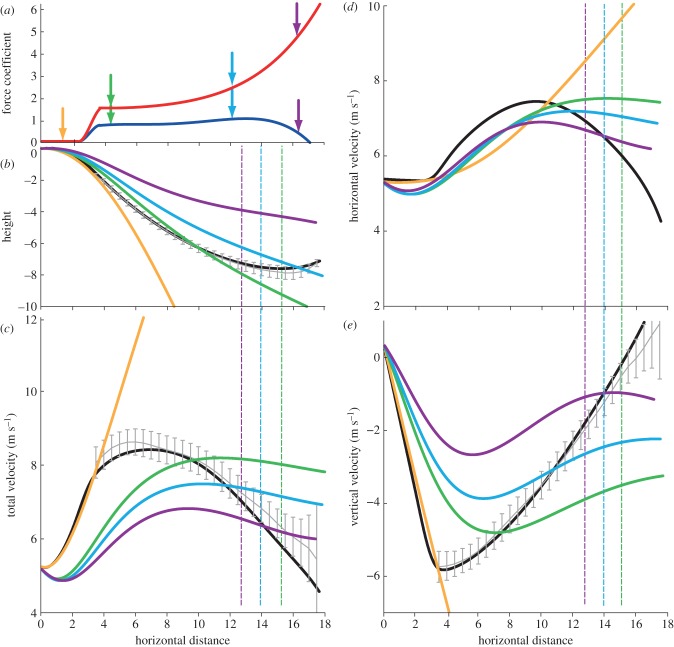
Figure 6.

Comparison of glide simulations. (a) Force coefficients used to generate the simulation that best matched the observed glides: C_L, red; C_D, blue. Before 3.5 m, C_L and C_D are constant and determined by an optimization scheme; after 3.7 m they are derived from observed glides. Coloured arrows highlight specific coefficients used in constant-coefficient simulations. These colours correspond to the line colours used in the remaining panels, such that the coefficients highlighted with the purple circles in (a) were used to create the simulations illustrated by the purple lines in (b) through (e). In (b) through (e), the black line represents the best-matched simulation, and the grey lines with error bars represent the observed data. The best-matched simulation and observed data are similar but not identical because the simulation is based on a polynomial fit rather than the original data. Dashed lines represent distance where equilibrium conditions are met. (b) Comparison of two-dimensional trajectories of simulations with different constant force coefficients, (c) comparison of total velocity of simulations, (d) comparison of horizontal velocities of simulations and (e) comparison of vertical velocity of simulations. (Online version in colour.)

Simulations generated using constant coefficients did not reach equilibrium for the first several metres of the glide. In these simulations, the velocities increased initially in association with gravity, then oscillated around and eventually approached a constant value (figure 6c–e). The magnitude of the force coefficients used for these simulations affected the shape of the trajectory, the GR, velocity and the point at which equilibrium was attained. Simulated glides with higher coefficients (figure 6, purple and blue) had shallower and slower glides, and reached equilibrium sooner than simulations with lower coefficients (orange and green). The simulation that used the average observed coefficients and L/D (blue) produced a similar GR, but slower average velocity than observed glides.

All the simulations created using observed constant force coefficients did reach equilibrium conditions within 18 m, the observed range of horizontal distance (figure 6b–e, dashed lines). The distance and height lost before reaching equilibrium was determined by the magnitude of the coefficients used. The simulations using higher coefficients, values similar to those observed at the end of the glides (figure 6, purple lines), achieved equilibrium at 10 m of horizontal distance and 2 m change in height. The simulations that attained the same mean GR as the observed glides (blue lines) achieved equilibrium at 13 m of distance and 3 m change in height. The simulations with low lift and drag coefficients (orange lines) reached equilibrium only after more than 20 m loss in height, long after ground contact would have occurred, despite having higher L/D than other simulations (e.g. green lines).

Comparing all simulations, GR and AGV were inversely proportional. AGV is proportional to GR^−1.87 (r² = 0.994) (figure 7). The best-matched simulation, characterized by variable force coefficients, did not, however, follow this trend. The performance of that simulation fell above the performance curve generated by the constant-coefficient simulations. Compared with a constant-coefficient simulation with an equivalent GR, AGV is 27 per cent faster in the best-matched simulation, and compared with a constant-coefficient simulation with an equivalent AGV, GR is 46 per cent greater in the best-matched simulation.

Figure 7.

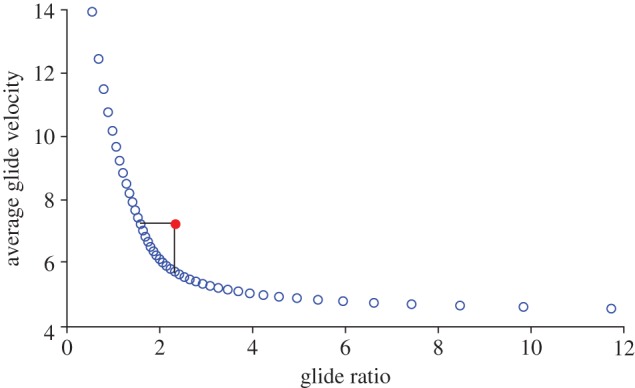
Theoretical performance trade-off between glide ratio (GR) and average glide velocity (AGV). The blue circles represent the performance from the constant-coefficient simulations. All coefficients used were taken from different points during the mean observed glide. Velocity decreases with GR^−1.87 (r² = 0.997). The red circle, which lies above the performance curve, shows the performance from the ‘best-matched’ simulation, which also represents the mean observed performance. (Online version in colour.)

4. Discussion

4.1. Equilibrium gliding and natural behaviour of northern flying squirrels

Although many studies have assumed that gliding mammals glide with equilibrium conditions, in which lift and drag are constant and their sum balances body weight, the flying squirrels in this study demonstrated neither balanced nor constant forces at any point during any glide. All glides showed net acceleration in either the vertical and/or horizontal direction at all times, and the magnitude of the accelerations changed continuously over each glide (figure 4a,b). There are two possible, but not mutually exclusive, explanations for the observed lack of equilibrium conditions. First, gliders may not have had sufficient space and time to reach equilibrium. Second, if gliders actively changed wing configuration to modulate aerodynamic forces, they would not experience long periods of equilibrium gliding, regardless of glide length. Our analyses suggest that both factors may be relevant for these animals.

If a glider adopts a static pose, and, therefore, constant force coefficients, the glider will oscillate around and eventually approach an equilibrium velocity after a certain amount of height lost and horizontal distance travelled [5]. Our constant force coefficient simulations reveal that equilibrium conditions are attainable for animals the size of G. sabrinus within the observed glide distances. The simulations with the higher observed force coefficients attained equilibrium velocity in as little as 10 m of horizontal travel and 2 m loss in height. All simulations that used coefficients from the observed range attained equilibrium velocity within 16 m of horizontal distance and 8 m of height loss. Approximately half of the observed glides were 10 m or shorter; the simulations suggest that equilibrium is not possible for those glides. For all glides longer than 10 m, however, nearly half of the glides we recorded, equilibrium gliding is physically possible, although the animals never used constant velocity gliding (figure 5a). Instead, the squirrels appear to actively avoid constant speed, given that the distance at which they would achieve equilibrium conditions, 12 m as determined by our simulations (figure 6, cyan), is the distance at which L/D began to increase in the observed glides (figure 5e,f). We suggest that northern flying squirrels are physically unable to achieve equilibrium gliding conditions during relatively short glides, and avoid equilibrium during longer glides by active aerodynamic modulation. We note that the predicted time and distance to achieve equilibrium will vary with wing loading, and this would change the minimum distance at which equilibrium conditions can be achieved.

Although the passive motion of balanced and constant forces would require constant force coefficients, the squirrels in this study appear to actively modulate their equivalent lift and drag coefficients in a consistent manner, both throughout and among glides (figure 5e). For wings in general, aerodynamic force coefficients are adjusted by two different mechanisms: changing wing orientation, specifically angle of attack, and changing wing shape. For an aerofoil that is not stalled, both C_L and C_D increase with increasing angle of attack. Here, during the first 12 m of the glide both C_L and C_D increased, and because they increase together, the change in equivalent coefficients could be caused solely by a change in angle of attack or by a change in wing area. After 12 m, the coefficients change in opposite directions; C_L increased, whereas C_D decreased. This implies that during the second half of the glide, the changes in the force coefficients were caused by changes in wing and/or body shape, rather than changes in angle of attack.

4.2. Natural gliding behaviour and mechanics

Non-equilibrium glides performed by flying squirrels were characterized by a systematic, consistent pattern of changing equivalent force coefficients (figure 5e). We characterize these glides as having three phases: an initial phase characterized by a streamlined, ballistic dive with low equivalent force coefficients; a middle phase characterized by moderate equivalent force coefficients and a moderate L/D of around 2.0; and a final phase characterized by very high lift coefficients, lower drag coefficients, and high L/D. The timing of changing equivalent force coefficients interacts with changing velocity and glide angle, resulting in characteristic sequential changes in net aerodynamic forces and typical glide trajectories (figure 8).

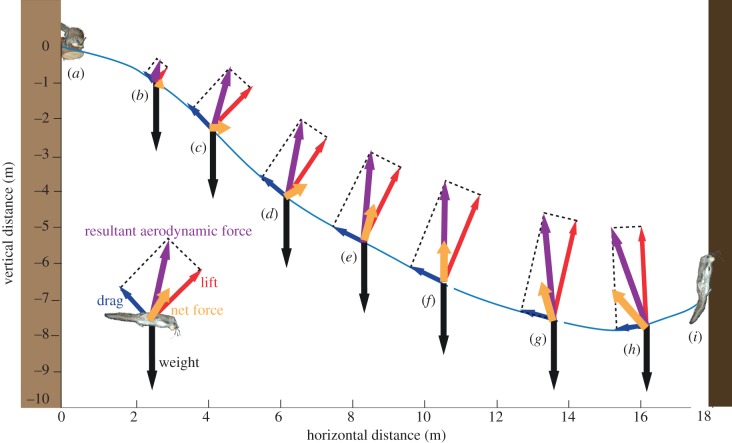
Figure 8.

Model of a flying squirrel glide trajectory showing changes in aerodynamic and net forces. Black arrow represents one body weight for scale. (a) Launch point: squirrels launched with a velocity approximately 5.25 m s⁻¹. (b) For the first 3 m, squirrels maintained small force coefficients, maximizing acceleration due to gravity, and increasing total glide velocity. After sufficient speed was attained, the force coefficients increased. (c) At the maximum glide angle, the vertical component of aerodynamic force equalled body weight. The net force now is entirely in the forward horizontal direction, increasing velocity beyond equilibrium velocity. Aerodynamic force continues to increase as speed increases. After this point, vertical aerodynamic force exceeds gravity and causes the glide trajectory to curve up, decreasing glide angle. (d) Peak velocity is achieved. Total velocity decreases because vertical velocity decreases faster than horizontal velocity increases, owing to forces. (e) While velocity is decreasing, C_L and C_D increase to continue to generate force as the animal slows. (f) As the glide path continues to flatten, resultant aerodynamic force is reoriented in an increasingly rearward direction. At 10 m, the resultant is vertical, and there is no horizontal acceleration. (g) Resultant aerodynamic force is now oriented partially rearward, causing rearward acceleration and increasingly slowing the squirrel. C_D and, consequently, drag, begin to decline to minimize this effect. (h) C_D continues to decrease to mitigate the effect of drag slowing the glide. This changes L/D, orienting the force slightly more forward, and extending the glide. (i) Landing.

The initial phase of the squirrels' gliding is ballistic with little aerodynamic force opposing gravity or the momentum present at launch (figure 8b). Although we did not directly record the first 3 m of the glide, our simulations suggest that the only way for the squirrels to attain the position and velocity we observed when they entered the camera field of view (figure 8c) is by virtue of relatively high launch velocity, approximately 5.4 m s⁻¹, and low force coefficients (C_L = 0.05, C_D = 0.05) during the first few metres (figure 6). We note that these are equivalent coefficients because our calculations assume constant wing area, but the same effect would result from higher coefficients and a smaller fraction of the membrane deployed. Nevertheless, these are reasonable aerodynamic coefficients for a streamlined body [27,28]. After the initial phase, C_L and C_D increased to approximately 1.5 and 0.8, respectively, increasing lift and drag, which reduces the sinking velocity and makes the glide shallower. Gliding steeply in this manner also leads to an increase in horizontal speed because it results in significant forward force: lift is perpendicular to the direction of travel, so at steeper glide angles, the lift vector has a larger forward horizontal component. At the steep glide angles we observed, the forward horizontal component of the lift vector was approximately twice the rearward horizontal component of the drag vector (figure 8c). Hence, the animals experienced a substantial net forward force, increasing horizontal velocity even after vertical velocity has started to decrease. Net velocity peaked at approximately 8.5 m s⁻¹ between 5 and 6 m horizontal distance from launch (figures 5a and 7d).

The middle, cruising phase of the glide is characterized by constant rates of change in most parameters. This period starts after a peak in net velocity. As the animal slows it gradually increases its equivalent force coefficients (C_L by approx. 50% and C_D by approx. 25%), compensating for the force reduction resulting from decreasing velocity (figures 5e and 7d–f). Throughout this phase, lift, which is already greater than one body weight, continues to increase at a consistent rate. Glide angle, vertical and total velocities, forces and L/D all change at relatively constant rates (figure 5a,c,d,f). This phase persists until horizontal velocity peaks, after which the net velocity begins decreasing more rapidly.

Throughout the middle phase, the glide angle becomes shallower, causing the direction of travel and force vectors to rotate rearward. As the net force rotates from more forward (figure 8e) to vertical (figure 8f) to more rearward (figure 8g), the horizontal acceleration gradually changes from positive to zero to negative, and horizontal velocity increases, peaks, then decreases. At this point, both horizontal and vertical velocities are decreasing and cause glide velocity to slow at an increasing rate. This slowing effect is ameliorated by changes in L/D during the final phase.

The final phase, approximately a third of the glide, is characterized by dramatic changes in the L/D (figure 5e), brought about by large and opposing changes in the force coefficients (figure 5e). When horizontal velocity begins to decrease, the squirrels further increase C_L to maintain lift during reduced velocity, and decrease C_D, thereby minimizing deceleration. The combined effect rotates the net aerodynamic force vector forward, reducing the horizontal rearward force and extending glide length.

The increase in lift and L/D near the end of a glide may contribute to the mechanics of landing, reducing the need for a sudden pull-up manoeuvre. When lift and resultant force exceed body weight, and are oriented upward and rearward, the glider's downward trajectory rotates upward (figure 8g,h). With lift relatively high, as velocity decreases, the squirrel's trajectory curves upward at an increasing rate until the animal arrives at the tree, its body oriented vertically. Thus, a landing manoeuvre for long glides is a natural end product of the behaviour that extends the glide via high lift and low drag, instead of a specific manoeuvre in which a glider induces stall and slows for landing using high drag.

4.3. High lift coefficients and measurement uncertainty

The equivalent lift coefficients exhibited by flying squirrels are high in comparison to most human-engineered aircraft. While many aircraft wings would stall with C_L well under 2.0, our analysis suggests flying squirrels can use lift coefficients considerably higher than that (figure 5e). Laboratory experiments with flying squirrels and sugar gliders observed lift coefficients between two and three for the middle region of very short glides [19,20]. The relatively high equivalent coefficients we observe during the middle region of glides in this study fall within that same range, and only exceed that range towards the end of the glide. These high values could possibly be attained by squirrels using a partially separated flow regime. Potential mechanisms that could generate these abnormally large lift coefficients include near-stall conditions and the augmentation of lift by leading edge vortices similar to those observed on low aspect ratio and delta wings, respectively [29,30].

The terminal portion of the glide shows more unusual aerodynamic performance, where we find high lift simultaneous with low drag. However, examples of engineered wings exhibit comparable force coefficients. The Liebeck aerofoil (C_L = 3.06 and C_D = 0.005), also a highly cambered thin wing, is one such example [31]. Similarly, exceptionally high values of L/D have been observed in gliding colugos [17]. We acknowledge that these are extreme force coefficients and must be viewed with some caution. At this stage of the glide, digitizing and differentiation errors are greatest (see the electronic supplementary material) and, as mentioned above (§2.5), equivalent force coefficients are sensitive to errors in estimation of body mass and wing area. Nevertheless, the combination of high lift and low drag prior to landing appears to be robust, although the actual coefficients may not be as extreme as the data suggest. Moreover, the overall conclusions about equilibrium and varying coefficients are not changed by this uncertainty.

4.4. Benefits of varying aerodynamic force coefficients

The consistency and repeatability of northern flying squirrels' three-dimensionally complex glide paths, particularly in the likely presence of unsteady flow conditions, suggests that these animals are able to exert at least some degree of active control over interaction of the gliding wing and local airflow. Varying C_L and C_D over the course of a glide allows squirrels to achieved greater whole-glide performance, GR and AGV than would be possible with constant force coefficients. Our simulations using constant force coefficients show that AGV scales negatively with GR; higher speed incurs a poorer GR along a specific performance curve (figure 7). Lower force coefficients give faster but shorter glides, whereas high coefficients with high L/D give longer but slower glides. However, by systematically varying C_L and C_D during the glide, squirrels achieved performance above the simulation curve (figure 7, red symbol). The best-matched simulation, which uses the same pattern of changing coefficients as the observed glides, shows a 46 per cent higher GR compared with a constant-coefficient simulation with the same AGV, and a 27 per cent faster AGV compared with a constant-coefficient simulation with the same GR. Although some constant-coefficient simulations had either higher GR or faster AGV than the best-matched simulation, no constant-coefficient simulation was superior on both counts. Observed glides, such as the best-matched simulation, all had both higher GRs and faster AGVs than all constant-coefficient simulation cases between the equivalent GR and AGV cases (figure 7).

To achieve both a combination of higher GR and AGV, squirrels used both strategies from the two extremes of GR versus AGV performance curve in the same glide. The squirrels used low equivalent coefficients at the beginning of the glides to achieve relatively high speed, and then changed to higher equivalent coefficients with a higher L/D to achieve greater distance and a better GR. Had the squirrels started with high and constant coefficients, they would not have quickly approached a slower equilibrium velocity, and would not have generated more than one body weight of lift for any substantial duration. In contrast, by switching from low to high coefficients, the squirrels generated more than one body weight of lift for most of the glide, minimizing loss in height and even gaining height near landing (figure 5d), a feat not possible if force coefficients remain constant.

This combined approach is particularly effective because of the timing and order in which squirrels vary equivalent force coefficients. By using low equivalent force coefficients early in the glide to achieve a relatively high speed, then switching to higher equivalent force coefficients further along the trajectory, they are able to produce more aerodynamic force later in the glide than if had they started with high coefficients. This result differs from that of Willis et al. [6], in which varying force coefficients in a gliding model did not produce significant improvements in GR. However, in that theoretical study, C_L was always assumed to be less than one and C_D was a specific function of C_L, and neither restriction was present in the glides we observed in northern flying squirrels.

Both GR and AGV have ecological consequences. The higher the GR, the less energy a squirrel has to spend climbing to travel a given horizontal distance during a glide. If energetic efficiency was the only selective criterion driving gliding behaviour, we would expect squirrels to glide in a manner that maximizes GR. We observe that squirrel glides do not maximize GR, which suggests that increased absolute speed may also be beneficial, perhaps for several reasons. First, higher flight speed may confer greater stability. In the event of perturbations, unequal forces across the wings will lead to corrective body rotations, and corrective forces can be produced with smaller postural adjustments at higher speeds because aerodynamic forces scale with velocity squared. Similarly, manoeuvres can be accomplished more efficiently at higher speeds. Second, gliding faster reduces squirrels' commute times, in turn reducing total foraging time and exposure to predators and the elements. Squirrels hoard, collecting food and storing it in nests or food caches [32]. Faster commute times allow for more round trips between a food source and a cache in a given amount of time, and this may provide a benefit when many individuals are competing for the same, limited patch of food.

4.5. Comparison of flying squirrels and other gliders

Gliding has evolved independently among mammals at least nine times: in three families of marsupials (Order Diprotodontia: Families Acrobatidae, Petaurdiae and Pseudocheridae [12]), five times in placental mammals (Order Dermoptera: Family Cynocephalidae; Order Rodentia: Families Sciuridae, Anomaluridae, Eumyidae (fossil only [33]), Gliridae (fossil only [34]) [1,15]), and in another order that is more basal in mammal phylogeny (Order Volaticotheria, Family Volaticotheriidae, fossil only [35]). Although no study has measured the time-resolved glide trajectories for any of these animals, a variety of studies have examined whole-glide performance (GR and AGV) in different mammalian gliders, and those provide a basis for comparison with our results. The mean GR we observed in this study was similar to the GRs previously reported for G. sabrinus and other gliding mammals (table 3). Similarly, magnitudes of whole-body accelerations in our study were similar to those measured with accelerometers on gliding colugos in the field [9]. The launch velocity we recorded was a little more than twice that recorded for a congeneric species of flying squirrel, Glaucomys volans [37]. This difference may be due to the smaller body size of G. volans and/or motivation due to setting, given that only 1.5 m vertical distance was available for gliding in that experimental set-up.

Table 3.

Glide ratios (GRs) and wing loadings in mammalian gliders.

species	common name	n	mean GR	maximum GR	wing loading (N m−2)	references
MARSUPIALIA
Petauridae
Petaurus gracilis	mahogany glider	31	1.91	2.50	n.a.	[12]
Petaurus breviceps	sugar glider	28	1.82	2.47	45–59a	[12]
Petaurus norfolcensis	squirrel glider	25	1.31	4.4	n.a.	[36]
RODENTIA
Sciuridae
Glaucomys sabrinus	northern flying squirrel	58	1.93	2.36	56–61a	this study
Glaucomys sabrinus	northern flying squirrel	100	1.98	n.a.	56–61a	[11]
Glaucomys volans	southern flying squirrel		1.53	n.a.	44.23b	[15]
Petaurista leucogenys	Japanese giant flying squirrel	150	1.87	3.50	n.a.	[10]
Petaurista petaurista	giant red flying squirrel		n.a.	n.a.	120a	[14]
Pteromys volans	Siberian flying squirrel	66	1.8	3.3	n.a.	[18]
Anomaluridae
Anomalurus derbianus	Lord Derby's anamolure	2	2.21	2.24	69–93a	[16]
DERMOPTERA
Cynocephalidae
Galeopterus variegatus	colugo	1	n.a.	11.3	49–71a	[17]

^aWing loading from Stafford et al. [10].

^bWing loading from Bishop [19].

The glide simulations we carried out produced trajectories with oscillating velocity profiles similar to those from simulations based on flying snakes [5], but the squirrel glide simulations produced different overall performance values. Simulations based on squirrel wing loading and coefficients approached equilibrium at approximately 2.1 s for a wide range of force coefficients, with distance varying according to glide velocity. Simulations based on snakes approached equilibrium after 4 s.

4.6. Evolution of flapping flight

The evolution of a flapping flyer from a gliding ancestor would require many changes in morphology, physiology, neuromechanics and behaviour. However, much discussion about the plausibility of this transition starts with a passive glider at equilibrium, and focuses on changes in wing length to increase lift and development of a downstroke to redirect lift into thrust [2–4]. It has been suggested that a gliding to flapping transition is not mechanistically possible because motions of a glider's wing that increase or redirect force would reduce lift and stability [3]. A glider in equilibrium generates only enough aerodynamic force to support body weight. Hence, any motion that might sacrifice lift for thrust, or generate no lift while repositioning the wings would cause the animal to fall faster, exhibiting poorer glide performance and consequently poorer fitness. In addition, wing flapping leads to fluctuations in the relative locations of the centre of mass and centre of pressure, which can cause instability in pitch and lead to reduced glide performance, particularly for mammals, which possess relatively massive wings [38]. Therefore, an evolutionary transition from gliding to flapping requires sensory, motor and behavioural capabilities that can compensate for the instabilities in motion and airflow that reduce glide performance. We propose that the following are particularly crucial for any flapping to gliding transition: the ability to detect the effect of airflow on body accelerations and rotations; the ability to control body accelerations and rotations in and about all three axes; and the ability to generate lift greater than body weight. A glider with these sensory, motor and behavioural abilities could be a plausible intermediate between an equilibrium glider and an animal capable of stable flapping flight, and would be exapted for powered flight.

To what degree might flying squirrels meet these criteria? The ability of northern flying squirrels to perform consistent and repeatable glides in an aerodynamic regime where unsteady forces are dominant indicates that the squirrels have the ability to sense and respond to their motion and surroundings. Like in other vertebrates, vestibular and proprioceptive signals convey information allowing squirrels to detect body accelerations, rotations and changes in position. In addition, gliding squirrels may have the ability to detect changes in flow over the wings that enables rapid responses to relevant aerodynamic cues. Unsteady flow phenomena, such as leading edge vortices and partial stall can be unpredictable, and a nervous system able to sense changes in flow or pressure gradients and to effect appropriate compensatory responses would be highly advantageous during gliding [39]. We observed consistent and repeatable glides in an aerodynamic regime where unsteady forces are likely to be significant, as illustrated by extremely high lift coefficients, which suggests that flying squirrels possess such neurophysiological mechanisms. At present, we hypothesize that these responses could be based, at least in part, on stretch receptors in the wing membrane muscles [40], or wing membrane sensory hairs similar to vibrissae or the as yet poorly understood sensory hairs of bats [41,42], but it is possible that the vestibular system, some other unidentified sensory input, and/or a combination of types of sensory information are needed. Animals that use flapping flight, such as bats, would also require the ability to sense and respond to unsteady and dynamically changing flow environments, hence their evolutionary origin from a lineage in which such mechanisms are present is probable.

In terms of movement patterns, flying squirrels actively manipulate their wings in a way that modulates aerodynamic force magnitude and direction. By changing wing posture, both flying squirrels and marsupial sugar gliders change aerodynamic force coefficients and resultant body rotations [19,20]. Theoretically, by altering position of the fore- and hindlimbs, tension of intrinsic muscles of the wing membrane, shape of the propatagium, tail position and overall body orientation, mammalian gliders have the potential to generate a wide variety of wing shapes and force coefficients. In this study, over the course of a glide, we observed C_L change from approximately 1.5 to approximately 4.5, resulting in an increase in lift of at least 300 per cent (figure 5e), and given that our simulations suggest that C_L can be lowered to almost zero, it is clear that these gliders have tremendous range in lift generating capability. Flying squirrels can also manipulate drag coefficients over a range of approximately 0 to approximately 1, both in tandem with and opposing lift coefficients (figure 5e). As a consequence, they are able to rapidly modulate L/D, which facilitates changes in orientation of aerodynamic force between the upward and forward directions. Readily able to move left and right limbs independently, northern flying squirrels can likely modulate the aerodynamic characteristics of their left and right wings independently, leading to roll and yaw rotations and sideways accelerations. These gliders thus appear capable of controlling acceleration in all three translational axes allowing them to direct their trajectory, and all three rotational axes, allowing them to control stability.

A third crucial capability necessary for powered flight is the ability to generate more than one body weight of lift. The ability, at minimum, to counteract body weight is crucial because this allows for net lift, averaged over the wingbeat cycle, to balance body weight, even when there are instances within the cycle in which lift is less than weight. Flapping flight typically involves dynamic changes in the magnitude of lift, with lift dropping below weight to zero or even to negative values during portions of the upstroke, when the wing is repositioned for the next downstroke [38,39,43,44], Over a longer timescale, flap-bounding birds, such as zebra finches, alternate between periods of flapping and periods in which they adopt a tucked-wing posture relying on momentum [43]. If a glider does not have the ability to generate lift that is greater than one body weight, then it cannot move its wings to trade lift for thrust or reposition its wings without falling faster. However, the squirrels in this study generated more than one body weight of lift for most of the glide and peaked at 1.5× body weights. Deficits in lift that might arise from wing movement or reorientation could be easily balanced by these periods of lift generation greater than body weight.

In sum, northern flying squirrels do not glide at equilibrium; instead they modulate and redirect aerodynamic force, presumably via movement and/or shape change of wings, in a highly controlled and repeatable fashion. They demonstrate this ability in the context of an aerodynamic regime in which unsteady forces are likely dominant, given the very high angles of attack and lift coefficients we observe in their flight performance. We propose that these animals are more likely to be representative than unique among gliding mammals, and that, therefore, the acquisition of some critical elements required for the evolution of stable flapping flight are not rare, but relatively common evolutionary events within mammals. Multiple lineages of gliders may, thus, be exapted for controlled flapping flight, and improved acceleration when selection favours greater manoeuvrability.

5. Conclusions

We conclude that northern flying squirrels carrying out glides in their natural habitat did not glide at equilibrium, resulting from lack of horizontal distance/height to reach equilibrium at the shorter glide distances and active control of their trajectories at all distances. The squirrels performed glides with unbalanced and continuously changing forces and force coefficients. By systematically varying force coefficients, the squirrels achieved higher GRs and faster velocities than we predict are possible from a constant force coefficient glide. The pattern of force coefficient change indicates that flying squirrels actively change their wing shape and orientation. Gliders with this behaviour could be a mechanistically plausible intermediate between simple static-wing or constant-coefficient gliders and powered flappers.