Abstract
It has become clear that water should not be treated as an inert environment, but rather as an integral and active component of molecules. Here, we consider molecules and their hydration shells together as single entities. We show that: (1) the rate of association of molecules should be determined by the energetic barriers arising from interactions between their hydration shells; (2) replacing non-polar atoms of molecular surfaces with polar atoms increases these barriers; (3) reduction of the hydration shells during molecular association is the driving force for association not only of non-polar, but of polar molecules as well; (4) in most cases the dehydration of polar atoms during molecular association thermodynamically counteracts association; (5) on balance the thermodynamic stability of associated complexes is basically determined by the action of these two opposing factors: reduction of the hydration shells and dehydration of polar atoms; (6) molecular crowding reduces the energetic barriers counteracting association and changes the thermodynamic stability of associated complexes. These results lead to a mechanism for biomolecular recognition in the context of which the formation of unique structures is provided by rapidly forming kinetic traps with a biologically necessary lifetime but with a marginal thermodynamic stability. The mechanism gives definitive answers to questions concerning the heart of specific interactions between biomolecules, their folding and intracellular organization. Predictions are given that can be subjected to direct experimental tests.
Keywords: Water, Protein folding, Enzymatic cycle, Molecular crowding, Intracellular organization
1. Introduction
It has become increasingly clear (see for example, Ref. Levy and Onuchic, 2006) that water plays active roles in intra- and inter-molecular associations. However, despite knowledge of an abundance of structures of water soluble molecules including the native structures of thousands proteins, nucleic acids, and their complexes (Berman et al., 2000), the role of water in the formation of molecular structures is still not clearly understood.
Hydrogen bonding is central to the actions of water molecules. A water molecule can participate in four hydrogen bonds (H-bonds). These bonds form a tetrahedrally ordered array in ice whereas liquid water is a disordered network of such hydrogen-bonded molecules in which H-bonds are loose, though in different ways (for details, see for example Refs. Saenger, 1984; Jeffrey, 1997; Finkelstein and Ptitsyn, 2002). However, people often use another model owing to its simplicity and convenience in describing the thermodynamic properties of water—and we may use it as well. In this model the majority of H-bonds existing in ice persist in liquid water and only some of the H-bonds are broken. The available data suggest that at 37 °C ~15% of the H-bonds are disrupted. I.e. in the average one H2O molecule in liquid water at the physiological temperatures should participate in ~3.4 H-bonds.
Any molecular surfaces including the surfaces of simple ions, such as Na+ and Cl− (in the following all simple ions will formally be considered as small molecules), impose restrictions on hydrogen bonding in their hydration shell. Therefore the behavior of water molecules and hence their free energies are changed within the hydration shells depending on the size and geometry of the surfaces of molecules and distribution of the surface polar and non-polar atoms. The water molecules interacting directly with the surface (the first layer of the hydration shell) undergo the most change, and outside the first 2–3 layers the behavior of water molecules is similar to that of those in bulk water (Saenger, 1984; Nakasako, 2004). All of this suggests that a molecule and its hydration shell should be considered together as a single entity. Below we deduce the free energy curves with emphasis on the activities and energetics of water molecules within the hydration shells.
2. Results
2.1. Hydrogen bonds that are most often formed by the polar atoms in biomolecular systems
The behavior of water molecules is basically determined by their capacity to form H-bonds. Therefore, prior to an analysis of the free energy curves for molecular interactions in water let us recall the properties of H-bonds. Consider the H-bonds O–H⋯O, O–H⋯N, N–H⋯O, N–H⋯N, which are common in biomolecular systems. The lengths of these H-bonds are 2.8–3 Å. This length agrees closely (Ramachandran and Sasisekharan, 1968; Scheraga, 1968) with the van der Waals contact distances in pairs OO, ON and NN. The energy of these H-bonds (the enthalpy of their disruption in a vacuum) is about 20 kJ/mol (4.18 J = 1 cal). This energy strongly exceeds the energy of other non-covalent interactions such as van der Waals contacts: the energy of one H-bond is equal to the energy of about 50 pairs of van der Waals contacts (Scheraga, 1968). In addition to H-bonds formed by O and N, the H-bonds formed with the participation of the sulphur atom S every so often are observed in biomolecular systems. As in the case of O and N, the sulphur atom S can also be a proton donor or acceptor. However, the “sulphur” H-bonds are weaker (their energy is E15 kJ/mol) than that formed by O and N (Donohue, 1969; Jeffrey, 1997).
A special comment should be made about H-bonds in the aqueous environment. H-bonding between two polar atoms of molecules replaces two H-bonds formed by these polar atoms with two water molecules and an additional H-bond is formed by these two freed water molecules. The energy (enthalpy) balance of this reaction is close to zero: two bonds are replaced by two bonds. However, the entropy of the water molecules increases since they are no longer bonded to the polar atoms but only mutually H-bonded and free to go anywhere. This entropy increase caused by the water dimer release is approximately equal to an entropy increase resulting from the molecule H2O transition from ice to liquid water (in both cases one particle becomes free in its movements). A simple estimation (see for example, Ref. Finkelstein and Ptitsyn, 2002) shows that a decrease of the free energy caused by an increase of the entropy of the water dimer is about 6 kJ/mol. This value can formally be considered as the energy of an intra- or inter-molecular H-bond in the aqueous environment. Although not strictly correct, this approximation is often used for convenience.
H-bonding between two polar atoms of molecules is accompanied by transition of water molecules surrounding the polar atoms from the hydration shell of molecules into bulk water and 6 kJ/mol is a part of the free energy that is changed during the transition. Therefore, a decrease of the free energy by 6 kJ/mol is properly considered as a part of the free energy of the hydration shell of molecules. We must also consider changes in the numbers of H-bonds. Decreases or increases of the number of H-bonds by N should contribute +N × 20 kJ/mol or −N × 20 kJ/mol (20 kJ/mol is the energy of an H-bond) to the change of the free energy of water solution. It is important to remember it since as we will see, these critical energetic properties have major consequences for the rates of formation and stabilities of associated molecules.
2.2. The changes of the free energy during the coming together of two non-polar molecules: Spherical non-polar molecules as an idealized example
The formation of the hydration shells of molecules should be accompanied by a change in the free energy of water because any molecular surface restricts the possible configurations of hydrogen bonding within the hydration shells. Despite these restrictions, the overall amount of hydrogen bonding on the surface of small non-polar molecules remains relatively unchanged. Therefore the change of the free energy of water on the surface of small non-polar molecules is largely entropic and not enthalpic (Chandler, 2002, 2005). However, in the case of the extended surfaces of non-polar molecules not all four H-bonds of water molecules can persist near to the surfaces (regardless of its orientation on the extended molecular surfaces) because some of the bonding moieties are directed toward the non-polar surface. Thus, such water molecules can have typically three or fewer H-bonds depending on the local curvature of the surface; i.e., the loss of H-bonds, each increasing free energy by ~20 kJ/mol, takes place in the hydration shell of large non-polar molecules. This energetic effect – the loss of hydrogen bonding – drives the segregation of non-polar molecules from water (Chandler, 2002, 2005).
As an idealized example, consider the changes in free energy during the coming together of spherical, non-polar molecules. The free energy G of an aqueous solution can be divided into two components: the free energy (Gm) of the molecules themselves and the free energy (Gw) of water. Assume that H1 and H2 are the thickness of the hydration shells of two spherical molecules (the thickness of the hydration shell of 2–3 layers may be estimated to be about 8–12 Å since the maximum steric size of H2O molecule is about 4 Å). Let us set Gm and Gw at zero when the distance “D” between the surfaces of two spherical non-polar molecules is vastly larger than H1 + H2, and then consider how Gw and Gm change as D decreases.
Gw should begin to increase when the hydration shells are close enough (Fig. 1A, position 1) to clamp one–two layers of water molecules between them (H1 + H2 + 4Å < D < H1 + H2 + 8 Å). In this case a small decrease in mobility of the clamped molecules will initiate modest increase in the entropy component of Gw. Then, as D further decreases to H1 + H2 the clamped molecules will be released but Gw does not return to “0” because the now interacting hydration shells (Fig. 1A, position 2) are more restricted than they were when interacting with bulk solvent. This should lead to the additional loss of H-bonds within the hydration shells. Therefore Gw at D ≈ H1 + H2 should basically be determined by the additional loss of H-bonds, i.e. Gw should has a positive value of N × 20 kJ/mol where 20 kJ/mol is the energy of an H-bond and N is the number of the additionally lost H-bonds. The latter is proportional to an area (S) of the surface–surface contact formed by the hydration shells at D ≈ H1 + H2 (Fig. 1A, position 2).
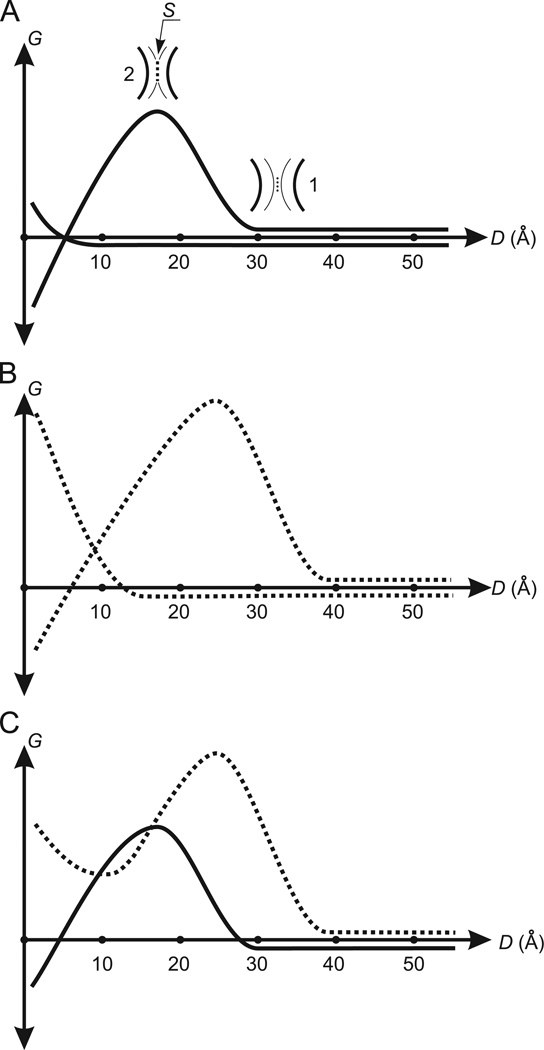
Fig. 1.
Changes of the free energy during the coming together of spherical molecules in water: (A) the coming together of non-polar spherical molecules. G is the free energy. D is the distance between the surfaces of molecules. The curve forming the energy barrier is the free energy Gw. The other curve is the free energy Gm. 1 is one layer of water molecules (dots) clamped between the hydration shells (fine arcs). The black bold arcs are the surfaces of molecules. The clamped water molecules determine the beginning of the increase of Gw. 2 is the surface–surface contact (the broken line S) formed by the hydration shells. An area of S determines the maximum value of Gw. (A) Demonstrates a case when the driving force for molecular association (decreasing Gw) successfully withstands the counteracting force (increasing Gm). (B) The curves Gw and Gm (broken) describing the coming together of spherical molecules having the surface enriched by polar atoms. In comparison with the curves Gw and Gm for non-polar molecules in (A), the energy barrier in Gw and the beginning of the increase of Gm are shifted to the right. The height of the energy barrier in Gw is increased. (C) The total curve for Gw and Gm (the Gmw-potential). The broken and unbroken curves are the Gmw-potentials for molecules having the surface enriched by polar atoms and for non-polar molecules, respectively.
At D < H1 + H2, Gw should begin decreasing because of the expulsion of the shell water molecules located between molecules into bulk water where they exhibit more favorable interactions. Gw will have negative values when D < 4 Å because at such D the hydration shell water molecules located between molecules will be freed to solvent. Thus, the changes of Gw caused by decreasing D should originally form an energetic barrier (the Gw-barrier), and then Gw should decrease down to a negative value (Fig. 1A). The Gw-barrier should be formed in the distance D interval of about (H1 + H2) ± 8 Å where (H1 + H2) is the D-coordinate of the Gw-barrier peak.
2.3. Gm always increases during association of non-polar molecules
The association of molecules is accompanied only by increases in Gm. This occurs because of the entropy loss and loss of van der Waals contacts (steric contacts). The first is evident. As for steric contacts, water molecules can be tightly packed not only on spherical molecules, but on any accessible molecular surfaces since hydrogen bonding between water molecules occurs practically without disruption of the van der Waals contacts between their oxygen atoms. A simple calculation shows that the number of molecular surface–water molecule steric contacts on two surfaces exceeds the number of the molecular surface–molecular surface steric contacts formed by two surfaces even when these two surfaces are complementary. This means that removal of water between molecules during their association is accompanied by a decrease in steric contacts within interacting parts of the molecules. The steric contact decrease should begin when 2–1 layers of water molecules are arranged between the molecules, i.e. when D reaches ~8–4 Å Gm should begin increasing. Then, the maximum value of Gm should be reached when the shell water molecules between molecules are expelled (D < 4 Å; Fig. 1A).
2.4. The Gmw-potential
The total curve of the free energy Gmw (the Gmw-potential) is the sum of Gm and Gw curves (Fig. 1A) and is also shown in Fig. 1C (unbroken curve). The Gmw-potential includes the Gw-barrier to association. To a rough approximation the barrier height is equal to N × 20 kJ/mol, where N is the number of lost H-bonds and is proportional to an area S (Fig. 1A, position 2). The average time (τ) required to overcome the barriers of N × 20 kJ/ mol at T = 300 K and N = 1–6 is equal to 10−9.5, 10−6, 10−2.5, 101, 104.5 and 108 s, respectively (Lim et al., 2005). These values of τ demonstrate that the time required to overcome barriers to association are exquisitely sensitive to N and, therefore, S. Clearly, molecular orientations that minimize S facilitate association. We return to this point below.
The Gmw-potential at D < 4 Å is determined by two opposing factors, both of which are due to the removal of water molecules from the hydration shells to bulk water. One factor is reduced Gw which is always negative and is the driving force for association. The other one is increasing Gm, which is always positive and opposes association. It follows from the available data that the value of Gmw = Gw + Gm at D < 4 Å is always negative in the case of non-polar molecules. This no surprise, since the Gmw-potential at D < 4 Å is basically determined by the increase in the number of H-bonds for the water molecules released from hydration shells (reducing Gw) and loss of van der Waals contacts for the dehydrated surfaces (increasing Gm). As it was noted above the energy of one H-bond is 1.5 orders greater than the energy of a van der Waals contact. For this reason Gmw = Gw + Gm < 0, i.e. well-known hydrophobic “interactions” take place that stabilize the molecular complexes formed by non-polar molecules.
2.5. The changes in the curve Gw caused by the polar atoms of molecules
Assume that all or part of non-polar atoms on the surfaces of considered spherical molecules are uniformly replaced by polar atoms. H-bonds formed by water molecules with these polar atoms will compensate, but always only partially, an increase of the free energy of water molecules in the hydration shells. An imperfect compensation is conditioned by the following two reasons. First, a water molecule on a molecular surface loses from 0.4 to 2.4 out of its 3.4 tetrahedrally oriented H-bonds. A loss of these H-bonds cannot be compensated by polar atoms of the surface because for steric reasons a water molecule can form only one H-bond with a polar atom. Second, the orientations and mobility of water molecules hydrogen bonded to a polar atom are sharply restricted. The free energy of two anchored molecules (see above) increases by about 6 kJ/mol, and furthermore, the shell molecules in the vicinity of the anchored molecules additionally lose the entropy and H2O–H2O H-bonds. Besides the above factors, in the case of charged polar atoms a decrease in the entropy of the hydration shell molecules also occur because of the ordering of water molecules around the charged atoms. Thus, an increase of the free energy of water molecules on the surfaces of non-polar molecules can only partially be reduced by substitution of polar atoms for non-polar ones. This, in turn, means that as in the case of non-polar molecules (Fig. 1A), the value of Gw at small D between polar molecules should always be negative too (Fig. 1B).
Anchoring water molecules on a polar atom restricts the possible configurations of hydrogen bonding and so increases the thickness of the hydration shell in the vicinity of the polar atom. A radius of solvated polar atoms is v0 + d0, where v0 is the van der Waals radius of polar atoms (~1.5 Å) and d0 is the thickness of the hydration shell (8–12 Å). Because shell surface area depends on (v0 + d0)2, an increase in the shell thickness by one water layer leads to a several-fold increase of the surface of the hydration shell of a polar atom. This should lead to increased S when the hydration shell of a polar atom participates in the formation of the Gw-barrier, i.e. an increase of the Gw-barrier should take place. Therefore the Gw-barrier will increase with increasing the density of polar atoms on the surface of spherical molecules; and besides increasing the height of the Gw-barrier, the D-coordinate of its peak will also increase because of the rise in thickness of the hydration shells. Thus, we can conclude that surface polar atoms change the curve Gw, increasing both the Gw-barrier and the D-coordinate at its peak (compare the curves for Gw in Fig. 1A and B).
2.6. The effect of polar atoms of molecules on the run of the Gm curve
With solutes containing polar atoms, H-bonds and electrostatic interactions are the basic factors determining the shape of the Gm curve. After dehydration of the polar atoms caused by molecular association, the H-bond donors and acceptors released from the water molecules cannot often form new H-bonds. This occurs because the number of the released donors is not equal to the number of released acceptors and, even when there are equal numbers of donors and acceptors, as a rule they cannot be brought together for hydrogen bonding. Consequently, H-bonds during molecular association make a positive contribution to the change of Gm because molecular association is accompanied by a decrease of the number of H-bonds formed by polar atoms of molecules. In other words, dehydration causes a decrease of the number of H-bonds formed by polar atoms and thus opposes molecular association.
As to electrostatic interactions, they cover the interactions of separate charges, dipoles and quadrupoles. Here, we consider only the interactions of separate charges because they are a few times stronger than interactions between dipoles, while interactions of dipoles are stronger than those between quadrupoles. According to classical electrostatics, a sphere of charge q and radius R in a medium of permittivity ε has the energy U = q2/2εR. The transfer of charged groups from water (ε ≈ 80) into the medium between the interacting molecular surfaces (ε ≈ 3) strongly increases the free energy. Even the transfer of a close pair of oppositely charged particles increases the free energy by about 150 kJ/mol (the estimations of energy and ε see for example Refs. Saenger, 1984; Scheraga, 1968; Finkelstein and Ptitsyn, 2002; Fersht, 1999). Experiment shows that e of 40–80 should be used when considering the energy (U = qiqj/εrij) of interactions between the surface charges qi and qj and such ε is retained even when rij is about 3 Å (a direct van der Waals contact). In this case the free energy of repulsion and attraction is ±12 kJ/mol at ε ≈ 40 and ±6 kJ/mol at ε ≈ 80. The energy of attraction and repulsion that occurs as the surfaces draw together is small because ε ≈ 80 and rij ≫ 3 Å. All of this indicates that electrostatic interactions also oppose molecular association by increasing the Gm component of the free energy and this is basically performed by the dehydration of charged groups.
An increase of Gm caused by dehydration of polar atoms of molecules can thus be considered the counteracting force for molecular association. This force should begin to act when D reaches ~12–8 Å, the distance occupied by 3–2 layers of water molecules in the hydration shells. Here, interactions between the inner layers of the hydration shells restrict the formation of H2O-polar atom H-bonds. Then, Gm should continue to increase as D decreases, reaching its maximum when all the shell water molecules between molecules are expelled; i.e., at D < 4 Å (Fig. 1B).
It is clear that a progressive increase of the density of polar atoms on molecular surfaces will be accompanied by progressive strengthening the counteracting force. At the limit when the surfaces of molecules are saturated with polar atoms, the energy losses caused by dehydration of polar atoms can significantly exceed the energy gained by reduction of the hydration shells during molecular association. In other words, saturation of molecular surfaces with polar atoms can lead to shifting the Gmw-potential curve to the left of the Gw-barrier from negative into positive territory (Fig. 1C), i.e. the association of molecules can be prohibited by increasing the density in distribution of polar atoms on molecular surfaces.
2.7. Generalization to interactions between molecules having arbitrary geometric parameters and distribution of the surface polar atoms
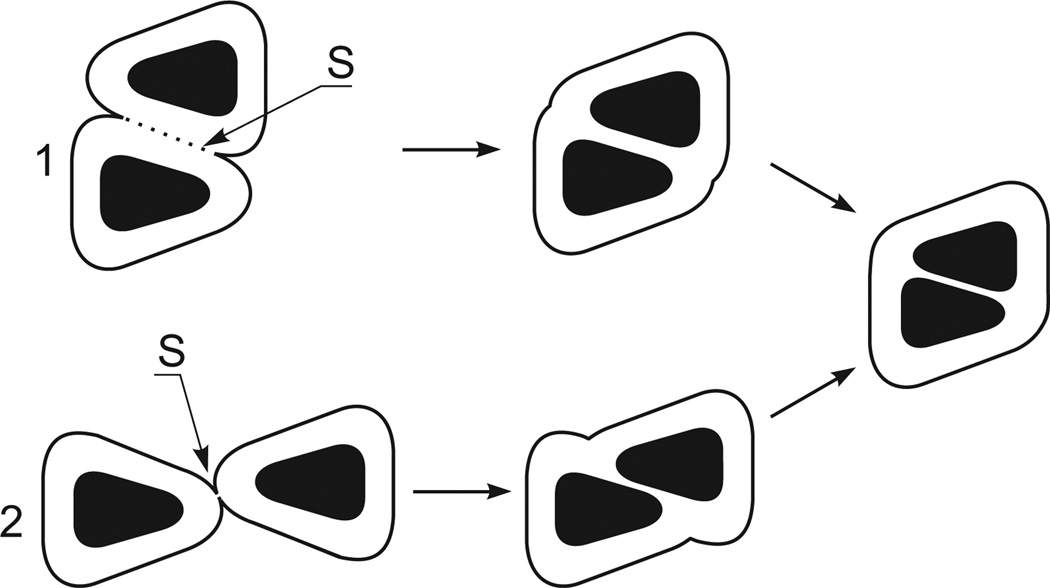
Actual molecules, as a rule, are not perfectly spherical and their surface polar atoms are nonuniformly distributed. However, it is clear that interactions between actual molecules should also be described by Gmw-potentials, with the difference that these potentials depend on such factors as the mutual orientations of molecules, their movements relative to each other, the size and geometry of molecular surfaces and distribution of polar and nonpolar atoms on these surfaces. These factors determine the size of the area S, the driving and counteracting forces for molecular association. In Fig. 2, for example, the area S in pathway 2 is significantly smaller than that in pathway 1. This example demonstrates that the mutual orientation of molecules during the formation of the contact between their hydration shells kinetically controls the pathways for molecular association since the size of area S determines the height of the Gw-barrier. The distribution of the surface polar atom also determines the height of the Gw-barriers since the polar atoms of molecules elevate the Gw-barriers.
Fig. 2.
Relationship between S and the mutual orientations of molecules (black bodies) during their association in water. The fine lines are the surfaces of the hydration shells. 1 and 2 are different variants of the coming together of molecules, ending with the same association. The figure demonstrates that S (and thus Gmw) in variant 2 is far less than S in variant 1.
A relationship between the driving force for molecular association (reduction of the hydration shells during the association) and the above-listed factors is evident. As to the counteracting forces, they strongly depend on the capacity of the dehydrated polar atoms to form inter-molecular H-bonds and bonds between oppositely charged atoms. This capacity is controlled by distribution of polar atoms on molecular surfaces.
Thus, we see that interactions between actual molecules can also be described by Gmw-potentials by introducing corrections for the size and geometry of actual molecules and distribution of their polar atoms. Our preliminary results based on these corrections simply explain why the association of polar molecules occurs slowly, or does not occur, or leads to unique molecular complexes. To show the broad utility of the Gmw-potential, below we briefly discuss its implications for biomolecular recognition which are the heart of many biomolecular processes. We also use it to explain the general intracellular distributions of biomolecules.
2.8. Application of the Gmw-potential to biomolecular recognition: selective inter and intra-molecular associations
Biomolecular recognition is performed not only between molecules (selective inter-molecular association), but also between mobile elements within a macromolecule (selective intra-molecular association). Both inter-molecular recognition and intra-molecular recognition can occur between partners having fixed or fluctuating structures, as in the case of protein folding or the formation of substrate–enzyme complexes. Recognition typically occurs within time intervals of about 10−3–1 s. Such times are observed for the formation of substrate–enzyme complexes (Fersht, 1999), in protein folding (Shulz and Schirmer, 1979) and during the assembly of protein–protein, RNA–protein and RNA–RNA complexes when protein chains are synthesized in the ribosome (Wilson et al., 2002). Assuming that H-bond disruption within hydration shells is the dominant process that determines the Gw-barriers during such associations, then these times would correspond to N of 3 to 4 H-bonds (see above). Greater the Gw-barriers would not be compatible with such molecular associations occurring within this time scale.
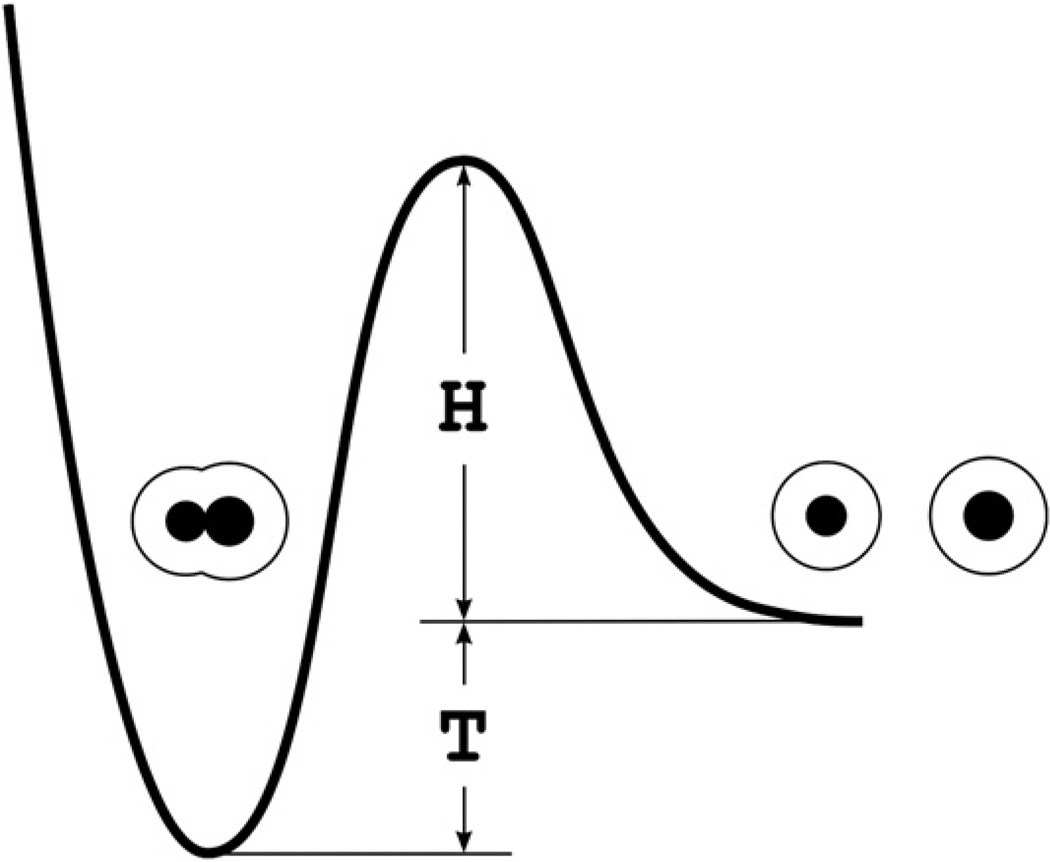
It follows from the above consideration that biomolecular recognition should be controlled not only thermodynamically but kinetically as well. We may think of biomolecular recognition as a fast molecular association leading to the formation of a unique associated complex with a biologically relevant lifetime. The associated complex can be considered as a rapidly formed kinetic trap (the rf-trap; Fig. 3). The average rate of the entry into the rf-traps should be determined by the Gw-barrier the height (H) of which is less than or equal to (3–4) × 20 kJ/mol. The lifetime of an rf-trap is the average time required to overcome the barrier with the height H + T, where T is the thermodynamic stability of the rf-trap (Fig. 3). Importantly, the barrier height H + T should provide biologically relevant lifetimes for rf-traps.
Fig. 3.
An associated complex as the rf-trap. Black spheres are dissolved molecules. The fine lines are the surfaces of their hydration shells. H is the height of the Gw-barrier determining the average rate of the entry into the rf-trap. This height is less than or equal to (3–4) × 20 kJ/mol. T is the thermodynamic stability of the rf-trap. A lifetime of the rf-trap is the average time required to overcome the barrier with the height H + T.
It is surprising that despite an abundance of different biomolecular surfaces, as a rule, only one of many possible rf-traps forms spontaneously. This is easily understood if it is recalled that polar atoms should increase Gw-barriers and Gm. For this reason the increase of a share of the surface polar atoms should lead to decreasing the total number of kinetic traps and primarily the rf-traps. A large share of polar atoms should lead to full elimination of the rf-traps. Therefore the formation of a unique rf-trap is most likely in the vicinity of the point of total disappearance of the rf-traps caused by increasing the share of polar atoms. This means that the biomolecular recognition should basically be provided by the rf-traps with a biologically necessary lifetime but with marginal thermodynamic stability.
The above scenario for the biomolecular recognition correlates well with the available data: most globular protein and nucleic acid structures are truly marginally stable (Privalov and Khechinashvili, 1974; Filimonov, 1986; Makhatadze and Privalov, 1995; Taverna and Goldstein, 2002), with a ΔFfolding value (−T in our model) of about −40 kJ/mol to −80 kJ/mol. The height H in the rf-traps is about (3–4) × 20 kJ/mol (see above). Consequently, the height H + T is 100–160 kJ/mol. For these values for H + T, the average lifetime of an rf-trap is between 104.5 and 1015 s. These times are on the same scale as the lifetimes of various proteins. All of this clearly demonstrates that biomolecular recognition can be provided by rf-traps with biologically relevant lifetimes while having marginal thermodynamic stabilities.
2.9. The influence of intracellular molecular crowding on the stability and broad distribution of biomolecules in cells
Let us designate a complex consisting of a molecule and its hydration shell as an hsm-complex. When the concentration of hsm-complexes is low they are randomly distributed in solution. The opposite situation takes place in living cells where molecular crowding and the intracellular compartmentalization of the various non-associated molecules are observed. In the framework of the Gmw-potential a cell molecular crowding should lead to a non-random distribution of hsm-complexes. To demonstrate it, let us roughly represent small to large biomolecular hsm-complexes as spherical ones with radiuses of 20–60 Å, including 10 Å hydration shells. When identical spherical hsm-complexes are tightly packed they occupy 75% of the total volume and the distance between the surfaces of the molecules of adjacent hsm-complexes is 20 Å (the average thickness of two hydration shells). Simple calculations show that when the spherical hsm-complexes with radiuses of 20–60 Å are tightly packed their biomolecular components occupy from 10% to 43% of total volume. This range is in excellent agreement with experimental observations of macromolecules in physiological fluids (Zhou et al., 2004). This leads to conclusion that under molecular crowding conditions in cells the average distance between the surfaces of adjacent molecules is about 20 Å.
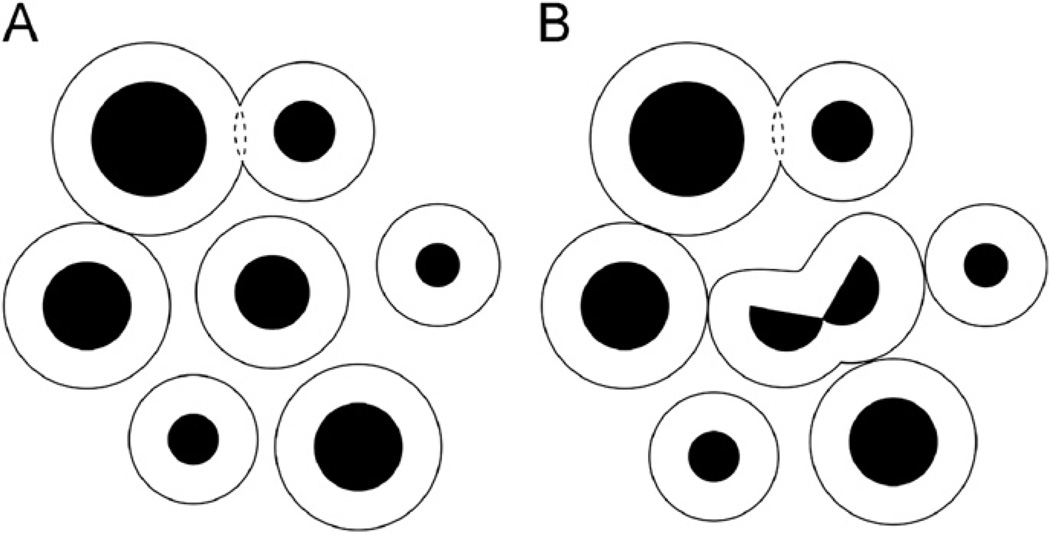
According to the Gmw-potential, when the distances between the molecular surfaces are 20 ± 10 Å the interactions between hsm-complexes are described by the Gw-barrier part of the Gmw-potential curves (Fig. 1C). For this reason a change of the free energy should be caused by any changes in the distribution of hsm-complexes. Consequently, under molecular crowding conditions a random intracellular distribution of molecules should be prohibited and the biomolecular hsm-complexes should exist in the “packed” state (Fig. 4A) with the minimal value of the free energy. However, it should be noted that in living cells the packed state is constantly rearranged due to changing the concentrations of different types of molecules caused by carrying out the metabolic processes. Thus, we see that understanding of the Gmw-potential allows one to give a clear knowledge of a mechanism of the intracellular distribution of molecules as the packing of hsm-complexes.
Fig. 4.
The packing of hsm-complexes under intracellular molecular crowding conditions. Black spheres are dissolved molecules. The fine lines are the surfaces of their hydration shells: (A) the hsm-complexes are closely spaced down to overlapping the hydration shells: the interactions between hsm-complexes are described by the Gw-barrier part of the Gmw-potential curves. (B) Break-up of the molecule into two parts at the center of the figure. Disruption of this molecule leads to the formation of the hydration shell–hydration shell contacts between the disrupted hsm-complex and neighboring hsm-complexes.
Another interesting consequence follows from the Gmw-potential: the thermodynamic stability of different structures of an hsm-complex should depend on crowded cellular environments. Under molecular crowding conditions in cells the structural transformations of an hsm-complex are accompanied by changes in the interactions of this complex with neighboring hsm-complexes (see the hsm-complex at the center of Figs. 4A and B). The changes of the free energy caused by these interactions are determined by the Gw-barrier part of the Gmw-potential curves. Therefore these free energy changes can be sufficiently large to stabilize or destabilize different structures formed by the molecule at the center of the Figs. 4A and B. Thus, the stability of different structures of a molecule and, therefore, choosing among them can be significantly determined by crowded cellular environments. In fact, this means that the changes in intracellular molecular crowding can lead to the structural transformations of hsm-complexes including changing molecular recognition.
2.10. Other applications of the Gmw-potential
The results obtained in this work demonstrate that the curves of Gm, Gw and Gmw are powerful enough to explain qualitatively the kinetics and thermodynamics of association of both polar and non-polar molecules. Furthermore, these curves provide definitive answers to the questions concerning the principles of biomolecular recognition and intracellular distributions of molecules. A natural extension of the obtained results would be computer graphics modeling of a great diversity of biomolecular processes in which the recognition plays the determining role. Such molecular processes, for example, are biopolymer folding and the enzymatic cycle.
Biopolymer folding should be considered an intra-molecular recognition of fluctuating molecular structures formed by different sections of the unfolded chain of a biopolymer. There are strong limitations on the number of the rf-traps providing the formation of fluctuating structures and their recognition. The lifetime of fluctuating structures, with rare exception (helical and other regular structures), is short in order to overcome even small Gw-barriers, and, furthermore, the number of small Gw-barriers allowing the fast association of fluctuating structures (especially adjacent ones along the chain) is strongly restricted when the fluctuating structures belong to one polymer. Therefore, it seems plausible that the computer graphics modeling of biopolymer folding will lead to satisfactory results at least in considering small biopolymer chains.
The Gmw-potential gives an insight into all three basic physical stages of the enzymatic cycle, namely, recognition of substrates, decreasing the activation barriers and expelling the products of enzymatic reactions. It is known that a concave form is a peculiarity of enzyme active centers. Our preliminary results show that concave centers are preferential for kinetic and thermodynamic reasons. The hydration shells of the substrate portions interacting with enzyme active centers have convex surfaces. It is geometrically evident that a steric contact formed by a convex surface with a concave surface significantly exceeds the surface–surface contacts formed by a convex surface with a flat or another convex surface. This means that in comparison with the hydration shells of flat and convex active centers, the hydration shell of concave active centers strongly reduces the number of small Gw-barriers allowing the fast association of molecules with the active center, i.e. the hydration shell of concave active centers provides the higher-order kinetic selection of substrates.
Concave centers have also a thermodynamic advantage: the interaction of substrates with a concave active center leads to the removal of a greater amount of water molecules from the hydration shells. Moreover, because a relatively great fraction of the water molecules in a concave hydration shell are high energy, first layer water molecules, their expulsion more sharply reduces Gw at D < 4 Å, stabilizing transition states. This reduced Gw allows one to distort, for example, the low-energy conformation of the attacked grouping into a higher energy conformation in order to reduce the activation barriers of enzyme reactions. Finally, the marginal stability of the rf-trap formed by an enzyme and its substrate serves dual functions in the enzymatic cycle. Besides the recognition of substrates, it is also required for the products of enzymatic reactions to be expelled from the active center thanks to small increasing the energy caused by transformation of substrates into products.
2.11. Experimentally testable predictions of the theory
Let us formulate the two thermodynamic predictions concerning a relationship between the concentrations and thermodynamic stability of dissolved globular proteins and their complexes. The thermodynamic stability at low concentrations of globular proteins is the change of the free energy caused by the transition of a native structure of a globular protein into an unfolded state. At moderately high concentrations of globular proteins this stability is changed by interactions between the hydration shells of unfolded protein chains. According to the Gmw-potential these interactions should additionally increase protein stability because they are described by the Gw-barrier curves having positive values.
Thus, we can formulate the following theoretical prediction: an increase of the concentration of globular proteins should be accompanied by an increase of their thermodynamic stability. The transition of a native structure into an unfolded state increases the geometric size of a protein chain. For this reason an increase of the stability should begin at protein concentrations such that several layers of water molecules are observed between the surfaces of the hydration shells of adjacent globules. Stated within our theory, the thermodynamic stability of globular proteins should grow with an increase of their concentration and should be maximal at the concentration where the hydration shells of unfolded protein chains are at the peak of the Gw-barrier curve because folding would reduce Gw.
The free energy of solution should increase at the concentrations of globular proteins that provide for interactions between their hydration shells. This energy increase should be maximal at the native protein concentrations that place molecules at the peak of the Gw-barriers. However, this energy increase can significantly or completely be eliminated by specific association of protein molecules or by their full aggregation including crystallization. Consequently, we can formulate the following second thermodynamic prediction: when protein molecules are placed at the peak of the Gw-barriers they should exhibit maximal aspiration to specific association, or full aggregation, or crystallization.
3. Conclusions
The main result of the work is the Gmw-potential successfully describing the drawing together of molecular surfaces in water. An analysis of the diversified biomolecular processes including the experimentally testable theoretical predictions demonstrate that the Gmw-potential provides exhaustive answers to the longstanding questions, as for instance, why proteins are marginally stable.
The results obtained from this work demonstrate that there are strong grounds for believing that the Gmw-potential theory can be used as a tool for providing insights into mechanisms of the formation of molecular structures and of the functioning of living cells. Consider such an example. In living cells the concentrations of many dissolved molecules are changing constantly as a result of metabolic processes. Under molecular crowding conditions in cells these concentration changes should shift the positions of the biomolecular hsm-complexes within the Gw-barrier curves and so affect the rates of the formation and stabilities of molecular structures. This, in turn, means that the concentration changes caused by metabolic processes can be accompanied by disruption of some molecular complexes and by the formation of new ones. Specifically, this can lead to changing molecular recognition. All of this makes it clear that the implementation of the Gmw-potential can really provide new insights into the functioning of living cells.
Acknowledgments
We thank A. Bogdanov, A. Liljas, J. Macosko, and K. Nierhaus for critical reading of the manuscript; and O. Nikonov for technical assistance. This work was supported by the Russian Academy of Sciences and grants (to M.B.G.) from the Program on Molecular and Cellular Biology RAS. J.F.C. was supported by NIH grant GM077194.
References
- Berman HM, et al. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandler D. Two faces of water. Nature. 2002;417:491. doi: 10.1038/417491a. [DOI] [PubMed] [Google Scholar]
- Chandler D. Interfaces and the driving force of hydrophobic assembly. Nature. 2005;437:640–647. doi: 10.1038/nature04162. [DOI] [PubMed] [Google Scholar]
- Donohue J. On N–H···S hydrogen bonds. J. Mol. Biol. 1969;45:231–235. doi: 10.1016/0022-2836(69)90102-8. [DOI] [PubMed] [Google Scholar]
- Fersht A. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding. New York: W.H. Freeman; 1999. [Google Scholar]
- Filimonov V. Thermodynamic Data for Biochemistry and Biotechnology. Springer, Berlin, Heidelberg; New York, Tokyo: 1986. The thermodynamics of conformation transitions in polynucleotides; pp. 377–401. [Google Scholar]
- Finkelstein AV, Ptitsyn OB. Protein Physics. Academic Press; 2002. [Google Scholar]
- Jeffrey GA. An Introduction to Hydrogen Bonding. Oxford University Press; 1997. [Google Scholar]
- Levy Y, Onuchic JN. Water mediation in protein folding and molecular recognition. Annu. Rev. Biophys. Biomol. Struct. 2006;35:389–415. doi: 10.1146/annurev.biophys.35.040405.102134. [DOI] [PubMed] [Google Scholar]
- Lim VI, Curran JF, Garber MB. Ribosomal elongation cycle: energetic, kinetic and stereochemical aspects. J. Mol. Biol. 2005;351:470–480. doi: 10.1016/j.jmb.2005.06.019. [DOI] [PubMed] [Google Scholar]
- Makhatadze GI, Privalov PL. Energetics of protein structure. Adv. Protein Chem. 1995;47:307–425. doi: 10.1016/s0065-3233(08)60548-3. [DOI] [PubMed] [Google Scholar]
- Nakasako M. Water–protein interactions from high-resolution protein crystallography. Philos. Trans. R. Soc. London. 2004;B359:1191–1206. doi: 10.1098/rstb.2004.1498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Privalov PL, Khechinashvili NN. A thermodynamic approach to the problem of stabilization of globular protein structure: a calorimetric study. J. Mol. Biol. 1974;86:665–684. doi: 10.1016/0022-2836(74)90188-0. [DOI] [PubMed] [Google Scholar]
- Ramachandran GN, Sasisekharan V. Conformation of polypeptides and proteins. Adv. Protein Chem. 1968;28:283–437. doi: 10.1016/s0065-3233(08)60402-7. [DOI] [PubMed] [Google Scholar]
- Saenger W. Principles of Nucleic Acid Structures. Springer; New York: 1984. [Google Scholar]
- Scheraga HA. Calculation of conformations of polypeptides. Adv. Phys. Org. Chem. 1968;6:103–183. [Google Scholar]
- Shulz GE, Schirmer RH. Principles of Protein Structure. New York, Heidelberg, Berlin: Springer-Verlag; 1979. [Google Scholar]
- Taverna DM, Goldstein RA. Why are proteins marginally stable? Proteins Struct. Funct. Genet. 2002;46:105–109. doi: 10.1002/prot.10016. [DOI] [PubMed] [Google Scholar]
- Wilson DN, et al. Protein synthesis at atomic resolution: mechanistics of translation in the light of highly resolved structures for the ribosome. Curr. Prot. Pept. Sci. 2002;3:1–53. doi: 10.2174/1389203023380846. [DOI] [PubMed] [Google Scholar]
- Zhou B-R, Liang Y, Du F, Zhou Z, Chen J. Mixed macromolecular crowding accelerates the oxidative refolding of reduced, denatured lysozyme. J. Biol. Chem. 2004;279:55109–55116. doi: 10.1074/jbc.M409086200. [DOI] [PubMed] [Google Scholar]