Insect wet steps: loss of fluid from insect feet adhering to a substrate

Abstract

Reliable attachment ability of insect adhesive pads is proposed to be due to pad secretion. It has been shown that surface roughness strongly reduces adhesion forces of insect pads. This effect has been explained by decreased contact area and rapid fluid absorption from the pad surface by rough surfaces. However, it remains unclear how the fluid flows on rough substrates having different roughness parameters and surface energy. In this paper, we numerically studied the fluid flow on rough substrates during contact formation. The results demonstrate that an increase in the density of the substrate structures leads to an increase in fluid loss from the pad: substrates with a fine roughness absorb pad fluid faster. Decreased affinity of the solid substrate to the fluid has a more remarkable effect on the fluid loss and leads to a decrease in the fluid loss. With an increase in the aspect ratio of the substrate irregularities (porosity), the fluid loss is decreased. The numerical results obtained agree well with previous observations on insects and experimental results on nanoporous substrata. The significance of the obtained results for understanding biological wet adhesives is discussed.

1. Introduction

Adhesive pads of insects rely on wet adhesion caused by pad fluid [1–6] and have been repeatedly reported as having excellent attachment properties and high contact reliability [7–10]. In such wet adhesive systems, a liquid is squeezed out of tight contacts and builds bridges between two surfaces that are close to each other. The presence of pad secretion produced by specific epithelia in the contacts is crucial for generating strong attractive forces and therefore a strong friction [11,12]. Aside from van der Waals and Coulomb forces, attractive capillary forces mediated by the pad secretion are an important factor in the mechanism of insect attachment [12,13].

Insect pad secretion contains non-volatile, lipid-like components. Secretions in some insects are most probably emulsions containing water- and lipid-based components [7,12,14,15]. This indicates that secretions may serve various mechanical strategies in making contact. The beetle pad secretion was previously found to behave as a fluid with high viscosity (about a hundred times that of water viscosity) [16]. Besides high viscosity, beetle pad secretion has a decreased evaporation rate, which is a crucial issue for micrometre-sized droplets (1–7 µm). This ensures that the adhesion is robust under a variety of conditions [16]. No specific complex fluid behaviour is required during locomotion. Insect adhesive pad secretion forms capillary bridges between setae and substrate, increasing the contact area and hence the adhesion and friction forces. An additional mechanism preventing insects from slipping on smooth substrates is supported by non-Newtonian properties of the pad secretion, which is actually an emulsion [12,17]. This mechanism probably results from the existence of a yield stress for such emulsions, when an emulsion droplet contains small enough sub-droplets.

However, strong attachment ability to smooth surfaces is not such a big challenge for insects. In a series of experiments, it was shown that surface roughness strongly influences the attachment of insects. So, it has been shown that insects generate a much higher friction on either smooth surfaces or surfaces with a large roughness (above 3 µm), whereas the friction generated by the adhesive pads of insects is the lowest on substrates with a roughness ranging from 0.3 to 3 μm [7,18,19]. Wet attachment devices of insects are more effective than dry ones on rough substrates, because the effective pad contact area is much larger when pad secretion covers substrate peculiarities [20].

Many micro-structured surfaces of plants strongly reduce insect attachment forces [21–30]. To explain anti-frictional properties of plant substrates covered with microscopic wax crystals, one recently proposed hypothesis has suggested that micro- and nano-structured surfaces may absorb the fluid from the surface of adhesive pads [31]. Intuitively, it is clear that fluid loss must be higher on rough surfaces. It has been recently shown that on porous substrates, insects may produce significantly reduced forces, partially due to absorption of the fluid from the pads by a porous media [32]. In this case, the reduced friction may be explained by a reduction of the fluid contact area, if the rate of fluid loss is significantly higher than the rate of fluid production [33]. However, it remains unclear how the fluid flows on substrates with different roughness and different surface energy. In this paper, we made numerical simulations to study how the fluid flows to rough substrates during subsequent contact formation. The following questions were asked: (i) is the wetting of the rough substrate stronger compared with the flat one? (ii) Does the amount of fluid remaining on the insect pad after the insect runs on a substrate, depend on the structure's density on the substrate? (iii) How does the aspect ratio of the substrate asperities and the surface energy of the substrate (substrate affinity to the fluid) influence the amount of fluid lost during sequential contact formation?

2. Results

2.1. Microscopic observations of fluid prints

To visualize fluids in contact, we examined the footprints of attachment pads in the flies Episyrphus balteatus (Diptera, Syrphidae) and Calliphora vicina (Diptera, Calliphoridae) using a phase contrast light microscope and cryo-SEM. Insect tarsi were cut-off from anaesthetized animals using a fine razor blade and were subsequently brought into contact with a glass slide using fine forceps. Contact was formed by applying a slight shear movement, as previously described to be the natural movement in contact formation in flies [34]. Samples were mounted on metal holders, frozen in liquid nitrogen and transferred to the Hitachi S-4800 cryo-SEM (Hitachi High-Technologies Corp., Tokyo, Japan) equipped with a Gatan ALTO 2500 cryo-preparation system (Gatan Inc., Abingdon, UK). Possible contamination by frozen crystals of condensed water was eliminated by sublimating samples for 2 min (sample at −90°C, cooler at −140°C). After sublimation, samples were sputter-coated with gold–palladium (thickness of 3–6 nm) in the preparation chamber, and examined in the SEM at accelerating voltage of 3 kV at −120°C (for details of sample preparation, see Gorb [35]). Prints on substrates with different roughness were made by artificial micro-patterned polymer samples [36], which were initially covered by a thin layer of oil (Mobile DTE oil ISO VG 46, ExxonMobil Lubricants and Specialties Europe, Antwerp, Belgium). The prints were visualized, using a stereo microscope M 205A (Leica, Wetzlar, Germany).

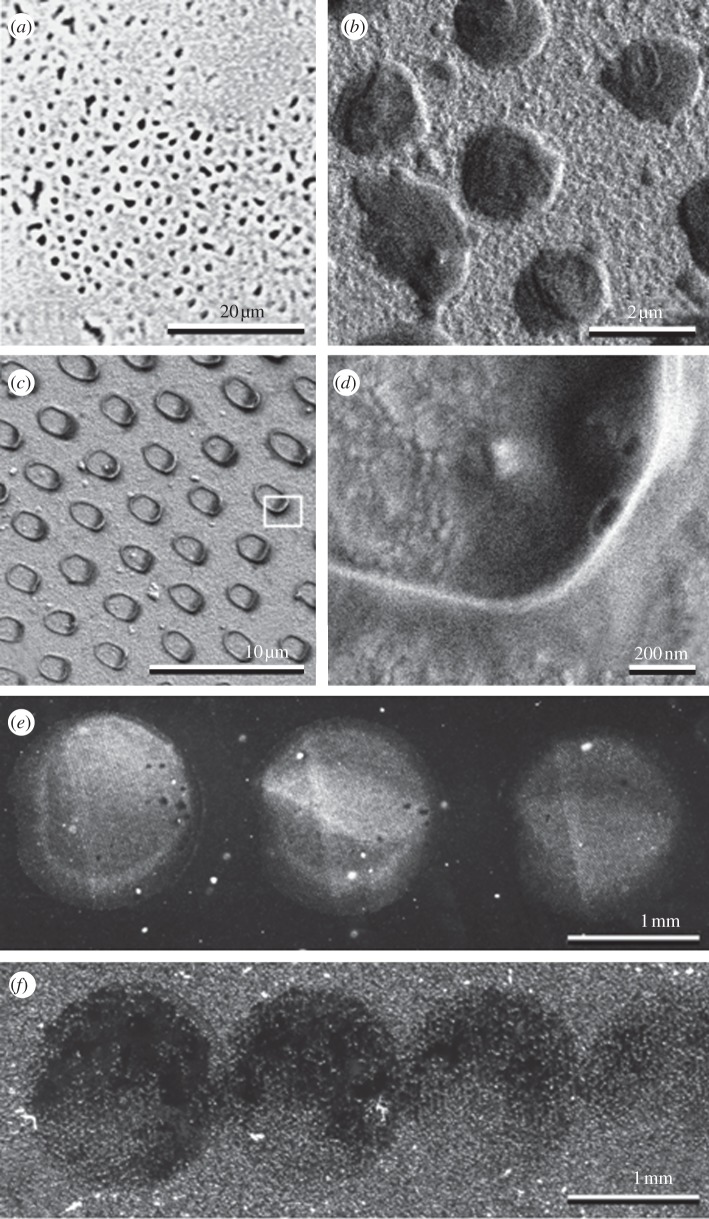
Examples of insect footprints on smooth substrates are shown in figure 1a–d. The phase contrast light microscopy images show that fly footprints have a hexagonal pattern of discrete fluid droplets corresponding to the distribution of the tenent hairs of the attachment pad (figure 1a). Cryo-SEM images demonstrate that the shape of the droplets remaining on the substrate and frozen, after breaking the contact between the insect's foot and the substrate, is convex (figure 1b). When the foot in contact with the substrate is first frozen and then the contact between the foot and the substrate broken, the frozen droplets remaining on the substrate are concave. The concave shape might appear, because the largest portion of fluid is pressed out of the contact thus leading to the meniscus-like appearance of the fluid at the circumference of the contact (figure 1c,d). If the fluid is not renewed, its amount, in a series of prints/steps, decreases. Such a decrease was observed to be greater on rough substrata (figure 1e,f).

Figure 1.

(a–d) The footprints of insects and (e,f) fluid residues from contacts built by oil-coated micro-structured artificial material. (a) The fly (Episyrphus balteatus) footprint, phase contrast microscopy. (b) The cryo-SEM images of the fly (Calliphora vicina) footprint. The liquid residue (c,d) after freezing of the fly foot with liquid interface adhering to the surface and further contact breakage by removal of the foot. Serial prints by artificially produced micro-structured oiled polyvinyl siloxane samples on smooth (e) and on rough (R_a = 1.31 µm) (f) substrates. In (e) and (f), note the different amount of oil left on the substrate in the subsequent prints.

2.2. Fluid loss model

For a qualitative explanation of fluid transfer from elastic setae to a rough substrate in a series of prints, a two-dimensional discrete model was proposed. In the numerical, experiment fluid was initially only on the surface of seta. Afterwards that surface was brought into contact with the surface of substrate. The system was equilibrated for some time. Then, the surfaces were separated. The fluid fraction remained on the elastic surface in 10 approach/withdrawal cycles that were analysed. The fluid distribution between the two interacting surfaces is described by time-dependent fluid density variations. The two surfaces have a different affinity to the fluid. The model includes a term stabilizing the fluid density. The model seta is elastic and can conform to the substrate surface.

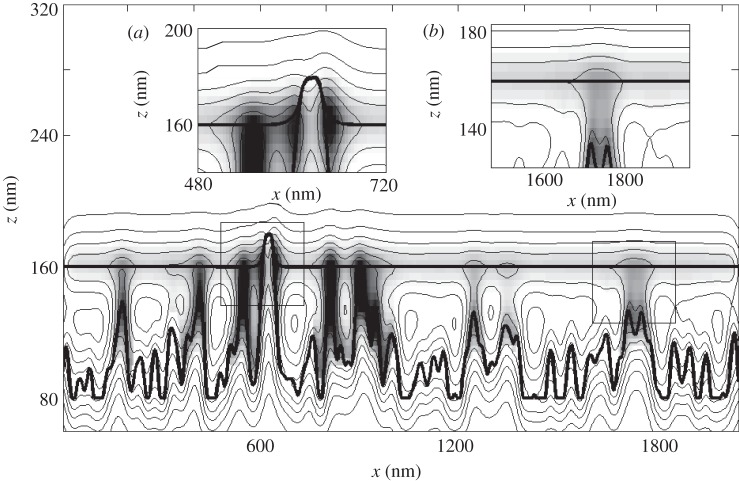
Our model is based on a standard approach of physical kinetics [37]. It includes two contacting surfaces with a liquid layer between them. The surfaces are defined on a grid uniform in the x-direction (figure 2). The lower surface is assumed to be non-deformable, and represents a typical rough rigid substrate. Generally, it has a complex, even fractal [38,39] structure, which, for the purposes of the present work, is generated by means of accumulation of the modes having different wavenumbers [40,41]. Below, we use either a sum of randomly positioned Gaussians or just one periodic component. The upper surface corresponds to the adhesive pad of the insect or to one part of it, which is normally flexible and adaptable to the substrate profile [42–44]. As a simplest approximation, the adjusted geometry of the upper surface can be found using the following equation:

2.1

Figure 2.

Conceptual scheme of the numerical experiment. Two potential minima which correspond to the surfaces modelling elastic setae (upper surface) and rough substrate (down surface) are shown by thick lines. Potential relief is presented by the thin lines of the contour plot. Fluid density (liquid layer thickness) is shown as a greyscale map. Darker colour corresponds to higher density. Two different meniscus types, described in the text, are shown in insets (a) and (b).

where K is an upper surface effective stiffness (3 × 10⁷ m⁻¹), z_u(x) is a function that describes an upper surface, z_0,u is zero level of z_u and corresponds to the effective loading.

Individual cases of fluid layer distribution (trial distribution) near the upper surface are modelled as uniform density along the surface and a Gaussian one in a perpendicular direction, with a half maximum width of approximately 50 nm [45] corresponding to the fluid layer thickness and estimated from figure 1b,d.

Chemical potential for fluid in the arbitrary point i between the surfaces is modelled by Morse potential: U_i,j,k(x,z) = U_0,k(1−exp{−r_ij/r₀})². Here, r_ij is a distance from this point to a point j on a surface k = 1,2 (upper or lower), r₀ = 25 nm. An impact to the total potential from the discrete segments used in numerical simulation is proportional to the length of the segments. Owing to non-uniform discretization along the z-axis, this length is proportional to the factor 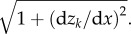As a result, total surface potential takes the following form:

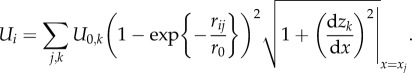2.2

During simulation, a fluid flow from the upper to the lower surface is studied. Initially, the fluid is only on the upper surface. Then, the two surfaces are brought into contact for 100 ms. This time was selected as approximately corresponding to the time a single insect foot is in contact with a substrate during walking (A. Kovalev & J. Langowski 2009, unpublished data). During this time, the fluid is allowed to redistribute between the surfaces according to the following kinetic equation:

2.3

where ρ(x,z) is an effective particle density of the liquid, Δ is a Laplace operator, η_eff is a diffusion coefficient or effective surface tension (6 × 10^–4 m² s⁻¹), γ is the characteristic time necessary to form a liquid bridge between setae and substrate (10 ms, the time needed to establish the equilibrium contact for a wet spatula of a Colorado beetle attachment pad [16]). This time is proportional to the fluid viscosity [16]. Local term in equation (2.3) ρ[U−(ρ−1)(2ρ−1)] has a standard form for the chemical potential defined by equation (2.2). To fulfil the principle of mass conservation in the absence of liquid sources or drains, we included an additional operation into numerical procedure that keeps the total amount of liquid fixed at each iteration step.

After a contact time of 100 ms, the surfaces are separated. In each spatial point, the fluid redistributes between the surfaces. The amount of the liquid must be divided according to the mutual relation between local surface potentials in a given point. In other words, the fluid remains on the surface with deeper local potential. The next cycle starts with the remaining fluid homogeneously redistributed on the upper surface and brought into contact with a new dry rigid surface. This procedure is repeated 10 times. The upper surface loses fluid at each cycle. It is convenient to characterize the process by a fraction of the fluid remaining on the upper surface normalized to an initial amount of the fluid. We will use such a ‘fraction’ as a main parameter below.

2.3. Numerical results

Figure 2 presents a typical experimental configuration. Potential minima for the upper and lower surface are shown by thick contour lines. The density of the liquid is displayed as a greyscale map. One can see how the fluid is redistributed in a total potential formed by both surfaces. The fluid occupies the potential minima and forms clearly seen liquid bridges. Two basic types of such bridges can be easily distinguished in the picture. One type, appearing around the straight contact of the surfaces, is shown in inset (a) in figure 2. For such contacts, the liquid meniscus with high-density surrounds the contacting surfaces. The second type is built in the areas in close proximity to the surfaces. It is presented in the subplot (figure 2b). In this case, both the fluid density and flow rate monotonically decrease with an increasing distance between the surfaces.

2.3.1. Density of the structures

Let us study separately the dependence of the draining rate on chemical and geometrical properties of the rigid surface. Keeping this in mind, it is useful to momentarily exclude the random factor and use a regular hard surface with just one periodic component. In this case, one can determine a dependence of liquid loss on the structure's density n_s, which equals the number of structures per 1 µm. All the menisci in this case are of the type shown in figure 2a.

The liquid fraction remaining on the upper surface during consecutive approach–retraction cycles is presented in figure 3 in a logarithmic scale. The family of curves here displays a dependence of the fluid fraction on the structure's density n_s. It is important to note that the curves here are close to the exponent (linear in a logarithmic scale) at high n_s only, but differ from it when n_s decreases, due to the nonlinear nature of equation (2.3). The fraction of the fluid finally left on the upper surface after all the approach–retraction cycles for different values of n_s is summarized in the inset of figure 3. Fast non-hyperbolic decay of the remaining fluid fraction depending on n_s is shown, inset of figure 3. The reason for such dependence is that fluid loss is controlled by two factors: number of menisci and flow path length (the average distance the fluid has passed over during the contact time). Both these factors are proportional to n_s. It is important to note that about 10 per cent of the fluid remains on the soft upper surface after 10 contact cycles for a structure's density equals to 2 μm⁻¹.

Figure 3.

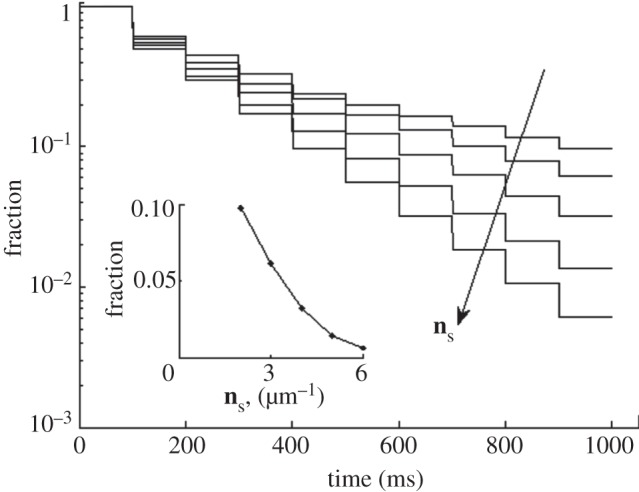
Liquid fraction remaining on the elastic setae (upper surface) in sequential approach–retraction to the structured substrate. The tendency of structure density growth, n_s, is marked by the arrow. Dependence of the fraction after the final approach–retraction cycle on n_s is shown in the inset.

2.3.2. Surface energy

The chemical potential of the substrate in the sense of affinity to the fluid (analogous to the surface energy) was analysed as a second factor influencing the fluid redistribution between contacting surfaces. The ratio between the affinities of the surfaces is chosen as a characteristic parameter: μ = U_0,up/U_0,down. Here, U_0,up and U_0,down are the coefficients in equation (2.2) for upper and lower surfaces, respectively. A set of curves in figure 4 represents the fraction kinetics in a logarithmic scale for different μ values (n_s was fixed to 4 μm⁻¹). Because of the nonlinearity of equation (2.3), the shape of the kinetic curves differs from the simply expected exponent. It is especially pronounced at μ < 1. The liquid fraction remaining on the upper surface after 10 approach–retraction cycles is shown in the inset of figure 4. It is seen from the figure that the ratio of affinities μ has a more vigorous influence on the fraction than the period. If the upper surface has a two times higher affinity to the fluid, it will lose just 43 per cent of the fluid after 10 contact cycles.

Figure 4.

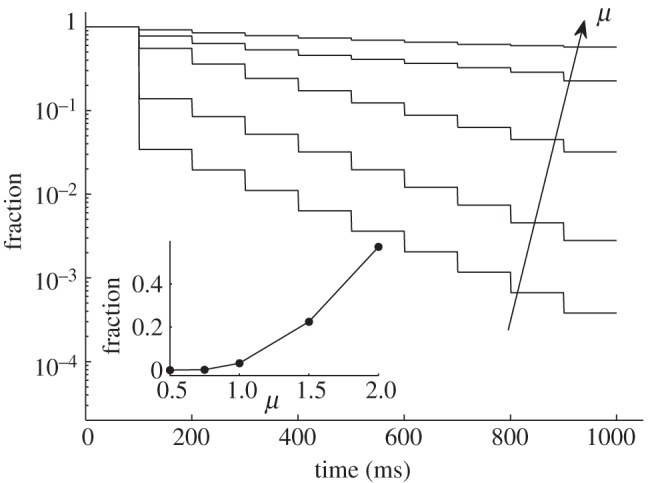
Liquid fraction remaining on the elastic setae (upper surface) in sequential approach–retraction to the substrate with different affinity to the liquid μ. The tendency of μ growth is marked by the arrow. Dependence of the fraction after the final approach–retraction cycle on μ is shown in the inset.

2.3.3. Roughness amplitude

Next, the influence of roughness amplitude of the hard surface on the fraction of the remaining fluid was studied. The family of the kinetic curves for different roughness amplitudes is shown in figure 5 at fixed parameters: μ = 1 and n_s = 4 μm⁻¹. The inset summarizes the fraction values after 10 contact cycles for different roughness amplitudes. It is seen directly from the figure that the remaining fraction for a random surface is higher than that for the periodic one. Two factors may be responsible for this. The average number of menisci is the same for both fractal and periodic surfaces, but some of them are of type (b) (figure 2b), and produce different impacts on the fluid flow. According to the kinetic equation, the flow rate for the remote contacts is lower. Additionally, the distance between neighbouring peaks here is not regular, and mean flow time is longer for the random surface.

Figure 5.

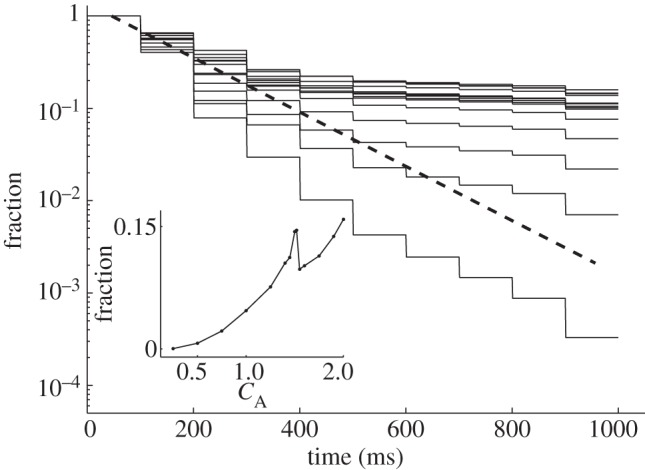
Liquid fraction remaining on the elastic setae (upper surface) in sequential approach–retraction to the substrate with different effective roughness aspect ratios. Expected liquid loss on a completely flat substrate is shown by a dashed line. Dependence of the fraction after the final approach–retraction cycle on the roughness amplitude is shown in the inset.

A simple geometric sequence is expected for the contact between absolutely flat surfaces. Such a sequence corresponds to exponential decay and it is displayed in figure 5 by the dashed line. The fluid loss rate is proportional to the amount of liquid. That is why, for some ranges of roughness, the rate of the fluid redistribution is initially faster than the expected exponent, but becomes slower for the later approaches. For a small roughness, the initial loss rate is typically higher than for a flat contact. Because a soft surface fits the smooth structures better, the fluid can directly reach the pits in the hard surface. Besides, the effective area of the lower surface is bigger than it is for the flat one. At a roughness amplitude of C_A = 1.5, the aspect ratio of the basic structures is close to unit. This changes the impact of the surface tension (presented by the Laplacian term in equation (2.3)) to the kinetics and leads to better conservation of the liquid fraction on the upper surface. This effect manifests itself by a local peak seen in the inset to figure 5. In the main part of the figure, this peak corresponds to an area densely filled by a majority of the curves.

3. Discussion

The aim of this study was to estimate the fluid expended by an insect running on different rough surfaces, because the presence of the fluid contributes to the attachment enhancement on rough surfaces [46–48]. Capillary forces are limited by vapour/cavitation pressure. Hence, there is an optimal volume of pad secretion at which the pad adhesion reaches its maximum. Secretion accumulated during a few minutes floods the attachment pads (figure 1c,d) [33]. In the flooded state, the capillary forces and pad adhesion are reduced. Yet after an insect takes several steps (seven steps for a cockroach on a smooth substrate), the pad secretion volume approaches a stationary state in which the accumulated secretion is largely transferred to the substrate and the fluid loss on the substrate is compensated with a rather slow influx of fluid [33]. High fluid loss on rough substrates (figure 1e,f) causes adhesion reduction. This is due to the reduction of fluid contact area and therefore reduction of capillary forces. The ability to adhere to rough substrates provides some important benefits to insects such as occupying new food sources, reducing competition with other species and escaping parasites/predators that are unable to stay on such substrates. The influence of surface roughness on insect attachment has been proved experimentally in several studies [7,10,19,20,46,48]. Below, the model used in this study and the influence of the structure's density, the surface energy and the roughness amplitude on the fluid loss based on the model are discussed.

3.1. Model

A simplified, two-dimensional model of the fluid dynamics was established in this paper for theoretical description of the fluid loss from an insect foot during locomotion. Instead of the precise solution of the non-equilibrium fluid flow, we were interested in the long-term fluid redistribution between contacting surfaces. Simplified fluid representation includes the term stabilizing the fluid density. The model lacks the precision of an exact physical model, but does allow a semi-quantitatively description of the system behaviour in a large parameter space, thanks to the model's simplicity.

3.2. Density of structures

In this numerical study, the higher density of the substrate irregularities leads to a stronger fluid loss from the adhesive pad. This effect may be responsible for the reduced friction of insect adhesive pads on fine roughness (0.3–1.0 µm). The reduced friction has been explained earlier by the specific geometry of spatula-like terminal elements of insect tenent setae [19,48] and their thickness [44] that are able to generate sufficient contact with large surface irregularities. Interestingly, many plant surfaces, to which insects fail to adhere, have such a critical roughness owing to the presence of tiny wax crystals on their surfaces [31].

Recently, it has been experimentally demonstrated that the behaviour of fluid drops on solid smooth surfaces differs essentially, if compared with that on nanoporous ones [32]. On smooth surfaces, after an oil drop had been stabilized, the contact angle (CA) remained almost the same over a certain period of time, whereas on nanoporous surfaces, CA–time curves showed a fast decrease in the CA during the first 20 s after drop deposition. This effect was explained by rapid absorption of the fluid by the porous medium just after drop deposition and following stabilization of CA owing to the ‘saturation’ of the porous surface by the absorbed fluid [32]. These experimental results and results of the present numerical simulation led us to an important biological conclusion that the use of wet adhesive pads for attachment purposes may be much more costly during locomotion on micro- and nanorough surfaces, especially, if the fluid is lipid-like.

3.3. Surface energy

Results of this study show that liquid loss can be minimized, if the surface energy of the pads (their affinity to the fluid) is high enough. This conclusion is based on the existence of an optimal amount of fluid between the pad and the substrate that enhances adhesion [47]. Therefore, wet adhesion is dependent on the duration of contact, especially if the fluid is continuously produced by the pad onto the contact area with the substrate: a contact time that is too long leads to reduced adhesion owing to a fluid layer that is too thick [20,49].

On the other hand, the pads affinity to the fluid should not be too high; otherwise, the substrate will not be sufficiently wetted. In that case, one can assume the influence of capillary water condensation and therefore environmental humidity on the fluid behaviour in contact between the pad and the substrate [50]. If the substrate affinity to the fluid is very high, then the fluid can wet the substrate well, but will be taken from the pad very quickly. This situation may lead to adhesion reduction owing to the thick fluid layer causing a hydroplaning effect, as previously observed for the superhydrophilic surface of the peristome in the carnivorous plants of the genus Nepenthes [51]. The previously observed biphasic fluids of insects [7,12,14,15] represent how sufficient but average affinity to the fluid for almost any natural substrate (presumably, μ > 1) may be kept. Because hydrophilic surfaces have a high affinity to the water-based component of the pad secretion and non-polar surfaces have a high affinity to the lipid-based component, the wetting of the substrate will be always fulfilled, and the fluid will not be rapidly absorbed from the pad (if the pad affinity to the pad secretion is higher than the substrate affinity).

3.4. Roughness amplitude

According to the numerical simulations performed, an abundant fluid loss from the adhesive pad takes place on a fine roughness (high density and low amplitude of the substrate irregularities). The fraction decreases with decreasing roughness amplitude; however, the contact area between fluid and substrate decreases for roughness amplitudes smaller than one. Presumably, different amounts of the fluid are produced by the pad glands of insects on different substrates, but this hypothesis has, as yet, no experimental evidence. Fluid production on demand may reduce its loss on rather flat surfaces or on those with a fine roughness. Interestingly, on rough substrata having an aspect ratio close to one, the fluid loss of the studied system has a local minimum. This fact should be taken into account when comparing wet attachment to substrata with different roughness.

4. Conclusion

The applied numerical approach to study fluid dynamics during contact formation by adhesive wet pad of insects shows that an increase in the periodicity length of the substrate leads to a decrease in fluid loss from the pad. In other words, substrates with a fine roughness take up pad fluid faster. Increased affinity of a solid substrate to the fluid leads to an increase in the fluid loss from the pad. With an increase in the aspect ratio of substrate irregularities the fluid loss is decreased. The numerical results obtained agree well with previous observations on insects and with experimental results on fluid absorption on nanoporous substrata.