Energy for Wild-Type Acetylcholine Receptor Channel Gating from Different Choline Derivatives

Abstract

Agonists, including the neurotransmitter acetylcholine (ACh), bind at two sites in the neuromuscular ACh receptor channel (AChR) to promote a reversible, global change in protein conformation that regulates the flow of ions across the muscle cell membrane. In the synaptic cleft, ACh is hydrolyzed to acetate and choline. Replacement of the transmitter’s ester acetyl group with a hydroxyl (ACh→choline) results in a +1.8 kcal/mol reduction in the energy for gating generated by each agonist molecule from a low- to high-affinity change of the transmitter binding site (ΔG_B). To understand the distinct actions of structurally related agonist molecules, we measured ΔG_B for 10 related choline derivatives. Replacing the hydroxyl group of choline with different substituents, such as hydrogen, chloride, methyl, or amine, increased the energy for gating (i.e., it made ΔG_B more negative relative to choline). Extending the ethyl hydroxide tail of choline to propyl and butyl hydroxide also increased this energy. Our findings reveal the amount of energy that is available for the AChR conformational change provided by different, structurally related agonists. We speculate that a hydrogen bond between the choline hydroxyl and the backbone carbonyl of αW149 positions this agonist’s quaternary ammonium group so as to reduce the cation-π interaction between this moiety and the aromatic groups at the binding site.

Introduction

Nicotinic acetylcholine receptor channels (AChRs) mediate fast chemical transmissions between nerve and muscle. This membrane protein undergoes a global allosteric gating transition between a low-affinity/closed-channel structure and a high-affinity/open-channel structure (C↔O), both with and without ligands present at its two transmitter binding sites (1–4). Agonist molecules, including the neurotransmitter acetylcholine (ACh), bind with a low affinity to two target sites in the protein that can switch to a higher-affinity conformation. As a consequence, when agonists are present at the binding sites, the probability of being in the open conformation (P_o) increases, and cations enter and depolarize the muscle cell, which eventually may contract.

Many different ligands can activate AChRs, but to different maximum extents. ACh is able to open transiently neuromuscular AChRs nearly completely (P_o^max ∼ 0.96). In the synaptic cleft, free ACh is hydrolyzed by acetylcholinesterase to acetate and choline, which has a hydroxyl group in place of the neurotransmitter’s ester acetyl group. This molecular replacement decreases the diliganded gating equilibrium constant (E₂) by ∼550-fold (5–8), so synaptic choline hardly activates these AChRs (P_o^max ∼ 0.05). Here, we seek to understand the nature of the atomic interactions that determine the extent to which a bound ligand activates AChRs.

As a member of the pentameric ligand-gated ion channel family, the adult neuromuscular AChR is composed of five homologous subunits (α1₂βδε) that fold into covalently linked extracellular and transmembrane domains (9). The channel’s gate region is located in the central pore of the transmembrane domain, and the two transmitter binding sites are in the extracellular domain at the α-δ and α-ε subunit interfaces. X-ray structures of AChR homologs bound with ligand (10–13) and mutational analyses (14–18) have revealed that the agonist’s quaternary ammonium group is surrounded by a cluster of aromatic residues, mostly in the α subunit.

The magnitudes of E₂ and P_o^max are determined by the amount of binding energy contributed by the agonist molecule toward the full C↔O gating isomerization. This energy, ΔG_B, is equal to the difference in binding energy, i.e., high versus low affinity (to O versus to C; Fig. S1 in the Supporting Material). Our approach was to measure ΔG_B for a variety of related choline derivatives to explore which aspects of the ligand’s structure correlate with the energy it provides to gating in adult mouse neuromuscular AChRs with wild-type (WT) binding sites. Specifically, we hoped to identify atoms of the agonist that are responsible for setting ΔG_B. For ACh, the source of ΔG_B energy is mainly interactions of its cation moiety with three aromatic groups in the α subunit (19), by cation-π forces (20). Many different agonists (including choline) have quaternary ammonium groups, and we wondered why some of these provide less energy for gating compared with ACh.

One can estimate ΔG_B experimentally by invoking a cyclic model for activation (Fig. S1) (21,22). The two adult-type AChR transmitter binding sites provide approximately equal energies for both ACh and choline (23). Hence, from a detailed balance, the ratio of the gating equilibrium constants with two versus without any agonists (E₂/E₀) is equal to the ratio of the C versus O equilibrium dissociation constants squared (K_d/J_d)². E₂ is estimated for each agonist as the ratio of the diliganded opening versus the closing rate constants (E₂ = f₂/b₂), which in turn are measured from interval durations of single-channel currents obtained at high agonist concentrations. The energy (in kcal/mol) provided by the affinity change for the agonist at each site is ΔG_B = −0.59 ln(K_d/J_d), or, equivalently

$$2\Delta {\text{G}}_{\text{B}}=-0.59\text{ln}\left(\frac{{\text{E}}_2}{{\text{E}}_0}\right)$$ (1)

The WT unliganded gating equilibrium constant at −100 mV is E₀ = 7 × 10⁻⁷ (2,3,23). Because this value is agonist independent, to estimate ΔG_B, all we need to measure is the ratio of rate constants, f₂/b₂, for each ligand.

Substantial evidence indicates that there are one or more brief intermediate states between the C and O ground states (8,24–27). For a sequence of reactions, the net energy difference between the end states is equal to the sum of the energy changes of all of the intermediate transitions. The experimental E₂ and ΔG_B values we report below pertain to the complete transition between diliganded C and O. Our measurements do not distinguish at which point(s) in the gating sequence the energy from the affinity change is realized.

Most agonists are cations that can block the channel pore (Fig. S2). When the channel-blocked state is brief, the single-channel current amplitude decreases, which makes it difficult to measure interval durations using high agonist concentrations. By depolarizing the membrane and using background mutations that compensate for the effect of depolarization on E₂, it is possible to measure precisely the interval durations without the interference from channel block (5). These experiments show that ACh, tetramethylammonium (TMA), and choline provide an average of ΔG_B = −5.1, −4.5, and −3.3 kcal/mol/ligand toward the gating isomerization, respectively. Here we attempt to rationalize these energy differences based on ligand and protein structures.

We measured ΔG_B for 10 choline derivatives. Our findings reveal the amount of energy that is available for the AChR conformational change provided by these ligands.

Materials and Methods

Mutagenesis and expression

Mutant cDNAs of the mouse AChR α and ε subunits listed in Table S1 and Table S2 were created using the QuikChange Site-Directed Mutagenesis Kit (Stratagene) and confirmed by dideoxy sequencing. HEK 293 cells were transiently transfected with WT and mutant subunit cDNAs by calcium phosphate precipitation. Approximately 3.5 μg of AChR α, β, δ, and ε subunit DNA was added to each 35-mm culture dish in a 2:1:1:1 ratio, along with cDNA for green fluorescent protein (GFP), as a transfection marker. After ∼16 h of incubation at 37°C, the cells were washed with fresh culture medium.

Electrophysiology and kinetic analysis

Single-channel currents were recorded at 23°C in a cell-attached configuration within ∼48 h post-transfection. The bath solution contained (in mM) 142 KCl, 5.4 NaCl, 1.8 CaCl₂, 1.7 MgCl₂, 10 HEPES/KOH (pH 7.4). The pipettes were filled with agonist diluted with Dulbecco’s phosphate-buffered saline containing (in mM) 137 NaCl, 0.9 CaCl₂, 2.7 KCl, 1.5 KH₂PO₄, 0.5 MgCl₂, and 8.1 Na₂HPO₄ (pH 7.4). To reduce channel block by the agonist, the pipette potential (V_p = −V_membrane) was held at −100 mV (Fig. S2), except for experiments with betaine, which is not a channel blocker (V_p = +100 mV).

In experiments with cholamine (pK_a = 7.1), the HEPES buffer was replaced with 50 mM TABS (N-tris(hydroxymethyl)methyl-4-aminobutanesulfonic acid) or 50 mM MOPSO (3-morpholino-2-hydroxypropanesulfonic acid) to achieve a pH of 9.0 or 6.1, respectively. Using these buffers at pH 6.1 or 9.0 did not affect the E₂^choline estimate. The primary amine of cholamine is 91% in the protonated, charged form at pH 6.1, and 99% deprotonated at pH 9.0 (28). A saturating concentration of cholamine (at pH 6.1 and 9.0) was reached at ∼5 mM.

Single-channel currents were filtered at 20 kHz and digitized at a sampling frequency of 50 kHz. Kinetic analyses were performed with the use of QuB software (http://www.qub.buffalo.edu). Currents from clusters of openings (Fig. 1 A) were idealized into noise-free interval durations with the SKM algorithm. The interval durations were fitted by a reaction scheme that had a gating step (A₂C↔A₂O, where A is the agonist) and another step representing occasional sojourns entry in a nonconducting, presumably desensitized state attached to A₂O (29). The diliganded forward (f₂) and backward (b₂) gating rate constants were estimated from the idealized intracluster interval durations obtained at a saturating agonist concentration by means of a maximum-interval likelihood algorithm (Table S1). Saturation was defined as the concentration of agonist that elicited the maximum f₂ value (the apparent f₂ did not change with a further increase in concentration). To assess saturation, f₂ was measured at agonist concentrations of (at least) 50, 100, and 140 mM. The diliganded gating equilibrium constant was calculated as E₂ = f₂/b₂. A 2-fold change in E₂ translates to a ∼0.2 kcal/mol difference in ΔG_B, which is approximately our resolution limit.

Figure 1.

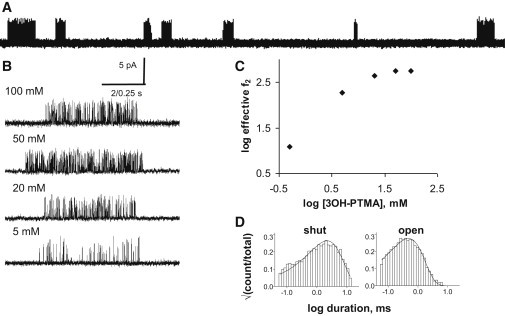
Estimating ΔG_B from single-channel currents. The agonist was 3OH-PTMA. (A) At low time resolution, openings (up; V_m = +100 mV) are clustered. Within a cluster, a single AChR switches repeatedly between C and O; between clusters, all AChRs in the patch are desensitized. (B) Higher-time-resolution view of clusters at different levels of [3OH-PTMA]. (C) The effective opening rate (inverse intracluster shut time) increases with increasing [3OH-PTMA] to reach an asymptote at >20 mM, signifying binding-site saturation. (D) Closed and open interval duration histograms at 100 mM [3OH-PTMA]. At V_m = +100 mV and with the εS450A background mutation, the measured f₂ and b₂ were 564 s⁻¹ and 2764 s⁻¹, respectively (E₂ = 0.20). These background perturbations combined increase E₀ (and hence E₂) by 1.36-fold, so the corrected E₂ value (−100 mV, WT) is 0.15 (Table S1 and Table S2). From Eq. 1, for 3OH-PTMA, ΔG_B = −3.6 kcal/mol.

To allow greater accuracy in the measurements, we used background mutations to generate f₂ and b₂ values that were in an easily measurable range (5). The effects of these substitutions, both alone and in combination, were previously calibrated and shown to change E₀ but have no effect on the affinity ratio. From the cycle, E₂ = E₀(K_d/J_d)², so adding perturbations that change only E₀ result in an equivalent change in E₂, which is what we measured. Rather than struggle with quantifying single-channel current intervals that were either too brief for accurate rate constant estimation or too long-lived to allow clear cluster definition, we added mutations simply to adjust E₀ to produce interval durations that were well within the time resolution of our equipment, software, and analysis protocols. With this engineering approach, we were able to measure the experimental gating rate constants accurately and then calculate what E₂ would have been under a reference condition (−100 mV, 23°C, adult WT mouse AChRs).

For example, consider the results for the agonist BTMA (Table S1). The measurements were obtained at +100 mV and with two background mutations, αS450W and αD97I. These three perturbations each change E₀ by factors of 0.08, 9.9, and 0.4, respectively (Table S2). It was previously established that the effects of these specific perturbations are independent of each other and of ΔG_B (5). Together, these three perturbations increase E₀ (and E₂) by (0.08)(9.9)(0.4) = 0.32-fold (5,19). The experimentally observed E₂ for BTMA on this background was 0.78, so the E₂ value we calculate for the reference condition is 0.78/0.32 = 2.44.

In some cases, other or additional loss- or gain-of-function background mutants (αD97A, αD97N, αD97I, αY127F, αS269I, and εL269F) were used to decrease or increase the opening rate constants to allow cluster formation and ΔG_B measurements of high- and low-efficacy agonists (Table S2) (30–35). Again, these mutations were all previously shown to change only E₀ (independently) and not ΔG_B. As described above, we divided the observed E₂ value by the net fold change of the background construct to estimate the E₂ value at the reference condition. Both the observed and background-corrected E₂ values are given in Table S1.

The intrinsic gating equilibrium constant at V_m = −100 mV is E₀ = 7 × 10⁻⁷ (2,3). If the two binding sites are equivalent, then the energy that an agonist provides toward gating is given by Eq. 1. So far, this has been shown to be the case only for ACh and choline (23), but we assumed that this was also true for the other agonists. The coupling free energy of perturbation cycle analysis was calculated as ΔG_B ^mod1&2/(ΔG_B ^mod1 − ΔG_B ^mod2), where mod represents an agonist modification such as tail elongation or addition of a hydroxyl. The error limits (SEM) for ΔG_B were calculated as described elsewhere (19).

We use the term “gating” to refer to the complete, C↔O allosteric transition rather than the ultimate molecular movement that allows water and ions to cross the membrane. Within the C↔O gating isomerization, the AChR passes through brief intermediate states. Such sojourns were too short-lived to be detected as discrete intervals in our experiments. However, this does not affect the ΔG_B estimates. Our energy measurements are based on E₀, E₂, and the thermodynamic cycle. Given a sequential gating scheme with explicit intermediate states, these experimental equilibrium constants are just the products of all of the microscopic ones across the sequence. Our objective was to estimate the total energy difference between the A₂C and A₂O ground states, and the presence of intermediate states between these two positions along the gating reaction coordinate is not relevant to that goal.

Homology modeling

Molecular modeling was performed using the ZMM program (http://www.zmmsoft.com), which employs the Monte Carlo minimization algorithm (MCM) to search for energetically favorable conformations (36). Atom-atom interactions were calculated using the AMBER force field (37). A cutoff distance of 8 Å was used for nonbonded interactions. Electrostatic interactions were calculated using a distant- and solvent-exposure-dependent dielectric function (38). Hydration energy was calculated using the implicit-solvent method (39). An explicit water molecule was initially constrained to the backbone oxygen of δN109 and backbone nitrogen of δL121. In subsequent MCM trajectories the constraints were removed, but the water molecule did not move away from these residues. This explicit water was suggested to be important for ACh binding (40), but we found that it was not important for the binding of TMA and choline. Ionizable residues of the protein were treated as neutral (39). The atomic charges of ligands were calculated by the AM1 method (41) using the MOPAC program (http://www.mopac.com). Bond angles of the ligand were allowed to vary in energy minimizations.

Our model of the mouse muscle AChR included the α and δ subunits of the extracellular domain, which were built according to the X-ray structure of Aplysia california ACh binding protein (AChBP) bound with epibatidine (PDB code 2BYQ (11)). The extracellular domain of the neuromuscular AChR α1 subunit has a sequence similarity of 64% with the A. californica AChBP versus 59% with Lymnaea stagnalis. The sequences of AChBP and AChR were aligned as shown in Table S3. The AChR transmembrane domain and the AChR loop insertions of the extracellular domain, which are not present in AChBP, were not modeled. The homology model was MC-minimized until 2000 consecutive energy minimizations did not decrease the energy of the apparent global minimum found. During energy minimizations, the α carbons of the protein were constrained to the template structure by pins, which are flat-bottom energy constraints that allow atoms to deviate penalty-free up to 1 Å from the template, and impose a penalty of 10 kcal/mol/Å for larger deviations.

We searched for the optimal positions and orientations of choline and TMA using a multi-MCM protocol (42,43). First, we generated 20,000 random starting points of the ligand within a cube of 7 Å in length. The size of the cube covered the transmitter binding site. Each starting point was optimized in an MCM trajectory of five steps to remove steric overlaps with the protein. Two hundred lowest-energy structures found at this stage were further MC-minimized in longer trajectories to refine the protein-ligand complexes. These trajectories were terminated after 1000 consecutive steps did not improve the best minimum found. The 10 best ligand-receptor complexes were analyzed. Although no specific energy terms were used for π-cation interactions, these interactions were accounted for by partial negative charges at the aromatic carbons (44).

Chemical synthesis

Six choline derivatives were synthesized because they were commercially unavailable as quaternary salts or their salt forms were unsuitable for electrophysiology experiments with an Ag-AgCl electrode. Tertiary amines were quaternized using methyl tosylate to prepare 3-hydroxypropyltrimethylammonium tosylate, 2-hydroxypropyltrimethylammonium tosylate, 4-hydroxybutyltrimethylammonium tosylate, and butyltrimethylammonium tosylate. Trimethylamine was alkylated to produce ethyltrimethylammonium bromide and propyltrimethylammonium bromide. For further details about the quaternization of amines, see the Supporting Material.

Results

Choline has a quaternary ammonium group and a hydroxyl group connected by an ethyl linker. We refer to the carbon to which the hydroxyl group is attached to as C2. We investigated three sets of choline derivatives by 1), extending the hydroxyethyl tail of choline to hydroxypropyl and hydroxybutyl; 2), extending the alkyl tail of TMA (without the hydroxyl group) from methyl to ethyl, propyl, and butyl; and 3), substituting the hydroxyl group at C2 with different functional groups. We chemically synthesized six of the choline derivatives using alkylation techniques as described in the Supporting Material.

Fig. 1 shows single-channel currents from AChRs activated by 3-hydroxypropyltrimethylammonium (3OH-PTMA) at a membrane potential of +100 mV. At −100 mV, this agonist blocks the channel and reduces the current amplitude. To avoid this problem, we depolarized the membrane to +100 mV and effectively eliminated such a fast channel block. Accordingly, the (outward) single-channel current amplitude was 4.3 pA in the presence of 100 mM 3OH-PTMA (Fig. 1 B, top). The effective opening rate constant (f₂) increased with increasing concentrations of the ligand to reach a plateau at ∼20 mM, which demonstrates that at this concentration the binding sites were fully occupied by agonist molecules (Fig. 1 C). After correcting for the background perturbations, we estimate E₂ = 0.15 for 3OH-PTMA (−100 mV, WT AChRs). We calculate (Eq. 1) that this agonist provides ΔG_B = −3.6 kcal/mol/ligand for gating (Table 1). 3OH-PTMA provides 1.5 kcal/mol less favorable energy for gating than ACh, but 0.3 kcal/mol more favorable energy than choline.

Table 1.

Energy estimates for choline derivatives

Ligand	E2 ± SEM	√(E2/E0) ± SEM	ΔGBa ± SEM, (kcal/mol)
ACh, acetylcholine	25.40b	6024	−5.1
Set 1: Extending the alkyl tail of TMA
TMA, tetramethylammonium	2.54b	1905	−4.5
ETMA, ethyltrimethylammoniumc	0.25 ± 0.11	597 ± 136	−3.8 ± 0.1
PTMA, propyltrimethylammoniumc	0.29 ± 0.13	644 ± 143	−3.8 ± 0.1
BTMA, butyltrimethylammoniumd	2.44 ± 0.18	1867 ± 116	−4.4 ± 0.03
Set 2: Extending the hydroxyethyl tail of choline
Choline,2-hydroxyethyltrimethylammonium	0.05b	256	−3.3
3OH-PTMA, 3-hydroxypropyltrimethylammoniumc	0.15 ± 0.03	464 ± 54	−3.6 ± 0.1
4OH-BTMA, 4-hydroxybutyltrimethylammoniumc	0.71 ± 0.34	1010 ± 248	−4.1 ± 0.1
Set 3: Substitutions at carbon#2 position
ClCho, 2-chloroethyltrimethylammonium	0.19 ± 0.12	523 ± 160	−3.7 ± 0.2
2OH-PTMA, 2-hydroxypropyltrimethylammoniume	0.02 ± 0.01	170 ± 34	−3.0 ± 0.1
Cholamine (pH 9.0), 2-aminoethyltrimethylammoniume	0.04 ± 0.01	243 ± 33	−3.2 ± 0.1
Cholamine (pH 6.1), 2-aminoethyltrimethylammoniumf	0.0012 ± 0.001	42 ± 23	−2.2 ± 0.3
Betaine, 2-aminoethanoic acid or trimethylglycineg	1.6E-5 ± 9.3E-6	4.7 ± 1.4	−0.9 ± 0.2

E₂ values were corrected for the following background constructs: ^cεS450A, ^dεS450W+αD97I, ^eεL269F, ^fεL269F+αD97N, and ^gα(D97A+Y127+S269I). See Table S1 for the uncorrected values and Table S2 for the effects of the backgrounds on E₀.

^aΔG_B = −0.59·ln[√(E₂/E₀)].

^bPreviously published E₂ measurements (5).

Extending the ethyl tail of choline with or without a hydroxyl group

We first examined ligands with a quaternary ammonium group and various tail lengths, with and without a terminal hydroxyl group. These derivatives were ethyltrimethylammonium (ETMA), propyltrimethylammonium (PTMA), 3-hydroxypropyltrimethylammonium (3OH-PTMA), butyltrimethylammonium (BTMA), and 4-hydroxybutyltrimethylammonium (4OH-BTMA) (Fig. 2, A and B).

Figure 2.

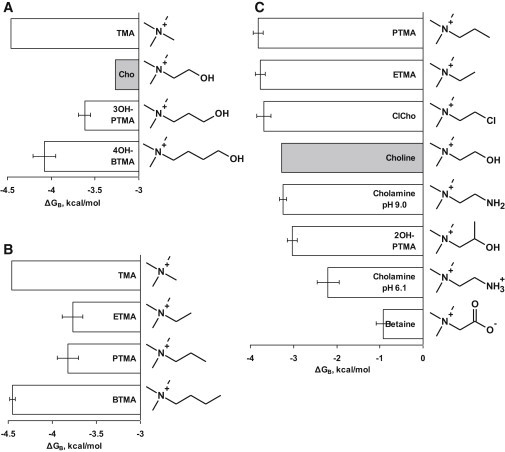
Binding energies and chemical structures of three sets of choline derivatives. (A) Extending the hydroxyethyl tail of choline to hydroxypropyl and hydroxybutyl (TMA shown for comparison). (B) Extending the alkyl tail of TMA from methyl to ethyl, propyl, or butyl. (C) Substituting the hydroxyl group of choline at C2 with different functional groups. Ligands with H-bonding ability are weaker agonists.

Choline and ETMA, which have the same tail length, provided the least favorable binding energy for gating from this group of agonists (Table 1). A longer tail resulted in more favorable (more negative) binding energies (Fig. 2 A). However, this apparent pattern did not apply to TMA, which is one methylene shorter than choline but provides only slightly less energy than does ACh. ΔG_B for TMA is ∼0.7 kcal/mol more favorable than for ETMA and ∼1.2 kcal/mol more favorable than for choline. The order of binding energy with respect to tail length was as follows: ethyl ≈ propyl < butyl ≈ methyl.

When we compared derivatives with or without a hydroxyl group, we found that in all cases, those without the hydroxyl provided more favorable energy (Fig. 2, A and B; Table 1). The hydroxyl group had an unfavorable effect (made ΔG_B more positive) of +0.5 kcal/mol (ETMA versus choline), +0.2 kcal/mol (PTMA versus 3OH-PTMA), and +0.4 kcal/mol (BMTA versus 4OH-BTMA).

Considering the above ligands, choline provided the least energy for gating because it possesses both of the unfavorable characteristics (i.e., an ethyl tail length and a hydroxyl group).

Substitutions at C2 position

Fig. 2 C compares the binding energies of choline derivatives having different substitutions at C2. The hydroxyl of choline was substituted with a chloride (chlorocholine), hydrogen (ETMA), methyl (PTMA), amine (cholamine at pH 9.0), ammonium (cholamine at pH 6.1), a hydroxyl and methyl (2OH-PTMA; 2-hydroxypropyltrimethylammonium), or carboxylic acid (betaine, also called trimethylglycine).

Compared with choline, four of these seven substitutions reduced the binding energy, by 0.1–2.4 kcal/mol. The order of effect was as follows: amine > hydroxyl and methyl > ammonium > carboxylic acid. Three of the substitutions at C2 provided a more negative ΔG_B energy than choline. Chloride, hydrogen, or a methyl group made ΔG_B more negative compared with choline, by ∼0.5 kcal/mol. A difference between the two groups of derivatives, which either decrease or increase the energy from the affinity change, is their H-bonding ability. The derivatives that readily H-bond had a less favorable ΔG_B than those without H-bonding ability.

Betaine deserves special mention because it is a physiological ligand (the oxidation product of choline) and because it is the only agonist that we have studied so far that provides substantially less binding energy than choline. Betaine is a zwitterion and is neutral at pH 7 and has a positive charge at the quaternary ammonium center and a negative charge at the carboxylic group. This agonist provides only ∼−0.9 kcal/mol toward gating. It is still an agonist, but is so weak as to be nearly a pure antagonist. Betaine binds with almost equal affinities to the C and O conformations, and therefore hardly promotes the gating isomerization. We did not measure the affinity of the resting AChR for betaine, so we do not know whether this ligand is an antagonist under physiological conditions.

Φ analysis

The opening rate constant versus the gating equilibrium constant (Table S1) for the choline derivatives is plotted on a log-log scale in Fig. 3. The slope of the linear fit of this rate-equilibrium relationship is called Φ, which estimates the relative timing of the energy change of the binding site’s affinity change in the gating isomerization of the protein. A Φ-value of one suggests an earlier energy change event, whereas zero suggests a later event. Plotting the results for all of the agonists, including ACh, TMA, and water (no ligand) (3), we estimate Φ^agonist = 0.90 ± 0.02 (r² = 0.996), which is similar to values previously estimated for more traditional agonists (0.93 in Grosman et al. (45)). The correlation was the same for all ligands, including water, over a >10 million-fold range in gating equilibrium constant.

Figure 3.

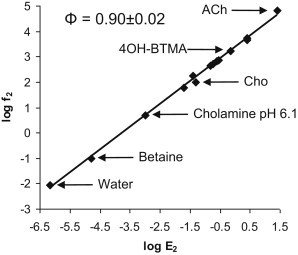
Rate-equilibrium analysis of choline derivatives. On a log-log scale, the opening rate constant (f₂) is plotted against the gating equilibrium constant (E₂). The slope of the linear fit (Φ) was 0.90 ± 0.02. The agonists in this plot are (from top to bottom) ACh, TMA, BTMA, 4OH-BMTA, PTMA, ETMA, ClCho, 3OH-PTMA, cholamine pH 9.0, Cho, 2OH-PTMA, cholamine pH 6.1, betaine, and water (no added ligand).

Homology model of AChR with TMA or choline

To further understand the binding energy estimates, we turned to molecular modeling. We used the x-ray structure of A. californica AChBP (11) to build a homology model of the AChR transmitter binding site. We randomly sampled 20,000 orientations of TMA or choline in the AChBP-based model of AChR (Fig. 4 A; Table S3), which after multi-MC-minimization yielded 10 most-favorable complexes.

Figure 4.

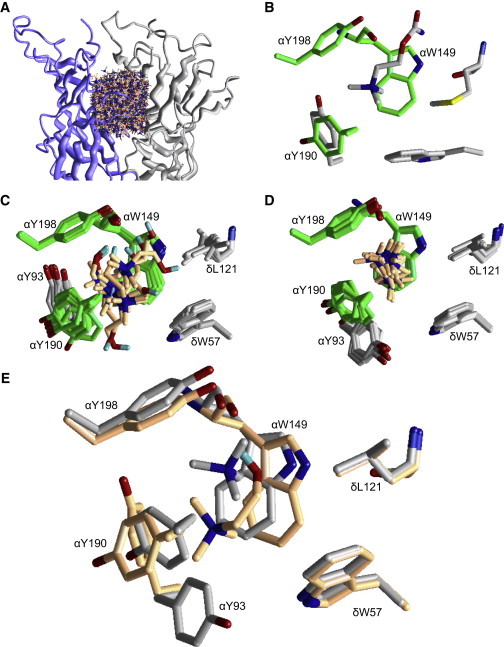
AChBP-based homology model of the AChR transmitter binding site with TMA and choline. (A) 1000 of the 10,000 randomly sampled orientations and positions of choline within the AChR transmitter binding site. The backbones of the α and δ subunits are presented as smooth ribbons. The ligand is shown in wireframe format, but its ammonium group is shown as a dark ball. (B) X-ray structure of Lymnaea AChBP bound with carbamylcholine (PDB accession number 1uv6). The aromatic triad is in green (AChR numbering). (C) The 10 most favorable binding modes of choline. Only residues within 4 Å from the ligand are shown as sticks. For clarity, the backbone atoms of the highlighted residues are not shown, except for αW149 and δL121. In six of the 10 modes, there is an H-bond between the choline hydroxyl and the backbone carbonyl of αW149. (D) The 10 most favorable binding modes of TMA. (E) Comparison of favorable binding modes of choline versus TMA. The relative position of the quaternary ammonium group within the aromatic triad (αW149, αY190, and αY198) is different for these two agonists. Although αY93 adopts alternative rotamers in TMA versus choline, this aromatic group likely contributes little to ΔG_B.

The 10 most favorable binding modes of choline and TMA are shown in Fig. 4, C and D. As expected, the ammonium group of the agonist was positioned between aromatic residues of the α subunit. The largest stabilizing contributions to agonist binding were from αW149, αY190, and αY198 (Table S4). In agreement with electrophysiology experiments (19), the computations show that this aromatic triad provides most of the total ligand-receptor energy. Weaker binding energies were from αY93, δW57, and δL121, each of which interacts with the agonist by <10% of the total ligand-receptor energy.

Among the energetically most favorable modes, the position of the quaternary ammonium group of choline did not deviate much; however, the agonist tail did adopt a variety of orientations. In most of the favorable modes, choline’s hydroxyl formed an H-bond with the backbone oxygen of αW149, which in effect slightly altered the position of its ammonium group compared with that of TMA, with respect to the aromatic groups of αW149 and αY190 (Fig. 4 E). In particular, the ammonium group of TMA is closer to the indole ring of αW149 compared with that of choline. This is in agreement with our structure-activity studies, which showed that removal of the hydroxyl group produces more active compounds. We hypothesize that this backbone-hydroxyl H-bond causes, in part, the more-positive ΔG_B for choline relative to TMA.

The modeling also shows that the αY93 side chain is in different orientations with TMA versus choline because of a rotation about the C_α-C_β bond. This aromatic group provides little energy for gating by ACh (Table S4 (19), so we do not think that this structural variation is important with regard to ΔG_B for TMA versus choline.

Discussion

Measuring agonist structure-activity relationships has long been a core experimental approach in pharmacology. For neuromuscular AChRs, the activity part of this relationship has been measured at increasingly mechanistic levels, from muscle contraction to membrane potential, membrane current, gating equilibrium constant, and now, energy from the affinity change. In the experiments reported here, the binding site was WT, and hence the ΔG_B and E₂ values had a fixed relation (Eq. 1). However, the method we used allows for ΔG_B measurements in AChRs with mutations of binding-site amino acids, in which case E₀ may not be the same as in the WT (46). This approach allows the structure part of the relationship to be expanded to include both the agonist and groups of the protein with which it interacts (19). In our view, ΔG_B is the appropriate quantitative index to use to rank the activity of agonists (Fig. 2).

E₂ values for some partial agonists of adult-type mouse neuromuscular AChRs with WT binding sites have been reported previously (5,8,26,45,47–51). We chose to investigate other partial agonists, particularly choline derivatives, because technical advances have made it possible to obtain more accurate estimates of ΔG_B. Specifically, we can 1), separate measurements of the gating rate constants without contamination from channel block and desensitization (5); 2), measure the energy (ΔG_B) contributed by the affinity change for the agonist because the value of the intrinsic gating equilibrium constant (E₀) is known (2,3); and 3), engineer predictable AChR gating rate constants to measure E₂ accurately for high-efficacy or low-efficacy agonists (5).

Each choline provides −3.3 kcal/mol for gating from the affinity change, compared with −5.1 kcal/mol for ACh and −4.5 kcal/mol for TMA. One of our goals was to identify the structures and interactions that are responsible for the +1.2 kcal/mol energy difference between choline and TMA. We selected choline derivatives that differed by only one or a few atoms. Our approach was to identify the specific atoms that could increase or decrease ΔG_B relative to choline. For example, elongating the alkyl tail by one -CH₂- (PTMA versus BTMA) makes ΔG_B more negative by −0.6 kcal/mol, and replacing the terminal -H with -OH (ETMA versus choline) makes ΔG_B more positive by +0.5 kcal/mol.

We can ask whether these two kinds of substitutions have energetically independent consequences. Fig. 5 shows a perturbation cycle analysis, which suggests that these substitutions are almost independent, so we conclude that it is the tail methyl group of BTMA that provides the −0.6 kcal/mol toward gating, rather than a wholesale change in the location of the ligand within the binding pocket. With this dissection, we estimate that for choline, C2 makes ΔG_B more positive by +0.7 kcal/mol (TMA versus ETMA) and the hydroxyl makes ΔG_B more positive by +0.5 kcal/mol (ETMA versus choline). Choline is a particular low-efficacy agonist among this group because it has two structural elements, each of which independently reduces the energy from the affinity change by ∼+0.6 kcal/mol.

Figure 5.

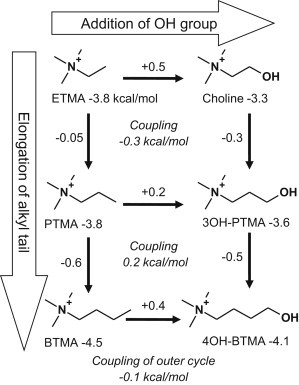
Perturbation-cycle analysis of choline derivatives. Addition of an OH group (horizontal arrows) and elongation of the alkyl tail (vertical arrows) are weakly coupled (by <0.3 kcal/mol), and thus the substitutions are nearly independent and additive. This suggests that these ligands bind similarly, and hence that ΔG_B differences can be attributed to specific atoms.

The Φ value for the agonists we examined was ∼0.9, which is consistent with previous measurements for other ligands. Φ gives the relative point in the reaction when the perturbed structural element changes energy. The high Φ-value for all of these agonists suggests that with WT binding sites, the affinity change occurs relatively early in the forward gating isomerization, which likely proceeds through a sequence of one or more intermediate microstates. However, it is important to emphasize that the ligand need not be the first structural element to change energy in gating. For example, residues near the C-terminus of the αM2 helix (the M2-cap) have Φ-values of ∼1, suggesting that this region of the protein changes energy at the same time (or before) the binding sites in the forward isomerization. Also, the Φ-values of some binding-site residues that contribute to the affinity ratio are lower in unliganded versus diliganded gating (19). The agonist has no momentum, so there is no a priori reason to assume that channel opening begins with the affinity-change/binding-site rearrangement, or indeed at any other particular place in the protein. Despite the high Φ-values that have been measured so far for agonists and binding-site residues, it is possible that the mechanical work of the channel-opening conformational change initiates at some region other than the transmitter binding sites.

There is general agreement that the ammonium group of AChR agonists forms cation-π interactions with aromatic residues located in the subunit interface. The benzene/indole rings of the aromatic triad, which is comprised of αW149, αY190, and αY198, provide the majority of the ΔG_B energy (∼−2 kcal/mol/ring) for ACh (19). ACh, TMA, and choline each possess a quaternary ammonium, but their ΔG_B values vary substantially. We considered the extents to which the ΔG_B differences between agonists might arise from differences in their intrinsic cation-π binding strengths or in their positions within the aromatic field.

The strength of a cation-π interaction is influenced by an electrostatic force between the cation and the quadrupole moment of the aromatic ring (20). The receptor provides Tyr and Trp aromatic rings, and the agonist provides a positively charged ammonium group. Ab initio calculations predict that the intrinsic cation-π ability of both the aromatic groups and the agonist ammonium group varies, in the order Trp>Tyr≈Phe (52) and TMA>ETMA>TEMA (triethylmethylammonium), with the difference between TMA and ETMA calculated to be ∼+0.3 kcal/mol (49). This value is less than our observed difference of +0.7 kcal/mol. Partial charge calculations using MOPAC show that the quaternary ammonium group (C₄H₁₁N) of ACh is only slightly more positive (+0.94) than choline (+0.87), a difference that is probably too small to account for the experimental ΔG_B difference between these ligands. It appears that the experimental ΔG_B differences cannot be attributed to the intrinsic properties of the agonist’s quaternary ammonium group.

An H-bond acceptor four or five bonds removed from the ammonium group was found to be a critical determinant for longer agonists, such as ACh, carbamylcholine, nicotine, and epibatidine (40). As seen in the x-ray structure of AChBP bound with nicotine (PDB code 1UW6 (10)), the H-bond acceptor of the agonist forms an H-bond with a structural water molecule interacting with the backbone of L102 and M114 (in AChBP numbering) of the complementary side. Thus, some larger agonists are stabilized by both a cation-π interaction with the aromatic triad and also by an energetically favorable H-bond with the complementary subunit. Shorter agonists, such as TMA and choline, do not possess this H-bond acceptor and therefore do not have this additional, favorable interaction with the protein.

TMA provides 0.6 kcal/mol less favorable binding energy than ACh, and 1.2 kcal/mol more favorable binding energy than choline. The structure-activity relationships show that a hydroxyl at carbon 2 or 3, or an amine at carbon 2 (within three bonds away from the agonist ammonium group) is unfavorable. In our AChR homology model, choline adopts an energetically unfavorable binding mode by H-bonding with the backbone carbonyl of αW149. A comparison of the choline and TMA binding modes reveals that the location of the quaternary ammonium group relative to the αW149 and αY190 side chains is displaced (Fig. 4 E). We hypothesize that the H-bond donor of choline forms an interaction with the backbone carbonyl of αW149, which alters the position of the quaternary ammonium group to reduce the strength of the cation-π interaction with the αW149 indole and the αY190 and αY198 benzene elements of the triad (Table S4). This would explain why choline, cholamine, 2OH-PTMA, and 3OH-PTMA are less efficacious than the other choline derivatives, such as TMA, chlorocholine, 4OH-BTMA, ETMA, PTMA, and BTMA, which would not H-bond with the backbone of αW149.

In summary, the relatively small ΔG_B from choline can be attributed to a combination of interactions at C2 and the hydroxyl group. We hypothesize that the hydroxyl group forms an H-bond with the αW149 backbone carbonyl, which serves to position the quaternary ammonium group within the aromatic residues of the binding site so as to reduce cation-π forces relative to agonists that do not form this H-bond. This hypothesis predicts that the ligand stabilization energy from the aromatic groups should be smaller for choline than for TMA and ACh. However, because the unfavorable interaction of choline is with a backbone atom, it does not shed light on the possibility that neuromuscular AChRs evolved to derive different binding energies for the transmitter versus its breakdown product. Further experimental analyses of choline and its derivatives using AChRs with binding-site mutations may reveal the full complement of the sources of energy for gating by agonists.