Taste of Sugar at the Membrane: Thermodynamics and Kinetics of the Interaction of a Disaccharide with Lipid Bilayers

Abstract

Sugar recognition at the membrane is critical in various physiological processes. Many aspects of sugar-membrane interaction are still unknown. We take an integrated approach by combining conventional molecular-dynamics simulations with enhanced sampling methods and analytical models to understand the thermodynamics and kinetics of a di-mannose molecule in a phospholipid bilayer system. We observe that di-mannose has a slight preference to localize at the water-phospholipid interface. Using umbrella sampling, we show the free energy bias for this preferred location to be just −0.42 kcal/mol, which explains the coexistence of attraction and exclusion mechanisms of sugar-membrane interaction. Accurate estimation of absolute entropy change of water molecules with a two-phase model indicates that the small energy bias is the result of a favorable entropy change of water molecules. Then, we incorporate results from molecular-dynamics simulation in two different ways to an analytical diffusion-reaction model to obtain association and dissociation constants for di-mannose interaction with membrane. Finally, we verify our approach by predicting concentration dependence of di-mannose recognition at the membrane that is consistent with experiment. In conclusion, we provide a combined approach for the thermodynamics and kinetics of a weak ligand-binding system, which has broad implications across many different fields.

Introduction

The recognition of carbohydrates at the cell membrane is known to mediate cell adhesion, infection of cells by pathogens, and many types of intracellular signaling responses. Many pathogenic virulent factors are carbohydrates, and initial infection involves recognition of these virulent factors by host phospholipid membrane (1,2). For example, mycobacterium tuberculosis, which causes tuberculosis, interacts with the host cell membrane primarily through a cell-surface associated glycolipid, lipoarabinomannan. The di-mannose molecule that caps lipoarabinomannan is a key virulent factor, and the recognition defined by the mannose-membrane interaction has been implicated in the initiation of TB pathogenesis (3–6). Another important aspect of carbohydrate-membrane interactions is that carbohydrates are known to increase membrane stability under dehydration and temperature stress. Thus, they help to maintain membrane integrity (7–10). Experimental and simulation studies have been extensively conducted to understand the mechanism of these stabilization effects (11–22).

There are currently two opposing views about the interaction of carbohydrates with phospholipid membranes: the water replacement hypothesis and the water entrapment hypothesis (23–26). The water replacement hypothesis suggests a direct interaction of sugars and the phospholipid interface with sugars being able to substitute for water molecules at the phospholipid interface and stabilize the membrane under dehydration (23,24). In contrast, the water entrapment hypothesis concludes that sugars are preferentially expelled from the hydration zone of phospholipids with sugars concentrating residual water molecules close to the phospholipid interface, stabilizing the membrane under dehydration (25,26). Molecular-dynamics simulations (12,13,15–19,21,22) have supported the water replacement hypothesis with the observation of direct interactions between carbohydrates and lipid molecules.

A recent experimental study by Andersen et al. (11) provided a consistent view that reconciled the two contradictory views: they found that binding of small sugars to the phospholipid bilayer dominates the interaction at low concentration, while sugars gradually become expelled from the membrane surface at high concentration (above ∼0.2 M). With these new findings, we seek to explore the thermodynamics and kinetics of a disaccharide molecule as it interacts with a phospholipid bilayer, with competing forces driving localization of this molecule in water and at the water-phospholipid interface.

In this combined computational and theoretical study, we consider a di-mannose molecule in two different water-phospholipid bilayer systems. We primarily use all-atom molecular-dynamics simulations to elucidate thermodynamics and kinetics. Potential of mean force calculations are used to extract localization tendencies. We use a two-phase model to quantify entropic contributions of water released from the water-phospholipid interface to bulk water phase upon di-mannose binding. Our results suggest that the direct interaction of di-mannose with membrane has a short residence time, with di-mannose exhibiting a small free energy bias toward the water-phospholipid interface, and this bias is driven by maximizing the water entropy of the whole system. We have also developed an analytical model to describe the carbohydrate ligand binding to a two-dimensional membrane surface. We evaluate kinetics directly from simulations and from this analytical model. Kinetics calculations show that association and dissociation are fast and weak for a ligand interacting with a two-dimensional surface. Finally, we reproduce a concentration dependence of di-mannose interaction with phospholipid bilayer as has been observed by Andersen et al. (11).

Methods

System

We study two phospholipid molecules, 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and 1,2-dioleoyl-sn-glycero-3-phosphatidylcholine (DOPC), which are the most prevalent phospholipid molecules that form the bilayer of eukaryotic cell membranes (27). They have the same PC headgroup but differ from each other by the degree of saturation and length of the acyl chains. POPC has one saturated (C16) and one mono-unsaturated acyl chain (C18), whereas DOPC has two mono-unsaturated acyl chains (C18). The membrane systems were built using the CHARMM-GUI membrane builder (28). Each system consists of 72 lipid molecules of pure POPC or DOPC with 36 lipids on each leaflet. Two levels of hydration are explored with water layer thickness of 1.5 nm or 2.5 nm on each side. Each system was equilibrated for 10 ns before incorporating a carbohydrate molecule. The carbohydrate molecule is di-mannose, α-D-mannose-(1,2)-α-D-mannose.

Simulation details

All simulations were carried out using the GROMACS 4.5.1 program (29). The CHARMM c36 force field (30–32) was used for lipids and carbohydrates. The CHARMM TIP3P (33) water model was used to represent explicit water. The sugar-membrane system was simulated under constant pressure (1 bar) and constant temperature (303 K) (NPT) with periodic boundary conditions, as in the original article by Klauda et al. (32). During NPT runs, Nosé-Hoover thermostat was used for temperature control with a 1.0-ps coupling constant (34,35), and Parrinello-Rahman extended-ensemble coupling was used for pressure control with a coupling constant 0.5 ps (36). Long-range electrostatic interactions were treated using the particle-mesh Ewald method (37). The van der Waals interactions were treated using a switching function to reduce the potential to zero from 1.1 to 1.2 nm. All bond interactions involving hydrogen atoms were constrained using SETTLE (38) and LINCS (39) to allow for a 1-fs integration time step to be used. To get enough statistics for kinetic parameter estimation, all systems were simulated at least three times using different random seeds with two simulations being 110-ns-long and a third one being 210-ns-long with frames saved every 2 ps. All the analysis is done for all the trajectories excluding the first 50 ns, unless otherwise stated.

Potential-of-mean-force calculations

The umbrella sampling method (40–42) was used to calculate the potential of mean force (PMF) for di-mannose affinity toward the water-phospholipid system with water thickness of 2.5 nm on each leaflet. With the symmetry of the phospholipid bilayer in the x-y plane, the reaction coordinate was taken as the distance in the z direction between the center of mass of di-mannose and the center of mass of the phospholipid bilayer. A total of 24 windows were used with a window size of 0.1 nm and a force constant of 1000 kJ/(mol⋅nm²) to guarantee sufficient overlap between neighboring windows. Each of the windows was simulated for 45 ns to ensure convergence, and the last 30 ns were used for PMF analysis. We used the weighted histogram analysis method (43) to construct PMF, and the standard error was calculated on five blocks, each of 6 ns, for all the windows.

Entropy calculations

We utilized the two-phase thermodynamics model of Lin et al. (44,45) to accurately calculate absolute entropy of water at the phospholipid bilayer interface and far from the interface (bulk water). The translational and rotational density of states of water molecules (g(ν), where ν is frequency) is partitioned into a gaslike g^g(ν) and solidlike g^s(ν) component,

$$g\left(\nu \right)=g^g\left(\nu \right)+g^s\left(\nu \right)=\frac{2}{k_{\text{B}}T}\underset{\tau \to \mathrm{\infty }}{\lim }\underset{-t}{\overset{t}{\int }}C\left(t\right)e^{-2\pi \nu i}dt,$$

where g(ν) is the Fourier transform of the velocity-autocorrelation function (VAC) C(t), and T is the temperature of the simulation system. C(t) is either the mass-weighted VAC of the center-of-mass velocities,

$$C_{\text{trans}}\left(t\right)=\sum _{i=1}^{N}m\stackrel{\rightharpoonup }{v_i\left(t\right)}\cdot \stackrel{\rightharpoonup }{v_i\left(0\right)}$$

or the moment of inertia-weighted angular VAC,

$$C_{\text{rot}}\left(t\right)=\sum _{i=1}^N\sum _{j=1}^3{I}_j{\omega }_{ij}\left(t\right){\omega }_{ij}\left(0\right)$$

where N is the total number of water molecules in the system, m is the mass of a water molecule, $\stackrel{\rightharpoonup }{v_i\left(\tau \right)}$ is the translational velocity of water molecule i, I_j is the j^th principle moment of inertia of a water molecule, and ω_ij(τ) is the angular velocity of water molecule i. Finally, the translational/rotational entropy of water can be calculated by assigning the appropriate weight, λ, to the gaslike and solidlike components and do the following integration,

$$S=k_b\underset{0}{\overset{\mathrm{\infty }}{\int }}(g^g\left(\nu \right){\lambda }^g\left(\nu \right)+g^s\left(\nu \right){\lambda }^s\left(\nu \right)d\nu ,$$

$$g^g\left(\nu \right)=\frac{g_0}{1+{\left(\frac{\pi g_0\nu }{6fN}\right)}^2},$$

$${\lambda }^s\left(\nu \right)=\frac{\beta h\nu }{\exp \left(\beta h\nu \right)-1}-\text{ln}\left[1-\text{exp}\left(-\beta h\nu \right)\right],$$

$${\lambda }^g\left(\nu \right)=\frac{1}{3}\frac{S^{HS}}{k_{\text{B}}},$$

where k_B is Boltzmann’s constant; h is the Planck’s constant; β = 1/k_BT; g₀ is the density of states at frequency zero; S^HS is the hard-sphere entropy determined from the Carnahan-Starling equation of state (46); and f is the fluidicity factor defined in the work of Lin et al. (44,45). Translational and rotational VACs C(t) for interface and bulk water were determined from five 20-ps simulations, and velocities and coordinates were saved every 4 fs.

Results

Comparative simulations of DOPC and POPC bilayers

To start, we verified the accuracy of our phospholipid bilayer simulations by calculating the area per lipid and the deuterium order parameters for POPC and DOPC phospholipid bilayers. Fig. 1 (also Fig. S1 in the Supporting Material) shows the area per lipid (APL) for both POPC and DOPC simulations. The APL for POPC is 66.08 ± 0.14 Å²/lipid and for DOPC is 67.17 ± 0.15 Å²/lipid. DOPC has a slightly larger APL compared to POPC. Those numbers agree well with the experimental values (47,48). The deuterium order parameters show that the saturated sn-1 acyl chain is less flexible than the sn-2 monounsaturated acyl chain of POPC. This is consistent with the observation that unsaturation due to double bonds results in kinks in the hydrocarbon tails, making the lipids more difficult to pack (49). The two acyl chains of DOPC show similar order parameters to those of the sn-2 acyl chain of POPC. The mono-unsaturation in both tails of DOPC results in an overall higher flexibility of the acyl chains. The slightly larger APL for DOPC than POPC is a direct consequence of the higher degree of tail flexibility. Although two levels of hydration for POPC and DOPC phospholipid bilayers are considered, no noticeable difference between them is observed (see Table S1 in the Supporting Material). Following results are reported for high level of hydration with 2.5-nm water thickness on each leaflet in the system.

Figure 1.

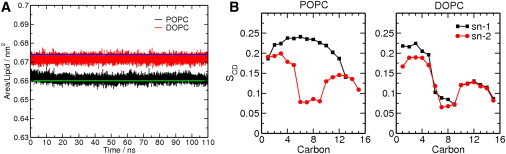
(A) Area per lipid (APL) of the POPC and DOPC phospholipid bilayers as a function of time for one 110-ns simulation. (Solid green line) Experimental APL for POPC 66.0 Å²/lipid (47); (solid blue line) experimental APL for DOPC, 67.4 Å²/lipid (48). (B) The deuterium order parameters for the two-acyl chains of POPC and DOPC molecules in the system.

Location of di-mannose in water-phospholipid bilayer system

Density profiles were calculated from trajectories of simulations of the two phospholipid systems to determine the location of di-mannose in the water-phospholipid system. The di-mannose density is mainly distributed in the water phase with small density peaks at the water-phospholipid interface (Fig. 2). Our single disaccharide density profiles are similar to previous disaccharide MD simulations with higher sugar concentration (15,16). In the simulations with 2.5-nm water thickness, di-mannose is found at the interface (within 0.7 nm above and below the bilayer) with a probability of 0.35 ± 0.03 compared to a probability of 0.25 ± 0.02 in the same thickness of bulk water. No significant difference was observed when comparing DOPC and POPC systems. As expected, we observed that the amplitude of the density peaks at the interface, and the probability of localization, is higher in the DOPC system with a 1.5-nm water layer than with a 2.5-nm water layer (see Fig. S2). The reason for the higher probability is that the interaction of di-mannose with the phospholipid membrane is not strong enough for it to adsorb and stick to the interface. Instead, di-mannose drifts in the water phase between interactions. In the DOPC system with 2.5-nm water layer, di-mannose spends more time in the thicker water layer before it comes back to interact with phospholipid molecules.

Figure 2.

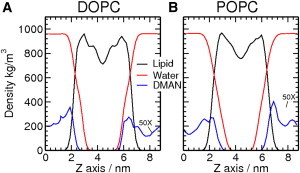
The density profile for the DOPC (A) and POPC (B) systems with 2.5-nm water layer. Water density (red), phospholipid density (black), and the di-mannose density (blue). The di-mannose density is amplified by 50 times to give better clarification. The Z axis is the direction perpendicular to the water-phospholipid interface (XY plane).

Temporal profile of di-mannose interaction with lipid bilayer

Next, the residence time of di-mannose at the water-phospholipid interface was characterized for DOPC and POPC (Fig. 3). If there are hydrogen-bond interactions between di-mannose and phospholipid for three consecutive frames, then di-mannose is considered to be at the interface. Similarly, di-mannose is considered to be off-interface if there is no hydrogen-bond interaction for three consecutive frames. We found that most of the interaction events have a short residence time (<50 ps), and few interaction events have a long residence time (>0.5 ns). Overall, the temporal profile of di-mannose with lipid can be described as a touch-and-go event with a short residence time. During long-residence time events, we find that di-mannose directly interacts with the oxygen atoms of the lipid phosphate group and localizes underneath the choline group. Again, no difference is observed between DOPC and POPC systems.

Figure 3.

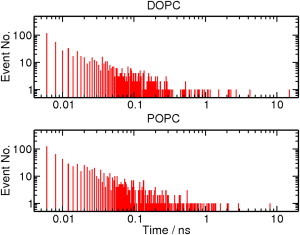
Characterization of residence time for di-mannose interaction with phospholipid for all the simulations of the DOPC and POPC systems with 2.5-nm water layer. Residence times are plotted against number of events (Event No.).

Affinity of di-mannose to lipid bilayer

As shown in Fig. 2, di-mannose drifts in the water phase with a low probability of localizing at the water-lipid interface. To better characterize the affinity of di-mannose to membrane, the PMF was calculated using umbrella sampling taking the distance in the z-axis direction between the center of mass of di-mannose and the phospholipid bilayer (see Methods). Because no difference is observed between DOPC and POPC systems, we focus on the PMF of the DOPC system (Fig. 4). The di-mannose is free to tumble in the PMF calculation and the free energy is averaged on all the possible orientation at the same z-axis distance, which introduced roughness in the PMF plot. The minimum of PMF locates at 2.55 nm from the center of the phospholipid bilayer with an energy bias of −0.42 kcal/mol. The inset in Fig. 4 shows the di-mannose location in the sugar-membrane system at the PMF energy minimum. This location is at the water-phospholipid interface where di-mannose has direct interaction with phospholipid molecules. The magnitude of the free energy bias is small and is comparable to the room temperature fluctuation (k_BT = 0.59 kcal/mol).

Figure 4.

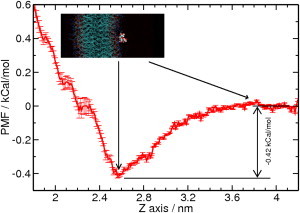
Potential of mean force for di-mannose location in the DOPC system. The reaction coordinate is the distance in the z axis between center of masses of di-mannose and the phospholipid bilayer. (Inset) Location of di-mannose in the sugar membrane system at the energy minimum.

PMF shows only a small preference, and it may fall within the error due to inaccuracies associated with free energy calculations. According to the studies of Shirts et al. (50), the accuracy of free energy calculations depends on sampling of relevant configurations, the statistical error, the systematic error, and true convergence. In our calculations, the correlation time of di-mannose translation along the PMF order parameter is in the subnanosecond regime, and we have performed sampling for 45 ns in each window. This ensures that the results in the MD simulations are independent of initial conditions and the observed convergence is reliable. We performed block averaging to estimate the statistical error (0.05 Kcal/mol) in the PMF calculations and it is provided as error bars in Fig. 4. Based on the studies of Kobrak (51), the systematic error and statistical error will be determined by the width of the sampling window, and they have shown that systematic error is smaller than the statistical error. In the studies by Shirts et al. (50), the systematic error on PMF calculations on a similar system is estimated to be smaller than 0.1 Kcal/mol for different widths of sampling windows. Regarding convergence, we have checked sufficient overlapping of the sampling histograms. Also, an increase in sampling time did not change the value of PMF (data not shown).

Enthalpic and entropic contributions to affinity of di-mannose to lipid bilayer

We calculated the interaction energies for di-mannose and the absolute entropy change for interface water released to bulk water when di-mannose binds to phospholipids. To consider the enthalpic contributions, we calculated the total potential energy of the system when di-mannose is in water phase and when di-mannose is at the water-phospholipid interface. No difference is observed for the two cases within errors, which means that there is no enthalpic preference for the di-mannose location.

Next, we calculated the key entropic contributions. Because the di-mannose interaction with the phospholipid bilayer does not affect phospholipid bilayer properties, we assume the entropy change coming from the phospholipid molecules in the system is negligible, and the entropy change of the system is directly related to the entropy change of water and di-mannose. Also, we calculated the diffusion coefficient of di-mannose at different locations to justify neglecting the entropy change contribution from di-mannose. The di-mannose diffusion coefficient was 1.85 ± 0.13 1 × 10⁻⁶ cm²/s in water phase and 0.18 ± 0.06 1 × 10⁻⁶ cm²/s at the water-phospholipid interface. The reduced diffusion at the water-phospholipid interface is because of the interaction between di-mannose and phospholipids as well as the hydrodynamic effects at the interface (52). Those diffusion coefficients are much smaller than water diffusion coefficients, so we further neglect the entropy contribution from di-mannose.

Therefore, we accurately calculated the absolute entropy of water at the interface and far from the interface (bulk water) using the two-phase thermodynamics model of Lin et al. (see Methods). The translational and rotational VACs for the two waters relax in a similar manner at very short timescales, and this is also revealed in the similarities between the densities of states at the high frequencies (Fig. 5). The peak of the density of states has a blueshift for both translational and rotational motion going from bulk to the interface, which suggests that interface waters are more tightly bound than bulk waters. The absolute entropy shows that by releasing interface water to bulk, there is an entropy gain of 0.727 kcal/mol (Table 1). Thus, there is a propensity for the system to have more bulk waters to maximize the entropy of the system. When di-mannose locates at the water-phospholipid interface, it will share hydration water with phospholipids, thus resulting in fewer water molecules at the interface. The total entropy of the system will increase as a result of di-mannose location at the water-phospholipid interface.

Figure 5.

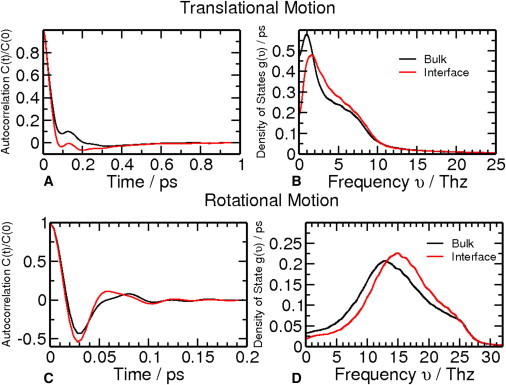
Translational and rotational velocity autocorrelation function (A and C) and density of states (B and D) for interface water and bulk water.

Table 1.

Entropy of water at the interface and far from interface (bulk water) at 303.0 K

Properties	Interface water	Bulk water
gtrans(ν = 0) ps	0.187 ± 0.005	0.480 ± 0.007
grot(ν = 0) ps	0.019 ± 0.001	0.033 ± 0.001
ftrans	0.219 ± 0.003	0.347 ± 0.002
frot	0.065 ± 0.001	0.087 ± 0.001
Strans (kcal/mol)	3.477 ± 0.008	3.964 ± 0.014
Srot (kcal/mol)	0.881 ± 0.012	1.122 ± 0.009
Stot (kcal/mol)	4.358	5.086

S_tot = S_trans + S_rot.

Kinetics of di-mannose interaction with lipid bilayer

We derive an analytical diffusion-reaction model to characterize the interaction between di-mannose and a phospholipid bilayer to extract kinetic information. In this association process, the two interacting partners are di-mannose (M) and phospholipid bilayer (P). M diffuses in the water-phospholipid bilayer system under the influence of a potential and interacts with the phospholipid bilayer to form an interaction complex M^∗P. The kinetic scheme can be described as

$$\begin{array}{c}{k}_{\text{on}}\\ \mathit{M}+\mathit{P}\rightleftharpoons \mathit{M}\mathit{\ast }\mathit{P}\\ k_{\text{off}}\end{array}$$

where k_on is the association rate constant from M and P to M^∗P and k_off is the dissociation rate constant from M^∗P to M and P.

These kinetic rate coefficients are extracted from simulations by deriving an analytical model that accounts for a ligand interaction with a two-dimensional surface. A ligand diffusing in a box is shown (Scheme 1). At the surfaces that make up the sides of the box we impose periodic boundary conditions so that the x and y directions are essentially infinite. In the z direction, the bottom surface of the box, z = 0, is an absorbing surface, while the top of the box, z = L_z, is reflecting.

Scheme 1.

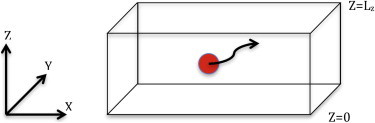
Schematic description of ligand diffusion in a box was used to derive an analytical expression for the binding rate constant for ligand binding with a 2-D surface. The red circle represents the ligand. Z=0 plane is an absorption plane, Z=L_z plane is a reflection plane and periodic boundary condition is applied in the x and y directions.

The association constant k_on for a ligand in the box, to reach the absorbing surface, is inversely related to the average mean first-passage time for the ligand to hit the surface:

$$k_{\text{on}}=\frac{1}{\langle w\rangle R}.$$

R is the effective lipid concentration in the volume, i.e., R = 1/(AL_z). Here, A is the size of the phospholipid surface and L_z is the thickness of the water layer in which sugar diffuses. Thus, we have

$$k_{\text{on}}=\frac{A{L}_z}{\langle w\rangle }.$$

The 〈w〉 can be obtained in two ways: 1), We could obtain 〈w〉 directly from the simulations. Alternatively, 2), one could derive an analytical expression in the diffusion-limited case that relates 〈w〉 to the diffusion coefficient of di-mannose as shown below. In the first approach, the average mean first-passage time is calculated directly from simulations by monitoring the time di-mannose, starting from different z, spent in water phase before hitting and forming complex with phospholipid. We obtain 〈w〉 =1.28 ns from MD simulations, and therefore k_on = 2.10 × 10¹⁰ M⁻¹ s⁻¹. The corresponding dissociation constant is k_off = 1/T_i, where T_i is the average interaction time of di-mannose with phospholipid. With T_i = 0.12 ns directly from simulation, we get k_off = 8.33 × 10⁹ s⁻¹.

Derivation of analytical expression for average mean first-passage time

From Shoup and Szabo (53), the general diffusion-limited mean first-passage time, w(x, y, z), for a particle starting at a position with coordinates (x, y, z) to reach an absorbing surface satisfies the partial differential equation,

$$e^{\beta V}\nabla \cdot e^{-\beta V}\mathit{D}\cdot \nabla w+1=0,$$ (1)

where β = 1/k_BT; D is the diffusion coefficient of the ligand; and V is the potential energy of interaction between the particle and the surface, where the latter two are (x, y, z)-dependent. Because of the periodic boundary conditions w, D and V are only functions of z. Therefore, Eq. 1 reduces to

$$e^{\beta V\left(z\right)}\frac{d}{dz}\left[e^{\beta V\left(z\right)}D\left(z\right)\frac{dw\left(z\right)}{dz}\right]+1=0.$$ (2)

Carrying out the integration after rewriting Eq. 2,

$$e^{\beta V\left(z\right)}D\left(z\right)\frac{dw\left(z\right)}{dz}+\underset{0}{\overset{z}{\int }}{e}^{-\beta V\left(m\right)}dm=const={\alpha }_1.$$ (3)

At z = L_z, dw/dz = 0, so

$${\alpha }_1=\underset{0}{\overset{L_z}{\int }}{e}^{-\beta V\left(m\right)}dm.$$

Rewriting Eq. 3 and integrating again,

$$w\left(z\right)={\alpha }_2+\underset{0}{\overset{z}{\int }}\frac{e^{\beta V\left(z\right)}}{D\left(z\right)}dzI\left(z\right).$$ (4)

Applying boundary condition w(0) = 0 at z = 0, we get α₂ = 0 and

$$I\left(z\right)=\underset{z}{\overset{L_z}{\int }}{e}^{-\beta V\left(x\right)}dx.$$

In the case where V(z) = V0e^−λz and βV₀ < 1,

$$e^{-\beta V\left(z\right)}\approx 1-\beta V_0{e}^{-\lambda z}.$$

Here, λ is the decay constant of the bias potential.

Then,

$$I\left(z\right)=\underset{z}{\overset{L_z}{\int }}{e}^{-\beta V\left(x\right)}dx=\underset{z}{\overset{L_z}{\int }}\left[1-\beta V_0{e}^{-\lambda z}\right]dx=\left(L_z-z\right)+\frac{\beta V_0}{\lambda }\left[e^{-\lambda L_z}-e^{-\lambda z}\right]$$

and substituting I(z) in Eq. 4 and integrating for w(z) gives

$$w\left(z\right)=\frac{1}{D}\underset{0}{\overset{z}{\int }}dz{e}^{\beta V\left(z\right)}I\left(z\right)=\frac{1}{D}\left[L_{z}z-\frac{z^2}{2}+\frac{\beta V_0}{\lambda }z{e}^{-\lambda L_z}+\frac{\beta V_0}{{\lambda }^2}\left[e^{-\lambda z}-1\right]\right]-\frac{\beta V_0}{D}\left[-\frac{L_z}{\lambda }{e}^{-\lambda z}+\frac{\lambda z+1}{{\lambda }^2}{e}^{-\lambda z}-\frac{1}{{\lambda }^2}-\frac{\beta V_0}{{\lambda }^2}{e}^{-\lambda L_z}\left[e^{-\lambda z}-1\right]+\frac{\beta V_0}{2{\lambda }^2}\left[e^{-2\lambda z}-1\right]\right].$$

Finally, the average value for w is

$$\langle w\rangle =\frac{\underset{0}{\overset{L_z}{\int }}w\left(z\right)dz}{L_z}=\frac{1}{D}\left[\frac{L_z^2}{3}+\frac{\beta V_0}{{\lambda }^2}\right],$$

during which we assume that $e^{-\lambda L_z}\approx 0$ (details are in the Supporting Material). The first term in 〈w〉 is the pure diffusion result. Because V_o is negative, the presence of potential reduces the time for the particle to reach the surface.

In our case, V₀ = −0.498 kcal/mol, and λ = 2.61 nm⁻¹ (the fitting of the PMF is shown in Fig. S3). With A as 24.18 nm², L_z as 1.85 nm, and using D from different sources, we get a range of k_on as shown in Table 2.

Table 2.

The association constant k_on for different diffusion constant D

	Diffusion coefficient D (1 × 10−6 cm2/s)	〈w〉 ns	kon (M−1 s−1)	koff (s−1)	Keq = kon/koff (M−1)
Literaturea	4.3	2.41	1.12 × 1010	8.33 × 109	1.34
Simulationb	1.98	5.23	5.15 × 109	8.33 × 109	0.62
Modelc	5.6	1.85	1.45 × 1010	8.33 × 109	1.74

^aUsed the diffusion coefficient of sucrose here (58).

^bDi-mannose in bulk water MD simulation to get diffusion coefficient.

^cDepending on the PDB structure to calculate diffusion coefficient using HYDROPRO (59).

Effect of mannose concentration

Our studies so far showed that a single di-mannose molecule displays a small preference to be localized at the water-phospholipid interface rather than in the aqueous phase (Figs. 2 and 4). To quantify how that localization would be affected at higher concentrations of di-mannose, we calculate a titration curve for di-mannose binding to the phospholipid bilayer. Here we assume that each di-mannose molecule binds independently to the phospholipid binding site with the same affinity and consider the same model as that in the previous section:

$$\mathit{M}+\mathit{P}\stackrel{{\mathit{K}}_{\mathit{eq}}}{\leftrightarrow }\mathit{M}\mathit{\ast }\mathit{P}.$$

The total number of di-mannose binding sites for the phospholipid bilayer from MD simulations is 18, as one di-mannose interacts with four headgroups of phospholipid molecules, and the total number of phospholipid molecules was 72. The volume of box was used to calculate the total concentration of phospholipid-binding sites. The concentration of the sugar-membrane complex is

$$\left[M\ast P\right]=K_{\text{eq}}{\left[M\right]}_{\text{bulk}}{\left[P\right]}_{\text{bulk}},$$

where [M]_bulk and [P]_bulk refer to the bulk concentration of sugar and available sugar-binding sites on the phospholipid bilayer, respectively. We calculate the concentration of complex as a function of total concentration of di-mannose. The total concentration of di-mannose and phospholipid-binding sites are given by the expressions

$${\left[M\right]}_t={\left[M\right]}_{\text{bulk}}+\left[M\ast P\right],$$

$${\left[P\right]}_t={\left[P\right]}_{\text{bulk}}+\left[M\ast P\right].$$

By combining these three equations above, we can obtain the concentration of the complex. The probability distribution of di-mannose in the simulation box (see Fig. S4) shows that all the di-mannose bound to lipid occurred in a 1.0-nm slab above and below the phospholipid bilayer. Then, the local concentration of di-mannose near the phospholipid bilayer can be calculated using the formula

$${\left[M\right]}_{\text{local}}=\left[M\ast P\right]\ast \frac{V_{\text{box}}}{V_{\text{slab}}},$$

where V_box is the volume of the box and V_slab is the volume of the 2.0-nm slab. Fig. 6 shows ([M]_local − [M]_bulk) versus [M]_bulk. This plot is similar to the measured plot of Fig. 3 in Andersen’s article (11) because Γ₃ from that work is proportional to ([M]_local − [M]_bulk). Here we use K_eq = 2.52 M⁻¹, the value obtained from the simulations. At very low sugar concentration, di-mannose prefers to localize at the phospholipid-water interface driven by the small energy bias due to attractive hydrogen-bonding interactions between di-mannose and phospholipid molecules. However, as the di-mannose concentration increases, all available phospholipid-binding sites become occupied with di-mannose. Eventually, [M]_local remains constant with increasing sugar concentration as the sites at lipid-water interfaces are fully occupied. As a result, further increase in sugar concentration increases only [M]_bulk. That leads to negative value for ([M]_local − [M]_bulk). This behavior is a direct result of the small energy bias of di-mannose to be located at the phospholipid-water interface and a low affinity of binding. The result is also consistent with both attraction and exclusion components for sugar interaction with a phospholipid bilayer.

Figure 6.

Sugar binding to the phospholipid bilayer as a function of sugar concentration. [M]_local and [M]_bulk correspond to the concentration of the dimannose close to the lipid bilayer (local) and in bulk solvent respectively.

Discussion

Disaccharide interactions with DOPC or POPC bilayers can be characterized at best as touch-and-go events. Consequently, di-mannose exhibits a small density peak at the water-phospholipid interface and spends most of the time drifting in the water phase. When a di-mannose molecule reaches the water-phospholipid interface, local fluctuations of lipids may provide a cavity large enough to accommodate the molecule. This leads to localization of di-mannose. Upon localization at the interface, it forms several hydrogen bonds with headgroups of multiple phospholipid molecules that can stabilize membrane structure under dehydration conditions. Specifically, hydrogen bonds with oxygen atoms of the phosphate group tend to show a long lifetime. Our observation of a series of interaction events is consistent with the water replacement hypothesis. Only 3.9% of the total interaction events have a residence time longer than 0.5 ns, indicating that the di-mannose interaction with phospholipid molecules is weak. Although the area per lipid of DOPC is slightly larger than POPC, and the tails of DOPC are more flexible than POPC, we do not see any noticeable difference in di-mannose interactions with these two phospholipid bilayers.

PMF calculations indicate that di-mannose has only a weak preference for the water-phospholipid interface. The PMF shows a small energy minimum of −0.42 kcal/mol at 2.55 nm perpendicular to the bilayer plane from the center of mass of the phospholipid bilayer that is at the top of the interface. This small energy bias drives di-mannose to localize at the water-phospholipid interface. However, this energy bias is comparable to the thermal fluctuations at room temperature, and these fluctuations tend to delocalize di-mannose away from the interface. This is the reason why most of the di-mannose phospholipid interactions exhibit a short residence time.

The calculated PMF explains the reason why Andersen et al. (11) observed the coexistence of attractive and exclusive components when sugar interacts with a phospholipid bilayer. Because sugar has a preferred location at the interface with low energy bias, the attractive component is weak, and sugar binding to the interface is a dynamic process. At low concentration of sugar, most sugars bind to the interface under the small energy bias, thus the dominant component is attractive. At high concentration, sugar binding is saturated because of the small energy bias. This results in a small portion of sugars bound, while a large portion of sugars are free from the interface. Thus, the dominant component is exclusive.

We further quantified key enthalpic and entropic contributions to this low free energy bias of di-mannose toward the water-phospholipid interface. From the evaluation of the total potential energies of the system, we find that there is no enthalpic preference for di-mannose to be located in bulk water or at the water-phospholipid interface. This finding is inconsistent with recently reported interaction energies from quantum mechanical calculations, which found that mannose interaction with a phospholipid molecule was stronger than its interaction with a water molecule (54). We note that those calculations considered interactions between single molecules of sugar and water/phospholipid. However, MD simulations showed that bulk effects are dominant and overwhelm the individual molecule interactions.

We found that the slight free energy bias of di-mannose to localize at the water-phospholipid interface is driven by maximization of the entropy of waters in the system. Our calculations show that by releasing water from the interface to bulk water, there is an entropy gain of 0.727 kcal/mol. This increased entropy of water is verified by our calculation of diffusion coefficients of water at different layers. The two-dimensional diffusion coefficients of different layers of water from the interface are shown in Table 3. All water diffusion coefficients are much larger than the diffusion coefficients of di-mannose in water and at the water-phospholipid interface. Again, this is the reason for neglecting the entropy change contribution from di-mannose. Waters far from the interface (Layer 4) have the largest two-dimensional diffusion coefficient, and the three-dimensional diffusion coefficient (5.82 1 × 10⁻⁵ cm²/s) is the same as CHARMM TIP3P bulk water (55). Waters close to the interface (Layer 1) have the smallest two-dimensional diffusion coefficient (0.32 1 × 10⁻⁵ cm²/s).

Table 3.

Two-dimensional diffusion coefficients for different layers of waters

	nm	D 1 × 10−5 cm2/s	SD
Layer 1	0 ∼ 0.35	0.32	0.054
Layer 2	0.35 ∼ 0.7	4.86	0.38
Layer 3	0.7 ∼ 1.05	5.38	0.54
Layer 4	1.5 ∼ 1.85	5.43	0.65

A smaller water diffusion coefficient is a manifestation of low entropy of water at the phospholipid interface. When one molar di-mannose locates at the interface of the phospholipid bilayer, ∼15 mol of interface waters will be released to become bulk waters. This change will increase the total entropy of the system. The entropy change of released water will dominate the entropy change during di-mannose binding. A similar entropy effect to drive peptide/protein to be located at the interface of a reverse micelle with <1 kcal/mol energy bias has previously been observed by Tian and García (56,57) without detailed quantification of water entropy change.

In addition, we quantified the kinetics of this system in terms of association and dissociation constants that describe the weak affinity toward the phospholipid bilayer. In a case like this, when a ligand binds to a two-dimensional surface, these rate constants are determined by the average mean first-passage time, 〈w〉. In the Results, we developed a simple analytical diffusion-reaction model to obtain an expression for 〈w〉 in the diffusion-limited regime. Using that and the free energy bias from PMF, we obtain a k_on as shown in Table 2. According to this model, when sugar diffuses freely in the water-phospholipid system,

$$k_{\text{on}}=\frac{A{L}_z}{\langle w\rangle },$$

and we derive

$$\langle w\rangle =\frac{1}{D}\left[\frac{L_z^2}{3}+\frac{\beta V_0}{{\lambda }^2}\right],$$

when there is a small free energy bias to be at the water-lipid interface. However, this average mean first-passage time can also be calculated directly from simulations from the average time a sugar, starting from different locations, spends in the water phase before it interacts with phospholipid. That provided an alternate way to calculate k_on. Considering w = 1.28 ns from MD simulations, we get kon = 2.10 × 10¹⁰ M⁻¹ s⁻¹. This directly calculated effective association constant is larger than that obtained from the analytical model, and appears to be consistent with experimental observations. These key rate constants should be very useful for studies that target sugar-based drug discovery or biomarker development.

Similar to experimental observation by Andersen et al. (11), we find that di-mannose prefers to be at the phospholipid-water interface and in the aqueous phase at low and high sugar concentrations, respectively. This is consistent with the coexistence of both attractive and exclusive interactions between the sugar and phospholipid molecules and a direct result of low affinity of di-mannose to lipid-water interface. We observe that the saturation occurs at 0.05 M, i.e., most of the binding sites for sugar on the phospholipid bilayer are occupied. This discrepancy compared to the experimental value of 0.2 M may be the result of using the same equilibrium constant for all binding events of di-mannose to the lipid bilayer. It is possible that the binding of a few di-mannose molecules to the phospholipid bilayer can increase the area per lipid and alter the binding constant of further di-mannose molecules to the lipid. In addition, we should consider that the equilibrium constant could be biased by the force field used in the simulations and this value may be underestimated in our MD simulations.

Conclusion

For the first time, to our knowledge, we take a combined approach of computational and analytical methods to understand the thermodynamics and kinetics of a di-mannose molecule in a phospholipid bilayer system. Our results show that disaccharide associations with pure phospholipid bilayers such as DOPC and POPC have predominantly short residence time. Slight differences between DOPC and POPC bilayers do not introduce any noticeable differences toward the recognition of a sugar molecule. Di-mannose has a small free energy bias to be located at the water-phospholipid interface, and this bias explains the observation of Andersen et al. of a coexistence of both attraction and exclusion mechanisms (11). We find that the small energy bias is driven by the maximization of water entropy in the system. Then we developed an analytical model with molecular-dynamics simulations to extract kinetic information. This model should be applicable to a wide range of problems involving molecular recognition of a weakly bound ligand on two-dimensional surfaces such as membranes. Finally, our combined approach is verified by reproducing the experimental concentration dependence of sugar binding with a lipid bilayer by using both the thermodynamic and kinetic information from our study.