Abstract
Several intracellular processes are governed by two different species of molecular motors, fast and slow ones, that both move in the same direction along the filaments but with different velocities. The transport of filaments arising from the cooperative action of these motors has been recently studied by three in vitro experiments, in which the filament velocity was measured for varying fraction of the fast motors adsorbed onto substrate surfaces in a gliding assay. As the fast motor fraction was increased, two experiments found a smooth change whereas the third one observed an abrupt increase of the filament velocity. Here, we show that all of these experimental results reflect the competition between fast and slow motors and can be understood in terms of an underlying saddle-node bifurcation. The comparison between theory and experiment leads to predictions for the detachment forces of the two motor species. Our theoretical study shows the existence of three different motility regimes: 1), fast transport with a single velocity; 2), slow transport with a single velocity; and 3), bistable transport, where the filament velocity stochastically switches between fast and slow transport. We determine the parameter regions for these regimes in terms of motility diagrams as a function of the surface fraction of fast motors and microscopic single-motor parameters. An abrupt increase of the filament velocity for an increasing fraction of fast motors is associated with the occurrence of bistable transport.
Introduction
Intracellular cargo transport of organelles and vesicles along cytoskeletal filaments is an essential biological process (1) that is carried out by molecular motors. These motors act as enzymes for nucleotide hydrolysis and are able to convert chemical energy into mechanical work. Cytoskeletal motor proteins such as kinesin, dynein, and myosin step along cytoskeletal filaments and transport cargo in a unidirectional manner. The properties of single molecular motors have been studied extensively both experimentally and theoretically in the last two decades. However, cargos are often transported by groups of cooperating molecular motors (2,3). Intracellular cargos are typically transported by small teams of cooperating molecular motors as theoretically studied by Klumpp and Lipowsky (4), Beeg et al. (5), and Driver et al. (6) for motors of the same type. In the in vitro gliding assays, where filaments are pulled by molecular motors adsorbed on a surface, large ensembles of motors can cooperate as has been studied theoretically (7–9) and experimentally (10). Groups of cooperating motors can also contain different types of motors with the same directionality (11), or different types of motors with different directionality such as kinesin and dynein motors (12–14).
As a result of such cooperative transport, complex motility patterns are observed that can serve important biological functions: cooperation of identical motors can increase the run-length (4) or groups of motors with different directionality can give rise to bidirectional transport (15), which allows for cargo transport in different directions. Here we study the cooperation of molecular motors with the same directionality but with different velocities (i.e., fast and slow motors), and find that a cooperative transport mechanism leads to three distinct motility regimes and to bistable switching between fast and slow transport.
Recently, important intracellular processes have been identified which involve the function of two types of kinesin motors such as kinesin-II and OSM-3 (kinesin-2 family) in the assembly of cilia (11,16), or Xkid (kinesin-10 family) and Xklp1 (kinesin-4 family) in chromosome positioning (17). All of these processes involve two types of kinesin motors walking along microtubules towards the plus-end but with different velocities. The two types of kinesin motors are therefore called fast and slow motors henceforth. We still know relatively little about the exact biological function of these transport systems, but velocity control of cargo transport is one possibility.
In vitro gliding assays are a suitable and important tool to understand the cooperative transport processes for fast and slow motors. In such gliding assays, cytoskeletal filaments are pulled by two types of molecular motors whose motor tails are immobilized on a solid surface. So far, three independent experimental studies of gliding assays with different types of kinesin motors have been performed: fast OSM-3 and slow kinesin-II motors are used by Pan et al. (16), fast wild-type and slow mutant kinesin-1 motors by Larson et al. (18), and fast Xklp1 and slow Xkid motors by Bieling et al. (17). In all three assays, the gliding velocities of microtubules were measured for different surface concentrations of fast motors with a fixed total motor surface density. In all three experiments, the gliding velocity showed a nonlinear dependence on the surface concentration of fast motors and varied between the speed of a single slow and a single fast motor in all of those experiments. However, there are also qualitative differences in the results of the three experiments: in the gliding assay by Larson et al. (18), the gliding velocity showed a switchlike, abrupt transition from slow to fast motion upon increasing the surface concentration of fast motors, whereas it changed smoothly in the other two experiments. This different evolution of the cooperative transport properties with increasing fraction of the fast motors remains to be understood in terms of the single motor properties. Similar phenomena have also been observed for gliding assays consisting of myosin and actin filaments (19).
To understand the different experimental results and the underlying dynamics of cargo transport by fast and slow motors, we study gliding assays using several theoretical methods. To begin, we use a master equation approach to describe the stochastic processes of binding and unbinding of motor proteins during filament transport. The master equation results are corroborated by microscopic Brownian (or Langevin) dynamics simulations (20–22), in which the stochastic stepping, binding, and unbinding of motors as well as the force transduction onto microtubules are taken into account, and in which microtubules perform an overdamped motion driven by thermal and motor forces. Finally, we also derive a simplified mean field equation from the master equation, which allows us to analyze the bifurcation behavior resulting from the competition between fast and slow motors.
Using these approaches, we identify three types of stationary states or motility regimes, which exhibit different probability distributions for the microtubule velocities:
Regime 1. Fast transport with unimodal velocity distributions.
Regime 2. Slow transport with unimodal velocity distributions.
Regime 3. Bistable transport with a bimodal velocity distribution corresponding to stochastic switching between fast and slow transport.
Our theory provides a quantitative description for the qualitatively different behavior as observed in the three experiments reported in Pan et al. (16), Bieling et al. (17), and Larson et al. (18). This allows us to extract values for the detachment forces of the two motor species from the experimental data.
Using the mean field approach, we derive motility diagrams for the cooperative transport behavior as a function of the fraction of fast motors adsorbed onto the substrate surface and of single motor parameters such as the ratio of detachment forces of fast and slow motors. The mean field approach allows us to predict where bistable transport occurs as a function of these parameters. On the one hand, these predictions can be tested experimentally; on the other hand, new experimental results about the three motility regimes will enable us to deduce refined values for single motor parameters based on these motility diagrams.
Results
Velocity as a function of the fraction of fast motors
In the three gliding assay experiments in Pan et al. (16), Bieling et al. (17), and Larson et al. (18), the velocity of microtubules was measured as a function of the fraction of fast motors adsorbed onto the gliding surface; for surface densities σf and σs of fast and slow motors, respectively, this fraction is given by σf/(σf + σs). For increasing fractions of fast motors, large velocity fluctuations and an abrupt transition from slow to fast transport have been observed in Larson et al. (18) for wild-type and mutant kinesin-1 motors, whereas a smooth crossover from slow to fast filament transport was observed in Pan et al. (16) for kinesin-II and OSM-3 and in Bieling et al. (17) for Xkid and Xklp1.
To understand these different behaviors, we consider filament transport by a fixed number of Nf fast and Ns slow motors, which can attach to or detach from the filament. For the total number N ≡ Nf + Ns of transporting motors, we will use a typical value N ≃ 10, which was estimated in Larson et al. (18), for all three experiments. In a gliding assay, Nf and Ns are actually fluctuating in time because the filament moves, whereas the motors are anchored to the substrate such that there is a constant exchange in the pool of motors available for binding. The numbers Nf and Ns of available motors are Poisson-distributed (21), which implies that fluctuations around the average values can be neglected for sufficiently large Nf and Ns. The numbers Nf and Ns of available motors are proportional to the corresponding surface motor densities σf and σs, the motor attachment lengths ℓf and ℓs (which depend on the length and the elastic properties of the respective motor stalks), and the filament length L (20). Assuming identical motor attachment lengths ℓf = ℓs for fast and slow motors, the fraction of fast motors on the gliding surface equals the fraction of fast motors available for binding, i.e., Nf/N = σf/(σs + σf), which is henceforth used as a control parameter.
Our theory can also be applied, with small modifications, to the complementary situation of cargo transport by slow and fast motor along a microtubule, where Nf and Ns are fixed numbers of fast and slow motors whose stalks are firmly bound to the cargo, in analogy to the situation considered in Klumpp and Lipowsky (4) and Müller et al. (15).
In our model, we characterize each motor species by six microscopic motor parameters (see Table 1; note subscripts f for fast motors, s for slow motors): motors bind to a microtubule with binding rates π0f and π0s; they unbind with an unbinding rate ϵ0f and ϵ0s. The unbinding rate increases exponentially under a load force, and the associated force scales are given by the detachment forces Fdf and Fds. When bound to a microtubule, unloaded motors walk with velocities vf and vs. Fast motors are always under resisting load forces from slow motors, and their velocities decrease linearly and reach zero at the stall force Fsf. Slow motors, on the other hand, are always subject to assisting forces. Also for assisting forces, we assume a linear force-velocity relation, which is characterized by a force Fss. In principle, the force Fss could be different from the stall force for the slow motors. For simplicity, we assume Fs ≡ Fss = Fsf in the following.
Table 1.
Motor parameter values used in the theoretical calculations and simulations and derived dimensionless parameters according to Eq. 4
| Parameter | Larson et al. (18) |
Pan et al. (16) |
Bieling et al. (17) |
|---|---|---|---|
| Fast motor | |||
| Wild kinesin-I |
OSM-3 |
Xklp1 |
|
| Slow motor | |||
| Mutant kinesin-1 | Kinesin-II | Xkid | |
| Binding rate, fast π0f | 5/s (32) | 5/s (32) | 5/s (32) |
| Binding rate, slow π0s | 5/s (18,32) | 5/s (32) | 5/s (32) |
| Unbinding rate, fast ϵ0f | 1/s (33,34) | 1/s (33,34) | 1/s (33,34) |
| Unbinding rate, slow ϵ0s | 1/s (18,33,34) | 1/s (33,34) | 1/s (33,34) |
| Detachment force, fast Fdf | 3 pN (34) | 6 pN (this work) | 6 pN (this work) |
| Detachment force ratio η ≡ Fds/Fdf | 0.45(23) | 3.3 (this work) | 1.9 (this work) |
| Stall force, fast Fsf | 6 pN (34) | 6 pN (34) | 6 pN (34) |
| Stall force, slow Fss | 6 pN (18,34) | 6 pN (34) | 6 pN (34) |
| Zero load velocity, fast vf | 0.522 μm/s (18) | 1.09 μm/s (16) | 1.0 μm/s (17) |
| Zero load velocity, slow vs | 0.034 μm/s (18) | 0.34 μm/s (16) | 0.1 μm/s (17) |
| 5 | 5 | 5 | |
| 2 | 1 | 1 | |
| 0.065 | 0.31 | 0.1 | |
During filament transport, fast and slow motors bind and unbind from the filament. The dynamic state of the system is described by the numbers nf of fast and ns of slow active motors which are attached to the filament. These numbers are stochastic variables fluctuating between 0 ≤ nf ≤ Nf and 0 ≤ ns ≤ Ns during filament transport. In the Supporting Material, we obtain the master equation for the probability p(nf, ns, t) that the filament is transported by nf fast and ns slow motors at a given time t. To describe the steady-state transport properties such as the average filament velocity, we solve the master equation in the stationary state for given numbers Nf and Ns numerically, to obtain the stationary probability distribution p(nf, ns).
The average velocity of microtubules has been measured by all three experimental groups in Pan et al. (16), Bieling et al. (17), and Larson et al. (18) for increasing fractions of fast motors Nf/N. Within our master equation approach, the average velocity of microtubules in a stationary state can be calculated from the probability p(nf, ns) by
| (1) |
where vm(nf, ns) is the stationary state velocity of the microtubule for given numbers nf and ns of fast and slow active motors. As shown in Eq. 1, the microtubule velocity vm(nf, ns) is uniquely determined as a function of the motor numbers nf and ns by the two conditions referenced in Models and Methods.
In Fig. 1, we compare the average velocities of microtubules, which we calculate using numerical solutions of the stationary state master equation for the probability distribution p(nf, ns) and Eq. 1, for different fractions Nf/N of fast motors with the available experimental data from (A) Larson et al. (18), (B) Pan et al. (16), and (C) Bieling et al. (17). Data points are experimental results; the solid curves are our theoretical calculations using the motor parameter values from Table 1 and a value of N = 10 for the total number of available motors. The theoretical calculations agree very well with the experimental data. There are no fitting parameters in Fig. 1 A for the assays with wild-type and mutant kinesin-1 motors by Larson et al. (18) as all single motor parameters are known.
Figure 1.
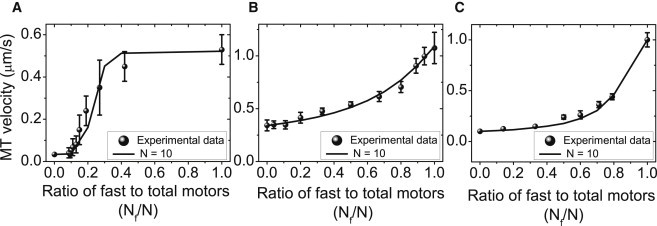
Comparison of experimental data (points) and corresponding theoretical calculations (solid lines) for the microtubule transport velocity as a function of the fraction of fast motors Nf/N for three different types of gliding assays with fast and slow motors: (A) for fast wild-type and slow mutant kinesin-1 motors (18), (B) for fast OSM-3 and slow kinesin-II motors (16), (C) for fast Xklp1 and slow Xkid motors (17). All three experimental data sets are well described by our theory based on the master equation approach and Eq. 1 with parameter values as given in Table 1.
For wild-type kinesin-1, all parameters are known from single-molecule experiments (see Table 1). For the mutant kinesin-1 motor used in Larson et al. (18), it is believed that only the velocity of the motor is reduced by a factor of 15 because of the five point mutations while the other motor parameters remain unchanged (see Table 1). In Uemura et al. (23), an asymmetry for detachment forces Fd under resisting and assisting forces has been measured for kinesin-1. Because slow mutant kinesin-1 motors are only subject to assisting forces from fast kinesin-1 motors, whereas fast wild-type kinesin-1 motors are only subject to resisting forces from slow mutant kinesin-1 motors, this asymmetry gives rise to different detachment forces Fdf and Fds for fast and slow motors.
Only a few parameters are known for kinesin-II and OSM-3 used in the experiments by Pan et al. (16), as well as for Xkid and Xklp1 used in the experiments by Bieling et al. (17). We assume the same values for binding and unbinding rates and for the stall force as for kinesin-1 and the other motors. Given the experimental data on gliding velocities, we then use the detachment forces of fast and slow motors as fit parameters, which give the solid curves in Fig. 1, B and C. The fits are very sensitive to the detachment force ratio,
| (2) |
of slow and fast motors. Using this procedure, we find Fdf ≃ 6 pN for OSM-3 and η ≃ 3.3 (i.e., Fds ≃ 20 pN for kinesin-II) for the experimental data by Pan et al. in Fig. 1 B and Fdf ≃ 6 pN for Xklp1 and η ≃ 1.9 (i.e., Fds ≃ 12 pN for Xkid) for the experimental data by Bieling et al. in Fig. 1 C. This demonstrates that we can derive predictions for microscopic motor parameters from the comparison between our theory and experimental gliding assay data.
Three motility states, bikinetic transport
The further characterization of the dynamic behavior during filament transport is based on an analysis of the stationary probability distribution p(nf, ns), as obtained from numerical solution of the stationary master equation. We find three types of probability distributions representing three different motility states:
-
1.
Fast transport characterized by a single maximum at motor numbers nf > ns corresponding to filament transport dominated by fast motors and with a large velocity.
-
2.
Slow transport characterized by a single maximum at motor numbers ns > nf corresponding to filament transport dominated by slow motors with a small velocity.
-
3.
Bistable transport characterized by a distribution with two maxima at nf > ns and ns > nf, corresponding to a bistable transport switching stochastically between a fast and slow transport velocity. This last motility regime could therefore be called bikinetic transport.
Three examples for the corresponding stationary distributions p(nf, ns) are shown in Fig. 2, A–C. For the motility regimes of fast and bistable transport shown (Fig. 2, A and C), we used parameters as in the experiments by Larson et al. (18) (see Table 1, left column, with detachment forces satisfying η = 0.45 and fractions of fast motors of Nf/N = 0.4 in Fig. 2 A and Nf/N = 0.2 in Fig. 2 C). For the motility regime of slow transport in Fig. 2 B, we also used a small fraction of fast motors, i.e., Nf/N = 0.2, but an increased detachment force for slow motors corresponding to η = 4.
Figure 2.
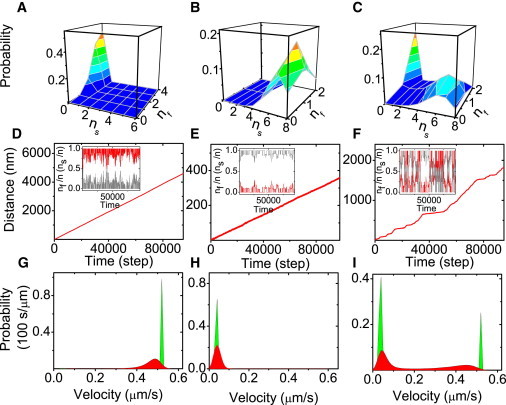
Comparison of microtubule transport in the three different motility regimes for wild- and mutant types of kinesin-1 corresponding to the experiments in Larson et al. (18) (with single motor parameters as given in Table 1, left column): (A, D, and G) fast transport in motility regime 1 for Nf/N = 0.4 and η = 0.45; (B, E, and H) slow transport in motility regime 2 for Nf/N = 0.2 and η = 4 (corresponding to a larger detachment force of slow motors); and (C, F, and I) bistable transport in motility regime 3 for Nf/N = 0.2 and η = 0.45. (A–C) Stationary probability distribution p(nf, ns) to find nf fast motors and ns slow motors attached to the microtubule from the master equation approach (blue corresponding to low probabilities, yellow and orange to high probabilities). For bistable transport (C), the distribution p(nf, ns) is bimodal. (D–F) Center-of-mass displacements (in nm) of the microtubules as a function of time from microscopic Brownian dynamics simulations (in simulation steps Δt = 0.1 ms) as described in Models and Methods (see main text). (Insets) Corresponding trajectories of fractions nf(t)/n(t) (red) of fast and ns(t)/n(t) (gray) of slow motors attached to the microtubule (n(t) = nf(t) + ns(t)). In fast transport (D) the fraction of fast motors is high, in slow transport (E) the fraction of slow motors is high, whereas in the bistable transport regime (F) both microtubule velocity and motor fractions exhibit bistable stochastic switching. (G–I) Microtubule velocity distributions both from the master equation approach (green) and from microscopic Brownian dynamics simulations (red). For bistable transport (I), the velocity distribution is bimodal.
From the probability distribution p(nf, ns) in the space of motor numbers nf and ns, we can directly obtain the probability distribution p(v) for the transport velocity of the filament because vm = vm (nf, ns) is uniquely determined by the motor numbers nf and ns (see Models and Materials and Eq. 7). This distribution is given by
| (3) |
Typical results for the velocity distribution in the three motility regimes are shown in Fig. 2, G–I. For fast and slow transport, the single maximum in the probability distribution p(nf, ns) also leads to a unimodal velocity distribution (see Fig. 2, A and G, for fast and Fig. 2, B and H, for slow transport). For bistable transport, on the other hand, two maxima in the probability distribution p(nf, ns) give rise to a bimodal velocity distribution as shown in Fig. 2, C and I.
The different dynamic behavior is also seen in microscopic Brownian dynamics simulations, where we solve the coupled motor and filament equations of motion (see Models and Methods). The trajectories of the microtubule center of mass are recorded to determine the walked distances of the microtubule center of mass along its trajectory as a function of time. The resulting trajectories are shown in Fig. 2, D–F. For fast and slow transport, the trajectories exhibit a unique slope corresponding to a single velocity (see Fig. 2, D and E). For bistable transport, the trajectories switch stochastically between two slopes corresponding to a bimodal velocity distribution as shown in Fig. 2 F.
In Fig. 2, G–I, we also compare the velocity distributions from the master equation approach to the velocity distributions from Brownian dynamics simulation trajectories. We find good agreement for the most probable velocities in all three motility regimes. The peak width of the velocity distributions from microscopic simulation trajectories is larger because of additional fluctuations in the numbers Nf and Ns of available motors, which we neglected in the master equation approach.
The existence of three motility regimes also explains the different experimental results (16–18) for the evolution of the microtubule velocity with increasing fraction Nf/N of fast motors. In all three experiments, the system starts at small fractions of fast motors in the motility regime of slow transport with a unimodal velocity distribution with a single peak at small velocities and eventually reaches the motility regime of fast transport with a unimodal velocity distribution having a single peak at high velocities. For the smooth increase of the average microtubule transport velocity as observed in Pan et al. (16) and Bieling et al. (17), the single peak of the unimodal velocity distribution shifts to higher velocities while the velocity distribution remains unimodal all the time. For the abrupt transition as observed in Larson et al. (18), on the other hand, the transition proceeds via an intermediate bistable motility regime where the velocity distribution develops a second peak at high velocities, which coexists with the low-velocity peak, before the low-velocity peak vanishes. The bistability and coexistence of two velocities in the transition regime explains the pronounced velocity fluctuations that have been found in Larson et al. (18) (see large error bars in Fig. 1 A in the transition region).
Motility diagrams
To understand the mechanism responsible for bistable transport in more detail, we have to compare the properties of the different molecular motors involved in the three experiments. The system with wild-type and mutant kinesin-1 motors from Larson et al. (18), which exhibits the abrupt velocity transition, is characterized by a rather small ratio Fdf/Fs = 0.5 of detachment to stall force for wild-type kinesin-1 and an even smaller ratio Fds/Fs = 0.225 for the mutant kinesin-1 motors (see Table 1, left column). These small values indicate that motors easily unbind from the microtubule at typical stall forces, which also represent typical load forces. Therefore, an unbinding cascade can be triggered. During transport, force balance is established between the group of fast and slow motors, where the load force is equally shared among motors of the same type. Once a fast or slow motor unbinds from the microtubule, the remaining fast or slow motors must sustain a higher load force, which leads to further unbinding events, until all fast or slow motors are unbound from the microtubule. Such unbinding cascades give rise to a bistable switching of the microtubule transport velocity: if the slow motors unbind, the microtubule velocity switches to the velocity vm ≈ vf of fast motors; if fast motors unbind, it switches to vm ≈ vs. Indeed, we observe such unbinding cascades in our microscopic Brownian dynamics simulations for the bistable motility regime, as can be seen in the inset in Fig. 2 F for Nf/N = 0.2.
In the other two assays in Pan et al. (16) and Bieling et al. (17), where the microtubule velocity changes smoothly, we obtain larger values Fdf/Fs = 1 and Fds/Fs > 1 from our fits to the experimental data (see Table 1, middle and right columns). This means that, in these cases, slow motors have a detachment force that is even larger than the stall force. Therefore, slow motors remain bound to the microtubule if fast motors exert more load force for increasing Nf/N, which suppresses unbinding cascades. Then the numbers of slow and fast motors participating in microtubule transport is only gradually changing and the velocity changes smoothly if the fraction of fast motors is increased.
This suggests that small detachment forces of slow and fast motors, as compared to stall forces, are a necessary condition for an abrupt velocity transition upon increasing the fraction of fast motors. To discuss this issue more systematically, we derive motility diagrams for all three assays, where the extents of the three motility regimes can be read off as a function of microscopic motor parameters. These motility diagrams are based on a mean field equation for the ratio 〈nf〉/〈ns〉 of the average numbers of bound fast to bound slow motors (see Eqs. 17 and 18). In this mean field equation, we identify the following set of five dimensionless control parameters,
| (4) |
which determine the behavior of the system. In the following, we mainly focus on the ratio η of detachment forces and the most important experimental control parameter, which is the fraction of available fast motors.
In Fig. 3 we show solutions of the mean field equation for the average fraction of bound fast motors 〈nf〉/(〈nf〉 + 〈ns〉) as a function of the ratio of detachment forces η for motor parameters appropriate for wild-type and mutant kinesin-1 as used in the experiments in Larson et al. (18) (see Table 1, left column). The fraction of available fast motors is fixed at Nf/N = 0.5. Fig. 3 clearly shows that solutions of the mean field equation can bifurcate, and the mean field equation can have one, two, or three different solutions. Bifurcations take place both at a lower critical value ηl and at an upper critical value ηu. In the parameter range ηl < η < ηu between these critical values, we find three solutions; below ηl and above ηu only a single stationary state exists. From a stability analysis, we find that the system is bistable, i.e., the upper and lower solutions are stable, while the middle branch is unstable; thus, the system undergoes saddle-node bifurcations at ηl or ηu.
Figure 3.
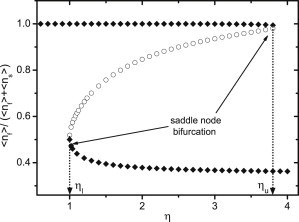
Bifurcation diagram for the gliding assay with wild and mutant types of kinesin-1 motors (18). It shows all solutions of the mean field equation for 〈nf〉/(〈nf〉 + 〈ns〉) as a function of the detachment force ratio η for a fixed fraction of fast motors Nf/N = 0.5. (Solid diamonds) Stable solutions. (Open circles) Unstable solutions. The bifurcation at the lower critical ηl and the upper critical ηu is of the saddle node type. For η < ηl, there is a single stable mean field solution at a high fraction of fast motors corresponding to the motility regime 1 of fast transport. For η > ηu, there is a single stable mean field solution at a low fraction of fast motors corresponding to the motility regime 2 of slow transport. For ηl <η < ηu, we find two metastable and one unstable solution corresponding to the bistable transport regime 3.
The existence of a single stationary state corresponds to a single solution for the average microtubule velocity and, thus, to a unimodal velocity distribution in the master equation approach. For η < ηl, i.e., small detachment forces of slow motors, slow motors detach easily, and we find transport with 〈nf〉/(〈nf〉 + 〈ns〉) ≈ 1, i.e., essentially by fast motors only. Correspondingly, we can identify the parameter regime η < ηl as the motility regime of fast transport. For η > ηu, on the other hand, detachment forces of slow motors are large, and slow motors remain bound to the microtubule, and we find transport with 〈nf〉/(〈nf〉 + 〈ns〉) < 0.5, i.e., predominantly by slow motors. Correspondingly, we can identify the parameter regime η > ηu as the motility regime of slow transport.
In the intermediate regime ηl < η < ηu, there are two metastable solutions of the mean field equations corresponding to fast and slow transport. Bistability of the mean field solutions therefore corresponds to a bimodal velocity distribution in the master equation approach such that the intermediate parameter regime ηl < η < ηu is the motility regime of bistable transport.
The bifurcation values ηl and ηu depend on the fraction Nf/N of fast motors and the remaining control parameters from Eq. 4, and we characterize the parameter regimes for the three different motility states by calculating the critical values ηl and ηu as a function of Nf/N. The results for wild-type and mutant kinesin-1 motors as in the assays by Larson et al. (18) (motor parameters from Table 1, left column) are shown in the motility diagram in Fig. 4 A in the (Nf/N, η) parameter plane. The open red circles represent numerical results for the upper and lower critical values ηl and ηu. The motility regime of bistable transport is enclosed by the red open circles. Outside this regime, there is just a single stable stationary state corresponding to the motility regimes of fast or slow transport. This is also demonstrated by three different velocity distributions, which have been calculated from the master equation approach. In Fig. 4 A, the vertical dashed black line for fixed Nf/N = 0.5 corresponds to the parameter regime, for which the detailed bifurcation behavior of the fraction 〈nf〉/(〈nf〉 + 〈ns〉) of fast motors is shown in the bifurcation diagram Fig. 3.
Figure 4.
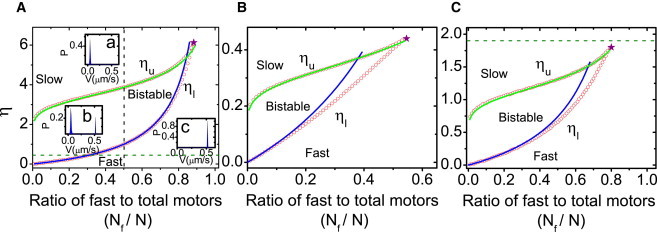
Motility diagrams for the three different microtubule gliding assays studied experimentally in Refs. (16–18) as a function of the parameters η and Nf/N: (A) For wild-type and mutant kinesin-1 motors (18), (B) for OSM-3 and kinesin-II motors (16), and (C) for Xklp1 and Xkid motors (17). (Open red circles) Numerical results for the lower and upper critical values ηl and ηu. (Solid blue and green curves) Obtained from analytical approximations of Eqs. 5 and 6, respectively (see also the Supporting Material). (Stars) Critical points. The region enclosed by red open circles represents the bistable motility regime. This is further illustrated by the insets in (A), which show velocity distributions from the master equation approach for values (a) η = 5.0, (b) η = 1.5, and (c) η = 0.5 at Nf/N = 0.5. In the bistable motility regime, the velocity distribution is bimodal (inset b), while there is only one stationary state with a unimodal velocity distribution outside of this region, corresponding to slow transport (inset a), or fast transport (inset c). The bifurcation diagram in Fig. 3 shows the detailed bifurcation behavior (vertical dashed black line) in diagram A. (Horizontal dashed green lines) Parameters explored experimentally in (A) Larson et al. (18) and (C) Bieling et al. (17). In Pan et al. (16), a value η = 3.3 outside the diagram B was realized experimentally.
Fig. 4 A also shows that there is a critical point, which limits the bistable motility regime, and which is located at (Nf,c/N, ηc) = (0.883, 6.13). Motility regimes of fast and slow transport are connected by a smooth crossover whenever we move along a trajectory in parameter space that runs around the bistable motility regime, which terminates at the critical point. The dashed green line in Fig. 4 A is given by η = 0.45 and represents the experimental parameters from Larson et al. (18). This line clearly enters the bistable motility regime resulting in an abrupt transition, because η = 0.45 is far below the critical point value ηc = 6.13. The motility diagram in Fig. 4 A then allows us to read off critical fractions of fast motors for the transitions between the bistable and slow or fast motility regimes.
We find a transition from bistable to fast transport for Nf/N ≃ 0.31, whereas the other transition from slow to bistable transport is close to vanishing for Nf/N (see Fig. 4 A). These results are in agreement with the master equation result for the location of the abrupt velocity transition (see Fig. 1 A). Because the ratio Nf/N of fast to total motors can be changed easily in experiments, the prediction of a transition from a bistable state with bimodal velocity distribution to a state with unimodal velocity distribution at Nf/N ≃ 0.31 can be tested experimentally for this system. The horizontal green dashed line in Fig. 4 A corresponds to the parameter range explored experimentally in Larson et al. (18), which implies that the observed abrupt increase of the filament velocity is a consequence of bistability.
We obtain analogous motility diagrams for the other two experimentally studied assays as shown in Fig. 4 B for kinesin-II and OSM-3 motors and in Fig. 4 C for Xkid and Xklp1 motors with parameters as given in Table 1 (middle and right columns). The critical points obtained for these assays are (Nf,c/N, ηc) = (0.55, 0.44) and (Nf,c/N, ηc) = (0.80, 1.81), respectively. However, the values η ≃ 3.3 we obtained for kinesin-II and OSM-3 motors from fitting the average velocity data is larger than the critical value ηc = 0.44 and, similarly, the value η ≃ 1.9 for Xkid and Xklp1 motors is larger than the critical value ηc = 1.81 (see green dashed line in Fig. 4 C). Therefore, according to the motility diagrams shown in Fig. 4, B and C, we predict that only unimodal velocity distributions should be observable in these gliding assays with a smooth crossover from slow to fast transport in accordance with the experimental observations.
Finally, we can derive analytical estimates for the two branches of critical values. The lower branch ηl is obtained in the limit of small 〈nf〉/〈ns〉 ≪ , the upper branch in the limit of large 〈nf〉/〈ns〉 ≫ . Details of the calculations are contained in the Supporting Material. For the lower branch, we find a dependence
| (5) |
on the fraction of fast motors (solid blue curve in Fig. 4 A). For the upper branch, we obtain a logarithmic dependence
| (6) |
(solid green curve in Fig. 4 A). Both results show good agreement with the numerical calculations.
In the Supporting Material we also discuss motility diagrams in the (Nf/N, ) and (Nf/N, ) parameter planes, which exhibit a similar topology with a bounded parameter region for the bistable motility regime 3 with bimodal velocity distribution. These parameter regions always terminate in critical points.
Models and Methods
Brownian dynamics simulations
We have introduced a microscopic Brownian (or Langevin) dynamics simulation model for gliding assays in the literature (20–22). Here we use these Brownian dynamics simulations to study the motion of a single microtubule transported by two types of kinesin motors in the two-dimensional gliding plane. The stochastic discrete motor stepping and stochastic binding and unbinding of motors from the microtubule are included in the model.
The microscopic simulation model contains the microtubule, motor heads, and polymeric motor stalks as three types of degrees of freedom. Two types of kinesin motors are distributed randomly in the two-dimensional substrate plane. To simulate the microtubule motion, we use Brownian (or Langevin) dynamics and solve the overdamped equation of motion for a rigid microtubule under forces and torques from attached motors, thermal forces and torques, and frictional forces and torques numerically. During each simulation time step, we update the microtubule position and orientation according to the equation of motion and the positions of the attached motor heads according to the force-velocity relation of motors. The forces from the stretched motor stalks, which are built, from the stepping of motor heads along the microtubule are transmitted on both the microtubule and the attached motor heads. Motor stalks equilibrate fast for given positions of the motor head and motor tail anchored on the substrate. Therefore, the forces for the stretched motor stalks can be recalculated after updating the motor head or the microtubule positions by applying the equilibrium force-extension relation of the motor stalk spring. The simulations are performed by advancing motor head positions and the microtubule position and orientation in discrete time steps. The discrete time step Δt is taken to be 0.1 ms if not mentioned otherwise. Details of the simulation are described in Kraikivski et al. (20), Kierfeld et al. (21), and Li et al. (22).
Master equation approach
The numbers of nf fast and ns slow motors that actually bind and transport the microtubule vary stochastically within the intervals 0 ≤ nf ≤ Nf and 0 ≤ ns ≤ Ns because of stochastic binding and unbinding of motors (Fig. 5 A). The state of the filament can then be described by the pair (nf, ns). The probability p(nf, ns, t) to find the filament with nf fast and ns slow motors attached at time t describes the stochastic properties of the system and satisfies a master equation, which is given in the Supporting Material.
Figure 5.
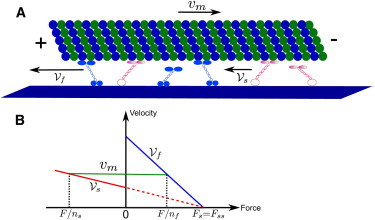
Filament gliding assay with fast (blue) and slow (red) molecular motors. (A) One microtubule is transported by two types of kinesin motors with velocity vm. The two types of motors walk along the microtubule to the plus-end with different velocities for slow and fast motors, respectively. (B) Force-velocity relations for fast and slow motors. A piecewise linear relation is taken for both types of motors. Fast motors are always pulled backward by resisting force F > 0 while slow motors are always pulled forward by assisting forces F < 0.
The master equation contains rates πf and ϵf for binding and unbinding of a fast motor as well as πs and ϵs for binding and unbinding of a slow motor, which are functions of the state (nf, ns) of the system. These rates are force-dependent.
We can derive these rates under the assumption of:
Condition 1. Force balance and equal force sharing.
Condition 2. Equal velocities of all motors.
Then, by assuming that motor stepping happens much faster than binding and unbinding of motors, we can use Conditions 1 and 2 with fixed motor numbers ns and nf.
We take the binding rates π = π0 of a single motor to be independent of load force because unbound motors can always bind to filaments from their relaxed state (4,15). The unbinding rate of a motor depends on its load force F and is given by Bell (24) and Svoboda and Block (25) ϵ(F) = ϵ0exp(|F|/Fd), where ϵ0 is the unbinding rate at zero load force and Fd defines the detachment force.
Fast motors will experience resisting forces F ≥ 0 because they move faster, while slow motors will be pulled forward and subject to assisting forces F ≤ 0. As shown in Fig. 5 B, we assume for both motors types linearly decreasing force-velocity relations (25–29) with vf and vs as velocities of unloaded motors and stall forces Fsf and Fss. As pointed out above, we assume Fs ≡ Fss = Fsf for simplicity.
With the load force F− < 0 acting on each slow motor and the resisting load force F+ > 0 acting on each fast motor, Condition 1 (force balance and equal force sharing between all attached nf fast and ns slow motors) leads to nfF+ = −nsF− ≡ F(nf, ns), where F(nf, ns) > 0 is the absolute value of the total force acting on each motor group. We neglect a small frictional force on the microtubule, as discussed in the Supporting Material.
Using Condition 2 (equal velocities of all motors and the microtubule) then leads to a microtubule velocity of
| (7) |
where n ≡ nf + ns is the total number of bound motors and the total force F(nf, ns) acting on each motor group,
| (8) |
Using this force, we can calculate the effective unbinding rates in a state (nf, ns) characterized by the numbers of bound fast and slow motors. The effective unbinding rates ϵf and ϵs of fast and slow motors from the microtubule in the state (nf, ns) are
| (9) |
| (10) |
The parameters ϵ0f and ϵ0s denote the unbinding rates of a single fast and slow motor at zero load force, and Fdf and Fds denote the detachment forces for fast and slow motors, respectively. The effective binding rates πf and πs of fast and slow motors in state (nf, ns) are
| (11) |
| (12) |
The parameters π0f and π0s denote the corresponding binding rates of fast and slow motors. Analogous expressions have also been obtained in Larson et al. (18), based on the theoretical framework as developed in Müller et al. (15). Using these unbinding and binding rates in the master equation, we can calculate the stationary probability distributions p(nf, ns) that the filament is transported by nf fast and ns slow motors numerically.
Mean field approach
It is difficult to solve the full master equation analytically or to identify the relevant control parameters governing transitions between different types of solutions corresponding to different motility states. Therefore, we also introduce an approximative mean field theory that can be used to derive and analyze dynamic equations for the mean numbers
of bound fast and slow motors analytically (30,31). We rescale these average numbers using the total numbers of available motors Nf and Ns, respectively, and define
| (13) |
which become continuous variables for large Nf and Ns. From the master equation, we obtain equations for these two rescaled mean motor numbers,
| (14) |
| (15) |
where we assumed equal binding and unbinding rates for fast and slow motors for simplicity, i.e., π0 ≡ π0f = π0s and ϵ0 ≡ ϵ0f = ϵ0s. In deriving the mean field equations (Eqs. 14 and 15), we used mean field approximations of the type
| (16) |
which become exact only for sharply peaked distributions p(nf, ns).
Using the result from Eq. 8 for the force F(nf, ns) on each motor group, we can obtain a closed set of dynamical mean field equations for and . In a stationary state , we can divide both equations to obtain a single stationary mean field equation for the ratio
| (17) |
which takes the form
| (18) |
Here we used the set of expressions from Eq. 4 of five dimensionless control parameters, which determine the behavior of the system within mean field theory. The mean field equation, Eq. 18, shows that η, , and are likely to be the most important microscopic motor parameters because they enter the exponential factors of the equation, whereas the parameter plays only a minor role. Therefore, we focused on the parameter η and consider the dependence on and in the Supporting Material.
At ηl and ηu, the solution of the mean field equation (Eq. 18), , bifurcates into three solutions, as shown in Fig. 3 for wild-type and mutant kinesin-1. The additional bifurcation condition is . Solving and simultaneously, we can efficiently calculate ηl and ηu numerically as a function of the fraction of fast motors Nf/N. At the critical point, ηu and ηl merge. The critical point can be calculated using the additional third condition .
Discussion
We have developed a unified theoretical description for filament transport by slow and fast kinesin motors in gliding assays, which explains the results of three independent experiments (16–18). In these experiments, the velocities of the microtubules have been measured as a function of the surface fraction of fast motors for different types of kinesin motors. Whereas the microtubule velocity exhibits an abrupt transition in the assays by Larson et al. (18) using wild-type and mutant kinesin-1 motors, the velocity increases smoothly in the assays by Pan et al. (16) with kinesin-II and OSM-3 motors and by Bieling et al. (17) with Xkid and Xklp1 motors. We were able to explain this surprisingly different behavior in a quantitative manner (Fig. 1) using a theory based on single motor parameters.
Using a master equation approach, the different experimental results can be explained quantitatively by using different detachment forces for molecular motors. As shown in Fig. 1, we are able to describe all three experimental results for the filament velocities as a function of the surface fraction of fast motors by using the same master equation approach but different motor parameters as given in Table 1. No fitting parameter has been used for the assay by Larson et al. with wild-type and mutant kinesin-1 motors, while the motor detachment forces were viewed as fit parameters for the other two assays. This allows us to determine these microscopic motor parameters from the comparison of experimental data and theory.
Solving the master equation, we obtained the stationary velocity distributions of the microtubule. Based on these velocity distributions, we can identify three distinct motility regimes: 1), fast and 2), slow transport with a unimodal velocity distribution; and 3), bistable (or bikinetic) transport where the microtubules stochastically switch between fast and slow transport. All three motility regimes were confirmed by Brownian dynamics simulations.
We find that the abrupt transition in the velocity as observed in one experiment (18) is a result of relatively small detachment forces. Such forces give rise to motor unbinding cascades, which we identified as the main mechanism for bistability and velocity switching.
To characterize the influence of single motor properties in detail, we used a mean field approach and identified the relevant single motor control parameters, such as the ratio of detachment forces η, the ratio of stall to detachment force , the velocity mismatch between slow and fast motors (see Eq. 4). The fraction of available fast motors Nf/N is the most important experimental control parameter. Based on the mean field equation (see Eq. 18), we calculated motility diagrams in the (Nf/N, η) parameter plane for the assay by Larson et al. (see Fig. 4 A), and for the other two assays (see Fig. 4, B and C).These motility diagrams exhibit a bounded parameter region, where we find two stable solutions to the mean field equation, which corresponds to the bistable transport regime with a bimodal velocity distribution. Outside this bounded parameter region, we find a single mean field solution corresponding to the motility regimes of fast or slow transport.
We also obtained approximative analytical expressions for the boundaries of the bistable motility regime. The boundaries terminate in a critical point. If the single motor parameters are known as they are known for wild-type and mutant kinesin-1 motors, then the motility diagram allows us to predict the fractions Nf/N of fast motors bikinetic transport (with bistable switching between fast and slow transport) that should be observable in experiments. Vice versa, knowing the range of fractions Nf/N of fast motors, where transport is bistable from experiments, we can deduce single motor parameters such as the motors’ detachment forces.
Our theory applies not only to microtubule transport in gliding assays but to cooperative cargo transport by slow and fast motors along a filament as well. Therefore, cargos transported by slow and fast motors can exhibit transport with bistable velocity switching in the parameter regions quantified in the motility diagrams.
Acknowledgments
After submission of our manuscript, we were informed by Yunxin Zhang that he has derived equations similar to our Eqs. 7 and 8 for the cooperative transport of filaments by fast and slow motors.
Supporting Material
References
- 1.Bray D. Garland; New York: 2001. Cell Movements: From Molecules to Motility. [Google Scholar]
- 2.Lipowsky R., Beeg J., Müller M. Cooperative behavior of molecular motors: cargo transport and traffic phenomena. Physica E. 2010;42:649–661. [Google Scholar]
- 3.Holzbaur E.L., Goldman Y.E. Coordination of molecular motors: from in vitro assays to intracellular dynamics. Curr. Opin. Cell Biol. 2010;22:4–13. doi: 10.1016/j.ceb.2009.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Klumpp S., Lipowsky R. Cooperative cargo transport by several molecular motors. Proc. Natl. Acad. Sci. USA. 2005;102:17284–17289. doi: 10.1073/pnas.0507363102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Beeg J., Klumpp S., Lipowsky R. Transport of beads by several kinesin motors. Biophys. J. 2008;94:532–541. doi: 10.1529/biophysj.106.097881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Driver J.W., Jamison D.K., Diehl M.R. Productive cooperation among processive motors depends inversely on their mechanochemical efficiency. Biophys. J. 2011;101:386–395. doi: 10.1016/j.bpj.2011.05.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Leibler S., Huse D.A. Porters versus rowers: a unified stochastic model of motor proteins. J. Cell Biol. 1993;121:1357–1368. doi: 10.1083/jcb.121.6.1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jülicher F., Prost J. Cooperative molecular motors. Phys. Rev. Lett. 1995;75:2618–2621. doi: 10.1103/PhysRevLett.75.2618. [DOI] [PubMed] [Google Scholar]
- 9.Badoual M., Jülicher F., Prost J. Bidirectional cooperative motion of molecular motors. Proc. Natl. Acad. Sci. USA. 2002;99:6696–6701. doi: 10.1073/pnas.102692399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bieling P., Telley I.A., Surrey T. Processive kinesins require loose mechanical coupling for efficient collective motility. EMBO Rep. 2008;9:1121–1127. doi: 10.1038/embor.2008.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Snow J.J., Ou G., Scholey J.M. Two anterograde intraflagellar transport motors cooperate to build sensory cilia on C. elegans neurons. Nat. Cell Biol. 2004;6:1109–1113. doi: 10.1038/ncb1186. [DOI] [PubMed] [Google Scholar]
- 12.Rogers S.L., Tint I.S., Gelfand V.I. Regulated bidirectional motility of melanophore pigment granules along microtubules in vitro. Proc. Natl. Acad. Sci. USA. 1997;94:3720–3725. doi: 10.1073/pnas.94.8.3720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pilling A.D., Horiuchi D., Saxton W.M. Kinesin-1 and Dynein are the primary motors for fast transport of mitochondria in Drosophila motor axons. Mol. Biol. Cell. 2006;17:2057–2068. doi: 10.1091/mbc.E05-06-0526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Welte M.A. Bidirectional transport along microtubules. Curr. Biol. 2004;14:R525–R537. doi: 10.1016/j.cub.2004.06.045. [DOI] [PubMed] [Google Scholar]
- 15.Müller M.J., Klumpp S., Lipowsky R. Tug-of-war as a cooperative mechanism for bidirectional cargo transport by molecular motors. Proc. Natl. Acad. Sci. USA. 2008;105:4609–4614. doi: 10.1073/pnas.0706825105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pan X., Ou G., Scholey J.M. Mechanism of transport of IFT particles in C. elegans cilia by the concerted action of kinesin-II and OSM-3 motors. J. Cell Biol. 2006;174:1035–1045. doi: 10.1083/jcb.200606003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bieling P., Kronja I., Surrey T. Microtubule motility on reconstituted meiotic chromatin. Curr. Biol. 2010;20:763–769. doi: 10.1016/j.cub.2010.02.067. [DOI] [PubMed] [Google Scholar]
- 18.Larson A.G., Landahl E.C., Rice S.E. Mechanism of cooperative behavior in systems of slow and fast molecular motors. Phys. Chem. Chem. Phys. 2009;11:4890–4898. doi: 10.1039/b900968j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cuda G., Pate E., Sellers J.R. In vitro actin filament sliding velocities produced by mixtures of different types of myosin. Biophys. J. 1997;72:1767–1779. doi: 10.1016/S0006-3495(97)78823-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kraikivski P., Lipowsky R., Kierfeld J. Enhanced ordering of interacting filaments by molecular motors. Phys. Rev. Lett. 2006;96:258103. doi: 10.1103/PhysRevLett.96.258103. [DOI] [PubMed] [Google Scholar]
- 21.Kierfeld J., Frentzel K., Lipowsky R. Active dynamics of filaments in motility assays. Eur. Phys. J. Spec. Top. 2008;157:123–133. [Google Scholar]
- 22.Li X., Lipowsky R., Kierfeld J. Critical motor number for fractional steps of cytoskeletal filaments in gliding assays. PLoS ONE. 2012;7:e43219. doi: 10.1371/journal.pone.0043219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Uemura S., Kawaguchi K., Ishiwata S. Kinesin-microtubule binding depends on both nucleotide state and loading direction. Proc. Natl. Acad. Sci. USA. 2002;99:5977–5981. doi: 10.1073/pnas.092546199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 25.Svoboda K., Block S.M. Force and velocity measured for single kinesin molecules. Cell. 1994;77:773–784. doi: 10.1016/0092-8674(94)90060-4. [DOI] [PubMed] [Google Scholar]
- 26.Coppin C.M., Pierce D.W., Vale R.D. The load dependence of kinesin’s mechanical cycle. Proc. Natl. Acad. Sci. USA. 1997;94:8539–8544. doi: 10.1073/pnas.94.16.8539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kojima H., Muto E., Yanagida T. Mechanics of single kinesin molecules measured by optical trapping nanometry. Biophys. J. 1997;73:2012–2022. doi: 10.1016/S0006-3495(97)78231-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Visscher K., Schnitzer M.J., Block S.M. Single kinesin molecules studied with a molecular force clamp. Nature. 1999;400:184–189. doi: 10.1038/22146. [DOI] [PubMed] [Google Scholar]
- 29.Carter N.J., Cross R.A. Mechanics of the kinesin step. Nature. 2005;435:308–312. doi: 10.1038/nature03528. [DOI] [PubMed] [Google Scholar]
- 30.Müller, M. 2008. Bidirectional transport by molecular motors. Ph.D. thesis, University of Potsdam, Potsdam, Germany.
- 31.Zhang Y. Properties of tug-of-war model for cargo transport by molecular motors. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;79:061918. doi: 10.1103/PhysRevE.79.061918. [DOI] [PubMed] [Google Scholar]
- 32.Leduc C., Campàs O., Prost J. Cooperative extraction of membrane nanotubes by molecular motors. Proc. Natl. Acad. Sci. USA. 2004;101:17096–17101. doi: 10.1073/pnas.0406598101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Vale R.D., Funatsu T., Yanagida T. Direct observation of single kinesin molecules moving along microtubules. Nature. 1996;380:451–453. doi: 10.1038/380451a0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Schnitzer M.J., Visscher K., Block S.M. Force production by single kinesin motors. Nat. Cell Biol. 2000;2:718–723. doi: 10.1038/35036345. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


