Abstract
Implicit membrane models usually treat the membrane as a hydrophobic slab and neglect lateral pressure/curvature stress effects. As a result, they cannot distinguish, for example, PE from PC lipids. Here, the implicit membrane model IMM1 is extended to include these effects using a combination of classical thermodynamics and membrane elasticity theory. The proposed model is tested by molecular dynamics simulation of the peptides alamethicin, melittin, cyclotide kalata B1, 18A, and KKpL15. The lateral pressure term stabilizes interfacial binding due to the negative pressure at the hydrocarbon-water interface. In agreement with experiment, increase in the peptide/lipid molar ratio shifts the equilibrium from the interfacial to the transmembrane orientation. Simulations of mixed DOPC/DOPE bilayers show that increase of the DOPE mole fraction in general stabilizes interfacial orientations and destabilizes transmembrane orientations. The extent of the stabilization or destabilization varies depending on the exact position of the peptides. The computational results are in good agreement with experiments.
Introduction
Although spontaneously self-assembled phospholipid bilayers or biological membranes are tension-free, the local pressure within membranes is depth-dependent and can reach several hundred atmospheres (1,2). This inhomogeneous distribution of the pressure along the membrane normal originates from the interaction between the membrane constituents and the balancing hydrophobic effect on exposure of the lipid chain to water at the polar-apolar interface. The resulting lateral pressure profile features two positive pressure peaks in the acyl-chain and headgroup regions, and a negative pressure peak at the interface (1,2).
The microscopic lateral pressure is related to the macroscopic elasticity of the membrane through its moments along the normal. The first moment is related to the mean curvature modulus kc and spontaneous curvature co (3),
| (1) |
The value of kc can be experimentally determined by the methods of thermal fluctuation of bending (4,5), pipette-aspiration (6), or dual-solvent stress (7,8). The second moment is related to the Gaussian curvature modulus (3),
| (2) |
In Eq. 2, δ is the position of the neutral plane (the plane of inextension), which is usually found to lie close to the interface (9–11). The value can be measured by the response of cubic QII-phase dimensions to varying water content (9), or observation of Lα-QII phase coexistence (11). Equations 1 and 2 provide a link between the lateral pressure profile and the curvature stress of the membrane.
Although the lateral pressure is widely accepted as an inherent property of lipid membranes, its direct measurement is not yet possible. Indirect methods include the use of 2H-NMR (12) and fluorescent probes (13); however, the results are not reliable due to uncertainties in the interpretation of the experiments. As an alternative, lateral pressure data have been obtained by theoretical and computational methods such as mean-field theory (MFT) (14–21) and molecular dynamics (MD) simulations (22–33). The MD simulations enable the calculation of the pressure profile across the entire bilayer, by representing the lipids explicitly with atomistic (22–31) or coarse-grained models (32,33). The results, however, do not agree very well with each other, indicating that the calculation is sensitive to the simulation protocol and/or the force field (24). The best-known MFT studies are those of Cantor (18–21). The MFT approach has the advantage of not being subject to statistical errors due to inadequate sampling. However, the assumption of a uniformly packed hydrophobic core of the bilayers may be problematic (23). Other computational approaches, such as dissipative particle dynamics (34) and Monte Carlo simulations (35), have also been used to obtain the pressure profile.
The lateral pressure is affected by variations in lipid composition. Cantor (20) investigated the influence of chain unsaturation and showed that, due to the difference in the packing of the chains, double bonds close to the headgroup have much stronger effect on the lateral pressure than those at the end of the chain. In addition, broadly distributed double bonds lead to broad pressure distribution as well, without significantly changing the thickness of the bilayer. This study also showed that even small quantities of cholesterol can cause significant changes to the pressure profile, characterized by a position shift toward the membrane interior and a maximum magnitude decrease adjacent to the interface. This effect is opposite to that of adding small solutes such as short-chain alcohols or general anesthetics. As for the influence of headgroups, not yet confirmed by computations, experiments suggest that conical-shaped nonbilayer lipids may induce a pressure decrease in the headgroup region and an increase in the acyl-chain region (36).
One of the reasons that the study of membrane lateral pressure has attracted great interest is that the variation in lipid composition could influence the conformation and function of membrane proteins and peptides. For example, higher conductance states of the alamethicin ion channel were found to be more probable in dioleoylphosphatidylethanolamine (DOPE) than in dioleoylphosphatidylcholine (DOPC) (37), perhaps due to the preference of DOPE for the oligomeric state of the peptide (38). Escherichia coli leader peptidase, an integral membrane protein crucial for the protein secretion pathway, was shown to have a preference for nonbilayer lipids over phosphatidylcholine and phosphatidylglycerol upon insertion into lipid monolayers (39). The transition free energy of rhodopsin between the meta-I and meta-II states was found to exhibit a linear dependence on the spontaneous curvature of DOPC/DOPE mixtures (40). Finally, the activity of peripheral membrane proteins such as protein kinase C (41,42), phospholipase A2 (43), and CTP:phosphocholine cytidylyltransferase (43,44) was also reported to be affected by nonbilayer lipids.
In recent years, implicit solvation models have increasingly been applied to MD simulation of peptides in membranes due to their computational efficiency (45). These models have been extended to account for the effect of surface charge (46–49), transmembrane voltage (50), aqueous pores (51–53), and recently membrane dipole potential (54). Despite its importance, the lateral pressure has not yet been incorporated into implicit membrane models. As a result, it is not possible to model the effects of lipid composition, such as, for example, the change from PC to PE. Because the lateral pressure profile has a well-defined shape across lipid bilayers, in this study we represent the pressure as an external field, and incorporate it into the IMM1 implicit membrane model (45). The proposed model is used to study the influence of peptide/lipid molar ratio and lipid composition on the membrane binding energy and configuration of the peptides alamethicin, melittin, cyclotide kalata B1 (KB1), 18A, and KKpL15.
Theory
Upon peptide binding, the total area AB of a bilayer is given by (1)
| (3) |
where aL is the area per lipid; aP is the peptide cross-sectional area; and nL and nP are the moles of lipid and peptide, respectively. From Eq. 3, we get
| (4) |
Based on Eq. 4, if the bilayer expands by the full peptide cross-sectional area , there is no compression of the lipids. On the other hand, if the bilayer does not expand at all , the lipids are compressed by the full peptide cross-sectional area (1). Because the true expansion of a bilayer is hard to estimate and depends on the experimental situation, here we write as
| (5) |
where λ is defined as the expansion coefficient, which can range from 0 to 1. In this study, it is treated as an adjustable parameter, tentatively set to 0.5. From Eqs. 4 and 5, we get
| (6) |
Because aP varies along the membrane normal, Eq. 6 has to be rewritten as
| (7) |
To insert a peptide into the bilayer at infinite dilution (infinitesimal peptide/lipid molar ratio nP/nL), one needs to do work against the pressure profile (1,18),
| (8) |
| (9) |
When λ = 0 (the bilayer does not expand at all), Eq. 9 can be simplified as
which is consistent with Eq. 2 in Cantor (18).
To calculate W in Eq. 9 in our model, a bilayer is evenly divided into slabs from the center (z = 0 Å) to a position in water (z = 30 Å) where the pressure is taken to be 0. The thickness of the slabs is set to h = 0.1 Å, a value much smaller than the size of any atom. Therefore, within each slab, both aP and p can be treated as approximately independent of z, and Eq. 9 is then written as
| (10) |
where k runs over all slabs.
At finite nP/nL, one has to take into account that the lateral pressure profile itself is affected by the presence of peptides. Thus, the lateral pressure within each slab is a function of the peptide cross-sectional area (1), and Eq. 10 has to be rewritten as
| (11) |
The explicit form of pk(aP,k) can be obtained based on thermodynamics. At constant temperature the relation between the lateral pressure pk and total volume of lipids VL,k at slab k upon peptide binding is given by
| (12) |
where KA,k is the compressibility modulus of the slab. Integration of Eq. 12 gives
| (13) |
where pok and VoL,k are the lateral pressure and total volume of lipids in the pure bilayer, and ΔVL,k = VL,k − VoL,k. If the stress caused by peptide binding is small, Eq. 13 can be approximated as
| (14) |
Because the stress is in-plane, we have
| (15) |
Noting that
and
Eq. 15 can be written as
| (16) |
In Eq. 16, ap,k is the peptide cross-sectional area, and aoL is the area per lipid in the pure bilayer. From Eq. 14 and Eq. 16, we get
| (17) |
Based on Eq. 17, Eq. 11 can be written as
| (18) |
The second term on the right-hand side of Eq. 18 is caused by the lateral compression of lipids upon peptide binding at finite nP/nL. The same term, with λ = 0, was derived in a different way by Huang (55). In summary, Eq. 18 is the discrete form of the work against the lateral pressure for inserting a peptide into a bilayer. It extends the equation given by Cantor (18) in two ways:
-
1.
It takes into consideration the pressure change caused by the compression of lipids upon peptide binding at finite nP/nL; and
-
2.
It takes into consideration the bilayer area expansion by introducing an expansion coefficient.
Because Eq. 14 is inaccurate at high nP/nL, in our simulations W was calculated based on Eq. 13, which gives
| (19) |
where β = ((1 − λ)/aoL)(nP/nL).
Methods
Implicit membrane model IMM1
IMM1 (45) is an extension of the EEF1 energy function for proteins in solution (56). In EEF1 and IMM1, the effective energy (potential of mean force) is the sum of the extended atom CHARMM energy function and a term describing the solvation free energy,
| (20) |
where ΔGislv is the solvation free energy of atom i, rij is the distance between i and j, fi is the solvation free energy density of i (a Gaussian function of rij), Vj is the volume of atom j, and ΔGiref is the solvation free energy of a fully solvent-exposed atom. In addition, the dielectric constant is distance-dependent and the ionic side chains are neutralized to account for the screening effect of the surrounding solvent. The membrane bilayer is represented by a hydrophobic slab centered at the plane z = 0 Å. The thickness of the slab depends on lipid type and typically ranges between 20 Å and 30 Å. In IMM1, the solvation parameters are linear combinations between the values pertaining to water and to cyclohexane, with a continuous transition between water and membrane environments. In addition, the dielectric screening is attenuated in the membrane. The surface potential can be treated using the Gouy-Chapman theory (48) and the dipole potential can be treated by adding a sigmoidal potential field along the membrane normal on both bilayer leaflets (54).
The peptide cross-sectional area
To obtain ap,k in Eq. 18, we make the assumption that the cross-sectional area of a peptide can be calculated by summing over individual atoms,
| (21) |
where ai is the cross-sectional area of atom i, and i runs over all atoms occupying slab k. Overlaps between bonded atoms and interstitial spaces are taken into account in an approximate fashion. Treating each atom as an ideal sphere, the cross-sectional area is a function of the distance between the center of the atom (zi) and the position of the slab plane (z′k), as
| (22) |
In Eq. 22, Ri is the radius of the atom, which is calculated by using the atomic volume Vi from the IMM1 solvation parameters (45) (Ri = (3Vi/4π)1/3) and is then empirically increased by 10% to account for the empty space between atoms.
Inserting Eq. 22 into Eq. 21 and doing the calculation for all slabs, a cross-sectional area profile along the membrane normal can be obtained. As a test, the calculation was performed on transmembrane and interfacial (Gly)22 helix and the result is given in Fig. 1. The highest areas of 300 Å2 and 45 Å2 for the interfacial and transmembrane orientations are very close to the 270 Å2 and 53 Å2 calculated with an ideal helix model (2.3 Å for helix radius, 1.8 Å for the average radius of backbone atoms, and 1.5 Å rise per residue along the helix axis).
Figure 1.
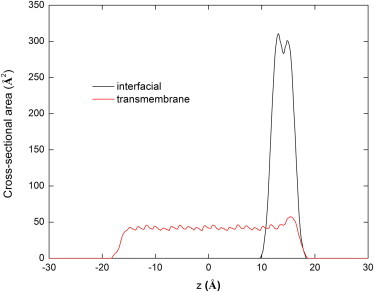
The cross-sectional area of transmembrane and interfacial orientations of a (Gly)22α-helix calculated as a sum of atomic contributions.
Fitting the lateral pressure profile of the DOPC bilayer
Because the lateral pressure profile of pure DOPC bilayer has been computed by several explicit MD simulations, a simple way to get pok in Eq. 18 would be to use these data directly. For more flexibility, however, and to impose consistency with experimental measurements, we fit the existing pressure distribution with an analytical function. The parameters controlling the position and width of the peaks and the magnitude at the interface are estimated by using the pressure profile from explicit MD simulations. The parameters for controlling the magnitude in the acyl-chain and headgroup regions are then calculated based on Eqs. 1 and 2.
Because the lateral pressure originates from the repulsion in the acyl-chain and headgroup regions and the cohesive tension at the interface (36), we decompose the pressure within a monolayer leaflet into three Gaussian components,
| (23) |
where a, b, and c are the parameters controlling the magnitude, position, and width of the pressure, respectively, and vary in each region. Based on Eq. 23, the first and second moments are given by
| (24) |
| (25) |
where and . The moments of the whole leaflet are linear combinations of the three components,
| (26) |
| (27) |
where subscripts A, I, and H denote the acyl chain, interface, and headgroup, respectively. Substituting from Eqs. 26 and 27 in Eqs. 1 and 2, we get
| (28) |
or
| (29) |
In Eq. 29, the pressure profile from Ollila’s simulation (27) was used to estimate m1A, m2A, m1I, m2I, m1H, m2H, and aI. The values kc, , and co were taken from experiments (57), in which kc = 4.0 × 10−20 J and = −0.8 kc. Finally, aA and aH can be calculated by solving Eq. 29, and then the whole pressure profile of the monolayer leaflet is given by
| (30) |
For a symmetric bilayer, the two leaflets will have the same lateral pressure profile. Extension to asymmetric bilayers is straightforward. In some previous atomistic MD simulations, a local maximum of pressure was obtained at the bilayer center, which is thought to be caused by the interdigitation of lipids from the opposing monolayer leaflets (24). This local maximum, however, was not reproduced in analytical theories and coarse-grained MD simulations. Even in those simulations that give the pressure maximum, its magnitude is not very large, so we do not expect it to have significant influence in our simulations. Therefore, this local maximum at the bilayer center is not included in our model.
The lateral pressure profile of mixed DOPC/DOPE bilayers
For mixed DOPC/DOPE monolayers, the spontaneous curvature c0 is a function of the mole fraction of DOPE (χ) (8),
| (31) |
where coDOPC and coDOPE are the spontaneous curvatures of DOPC and DOPE monolayers, whose values are −0.0066 Å−1 and 0.0431 Å−1, respectively (2). Inserting Eq. 31 into Eq. 29, the corresponding aA and aH can be calculated. The reasons that, in Eq. 29, the same parameters except for aA, aH, and co are used for DOPC and DOPE, are the following:
-
1.
Both lipids have the same type of acyl chains, which makes it reasonable to assume that the position and width of the pressure peaks do not change too much;
-
2.
The pressure at the interface is characterized by the contact of hydrocarbon with bulk water and is much the same for all lipids (2); and
-
3.
Experiments give similar kc values for DOPC and DOPE monolayers (57).
In Fig. 2, the lateral pressure profiles at χ = 0, 0.2, 0.4, 0.6, and 0.8 are plotted. It can be seen that the nonbilayer DOPE increases the pressure in the acyl-chain region and decreases it in the headgroup region, as suggested by both fluorescence (13) and 2H-NMR experiments (58–60).
Figure 2.
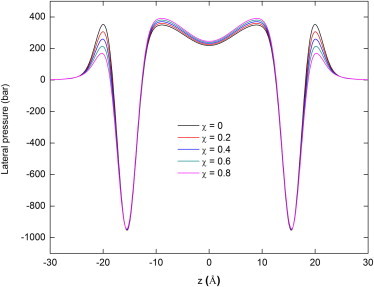
The lateral pressure profile of a mixed DOPC/DOPE bilayer at different mole fractions of DOPE.
The compressibility modulus and total energy of peptide binding
In this model, the compressibility modulus is treated as a constant along the membrane normal, and KA,k in Eq. 18 is assumed to be
| (32) |
where KA is the compressibility modulus of the bilayer, set to 240 mN/m for DOPC (10), and d is the bilayer thickness including both hydrocarbon (25.4 Å) and headgroup regions (20 Å). Because experiments give similar AoL and bilayer thickness for DOPC and DOPE (Table 1), for convenience the same parameters are used for DOPE. For KA, although experiments show that the PE headgroup stiffens lipid bilayers and increases the value of KA (61), we found that the influence of KA is very small compared to that of po, therefore the value of KA for DOPC is also used for DOPE. It is also worth mentioning that KA is affected by the pressure and thereby affected by nP/nL. However, within the range of nP/nL in our simulation the change in pressure is very small so that KA can be approximately treated as a constant. From Eqs. 18 and 32, we get
| (33) |
In Eq. 33, the first term is represented as ELAT because it is related to the lateral pressure of the pure bilayer, and the second term is represented as ECOM because it is related to the compressibility modulus. The total energy of peptide binding to the bilayer is then given by
| (34) |
where EIMM1 is the standard IMM1 energy.
Table 1.
Experimental parameters of DOPC and DOPE bilayers
| KA (mN/m)a | kc (10−20J)b | (J)b | co (Å−1)b | dl (Å)c | aoL (Å2)d | |
|---|---|---|---|---|---|---|
| DOPC | 240 | 4.0 | −0.8 | −0.0066 | 36 | 70 |
| DOPE | 240 | 4.5 | −0.0431 | 37 | 65 |
KA from Table 1 of Rawicz et al. (10), which is all ∼240 mN/m for more than 10 lipids. Therefore, the value of 240 mN/m is used for both DOPC and DOPE in this study.
See Marsh (2). These values are for monolayers.
dl from Table 1 of Rand and Parsegian (83), which is the distance between the center of the phosphate groups.
See Rand and Parsegian (83).
Molecular dynamics simulations
MD simulations were carried out at 300 K using the CHARMM program (62). Membrane and water were implicitly represented with IMM1. Five peptides were simulated: alamethicin, melittin, KB1, 18A, and KKpL15, whose sequences are given in Table 2. The simulations were done in a zwitterionic (neutral) bilayer, whose hydrocarbon thickness is set to 25.4 Å corresponding to the DOPC bilayer (63). The initial structures of the peptides were generated by CHARMM based on their sequences except KB1, for which the crystal structure was used. To study the influence of peptide/lipid molar ratio on peptide binding, simulations were performed on alamethicin in pure DOPC bilayer from nP/nL = 0.01 to 0.10 in 0.01 increments. To study the influence of nonbilayer lipids, simulations were performed on all peptides in mixed DOPC/DOPE bilayers at χ = 0, 0.2, 0.4, 0.6, and 0.8. In the second study, nP/nL = 0.01 was used for all peptides.
Table 2.
Sequences of the peptides studied
| Alamethicin | Ac-UPUAUAQUVUGLUPVUUEQF-OHa |
| Melittin | Ac-GIGAVLKVLTTGLPALISWIKRKRQQ-NH2 |
| KB1 | Ac-CGETCVGTCNTPGCTCSWPVCTRNGLPV-NH2 |
| 18A | Ac-DWLKAFYDKVAEKLKEAF-NH2 |
| KKpL15 | Ac-KKLLLLLLLDWLLLLLLLLKK-NH2 |
U stands for α-aminoisobutyric acid.
Each simulation run lasted 10 ns, and the average structures and energies of the last 5 ns were taken for analysis. The binding energy of the peptides was estimated as the average effective energy difference in membrane and water environments for the conformational ensemble generated by the membrane simulation,
| (35) |
where EiMBR and EiWAT are the effective energy in membrane and in water, respectively, and i runs through N = 2500 conformations saved at equal intervals within the last 5 ns of the simulation.
Results
Binding of alamethicin to a DOPC bilayer at various peptide/lipid molar ratios
Alamethicin is a 20-amino-acid helical peptide forming voltage-gated ion channels in lipid bilayers (64). Previous MD simulations with IMM1 showed that alamethicin can bind lipid bilayers in two orientations, one interfacial and one more deeply inserted (nearly transmembrane). The binding energy of the former is 1–2 kcal/mol lower than that of the latter (50,54). These simulations also showed that the N-terminus of the interfacial orientation is slightly tilted and buried under the interface, while the tilt angle between the transmembrane orientation and bilayer normal is ∼30°.
In this study, alamethicin was initially placed both parallel to the bilayer at the interface and inserted perpendicular to the bilayer. The peptide/lipid molar ratio nP/nL was initially set to 0.01. Both interfacial and transmembrane binding were observed in the simulation (Fig. 3); however, it can be seen from the figure that the N-terminus of our interfacial orientation is no longer tilted. Also, it was found that with the lateral pressure added to IMM1, the interfacial orientation is significantly stabilized, with binding energy now 8 kcal/mol lower than that of the transmembrane orientation (Table 3).
Figure 3.
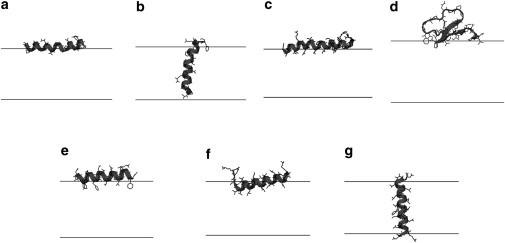
The average configuration of (a) interfacial alamethicin, (b) transmembrane alamethicin, (c) melittin, (d) KB1, (e) 18A, (f) interfacial KKpL15, and (g) transmembrane KKpL15 at nP/nL = 0.01 and χ = 0. The average helix contents calculated based on the structures from our simulations are: 85% for alamethicin, 80% for melittin, 84% for 18A, and 75% for KKpL15, which are a little higher than the corresponding experimental values of 71–74% (84), 76% (84), 70–76% (76), and 65–75% (77). The structures do not change significantly with nP/nL or χ. The lines denote the hydrophobic boundary of the bilayers.
Table 3.
Binding energy (kcal/mol) of alamethicin at various peptide/lipid molar ratios
| nP/nL | ΔEIMM1 | ΔELAT | ΔECOM | EBINDING |
|---|---|---|---|---|
| 0.01 | −7.6/−7.0 | 1.5/−7.1 | 0.0/0.1 | −6.1/−14.0 |
| 0.02 | −7.5/−7.0 | 1.5/−7.2 | 0.1/0.3 | −5.9/−13.9 |
| 0.03 | −7.5/−7.1 | 1.5/−7.0 | 0.1/0.4 | −5.9/−13.8 |
| 0.04 | −7.6/−7.0 | 1.5/−7.1 | 0.2/0.5 | −5.9/−13.6 |
| 0.05 | −7.5/−7.1 | 1.5/−7.1 | 0.2/0.7 | −5.8/−13.5 |
| 0.06 | −7.6/−7.1 | 1.5/−7.0 | 0.3/0.8 | −5.9/−13.3 |
| 0.07 | −7.6/−7.2 | 1.5/−7.1 | 0.3/1.0 | −5.8/−13.2 |
| 0.08 | −7.6/−7.2 | 1.5/−7.0 | 0.3/1.1 | −5.8/−13.1 |
| 0.09 | −7.5/−7.2 | 1.5/−7.0 | 0.4/1.2 | −5.7/−13.0 |
| 0.10 | −7.6/−7.2 | 1.5/−7.0 | 0.4/1.4 | −5.6/−12.8 |
The first number is for the transmembrane orientation and the second for the interfacial orientation. EBINDING = ΔEIMM1 + ΔELAT + ΔECOM, where Δ denotes the transfer from water to membrane. The average standard deviation is ∼0.1 kcal/mol.
To investigate the influence of peptide/lipid molar ratio on the binding, we increased nP/nL from 0.01 to 0.10 at 0.01 increments and repeated the simulation at each nP/nL. Because the transmembrane orientation has significantly higher relative binding energy, the peptide easily moves to the interfacial orientation in most of the simulations, even though it was initially placed perpendicular to the bilayer. Therefore, to obtain energy data for the transmembrane configuration, harmonic constraints were applied to the Cα atoms using the nP/nL = 0.01 structure as a reference. This way the binding energy of both orientations as a function of nP/nL was calculated and reported in Table 3. It can be seen from the table that the binding energy increases with nP/nL for both interfacial and transmembrane orientations. However, the increase is much larger for the former. Therefore, we expect equilibrium to shift gradually from the interfacial to transmembrane orientation as nP/nL increases. Experimentally, a transition from interfacial to transmembrane has been observed for many antimicrobial peptides, including alamethicin (65–67). This transition was attributed to the thinning of the bilayer caused by the interfacial binding of the peptides (55). Although the shift we observed is in agreement with experiment, experiment gives a threshold concentration of 0.02 for alamethicin binding on DPhPC bilayer (68), while we are not able to observe the transition on DOPC bilayer from nP/nL = 0.01 to 0.10. This may be because IMM1 has been parameterized without the inclusion of a lateral pressure term (see Discussion).
Binding of peptides to mixed DOPC/DOPE bilayers
Alamethicin
The effect of DOPE mole fraction on the binding energy of alamethicin was investigated separately for interfacial and transmembrane configurations. As before, harmonic constraints on the Cα atoms were employed to keep alamethicin transmembrane. The binding energy as a function of χ is plotted in Fig. 4 A (the contribution of all components is given in Table 4). From the figure it can be seen that for the interfacial orientation, the binding energy barely changes. For the transmembrane orientation, however, the binding energy increases with χ. This is consistent with experiment, which reported that in mixed DOPC/DOPE bilayers the binding free energy of transmembrane alamethicin increases linearly with the mole fraction of DOPE (38). From χ = 0 to 0.6, our binding energy for the transmembrane orientation increases by 0.5 kcal/mol, which is slightly smaller than the experimental value of 0.8 kcal/mol.
Figure 4.
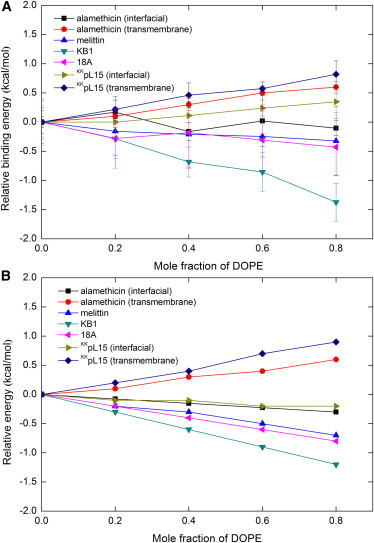
(A) The relative binding energy of the peptides on mixed DOPC/DOPE bilayers at various mole fractions of DOPE. (B) The relative energy calculated with the average binding structures obtained at nP/nL = 0.01 and χ = 0.
Table 4.
Binding energy (kcal/mol) at various mole fractions of DOPE
| χ = 0 | χ = 0.2 | χ = 0.4 | χ = 0.6 | χ = 0.8 | ||
|---|---|---|---|---|---|---|
| Alamethicin (interfacial) | ΔEIMM1 | −6.9 | −6.7 | −7.0 | −6.5 | −6.7 |
| ΔELAT | −7.1 | −7.3 | −7.3 | −7.6 | −7.6 | |
| ΔECOM | 0.1 | 0.1 | 0.1 | 0.2 | 0.1 | |
| EBINDING | −14.0 | −13.8 | −14.1 | −14.0 | −14.1 | |
| Alamethicin (transmembrane) | ΔEIMM1 | −7.6 | −7.6 | −7.6 | −7.6 | −7.6 |
| ΔELAT | 1.5 | 1.6 | 1.8 | 1.9 | 2.1 | |
| ΔECOM | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| EBINDING | −6.1 | −6.0 | −5.8 | −5.6 | −5.5 | |
| Melittin | ΔEIMM1 | −13.2 | −13.1 | −13.0 | −12.8 | −12.7 |
| ΔELAT | −8.1 | −8.4 | −8.6 | −8.8 | −9.0 | |
| ΔECOM | 0.1 | 0.2 | 0.2 | 0.2 | 0.2 | |
| EBINDING | −21.2 | −21.3 | −21.4 | −21.4 | −21.5 | |
| KB1 | ΔEIMM1 | −0.4 | -0.2 | −0.4 | −0.4 | −0.4 |
| ΔELAT | −5.4 | −5.9 | −6.1 | −6.2 | −6.8 | |
| ΔECOM | 0.1 | 0.2 | 0.1 | 0.1 | 0.1 | |
| EBINDING | −5.6 | −5.9 | −6.3 | −6.5 | −7.0 | |
| 18A | ΔEIMM1 | −5.0 | −5.1 | −4.9 | −4.8 | −4.8 |
| ΔELAT | −6.8 | −7.0 | −7.1 | −7.3 | −7.5 | |
| ΔECOM | 0.1 | 0.1 | 0.2 | 0.1 | 0.2 | |
| EBINDING | −11.7 | −11.9 | −11.8 | −12.0 | −12.1 | |
| KKpL15 (interfacial) | ΔEIMM1 | −26.1 | −26.0 | −25.7 | −25.3 | −24.9 |
| ΔELAT | −3.7 | −3.8 | −4.0 | −4.3 | −4.5 | |
| ΔECOM | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | |
| EBINDING | −29.6 | −29.6 | −29.5 | −29.4 | −29.3 | |
| KKpL15 (transmembrane) | ΔEIMM1 | −28.3 | −28.3 | −28.3 | −28.4 | −28.3 |
| ΔELAT | 2.9 | 3.0 | 3.2 | 3.5 | 3.7 | |
| ΔECOM | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| EBINDING | −25.4 | −25.2 | −24.9 | −24.8 | −24.6 |
Because the binding energy is an average from MD simulations, it is noisy and includes contributions not only from changes in lipid composition, but also changes in peptide configuration. To see how much the lipid composition alone contributes to the binding energy, energy calculations were performed on the average structure of the peptide from χ = 0 to 0.8. The result is given in Fig. 4 B and is consistent with that obtained using average energies.
Melittin
Melittin, a 26-amino-acid helical peptide, is the main proteinaceous constituent of honeybee venom. The orientation as well as insertion depth of melittin upon binding to membranes has been the subject of extensive debate. Experiments under various conditions suggest either a transmembrane or an interfacial orientation (69,70). Nevertheless, it is likely that interfacial binding is more reasonable for neutral bilayers with the hydrophobic thickness of DOPC (45). Therefore, at the beginning of our simulation, melittin was placed parallel to the bilayer at the interface.
During the simulations, melittin stayed primarily at the interface, with the C-terminus becoming slightly unstructured and moving toward the water, as shown in Fig. 3. Fig. 4 shows that the binding energy of melittin decreases by a very small amount (at ∼0.3 kcal/mol) from χ = 0 to 0.8. Experiment reported that melittin binds with similar affinity to liquid crystalline 1,2-Dielaidoyl-sn-glycero-3-phosphocholine (DEPC) and 1,2-Dielaidoyl-sn-glycero-3-phosphoethanolamine (DEPE) vesicles, albeit at different temperatures, while in the gel phase binding to DEPE is much weaker than to DEPC (71).
Cyclotide kalata B1
The cyclotides are a large family of peptides from plants, among which the prototypic cyclotide kalata B1 (KB1) is the most well studied and has been shown to bind (72) and disrupt phospholipid bilayers by a pore-forming mechanism (73). The cyclic knotted structure of KB1 is stabilized by three disulfide bridges, and binds to membranes via two hydrophobic loops (74). The starting structure of KB1 was taken from the Protein Data Bank (PDB:1NB1; www.wwpdb.org) and was placed with the hydrophobic loops at the interface.
During the simulation, the peptide stayed as the cyclic structure at the interface, with the two hydrophobic loops anchoring superficially into the hydrophobic core of the bilayer (Fig. 3). The C-terminus of the peptide is more flexible than the N-terminus. It can be seen from Fig. 4 that the binding energy of KB1 decreases by the largest amount among all peptides, and from χ = 0.1 to 0.2 the energy decreases by ∼0.2 kcal/mol. In a surface plasmon resonance experiment it was reported that the peptide/lipid molar ratio increases from 0.08 to 0.15 as the mole percentage of DOPE in DOPC vesicles increases from 10% to 20% (75). From this one can deduce a binding free energy decrease of ∼0.35 kcal/mol. The authors attribute the affinity for PE to specific interactions with the headgroup, but we find that a large portion of the affinity increase can be explained by lateral pressure/curvature stress effects.
18A
18A is a designed amphipathic peptide of 18 residues. CD experiments indicated that the peptide adopts mainly helical structure in membranes, and 2H-NMR showed that the insertion of the peptide occurs at the membrane interface (76). Based on this, the peptide was built as an ideal α-helix and placed initially parallel to the bilayer at the interface.
During the simulations the helical structure of 18A was perfectly maintained and the orientation remained interfacial (Fig. 3). The binding energy of 18A decreases by 0.3 kcal/mol from χ = 0 to 0.5 (Fig. 4). In experiment, it is reported that the binding free energy of 18A decreases by ∼0.5 kcal/mol as the mole fraction of DOPE in POPC/DOPE vesicles increases from 0 to 0.5 (76).
KKpL15
KKpL15 is a designed hydrophobic peptide of 21 residues. According to experiment, the peptide is helical and binds membranes at either transmembrane or interfacial orientation (77). Therefore, at the beginning of our simulation the peptide was placed both parallel to the bilayer at the interface and inserted perpendicular to the bilayer.
During the simulations, the helical structure of the peptide was maintained, except that the N-terminus of the interfacial orientation occasionally unfolded. From Fig. 3 it can be seen that the interfacial orientation lies right at the interface, while the transmembrane orientation spans completely across the hydrophobic core. In Fig. 4 A the binding energy of interfacial KKpL15 increases by 0.3 kcal/mol from χ = 0 to 0.8, while in Fig. 4 B the effective energy decreases by 0.2 kcal/mol. As explained above, Fig. 4 B gives the intrinsic contribution of the lipid composition while Fig. 4 A includes the effect of changes in peptide configuration or conformation. Note that in Table 4 ELAT of interfacial KKpL15 decreases with χ, while EIMM1 increases. In Fig. 4 A the binding energy of transmembrane KKpL15 increases by 0.8 kcal/mol from χ = 0 to 0.8. This indicates that the transmembrane orientation becomes less stable than the interfacial orientation as DOPE is added. In experiment, the transition between the two orientations of KKpL15 was studied with tryptophan fluorescence. A red-shift of the emission was observed as POPE was added to the POPC vesicles, indicating that nonbilayer lipids stabilize the binding of the interfacial orientation (77). This is in agreement with our calculations.
Discussion
In this study, we proposed a simple approach for implicit modeling of the lateral pressure across lipid bilayers. The pressure profile was treated as symmetric with respect to the bilayer center and was decomposed within each leaflet into components in the acyl-chain and headgroup regions and at the interface. Each component was represented by a Gaussian function. While the parameters for controlling the position and width of the pressure peaks and the magnitude at the interface were estimated by using the data from the previous MD simulations with explicit lipid models, those for the magnitude in the headgroup and acyl-chain regions were calculated based on the relation between the lateral pressure and monolayer bending elasticity. This treatment gives better compatibility with the implicit membrane model IMM1 and enables us to easily calculate the pressure profile at various lipid compositions. Based on the model, the interaction energy between the lateral pressure and peptide cross-sectional area consists of two terms: ELAT that arises from the lateral pressure of the pure lipid bilayer, and ECOM that arises from the lateral compression of lipids upon peptide binding and is proportional to the peptide/lipid molar ratio.
From Tables 3 and 4 it can be seen that in general the incorporation of the lateral pressure into IMM1 gives extra stabilization to the interfacial binding, as a result of the negative pressure at the bilayer interface. For alamethicin, this extra stabilization is ∼8 kcal/mol. With this extra term, IMM1 predicts the interfacial orientation to be substantially more stable than the transmembrane one. This seems inconsistent with experiment, in which alamethicin was found to bind lipid bilayers in transmembrane orientation even at very low concentrations (78). This may be because IMM1 was parameterized without the lateral pressure term. It contains an adjustable parameter (parameter a in Eq. 10 of Lazaridis (45)), which controls the intensity of electrostatic interaction inside the membrane. A decrease in this parameter from 0.85 to 0.80 would lower the binding energy of transmembrane alamethicin by 7 kcal/mol, while causing little change to interfacial alamethicin. Therefore, it is expected that by reparameterizing the electrostatic interaction, a relative binding energy between the two orientations that is more consistent with experiment could be obtained.
Another important impact of the proposed term is in the interfacial configuration of alamethicin. While standard IMM1 predicts significant tilt in the interfacial configuration, the lateral pressure term induces a configuration that is parallel to the membrane. A simple test of the validity of the lateral pressure term would be to perform explicit bilayer simulations of interfacial alamethicin starting from both tilted and untilted simulations. If this effect has been captured correctly, both simulations should converge to a parallel orientation.
As DOPE is added, the lateral pressure within the bilayer will change due to the different spontaneous curvature of DOPC and DOPE. From Fig. 4 it can be seen that, in general, DOPE stabilizes interfacial binding and destabilizes transmembrane binding. According to Eqs. 29 and 31, this change in binding energy is caused by the change in ELAT, and the difference in ELAT between two different mole fractions of DOPE (χ1 and χ2) is given by
| (36) |
Because transmembrane alamethicin and KKpL15 bind in the acyl-chain region of the bilayer (Fig. 3) where the pressure increases with χ, according to Eq. 36 ELAT increases as well. KB1 binds in the headgroup region where the pressure decreases, so ELAT decreases. The average position of melittin and 18A in the simulations is 15.9 Å and 16.1 Å from the bilayer center, which is between the interface and headgroup region, so ELAT also decreases, but by a smaller value. The average position of interfacial alamethicin and KKpL15 is 15.0 Å and 14.9 Å, so these two peptides have the least ELAT decrease with χ. The difference for interfacial KKpL15 in Fig. 4, A and B, as mentioned above, is caused by the change in EIMM1 as a result of the conformation change with χ.
In this model, possible bilayer expansion upon peptide binding was taken into account through an empirical expansion coefficient λ. Because the true expansion of a bilayer is hard to estimate and depends on the experimental situation, λ was arbitrarily set to 0.5. The value of λ influences the binding energy of peptides. For example, according to Eq. 33, an increase in λ will decrease the magnitudes of both ELAT and ECOM, which means that changing nP/nL or χ will cause smaller influence upon the orientation and binding energy of peptides in our simulations. On the other hand, if we decrease λ, the difference of peptide orientation and binding energy at various nP/nL or in χ in our simulation should become larger. The results obtained with the value 0.5 adopted here happen to be quite close to experiment. For example, experiment gives a binding free energy increase of 0.8 kcal/mol for transmembrane alamethicin from χ = 0 to 0.6, while the value predicted by our model is 0.5 kcal/mol. By further adjusting λ, even better agreement with experiment could be achieved.
The model is based on significant assumptions. For example, the bilayer is divided into slabs and each slab is treated as independent of the others. This assumption would be appropriate if the lipid chains were completely flexible and able to align exactly with the surface of the peptide. However, the bending rigidity of lipids varies with chain unsaturation (10) and content of cholesterol (79), and it is reasonable to expect that this variation can cause errors in the calculation of ELAT and ECOM. Also neglected are the thermodynamic consequences of the lipid rearrangements when a peptide is inserted. These effects have been calculated using mean field theories (80), but they are difficult to incorporate in analytical implicit membrane models.
Another factor that might cause errors is the absence of the bilayer surface deformation in our model. For example, when there is a hydrophobic mismatch between a transmembrane peptide and the bilayer, the surface of the bilayer around the peptide may grow or collapse until the local thickness of the bilayer is equal to the length of the peptide (81). While this deformation avoids the exposure of hydrophobic surfaces to water and grants the binding extra stabilization, it causes frustration to the bilayer curvature (82). To balance these two opposing forces, the peptide may adjust its binding state without causing any changes to the lateral deformation. An example for this is the association of rhodopsin in lipid membranes. While it is not likely to influence the cross-sectional area of the protein, it was proposed that the association could significantly relieve the membrane curvature strain of the monomeric binding state (82).
These concerns notwithstanding, our model provides an easy and fast way to take into account the effect of membrane lateral pressure in MD simulations and could be applied to larger systems and more complex problems. A potentially interesting application of the model would be to investigate the influence of lipid composition on the conformation and thus the function of membrane proteins. It would also be interesting to determine whether the model can be further improved by incorporating lipid bending rigidity, which would enable the investigation of the influence of lipid unsaturation and cholesterol on peptide/protein binding.
Acknowledgments
This work was supported by the National Science Foundation (grant No. MCB-1244207), and in part by the National Institutes of Health (grant No. SC1 GM087190). Infrastructure support was provided by Research Centers in Minority Institutions (grants No. 2G12RR03060-26A1/8G12MD007603-27) at the National Institutes of Health.
References
- 1.Marsh D. Lateral pressure in membranes. Biochim. Biophys. Acta. 1996;1286:183–223. doi: 10.1016/s0304-4157(96)00009-3. [DOI] [PubMed] [Google Scholar]
- 2.Marsh D. Lateral pressure profile, spontaneous curvature frustration, and the incorporation and conformation of proteins in membranes. Biophys. J. 2007;93:3884–3899. doi: 10.1529/biophysj.107.107938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Helfrich W. North-Holland; Amsterdam: 1981. Amphiphilic Mesophases Made of Defects. [Google Scholar]
- 4.Engelhardt H., Duwe H.P., Sackmann E. Bilayer bending elasticity measured by Fourier-analysis of thermally excited surface undulations of flaccid vesicles. J. Phys. Lett. (Paris). 1985;46:L395–L400. [Google Scholar]
- 5.Bivas I., Hanusse P., Aguerrechariol O. An application of the optical microscopy to the determination of the curvature elastic-modulus of biological and model membranes. J. Phys. (Paris) 1987;48:855–867. [Google Scholar]
- 6.Evans E., Rawicz W. Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 1990;64:2094–2097. doi: 10.1103/PhysRevLett.64.2094. [DOI] [PubMed] [Google Scholar]
- 7.Rand R.P., Fuller N.L., Parsegian V.A. Membrane curvature, lipid segregation, and structural transitions for phospholipids under dual-solvent stress. Biochemistry. 1990;29:76–87. doi: 10.1021/bi00453a010. [DOI] [PubMed] [Google Scholar]
- 8.Leikin S., Kozlov M.M., Rand R.P. Measured effects of diacylglycerol on structural and elastic properties of phospholipid membranes. Biophys. J. 1996;71:2623–2632. doi: 10.1016/S0006-3495(96)79454-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Templer R.H., Khoo B.J., Seddon J.M. Gaussian curvature modulus of an amphiphilic monolayer. Langmuir. 1998;14:7427–7434. [Google Scholar]
- 10.Rawicz W., Olbrich K.C., Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000;79:328–339. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Siegel D.P., Kozlov M.M. The Gaussian curvature elastic modulus of N-monomethylated dioleoylphosphatidylethanolamine: relevance to membrane fusion and lipid phase behavior. Biophys. J. 2004;87:366–374. doi: 10.1529/biophysj.104.040782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gawrisch K., Holte L.L. NMR investigations of non-lamellar phase promoters in the lamellar phase state. Chem. Phys. Lipids. 1996;81:105–116. [Google Scholar]
- 13.Templer R.H., Castle S.J., Klug D.R. Sensing isothermal changes in the lateral pressure in model membranes using di-pyrenyl phosphatidylcholine. Faraday Discuss. 1998;111:41–53. doi: 10.1039/a806472e. [DOI] [PubMed] [Google Scholar]
- 14.Szleifer I., Kramer D., Gelbart W.M. Curvature elasticity of pure and mixed surfactant films. Phys. Rev. Lett. 1988;60:1966–1969. doi: 10.1103/PhysRevLett.60.1966. [DOI] [PubMed] [Google Scholar]
- 15.Szleifer I., Ben-Shaul A., Gelbart W.M. Chain packing statistics and thermodynamics of amphiphile monolayers. J. Phys. Chem. 1990;94:5081–5089. [Google Scholar]
- 16.Szleifer I., Kramer D., Safran S.A. Molecular theory of curvature elasticity in surfactant films. J. Chem. Phys. 1990;92:6800–6817. [Google Scholar]
- 17.Xiang T.X., Anderson B.D. Molecular distributions in interphases: statistical mechanical theory combined with molecular dynamics simulation of a model lipid bilayer. Biophys. J. 1994;66:561–572. doi: 10.1016/s0006-3495(94)80833-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cantor R.S. The lateral pressure profile in membranes: a physical mechanism of general anesthesia. Biochemistry. 1997;36:2339–2344. doi: 10.1021/bi9627323. [DOI] [PubMed] [Google Scholar]
- 19.Cantor R.S. The influence of membrane lateral pressures on simple geometric models of protein conformational equilibria. Chem. Phys. Lipids. 1999;101:45–56. doi: 10.1016/s0009-3084(99)00054-7. [DOI] [PubMed] [Google Scholar]
- 20.Cantor R.S. Lipid composition and the lateral pressure profile in bilayers. Biophys. J. 1999;76:2625–2639. doi: 10.1016/S0006-3495(99)77415-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cantor R.S. Size distribution of barrel-stave aggregates of membrane peptides: influence of the bilayer lateral pressure profile. Biophys. J. 2002;82:2520–2525. doi: 10.1016/S0006-3495(02)75595-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lindahl E., Edholm O. Spatial and energetic-entropic decomposition of surface tension in lipid bilayers from molecular dynamics simulations. J. Chem. Phys. 2000;113:3882–3893. [Google Scholar]
- 23.Gullingsrud J., Schulten K. Lipid bilayer pressure profiles and mechanosensitive channel gating. Biophys. J. 2004;86:3496–3509. doi: 10.1529/biophysj.103.034322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Patra M. Lateral pressure profiles in cholesterol-DPPC bilayers. Eur. Biophys. J. 2005;35:79–88. doi: 10.1007/s00249-005-0011-0. [DOI] [PubMed] [Google Scholar]
- 25.Sonne J., Hansen F.Y., Peters G.H. Methodological problems in pressure profile calculations for lipid bilayers. J. Chem. Phys. 2005;122:124903. doi: 10.1063/1.1862624. [DOI] [PubMed] [Google Scholar]
- 26.Carrillo-Tripp M., Feller S.E. Evidence for a mechanism by which ω-3 polyunsaturated lipids may affect membrane protein function. Biochemistry. 2005;44:10164–10169. doi: 10.1021/bi050822e. [DOI] [PubMed] [Google Scholar]
- 27.Ollila O.H.S., Róg T., Vattulainen I. Role of sterol type on lateral pressure profiles of lipid membranes affecting membrane protein functionality: comparison between cholesterol, desmosterol, 7-dehydrocholesterol and ketosterol. J. Struct. Biol. 2007;159:311–323. doi: 10.1016/j.jsb.2007.01.012. [DOI] [PubMed] [Google Scholar]
- 28.Ollila S., Hyvönen M.T., Vattulainen I. Polyunsaturation in lipid membranes: dynamic properties and lateral pressure profiles. J. Phys. Chem. B. 2007;111:3139–3150. doi: 10.1021/jp065424f. [DOI] [PubMed] [Google Scholar]
- 29.Griepernau B., Böckmann R.A. The influence of 1-alkanols and external pressure on the lateral pressure profiles of lipid bilayers. Biophys. J. 2008;95:5766–5778. doi: 10.1529/biophysj.108.142125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Terama E., Ollila O.H.S., Vattulainen I. Influence of ethanol on lipid membranes: from lateral pressure profiles to dynamics and partitioning. J. Phys. Chem. B. 2008;112:4131–4139. doi: 10.1021/jp0750811. [DOI] [PubMed] [Google Scholar]
- 31.Jerabek H., Pabst G., Stockner T. Membrane-mediated effect on ion channels induced by the anesthetic drug ketamine. J. Am. Chem. Soc. 2010;132:7990–7997. doi: 10.1021/ja910843d. [DOI] [PubMed] [Google Scholar]
- 32.Ollila O.H.S., Risselada H.J., Marrink S.J. 3D pressure field in lipid membranes and membrane-protein complexes. Phys. Rev. Lett. 2009;102:078101. doi: 10.1103/PhysRevLett.102.078101. [DOI] [PubMed] [Google Scholar]
- 33.Baoukina S., Marrink S.J., Tieleman D.P. Lateral pressure profiles in lipid monolayers. Faraday Discuss. 2010;144:393–409. doi: 10.1039/b905647e. [DOI] [PubMed] [Google Scholar]
- 34.Venturoli M., Smit B. Simulating the self-assembly of model membranes. Phys. Chem. Comm. 1999;10:1–5. [Google Scholar]
- 35.Harries D., Ben-Shaul A. Conformational chain statistics in a model lipid bilayer: comparison between mean field and Monte Carlo calculations. J. Chem. Phys. 1997;106:1609–1619. [Google Scholar]
- 36.van den Brink-van der Laan E., Killian J.A., de Kruijff B. Nonbilayer lipids affect peripheral and integral membrane proteins via changes in the lateral pressure profile. Biochim. Biophys. Acta. 2004;1666:275–288. doi: 10.1016/j.bbamem.2004.06.010. [DOI] [PubMed] [Google Scholar]
- 37.Keller S.L., Bezrukov S.M., Parsegian V.A. Probability of alamethicin conductance states varies with nonlamellar tendency of bilayer phospholipids. Biophys. J. 1993;65:23–27. doi: 10.1016/S0006-3495(93)81040-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lewis J.R., Cafiso D.S. Correlation between the free energy of a channel-forming voltage-gated peptide and the spontaneous curvature of bilayer lipids. Biochemistry. 1999;38:5932–5938. doi: 10.1021/bi9828167. [DOI] [PubMed] [Google Scholar]
- 39.van Klompenburg W., Paetzel M., de Kruijff B. Phosphatidylethanolamine mediates insertion of the catalytic domain of leader peptidase in membranes. FEBS Lett. 1998;431:75–79. doi: 10.1016/s0014-5793(98)00733-9. [DOI] [PubMed] [Google Scholar]
- 40.Botelho A.V., Gibson N.J., Brown M.F. Conformational energetics of rhodopsin modulated by nonlamellar-forming lipids. Biochemistry. 2002;41:6354–6368. doi: 10.1021/bi011995g. [DOI] [PubMed] [Google Scholar]
- 41.Senisterra G., Epand R.M. Role of membrane defects in the regulation of the activity of protein kinase C. Arch. Biochem. Biophys. 1993;300:378–383. doi: 10.1006/abbi.1993.1051. [DOI] [PubMed] [Google Scholar]
- 42.Stubbs C.D., Slater S.J. The effects of non-lamellar forming lipids on membrane protein-lipid interactions. Chem. Phys. Lipids. 1996;81:185–195. doi: 10.1016/0009-3084(96)02581-9. [DOI] [PubMed] [Google Scholar]
- 43.Cornell R.B., Arnold R.S. Modulation of the activities of enzymes of membrane lipid metabolism by non-bilayer-forming lipids. Chem. Phys. Lipids. 1996;81:215–227. [Google Scholar]
- 44.Attard G.S., Templer R.H., Jackowski S. Modulation of CTP:phosphocholine cytidylyltransferase by membrane curvature elastic stress. Proc. Natl. Acad. Sci. USA. 2000;97:9032–9036. doi: 10.1073/pnas.160260697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lazaridis T. Effective energy function for proteins in lipid membranes. Proteins. 2003;52:176–192. doi: 10.1002/prot.10410. [DOI] [PubMed] [Google Scholar]
- 46.Spassov V.Z., Yan L., Szalma S. Introducing an implicit membrane in generalized Born/solvent accessibility continuum solvent models. J. Phys. Chem. B. 2002;106:8726–8738. [Google Scholar]
- 47.Im W., Feig M., Brooks C.L., 3rd An implicit membrane generalized Born theory for the study of structure, stability, and interactions of membrane proteins. Biophys. J. 2003;85:2900–2918. doi: 10.1016/S0006-3495(03)74712-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lazaridis T. Implicit solvent simulations of peptide interactions with anionic lipid membranes. Proteins. 2005;58:518–527. doi: 10.1002/prot.20358. [DOI] [PubMed] [Google Scholar]
- 49.Tanizaki S., Feig M. A generalized Born formalism for heterogeneous dielectric environments: application to the implicit modeling of biological membranes. J. Chem. Phys. 2005;122:124706. doi: 10.1063/1.1865992. [DOI] [PubMed] [Google Scholar]
- 50.Mottamal M., Lazaridis T. Voltage-dependent energetics of alamethicin monomers in the membrane. Biophys. Chem. 2006;122:50–57. doi: 10.1016/j.bpc.2006.02.005. [DOI] [PubMed] [Google Scholar]
- 51.Lazaridis T. Structural determinants of transmembrane β-barrels. J. Chem. Theory Comput. 2005;1:716–722. doi: 10.1021/ct050055x. [DOI] [PubMed] [Google Scholar]
- 52.Mihajlovic M., Lazaridis T. Antimicrobial peptides in toroidal and cylindrical pores. Biochim. Biophys. Acta. 2010;1798:1485–1493. doi: 10.1016/j.bbamem.2010.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Mihajlovic M., Lazaridis T. Antimicrobial peptides bind more strongly to membrane pores. Biochim. Biophys. Acta. 2010;1798:1494–1502. doi: 10.1016/j.bbamem.2010.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zhan H., Lazaridis T. Influence of the membrane dipole potential on peptide binding to lipid bilayers. Biophys. Chem. 2012;161:1–7. doi: 10.1016/j.bpc.2011.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Huang H.W. Free energies of molecular bound states in lipid bilayers: lethal concentrations of antimicrobial peptides. Biophys. J. 2009;96:3263–3272. doi: 10.1016/j.bpj.2009.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lazaridis T., Karplus M. Effective energy function for proteins in solution. Proteins. 1999;35:133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 57.Marsh D. Elastic curvature constants of lipid monolayers and bilayers. Chem. Phys. Lipids. 2006;144:146–159. doi: 10.1016/j.chemphyslip.2006.08.004. [DOI] [PubMed] [Google Scholar]
- 58.Marsh D., Watts A., Smith I.C.P. Dynamic structure and phase behavior of dimyristoyl phosphatidylethanolamine bilayers studied by deuterium nuclear magnetic resonance. Biochemistry. 1983;22:3023–3026. doi: 10.1021/bi00281a036. [DOI] [PubMed] [Google Scholar]
- 59.Perly B., Smith I.C.P., Jarrell H.C. Effects of replacement of a double bond by a cyclopropane ring in phosphatidylethanolamines: a 2H NMR study of phase transitions and molecular organization. Biochemistry. 1985;24:1055–1063. doi: 10.1021/bi00325a038. [DOI] [PubMed] [Google Scholar]
- 60.Cullis P.R., Hope M.J., Tilcock C.P.S. Lipid polymorphism and the roles of lipids in membranes. Chem. Phys. Lipids. 1986;40:127–144. doi: 10.1016/0009-3084(86)90067-8. [DOI] [PubMed] [Google Scholar]
- 61.Brown M.F., Thurmond R.L., Beyer K. Elastic deformation of membrane bilayers probed by deuterium NMR relaxation. J. Am. Chem. Soc. 2002;124:8471–8484. doi: 10.1021/ja012660p. [DOI] [PubMed] [Google Scholar]
- 62.Brooks B.R., Brooks C.L., 3rd, Karplus M. CHARMM: the biomolecular simulation program. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Rand, R. P. Structural parameters of aqueous phospholipid mixtures. http://www.brocku.ca/researchers/peter_rand/lipid/default.html.
- 64.Cafiso D.S. Alamethicin: a peptide model for voltage gating and protein-membrane interactions. Annu. Rev. Biophys. Biomol. Struct. 1994;23:141–165. doi: 10.1146/annurev.bb.23.060194.001041. [DOI] [PubMed] [Google Scholar]
- 65.Huang H.W., Wu Y. Lipid-alamethicin interactions influence alamethicin orientation. Biophys. J. 1991;60:1079–1087. doi: 10.1016/S0006-3495(91)82144-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.He K., Ludtke S.J., Huang H.W. Mechanism of alamethicin insertion into lipid bilayers. Biophys. J. 1996;71:2669–2679. doi: 10.1016/S0006-3495(96)79458-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Chen F.Y., Lee M.T., Huang H.W. Sigmoidal concentration dependence of antimicrobial peptide activities: a case study on alamethicin. Biophys. J. 2002;82:908–914. doi: 10.1016/S0006-3495(02)75452-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Chen F.Y., Lee M.T., Huang H.W. Evidence for membrane thinning effect as the mechanism for peptide-induced pore formation. Biophys. J. 2003;84:3751–3758. doi: 10.1016/S0006-3495(03)75103-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Frey S., Tamm L.K. Orientation of melittin in phospholipid bilayers. A polarized attenuated total reflection infrared study. Biophys. J. 1991;60:922–930. doi: 10.1016/S0006-3495(91)82126-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Bradshaw J.P., Dempsey C.E., Watts A. A combined x-ray and neutron diffraction study of selectively deuterated melittin in phospholipid bilayers: effect of pH. Mol. Membr. Biol. 1994;11:79–86. doi: 10.3109/09687689409162224. [DOI] [PubMed] [Google Scholar]
- 71.Batenburg A.M., van Esch J.H., de Kruijff B. Melittin-induced changes of the macroscopic structure of phosphatidylethanolamines. Biochemistry. 1988;27:2324–2331. doi: 10.1021/bi00407a013. [DOI] [PubMed] [Google Scholar]
- 72.Kamimori H., Hall K., Aguilar M.I. Studies on the membrane interactions of the cyclotides kalata B1 and kalata B6 on model membrane systems by surface plasmon resonance. Anal. Biochem. 2005;337:149–153. doi: 10.1016/j.ab.2004.10.028. [DOI] [PubMed] [Google Scholar]
- 73.Huang Y.-H., Colgrave M.L., Craik D.J. The biological activity of the prototypic cyclotide kalata b1 is modulated by the formation of multimeric pores. J. Biol. Chem. 2009;284:20699–20707. doi: 10.1074/jbc.M109.003384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Shenkarev Z.O., Nadezhdin K.D., Arseniev A.S. Conformation and mode of membrane interaction in cyclotides. Spatial structure of kalata B1 bound to a dodecylphosphocholine micelle. FEBS J. 2006;273:2658–2672. doi: 10.1111/j.1742-4658.2006.05282.x. [DOI] [PubMed] [Google Scholar]
- 75.Henriques S.T., Huang Y.-H., Craik D.J. Decoding the membrane activity of the cyclotide kalata B1: the importance of phosphatidylethanolamine phospholipids and lipid organization on hemolytic and anti-HIV activities. J. Biol. Chem. 2011;286:24231–24241. doi: 10.1074/jbc.M111.253393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Shintou K., Nakano M., Handa T. Interaction of an amphipathic peptide with phosphatidylcholine/phosphatidylethanolamine mixed membranes. Biophys. J. 2007;93:3900–3906. doi: 10.1529/biophysj.107.108399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Shahidullah K., London E. Effect of lipid composition on the topography of membrane-associated hydrophobic helices: stabilization of transmembrane topography by anionic lipids. J. Mol. Biol. 2008;379:704–718. doi: 10.1016/j.jmb.2008.04.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.North C.L., Barranger-Mathys M., Cafiso D.S. Membrane orientation of the N-terminal segment of alamethicin determined by solid-state 15N NMR. Biophys. J. 1995;69:2392–2397. doi: 10.1016/S0006-3495(95)80108-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Song J.B., Waugh R.E. Bending rigidity of SOPC membranes containing cholesterol. Biophys. J. 1993;64:1967–1970. doi: 10.1016/S0006-3495(93)81566-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Zemel A., Ben-Shaul A., May S. Membrane perturbation induced by interfacially adsorbed peptides. Biophys. J. 2004;86:3607–3619. doi: 10.1529/biophysj.103.033605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Killian J.A. Hydrophobic mismatch between proteins and lipids in membranes. Biochim. Biophys. Acta. 1998;1376:401–416. doi: 10.1016/s0304-4157(98)00017-3. [DOI] [PubMed] [Google Scholar]
- 82.Botelho A.V., Huber T., Brown M.F. Curvature and hydrophobic forces drive oligomerization and modulate activity of rhodopsin in membranes. Biophys. J. 2006;91:4464–4477. doi: 10.1529/biophysj.106.082776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Rand R.P., Parsegian V.A. Hydration forces between phospholipid-bilayers. Biochim. Biophys. Acta. 1989;988:351–376. [Google Scholar]
- 84.Vogel H. Comparison of the conformation and orientation of alamethicin and melittin in lipid membranes. Biochemistry. 1987;26:4562–4572. doi: 10.1021/bi00388a060. [DOI] [PubMed] [Google Scholar]


