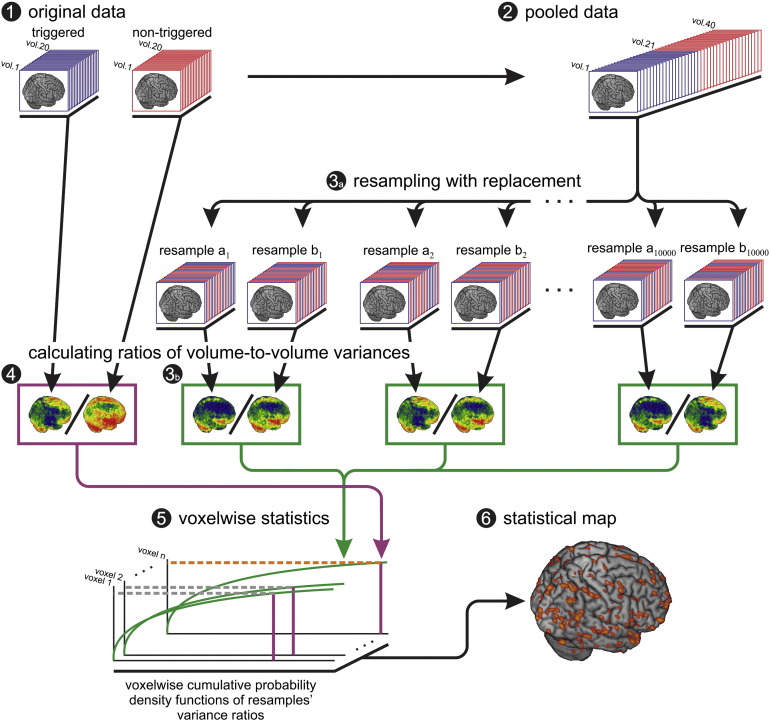
Fig. 2.
Flowchart of Bootstrap algorithm.
Because the distribution of signal intensity in a given voxel over repeated measurements cannot be assumed to be normal the parametric F-test may not provide accurate p-values. This bootstrap procedure is the non-parametric equivalent of the parametric F-test and provides unbiased p values. Step 1) Obtain data with (blue, nT = 20) and without triggering (red, nN = 20). Step 2) Pool the triggered and non-triggerred data Step 3) randomly draw (with replacement) N = nT + nN = 40 images from the pooled data. Consider the first 20 images as a pseudo dataset with triggering, the other 20 as a pseudo dataset without triggering. Repeat this re-sampling procedure 10,000 times, calculate the variance for each of the resamples of pseudo triggered (σb1T, σb2T,…, σb10000T) and pseudo non–triggered data (σb1N, σb2N,…, σb10000N) and their respective ratios (F1b, F2b, … F10000b) and store the results. Step 4), calculate the variance of the original triggered (σT) and the original non-triggered (σN) dataset and their ratio . Step 5), compare the F value of the original data (F) to the distribution of 10,000 pseudo Fb values obtained from the bootstrap re-sampling procedure. Step 6), identify voxels where fewer than 5 of the 10,000 pseudo Fb values are larger than the original F value. This corresponds to p < 0.0005 meaning that if the triggered and non-triggered data were drawn from the same distribution, there is less than 5 in 10,000 chance to obtain an F value that is as large; i.e. in a given voxel where there is no difference in variance there is only a 5/10000 chance that we would say there is.