Abstract
Toroidal shapes are often found in bio-molecules, viruses, proteins and fats, but only recently it was proved experimentally that toroidal structures can support exotic high-frequency electromagnetic excitations that are neither electric or magnetic multipoles. Such excitations, known as toroidal moments, could be playing an important role in enhancing inter-molecular interaction and energy transfer due to its higher electromagnetic energy confinement and weaker coupling to free space. Using a model toroidal metamaterial system, we show that coupling optical gain medium with high Q-factor toroidal resonance mode can enhance the single pass amplification to up to 65 dB. This offers an opportunity of creating the “toroidal” lasing spaser, a source of coherent optical radiation that is fueled by toroidal plasmonic oscillations in the nanostructure.
Spaser is a quantum amplifier of surface plasmons based on stimulated emission of radiation. It was introduced by Bergman and Stockman in 20031,2 as a nano-plasmonic counterpart of a laser that could generate intense coherent plasmonic fields and feed nanoscale plasmonic circuits. Since, there has been a surge of activity in this field, both theoretical and experimental3 (see Ref. 3, and references therein) culminated by a recent demonstration of the nano-particle-based spaser4, plasmonic laser5,6,7, and electrically pumped nanolaser8,9.
In a further development of the spaser concept the stimulated plasmonic oscillations were suggested to power up a nanoscale source of coherent radiation, the lasing spaser10. The key element of the lasing spaser is a plasmonic metamaterial, a two-dimensional array of plasmonic nano-resonators, which can support a high-Q collective and low radiation mode of excitation. This mode has the lowest dipole scattering loss when all resonators in the array oscillate in phase. An example of such mode is the anti-symmetric plasmon oscillations excited in weakly asymmetric split-ring resonators, the so-called trapped mode11. Engaging the trapped mode produces a narrow-diversion spatially coherent beam of radiation and substantially reduces the gain threshold compare to other gain-assisted solutions based on common electric and magnetic dipolar modes, including nanoshell12 and horseshoe13 plasmonic resonators.
In this letter we propose a lasing spaser that is fueled by previously overlooked toroidal dipolar mode of plasmonic coherent oscillations. This peculiar electromagnetic mode is formed by poloidal currents (i.e. currents flowing on a surface of a torous along its meridians14) and cannot be described in terms of the standard multipole expansion14,15; it couples very weakly to electromagnetic radiation and until recently remained elusive at microwave16 and optical frequencies17,18. Recently, Ögüt et al. proposed oligomer nanocavities with a near-field excitation source which makes the toroidal resonances prominent at visible frequencies19. We show that compare to the conventional magnetic dipolar response, engaging toroidal dipolar resonance in a near-IR active metamaterial enables to lower the levels of gain for loss compensation, optical amplification and lasing. The resonant toroidal mode also ensures stronger collective response of the metamaterial, which will lead to better spatial coherency and narrower diversion of the beam produced in the self-starting regime.
Results
Figures 1(a) shows a schematic diagram of the proposed toroidal lasing spaser. It is based on a two-dimensional array of plasmonic toroidal metamolecules embedded into a dielectric slab with optical gain. Each metamolecule occupies a rectangular unit cell t × ax × az and is formed by four identical U-shaped gold nano-resonators suspended in the dielectric with alternating orientations yielding 2-fold rotoinversion axis parallel to z-axis. The dimensions of the metamolecules ensure non-diffractive resonant operation of the metamaterial in the near-IR spectral range (see Fig. 1(b)).
Figure 1. Toroidal lasing spaser.
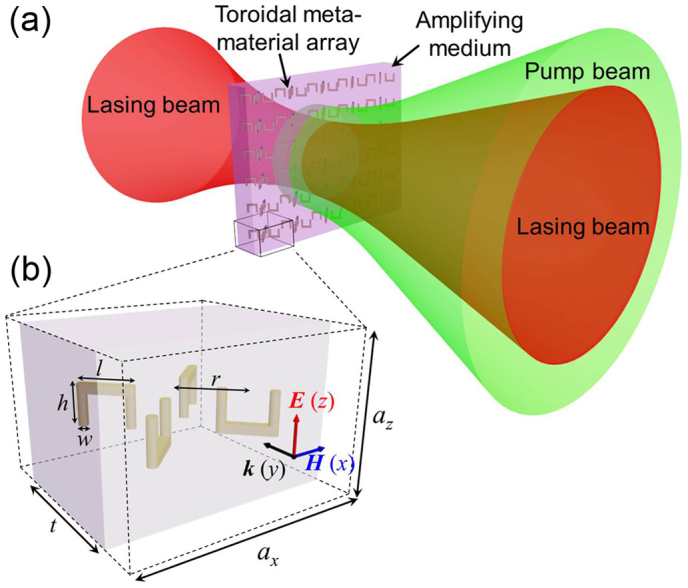
(a) Schematic diagram of the plasmonic toroidal lasing spaser. The structure comprises an amplifying medium slab (purple) supporting an array of plasmonic toroidal metamolecules. (b) Unit cell of the toroidal metamaterial, where ax = 1200 nm, az = 800 nm and t = 800 nm (thickness of the gain medium slab). It contains four gold U-shaped nano-resonators forming toroidal metamolecule with the following dimensions: l = 300 nm, h = 250 nm, r = 300 nm and w = 50 nm. k(y), E(z) and H(x) denote the direction of incident wave, polarization direction of electric and magnetic fields, respectively.
The optical response of the toroidal metamaterial was modeled by solving 3D Maxwell equations with full-wave finite-element method (COMSOL Multiphysics 3.5a). The permittivity of gold was described by Drude model20 with the damping constant γ set to 2π × 6.5 × 1012 s−1 and the plasma frequency ωp = 2π × 2.175 × 1015 s−1. Refractive index of the dielectric slab was n = 1.39, while its gain coefficient was assumed to be independent of frequency and as in Ref. 10 was introduced through imaginary part of the dielectric permittivity 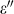 according to
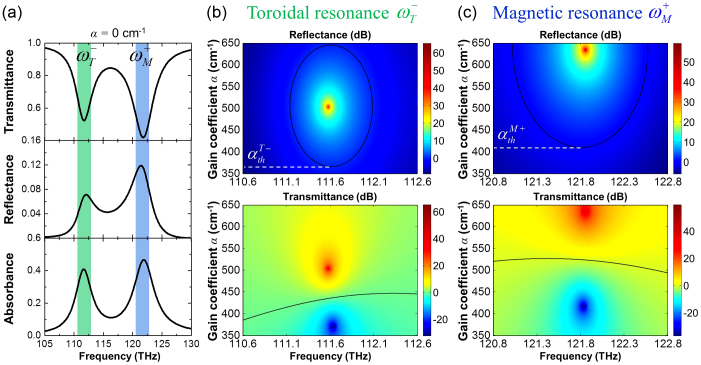
according to 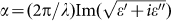 . Figure 2(a) shows the simulated transmittance, reflectance and absorbance spectra of the metamaterial slab without the presence of gain (α = 0 cm−1). The spectra show two resonances located at 111.7 THz and 121.8 THz respectively. Multipole decomposition of plasmonic currents resonantly induced in each metamolecule indicates that high-frequency resonance corresponds to conventional magnetic dipole response, while low-frequency resonance signifies the excitation of toroidal dipolar mode (see Figure 2(e) of Ref. 17). The toroidal resonance and magnetic resonance are excited because of the coupling effect of the front and back magnetic dipole pairs of SRRs16,17. Actually, the plasmonic metamaterials such as nanorod and nanowire exhibit the electric resonance depending on its geometrical properties and orientation with respect to the illuminating light21,22. Utilizing the retardation of the electric resonances induces localized field which resulting in a magnetic dipolar resonances within the intermediate spacer. Such interaction between the retardant fields has also been investigated that provides a very broad resonance in the field of negative index issue23,24. Moreover, not only the retardation of the electric resonances but also the magnetic resonances can provide particular plasmonic resonances, such as toroidal dipolar response16,17,18 and magnetic interaction in sterometamaterial25. The toroidal resonance is excited at the lower frequency due to the electric and magnetic dipole interaction at toroidal resonance shows a more stable and lower energy configuration than that at the magnetic resonance (see Ref. 17 for detailed discussion). The toroidal resonance shows local distribution of magnetic field lines curling around the metamolecule's symmetry axis at 111.7 THz. The mode is slightly distorted due to plasmonic loss, but as we show later, will be restored in the presence of gain.
. Figure 2(a) shows the simulated transmittance, reflectance and absorbance spectra of the metamaterial slab without the presence of gain (α = 0 cm−1). The spectra show two resonances located at 111.7 THz and 121.8 THz respectively. Multipole decomposition of plasmonic currents resonantly induced in each metamolecule indicates that high-frequency resonance corresponds to conventional magnetic dipole response, while low-frequency resonance signifies the excitation of toroidal dipolar mode (see Figure 2(e) of Ref. 17). The toroidal resonance and magnetic resonance are excited because of the coupling effect of the front and back magnetic dipole pairs of SRRs16,17. Actually, the plasmonic metamaterials such as nanorod and nanowire exhibit the electric resonance depending on its geometrical properties and orientation with respect to the illuminating light21,22. Utilizing the retardation of the electric resonances induces localized field which resulting in a magnetic dipolar resonances within the intermediate spacer. Such interaction between the retardant fields has also been investigated that provides a very broad resonance in the field of negative index issue23,24. Moreover, not only the retardation of the electric resonances but also the magnetic resonances can provide particular plasmonic resonances, such as toroidal dipolar response16,17,18 and magnetic interaction in sterometamaterial25. The toroidal resonance is excited at the lower frequency due to the electric and magnetic dipole interaction at toroidal resonance shows a more stable and lower energy configuration than that at the magnetic resonance (see Ref. 17 for detailed discussion). The toroidal resonance shows local distribution of magnetic field lines curling around the metamolecule's symmetry axis at 111.7 THz. The mode is slightly distorted due to plasmonic loss, but as we show later, will be restored in the presence of gain.
Figure 2. Absorbance, reflectance and transmittance spectra.
(a) Simulated spectral response of the toroidal metamaterial in the case of α = 0 cm−1. The magnetic and toroidal resonances are excited at the higher and lower frequency, respectively. Panels (b) and (c) show transmittance and reflectance spectra as a function of the gain coefficient α in the range from 350 to 650 cm−1 for magnetic and toroidal modes respectively. The intensity of transmittance and reflectance spectra is shown as color in dB scale, and the unity transmittance and reflectance is marked as black solid contour.
Figures 2(b) and 2(c) show how the reflectance and transmittance spectra of the toroidal metamaterial change as the gain coefficient α increases from 350 to 650 cm−1, revealing two distinct stages of the spectral transformation. The calculation of color maps in Figures 2(b) and 2(c) has a resolution of 1 × 10−3 THz. At first, an increase of the gain coefficient leads to an increase of reflectance and decrease of transmittance at both resonances. Upon achieving a threshold value, which are 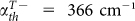 and
and 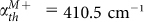 at magnetic and toroidal resonances respectively, the resonant reflectance reaches unity, while the transmittance drops to zero. A further increase of gain leads to rapid increase of both reflectance and transmittance, which reach a maximum of 60 dB at α = 635.5 cm−1 and 65 dB at α = 503.5 cm−1 for correspondingly magnetic and toroidal resonances. The first stage signifies gain-assisted reduction of the plasmonic losses, which become fully compensated near the threshold. At the second stage the resonant scattering from the plasmonic metamolecules exceeds the intensity of the incident (probe) beam in both transmission and reflection directions, and the metamaterial starts to operate as a single-pass small-signal optical amplifier.
at magnetic and toroidal resonances respectively, the resonant reflectance reaches unity, while the transmittance drops to zero. A further increase of gain leads to rapid increase of both reflectance and transmittance, which reach a maximum of 60 dB at α = 635.5 cm−1 and 65 dB at α = 503.5 cm−1 for correspondingly magnetic and toroidal resonances. The first stage signifies gain-assisted reduction of the plasmonic losses, which become fully compensated near the threshold. At the second stage the resonant scattering from the plasmonic metamolecules exceeds the intensity of the incident (probe) beam in both transmission and reflection directions, and the metamaterial starts to operate as a single-pass small-signal optical amplifier.
Discussions
To further quantitatively clarify the gain-assisted radiated enhancement of dipoles and multipoles, here we calculate the radiated power of electric and magnetic multipoles as well as toroidal dipole for different values of gain coefficient α. The field distribution and radiated power of the 1st metamolecule for α = 366 cm−1 (at lasing threshold) and α = 503.5 cm−1 (at transmittance maxima) are shown in Figures 3(a) and 3(b) respectively. We found, comparing our prior work (the Figure 2 of Ref. 17), the radiated power of toroidal dipole as well as electric and magnetic multipoles is enhanced after gain medium involved. The inset figures of Figures 3(a) and 3(b) show the magnetic energy in logarithm scale and the magnetic field distribution at the toroidal resonances for 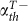 and
and 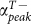 . The gain-assisted reduction of the plasmonic losses makes the much more uniform magnetic field distribution, which makes the joule loss of gold U-shaped SRR in NIR region is compensated showing a similar magnetic field distribution at toroidal resonance in microwave region (see Figure 3E of Ref. 16).
. The gain-assisted reduction of the plasmonic losses makes the much more uniform magnetic field distribution, which makes the joule loss of gold U-shaped SRR in NIR region is compensated showing a similar magnetic field distribution at toroidal resonance in microwave region (see Figure 3E of Ref. 16).
Figure 3. Dispersion of five strongest multipoles contributing to the metamaterial response.
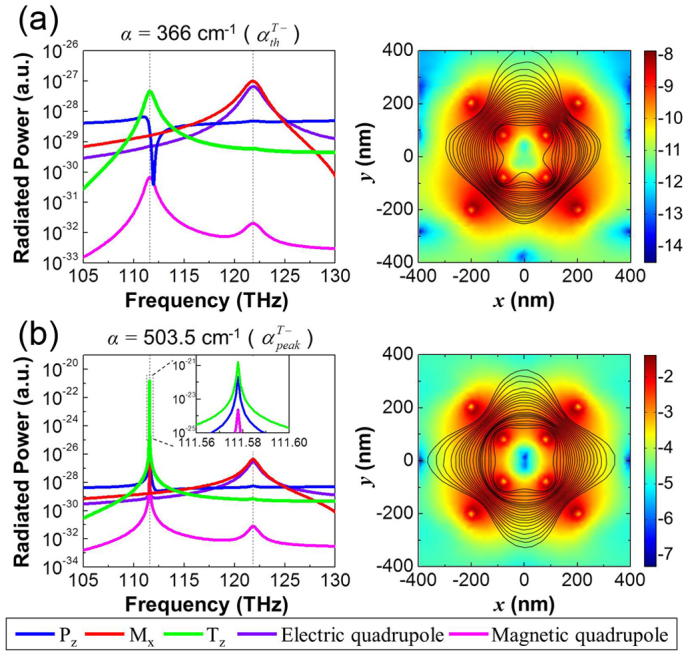
(a) Dispersion of radiated power in the case of threshold gain. (b) Dispersion of radiated power in the case of amplification maximum. Color map and black streamline show the magnetic energy in logarithm scale and the magnetic field distribution at the toroidal resonances for different values of gain coefficients. The inset of (b) presents the enlarged dispersion of radiated power around toroidal resonance.
Further changes expected in the metamaterial response at the toroidal and magnetic resonances in the presence of gain are illustrated in Figures 4(a) and 4(b). The calculation of the spectra for difference values of gain coefficients in Figures 4(a) and 4(b) has a resolution of 1 × 10−4 THz. In particular, one may observe that the width of both resonances decreases very rapidly with increasing gain and the resonances virtually collapse as their width reduces by about 3 orders of magnitude near the amplification maximum. The collapse is also accompanied by a rapid increase of the resonance quality factor, which exceeds 105 in the case of the toroidal dipolar mode.
Figure 4. Reflectance properties.
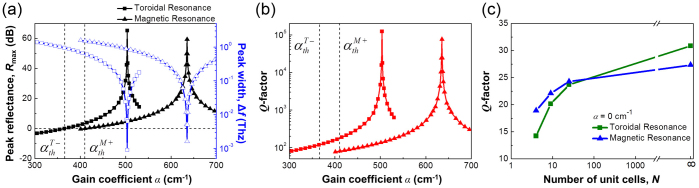
(a) Small-signal amplification (black) and spectral width (blue) of the reflectance peak at correspondingly toroidal and magnetic dipole resonances as a function of gain level in the slab. The horizontal dash line indicates unity reflectance. The vertical dash lines show the threshold gain 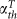 and
and 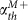 . (b) Q-factor of the toroidal (squares) and magnetic (triangles) dipolar resonances as functions of gain levels. (c) Q-factor as a function of the total number of metamolecules in the toroidal metamaterial array. Simulated data are represented by points for both toroidal resonance (green square) and magnetic resonance (blue triangle).
. (b) Q-factor of the toroidal (squares) and magnetic (triangles) dipolar resonances as functions of gain levels. (c) Q-factor as a function of the total number of metamolecules in the toroidal metamaterial array. Simulated data are represented by points for both toroidal resonance (green square) and magnetic resonance (blue triangle).
In the most cases on plasmonic metamaterials, the radiation loss and Joule loss are two key problems making the performance of plasmonic metamaterials become worse. The later problem could be eliminated by adding gain medium into a metamaterial system1,4. However, the radiation loss becomes stronger while gain increases. Therefore, for a very large gain value α, the excess of gain starts to dump plasmonic oscillations (just as losses do), which broadens the resonances and reduces the efficiency of amplification10. Besides, each individual mode has distinct optimal gain coefficient because the different values of the radiation loss.
Although both types of the metamaterial resonance show similar dependencies on the gain coefficient, we note that for the toroidal resonance all stages of the response transformation are achieved at markedly lower levels of gain. In particular, the threshold value of α is about 10% smaller here, while the level of gain that maximizes single-pass amplification in the metamaterial is reduced by more than 20%. Remarkably, at α ≈ 504 cm−1 the strength of the toroidal excitation exceeds that of the magnetic dipole by 5 orders of magnitude, as evident from Figure 3(b). We argue that this is because the toroidal dipolar excitation is spatially much more confined and exhibit much weaker coupling to free space (i.e. radiative loss) compare to the magnetic dipolar mode. Indeed, the field lines of the fully developed toroidal mode are self-terminated and completely localized within a well-defined region of the metamaterial's unit cell (see Figure 3(b)), which makes this type of electromagnetic excitation very different from the standard dipolar (and even quadrupolar) modes. In our case the plasmonic metamolecules resemble a nano-scale analogue of resonant cavities with highly reflecting mirrors, thus providing much more efficient transfer of energy from the gain medium to the toroidal mode. This also ensures lower gain threshold in the self-starting regime (i.e. lasing) at the toroidal resonance.
Importantly, the spatial extent of the toroidal mode in a metamolecule (and therefore its radiative loss) is reduced in the vicinity of other toroidal excitations due to partial cancellation of the magnetic-field vortices produced by each mode. Thus the toroidal resonance is also a collective effect, which should become stronger in large arrays. This is illustrated in Figure 4(c), where we plotted the quality factors of both magnetic and toroidal resonances as functions of the total number of metamolecules for the case of zero gain. One can see that the Q-factor of the toroidal resonance rises faster and appear to exceed the level of the magnetic resonance in the metamaterial arrays larger than 5 × 5. In the lasing regime the suppression of radiative loss due to collective behavior guarantees that the in-phase toroidal oscillations in a large number of the plasmonic metamolecules will win over other modes of excitation, generating spatially coherent diffraction-limited beam of optical emission normal to the array.
In conclusion, we have proposed and numerically studied near-IR toroidal lasing spaser, a metamaterial-based optical amplifier/source of coherent radiation fuelled by toroidal plasmons. Switching from magnetic to toroidal dipolar response at around 110 THz allows to achieve better coherency and bring the gain threshold down to the level of 366 cm−1, which can be provided by quantum cascade amplifiers in near-IR, such as quantum dots (QDs)26,27, quantum wells28,29, and organic dyes30. Such a high Q-factor of toroidal metamolecule with a narrow bandwidth of gain has applications, such as single pass amplifier which the certain frequency of incident wave can be amplified up to 65 dB (~3.16 × 106 times). The modeled sub-micron toroidal resonators can be fabricated using recently developed e-beam lithography technique with precise alignment31 or stress-driven assembly fabricated method32, while reducing their size would enable to blue-shift the resonant response and exploit other types of optical gain media.
Author Contributions
N.I.Z. and D.P.T. jointly conceived the idea. Y.-W.H. designed and performed the calculations. W.T.C., P.C.W. and V.A.F. assisted in the analyzing and discussion of the results. Y.-W.H., W.T.C. and V.A.F. prepared the manuscript. D.P.T. and N.I.Z. supervised and coordinated all the work. All authors commented on the manuscript.
Acknowledgments
The authors thank financial aids from National Taiwan University, National Science Council, Taiwan under grant numbers 101-3113-P-002-021, 100-2923-M-002-007-MY3 and 101-2112-M-002-023. Authors are grateful to EPSRC, UK and the Royal Society, London, the National Center for Theoretical Sciences, Taipei Office, Molecular Imaging Center of National Taiwan University and National Center for High-Performance Computing, Taiwan for their support.
References
- Bergman D. J. & Stockman M. I. Surface plasmon amplification by stimulated emission of radiation: Quantum generation of coherent surface plasmons in nanosystems. Phys. Rev. Lett. 90, 027402 (2003). [DOI] [PubMed] [Google Scholar]
- Stockman M. I. Spasers explained. Nat. Photonics 2, 327–329 (2008). [Google Scholar]
- Stockman M. I. Nanoplasmonics: past, present, and glimpse into future. Opt. Express 19, 22029–22106 (2011). [DOI] [PubMed] [Google Scholar]
- Noginov M. A. et al. Demonstration of a spaser-based nanolaser. Nature 460, 1110–1112 (2009). [DOI] [PubMed] [Google Scholar]
- Oulton R. F. et al. Plasmon lasers at deep subwavelength scale. Nature 461, 629–632 (2009). [DOI] [PubMed] [Google Scholar]
- Ma R.-M., Oulton R. F., Sorger V. J., Bartal G. & Zhang X. Room-temperature sub-diffraction-limited plasmon laser by total internal reflection. Nat. Mater. 10, 110–113 (2011). [DOI] [PubMed] [Google Scholar]
- Lu Y.-J. et al. Plasmonic nanolaser using epitaxially grown silver film. Science 337, 450–453 (2012). [DOI] [PubMed] [Google Scholar]
- Hill M. T. et al. Lasing in metallic-coated nanocavities. Nat. Photonics 1, 589–594 (2007). [Google Scholar]
- Hill M. T. et al. Lasing in metal-insulator-metal sub-wavelength plasmonic waveguides. Opt. Express 17, 11107–11112 (2009). [DOI] [PubMed] [Google Scholar]
- Zheludev N. I., Prosvirnin S. L., Papasimakis N. & Fedotov V. A. Lasing spaser. Nat. Photonics 2, 351–354 (2008). [Google Scholar]
- Fedotov V. A. et al. Spectral collapse in ensembles of metamolecules. Phys. Rev. Lett. 104, 223901 (2010). [DOI] [PubMed] [Google Scholar]
- Gordon J. A. & Ziolkowski R. W. The design and simulated performance of a coated nano-particle laser. Opt. Express 15, 2622–2653 (2007). [DOI] [PubMed] [Google Scholar]
- Sarychev A. K. & Tartakovsky G. Magnetic plasmonic metamaterials in actively pumped host medium and plasmonic nanolaser. Phys. Rev. B 75, 085436 (2007). [Google Scholar]
- Dubovik V. M. & Tugushev V. V. Toroid moments in electrodynamics and solid-state physics. Phys. Rep. 187, 145–202 (1990). [Google Scholar]
- Radescu E. E. & Vaman G. Exact calculation of the angular momentum loss, recoil force, and radiation intensity for an arbitrary source in terms of electric, magnetic, and toroid multipoles. Phys. Rev. E 65, 046609 (2002). [DOI] [PubMed] [Google Scholar]
- Kaelberer T., Fedotov V. A., Papasimakis N., Tsai D. P. & Zheludev N. I. Toroidal dipolar response in a metamaterial. Science 330, 1510–1512 (2010). [DOI] [PubMed] [Google Scholar]
- Huang Y.-W. et al. Design of plasmonic toroidal metamaterials at optical frequencies. Opt. Express 20, 1760–1768 (2012). [DOI] [PubMed] [Google Scholar]
- Dong Z.-G. et al. Optical toroidal dipolar response by an asymmetric double-bar metamaterial. Appl. Phys. Lett. 101, 144105 (2012). [Google Scholar]
- Ögüt B., Talebi N., Vogelgesang R., Sigle W. & van Aken P. A. Toroidal plasmonic eigenmodes in oligomer nanocavities for the visible. Nano Lett. 12, 5239–5244 (2012). [DOI] [PubMed] [Google Scholar]
- Linden S. et al. Magnetic response of metamaterials at 100 terahertz. Science 306, 1351–1353 (2004). [DOI] [PubMed] [Google Scholar]
- Kuwata H., Tamaru H., Esumi K. & Miyano K. Resonant light scattering from metal nanoparticles: Practical analysis beyond Rayleigh approximation. Appl. Phys. Lett. 83, 4625 (2003). [Google Scholar]
- Chen H.-A., Lin H.-Y. & Lin H.-N. Localized surface plasmon resonance in lithographically fabricated single gold nanowires. J. Phy. Chem. C 114, 10359 (2010). [Google Scholar]
- Dolling G. et al. Cut-wire pairs and plate pairs as magnetic atoms for optical metamaterials. Opt. Lett. 30, 3198–3200 (2005). [DOI] [PubMed] [Google Scholar]
- Garwe F. et al. Evaluation of gold nanowire pairs as a potential negative index material. Appl. Phys. B 84, 139–148 (2006). [Google Scholar]
- Liu N., Liu H., Zhu S. & Giessen H. Stereometamaterials. Nat. Photonics 3, 157–162 (2009). [Google Scholar]
- Plum E., Fedotov V. A., Kuo P., Tsai D. P. & Zheludev N. I. Towards the lasing spaser: controlling metamaterial optical response with semiconductor quantum dots. Opt. Express 17, 8548–8551 (2009). [DOI] [PubMed] [Google Scholar]
- Tanaka K., Plum E., Ou J. Y., Uchino T. & Zheludev N. I. Multifold Enhancement of Quantum Dot Luminescence in Plasmonic Metamaterials. Phys. Rev. Lett. 105, 227403 (2010). [DOI] [PubMed] [Google Scholar]
- Carrere H., Marie X., Lombez L. & Amand T. Optical gain of InGaAsN/InP quantum wells for laser applications. Appl. Phys. Lett. 89, 181115 (2006). [Google Scholar]
- Meinzer N. et al. Arrays of Ag split-ring resonators coupled to InGaAs single-quantum-well gain. Opt. Express 18, 24140–24151 (2010). [DOI] [PubMed] [Google Scholar]
- Tsuda A. & Osuka A. Fully conjugated porphyrin tapes with electronic absorption bands that reach into infrared. Science 293, 79–82 (2001). [DOI] [PubMed] [Google Scholar]
- Chen W. T. et al. Optical magnetic response in three-dimensional metamaterial of upright plasmonic meta-molecules. Opt. Express 19, 12837–12842 (2011). [DOI] [PubMed] [Google Scholar]
- Chen C. C. et al. Fabrication of three dimensional split ring resonators by stress-driven assembly method. Opt. Express 20, 9415–9420 (2012). [DOI] [PubMed] [Google Scholar]