Characterizing Protein Environmental Effects on Reduction Potentials of Metalloproteins

Abstract

Electron transfer proteins play critical roles in determining their reduction potentials by the degree of burial of the redox site within the protein and the degree of permanent polarization of the polypeptide around the redox site. Although continuum electrostatics calculations of protein structures can predict their net effect, quantifying how each contributes separately is difficult. Here, the burial of the redox site is characterized by a dielectric radius R_p, which is a Born-type radius for the protein, the polarization of the polypeptide is characterized by an electret potential φ_p, which is the average electrostatic potential at the metal atoms, and an electret-dielectric spheres (EDS) model of the entire protein is then defined in terms of R_p and φ_p. The EDS model shows that for a protein with a redox site of charge Q, the dielectric response free energy is a function of Q² while the electret energy is a function of Q. In addition, R_p and φ_p are shown to be characteristics of the fold of a protein and predictive of the most likely redox couple for redox sites that undergo different redox couples.

Introduction

In bioenergetic processes, electrons move over long distances by electron transfer reactions between electron carriers, which are generally redox sites within electron transfer proteins. The reduction potential E° of the redox sites determine the driving force for the reactions, with more favorable electron flow toward the redox site with larger E°. Since nature uses the same redox sites for many different processes, the protein environment surrounding each redox site must play a critical role in determining E°. Thus, understanding how the protein environment affects E° is essential for understanding structure-function relationships in electron transfer proteins.

Computational studies have played an important role in understanding reduction potentials of metalloproteins. Since E° is proportional to the negative of the free energy for the reduction reaction ΔG, the energetics can be divided into the inner sphere contribution ΔG_in, which is the energy of adding an electron to the redox site, and the outer sphere contribution ΔG_out, which is the change in the interaction energy of the redox site with the protein and solvent upon reduction of the redox site. Many earlier studies of proteins have assumed that ΔG_in for a given redox site is independent of the protein, and thus have focused on understanding relative values of E° between different proteins with the same redox site rather than the absolute value of E°[1–6]. However, deviations from experiment can be attributed to the missing inner sphere contribution so the calculations of reduction potentials versus the standard hydrogen electrode (SHE) for [4Fe-4S] proteins by Noodleman, Case, Bashford, and co-workers using density functional theory (DFT) for ΔG_in and Poisson-Boltzmann (PB) electrostatics for ΔG_out are an important step forward[7,8]. More recent studies[9] indicate that the non-hybrid functional used in those studies gives inner sphere energetics appear somewhat poorer compared to electrospray ionization - photoelectron spectroscopy (EI-PES) detachment energies of [4Fe-4S] cluster analogs measured by Wang and co-workers[10,11] although the geometries were better than some hybrid functionals.

Recently, our group has predicted E° for [4Fe-4S] proteins that are in excellent agreement with experiment (Figure 1) using a simple additive approach we refer to as DFT+PB in which ΔG_in is obtained by DFT calculations of gas phase redox site analogs and ΔG_out is obtained by PB calculations of the redox site in the protein using partial charges from the DFT calculation[12]. A key factor has been our calibration of the functionals and basis sets for the DFT calculations by comparing the calculated detachment energies of redox site analogs in the gas phase against EI-PES data[9]. Our DFT calculations also confirm that ΔG_in for the iron-sulfur clusters is relatively independent of environment[9], although the ligand dihedral conformation may tune it by ~200 mV[13]. The DFT+PB calculations show that the two major factors differentiating ΔG_out between proteins are the degree of burial of the redox site in the protein and the degree of permanent polarization of the polypeptide surrounding the redox site[12]. The degree of burial of the redox site determines the dielectric response of the surroundings. According to the Born solvation free energy, the dielectric response for an ion in solution is a function of the charge and radius of the ion and of the dielectric response of the solvent. On the other hand, for the redox site of a protein in aqueous solution, both the low protein dielectric and the high solvent dielectric will contribute; thus, the proximity of the redox site to the surface of the protein and therefore the solvent will affect the dielectric response. Moreover, previous results indicate the proximity to the surface is actually more important than the size of the protein[12]. In addition, the polypeptide in several Fe-S proteins[14] and cytochrome c[2] is polarized around the redox site, creating an electrostatic potential at the redox site that persists even in the limit of zero charge of the redox site[14]. Thus, such a protein is an “electret”, which is a material with quasi-permanent electrical polarization analogous to a permanent magnet[15]. The protein electret is maintained by the hydrogen-bonded, three-dimensional structure of the protein and can easily tune the reduction potential by appropriate mutations.

Figure 1.

Comparison of experimental versus calculated reduction potentials for the 2-/3- (below dashed line) and 1-/2- (above dashed line) couples. From left to right, Fe₄S₄(SCH₂CH₃)₄ (purple), Rg/RtHiPIP (red), Cv, Pr, Pa, and CaFds (blue), Av-ADP, Av, and CpFePs (green), Eh, Ev, Tt, Rt, Rf, and CvHiPIPs (red), and Cp/CvFd (blue).

Since both the burial of the redox site and the electret of the protein are important in determining ΔG_out and thus E°, quantifying each is useful for comparing different proteins; however, both are difficult to quantify. For instance, the solvent accessible surface area (SASA)[16] of the redox site can distinguish between partially exposed sites but not completely buried sites, which is important since the distance from the surface affects the dielectric response free energy even for a completely buried site. Also, while the number of hydrogen bonds to the redox site indicates the polarization of the backbone, the contribution of each hydrogen bond is highly dependent on the orientation and distance[17]. Here, using continuum electrostatics calculations of crystal structures, the dielectric radius of the protein R_p is defined to measure the degree of burial of the redox site within the protein and the protein electret potential φ_p is defined to measure the degree of permanent polarization of the protein surrounding the redox site. Next, the electret-dielectric sphere model is developed in terms of R_p and φ_p and used to explore how the two factors contribute to the redox properties of differing proteins. Specifically, R_p and φ_p are shown to be characteristic of the fold of a protein and, for a redox site that can undergo different redox couples, only certain values of R_p and φ_p are shown to be consistent with reduction potentials that are within the physiological range for each couple. The proteins examined here are homologous proteins from three families of [4Fe-4S]-proteins: HiPIP, ferredoxin (Fd), and nitrogenase iron protein (FeP), plus an example from each of three more families of redox proteins: the [1Fe]-protein rubredoxin (Rd), the blue-copper protein plastocyanin (Pc), and the heme-protein cytochrome c (cyt c) (Figure 2).

Figure 2.

The folds of TtHiPIP, CaFd, and AvFeP (top, left to right) and PfRd, TaCyt c, and PlPc.(bottom, left to right).

Methods

In the DFT+PB approach,[12] the total E° versus the standard hydrogen electrode (SHE) is decomposed as

$$-\mathit{nFE}°=\mathrm{\Delta }G°\approx \mathrm{\Delta }{G}_{\text{in}}+\mathrm{\Delta }{G}_{\text{out}}+\mathrm{\Delta }{G}_{\text{SHE}},$$ (1)

where n is the number of electrons transferred, F is the Faraday constant, and ΔG_SHE/F = 4.43 eV is the absolute electrode potential for the SHE[18]. Although values of 4.28 eV[19] and 4.34 eV[20,21] based on cluster-ion solvation data[22], this value is close to the IUPAC recommended value[23] and the differences will not significantly affect results[24]. ΔG_in is calculated using DFT as the difference in free energy between an oxidized and reduced redox site analog in the gas phase and ΔG_out is calculated using continuum electrostatics as the change in the interaction energy of the redox site with the surrounding protein and solvent upon reduction of the redox site. In the continuum electrostatics approach, the permittivity of the redox site is ε_c, permittivity of the protein is ε_p, and the permittivity of water is ε_w.

Calculations of R_p and φ_p

Two physical quantities are defined here to characterize a metalloprotein, utilizing continuum electrostatics calculations of a protein in a dielectric continuum solvent. Although partial charges of the redox sites have been calculated by us for the cases studied here, partial charges for redox sites are not always available. Thus, instead of using the partial charges of the redox site, a system of test charges equal to Q/M are distributed over the M metals of the redox site, where Q is equal to −1, so that the only parameters required available in standard protein force fields. Moreover, while it is possible to “fit” the model for each different charge state, or each different redox couple, the net charge Q is chosen as −1, again for generality in case the net charge of the redox site is not known and to limit the number of definitions. First, the dielectric radius of the protein R_p is defined using the Born solvation free energy equation as

$$R=\frac{Q^2}{2{\mathrm{\Delta }}_{\text{sol}}G}\left(\frac{1}{{\epsilon }_{\text{in}}}-\frac{1}{{\epsilon }_{\text{out}}}\right),$$ (2)

where Q = −1, ε_in = ε_p, and ε_out = ε_w. Δ_solG = Δ_solG_test is calculated using the PB equation for the system of test charges in place of the partial charges of the redox site in the protein cavity with permittivity ε_p and the solvent with permittivity ε_w (Figure 3, F). Next, the protein electret potential, φ_p, is defined as the average of the electrostatic potential at each metal atom in the redox site. It is calculated using the PB equation for a system consisting of the redox site cavity with no test or partial charges and permittivity ε_c, the protein cavity with the protein partial charges and permittivity ε_p, and the solvent with permittivity ε_w (Figure 3, G). The backbone contribution to the electret potential, φ_bb, is defined similarly except the side chain partial charges for each residue are set to zero. In the case of ferredoxin, partial charges for the other redox site in the 2- state are included in the calculation of φ.

Figure 3.

The solvation energy of A) the standard atomistic description of a protein by PB methods consists of the solvation energies of B) point charges at metal atoms within the redox site cavity, C) point charges at metal atoms within the protein cavity, and D) point charges at the protein atoms within both cavities. In the EDS model, B, C, and D, are represented by E) a point charge in a sphere of radius R_c representing the redox site cavity, F) a point charge in a sphere of radius R_c representing the protein cavity, and G) an electret potential, φ_p, due to the polarization of the protein environment.

Electret-Dielectric Spheres Model

The EDS model is a means of interpreting ΔG_out (such as from a full PB calculation) based on a physical model in terms of the two quantities R_p and φ_p, by modeling a redox-active protein as a point charge inside two concentric dielectric spheres immersed in a dielectric continuum solvent (Figure 3). The point charge inside the inner sphere represents the redox site while the outer sphere plus an associate electret represents the protein. The solvation free energy for this model is

$${\mathrm{\Delta }}_{\text{sol}}{G}_{\text{EDS}}=-\frac{Q^2}{2R_{\text{c}}}\left(1-\frac{1}{{\epsilon }_{\text{p}}}\right)-\frac{Q^2}{2R_{\text{p}}}\left(\frac{1}{{\epsilon }_{\text{p}}}-\frac{1}{{\epsilon }_{\text{w}}}\right)+Q{\phi }_{\text{p}},$$ (3)

where Q is the net charge of the redox site including both the metals and ligands, R_c is the radius of the redox site, R_p is radius of the protein, and φ_p is the electret potential. Since R_c is sensitive to the exact distribution of the partial charges, it is calculated separately for each couple according to

$$R_{\text{c}}=-\frac{(Q_{\text{red}}^2-Q_{\text{oxi}}^2)}{2\left({\mathrm{\Delta }}_{\text{sol}}{G}_{\text{test}}\right(R_{\text{c}}^{\text{oxi}})-{\mathrm{\Delta }}_{\text{sol}}{G}_{\text{test}}(R_{\text{c}}^{\text{red}}\left)\right)}\left(1-\frac{1}{{\epsilon }_{\text{p}}}\right).$$ (4)

The first two terms are an extension of the Born solvation free energy for a point charge Q inside two concentric dielectric spheres in a dielectric continuum, which has been used by Warshel to give a physical picture of the protein environment,[25] while the last term arises from the interaction of Q with φ_p, the permanent electrostatic potential due to the protein electret. Thus, the outer sphere contribution to E° in the EDS model is ΔG_EDS = Δ_solG_EDS(Q_red) − Δ_solG_EDS(Q_oxd), where Q_oxd and Q_red are the net charge of the redox site in the oxidized and reduced states, respectively.

All solvation energies and electrostatic potentials were calculated using APBS[26], a program for solving the Poisson-Boltzmann equation, as described fully elsewhere[24] and summarized briefly here. Radii for Connolly surfaces[16] of the proteins and redox sites and partial charges for the protein were from the CHARMM22 parameters[27]. Partial charges from our previous DFT calculations were used for the [4Fe-4S],[24] [1Fe],[28] and blue-copper[29] redox sites while CHARMM22 parameters were used for the heme, where the total charge of each redox site is an integer. The dielectric permittivity were chosen as ε_c=1, ε_p=4, and ε_w=78 and the ionic concentration was set to zero. A 51.2 Å × 51.2 Å × 51.2 Å box with 257 grid points in each direction was used for HiPIP, Fd, Rd, Pc, and cyt c while a 76.8 Å × 76.8 Å × 76.8 Å box with 385 grid points in each direction was used for FeP, at a constant 0.2 Å spacing for all proteins. Electrostatic potentials were calculated as the average over the potential at the eight grid points surrounding the atom of interest.

Crystal structures of the proteins were obtained from the Protein Data Bank (PDB)[30] and are listed in Table S1. Missing heavy atoms in the crystal structure were added from CHARMM22 parameters and hydrogen atom positions were added with HBUILD in CHARMM[31] version 35b1. For crystal structures containing more than one protein in the asymmetric unit or multiple side chain conformations, the calculated reduction potentials were averaged over all structures except for Eh HiPIP, where one structure was not used due to unusual Fe-S bond lengths. The redox site was defined to include all metal ligands up to the C_β for side chains of the protein. Thus, [Fe₄S₄(SCH₂)₄] was used for the [4Fe-4S] proteins, [Fe(SCH₂)₄] for Pf Rd, the copper, His39, His92, Cys89, and Met97 for Pl Pc, and the heme, His18, and Met80 for Ta cyt c. Note that while the calculation of ΔG_in terminates the ligand with a methyl group, the protein has a methylene group and the partial charges of the methyl group are redistributed accordingly for the calculation of ΔG_out[24].

Results and Discussion

Calculations of R_p and φ_p

The dielectric radii R_p (Eqn. 2) and the protein electret potentials φ_p were calculated for the six types of proteins (Table 1). The values of R_p follow the order Cyt c > HiPIPs > Fd ≈ Pc > Rd > FeP. While R_p, which reflects the burial of the redox site (Figure 4) but is also relatively independent of the size of the protein as measured by the molecular weight or number of residues. The values of φ_p follow a different order Pc < HiPIP < Cyt c < Rd ≈ Fd < FeP and the values of φ_bb, the contribution of the backbone to φ_p, have yet another order Pc Cyt c < HiPIP < Rd < Fd ≈ FeP. The backbone is the major contributor to φ_p, and interestingly, there is little correlation with the net charge of the proteins. The range in R_p, φ_p, and φ_bb for homologous proteins is relatively small while the difference between proteins with different folds is larger especially for φ_bb, indicating that R_p, φ_p, and φ_bb are characteristics of the protein folds. However, within a set of homologous proteins, the size of the protein appears to have more of an effect on R_p and the sequence has more of an effect on φ_p.

Table 1.

Properties of proteins and the calculated dielectric radii R_p and electret potentials at the redox site due to the full protein φ_p and the backbone φ_bb

Protein	Molecular Weight (D)	Number of Residues	Net Charge (e)	Rp (Å)	φp (eV)	φbb (eV)
HiPIP	8290 ± 900	75 ± 9	−2 ± 6	10.3 ± 0.4	0.39±0.15	0.36±0.04
Fd	8019 ± 2000	69 ± 16	−13 ± 4	8.9 ± 0.2	0.59±0.13	0.79±0.03
FeP	63988 ±4400	558 ± 24	−26 ± 9	6.4 ± 0.3	0.64±0.13	0.80±0.07
Pf Rd	5901	53	−8	6.7	0.59	0.68
Pl Pc	11466	105	−4	8.9	0.05	0.12
Ta Cyt c	11416	104	+9	11.2	0.47	0.21

Figure 4.

Spheres of radius R_p (red) located at the center of the metal sites and the Connolly surfaces (white) of TtHiPIP, CaFd, and AvFeP (top row, left to right) and Ta cyt c, Pl Pc, and Pf Rd (bottom row, left to right).

Electret-Dielectric Spheres Model

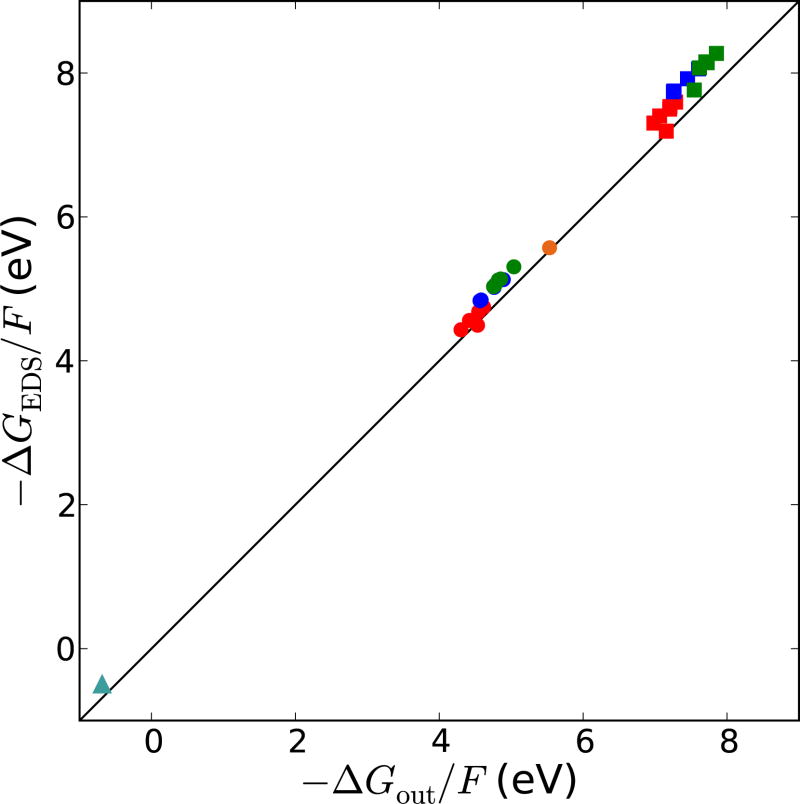
The electret-dielectric spheres model was used to calculate the redox energetics of the six proteins using R_p and φ_p For the calculations, R_c are 4.34 Å for [Fe₄S₄(SCH₂)₄] for the 1-/2-couple, (4.38 Å for [Fe₄S₄(SCH₂)₄] for the 2-/3- couple so the value for the 1-/2- is used), 3.46 Å for [Fe(SCH₂)₄] for the 1-/2- couple, and 3.35 Å for the blue copper site for the 1+/0 couple. The ΔG_EDS for the 1-/2- and 2-/3- couples in the concentric dielectric spheres of radius R_c and R_p with the appropriate φ_p are compared to the full PB calculation of ΔG_out (Figure 5) to see how well EDS can model the response to a change in the charge of the redox site. Although good agreement is expected since these quantities are derived from PB calculations albeit from a slightly different charge distribution of the redox site, the agreement also demonstrates that the EDS model is a way of decomposing the full PB calculation. Moreover, the important implication of the agreement is that the EDS model breaks down the solvation free energy into a dielectric response contribution, which depends on Q², and an electret contribution, which depends on Q. Thus, the degree of burial of the redox site will have a greater effect on the E° of redox sites with a larger absolute net charge, while the electret contribution to E° will be independent of the net charge. In addition, when the protein docks to a redox partner, R_p will increase if the redox site is buried by the redox partner but φ_p will be relatively unaffected so that only the dielectric response contribution to E° is expected to change significantly. One caveat is that the proteins are assumed to be fairly rigid so that neither the redox site nor the surrounding protein changes much upon reduction. This is thought to be true for the proteins studied here. For instance, even though nucleotide binding to FeP causes a conformational change that decreases the distance the [4Fe-4S]-cluster of FeP and the P-cluster of nitrogenase[32], the environmental change around the [4Fe-4S]-cluster has a small effect on E° (φ_p is reduced by < 0.05 eV and R_p increases by < 0.2 Å for Av FeP). Other metal sites such as the found in some copper proteins may experience significant changes in the coordination sphere, and other proteins undergo conformational changes. Thus, this approach should be considered a baseline, from which deviations can be studied.

Figure 5.

−ΔG_out/F versus − ΔG_EDS/F for the 1-/2- (circles) and 2-/3- (squares) redox couples of HiPIP (red), Fd (blue), FeP (green), Pc (cyan), and Rd (orange).

Classifying Redox Properties of Metalloproteins

A plot of R_p versus φ_bb shows that the burial of the redox site and the polarization of the backbone differ between non-homologous proteins but are relatively consistent within a given fold (Figure 6A), which demonstrates that such a plot can be used to classify protein types. Moreover, the values of R_p and φ_p are particularly interesting when comparing proteins with the same redox site when the site can achieve multiple redox couples, such as the [4Fe-4S] clusters. Since ΔG_in for two redox couples (−0.232 eV for 1-/2- and 3.452 eV for 2-/3-), the range of values of R_p and φ_p that correspond to a biological range of Eº from −0.6 V to 0.4 V can be found by solving Eqn. (3). When the values of R_p and φ_p for the [4Fe-4S] proteins are plotted along with the ranges consistent for each couple, the HiPIPs fall in the range corresponding to the 1-/2- couple, the Fd and FeP fall within the range corresponding to the 2-/3- couple (Figure 6B).

Figure 6.

A) R_p versus φ_bb for cyt c (purple), HiPIP (red), Fd (blue), FeP (green), Pc (cyan), and Rd (orange). B) R_p versus φ_p for HiPIP (red), Fd (blue), and FeP (green). The shaded area indicates the combination of R_p and φ_p that results in a E° between 0.4 V and E° = −0.6 V with ΔG_in = −0.232 eV (horizontal lines) for the 1-/2- couple or ΔG_in = 3.452 eV (vertical lines) for the 2-/3- couple.

Conclusions

The outer sphere contribution to the reduction potential for six types of metalloproteins are examined here in terms of the degree of burial of the redox site inside the protein and the permanent polarization of the protein around the redox site. The dielectric radius of the protein, R_p, is used to measure the degree of redox site burial and the protein electret potential, φ_p, is used to measure the permanent polarization. Using PB calculations, R_p is shown to be determined mainly by the burial of the redox site within the protein, with only slight dependence on the total size of the protein, while φ_p is shown to be due mainly to the backbone, although the side chains can alter the values somewhat. Thus, R_p and φ_p are mainly a function of the fold of the protein, but especially φ_p can be tuned by the sequence, which is consistent with our previous findings on the effects of fold and sequence[12].

The EDS model is a simple model of a redox protein that can be used to break down the total outer sphere response of the reduction potential into the dielectret response energy and the electret energy. Moreover, it shows that the dielectric response energy determined by R_p is dependent on Q² while the electret energy determined by φ_p is dependent on Q. The definitions of R_p and φ_p provide a useful way of quantitating comparisons of how redox site burial and protein polarization contribute to the redox properties of different proteins. R_p and φ_p, or better yet φ_bb, are characteristics of the fold and therefore are useful in identifying how an unknown protein may behave, especially in comparison to a known protein with the same redox site but perhaps different fold. In particular, R_p, and φ_p are shown to be useful for identifying the physiological couple for redox sites with more than one couple.