Variance of time-of-flight distribution is sensitive to cerebral blood flow as demonstrated by ICG bolus-tracking measurements in adult pigs

Abstract

Variance of time-of-flight distributions have been shown to be more sensitive to cerebral blood flow (CBF) during dynamic-contrast enhanced monitoring of neurotrauma patients than attenuation. What is unknown is the degree to which variance is affected by changes in extracerebral blood flow. Furthermore, the importance of acquiring the arterial input function (AIF) on quantitative analysis of the data is not yet clear. This animal study confirms that variance is both sensitive and specific to changes occurring in the brain when measurements are acquired on the surface of the scalp. Furthermore, when the variance data along with the measured AIF is analyzed using a nonparametric deconvolution method, the recovered change in CBF is in good agreement with CT perfusion values.

1. Introduction

The ability to monitor changes in cerebral blood flow (CBF) during the recovery of neurotrauma represents an important application for biomedical optics, since optical techniques are safe, non-invasive and portable, and are therefore easily applied at the bedside. Techniques that employ near-infrared light, such as continuous-wave near-infrared spectroscopy [1], frequency domain techniques [2], and time-resolved near-infrared spectroscopy (TR-NIR) [3] benefit from the relative transparency of tissue to light between 600 and 900 nm. Additionally, two important chromophores—oxyhemoglobin and deoxyhemoglobin—have spectral features in this bandwidth, and the only optical dye that is currently FDA-approved [4], indocyanine green (ICG) also has an absorption peak at 805 nm [5]. These properties readily allow the quantification of oxygenation and flow dynamics of the underlying tissue. However, a significant challenge to applying these techniques is that the light signal measured with probes positioned on the surface of the head must travel through the extracerebral layers (scalp, skull and CSF) before interrogating brain [6]. As a result, when developing an optical method to measure changes in brain oxygenation or CBF, both the sensitivity—i.e., the ability to reliably detect changes in CBF or hemoglobin concentrations —as well as the specificity—i.e., the confidence that a change in signal reflects only the brain and not the extracerebral tissue—must be investigated.

Dynamic contrast-enhanced (DCE) methods based on analysis of the statistical moments of measured distributions of times-of-flight of photons (DTOF) have been proposed as a way to increase the sensitivity to signal changes occurring in the brain [3]. Following an injection of the vascular tracer ICG, it is possible to record the concentration-dependent changes in three statistical moments of DTOFs: total number of photons, N, mean time-of-flight, <t>, and variance, V. To date, the moments-based technique has been applied to healthy volunteers [3,7], stroke patients [8,9], and other neurotrauma patients [10], and qualitative analysis strongly suggests that the time-dependent change in variance of the DTOF shows good sensitivity to absorption changes occurring in the brain. The work presented in this paper extends the previous moments-based methods to allow quantification of CBF changes and to confirm the sensitivity and specificity of the approach using an adult pig model.

Two quantification schemes are investigated in this paper. The time-to-peak (TTP) method has been highlighted by several groups [8,11,12] as a relatively straightforward method that can be applied to intensity normalized curves. As an alternative to this method, we also present a nonparametric deconvolution-based method [13–15] that enables the recovery of a relative blood flow index, dBF. This method differs from previously described quantitative deconvolution methods since only a relative blood flow index is recovered. The advantage of this approach compared to TTP measurements is that confounding effects due to arterial input function (AIF) are removed. We provide an overview of the theoretical basis for these two approaches within the context of moments-based analysis. Numerical simulations were used to demonstrate the influence of cerebral blood volume (CBV) and the AIF shape on TTP.

Using an adult pig model, we present the first within-subject comparison of moments collected on the surface of the scalp and moments collected directly on the brain. In Part A, the experiments involved manipulating the extracerebral layer to cause perturbations in both scalp blood flow and the extracerebral composition. In Part B, perfusion measurements were acquired directly on the brain and contralaterally on the scalp during normocapnia and hypocapnia—the latter causes CBF to decrease. Concomitant measurements were acquired by CT perfusion (CTP) for comparison.

2. Theory

2.1 Statistical moments of distributions of times-of-flight

Time-resolved near-infrared techniques measure the times-of-flight of individual photons at each detector over a few hundred milliseconds, building a histogram that approximates a distribution function. It has been demonstrated theoretically [16] and experimentally [17] that later time-bins correspond to a group of photons are statistically more likely to have interrogated deeper tissue structures. Therefore, changes in absorption of light in brain tissue, for example following the injection of dye, will differentially affect certain time bins in the DTOF. A transformation can be written as follows:

$$\Delta N_i={\displaystyle \sum _j^{}{A}_{i,j}\cdot \Delta {\mu }_{a,j},}$$ (1)

where ΔN_i is the change in the number of photons occurring in the i^th time-bin of the DTOF, Δμ_a,j is the change in absorption coefficient in the j^th layer, and A_i,j is the sensitivity matrix describing the transformation between these two functions. Since the experimentally measured DTOF is in reality a convolution between ΔN_i and the instrument response function (IRF), direct analysis of the DTOF is challenging [18]. A simpler approach is to use statistical moments, m_k, of the DTOF:

$$m_k(t)={\displaystyle \underset{t_1}{\overset{t_2}{\int }}{t}^{k}N(t)dt,}$$ (2)

where k is the order of the moment, and t₁ and t₂ are temporal integration limits. This approach reduces the dimension of the problem in Eq. (1), and the change in normalized moments is independent of the IRF [3]. Furthermore, it has been demonstrated previously that higher-order moments are more sensitive to changes occurring in deeper tissues [3]. A similar transformation to Eq. (1) can be written:

$$\Delta m_k={\displaystyle \sum _j^{}{A}_{{}_{k,j}}^{}\cdot \Delta {\mu }_{a,j}},$$ (3)

where A_k,j is the sensitivity matrix describing transformation between a change in the k^th moment and the change in absorption coefficient occurring in the j^th layer. The changes in three moments are used to describe the time-dependent changes that occur in the head following a bolus injection of dye: attenuation, A, which is related to the zeroth moment, mean time of flight, <t>, and variance of the DTOF, V. The mathematical definitions of these moments and the sensitivity factors corresponding to the change in these moments are given in Table 1 . Sensitivity factors can be determined with analytical [19] or Monte Carlo based methods [17,20].

Table 1. The three moments used in DTOF analysis, along with their formula and the abbreviations for their sensitivity factors.

Name	Related moment	Formula	Sensitivity factor
Attenuation	zeroth moment (area under the curve)	$A=\ln (m_0)$	MPP
Mean time of flight	first normalized moment	$\langle t\rangle =m_1/m_0$	MTSF
Variance	second centralized moment	$V=m_2/m_0-{\left(m_1/m_0\right)}^2$	VSF

MPP, mean partial pathlength; MTSF, mean time-of-flight sensitivity factor; VSF, variance sensitivity factor.

2.2 Indicator dilution theory

The previous section provides the mathematical basis for understanding how a change in the absorption coefficient of underlying tissues will produce a change in the measured moments. With dynamic contrast-enhanced techniques, this change in absorption is caused by the injection of an exogenous dye. If all other chromophores are assumed constant for the period of time required to collect a measurement, then the change in absorption coefficient in a tissue of interest as a function of time T is related to the tissue dye concentration, C, by

$$\Delta {\mu }_a(T)=C(T)\cdot \epsilon \cdot \ln (10),$$ (4)

where ε is the wavelength-dependent extinction coefficient of the dye. Following a bolus injection into a peripheral vein, the dye is delivered first to the heart, where it is subsequently pumped though the arterial circulatory system to all tissues of the body. According to the convolution theorem [21], the time-dependent tissue dye concentration is given by:

$$C(T)=F\cdot {\displaystyle \underset{0}{\overset{T}{\int }}{C}_a}(u)\cdot R(T-u)du,$$ (5)

where F is blood flow, C_a(T) is the time-dependent arterial concentration of dye (i.e., the AIF), and R(T) is referred to as the impulse residue function. R(t) represents the fraction of dye remaining in the tissue at time, T, following an idealized bolus injection. The convolution theorem can be derived from the Fick Principle and [22] provides additional details of this derivation. The function C_a(T) is common to all tissue regions in the body, while in contrast, R(T) and F are specific to each tissue region. Therefore, if C(T) is characterized from signal containing information from multiple regions of tissue, F and R(T) are in reality a weighted average of the tissue-specific functions represented in the probed region. In the case that the region-of-interrogation contains multiple layers of tissue, a more rigorous expression is found by combining Eqs. (3) and (4) with the convolution in Eq. (5), yielding the moment-specific solution:

$$\Delta m_k(T)={\displaystyle \sum _j^{}{F}_j\cdot \epsilon \cdot \ln (10)\cdot A_{k,j}^{}{\displaystyle \underset{0}{\overset{T}{\int }}{C}_a}(u)\cdot R_j(T-u)du}.$$ (6)

This convolution describes the fundamental relationship between the behavior of contrast agent in the tissue and the measured change in DTOF moments.

2.3 Quantification of blood flow changes

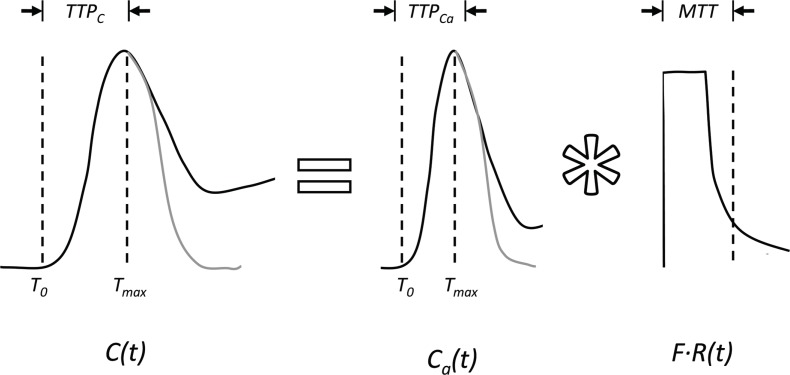
In this paper, we investigated two different approaches of measuring change in cerebral blood flow (CBF): the time-to-peak method and the relative deconvolution method. The time-to-peak of the tissue function (TTP_C) is defined as the time elapsed between the first appearance of dye, T₀, and the peak concentration of dye, T_max (Fig. 1 ).The time-to-peak can be related to CBF using the first moments of the tissue and arterial concentration curves. A property of a convolution is that the first moments are additive [23] and, therefore, Eq. (5) can be written as:

$${\langle t\rangle }_C={\langle t\rangle }_{Ca}+MTT.$$ (7)

The mean transit time (MTT), which is the first moment of the flow-scaled R(t), is equal to CBF/CBV (where CBV is cerebral blood volume) by the central volume principle [21]. Typically, tissue and arterial functions can be approximated by gamma variate functions [24]. However, over the interval T₀ < t ≤ T_max, these functions can be approximated by a symmetrical function, such as a Gaussian. In this case, the first moment equals the time-to-peak: ${\langle t\rangle }_C$ = TTP_C and ${\langle t\rangle }_{Ca}$ = TTP_Ca. Equation (7) can be rewritten as:

Fig. 1.

A depiction of the time-to-peak (TTP) method. Hypothetical tissue and arterial concentration curves including the effects of dye recirculation are shown by the solid black lines, along with their corresponding TTP values (TTP_C and TTP_Ca, respectively). The solid grey lines represent the first moments of the concentration curves without the effects of recirculation.

$$TT{P}_C=TT{P}_{Ca}+\frac{CBV}{CBF}.$$ (8)

Note that TTP_C not only depends on CBF, but also on CBV and TTP_Ca. Therefore, the influence of initial values of these two parameters must be considered when interpreting the relative change in TTP_C.

An alternative approach to characterizing the DCE curves is to perform a deconvolution to recover a relative blood flow index, dBF, representing the scalar quantity defined by the summation in Eq. (6). Generally, dBF for the k^th moment is

$$dB{F}_k={\displaystyle \sum _j^{}{F}_j\cdot \epsilon \cdot \ln (10)\cdot A_{k,j}^{}}.$$ (9)

It has been suggested that the variance of measurements acquired on the scalp has greater sensitivity to brain tissue and the influence of the extra-cerebral layers is relatively small [3]. If this is the case, the variance sensitivity factors for the extracerebral layers are approximately zero and the summation in Eq. (9) collapses to:

$$dB{F}_{\Delta V}\approx CBF\cdot \epsilon \cdot \ln (10)\cdot VSF,$$ (10)

where VSF is the sensitivity factor for the brain layer. If VSF remains constant between measurements, the change in dBF equals the true change in CBF (ΔCBF). To recover dBF, an algorithm incorporating physiologically derived constraints was used to stabilize the deconvolution, which is an inherently unstable process. This algorithm has been described and validated previously, both for CT perfusion [13], and near-infrared techniques in neonatal models [14,25] as well as in more complex multi-regional scenarios [1,15].

2.4 Influence of CBV and AIF on time-to-peak measurements

A series of numerical simulations were performed to determine the effect of CBV and AIF on the relationship between ΔTTP_C and ΔCBF. To investigate the effect of CBV, cerebral blood volume was related to cerebral blood flow according to the Grubb relationship [26]:

$$CBV=g\cdot CB{F}^{\gamma }.$$ (11)

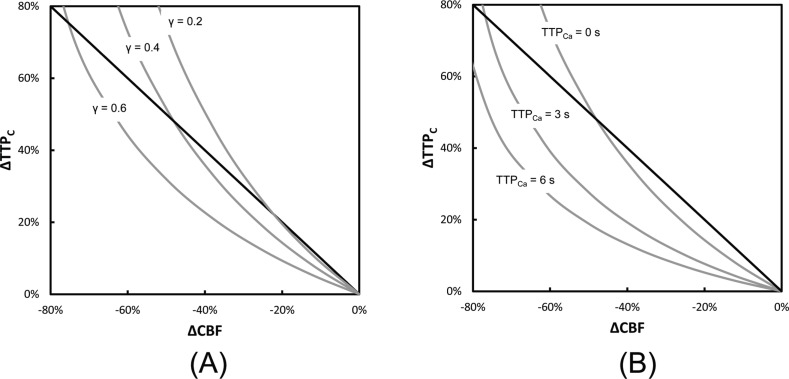
where g and γ are empirically derived parameters. Values for g and γ are described in the rhesus monkey as 0.8 and 0.38 [26], and similar CBV values have been measured in humans [27]. For the simulations, g was set to 0.8 and γ varied between 0.2 and 0.6 to investigate how the relationship between ΔTTP_C and ΔCBF (Eq. (8)) was affected by changes in CBV. In these simulations, TTP_Ca was set to zero, which represents the ideal case where the arterial input function is a Dirac delta function. The results are summarized in Fig. 2(A) . Similarly, the effect of TTP_Ca on Eq. (8) was performed by setting γ = 0.38 and varying TTP_Ca from 0 to 6 seconds. These results are summarized in Fig. 2(B).

Fig. 2.

The relationship between changes in tissue-curve TTP (ΔTTP_C) and changes in CBF (ΔCBF) (grey lines). (A) The effect of varying the relationship between CBV and CBF, which was performed using the Grubb relationship for γ = 0.2, 0.4 and 0.6, and setting TTP_Ca = 0. (B) The effect of varying the arterial TTP (TTP_Ca) from 0 to 6 s with γ set to 0.38. The solid lines show the negative unity slope for comparison.

The results of the simulations illustrated in Fig. 2 predict that the relationship between ΔTTP_C and ΔCBF can be strongly influenced by how CBV and CBF are related, and by the finite width of the AIF (i.e., TTP_CA).

3. Materials and methods

3.1 Instrumentation

A time-resolved near-infrared system, assembled in-house, was used for all optical measurements. A detailed description of this system and its characterization can be found in [28]. Briefly, a picosecond diode laser light source (LDH-P-C-810, PicoQuant, Germany) emitting at 802 nm, close to the peak absorption wavelength of ICG, was used. The laser output was attenuated by a neutral density filter to below ANSI safety limits for skin exposure (52.2 mW/cm² measured at fiber output compared to limit of 317 mW/cm² for 800 nm), and a pulse repetition rate of 80 MHz was used. The beam was coupled into a 1.5-m long multimode fiber (core = 400 μm and N.A. = 0.22; Fiberoptics Technology, Pomfret, CT) and directed onto the scalp. Photons exiting the tissue were collected by a fibre bundle 1.5 m long. The proximal end of the bundle was placed on scalp to provide measurements at a source-detector distance of 30 mm. The source and detector light-guides were held in place using a probe holder, constructed from black polychloroprene rubber. The distal end of the collection optode was secured in front of an electromechanical shutter (SM05, Thorlabs). Light transmitted through the shutter was passed through a bandpass filter (FEB800-10, Thorlabs) to remove fluorescence emission, before being collected by a Peltier-cooled photomultiplier tube (PMT). A photon count rate corresponding to roughly 1% of the laser repetition rate was used.

3.2 Animal experiments

All animal experiments were conducted following the guidelines of the Canadian Council on Animal Care and approved by the Animal Use Subcommittee at the University of Western Ontario. Duroc-cross pigs (n = 4) were acquired from a local supplier on the morning of the experiment. Animals were anesthetized with 1.75-3% isofluorane, tracheotomized and mechanically ventilated on an oxygen/medical air mixture. A femoral artery was catheterized to monitor heart rate and blood pressure and to collect blood gas samples. Body temperature was maintained between 37.5 and 38.5°C throughout the experiment.

Following a 1-h stabilization period, the rubber probe holder was placed on the head and fixed in place with tissue glue (Vetbond 1469SB, 3M Health Care, St. Paul, MN). The respiration rate, anesthetic levels and glucose levels were closely monitored and adjusted to ensure that physiological parameters remained stable throughout the experiment.

All four animals were included in Part A (i.e., the manipulation of the extracerebral layers) and two animals were included in Part B (i.e., the manipulation of CBF). In Part A, two sets of time-resolved measurements during inflow and washout of ICG (0.1 mg/kg, Cardiogreen, Sigma-Aldrich, St. Louis, MO) were acquired on the surface of the head. All measurements were separated by a delay of 20 min to allow sufficient time for clearance of the dye. After these scalp measurements, three incisions were made around the probe holder to reduce scalp blood flow. The tissue medial to the probe holder was left intact and the three incisions were cauterized to stop bleeding. Two sets of measurements were acquired under this ischemic scalp condition. After the exact position of the probe holder was marked, the underlying scalp was removed using the probe holder as a guide. Two measurements were acquired directly on the skull of the animals at approximately the same location as the previous measurements. Following the skull measurements, holes were carefully drilled through the skull in the same locations. Probes were inserted into the holes until they rested directly on the dura matter. In this way, two sets of time-resolved measurements were acquired on the brain.

In Part B, time-resolved measurements were acquired directly on the brain and then concomitantly on the contralateral scalp during normocapnia and hypocapnia. Computed tomography (CT) perfusion measurements were acquired using a CT scanner (LightSpeed QXi, GE Healthcare, Milwakee, WI) during normocapnia and hypocapnia. Each cine scan (80 kVp, 190 mA) was acquired for 40 s following injection of the contrast agent (1.0 mL/kg of 300 mg/mL 300-Isovue, Bracco Diagnostics Inc., Princeton, NJ) at an injection rate of 1 mL/s. Eight coronal slices (5 mm thick, temporal resolution of 1 s) were used to generate CBF maps using CT PERFUSION 4 software (GE Healthcare). Region-of-interests were drawn encompassing the cortical tissue of each hemisphere which approximate the region interrogated by the NIR light.

3.3 Data processing

Data processing was performed in the MATLAB programming environment (MathWorks, Natick, MA). Prior to the analysis, the distributions of times-of-flight of diffusely reflected photons were denoised using a three-step method which uses an Anscombe transformation, followed by wavelet denoising and then subsequent inverse Anscombe transformation, as described previously [18]. Denoising was done to reduce the susceptibility of higher moments to noise-related artifacts. Statistical moments were calculated from the denoised data sets using a previously described approach [20]. For calculating the moments, the upper integration limit was defined on the level of 5% of the maximum of the DTOF in order to reduce the influence of any remaining noise. Following subtraction of IRF contribution, moments were smoothed using the Savitzky-Golay algorithm (11.6 second window span, 6th order polynomial) to remove high-frequency components not related to dye kinetics.

Attenuation and variance of the DTOFs were analyzed using the time-to-peak method and the kinetic deconvolution method. When presenting the percent change in TTP, values were multiplied by −1 to facilitate comparison with the other indices. These four values were obtained for all time-resolved measurements. For Part A, analysis of differences between groups was performed using SPSS 17.0. Statistical significance was considered to be p < 0.05.

4. Results

4.1 Part A: Extracerebral manipulations

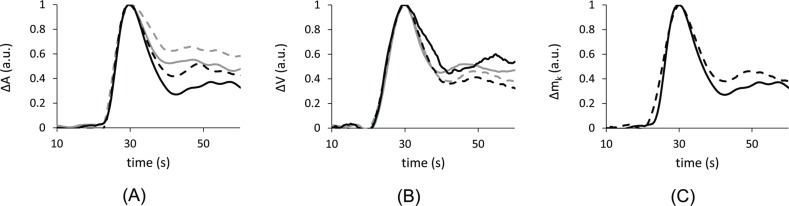
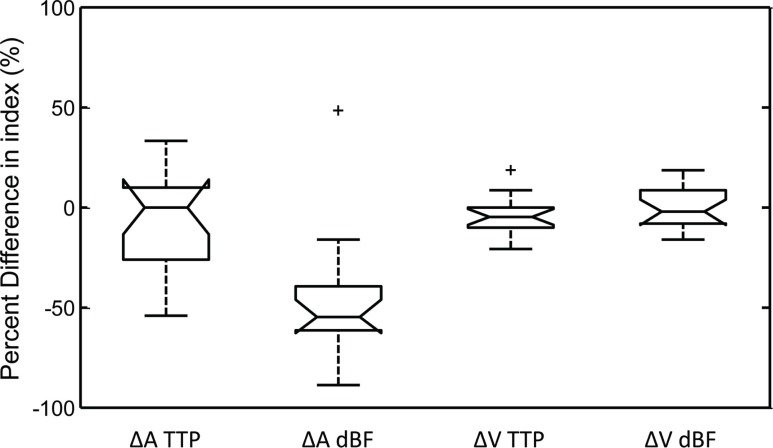
During these experiments, the extracerebral environment was manipulated in several ways to demonstrate the sensitivity of the measured parameters to perfusion changes in the different layers. Blood flow indices were determined under four conditions: (1) baseline, (2) following partial scalp ischemia, (3) probes placed on the skull, and (4) probes placed directly on the brain (17 data sets were collected from 4 animals). The shape of the tissue concentration curves acquired on the scalp showed large differences between the different moments of DTOFs (A, <t> and V). Furthermore, the higher order moments showed less variability when the extracerebral layer was manipulated compared to attenuation. Figure 3 shows the (A) attenuation ICG curves and (B) the variance ICG curves for one animal under the four conditions. This representative example was typical of all animals. Figure 3(C) shows the similarity between the ICG curves derived from the scalp variance measurements and the brain attenuation measurements.In terms of the qualitative blood flow indices (TTP and dBF) calculated from changes in attenuation (ΔA) and variance (ΔV) of the DTOF, Fig. 4 summarizes the percent difference between the measurements under the three extracerebral manipulations and the measurement directly on the brain. From the ΔA measurements, the average difference was −47.9 ± 7.8% for dBF and −8.0 ± 6.31% for TTP. From the ΔV measurements, the average difference was −0.2 ± 2.43% for dBF and by −3.5 ± 2.22% for TTP. The values for ΔV TTP, ΔV dBF, and ΔA TTP were not significantly different, but ΔA dBF was significantly lower than the other three parameters (p<0.001).

Fig. 3.

Representative curves from one animal (pig #2) under the four conditions. In this case, the thickness of the extracerebral layer was 10.2 mm. (A) Change in attenuation (ΔA) for measurements made on intact scalp (solid grey), ischemic scalp (dashed grey), skull (dashed black) and brain (solid black). (B) Change in variance (ΔV) for the same conditions. (C) ΔA measured on the brain (solid black) compared with ΔV measured on the scalp (dashed black).

Fig. 4.

Box-and-whisker plot of the difference in measured blood flow indices during the extracerebral manipulations compared to measurements acquired on the brain. Each parameter was evaluated from seventeen measurements acquired in four pigs. Boxes are bound by 1st and 3rd quartiles, with the centre line indicating the median. Error bars represent the range of the data, and crosses signify outliers. Only ΔA dBF was significantly different from the expected change of zero (p < 0.001). Additionally, none of ΔA TTP, ΔV TTP, or ΔV dBF differed significantly from each another, as measured by a paired t-test.

4.2 Part B: Hypocapnic challenge

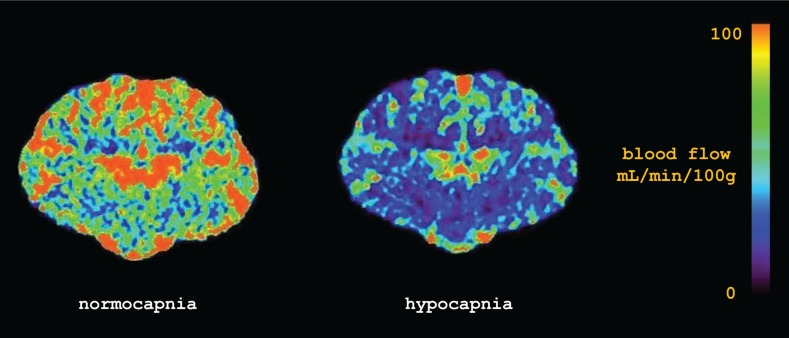
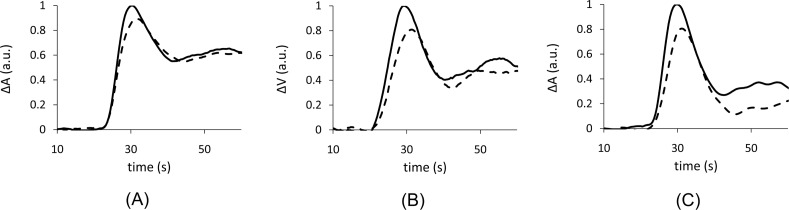
To augment the results of Part A, we further analyzed the sensitivity of the attenuation and variance TTP and dBF measurements to reductions in CBF caused by hypocapnia. Sequential bilateral measurements were made in two animals during normocapnia and hypocapnia. On the ipsilateral side, measurements were made directly on the brain and on the contralaterial side, measurements were made on the scalp. A reduction in CBF was observed during hypocapnia as depicted by the CBF maps generated by CT perfusion (Fig. 5 ).Qualitatively, a large reduction of amplitude was also observed in ΔV from the DTOFs measured on the contralateral site that reflected ΔA measured directly on the brain. There was also a decrease in ΔA measured on the scalp; however, it was less marked. Figure 6 provides a representative example of the ΔA and ΔV ICG curves during normo- and hypo- capnia.Table 2 summarizes the hypocapnic changes CBF and scalp blood flow measured by CT perfusion and the corresponding quantitative NIRS blood flow indices from the two animals. As a reference, the values obtained with the NIRS indices were compared to CBF values obtained by CT perfusion—the current clinical standard-of-care.

Fig. 5.

CT perfusion images of the brain from one animal during normocapnia and hypocapnia. The mean reduction in global CBF during hypocapnia was 43% in this case.

Fig. 6.

Representative curves from one animal under normocapnia (solid lines) and hypocapnia (dashed lines). (A) The change in attenuation (ΔA) made on intact scalp for the two conditions. (B) The change in variance (ΔV) made on intact scalp for the two conditions. (C) ΔA measured directly on the brain for the two conditions. Note: curves have been normalized to the maximum of the normocapnia curve.

Table 2. Percent change in the blood flow indices (TTP and dBF) obtained by analysis of attenuation (ΔA) and variance (ΔV) of DTOF during hypocapnia. Measurements were obtained directly on the brain and on the contralateral scalp. The error values are relative to the CBF change measured by CT perfusion (CTP). The thickness of the extracerebral layer was 10.2 mm and 11.2 mm for animal 1 and 2, respectively.

	Animal #1			Animal #2
	Percent Change	Error		Percent Change	Error
Ipsilateral (brain)
CTP brain	−32.0%	-		−44.4%	-
CTP scalp	-	-		-	-
ΔA TTP	−16.7%	15.3%		10.5%	54.9%
ΔV TTP	−21.1%	10.9%		4.5%	48.9%
ΔA dBF	−28.0%	3.9%		−45.5%	−1.1%
ΔV dBF	−31.6%	0.4%		−42.3%	2.1%
Contralateral (scalp)
CTP brain	−31.7%	-		−42.2%	-
CTP scalp	−19.1%	-		−29.3%	-
ΔA TTP	−16.7%	15.1%		−22.2%	20.0%
ΔV TTP	−20.0%	11.7%		−26.3%	15.9%
ΔA dBF	−20.9%	10.9%		−27.4%	14.8%
ΔV dBF	−31.6%	0.1%		−42.7%	−0.5%

5. Discussion and conclusion

A number of recent studies have suggested that the DTOF variance signal collected on the scalp is sensitive to decreased CBF in neurological disorders such as stroke [8,9]. The principle objective of this study was to verify these findings in an adult pig model in which scalp and cerebral blood flow could be manipulated. The results of Part A indicated that the ΔV signal was less sensitive to the extracerebral layer than the corresponding ΔA signal, as demonstrated by the greater variability in the shape of the ΔA ICG concentration curves over the different manipulations of the extracerebral layers. In general, the dynamics of the ΔA ICG curves reflected flow contributions from both scalp and brain. The curves shown in Fig. 3 illustrate that the ΔA signal acquired under the ischemic scalp condition resulted in the slowest kinetics, whereas the ΔA signal acquired directly on the brain have the fastest. The ΔA signals collected on the skull and the intact scalp demonstrated intermediate kinetics. The former was the most similar to the brain ICG curve since the thickness of the skull in this animal was only about 5 mm. Interestingly, the shape of the ΔA ICG curve acquired on the intact scalp was more similar to the ΔA signal collected on the skull rather than the signal acquired from ischemic scalp, despite the fact that the thickness of the extracerebral layer approximately doubled.

The influence on the extracerebral layer on the shape of the ΔA ICG curve is also reflected in the TTP and dBF measurements shown in Fig. 4. In both cases, the increased variability was not due to increased measurement error, but rather, it was attributed to the different flow contributions under the four conditions. The dBF measurements determined from the ΔA ICG curves that included an extracerebral layer were also consistently lower than the value determined from the brain ICG curve. This is because ΔA dBF represents a weighted average of the blood flow in each layer scaled by its mean partial pathlength. Therefore, the addition of each extracerebral layer resulted in a reduction in average blood flow within the region of interrogation

The faster ICG dynamics for the ΔA signal collected on the intact scalp would appear to be at odds with previous studies involving human subjects, in which a large difference in the shape of the ΔA and ΔV ICG curves was reported [3,8,29]. This apparent discrepancy can be attributed to differences in head anatomy between pigs and humans. We found that the pig’s scalp was highly vascularized and well perfused, likely to supply the thick temporalis muscles that originate at the temporoparietal region of the head. This observation was confirmed by CT perfusion, which revealed an average scalp blood flow of approximately 25 mL/min/100g. In contrast, scalp blood flow in the human head, as determined by a radioactive xenon clearance technique, was only about 5 mL/min/100g [30]. Given this difference, the ischemic scalp condition in Part A more closely reflects the intact human scalp.

In contrast to the ΔA signals, the ΔV ICG curves shown in Fig. 3(B) exhibited less sensitivity to the extracerebral tissue. In this case, there was a noticeable improvement in the similarity of the ICG curves acquired under the two extremes—i.e., on the brain and on the ischemic scalp—compared to the ICG curves obtained from the ΔA signal. This insensitivity to the top layers was also reflected in the lower variability observed in the ΔV TTP and dBF values across the four conditions, as shown in Fig. 4. As well, the underestimation of CBF by ΔA dBF was not observed when dBF was determined from the ΔV signals.

A secondary objective of this study was to compare two analytical methods of tracking change in CBF from the measured DTOF moments. The metric of choice in these studies has been time-to-peak, since it is relatively easy to calculate, and can be applied to normalized signals of variance of the DTOF. The ability to use the normalized signal makes TTP a robust longitudinal tool because it will be relatively insensitive to small changes in the signal amplitude, for example, from light coupling issues. This is a major benefit when using time-resolved equipment that is sensitive to light coupling and noise; however, time-to-peak also has some drawbacks that may not always be appreciated. In particular, a limitation of the TTP method is the implicit assumption that the AIF is consistent from measurement to measurement. In a clinical environment, it may be difficult to achieve an AIF of reproducible shape, since bolus injections are operator dependent, and the AIF depends on the cardiac output of the patient. For example, in the ipsilateral measurements acquired from animal #2 (Table 2), TTP measurements did not correctly identify the large decrease in CBF. Further investigation revealed that the arterial TTP changed in the opposite direction by 30%, obscuring the expected change in tissue TTP caused by hypocapnia. After adjusting the tissue TTP value to account for the unexpected change in arterial TTP, the change in ΔV TTP was −13.6% instead of 4.5%. In certain applications, such as inter-hemisphere comparisons in stroke patients, the absolute change in TTP (as opposed to the percent change in TTP) is independent of the arterial input function [8]. However, when percent change in TTP is used as a surrogate of percent change in CBF across serial injections of ICG, any variability in the arterial input function, including systemic physiological changes, will have a dramatic effect on the accuracy of the measurement.

Another important consideration with using the time-to-peak method as a surrogate CBF is that it also depends on CBV and the time-to-peak of the AIF (Eq. (8)). Therefore, it exhibits a non-linear relationship with CBF. The numerical simulations depicted in Fig. 2 demonstrate how the relationship between ΔCBF and ΔTTP can be altered by both the relationship between CBV and CBF (the Grubb relationship) and the finite width of the AIF. In these simulations, both effects cause the measured ΔTTP to be underestimated relative to the true change in CBF. Interestingly, when CBF decreases by about 80%, which would be similar to the expected perfusion reduction during clinical ischemia, this error is not as severe.

An alternative method to analyzing DCE data is derived from the convolution theory of tracer kinetics. If the AIF is measured, a deconvolution method can be used to recover the blood flow index, dBF, which is equal to the average blood flow in the region of interrogation weighted by the layer-specific sensitivity factor (Eq. (9)). In addition to accounting for variability in the AIF, the deconvolution method also decouples the effects of blood flow, blood volume and mean transit time. When ΔA is measured in the intact head, the acquired signal is highly sensitive to extracerebral tissue, and the average blood flow recovered by deconvolution will represent a weighted average of scalp and cerebral blood flow as shown in Fig. 4. In contrast, the region of interrogation represented in the ΔV signal has greater sensitivity to brain tissue and, therefore, the change in dBF better reflects the true change in CBF. Note that this relative approach is in contrast to previous methods that recover absolute CBF from time-resolved measurements acquired directly from the brain, or in a scenario where the scalp contribution is negligible. In these special cases, deconvolution of the ΔA signal permits recovery of absolute CBF in units of mL/min/100g, since the differential pathlength can be measured directly from the time-resolved data [25].

In Part B, concomitant measurements were acquired on the ipsilateral brain and the contralateral scalp during normocapnia and hypocapnia in two animals. In addition, CT perfusion measurements were acquired under the two conditions to measure scalp and cerebral blood flow. Table 2 summarizes the percent change in TTP and dBF caused by hypocapnia for both animals. Despite a small sample size, three observations can be made about these results. First, all four ΔV dBF values and the two ΔA dBF values derived from ispilateral measurements exhibited good agreement with the CBF values from CT perfusion. Second, contralateral ΔA dBF measurements were almost identical to the scalp blood flow values from CT perfusion. When considered along with the results of Part A, this suggests that ΔA is mainly interrogating the extracerebral layer, while ΔV is sensitive to the brain. Finally, all eight TTP measurements (when the corrected TTP measurement for animal #2 as described above is substituted) showed a consistent underestimation of the CBF change measured by CT perfusion. This underestimation occurred whether the measurements were acquired on the scalp or directly on the brain. The numerical simulations presented in Section 2.4 provide insight into this underestimation: the average arterial TTP in the animal experiments was about 4 seconds and the Grubb exponent, γ, was about 0.4 (determined from the CT perfusion data). For this combination, a 40% decrease in CBF is predicted to result in a roughly 20% change in TTP.

The salient finding of this study was that the variance of the DTOF was relatively insensitive to changes in extracerebral blood flow and optical properties caused by physically manipulating the extracerebral layers in the pig. A corollary finding was that the variance signal measured on the scalp was sensitive to changes in CBF. Finally, while both TTP and dBF obtained from the variance signal showed similar robustness in the presence of extracerebral variability, dBF had better sensitivity to hypocapnic CBF changes when compared to CT perfusion. This improvement suggests a benefit to measuring the AIF during acquisition of DCE time-resolved data. Despite differences in scalp blood flow in this animal model compared to humans, the methods presented in this study for measuring CBF changes are translatable to the human adult.