In vivo vibrometry inside the apex of the mouse cochlea using spectral domain optical coherence tomography

Abstract

Sound transduction within the auditory portion of the inner ear, the cochlea, is a complex nonlinear process. The study of cochlear mechanics in large rodents has provided important insights into cochlear function. However, technological and experimental limitations have restricted studies in mice due to their smaller cochlea. These challenges are important to overcome because of the wide variety of transgenic mouse strains with hearing loss mutations that are available for study. To accomplish this goal, we used spectral domain optical coherence tomography to visualize and measure sound-induced vibrations of intracochlear tissues. We present, to our knowledge, the first vibration measurements from the apex of an unopened mouse cochlea.

1. Introduction

Hearing is a multi-stage complex process. The external ear collects and funnels sound pressure waves to the tympanic membrane (eardrum). Vibrations of the tympanic membrane are carried through the middle ear ossicles, the malleus, incus, and stapes, and transferred to the auditory portion of the inner ear, the cochlea. The resultant pressure waves travel down the length of the fluid-filled cochlea and cause the organ of Corti to vibrate [1]. The organ of Corti transduces these mechanical vibrations into electrical signals that propagate along the auditory nerve to the brain. There is a gradient of the mass and stiffness of the organ of Corti along the length of the cochlea. These passive mechanical properties tune each region to a specific frequency of sound. Thus, the base of the cochlea resonates at higher frequencies and the apex at lower frequencies. In addition, the magnitude of the organ of Corti vibration is amplified in a nonlinear fashion because of force production by outer hair cells [2]. This amplifies vibrations at low sound levels more than high sound levels.

Previous experiments used laser Doppler vibrometry to investigate this process by measuring vibrations of the organ of Corti in large rodents such as gerbils [3], guinea pigs [4–6], and chinchillas [7]. Since sound transduction is directly based upon organ of Corti vibrations, these measurements provide an important way to understand basic mechanisms of hearing. However, these measurements are difficult because the cochlea is encased in bone and the intracochlear structures of interest are composed of soft tissues with low reflectance [8]. Thus, a small opening in the cochlear bone is usually made and reflective microbeads are positioned on the structures to be measured. Unfortunately, making an opening in the cochlea can damage the function, which reduces the likelihood of obtaining reliable results.

Our current understanding of structural proteins necessary for normal hearing has rapidly expanded within the last decade [9], and there are many strains of hearing-impaired mice due to mutations in these proteins. Since these mutations likely affect the organ of Corti vibratory pattern, it is highly desirable to be able to measure the vibration to understand disease pathophysiology [10]. The small size of the mouse cochlea makes routine laser Doppler vibrometry challenging because opening it is more likely to produce trauma that alters cochlear function. Only one group has been able to make vibration measurements in transgenic mice, and these measurements were made without opening the cochlea [11]. They used a self-mixing, laser-diode interferometer that was focused through the round window membrane to visualize the organ of Corti. Because of the relatively long depth of focus, one downside to this approach is that round window membrane vibration may contaminate the measurements [12]. As a result, the consistency of these measurements has been questioned [2].

In order to reliably and accurately measure vibrations of the organ of Corti within living mice, we developed a system based on optical coherence tomography (OCT), a noninvasive interferometric imaging technique. Previous OCT imaging experiments by our lab and others have shown it to be effective in resolving soft tissues within the cochlea, including the various substructures that compose the organ of Corti [13–16]. Vibration measurements have been made using OCT within the opened guinea pig cochlea in vivo [17,18]. Because the bone surrounding the mouse cochlea is thinner than that of the guinea pig cochlea, we sought to use OCT to perform in vivo vibrometry of the unopened mouse cochlea. Herein, we demonstrate the ability of our system to image inside the apex of the unopened, living mouse cochlea and to measure nanoscale vibrations of the organ of Corti.

2. Materials and methods

2.1. OCT system description

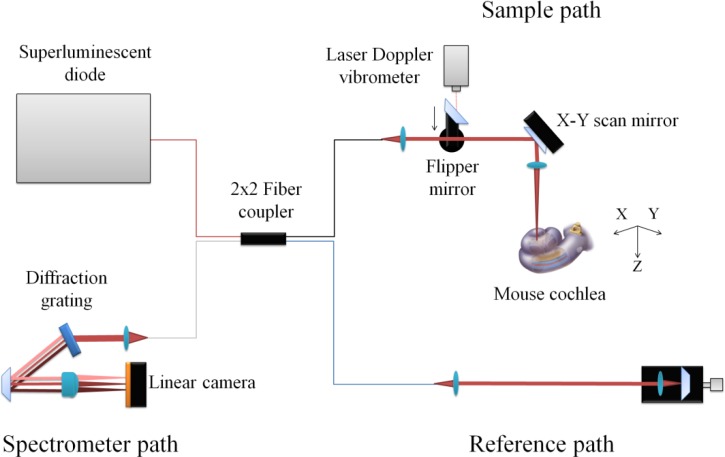
Previously, we described our spectral domain OCT system for in vitro cochlear imaging [13]. We have now modified it to improve our ability to collect in vivo vibrometric data. A schematic of the system is shown in Fig. 1 . The source was a superluminescent diode (SLD) running in high power mode (Broadlighter S930-B-I-10, Superlum, Ireland). The SLD has a center wavelength of ~935 nm and a spectrum full width at half maximum (FWHM) of ~70 nm. The SLD was connected to one end of a 2x2 (50:50) fiber-fused coupler (WA10500202B2111-BC1, AC Photonics, Santa Clara, CA). One of the output ports was directed to the X-Y scanning mirror (OIM101, Optics in Motion LLC, Long Beach, CA) of an upright microscope (MOM, Sutter Instruments, Novato, CA), which served as the sample arm. The other output port was used as the reference arm. The average power measured after the objective (an achromatic lens with a focal length of 100 mm) was ~4 mW.

Fig. 1.

Schematic of the spectral domain OCT system. A flipper mirror was used to direct either the light from the laser Doppler vibrometer or the superluminescent diode into the sample path.

The reflected light from both the sample and reference arms was combined in the fiber coupler. The resulting interferogram was recorded using a custom spectrometer based on a high speed line scan camera (AViiVA SM2 CL 2014, E2V, Tarrytown, NY). A camera integration time of 30 µs with a line rate of ~16 kHz was used for all data presented herein. The dynamic range of the line scan camera was ~70 dB, as referenced to the standard deviation of the dark current and read noise. To generate the depth-resolved sample reflectivity or A-line, the interferogram was transformed into k-space, linearized, and the magnitude of the Fourier transform was computed. All of the software used was custom written in MATLAB (MathWorks, Natick, MA). The signal-to-noise ratio of the system was ~90 dB and the axial resolution was ~10 µm. These were determined, respectively, by comparing the A-line peak of a mirrored surface to the standard deviation of a region 500 µm away and the FWHM of the A-line peak. The lateral resolution, determined experimentally by imaging microspheres, was ~10 µm.

2.2. Vibrometry using OCT

Before collecting vibration information, we first chose an axial line (A-line) of interest from a cross-sectional image (B-scan). We then recorded two M-scans (A-lines recorded as a function of time) with 5,000 time samples (A-lines) with a sample interval of 62 µs during sinusoidal stimuli with specific amplitude, frequency, and phase. Using coherently interleaved sampling [19], we improved our effective sampling rate by a factor of two by introducing a phase shift in the stimulus between the two M-scans and then interleaving to generate a 10,000 A-line M-scan with a sampling interval of 31 µs. For the depths of interest, a second Fourier transform was performed along the time axis of the interferometric phase (the angle of the first Fourier transform). The magnitude of the second Fourier transform was the vibration magnitude; the angle was the vibration phase. The vibration magnitude was converted to units of nanometer (nm) by multiplying by λ/(4πn), where λ is the center wavelength of the light source and n is the sample refractive index. For the intracochlear soft tissues, we assumed a refractive index of 1.4. We averaged multiple trials to ensure that our signal was above a noise threshold, defined to be the mean plus three times the standard deviation of the noise at nearby frequencies to the stimulus frequency.

2.3. Animal preparation

The Stanford University Institutional Animal Care and Use Committee approved the study protocol. Surgical access to the mouse cochlea was performed similarly to what was previously described for electrophysiological measurements [20,21]. Briefly, a five week old, wild-type mouse was first anesthetized with a ketamine/xylazine mixture and secured in a head holder. Supplemental doses of anesthesia were administered to ensure areflexia to paw pinches. The pinna was removed along with the muscles covering the bulla. The ramus of the mandible and the surrounding muscles were also removed to allow for a steeper incident imaging angle. The bulla was then carefully opened medial to the tympanic annulus to expose the cochlea. The mouse was then positioned on a heating pad atop a moveable platform under the OCT system. The platform could move in the x, y, and z directions and included an adjustable ear bar with an attached speaker and microphone (type 4182, NEXUS conditioning amplifier type 2690, Brüel & Kjær, Denmark). The ear bar was inserted into the ear canal of the mouse and secured. Sound stimuli were generated digitally using MATLAB and converted to analog signals using a digital-to-analog (DAQ) converter (PXI-6259, National Instruments, Austin, TX). The signal was sent to the speaker connected to the ear bar, which was calibrated with the microphone.

2.4. Plastic-embedded cochlear histology

The cochlea was first excised and the stapes removed. The cochlea was then bathed in a mixture of 2.5% glutaraldehyde and 1.5% paraformaldehyde in 0.1M phosphate buffered water (PB) at 4°C overnight. The following day, the cochlea was rinsed with dH₂O 3 times for 5 minutes and placed in 1% osmium tetroxide for 45 minutes. The cochlea was rinsed again with dH₂O 3 times for 5 minutes and placed in 0.12M EDTA in 0.1M PB with 1% glutaraldehyde, with the pH adjusted to 7. Next, the cochlea was placed on a gentle tilting shaker at room temperature and decalcified for 3 days. The EDTA solution was changed every day. Once decalcified, the cochlea was rinsed with dH₂O 2 times for 15 minutes. The cochlea was dehydrated in 50% ethanol and then 70% ethanol for 15 minutes each. This was followed by 2 changes of 95% ethanol and 4 changes of 100% ethanol for 15 minutes each. It was finally dehydrated for 30 minutes in propylene oxide (PO).

The cochlea was gradually incorporated into Araldite (percentages by volume: 46.6% Araldite 502 - #10900, 39.6% DDSA - #13710, 12.1% DBP - #13100, and 1.6% DMP-30 - #13600, Electron Microscopy Sciences, Hatfield, PA) through 1:1 mix of Araldite to PO for two hours and then 2:1 mix of Araldite to PO overnight at room temperature. OCT B-scans were collected at this point. Finally, the cochlea was immersed in Araldite for 2 hours in a vacuum at room temperature, orientated to the desired position in a coffin mold filled with degassed Araldite, and placed in 60°C to harden for at least three days. The specimen was sectioned serially with 10 μm thickness (RM2255, Leica, Buffalo Grove, IL). Sections were stained with 1:10 dilution of Epoxy Stain (#14950, EMS, Hatfield, PA) with dH₂O for two minutes and then washed in tap water. The dry sections were embedded with ClearMount (MMC0126, American MasterTech), and the coverslips were sealed with nail polish. The slides were viewed on an upright microscope (Axio Scope.A1, Zeiss, Germany), and images were taken using a color camera (AxioCam MRc, Zeiss, Germany).

3. Results

3.1. Vibrometry of piezo-electric membranes

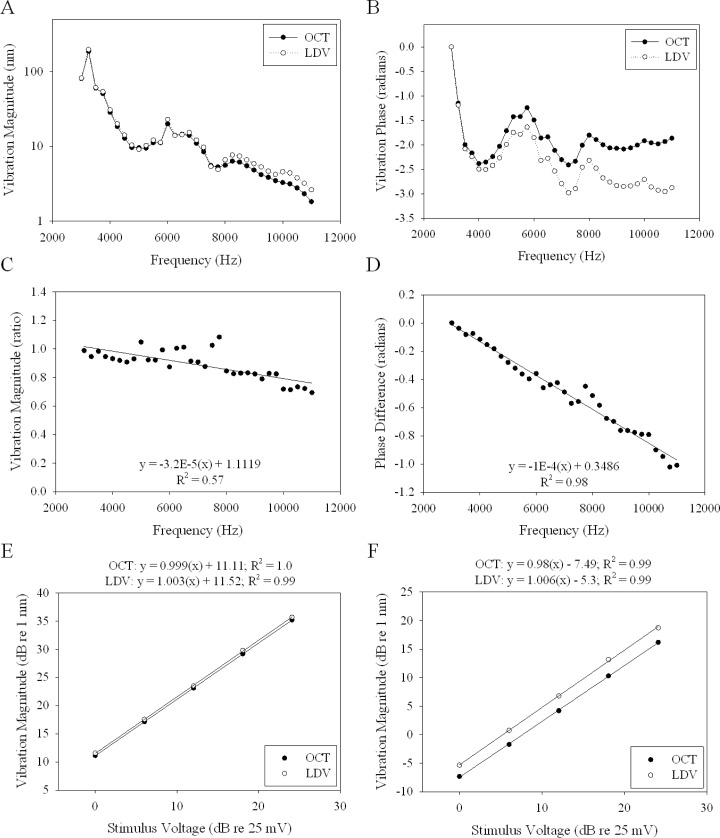
To characterize the frequency response of our OCT system, we made vibration measurements from the surface of a piezo-electric membrane at stimulus frequencies between 3 and 11 kHz with stimulus amplitudes of 200 mV. We compared the results to measurements made with a commercial laser Doppler vibrometer (LDV) (OFV-5000, Polytech, Irvine, CA) that we have used previously for in vitro cochlear experiments [21,22]. The LDV was incorporated into the sample path of the OCT system as shown in Fig. 1. The results are summarized in Figs. 2A to 2D. The frequency response demonstrates that there are various peaks and valleys due to the innate resonances of the piezo-electric membrane. Importantly, the vibration magnitude measured with our OCT system followed the same pattern as that measured by the LDV system. However, there was a roll-off in the magnitude as the period of the stimulus approached the integration time [19]. For simplicity, we approximated this roll-off with a linear fit, which yielded an equation with a slope of −0.032 kHz⁻¹ and a y-intercept of 1.1119. The x-intercept for this fit is 28.8 µs, which is similar to the roll-off that would be expected with our effective sampling rate of 31 µs. For all further presented data, we compensated for this roll-off using this frequency-dependent scaling factor.

Fig. 2.

(A) Plot of the piezo-electric membrane vibration magnitude, as measured by OCT and LDV, to stimulus frequencies between 3 and 11 kHz at a stimulus amplitude of 200 mV. (B) Plot of the piezo-electric membrane vibration phase to the same parameters as in (A). (C) The ratio of the magnitudes, OCT divided by LDV. The equation of the linear fit and the R² value are shown. (D) The phase difference, LDV – OCT. The equation of the linear fit and the R² value are shown. (E) Growth curves as measured by OCT and LDV to 4 kHz stimulus. The equation of the linear fit and the R² value are shown. (F) Growth curves as measured by OCT and LDV to 10 kHz stimulus. The equation of the linear fit and the R² value are shown.

There was also a frequency-dependent phase difference between the systems. The slope of the linear fit of the phase difference (LDV – OCT) was −0.1 radians/kHz. This was the result of a fixed phase delay between the two systems. To compensate for this artifact during our experiments, we referenced all phase values recorded from the intracochlear structures to phase values from the malleus/incus complex of the middle ear, essentially referencing the output to the input.

To test the amplitude response of our OCT system, we compared the slopes of growth curves measured on the piezo-electric membrane at 4 and 10 kHz with stimulus amplitudes of 25, 50, 100, 200, and 400 mV. We also compared the results to measurements made with a commercial LDV. The growth curves in response to a 4 kHz stimulus are shown in Fig. 2E. The growth curves in response to a 10 kHz stimulus are shown in Fig. 2 F. We found the slopes to be ~1 dB/dB as measured using both systems.

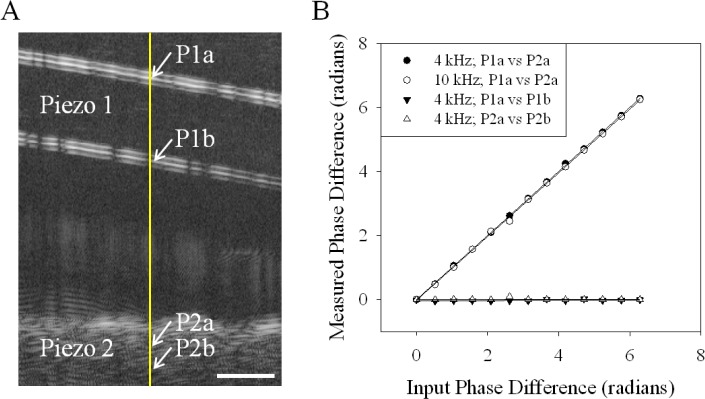
An important consideration for performing the desired experiment was to be able to measure the vibration of an intracochlear structure that lies deeper than the overlying bone which does not vibrate. We wanted to ensure that our approach permitted the simultaneous measurement of phase differences between structures at different depths along a single A-line. We positioned a piece of clear plastic attached to one piezo-electric membrane above another piezo-electric membrane with a piece of tape on top. A B-scan of this setup is shown in Fig. 3A . We then drove the two piezo-electric membranes with sinusoidal stimuli at the same frequency, but with different phase. We did this at both 4 and 10 kHz. We then compared the vibration phase at the depths pointed to by the white arrows in Fig. 3A. We looked at P1a vs P2a. For comparison, we also looked at the phase difference at different depths in each piezo-electric membrane, P1a vs P1b and P2a vs P2b. The input phase versus the measured phase is shown in Fig. 3B. There was excellent agreement between the expected and measured values.

Fig. 3.

(A) A B-scan image of the 2 piezo-electric membrane setup. Piezo 1 labels the transparent plastic that was attached to one piezo-electric membrane. Piezo 2 labels the tape atop the second piezo-electric membrane. The A-line that was recorded from is highlighted by the yellow line. The depths that were compared are indicated by white arrows and labeled P1a, P1b, P2a, and P2b. The scale bar is 200 µm. (B) The measured phase difference at two different depths plotted against the input phase difference to the two piezo-electric membranes at 4 or 10 kHz. 4 kHz; P1a vs P2a refers to a comparison between the labeled depths. The equation of the linear fit was y = 1.0015(x) – 0.0002 and the R² value was 0.99. 10 kHz; P1a vs P2a refers to a comparison between the labeled depths. The equation of the linear fit was y = 0.996(x) – 0.0243 and the R² value was 0.99. 4 kHz; P1a vs P1b refers to a comparison between the labeled depths. The equation of the linear fit was y = 0.0048(x) – 0.0425 and the R² value was 0.18. 4 kHz; P2a vs P2b refers to a comparison between the labeled depths. The equation of the linear fit was y = −0.0005(x) + 0.0084 and the R² value was 0.0013.

3.2. In vivo imaging at the apex of the unopened mouse cochlea

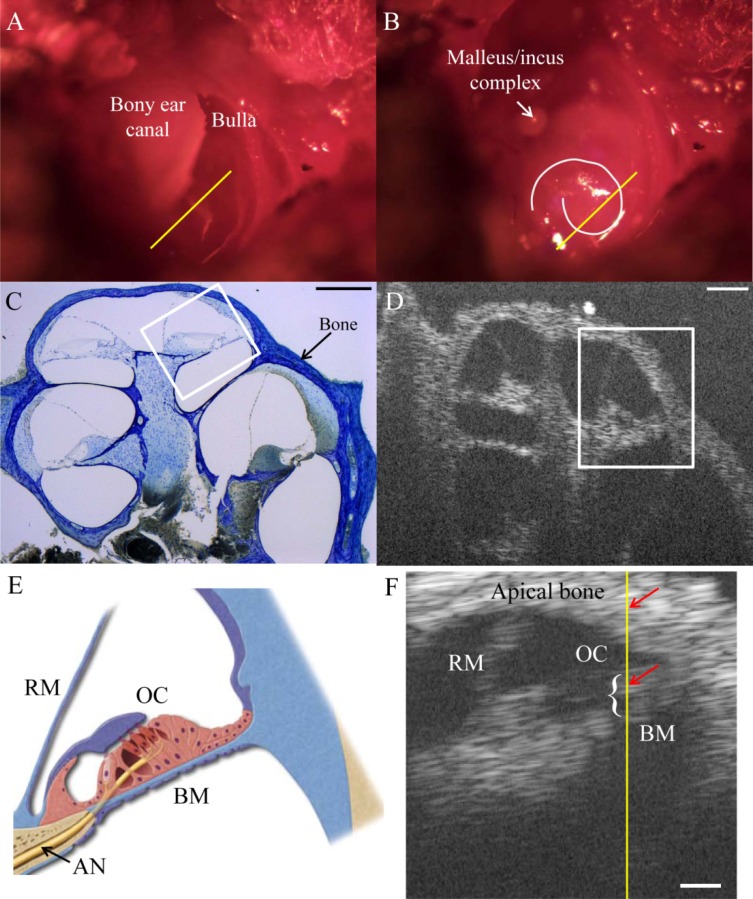
For the in vivo experiment, we first positioned the mouse on its side, with the left ear up. We then rotated the head counterclockwise until the malleus/incus complex of the middle ear was visible through the opening that was made in the bulla. We recorded the middle ear response to sound stimuli from 3 to 11 kHz at 80 dB SPL. We then tilted and rotated the mouse to view the apex of the cochlea. A camera image of the view is shown in Fig. 4A . The bony ear canal is labeled and covers half of the cochlea. The approximate scan path is shown in yellow. Figure 4B shows the view with the bony ear canal removed. The apical cochlear turn is highlighted in white. For reference, Fig. 4C shows a plastic-embedded histologic image of a cochlear cross-section at a position similar to the scan path. The otic capsule bone surrounding the cochlea is dark blue. Figure 4D shows an unaveraged OCT image of a cochlear cross-section from a fixed and decalcified cochlea in vitro. This whole cochlear view is not achievable in vivo because opening the bony ear canal fully damages middle ear function. The structures of interest are boxed in Figs. 4C and 4D. Figure 4E is a diagram depicting the structures of interest. A B-scan that was averaged 10 times showing the cross-sectional cochlear view in the living mouse is depicted in Fig. 4F. This B-scan was the right half of the scan path shown in Fig. 4A. This cross-sectional view was approximately a half turn from the mouse cochlear apex.

Fig. 4.

(A) Camera image of the view of the cochlea from the left ear of a mouse. The bony ear canal and opened bulla atop the cochlea are labeled. The approximate scan path is shown in yellow. (B) The view with the bony ear canal removed. The apical cochlear turn is highlighted in white. The approximate scan path is in yellow. (C) Histologic image of a cochlear cross-section. Bone is in dark blue. The structures of interest are boxed. The scale bar is 200 µm. (D) OCT cross-sectional B-scan of a fixed and decalcified cochlea in vitro. The structures of interest are boxed. The scale bar is 200 µm. (E) A cross-sectional diagram of the intracochlear structures. Ressiner’s membrane (RN), the organ of Corti (OC), basilar membrane (BM), and the auditory nerve fiber (AN) are labeled. (F) B-scan image of the organ of Corti in the living mouse that was averaged 10 times. The A-line where vibration measurements were made is shown in yellow. Each red arrow points to a depth for the representative vibration data shown in Figs. 5A and 5B. The white brace shows the depth range of the organ of Corti that was analyzed for Figs. 5C and 5D. The scale bar is 100 µm.

3.3. In vivo vibrometry at the apex of the unopened mouse cochlea

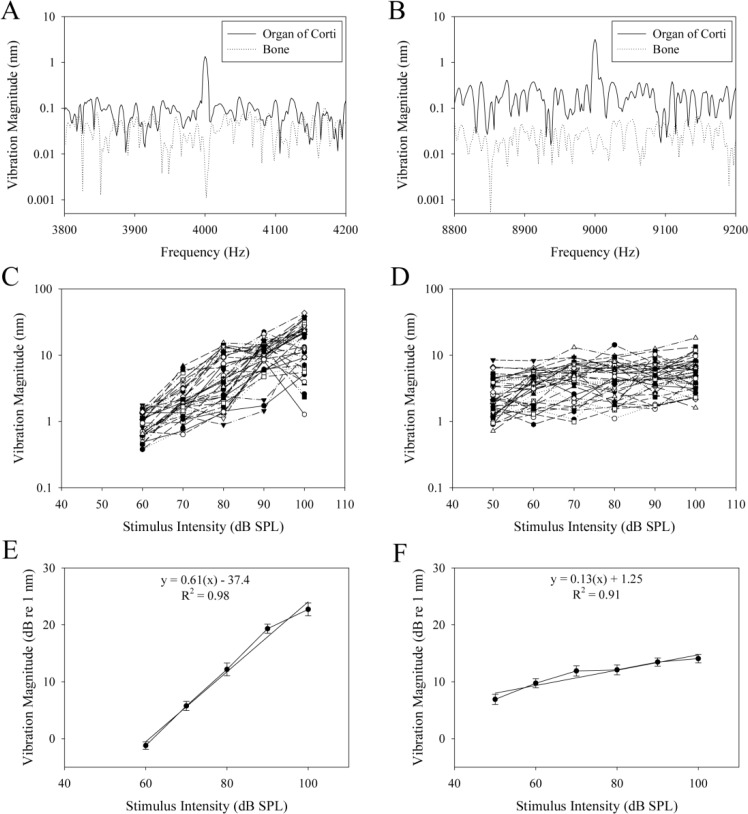
The vibration data from the A-line highlighted in Fig. 4F is summarized in Fig. 5 . We averaged multiple trials to lower the noise threshold. Each trial consisted of one interleaved M-scans of 10,000 A-lines. Because the organ of Corti displacement was greater with higher stimulus intensities, we averaged 25, 25, 16, 16, 9, and 9 trials for stimulus intensities of 50, 60, 70, 80, 90, and 100 dB SPL, respectively. Figures 5A and 5B show the frequency response to 4 kHz and 9 kHz sine wave stimuli, respectively, at 60 dB SPL. The presented data demonstrate vibration of the organ of Corti from one depth at the stimulus frequency. In contrast, data collected simultaneously from another depth within the overlying otic capsule bone demonstrate that there was no movement at the stimulus frequency. The two depths were pointed to by red arrows in Fig. 4F. Thus, our system was able to differentiate vibrations between different structures without contamination.

Fig. 5.

(A) Representative vibration magnitude in response to a 4 kHz stimulus at 60 dB SPL. (B) Representative vibration magnitude in response to a 9 kHz stimulus at 60 dB SPL. (C) Vibration magnitude in response to 4 kHz stimuli ranging from 60 to 100 dB SPL for all depths within the organ of Corti. There were no measureable responses above the noise threshold with a 50 dB SPL stimulus. (D) Vibration magnitude in response to 9 kHz stimuli ranging from 50 to 100 dB SPL for all depths within the organ of Corti. (E) Averaged data from (C) with standard errors. The equation of the linear fit and the R² value of the fit are shown. (F) Averaged data from (D) with standard errors. The equation of the linear fit and the R² value of the fit are shown.

To aggregate the data, we then went through each depth in the region indicated by the white brace in Fig. 4F and compared the vibration magnitude at the stimulus frequency to the noise threshold. This was done for all stimulus intensities. The magnitudes were recorded only if they were greater than the noise threshold. Figures 5C and D show growth curves of stimulus intensity versus vibration magnitude. In these examples, we show the vibrations measured at each depth within the region outlined by the brace in Fig. 4F for 4 kHz and 9 kHz, respectively. While the general trend demonstrates more displacement with higher stimulus intensity, there was some variability between depths. Figures 5E and 5F show the averaged curves from Figs. 5C and 5D, respectively. The vibration magnitude was converted to dB, referenced to 1 nm. The slope of the stimulus intensity versus vibration magnitude at 4 kHz was 0.61 dB/dB; the slope at 9 kHz was 0.13 dB/dB. The reason these slopes were <1 dB/dB is because of the nonlinear amplification within the organ of Corti.

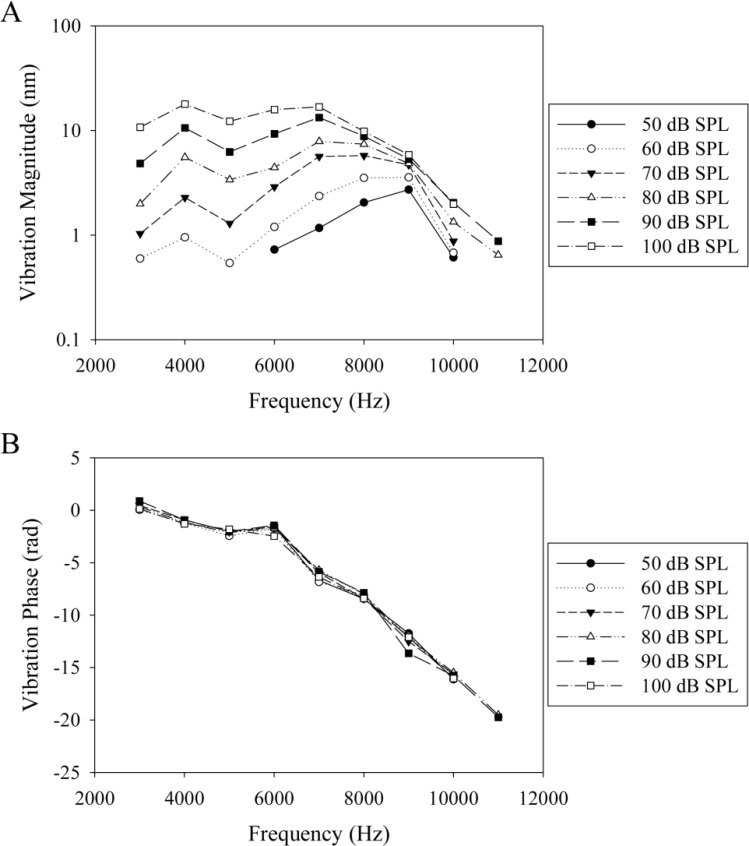
We then collected data over the frequency range of 3 to 11 kHz and averaged the responses from the depths within the organ of Corti, as shown in Fig. 4F. As seen in Fig. 6A , the region of the cochlea that we recorded from has a characteristic frequency (CF), defined as the resonance frequency at low stimulus intensities, of ~9 kHz. The CF shifts lower with increasing stimulus intensity, consistent with the cochlear nonlinearities found in larger rodents [1,7]. The vibration phase, as shown in Fig. 6B, was referenced to the phase of the malleus/incus complex. The progressive phase lag with increasing frequency is consistent with a traveling wave propagating along the length of the cochlea [1].

Fig. 6.

In vivo vibration magnitude (A) and phase (B) data from the organ of Corti at the apex of the unopened mouse cochlea.

4. Discussion

Herein, we demonstrate that spectral domain OCT can image the interior structures of the living mouse cochlea and measure nanoscale vibrations within the organ of Corti near the cochlear apex. The CF of the region we recorded from was ~9 kHz, which is close to the predicted characteristic frequency for a region approximately a half turn from the mouse helicotrema, the apical end of the cochlea [23]. Furthermore, the shape of the magnitude and phase plots and the 0.13 dB/dB slope of the stimulus intensity versus vibration magnitude at the CF are comparable to previous measurements from the cochlear base of larger mammals [6,7]. This suggests that the apical turn of the mouse cochlea functions similarly to the basal turn of larger rodents. As well, this research now opens up the possibility of investigating cochlear mechanics in transgenic mouse models of hearing loss.

An important consideration for this type of experiment is to manage animal motion. It takes less than three seconds to collect and save the raw camera data of a single trial of 10,000 A-lines at a specific stimulus frequency and amplitude. For our in vivo experiment, we chose to process and average the data before saving to reduce hard-drive usage. It took approximately an hour to collect the data at six different stimulus levels and nine different frequencies with the requisite averages. When fixed in place and anesthetized, the head of the mouse remained still over this time period, as assessed by viewing B-scans of the cochlea before and after the experiment. Nevertheless, it is certainly possible that small (<10 µm) movements could have occurred during this time. However, averaging the data over multiple depths was done to reduce the impact of such changes.

Ideally, we would like to analyze vibration depth-by-depth across multiple A-lines covering the entire organ of Corti. Two OCT studies in the opened cochlea of larger mammals have shown that this kind of information can provide insights into the interplay between the different components of the organ of Corti [17,18]. Because averaging multiple trials may still be needed to lower the noise threshold of vibration measurements inside the unopened cochlea, managing experimental times will be a concern. The fact that the surgical technique we used does not require opening the cochlea is a benefit however. It reduces the risk of trauma affecting experimental results, and thus, is expected to lead to increased reliability of our experimental preparations.

5. Conclusion

Spectral domain OCT can be used to measure vibrations at the apex of unopened mouse cochlea in vivo. Since the data are comparable to that measured with LDV without the risks associated with opening the cochlea, OCT represents a new standard for the measurement of vibrations of intracochlear tissues.