The Effect of Linkage Disequilibrium and Family Relationships on the Reliability of Genomic Prediction

Abstract

Although the concept of genomic selection relies on linkage disequilibrium (LD) between quantitative trait loci and markers, reliability of genomic predictions is strongly influenced by family relationships. In this study, we investigated the effects of LD and family relationships on reliability of genomic predictions and the potential of deterministic formulas to predict reliability using population parameters in populations with complex family structures. Five groups of selection candidates were simulated by taking different information sources from the reference population into account: (1) allele frequencies, (2) LD pattern, (3) haplotypes, (4) haploid chromosomes, and (5) individuals from the reference population, thereby having real family relationships with reference individuals. Reliabilities were predicted using genomic relationships among 529 reference individuals and their relationships with selection candidates and with a deterministic formula where the number of effective chromosome segments (M_e) was estimated based on genomic and additive relationship matrices for each scenario. At a heritability of 0.6, reliabilities based on genomic relationships were 0.002 ± 0.0001 (allele frequencies), 0.022 ± 0.001 (LD pattern), 0.018 ± 0.001 (haplotypes), 0.100 ± 0.008 (haploid chromosomes), and 0.318 ± 0.077 (family relationships). At a heritability of 0.1, relative differences among groups were similar. For all scenarios, reliabilities were similar to predictions with a deterministic formula using estimated M_e. So, reliabilities can be predicted accurately using empirically estimated M_e and level of relationship with reference individuals has a much higher effect on the reliability than linkage disequilibrium per se. Furthermore, accumulated length of shared haplotypes is more important in determining the reliability of genomic prediction than the individual shared haplotype length.

CURRENTLY, it is feasible in most plant and animal breeding programs to genotype individuals at low costs for many thousands of single-nucleotide polymorphisms (SNPs) spread across the whole genome. With a sufficiently large reference population containing individuals with phenotypes and genotypes, SNP effects can be estimated. Subsequently, estimated SNP effects and an individual’s genotype for each SNP can be used for genomic prediction of breeding values. Selection based on those genomic breeding values is called genomic selection (Meuwissen et al. 2001) and this method has high potential both in animal (e.g., Hayes et al. 2009a) and plant breeding (e.g., Heffner et al. 2009; Jannink et al. 2010). Many studies demonstrated higher reliabilities for direct genomic breeding values compared to breeding values based on pedigree information only, especially for juvenile individuals without phenotypic information (e.g., Meuwissen et al. 2001; Calus et al. 2008; VanRaden 2008).

The response to genomic selection relies on linkage disequilibrium (LD) between specific alleles of SNPs and quantitative trait loci (QTL) (Meuwissen et al. 2001); the stronger the LD, the higher the reliability of genomic predictions (Calus et al. 2008; Solberg et al. 2008). Since LD between QTL and SNP will decrease over generations, reliability of genomic prediction is expected to decrease without reestimating SNP effects in more recent generations (Muir 2007). However, the observed decrease in reliability of genomic predictions over generations following the generation in which SNP effects are estimated is higher than the expected decrease due to the decay of LD between SNP and QTL alone (Habier et al. 2007; Habier et al. 2010). This higher decrease in reliability is a result of decreasing family relationships (i.e., all nonzero additive genetic relationships) over generations of the selection candidates with the reference population, indicating that SNPs used for genomic selection not only capture LD between SNP and QTL, but capture family relationships among individuals as well (Habier et al. 2007; Gianola et al. 2009; Habier et al. 2010). Indeed, several studies already showed higher reliabilities for genomic predictions when selection candidates were more closely related to the reference population (e.g., Meuwissen 2009; Habier et al. 2010; Makowsky et al. 2011).

Separating effects of LD and family relationships on the reliability of genomic predictions is difficult because LD and family relationships are entangled. The extent of LD in a population is related with effective population size ($N_{\text{e}})$ (Sved 1971); the lower $N_{\text{e}}$, the higher the kinship level among individuals and the higher the extent of LD (Falconer and Mackay 1996). Besides that, LD can differ between families within breed (Dekkers 2004) and differs even more between diverged populations or breeds (De Roos et al. 2008; De Roos et al. 2009). A high marker density may enable achievement of similar LD between markers and QTL across breeds (De Roos et al. 2008); however, family relationships are still absent. Thus far, little is known about the effect of LD in situations without family relationships on the reliability of genomic predictions.

Deterministic formulas for predicting reliability of genomic prediction using population and trait parameters, which can be used before data on selection candidates are collected, are derived by Daetwyler et al. (2008) and Goddard (2009). Both formulas assume that selection candidates are unrelated to individuals from the reference population. Hayes et al. (2009d) applied the formula of Goddard (2009) to individuals that were related to the reference population; however, only simple family structures were used, such as selection candidates with full-sibs, half-sibs, or double first cousins in the reference population. A deterministic method for predicting the reliability of genomic prediction that accounts for any type of family structure, by using all relationships among animals in a population, was derived by VanRaden (2008). However, the method of VanRaden (2008) uses genotypes of selection candidates and reference individuals to predict individual reliabilities instead of population parameters to predict the average reliability for a population. Therefore, this formula can be applied only after genotypic data are collected on selection candidates in contrast to the previous two deterministic formulas (Goddard et al. 2011). Family structures occur in real data and, so far, possibilities of applying deterministic formulas based on population parameters to predict reliability of genomic prediction are limited in such situations.

The first objective of this study was to examine the effects of LD and family relationships on the reliability of genomic predictions. The second objective of this study was to investigate whether deterministic prediction formulas for the reliability of genomic prediction based on population parameters can be used in real data sets with a complex family structure between selection candidates and individuals in the reference population. This article is organized as follows: first, we start by describing a real reference population set and the different sets of selection candidates simulated based on information of the reference population. Thereafter, the different methods to predict the reliabilities of the selection candidates are explained. Finally, results are presented and discussed.

Materials and Methods

In this study, reliability of genomic prediction was predicted for five scenarios with simulated genotypes for selection candidates and using a reference population composed of real individuals with genotypic information. To create differences in LD and family relationships among the five scenarios, genotypes for the selection candidates were simulated using allele frequency, LD pattern, haplotypes, chromosomes, or family relationships from the reference population (Table 1). Finally, reliability of genomic prediction for each of the five scenarios was determined using two methods, namely those presented by: (1) VanRaden (2008), which explicitly accounts for family relationships between selection candidates and reference individuals, and (2) Daetwyler et al. (2008), where we aimed to account for family relationships by using an alternative way to estimate one of the parameters. For the last scenario, reliability was also empirically evaluated using observed phenotypic data and leave-one-out cross-validation.

Table 1 . Overview of the information from the reference population used in the simulations of the different scenarios.

Scenarios	Allele frequencies	LD pattern	Haplotypes	Chromosomes	Family relationships
FREQ	X
LD	X	X
HAP	X	X	X
CHR	X	X	X	X
FAM	X	X	X	X	X

Reference population

The reference population consisted of 529 genotyped Holstein–Friesian cows from the Netherlands. The cows were genotyped using the Illumina 50K SNP chip (Illumina, San Diego, CA), containing 54,001 SNPs. During a quality check, performed on a larger data set including those 529 cows, SNPs with a GCscore ≤0.2, a GTscore ≤0.55, a call rate ≤95%, a minor allele frequency ≤1%, deviating from Hardy–Weinberg equilibrium (χ² ≥600), and SNP that could not be assigned to a location on one of the chromosomes or were assigned to the X chromosome using the UMD3.0 bovine genome assembly from the University of Maryland were deleted. Individuals with Mendelian inconsistencies (Calus et al. 2011) between SNP data and pedigree in genotyped parent–offspring pairs and among sibs were removed. The software package Beagle (Browning and Browning 2007) was used to simultaneously phase the SNP data and impute any missing genotypes due to low call rates using the larger data set. One of the SNPs from each SNP pair with very high LD (i.e., r² >0.99) within the population of 529 individuals was deleted as well, to avoid problems of nonpositive definite matrices during the analyses. Finally, 35,002 SNPs remained for the purpose of the study.

The data set used in this study contained many close family relationships. In total, the population contained 117 mother–daughter pairs, 48 full-sib families with on average 2.27 individuals per family, 69 paternal half-sib families with on average 7.23 individuals per family, and 65 maternal half-sib families with on average 2.65 individuals per family.

Simulation of selection candidates

In this study, five different scenarios were considered in which genotypes of 529 selection candidates for 35,002 SNPs were simulated, using either the allele frequency, LD pattern, haplotypes, chromosomes, or family relationships from the reference population. The deterministic equations used to predict the individual reliabilities only used genotype information and considered variance components, so no phenotypes were simulated for the selection candidates. The last scenario was an exception to this, where we also used observed phenotypes for an empirical evaluation of the reliability.

FREQ:

The first scenario (FREQ) simulated selection candidates using only allele frequencies of the reference population to show the potential reliability of genomic prediction in the absence of LD and family relationships. This scenario allocated genotypes to the simulated individuals with probabilities calculated by using the observed allele frequencies in the reference population, assuming that the loci were independent and that the population was in Hardy–Weinberg equilibrium.

LD:

The second scenario (LD) used allele frequency and LD pattern between the SNPs of the reference population to simulate selection candidates, resulting in the potential reliability due to LD in the absence of family relationships. Only the 50 surrounding SNPs of a certain SNP were taken into account. To achieve this, a multivariate normal distribution was simulated by drawing one random number per SNP for each individual from a standard normal distribution, i.e., N(0,1). Those random numbers were multiplied with the Cholesky decompositions of the correlation matrices between the SNPs per chromosome from the reference population. Whenever this correlation matrix was not positive definite, it was bended following Jorjani et al. (2003). The correlation matrices were calculated from the phased allelic data and represent LD; i.e., the square of those values is the well-known LD measure $r^2$ (Hill and Robertson 1968).

The random numbers drawn from the multivariate normal distribution were translated into genotypes by calculating two cut-off values on the normal distribution for each SNP using the allele frequency ($p_i$) of the reference population: (1) a cut-off value with an area of size ${\left(1-p_i\right)}^2$ to the left of it and (2) a cut-off value with an area of size ${\left(p_i\right)}^2$ to the right of it. When the random number was below the first cut-off value (above the second cut-off value), the genotype of the individual for that SNP was set to −1 (1). When the random number was in between the two cut-off values, which was the case for a proportion of $2p_i\left(1-p_i\right)$ of the individuals, the genotype was set to 0.

HAP:

Two individuals coming from the same population are expected to share some haplotypes, even if they do not share a common ancestor in the recent past. In this third scenario (HAP), the reliability due to sharing haplotypes with individuals in the reference population was investigated. The number of haplotypes used was equal to the number of effective chromosome segments, $M_{\text{e}}$, present in the reference population (estimation of $M_{\text{e}}$ is explained later). For simplicity, all haplotypes were assumed to have an equal length in basepairs, although in reality haplotype length depends on LD structure of the genome. For each haplotype, 1058 ($529\times 2)$ haploid copies were present in the reference population. Simulating selection candidates was done by randomly drawing two copies per haplotype from those 1058 copies and combining them across haplotypes to form the genome of the simulated individual. The number of haploid haplotypes shared between a simulated individual and a specific reference individual was divided equally over the 529 reference individuals. Note that this scenario is a theoretical scenario and used as an intermediate between the LD and FAM scenario.

CHR:

VanRaden (2009) suggested a hypothetical scenario in which individuals are created by combining the best chromosomes present in a population to further increase the genetic progress. Although, e.g., chromosome substitution lines exist in mice by successive backcrossing of inbred lines (Nadeau et al. 2000; Singer et al. 2004), the scenario suggested by VanRaden (2009) is currently not feasible in practice for most animal and plant species. The reliability of those hypothetical individuals was investigated in this fourth scenario (CHR). As an alternative to picking the best chromosomes, we simulated individuals by randomly picking chromosomes from the reference population. Selection candidates in this scenario were in general simulated in the same way as in the HAP scenario, but instead of haplotypes, haploid chromosomes were used. The maximum number of haploid chromosomes shared between a simulated individual and a reference individual was restricted to one.

FAM:

For this last scenario (FAM), instead of simulating genotypes of selection candidates, genotypes of real individuals were used to include family relationships. Each of the selection candidates had at least one genomic relationship of at least 0.125 with one of the individuals in the reference population, which is equal to the relationship of an individual with its great-grandparent. Reliabilities for this scenario were predicted by deleting each individual once from the reference population and using the remaining 528 individuals as reference population. This approach is also known as leave-one-out cross-validation and the effect due to differences of the composition of the reference population by one individual on the reliability is expected to be negligible.

For an empirical evaluation of the reliability of genomic prediction in this scenario, precorrected phenotypes on milk production were used. For all 529 cows used as selection candidate and reference individual, precorrected phenotypes were available. A detailed description of the precorrection is given by Veerkamp et al. (2012).

All scenarios were set up such that allele frequencies across simulated selection candidates were expected to be similar to the allele frequencies observed in the reference population. Inspection of the simulated data showed that this was indeed the case. See supporting information, File S1, for the (simulated) genotypes and phenotypes.

Predicting reliability

Reliabilities were predicted in all scenarios using two different deterministic methods at a heritability of 0.1 and 0.6. One of the deterministic methods was also used to study the effect of size of the reference population on the magnitude of effects of LD vs. family relationships on the reliability of genomic prediction.

Besides both deterministic methods, reliabilities were also predicted using phenotypes on milk production in the FAM scenario. For a good comparison of the empirical and deterministic predicted reliabilities, the estimated heritability for milk production based on the empirical data was used as well to predict the reliability of genomic prediction in the FAM scenario using the deterministic methods.

VanRaden (2008):

The first method to predict reliability was derived by VanRaden (2008) and predicted reliability of genomic prediction separately for each selection candidate as

$$r_{\text{VR}}^2=\mathbf{c}{\left[\mathbf{G}+\mathbf{I}\left(\frac{{\sigma }_{\text{e}}^2}{{\sigma }_{\text{a}}^2}\right)\right]}^{-1}c\prime ,$$ (1)

in which c is a vector of genomic relationships of the selection candidate with each of the individuals in the reference population, G is the genomic relationship matrix of the reference population, I is an identity matrix, ${\sigma }_{\text{e}}^2$ is the residual variance, and ${\sigma }_{\text{a}}^2$ is the additive genetic variance. The heritability ($h^2$) of the trait is reflected by $\left(1-h^2\right)/h^2={\sigma }_{\text{e}}^2/{\sigma }_{\text{a}}^2$.

The genomic relationship matrix is calculated as $\text{G}=\text{X}\text{X}\prime /n$ (Yang et al. 2010), in which n is the number of SNPs. The X matrix contains standardized genotypes calculated as $x_{ij}=\left[g_{ij}-2\left(p_i-0.5\right)\right]/\sqrt{2p_i\left(1-p_i\right)}$, in which $g_{ij}$ codes the genotype at SNP locus i for individual j as −1 for a homozygote, 0 for the heterozygote, and 1 for the opposite homozygote and $p_i$ is the allele frequency of the second allele at locus i (for which the homozygote genotype is coded 1). Subtraction of $2\left(p_i-0.5\right)$ from the genotype code sets the average value of the estimated allele effects per locus to zero. Division by $\sqrt{2p_i\left(1-p_i\right)}$ results in unbiased estimates of the relationships among individuals using $XX\prime$. Diagonal elements were calculated in the same way as off-diagonal elements, following Goddard et al. (2011) and Meuwissen et al. (2011).

Another common approach is to calculate G as $Z{Z}^{\prime }/2{\displaystyle \sum }{p}_i\left(1-p_i\right)$, in which Z is calculated as $g_{ij}-2\left(p_i-0.5\right)$ (e.g., VanRaden 2008; Legarra et al. 2009). This approach gives less weight to alleles with a low allele frequency, resulting in a weighted G. Meuwissen et al. (2011) suggested that the approach of Yang et al. (2010), i.e., $G=X{X}^{\prime }/n$, would result in the best, unweighted, estimate of G when a high proportion of loci with low minor allele frequencies are used. Therefore, the approach of Yang et al. (2010) was used to calculate G in this study.

The vector including genomic relationships of the selection candidate with each of the individuals in the reference population is computed as $c=x_{2}X\mathit{\prime }/n$ (VanRaden 2008; Yang et al. 2010). In this calculation, X is the X matrix of the reference population and $x_2$ is the X matrix of the selection candidates, which becomes a vector when only one selection candidate at a time is evaluated. Similarly, c becomes a vector as well.

The calculated G and c are biased, because G and c are based on a sample of segregating loci from the whole genome of an individual (Powell et al. 2010; Goddard et al. 2011). For an unbiased estimate of G (i.e., $\widehat{G}$), we assume that (Yang et al. 2010)

$$\widehat{G}=G+E=A+\left(G-A\right)+E$$ (2)

in which E is a matrix with error terms due to sampling of the SNPs from the genome. The variances for those matrices are $\text{Var}\left(\widehat{G}-A\right)=\text{Var}\left(G-A\right)+\text{Var}(E)$ in which $\text{Var}(E)$ is equal to 1/n.

The unbiased $\widehat{G}$ was calculated by regressing G back to A as (Yang et al. 2010; Goddard et al. 2011)

$$\widehat{G}=A+\text{b}\left(G-A\right)$$ (3)

in which

$$b=\frac{\text{Var}\left(G-A\right)}{\left[\text{Var}\left(G-A\right)+\text{Var}\left(E\right)\right]}=\frac{\text{Var}\left(\widehat{G}-A\right)-\left(1/n\right)}{\text{Var}(\widehat{G}-A)}.$$ (4)

The sampling error on the elements in $\widehat{\text{G}}$ depend on the level of family relationships, which is accounted for by calculating the regression coefficient b separately for bins of family relationships in A (0–0.10, >0.10–0.25, >0.25–0.50, and >0.50) with calculated b’s of respectively 0.973, 0.976, 0.990, and 0.997. All parent–offspring relationships were expected to be 0.5 and those relationships were excluded from the regression. Besides that, only off-diagonal elements were regressed.

Elements of c were regressed back to A as well, resulting in unbiased $\widehat{c}$. For the FAM scenario, the regression for c was done in the same way as for G, because $\widehat{c}$ was directly obtained from $\widehat{G}$. For the other scenarios, all family relationships between selection and reference individuals were zero, resulting in an A matrix where all elements were zero. Therefore the regression coefficient used for regressing c reduced to $b=\text{Var}(C)/\left[\text{Var}\left(C\right)+1/n\right]$, in which C is a matrix containing all c vectors with genomic relationships between selection and reference individuals.

Daetwyler et al. (2008):

The second formula for predicting the reliability of genomic predictions was derived by Daetwyler et al. (2008),

$$r_{\text{D}}^2=\frac{N_{\text{p}}{h}^2}{N_{\text{p}}{h}^2+N_{\text{g}}},$$ (5)

in which $h^2$ is the heritability of the trait, $N_{\text{p}}$ is the number of individuals in the reference population, and $N_{\text{g}}$ is the number of independent loci underlying the trait. Assumptions underpinning this equation were: (1) loci are independent, (2) all loci have an effect, and (3) there are no family relationships between selection candidates and reference population. To account for the fact that segregating loci in real population are not independent, $N_{\text{g}}$ was replaced by $M_{\text{e}}$ in our study, as suggested by Daetwyler et al. (2008, 2010). Estimation of $M_{\text{e}}$ is explained later. The formula of Daetwyler et al. (2008) provides one reliability that applies to the whole group of selection candidates, whereas $r_{\text{VR}}^2$ provides a single reliability for each selection candidate.

Impact of reference population size:

The size of the reference population affects reliability of direct genomic values and, therefore, may also affect the magnitude of the effect of LD vs. family relationships on the reliability. For this reason, we predicted the reliability using the formula of Daetwyler et al. (2008) for all five scenarios with different reference population sizes, ranging from 100 to 60,000 individuals. Heritability and $M_{\text{e}}$ were assumed to be constant across different sizes of the reference population, reflecting a situation where reference individuals and selection candidates are a representative sample of the whole population.

Empirical estimation:

In the FAM scenario, reliability of genomic prediction was empirically evaluated using precorrected phenotypes on milk production. Genomic breeding values for milk production were calculated for all individuals using a GBLUP model in ASReml (Gilmour et al. 2009) and leave-one-out cross-validation. The GBLUP model used the same genomic relationship matrix as used for the deterministic prediction of the reliabilities and explicitly estimated variances for the trait in the model. The average reliability across all individuals in the reference population was calculated as the squared correlation between the phenotypes and the genomic breeding values, divided by the heritability, as explained in Verbyla et al. (2010). The heritability for this trait was estimated from the same GBLUP model when all 529 reference individuals were included.

Estimating $M_{\text{e}}$

The $M_{\text{e}}$ was estimated for each scenario using the genomic relationship matrix and the additive genetic relationship matrix. Only for the last scenario, FAM, we estimated $M_{\text{e}}$ based on the estimated $N_{\text{e}}$ as well, because this was the only scenario with a generation structure.

Based on the G and A matrix:

Goddard et al. (2011) showed that the variance of off-diagonal elements of G for unrelated individuals, all having expected values of zero, is about equal to the average of $r_{\text{LD}}^2$ (i.e., $\stackrel{-}{r_{\text{LD}}^2}$) as a measure of LD over all pairs of loci. This $\stackrel{-}{r_{\text{LD}}^2}$, and therefore the variance of G as well, is related with $M_{\text{e}}$ as $M_{\text{e}}=1/\stackrel{-}{r_{\text{LD}}^2}=1/\text{Var}(G)$. For related individuals, we can use $D=G-A$, in which G is the genomic relationship matrix and A the additive genetic relationship matrix, where the expected values for all elements of D are zero. This suggests that $\text{Var}\left(D\right)$ is related to $\stackrel{-}{r_{\text{LD}}^2}$ over all pairs of loci and, therefore, that $M_{\text{e}}$ for a specific population with related individuals can be estimated as

$$M_{\text{e}}=\frac{1}{\text{Var}\left(D\right)}.$$ (6)

In the formula for calculating D, G should contain the genomic relationships between reference individuals and selection candidates (Goddard et al. 2011). Following our earlier notation, here we use the $\widehat{C}$ matrix, containing all $\widehat{c}$ vectors with the relationships between selection and reference individuals. For the FAM scenario, A was calculated based on the pedigree. In the other scenarios, individuals were simulated without family relationships with the reference individuals and therefore lacked pedigree information. For those scenarios, additive genetic relationships between selection candidates and reference individuals were assumed to be zero.

Based on N_e:

For the FAM scenario, $M_{\text{e}}$ was also estimated based on $N_{\text{e}}$. In this study, we used the two most frequently used formulas, namely $M_{\text{e}}=2N_{\text{e}}L/\text{ln}\left(4N_{\text{e}}L\right)$ (Goddard 2009) and $M_{\text{e}}=2N_{\text{e}}L$ (Hayes et al. 2009d). In those formulas, L was the genome size that was assumed to be 31.6 M (Ihara et al. 2004). The required value for $N_{\text{e}}$ was estimated for the reference population. For each t generations back, $N_{\text{e}}$ is correlated with a mean $r_{\text{LD}}^2$ (i.e., $\stackrel{-}{r_{\text{LD}}^2}$) as a measure of LD over a chromosome segment with length $c=1/2t$ (Hayes et al. 2003), in which c is the length of the chromosome segment in morgans. All $r_{\text{LD}}^2$ of SNP intervals in between the chromosome segment length using $(t-0.1)$ and $(t+0.1)$ and assuming 1 cM = 1 Mb were averaged to calculate $\stackrel{-}{r_{\text{LD}}^2}$, which is used to estimate $N_{\text{e}}$ following $\stackrel{-}{r_{\text{LD}}^2}=1/\left(4N_{\text{e}}c+1\right)$ (Sved 1971). For t the values 1–5 were used and the final $N_{\text{e}}$ of the population was estimated as the mean $N_{\text{e}}$ over those last 5 generations.

Results

Reliabilities of the different scenarios

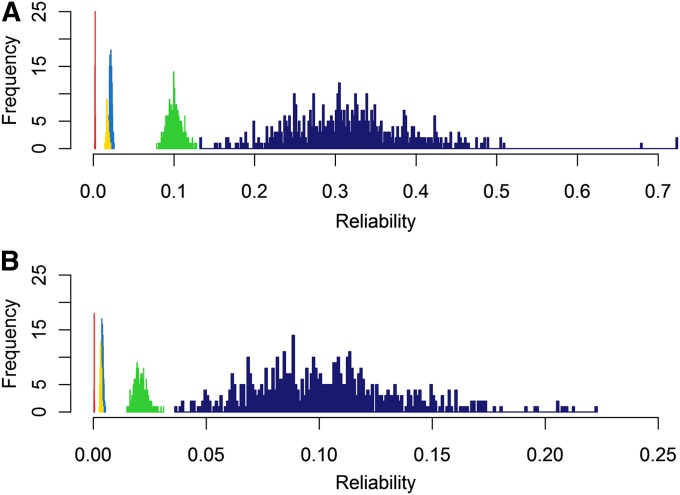
The different scenarios showed predicted reliabilities of 0.002 ± 0.0001 (FREQ), 0.022 ± 0.001 (LD), 0.018 ± 0.001 (HAP), 0.100 ± 0.008 (CHR), and 0.318 ± 0.077 (FAM) using the formula of VanRaden (2008) at a heritability of 0.6 (rel_VR; Figure 1A). This indicates that reliability of selection candidates that share only allele frequencies with the reference population was almost zero. Adding the LD pattern or haplotype information as information source used for simulating selection candidates slightly increased the reliability. Using chromosomes from the reference population to simulate selection candidates showed an increase in reliability of about 0.1. Adding family relationships between selection candidates and reference individuals resulted in a relatively high increase in reliability compared to the other scenarios (an increase of >0.3 compared to the FREQ scenario and >0.2 compared to the CHR scenario). So, the average reliabilities of genomic predictions increased by simulating selection candidates using an increasing amount of information from the reference population and this increase was highest when family relationships were added as an information source.

Figure 1 .

Histograms depicting distributions of reliabilities of genomic preditions using a reference population of 529 genotyped individuals at a heritability of 0.6 (A) and 0.1 (B) over the five different scenarios using different information sources from the reference population (from left to right). Red: Selection candidates simulated based on allele frequency of the reference population (FREQ). Yellow: Selection candidates simulated based on 837 haplotypes of equal length segregating in the reference population (HAP). Light blue: Selection candidates simulated based on LD pattern of the reference population (LD). Green: Selection candidates simulated based on haploid chromosomes segregating in the reference population (CHR); Dark blue: Individuals from the reference population (FAM).

Next to the increase in reliability when more information from the reference population was used to simulate selection candidates, variation in reliability among selection candidates increased as well (Figure 1A). Especially the variation in the FAM scenario, using family relationships between selection candidates and reference individuals, was high compared to the other scenarios and the reliabilities in that scenario ranged from 0.13 to 0.72. The distributions of the reliabilities overlapped between the HAP and CHR scenario. For the other scenarios, the distributions were not overlapping.

For all scenarios, rel_VR was lower at a heritability of 0.1 compared to a heritability of 0.6, but relative differences between and standard deviations of reliabilities within groups were similar to those observed at a heritability of 0.6 (Figure 1B).

Applying the formula of Daetwyler et al. (2008) to populations with a complex family structure

Another method used to predict reliability of genomic prediction is the formula of Daetwyler et al. (2008). A disadvantage of this formula is the inability to predict reliabilities for populations with a complex family structure. In this study, this disadvantage was overcome by estimating $M_{\text{e}}$ in the formula based on the genomic and additive genetic relationship matrix. At the same heritability, reliabilities predicted with the formula of Daetwyler et al. (2008), denoted as rel_D hereafter, were in good agreement with rel_VR presented before, being 0.003 (FREQ), 0.027 (LD), 0.021 (HAP), 0.129 (CHR), and 0.275 (FAM; Table 2). Those predicted rel_D values at a heritability of 0.6 were almost equal to rel_VR for the FREQ scenario and the difference was highest for the FAM scenario (0.043). At a heritability of 0.1, predicted rel_D and rel_VR were equal for the FREQ and LD scenario and the maximum difference was 0.044 (FAM).

Table 2 . Comparison of average reliabilities of genomic predictions at different heritabilities for five different scenarios obtained with the deterministic formulas of VanRaden (2008) (rel_VR) and Daetwyler et al. (2008) (rel_D), using the estimated number of effective chromosome segments (M_e).

$h^2$	Scenario	$M_{\text{e}}$a	Rel_VR	Rel_D
0.6	FREQ	122116	0.002	0.003
0.6	LD	11458	0.022	0.027
0.6	HAP	14627	0.018	0.021
0.6	CHR	2139	0.100	0.129
0.6	FAM	837	0.318	0.275
		805b		0.283
		7774c		0.039
0.1	FREQ	122116	0.0004	0.0004
0.1	LD	11458	0.004	0.005
0.1	HAP	14627	0.003	0.004
0.1	CHR	2139	0.021	0.024
0.1	FAM	837	0.104	0.059
		805b		0.062
		7774c		0.007

^a$M_{\text{e}}$ estimated based on the genomic and additive genetic relationship matrices (Equation 6).

^b$M_{\text{e}}$ estimated as $M_{\text{e}}=2N_{\text{e}}L/\left(\text{ln}\left(4N_{\text{e}}L\right)\right)$ (Goddard 2009).

^c$M_{\text{e}}$ estimated as $M_{\text{e}}=2N_{\text{e}}L$ (Hayes et al. 2009d).

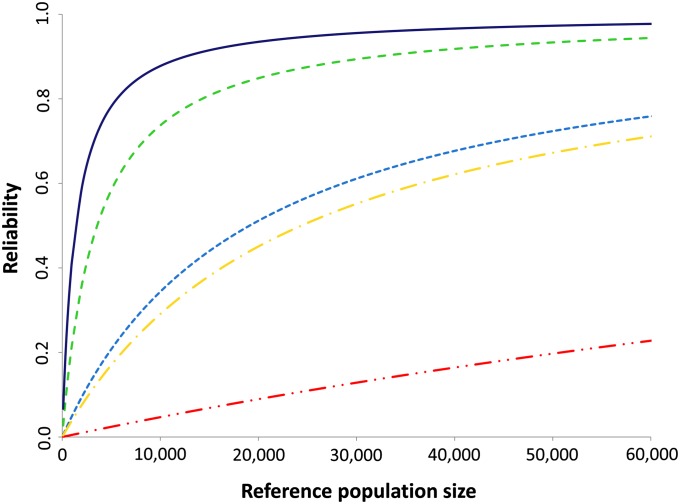
The formula of Daetwyler et al. (2008) was also applied to study the effect of size of the reference population on the magnitude of effects of LD vs. family relationships on the reliability of genomic prediction. Reliabilities at a heritability of 0.6 of all five scenarios using different sizes of the reference population are shown in Figure 2. For the FAM scenario, reliability shows a steep marginal increase by increasing reference population size at small initial sizes of the reference population. At reference population sizes of about 5000-10,000, when reliability approaches the maximum reliability of 1, the marginal increase in reliability starts to decline. For the LD scenario, the marginal increase is more gradual, so less steep at small sizes of the reference population and more steep at bigger sizes of the reference population. The increase in reliability is, however, still higher at small initial sizes of the reference population compared to bigger sizes. For the CHR, the pattern is in between the ones from the FAM and LD scenario, and for the HAP scenario, the pattern is more or less the same as for the LD scenario. For the FREQ scenario, the increase in reliability is almost linear across the considered range of reference population sizes. Those results indicate that the effect of LD vs. family relationship does indeed depend on the size of the reference population.

Figure 2 .

Predicted reliability of genomic prediction, at a heritability of 0.6 and different sizes of the reference population, obtained with the deterministic formula of Daetwyler et al. (2008) for the five different scenarios using different information sources from the reference population (from bottom to top). Red: Selection candidates simulated based on allele frequency of the reference population (FREQ). Yellow: Selection candidates simulated using 837 haplotypes of equal length segregating in the reference population (HAP). Light blue: Selection candidates simulated based on LD pattern of the reference population (LD). Green: Selection candidates simulated based on haploid chromosomes segregating in the reference population (CHR). Dark blue: Individuals from the reference population (FAM).

Empirical estimation

In the FAM scenario, empirical estimation of the reliability using leave-one-out cross-validation for milk production resulted in an estimated reliability of 0.291. At the heritability estimated for milk production in this data set (0.56), the FAM scenario showed a rel_VR of 0.305 and rel_D of 0.261. So, both deterministic predictions were very close to the empirically estimated reliability.

Calculating $N_{\text{e}}$ and $M_{\text{e}}$

The $N_{\text{e}}$ of the reference population was estimated to be 123 and this value was used to approximate the $M_{\text{e}}$ of the FAM scenario using two different formulas. The first formula, $M_{\text{e}}=2N_{\text{e}}L/\ln \left(4N_{\text{e}}L\right)$ (Goddard 2009), resulted in almost the same $M_{\text{e}}$ as based on the genomic and additive genetic relationship matrix and, therefore, predicted reliability using this value was in good agreement with rel_VR and rel_D (Table 2). The second formula, $M_{\text{e}}=2N_{e}L$ (Hayes et al. 2009d), showed an almost 10 times higher value for $M_{\text{e}}$, resulting in a much lower predicted reliability compared to rel_VR and rel_D.

Genomic relationship vs. reliability

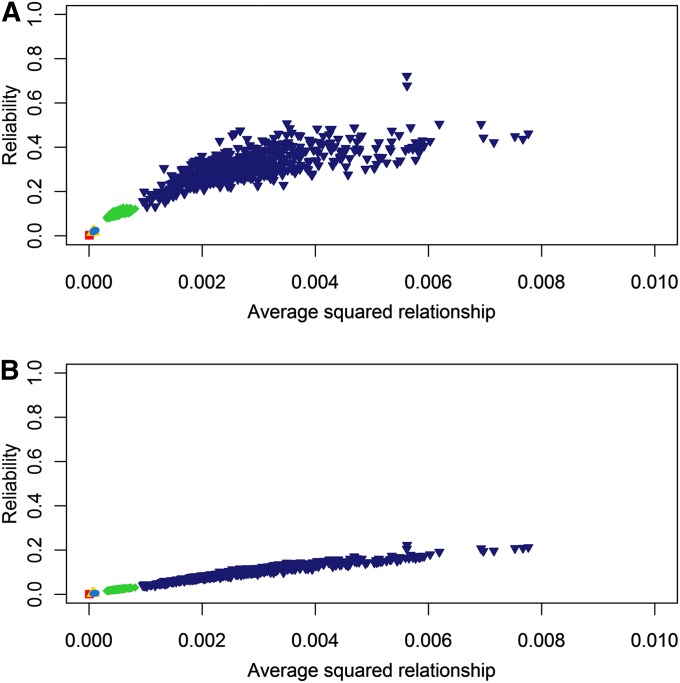
Since the reliability predicted with the formula of VanRaden (2008) was predicted separately for each individual, it was possible to evaluate the relation between genomic relationship and reliability. Average squared genomic relationship, which was found to be an accurate indicator of reliability in the study of Pszczola et al. (2012), also showed a high correlation with reliability in our study (Figure 3); the higher the average squared relationship with the reference population, the higher the reliability of genomic prediction. Fitting a linear regression line through the data presented in Figure 3A resulted in a model R² ranging from 0.51 to 0.60 (FREQ = 0.57, LD = 0.54, HAP = 0.58, CHR = 0.60, FAM = 0.51) at a heritability of 0.6. The mean and variance of the average squared genomic relationship within a scenario were both affected by the relationship with the reference population; i.e., using more information from the reference population to simulate the selection candidates resulted in a higher mean and variance of the average squared genomic relationship.

Figure 3 .

Average squared relationships to the reference population vs. the reliability of genomic predictions at a heritability of 0.6 (A) and 0.1 (B) for the five different scenarios using different information sources from the reference population (from left to right). Red: Selection candidates simulated based on allele frequency of the reference population (FREQ).Yellow: Selection candidates based on 837 haplotypes of equal length segregating in the reference population (HAP). Light blue: Selection candidates simulated based on LD pattern of the reference population (LD). Green: Selection candidates simulated based on haploid chromosomes segregating in the reference population (CHR). Dark blue: Individuals from the reference population (FAM).

The relation between average squared relationships and reliability at heritability values of 0.1 and 0.6 was very similar (Figure 3B). Nevertheless, average squared relationship predicted the reliabilities more accurately at a heritability of 0.1, with a R² of the regression model ranging from 0.92 to 0.94 (FREQ = 0.92, LD = 0.92, HAP = 0.92, CHR = 0.94, FAM = 0.93).

Discussion

Effect of LD and family relationships on reliability

The first aim of this study was to investigate the effects of LD and family relationships on the reliability of direct genomic values. The results indicate that family relationships between selection candidates and reference population can have a large effect on the reliability of genomic predictions compared to linkage disequilibrium per se.

The difference in reliability between selection candidates distantly and closely related to the reference population in our study was >0.5 at a heritability of 0.6. For breeding practices, it is therefore advisable to predict reliability for each selection candidate individually. However, it should be noted that both the general level and the variation of relationships within the data set used in our study was high, and the reference population was small. In data sets used for breeding practices, the difference in relationships among selection candidates may be lower and the size of the reference population may be higher, resulting in smaller differences in reliability.

The size of the reference population influences the relative effect of LD and family relationships on the reliability of genomic prediction; small reference populations result in a higher effect of family relationships compared to LD, and larger reference populations result in a higher effect of LD on reliability. Those results are in agreement with the results of Clark et al. (2012), who stated that the effect of family relationships is reduced at an increasing size of the reference population. Size of the reference population combined with the high general level of relationships between selection candidates and reference individuals in our study also explains at least part of the difference between our results and results of Habier et al. (2007), who found that less than half of the reliability of a population one generation younger than the reference population, including both parents, was due to family relationships.

Both deterministic approaches used in this study to predict the reliability of genomic prediction are based on a genomic relationship matrix. The genomic relationship matrix is quite consistent over different numbers of SNPs, with a correlation >0.98 when anywhere between ∼10,000 and 40,000 SNPs are used to set up the matrix (Rolf et al. 2010). Therefore, the conclusions of our study are supposed to be independent from the number of SNPs used to set up the genomic relationship matrix, provided that at least 10,000 SNPs are used.

The reliabilities achieved in the LD and HAP scenario are very similar. This indicates that most of the information coming from the considered haplotypes in the HAP scenario coincides with the information captured by the LD pattern in our data. Decreasing the number of haplotypes, and thereby increasing the haplotype length, will result in a higher additional amount of information captured in the HAP scenario compared to the LD scenario. The most extreme scenario of haplotypes in terms of their length is represented by the CHR scenario, which showed a considerably higher reliability than LD and HAP.

Length of haplotypes identical by descent between two individuals is related to the number of generations diverged from the common ancestor (Chapman and Thompson 2003; Browning 2008). The length of chromosome segments shared between individuals is, therefore, expected to be correlated with the level of family relationships between individuals (Sved 1971; VanRaden et al. 2011) and also with the reliability of genomic prediction. The results in our study do not completely agree with these expectations. In the CHR scenario, simulated individuals shared whole unrecombined chromosomes with the reference population. The genomic relationship and reliability was, however, lower than achieved in the FAM scenario, where individuals had shorter haplotypes in common with reference individuals. In the CHR scenario, selection candidates had only one long haplotype in common with any one reference individual; while in the FAM scenario, more shorter haplotypes were shared between a selection candidate and the same reference individual resulting in a higher relationship due to a higher accumulated length of shared haplotypes and, therefore, a higher reliability of genomic prediction. Moreover, this indicates that reliabilities of individuals composed of the best chromosomes present in a population, assuming this would be possible without going through the usual process of meiosis and recombination, as suggested by VanRaden (2009) and Cole and VanRaden (2011), may be substantially lower compared to individuals that have some degree of family relationship to one or more reference individuals. So, accumulated length of shared haplotypes between selection candidates and individuals in the reference population is more important than individual length of shared haplotypes.

Predicting the reliability for populations with a complex family structure

The second aim of this article was to investigate whether deterministic prediction formulas for the reliability of genomic prediction using population parameters can be used in situations with a complex family structure between selection candidates and the reference population. The results show that the formula of Daetwyler et al. (2008), using $M_{\text{e}}$ estimated based on the difference between genomic and additive genetic relationship matrices, yields similar predicted reliabilities for populations with a complex pedigree structure as using the formula of VanRaden (2008) and a cross-validation method based on observed phenotypes.

The formula of VanRaden (2008) can be used to predict the reliability of genomic prediction for populations with a complex family structure. Previous studies that performed an empirical evaluation of the formula of VanRaden (2008), which is equal to predicting the reliability based on the prediction error variance as shown by Strandén and Garrick (2009), in general overestimated the reliability (Hayes et al. 2009b; Lund et al. 2009; Thomasen et al. 2012). This overestimation can be reduced by regressing the genomic relationship matrix back to the additive genetic relationship matrix calculated from pedigree information (Goddard et al. 2011). In our study, using such a regressed genomic relationship matrix resulted in good agreement between the reliability predicted with the formula of VanRaden (2008) and the empirically estimated reliability.

Previous empirical evaluations of the formula of Daetwyler et al. (2008) all showed good agreement between empirically and deterministically derived reliabilities (Hayes et al. 2009c; Clark et al. 2012; Pryce et al. 2012). This formula assumes that selection candidates and reference individuals are unrelated. In our study, family structure between reference and selection individuals was taken into account in the prediction of $M_{\text{e}}$. Agreement between empirically estimated reliability and the reliabilities predicted with the formulas of VanRaden (2008) and Daetwyler et al. (2008) shows that the formula of Daetwyler et al. (2008) can also be applied to populations with a complex family structure, by using a value for $M_{\text{e}}$ that represents the family structure in the population.

The $M_{\text{e}}$ estimated as $2N_{\text{e}}L$ (Hayes et al. 2009d) was much higher, resulting in an unrealistically low reliability, compared to the $M_{\text{e}}$ and reliability estimated with $M_{\text{e}}=1/\text{Var}(G-A)$. The other formula used to estimate $M_{\text{e}}$, $M_{\text{e}}=2N_{\text{e}}L/\ln \left(4N_{\text{e}}L\right)$ (Goddard 2009), resulted in a similar value for $M_{\text{e}}$ as using $M_{\text{e}}=1/\text{Var}(G-A)$, indicating that the reliabilities of genomic prediction using $M_{\text{e}}=1/\text{Var}(G-A)$ were similar to those using $M_{\text{e}}=2N_{\text{e}}L/\ln \left(4N_{\text{e}}L\right)$ in the formula of Daetwyler et al. (2008).

Implications

Currently, more and more research is focused on the use of multibreed or multiline reference populations to enable genomic selection for smaller breeds or lines. Compared to within-breed genomic prediction, reliability of across-breed predictions may be lower due to differences in allele frequencies, LD pattern, and haplotypes among breeds (e.g., De Roos et al. 2008; Pryce et al. 2010; Goddard 2012) and because family relationships among full-bred individuals of different breeds are absent (VanRaden et al. 2011). In addition, breed-specific allele effects might exist (Spelman et al. 2002; Thaller et al. 2003), which further reduces the reliability of genomic prediction for multibreed populations.

A high marker density is expected to increase the consistency of LD between SNPs and QTL across breeds and the corresponding reliability (De Roos et al. 2008; Ibánẽz-Escriche et al. 2009). The problem of different allele frequencies and breed-specific allele effects can, however, not be solved by a higher marker density. Therefore, the expected reliability using a reference population of another breed is supposed to be lower than the reliability in the LD scenario in our study. Estimating $M_{\text{e}}$ for such scenarios, as shown in this study for populations with a complex family structure, is a potential starting point for predicting the reliability for those multibreed population structures.

Conclusion

In conclusion, our results showed that the level of family relationship between selection candidates and the reference population has a higher effect on the reliability of direct genomic values than linkage disequilibrium per se. Furthermore, accumulated length of shared haplotypes across a reference individual and a selection candidate are more important in determining the reliability of genomic prediction than individual length of shared haplotypes. And finally, existing deterministic formulas using population parameters can accurately predict the reliability of genomic prediction using reference populations with complex family structures by estimating the number of effective chromosome segments based on genomic and additive genetic relationship matrices.