Fundamental relationship between the noise properties of grating-based differential phase contrast CT and absorption CT: Theoretical framework using a cascaded system model and experimental validation

Abstract

Purpose: Using a grating interferometer, a conventional x-ray cone beam computed tomography (CT) data acquisition system can be used to simultaneously generate both conventional absorption CT (ACT) and differential phase contrast CT (DPC-CT) images from a single data acquisition. Since the two CT images were extracted from the same set of x-ray projections, it is expected that intrinsic relationships exist between the noise properties of the two contrast mechanisms. The purpose of this paper is to investigate these relationships.

Methods: First, a theoretical framework was developed using a cascaded system model analysis to investigate the relationship between the noise power spectra (NPS) of DPC-CT and ACT. Based on the derived analytical expressions of the NPS, the relationship between the spatial-frequency-dependent noise equivalent quanta (NEQ) of DPC-CT and ACT was derived. From these fundamental relationships, the NPS and NEQ of the DPC-CT system can be derived from the corresponding ACT system or vice versa. To validate these theoretical relationships, a benchtop cone beam DPC-CT/ACT system was used to experimentally measure the modulation transfer function (MTF) and NPS of both DPC-CT and ACT. The measured three-dimensional (3D) MTF and NPS were then combined to generate the corresponding 3D NEQ.

Results: Two fundamental relationships have been theoretically derived and experimentally validated for the NPS and NEQ of DPC-CT and ACT: (1) the 3D NPS of DPC-CT is quantitatively related to the corresponding 3D NPS of ACT by an inplane-only spatial-frequency-dependent factor 1/f ², the ratio of window functions applied to DPC-CT and ACT, and a numerical factor C_g determined by the geometry and efficiency of the grating interferometer. Note that the frequency-dependent factor is independent of the frequency component f_z perpendicular to the axial plane. (2) The 3D NEQ of DPC-CT is related to the corresponding 3D NEQ of ACT by an f ² scaling factor and numerical factors that depend on both the attenuation and refraction properties of the image object, as well as C_g and the MTF of the grating interferometer.

Conclusions: The performance of a DPC-CT system is intrinsically related to the corresponding ACT system. As long as the NPS and NEQ of an ACT system is known, the corresponding NPS and NEQ of the DPC-CT system can be readily estimated using additional characteristics of the grating interferometer.

INTRODUCTION

Although numerous studies have been conducted to demonstrate the feasibility of differential phase contrast (DPC) imaging^{1, 2, 3, 4, 5, 6, 7} and DPC computed tomography (DPC-CT) (Refs. ^{8, 9, 10, 11, 12, 13, 14, 15, 16}) using a Talbot-Lau interferometer, several questions remain unanswered on how to fully understand and optimize such systems for clinical applications. First, what are the potential performance limitations of a DPC-CT system in terms of contrast, noise, spatial resolution, and data acquisition speed? Second, how can the performance of a DPC-CT system be optimized to maximize its potential? Finally, given a radiation dose constraint and specific detection task for an in vivo clinical application, will DPC-CT provide better detectability than that of a conventional absorption CT (ACT) imaging system? To address these questions, it is fundamentally important to understand how the signal and noise propagate through the entire DPC-CT imaging chain. For a conventional absorption x-ray CT imaging system, the noise propagation through the image acquisition, reconstruction, and display have been thoroughly studied in recent years.^{17, 18, 19, 20, 21, 22, 23, 24} The results have played a pivotal role in attempts to optimize a CT imaging system for a specific imaging task. In this paper, we extend the success of the imaging science in ACT to DPC-CT to provide a foundation for optimizing a DPC-CT imaging system to meet the needs of a medical detection task.

Though initial studies examined the phase contrast mechanism itself, signal detection is ultimately influenced by both signal and noise levels. It is imperative that the noise properties of any new system be well understood before evaluating its clinical utility. Quickly following the initial introduction of grating-based DPC-CT, different research groups began to investigate the noise properties of the DPC-CT system. It was demonstrated^{15, 25} that for some materials under certain experimental conditions, DPC-CT may have superior contrast to noise ratio (CNR) compared to ACT, and the CNR for both DPC-CT and ACT is inversely proportional to the square root of exposure level. It was also discovered both theoretically^{25, 26, 27, 28} and experimentally²⁶ that the noise variance of DPC-CT system scales with the spatial resolution with an exponent of −1, rather than the value of −3 for two-dimensional (2D) ACT.²⁹ To compare the spatial correlation of noise in DPC-CT with that of ACT, the noise power spectrum (NPS) of DPC-CT was theoretically studied^{25, 27, 28} and experimentally measured³⁰ in the 2D case. The effect of the DPC-CT noise texture on low contrast detectability was studied using human observers.³¹ All of these studies highlight the importance of considering noise properties when evaluating a potential clinical system.

As is well known in the modern task-based imaging science framework developed for ACT,^{17, 18, 19, 20, 21, 22, 23, 24} the characterization of the system's detection performance must include the characterization of the modulation transfer function (MTF) for each link of the entire imaging chain, the three-dimensional (3D) NPS, the target imaging task, and the modeling of the potential confounding effects from variability of the anatomical background.^{32, 33, 34, 35, 36, 37, 38} Although the detection tasks will be application specific, the overall system performance can be characterized by combining the MTF, NPS, and signal nature into the generalized spatial-frequency-dependent noise equivalent quanta (NEQ). Recently, theoretical investigations with numerical simulations have been performed to study the NEQ of an idealized DPC-CT system.^{39, 40} These studies concluded that the total NEQ of a DPC-CT system could be either double³⁹ or identical to⁴⁰ that of the corresponding ACT system. However, a modified definition of NEQ was introduced for DPC-CT in Refs. ^{39, 40}. Their modified NEQ can be viewed as a result of multiplying the physical NPS of DPC-CT by a frequency dependent factor f ². In contrast, in this paper, a concept of absorption-equivalent NPS, $S_{\mathrm{eqv}}^{\mathrm{dpc}}\left(f\right)$, is introduced for DPC-CT in which the physical NPS is multiplied by a frequency independent factor ${(\overline{\mu }/\overline{\delta })}^2$. Using $S_{\mathrm{eqv}}^{\mathrm{dpc}}\left(f\right)$, the same definition of NEQ can be utilized to study the imaging performance of either contrast mechanism.

This work focuses on developing a cascaded systems model for DPC-CT imaging to investigate the potential relationship between the noise properties of a DPC-CT system and the associated ACT system. As demonstrated in earlier works, a grating interferometer based DPC-CT system enables one to simultaneously extract the associated ACT images as well. Therefore, it is expected that there should be some intrinsic relationship between the noise properties of the two types of images. The hardware difference between a conventional ACT system and a grating-based DPC-CT system is the insertion of the x-ray gratings that form the interferometer. The performance of such a DPC-CT system should therefore be quantitatively determined by the performance of the associated ACT system with additional factors to characterize the grating interferometer and image processing methods. The focus of this work is to explore these additional factors. Note that the performance of ACT may be degraded to some extent by the introduction of the Talbot-Lau interferometer. Therefore, if one intends to compare the noise performance of a DPC-CT system with that of an ACT system without gratings, a correction factor is needed. This is explained further in Sec. 6. Throughout the paper, our studies focus on the relationship between a DPC-CT system and the associated ACT system that includes the Talbot-Lau interferometer.

The layout of the paper is presented as follows: to be self-contained, a basic imaging model of DPC-CT, and the basic concepts of both NPS and NEQ are briefly reviewed in Sec. 2. In Sec. 3, we generalize the cascaded systems model of ACT to include both DPC-CT and ACT. Using the developed cascaded systems model, the propagation of both the signal and noise through the entire imaging chain are studied in detail. From this, two fundamental relationships are derived to link the NPS and NEQ of the DPC-CT system to the associated ACT system. These intrinsic relationships enable an understanding of the system performance of the DPC-CT system directly from the performance of the associated ACT system with some additional factors to characterize the grating interferometer, the data processing techniques, and the nature of the signal. In Sec. 4, the experimental methods used to validate these fundamental relationships are presented, with results presented in Sec. 5. Finally, discussion and conclusions are presented in Sec. 6. For convenience, a glossary of terms and symbols used in the paper is presented in Table 1.

Table 1.

Glossary of terms and symbols.

(u, v)	Detector column and row coordinates
(fv, fv)	Frequency coordinates corresponding to (u, v)
(x, y, z)	Spatial coordinates of the reconstructed image
(fx, fy, fz)	Frequency coordinates corresponding to (x, y, z)
f	Radial spatial frequency in the xy-plane;
	$f^2=f_x^2+f_y^2$
fN	Nyquist frequency
m	Total number of phase steps
mθ	Total number of projections of a CT acquisition
M	Geometric magnification factor
Nk	Measured photon density at phase step k
$N_{bk}^k$	Measured photon density at phase step k in the
	background scan
${\overline{N}}_0$	Mean photon density (per phase step) incident
	on the detector
μ	X-ray linear attenuation coefficient
δ	Decrement of the real part of refractive index
ε	Talbot-Lau interferometer efficiency factor
	(visibility of the modulation pattern)
ϕ	Phase shift of the modulation pattern
λ	X-ray wavelength
p2	Period of the modulation pattern
	and analyzer grating
zT	Fractional Talbot distance
do	G0-object distance
d1	G0-G1 distance
ai	Projection sampling interval along domain i
bi	Reconstr. sampling interval along domain i
T0	Transfer function due to finite focal spot
T3	Transfer function due to spread of optical
	photons
T5	Transfer function due to photodiode aperture
T10	Reconstruction kernel
T11	Apodization filter
T12	Interpolation filter
T13	Backprojection transfer function
Θ13	Backprojection transfer function of the noise
Sa	3D NPS of ACT
Sdpc	3D NPS of DPC-CT
Ta	3D MTF of ACT
Tdpc	3D MTF of DPC-CT
NEQa	3D NEQ of ACT
NEQdpc	3D NEQ of DPC-CT
Cg	Absorption-to-DPC geometric scaling factor

BRIEF REVIEW OF DIFFERENTIAL PHASE CONTRAST CT IMAGING, NOISE POWER SPECTRUM, AND NOISE EQUIVALENT QUANTA

Differential phase contrast imaging

Using a Talbot-Lau grating interferometer, DPC signals can be captured by measuring the lateral shift, ϕ, of interference patterns at the detector. The quantity ϕ (in radians) is related to the decrement, δ, of the real part of the object's refractive index^{4, 11, 26} according to

$$\varphi \left(u\right)=-\frac{2\pi z_{\mathrm{T}}}{p_2}\frac{\partial }{\partial u}\int \delta \left(\mathbf{r}\right)\mathrm{d}l,$$ (2.1)

where $z_{\mathrm{T}}=k{p}_2^2/\left(8\lambda \right)$ (k = 1, 3, 5, …) is the fractional Talbot distance, p₂ is the period of the analyzer grating G₂, and λ is the x-ray wavelength. In order to measure ϕ, a phase-stepping method^{2, 3} is used in which a partially transmissive grating, i.e., the G₂ grating, typically with a 50% duty cycle,^{3, 4, 6, 9, 10, 11, 15} is placed in front of the detector. This grating is translated by a fraction of the grating pitch along the u axis m times: u_g = kp₂/m (k = 1, 2, …, m), where m ⩾ 3 is the total number of phase steps used in data acquisitions. For each phase step, the measured photon density is given by

$$N^{\left(k\right)}\left(u\right)=N_0+N_1\cos \left[\frac{2\pi }{m}k+\varphi \left(u\right)\right],$$ (2.2)

where N^(k)(u) will be referred to as the raw projection data. In Eq. 2.2, N₀ and ϕ are determined, respectively, by the imaginary part (i.e., μ) and the decrement of the real part (i.e., δ) of the refractive index. Radiographs of both absorption contrast and DPC can be extracted from the raw projections as follows. For absorption contrast,

$$\int \mu \left(\mathbf{r}\right)\mathrm{d}l=-\ln \left[\frac{{\sum }_{k=1}^m{N}^{\left(k\right)}\left(u\right)}{{\sum }_{k=1}^m{N}_{bk}^{\left(k\right)}\left(u\right)}\right],$$ (2.3)

and for DPC,

$$\begin{array}{ccc}\hfill \varphi \left(u\right)& =& \arg \left[\sum _{k=1}^m{N}^{\left(k\right)}\left(u\right)\exp \left(-\mathrm{i}2\pi \frac{k}{m}\right)\right]\hfill \\ & & -\arg \left[\sum _{k=1}^m{N}_{bk}^{\left(k\right)}\left(u\right)\exp \left(-\mathrm{i}2\pi \frac{k}{m}\right)\right],\hfill \end{array}$$ (2.4)

where $N_{bk}^k$ denotes the detected photon fluence in the air (i.e., flood-field) scan, and the function, arg(a + ib), is defined as arg(a + ib) = arctan(b/a) if a ⩾ 0 and arg(a + ib) = [arctan(b/a) + π] otherwise. Equations 2.3, 2.4 demonstrate how radiographs of two different contrast mechanisms can be generated from a single acquisition. They also suggest that the noise properties of DPC-CT and ACT might be correlated since they were derived from the same x-ray intensity measurements.

Noise power spectrum

The noise power (Weiner) spectrum, is defined as the squared magnitude of the Fourier transform of an image containing only noise, averaged over an ensemble of images,¹⁹

$$S\left(f\right)=\underset{X\to +\infty }{\lim }\frac{1}{X}⟨{\left|{\int }_{X}n\left(x\right)\exp \left(-\mathrm{i}2\pi xf\right)\mathrm{d}x\right|}^2⟩,$$ (2.5)

where S denotes NPS and ⟨·⟩ denotes ensemble averaging. The NPS can be viewed as a decomposition of the noise variance σ² into its spatial frequency components. Therefore, the integral of NPS over f is equal to σ². An image dominated by high frequency noise power has a texture with fine graininess, while an image with excessive low frequency noise power has a patchy or coarse texture. For ACT, the NPS has been extensively investigated since the 1970s. Riederer et al.⁴¹ showed that it is proportional to G²(f)/f where G(f) is the reconstruction kernel used in the filtered backprojection (FBP) CT reconstruction. Wagner et al.⁴² and Hanson⁴³ investigated the relationship between large-area, low contrast detectabilities and the NPS of ACT imaging using signal detection theory. Kijewski and Judy⁴⁴ derived a discrete (digitized) expression of NPS for ACT. Boedeker et al.²¹ measured NPS and NEQ on multislice diagnostic CT scanners.

The NPS concept has been generalized to arbitrary n-dimensional (nD) digital images by Siewerdsen et al.²⁰

$$S\left(f_{1:n}\right)=\frac{b_{1:n}}{N_{1:n}}⟨|{\mathrm{DFT}}_{n\mathrm{D}}[I\left(x_{1:n}\right)-\overline{I}]{|}^2⟩,$$ (2.6)

where b_i denotes pixel size in domain i, N_i is the number of pixels of the ROI along domain i, DFT_nD denotes an nD discrete Fourier transform, I denotes a noise-only nD volume, and $\overline{I}$ is the mean DC value of the volumes. This framework is applicable not only to ACT, but also to any other linear system including DPC-CT. The unit of the nD NPS is determined by the physical nature of the signal as well as the dimensionality of the imaging system as

$$\left[S\left(f_{1:n}\right)\right]={\left[\mathrm{signal}\right]}^2{\left[\mathrm{domain}\right]}^n,$$ (2.7)

where the square brackets [·] denote the units of a quantity therein, and [domain] denotes the physical dimension of one domain in an nD space. For example, for 3D ACT with units of its signal determined by the linear attenuation coefficient μ, [S] = [mm⁻¹]² [mm]³.

Noise equivalent quanta

As shown in Eq. 2.7, the units of the NPS depend on the units of the image signal and thus are different between ACT and DPC-CT. By expressing the image noise in terms of the number of Poisson-distributed photons per unit length/area at each spatial frequency, an absolute scale of noise, the NEQ, can be introduced.⁴⁵ The frequency-dependent NEQ of a 2D axial CT is given by^{42, 43}

$$\mathrm{NEQ}\left(f\right)=\pi \left|f\right|\frac{T^2\left(f\right)}{S\left(f\right)},$$ (2.8)

where T denotes the system MTF and f denotes the radial spatial frequency in the axial (xy) plane throughout the paper. For a nD CT system, its NEQ is given by^{23, 57}

$$\mathrm{NEQ}\left(f_{1:n}\right)=\pi \left|f\right|\frac{T^2\left(f_{1:n}\right)}{S\left(f_{1:n}\right)}.$$ (2.9)

For ACT, the units of its NEQ are given by

$$\begin{array}{ccc}\hfill \left[\mathrm{NEQ}\left(f_{1:n}\right)\right]& =& \left[\pi \right|f\left|\right]\frac{\left[T^2\left(f_{1:n}\right)\right]}{\left[S\left(f_{1:n}\right)\right]}\hfill \\ & =& {\left[\mathrm{domain}\right]}^{-1}\frac{{\left[1\right]}^2}{{\left[\mu \right]}^2{\left[\mathrm{domain}\right]}^n}\hfill \\ & =& \frac{1}{{\left[\mathrm{domain}\right]}^{n-1}}.\hfill \end{array}$$ (2.10)

Therefore, the NEQ of a 3D absorption conventional x-ray cone beam CT (CBCT) using a planar detector have the units of [photons/mm²].²³ For DPC-CT, however, as its signal (δ) differs from that of ACT in both units and magnitude, an absorption-equivalent NPS ($S_{\mathrm{eqv}}^{\mathrm{dpc}}$) is introduced to define and calculate NEQ for DPC-CT. $S_{\mathrm{eqv}}^{\mathrm{dpc}}$ is given by

$$S_{\mathrm{eqv}}^{\mathrm{dpc}}\left(f_{1:n}\right)={\left(\frac{\overline{\mu }}{\overline{\delta }}\right)}^2{S}^{\mathrm{dpc}}\left(f_{1:n}\right),$$ (2.11)

where $\overline{\mu }$ and $\overline{\delta }$ are the mean output signals of ACT and DPC-CT, respectively. Note that the relative noise power at each spatial frequency component remains the same for both the physical NPS defined in Eq. 2.6 and the absorption-equivalent NPS defined in Eq. 2.11. Such an approach provides a common ground to directly compare the NEQs across DPC-CT and ACT.

NEQ( f ) is an important metric quantifying the overall performance of an imaging system. For example, it is directly related to the estimation of the detection performance of ideal observers by²³

$$\begin{array}{ccc}\hfill {\left(d^{\prime }\right)}^2& =& \int ...\int \frac{1}{\pi \left|f\right|}{\left|\Delta H\left(f_{1:n}\right)\right|}^2\mathrm{NEQ}\left(f_{1:n}\right)\mathrm{d}{f}_1\cdots \mathrm{d}{f}_n\hfill \\ & =& \int ...\int \frac{1}{\pi \left|f\right|}|\Delta H\left(f_{1:n}\right){|}^2\pi \left|f\right|\frac{T^2\left(f_{1:n}\right)}{S\left(f_{1:n}\right)}\mathrm{d}{f}_1\cdots \mathrm{d}{f}_n\hfill \\ & =& \int ...\int \frac{|\Delta H\left(f_{1:n}\right){|}^2{T}^2\left(f_{1:n}\right)}{S\left(f_{1:n}\right)}\mathrm{d}{f}_1\cdots \mathrm{d}{f}_n,\hfill \end{array}$$ (2.12)

where d ^′ denotes the ideal observer detectability index, ΔH(f) is the frequency representation of the difference between two hypotheses h₁ and h₂ (e.g., signal-present vs. signal-absent)

$$\begin{array}{ccc}\hfill \Delta H\left(f_{1:n}\right)& =& \int ...\int \left[h_1\left(x_{1:n}\right)-h_2\left(x_{1:n}\right)\right]e^{-\mathrm{i}2\pi (x_{1:n}·f_{1:n})}\hfill \\ & & \times \mathrm{d}{f}_1\cdots \mathrm{d}{f}_n.\hfill \end{array}$$ (2.13)

The units of |ΔH|² are [signal]²[domain]²ⁿ. Note that when calculating d ^′ using Eq. 2.12, the [signal]² dimension from the |ΔH|² term will always be normalized by the same dimension from the NPS based on Eq. 2.7, thus, the units of d ^′ are independent of the contrast mechanism of the imaging system and are always dimensionless.

INTRINSIC NOISE CHARACTERISTICS BETWEEN DPC-CT AND THE ASSOCIATED ABSORPTION CT: THEORETICAL STUDIES

This section presents our theoretical derivations of NPS and NEQ for both ACT and DPC-CT using a cascaded system model. As has been rightfully emphasized by Siewerdsen et al.,²⁰ a realistic CT system, even if it uses a single-row detector, is always 3D. Therefore, this paper focuses on the 3D analysis using a cascaded model. Two-dimensional results can be readily derived from the 3D results. An important assumption used in the derivation is that both DPC-CT and ACT signals are extracted from the same data acquisition with the interferometer gratings in the beam as described in Sec. 2A. This assumption provides a common ground for the comparison of the noise performance between the two contrast mechanisms.

Cascaded system model for DPC-CT and ACT acquisitions

Cascaded system analysis^{46, 47, 48} has been widely used in a variety of 2D (Refs. ^{49, 50, 51, 52, 53, 54, 55, 56}) and 3D (Refs. ^{23, 24, 36, 57}) imaging applications. Linearity and shift invariance are two basic assumptions used in the method. The method models the imaging chain as a series of discrete stages (e.g., gain, stochastic spreading, deterministic spreading, or sampling). The mean signal ${\overline{q}}_i$ and NPS S_i at stage i are determined from those at the previous stage (i − 1) by the mean gain ${\overline{g}}_{i-1}$, variance of the gain ${\sigma }_{g_i}^2$, MTF T_i, etc.

A DPC-CT system is capable of generating both DPC-CT and ACT images simultaneously from the same data set. This allows for a simple extension of the current cascaded system model to a DPC-CT system. Both rotating-anode x-ray tubes and indirect-detection flat panel detectors (FPD) have been used in DPC-CT systems.^{4, 7, 15, 58} Incident photons are diffracted by the Talbot-Lau interferometer before interacting with the detector, as shown in Fig. 1. Stages 1–7 are transfer stages in the indirect-detection FPD.^{49, 51} Stage 8 is added to account for the rebinning of the projection data.²³ The NPS of the raw projection data after Stage 8 is denoted as S₈. The transfer function related to the finite width of the x-ray focal spot (T₀) is a source of blur for systems with geometric magnification.^{57, 59, 60} Although T₀ degrades the system MTF [and therefore the NEQ based on Eq. 2.8], it does not influence the noise characteristics.⁵⁷ As a result, T₀ is not included in the analysis of NPS, but will be included in the NEQ analysis in Sec. 3C.

Figure 1.

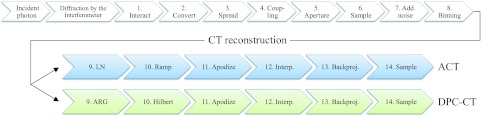
A schematic illustration of the cascaded system analysis model of image formation and reconstruction in DPC-CT/ACT.

The presented cascaded analysis in Sec. 3B starts from Stage 9, where the NPS of the two contrast mechanisms bifurcate into two different branches as shown in Fig. 1. X-ray scatter is neglected in the following analysis, though it could be incorporated following the methodology used by Prakash et al.⁵⁷ Other potentially relevant factors that will be neglected include nonuniformities in detector response, the heel effect, geometric misalignment, and beam hardening.

Characterizing the performance of the DPC-CT and ACT imaging chains: 3D NPS analysis

Stage 9: Data extraction

Because of the natural logarithm transformation (ln) in Eq. 2.3, the noise in the extracted absorption projections are related to the noise in the unprocessed raw projection data by²³

$$S_9^{\mathrm{a}}(f_u,f_v)=\frac{1}{{\left(m{\overline{N}}_0\right)}^2}{S}_8(f_u,f_v),$$ (3.1)

where the two spatial frequency components f_u, f_v are used to characterize the spatial frequency along the horizontal, u, and vertical, v, directions in the 2D detector plane.

In parallel to the ACT signal processing, the noise propagation of the DPC signal extraction described in Eq. 2.4 was previously analyzed²⁶ to find

$$S_9^{\mathrm{dpc}}(f_u,f_v)=\frac{2}{{\epsilon }^2}\frac{1}{{\left(m{\overline{N}}_0\right)}^2}{S}_8(f_u,f_v),$$ (3.2)

where $\epsilon ={\overline{N}}_1/{\overline{N}}_0$ is a parameter describing the efficiency of the grating interferometer component of the DPC-CT data acquisition system. ε is determined by the properties of the Talbot-Lau interferometer such as the aspect-ratio and duty-cycle of the gratings and intergrating distances. ε is independent of photon fluence and spatial frequency. The factor of 2 in the numerator of Eq. 3.2 reflects the fact that the photon usage will be effectively reduced by half when demodulation [e.g., Eq. 2.4] is used to retrieve phase information.

Stage 10: Reconstruction kernel

The FDK algorithm⁶¹ can be used to reconstruct both ACT and DPC-CT images. During the reconstruction, each projection is filtered with a reconstruction kernel only along the horizontal (u) direction. For ACT reconstruction, the reconstruction kernel is a ramp filter. As a result, the transfer function T(f) in this stage is given by

$$T_{10}^{\mathrm{a}}(f_u,f_v)=\left|f_u\right|.$$ (3.3)

In contrast, due to the differential nature of the projection data in DPC-CT a Hilbert filter should be used for the FDK reconstruction^{11, 62, 63, 64}

$$T_{10}^{\mathrm{dpc}}(f_u,f_v)=\frac{\mathrm{sgn}\left({\mathrm{f}}_{\mathrm{u}}\right)}{2\pi \mathrm{i}}.$$ (3.4)

The NPS for this stage is transferred deterministically

$$S_{10}(f_u,f_v)={\left|T_{10}(f_u,f_v)\right|}^2{S}_9(f_u,f_v),$$ (3.5)

where the transfer function T₁₀( f ) is different for ACT and DPC-CT as shown in Eqs. 3.3, 3.4, respectively.

Stage 11: Apodization window

In ACT, it is not uncommon to use an apodization filter (e.g., Hamming window) to suppress high-frequency noise in the final images and/or to tailor the MTF. In contrast, DPC-CT does not need additional image smoothing due to the low-frequency nature of its NPS.^{25, 27, 28, 30} In fact, a recent study showed that detectability in DPC-CT may actually benefit from a carefully chosen high-pass filter.⁶⁵ Therefore, the transfer functions in this stage are generally different for ACT and DPC-CT and are denoted as $T_{11}^{\mathrm{a}}$ and $T_{11}^{\mathrm{dpc}}$, respectively. The NPS for this stage is transferred deterministically as

$$S_{11}(f_u,f_v)=T_{11}^2(f_u,f_v)S_{10}(f_u,f_v).$$ (3.6)

Stage 12: Interpolation of the filtered projection

Interpolation is needed to approximate a continuous signal from digitized projections during the CT reconstruction. Bilinear and nearest-neighbor interpolation are the most commonly used methods. The transfer function associated with 2D bilinear interpolation is given by

$$T_{12}(f_u,f_v)={\mathrm{sinc}}^2\left(\pi f_u{a}_u\right){\mathrm{sinc}}^2\left(\pi f_v{a}_v\right),$$ (3.7)

and for nearest-neighbor, T₁₂ is given by

$$T_{12}(f_u,f_v)=\mathrm{sinc}\left(\pi f_u{a}_u\right)\mathrm{sinc}\left(\pi f_v{a}_v\right),$$ (3.8)

where a_i is the detector sampling interval along axis i. The reconstructions of ACT and DPC-CT often use the same interpolation method.

Stage 13: Backprojection

Due to the system magnification, the projection data should be scaled when they are backprojected to the image domain

$$S_{12M}(f_{y^{\prime }},f_z)=\frac{S_{12}(M{f}_u,M{f}_v)}{M^2}.$$ (3.9)

For idealized planar ACT, based on the well-known central slice theorem,⁶⁶ backprojecting a projection at a given view angle superimposes its power spectrum along a spoke in the frequency space through the origin and along direction determined by the projection angle. Thus, the NPS of the final reconstructed CT image is given by superimposing the NPS of each filtered projection data along its own spoke. The extent of superposition is directly proportional to the radial distance to the origin. Riederer et al.⁴¹ showed that, if the image is reconstructed from a total number of m_θ view angles equally spaced over π radians, the spoke density at radial frequency f is m_θ/(π|f|). Tward and Siewerdsen²³ generalized this relation to 3D CBCT with a geometric magnification by introducing a 3D transfer function

$${\left[{\Theta }_{13}^{\mathrm{a}}(f,f_z)\right]}^2=\frac{m_{\theta }}{\pi \left|f\right|}{M}^2{\left(\frac{\pi }{m_{\theta }}\right)}^2=\frac{\pi M^2}{m_{\theta }}\frac{1}{\left|f\right|},$$ (3.10)

where M was inserted to account for geometric magnification.

For DPC-CT, a multiplicative term ${\left(\frac{p_2}{2\pi z_{\mathrm{T}}}\right)}^2$ should be combined with ${\Theta }_{13}^{\mathrm{a}}$ according to Eq. 2.1

$${\left[{\Theta }_{13}^{\mathrm{dpc}}(f,f_z)\right]}^2=\frac{\pi M^2}{m_{\theta }}{\left(\frac{d_1}{d_{\mathrm{o}}}\right)}^2{\left(\frac{p_2}{2\pi z_{\mathrm{T}}}\right)}^2\frac{1}{\left|f\right|}.$$ (3.11)

The additional multiplicative term $\frac{d_1}{d_{\mathrm{o}}}$ accounts for the reduction in ϕ due to the divergent nature of the cone-beam.⁶d_o denotes the distance between the G₀ grating and the image object, and d₁ denotes the distance between the G₀ and G₁ gratings. Consequently, the NPS is transferred deterministically in this stage as²³

$$S_{13}(f_x,f_y,f_z)={\Theta }_{13}^2\left(f\right)S_{12M}(f,f_z).$$ (3.12)

Using the individual transfer functions given in Eqs. 3.10, 3.11, the transfer function can determined at this stage for ACT and DPC-CT, respectively.

Stage 14: Sampling of the 3D image matrix

A digital CT image is a sampled version of its continuous object function: δ(x, y, z) for DPC-CT and μ(x, y, z) for ACT. Sampling in the image domain with an interval of b_i along the ith domain (e.g., i = x, y, z for the three spatial directions) can be represented as a multiplication with a comb function $Ш\left(\frac{x}{b_x}\right)Ш\left(\frac{y}{b_y}\right)Ш\left(\frac{z}{b_z}\right)$, which corresponds to a 3D convolution with the function ${Ш}_{14}$ in the spatial frequency domain

$${Ш}_{14}(f_x,f_y)=\frac{1}{b_x}Ш\left(b_x{f}_x\right)\frac{1}{b_y}Ш\left(b_y{f}_y\right)\frac{1}{b_z}Ш\left(b_z{f}_z\right).$$ (3.13)

This results in

$$S_{14}(f_x,f_y,f_z)=S_{13}(f_x,f_y,f_z)⊛{Ш}_{14}(f_x,f_y,f_z),$$ (3.14)

where b_i is the sampling interval along axis i in the coordinate system of the reconstructed images and ⊛ represents the 3D convolution operation. Stage 14 affects the NPS of ACT by causing aliasing, as noise power from above the Nyquist frequency determined by the sampling interval wraps around to increase noise power at lower frequencies.⁴⁴ For DPC-CT, the magnitude of aliasing is expected to be reduced due to the low-frequency nature of its NPS.³⁰

Combining the stages

Based upon the cascaded system model, the individual 2D NPS for both ACT and DPC-CT can be written in terms of S₈ and the transfer functions from Stages 9 through 14. For ACT,

$$S^{\mathrm{a}}=\frac{1}{{\left(m{\overline{N}}_0\right)}^2}{\left[T_{10}^{\mathrm{a}}{T}_{11}^{\mathrm{a}}{T}_{12}{\Theta }_{13}^{\mathrm{a}}\right]}^2{S}_8⊛{Ш}_{14}.$$ (3.15)

In contrast, the NPS of the DPC-CT imaging chain is given by

$$S^{\mathrm{dpc}}=\frac{2}{{\epsilon }^2}\frac{1}{{\left(m{\overline{N}}_0\right)}^2}{\left[\left|T_{10}^{\mathrm{dpc}}\right|T_{11}^{\mathrm{dpc}}{T}_{12}{\Theta }_{13}^{\mathrm{dpc}}\right]}^2{S}_8⊛{Ш}_{14}.$$ (3.16)

Due to the fact that the decrement δ and the linear attenuation coefficient μ have different physical units, the resulting noise power spectra for ACT and DPC-CT also carry different physical units. The unit of the 3D ACT NPS, S^a, is [μ² mm³] or [mm⁻² mm³]. In contrast, the 3D DPC-CT NPS, S^dpc, has a unit of area: [δ² mm³] or [mm³].

Relationship between the 3D NPS of DPC-CT and ACT

Equations 3.15, 3.16 indicate that the 3D NPS of DPC-CT and ACT are intrinsically related. Except in cases of severe aliasing, ratio of the NPS between the two contrast mechanisms can be approximated as

$$\begin{array}{ccc}\hfill \frac{S^{\mathrm{dpc}}}{S^{\mathrm{a}}}& \approx & \frac{2}{{\epsilon }^2}{\left|\frac{T_{10}^{\mathrm{dpc}}}{T_{10}^{\mathrm{a}}}\right|}^2{\left[\frac{T_{11}^{\mathrm{dpc}}}{T_{11}^{\mathrm{a}}}\right]}^2{\left[\frac{{\Theta }_{13}^{\mathrm{dpc}}}{{\Theta }_{13}^{\mathrm{a}}}\right]}^2\hfill \\ & =& \frac{2}{{\epsilon }^2}\frac{1/{\left(2\pi \right)}^2}{f^2}{\left[\frac{T_{11}^{\mathrm{dpc}}}{T_{11}^{\mathrm{a}}}\right]}^2{\left(\frac{d_1}{d_{\mathrm{o}}}\frac{p_2}{2\pi z_{\mathrm{T}}}\right)}^2\hfill \\ & =& \frac{C_{\mathrm{g}}}{f^2}{\left[\frac{T_{11}^{\mathrm{dpc}}}{T_{11}^{\mathrm{a}}}\right]}^2,\hfill \end{array}$$ (3.17)

where f, defined as $f^2=f_x^2+f_y^2$, is the radial frequency in the axial plane, and C_g is a dimensionless factor that is determined by the geometry and efficiency ε of the interferometer

$$C_{\mathrm{g}}=\frac{1}{2{\pi }^2{\epsilon }^2}{\left(\frac{d_1}{d_{\mathrm{o}}}\frac{p_2}{2\pi z_{\mathrm{T}}}\right)}^2.$$ (3.18)

Equation 3.17 shows: (1) the NPS of DPC-CT can be quantitatively determined from the NPS of the associated ACT by a spatial-frequency-dependent factor 1/f ², the ratio of the reconstruction window functions, $T_{11}^{\mathrm{dpc}}/T_{11}^{\mathrm{a}}$, and an interferometer-related factor C_g; (2) this relationship depends on neither DPC-CT's nor the associated ACT's exposure level; (3) this relationship does not depend on the properties of the x-ray tube and detector except their geometric setup. This relationship provides an approach to quantitatively estimate the noise properties of DPC-CT from the associated ACT, provided that C_g is given or can be modeled. Note that some errors may occur in the estimate when aliasing effects are severe. In such cases, the convolution with ${Ш}_{14}$ would play an increasingly important role in the NPS expressions in Eqs. 3.15, 3.16.

Characterizing the performance of the DPC-CT and ACT imaging chains: 3D NEQ analysis

Based on Eq. 2.9, the NEQs of 3D ACT and 3D DPC-CT are given by

$${\mathrm{NEQ}}^{\mathrm{a}}(f_x,f_y,f_z)=\pi \left|f\right|\frac{{\left[T^{\mathrm{a}}(f_x,f_y,f_z)\right]}^2}{S^{\mathrm{a}}(f_x,f_y,f_z)}$$ (3.19)

and

$${\mathrm{NEQ}}^{\mathrm{dpc}}(f_x,f_y,f_z)=\pi \left|f\right|\frac{{\left[T^{\mathrm{dpc}}(f_x,f_y,f_z)\right]}^2}{S_{\mathrm{eqv}}^{\mathrm{dpc}}(f_x,f_y,f_z)},$$ (3.20)

where $S_{\mathrm{eqv}}^{\mathrm{dpc}}$ has been defined in Eq. 2.11, and T^a and T^dpc denote 3D MTFs of the ACT system and the DPC-CT system, respectively. For an ACT system, its MTF can be written as the multiplication of a series of transfer functions T_i in the imaging process.²³ These include the transfer functions associated with the spread of secondary quanta in the scintillator (T₃), the integration of secondary quanta within the finite pixel aperture (T₅), the apodization filter during the reconstruction (T₁₁), and the interpolation during the reconstruction (T₁₂). In addition, there is a transfer function T₀ associated with the system magnification M and the focal spot MTF T_spot by^{57, 60}

$$T_0=T_{\mathrm{spot}}\left(\frac{M-1}{M}f,\frac{M-1}{M}{f}_z\right).$$ (3.21)

The difference between T_spot and T₀ is that the former is defined at the focal spot plane, and is thus independent of magnification, while the latter is defined at the object plane and varies with M. T^a is therefore given by

$$T^{\mathrm{a}}=T_0{T}_3{T}_5{T}_{11}^{\mathrm{a}}{T}_{12}.$$ (3.22)

For DPC-CT, in addition to the above transfer functions, the system MTF may also be altered by the nonuniform frequency response of the grating interferometer, which is defined as the MTF of the Talbot-Lau interferometer (T_TL). T^dpc is given by

$$T^{\mathrm{dpc}}=T_0{T}_{\mathrm{TL}}{T}_3{T}_5{T}_{11}^{\mathrm{dpc}}{T}_{12}.$$ (3.23)

Note that in Eqs. 3.22, 3.23, the apodization filter T₁₁ may be different in ACT and DPC-CT. Based on the NPS relationship described in Eq. 3.17 and the MTF expressions in Eqs. 3.22, 3.23, the ratio of the NEQ between DPC-CT and the associated ACT is given by

$$\begin{array}{ccc}\hfill \frac{{\mathrm{NEQ}}^{\mathrm{dpc}}}{{\mathrm{NEQ}}^{\mathrm{a}}}& =& {\left[\frac{T^{\mathrm{dpc}}}{T^{\mathrm{a}}}\right]}^2{\left[\frac{S^{\mathrm{a}}}{S_{\mathrm{eqv}}^{\mathrm{dpc}}}\right]}^2\hfill \\ & \approx & {\left(\frac{\overline{\delta }}{\overline{\mu }}\right)}^2{T}_{\mathrm{TL}}^2\frac{f^2}{C_{\mathrm{g}}}.\hfill \end{array}$$ (3.24)

Note that the physical dimension of f compensates for the physical dimension of $\overline{\mu }$ to make this ratio dimensionless.

Equation 3.24 shows that the NEQ of DPC-CT is related to the associated ACT's NEQ in terms of (1) the ratio of the mean output signals between the two contrast mechanisms, (2) the interferometer MTF T_TL, (3) the square of axial radial frequency f, and (4) the design and quality of the interferometer (C_g). Consequently, one can also quantitatively determine the NEQ of a DPC-CT system from the NEQ of the associated ACT system using Eq. 3.24.

EXPERIMENTAL VALIDATION OF THE DERIVED INTRINSIC RELATIONSHIPS

This section presents experimental methods to validate Eq. 3.17, i.e., the 3D NPS of DPC-CT can be determined from that of the associated ACT and vice versa. In addition, experimental methods to measure the 3D MTF and NEQ of DPC-CT and the associated ACT will be presented.

Imaging acquisition system and acquisition parameters

The image acquisition system is a multicontrast cone-beam CT benchtop constructed by the authors' group.¹⁵ The system uses a rotating-anode x-ray tube (Varian G1582, Palo Alto, CA) with 0.3 and 1.0 mm nominal focal spot, and a flat-panel detector (Rad-icon Shad-o-Box 2048, Sunnyvale, CA) with 48 × 48 μm native pixels across a 1024 × 2048 array. The native pixels were 2 × 2 binned after readout, giving an effective size of 96 μm along both directions. Three gratings (G₀, G₁, and G₂) were used in the data acquisition system. The G₂ grating has a pitch p₂ = 4.5 μm and was placed at the first fractional Talbot distance (z_T = 18.5 cm). The system has a magnification of 1.2, and field of view (FOV) of 58 mm in diameter for the axial (xy) plane and 58 × 41 mm in the sagittal (yz)/coronal (xz) planes. The fan and cone angles of the system are 1.8° and 1.3°, respectively. The small beam divergence for this setup justifies the assumption of shift-invariance used in the theoretical analysis.

For the CT acquisition, 360 projections were acquired at 1° angular intervals with the x-ray tube operating at 40 kVp and 10 mA. At each projection view, the exposure time was 40 s, divided over 8 phase steps. Absorption and DPC projections were extracted from the same intensity data using Eqs. 2.3, 2.4, then reconstructed using the FDK algorithm with bilinear interpolation. Depending on the contrast mechanism, either the ramp filter (ACT) or the Hilbert filter (DPC-CT) was used. No apodization filter was applied, therefore, $T_{11}^{\mathrm{a}}=T_{11}^{\mathrm{dpc}}=1$. The reconstruction matrix size is 360 × 360 × 360. The reconstructed images have an isotropic voxel size of 80 μm.

NPS measurements

Two back-to-back scans of a cylindrical water phantom (diameter 25.6 mm) were reconstructed and subtracted to generate noise-only 3D ACT and DPC-CT image volumes. The 3D NPS was measured from the 3D DFT of its subvolumes²⁰

$$\begin{array}{c}\hfill S(f_x,f_y,f_z)=\frac{b_x}{N_x}\frac{b_y}{N_y}\frac{b_z}{N_z}\frac{⟨|{\mathrm{DFT}}_{3\mathrm{D}}[I(x,y,z)-\overline{I}]{|}^2⟩}{2},\end{array}$$ (4.1)

where I(x, y) denotes each of the 27 partially overlapped volumes of interest (VOI), and $\overline{I}$ denotes the average DC value of all the VOIs. The factor of 2 in the denominator accounts for the doubling of noise variance caused by the subtraction of the two image volumes. Matrix size and voxel size of each VOI are N_x = N_y = N_z = 180, and b_x = b_y = b_z = 0.08 mm, respectively. The symbol ⟨·⟩ denotes ensemble averaging across the 27 VOIs. Along each frequency axis, the NPS was computed within [−f_N, f_N] sampled over 360 frequency bins (Δf = f_N/180), where f_N denotes the Nyquist frequency determined by the sampling rate of the projection data and system magnification

$$f_{\mathrm{N}}=\frac{1}{2}\frac{M}{\Delta u}=\frac{1.2}{2\times 0.096\mathrm{mm}}=6.25{\mathrm{mm}}^{-1}.$$ (4.2)

To validate the NPS relationship [Eq. 3.17], the numerical values of C_g for the experimental system used in this study were also experimentally determined as follows: based on Eq. 2.2, the interferometer efficiency factor ε was measured using

$$\epsilon =⟨\frac{2\left|{\sum }_k{N}^k\exp \left(-\mathrm{i}2\pi \frac{k}{m}\right)\right|}{{\sum }_k{N}^k}⟩.$$ (4.3)

The ensemble averaging was performed across a 200 × 200 ROI located at the center of each projection image and then across the 360 projection views. This ensemble average yielded a result of ε = 0.11 ± 0.02. For the system used in this study, d_o = 134.6 cm and d₁ = 148.6 cm, thus, the numerical value of C_g is

$$C_{\mathrm{g}}=\frac{1}{2{\pi }^2{\epsilon }^2}{\left(\frac{d_1}{d_{\mathrm{o}}}\frac{p_2}{2\pi z_{\mathrm{T}}}\right)}^2=7.65\times {10}^{-11}.$$ (4.4)

To quantify the accuracy of the calculated NPS (S_c) against the measured NPS (S_m), the relative root mean square error (rRMSE) is used

$$\mathrm{rRMSE}\left({\mathbf{S}}_{\mathbf{c}}\right)=\frac{\frac{1}{\sqrt{N_S}}{\Vert {\mathbf{S}}_{\mathbf{c}}-{\mathbf{S}}_{\mathbf{m}}\Vert }_{{\ell }_2}}{\max \left({\mathbf{S}}_{\mathbf{m}}\right)-\min ({\mathbf{S}}_{\mathbf{m}})}\times 100\%,$$ (4.5)

where N_S is the total number of elements in the 3D matrix S_m.

MTF measurements

In this paper, the 3D MTF was approximated as a product of the 2D axial MTF (T_2D) and the 1D MTF along the f_z-direction (T_z). The experimental measurements of 3D MTF of a DPC-CT system are not as straightforward as that of the well-known process for the associated ACT system. Fortunately, the problem is simplified by the one-dimensional (1D) nature of the gratings used in the present experiments: 1D grating structures and grooves were used in the Talbot-Lau interferometer, and the grating structures are parallel to the rotation axis of the data acquisition system. Thus, the current DPC-CT system does not introduce additional mechanism to alter the spatial resolution along the z-direction. Namely, the MTFs of the DPC-CT system and the associated ACT system have the same f_z dependence, and therefore the same T_z

$$T^{\mathrm{dpc}}(f,f_z)=T_{2\mathrm{D}}^{\mathrm{dpc}}\left(f\right)T_z\left(f_z\right),$$ (4.6)

$$T^{\mathrm{a}}(f,f_z)=T_{2\mathrm{D}}^{\mathrm{a}}\left(f\right)T_z\left(f_z\right).$$ (4.7)

In this study, the 3D ACT MTF T^a(f, f_z), the 2D MTF $T_{2D}^{\mathrm{dpc}}\left(f\right)$, and $T_{2D}^{\mathrm{a}}\left(f\right)$ were measured separately. Using Eq. 4.7, one can derive the common factor T_z(f_z) and use it in Eq. 4.6 to generate the desired 3D MTF for DPC-CT.

A tantalum sphere (ϕ = 258 μm, suspended in a tube of gelatin) was scanned using the system to obtain its volumetric ACT images. The scan was performed over 720 views with a 0.5° angular interval. A FOV of 1.6 mm with 10 μm pixel size was reconstructed. No apodization function was applied. Other acquisition parameters were identical to those used in Sec. 4B. The measured ACT volume was deconvolved with the true 3D profile of the sphere to obtain the volumetric spread function and the corresponding 3D ACT MTF T^a(f, f_z).

The 2D MTFs were measured using the reconstructed axial ACT and DPC-CT images of a custom-built MTF phantom. Although it is a common practice to scan a high density small object to measure the axial MTF of conventional ACT,^{17, 67, 68} the use of a material with extremely high density should be avoided when measuring the MTF of DPC-CT to avoid phase wrapping. In addition, one cannot use extremely small objects to measure the MTF in DPC-CT, because the DPC-CT system is not sensitive to objects contained entirely within a detector pixel. The MTF phantom used in this study was constructed using a graphite rod (0.3 mm B Pentel super lead), which is made of graphite mixed with a polymer binder. The rod was held in a water cylinder with an outer diameter of 25 mm. Such a deliberate phantom design was able to avoid phase wrapping while generating sufficiently strong phase signal in the DPC projections. A FOV of 4 mm with 10 μm pixel size was reconstructed. Other acquisition and postprocessing parameters are identical to those used in the 3D ACT MTF measurement. For each contrast mechanism, 100 axial slices were reconstructed and carefully registered before slice-averaging was performed for the purpose of noise reduction. Line profiles through the center of the phantom were measured then radially averaged. The finite width of the graphite rod was corrected using deconvolution. Finally, the 3D MTF of DPC-CT was calculated using Eq. 4.6.

NEQ measurements

The 3D NEQ of ACT was calculated using Eq. 3.19. To calculate the 3D NEQ of DPC-CT, first, $\overline{\mu }$ and $\overline{\delta }$ were measured in a 180 × 180 × 180 VOI located inside the water phantom, then $S_{\mathrm{eqv}}^{\mathrm{dpc}}$ was calculated using Eq. 2.11, and finally the DPC-CT NEQ was calculated using Eq. 3.20.

Since the 3D NEQ of both ACT and DPC-CT are expected to be radially symmetric in the axial plane due to the radial symmetry of both the MTFs and NPS, each 3D NEQ can be rendered as a 2D slice NEQ(f, f_z) obtained by radial averaging.

Note that both object material and x-ray beam energy must be considered when comparing the NEQs of the two contrast mechanisms, because both $\overline{\delta }$ and $\overline{\mu }$ in Eq. 2.11 are material and energy dependent. To demonstrate an example of the material dependence of NEQs, their values were recalculated when the material of the NPS phantom was changed from water to acrylic. The results are presented in Sec. 5C.

Ideal observer performance with simple detection tasks

In order to demonstrate the utility of the NEQ, the ideal observer detectability indices for simple disc-detection tasks were computed based on Eq. 2.12. Two hypotheses of each task were: hypothesis h₁, presence of an acrylic disc in a uniform water background; hypothesis h₂, absence of the disc (water only). The task functions were calculated using Eq. 2.13. To understand how the detectability index changes with the frequency content of the imaging task, each task used one out of a group of 12 discs with distinct diameters ranging from 0.4 to 4.8 mm.

EXPERIMENTAL RESULTS

Noise power spectrum

In Fig. 2, 3D NPS for ACT and DPC-CT are rendered as stacks of interleaved axial slices. The center of the central slice of a stack corresponds to S(f_x = 0, f_y = 0, f_z = 0). Each slice is separated from another by f_N/4 along f_z. Figure 2a is the NPS of ACT measured from the experimental cone beam ACT data. The fact that the ramp filter imposes a low weight on the low f region, when combined with the blurring caused by other transfer functions in Eq. 3.15, leads to the observed midpass feature in the axial planes of the ACT NPS. The observed drop along the f_z axis is caused by detector blurring along the v-axis (parallel to the rotation axis of the data acquisition system) as well as the interpolation along z-axis in the FDK reconstruction. In contrast, Fig. 2b is the experimentally measured NPS of DPC-CT, which shows a low-pass feature primarily caused by the use of the Hilbert filter in the DPC-CT reconstruction.

Figure 2.

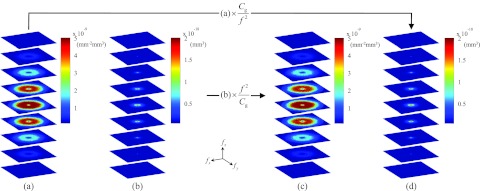
Axial cuts through the 3D NPS. Frequency range along each axis is [−6.25, 6.25] mm⁻¹. (a) and (b) NPS of ACT and DPC-CT, respectively, measured from experimental data. (c) The NPS of ACT calculated from the experimental NPS of DPC-CT in (b). (d) The NPS of DPC-CT calculated from the experimental NPS of ACT in (a).

As shown in Eq. 3.17, the 3D NPS of one contrast mechanism can be quantitatively calculated from the other if the NPS of the other contrast mechanism is known. In this study, $T_{11}^{\mathrm{dpc}}=T_{11}^{\mathrm{a}}$ has been used. Figure 2d shows the quantitatively calculated NPS of DPC-CT from the experimentally measured NPS of ACT using the multiplier C_g/f ². In contrast, Fig. 2c shows the quantitatively calculated NPS of ACT from the experimentally measured NPS of DPC-CT using the multiplier of f ²/C_g. The rRMSE of the calculated NPS of ACT is 2.8%, while the rRMSE of the calculated NPS of DPC-CT NPS is about 0.083%. The errors are likely to be caused by aliasing in the measured NPS. These results demonstrate that the 3D NPS of DPC-CT can be estimated from that of ACT with high accuracy, and vice versa, using the NPS relationship in Eq. 3.17.

Additionally, as shown in Fig. 2, the NPS of the two contrast mechanisms demonstrate the expected rotational symmetry in each axial plane. Therefore, a radial-averaging process is justified. Sample line plots are shown in Figs. 3c, 3f, from which one can easily appreciate the significant difference in the NPS along the f axis between ACT and DPC-CT. Note that a direct comparison of the magnitude of NPS between the two modalities should be avoided, as they have different physical units due to the difference in the nature of the measured signals.

Figure 3.

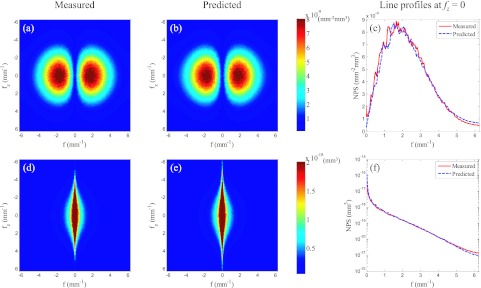
Because of the radial symmetry of the 3D NPS in Fig. 2, a 2D axial plane at a given f_z can be reduced to a line by radial-averaging, and the 3D NPS can be reduced to 2D NPS planes S(f, f_z), as shown here. The first row shows the NPS of ACT, and the second shows the NPS of DPC-CT. The predicted NPS were calculated from the measured NPS of the other contrast using Eq. 3.17. Line profiles in (c) and (f) are along f_z = 0 [note that the DPC-CT line plots in (f) are on a semilog scale].

Modulation transfer function

The cross sections of 3D MTF of ACT and DPC-CT are presented as 2D slices: T^a(f, f_z) in Fig. 4a and T^dpc(f, f_z) in Fig. 4b. The line plots T^a(f, f_z = 0) and T^dpc(f, f_z = 0) are presented in Fig. 4c. As expected and shown in Fig. 4c, the spatial resolution of DPC-CT in the axial plane is slightly inferior to that of ACT due to the presence of the Talbot-Lau interferometer MTF T_TL. In the axial plane, the spatial frequencies at the 10% MTF levels were 5.10 (ACT) and 4.23 mm⁻¹ (DPC-CT), which corresponds to spatial resolutions of 98 and 118 μm, respectively. Along the z-direction, the spatial frequency at the 10% MTF levels is 5.38 mm⁻¹ for both systems.

Figure 4.

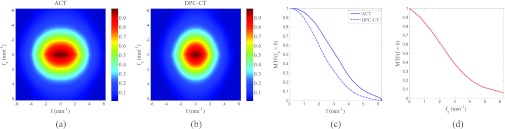
Because of the radial symmetry in the (f_x, f_y) plane, the 3D MTFs of ACT and DPC-CT can be visualized using their 2D slice in the (f, f_z) plane, as shown in (a) and (b). Horizontal and vertical line profiles of the MTFs through the origin (f = 0, f_z = 0) were plotted in (c) and (d), respectively. In (d), only one line is shown because the MTF along f_z is the same for both contrast mechanisms.

Noise equivalent quanta

Using the measured 3D MTF and NPS of both DPC-CT and ACT, one can proceed to generate a 3D NEQ provided the mean signals of ACT and DPC-CT images are given. The mean signal values measured under the presented experimental conditions are $\overline{\mu }=0.0371$ mm⁻¹ and $\overline{\delta }=2.99\times {10}^{-7}$. Because of their radial symmetry in the axial (xy) plane, the 3D NEQ can be represented by their coronal/sagittal 2D cross sections through the origin [Fig. 5a for ACT and Fig. 5b for DPC-CT]. Axial cross sections of the NEQ through the origin have also been generated as shown in Figs. 5d, 5e for ACT and DPC-CT, respectively. The NEQ of ACT demonstrates a relatively weak frequency dependence. In contrast, the NEQ of DPC-CT shows a strong bandpass behavior in the axial plane. The NEQ of DPC-CT is limited by a low frequency divergence in the NPS and is constrained by the MTF at high frequencies. Under the presented experimental conditions, the NEQ of DPC-CT peaks at f = 3.09 mm⁻¹. The crossover frequency of the two NEQ is 1.15 mm⁻¹, beyond which DPC-CT demonstrates an advantage compared with ACT. This is consistent with the result of a human observer study.³¹ In order to demonstrate the effect of changing the object material, Fig. 6 shows the predicted NEQ of both systems if the object material is changed from water to acrylic. For ACT, the difference in NEQ between water and acrylic is negligible. For DPC-CT, however, switching to acrylic leads to appreciable increase in NEQ because of this material's larger δ value (δ_acrylic = 3.38 × 10⁻⁷).¹⁵

Figure 5.

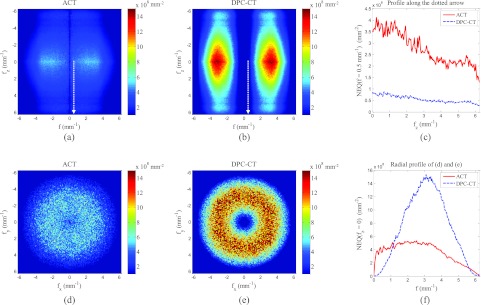
2D planes through the 3D NEQ. (a) and (b) Averaged NEQ(f, f_z) while (d) and (e) show a central axial plane of NEQ(f_x, f_y) with f_z = 0. (a) and (b) show less uncertainty because of the radial averaging. (c) shows line profiles of the NEQ along the dotted arrow in (a) and (b). (f) shows the radial profile of (d) and (e).

Figure 6.

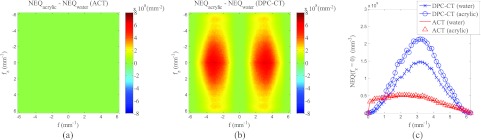
(a) Difference between the ACT NEQ measured using an acrylic phantom and the NEQ in Fig. 5a, which were measured using a water phantom of the same size. (b) Difference between the DPC-CT NEQ measured using the acrylic phantom and that measured by the water phantom [Fig. 5b]. (c) shows line profiles of the NEQ along f as a function of contrast mechanisms and phantom materials.

While the NEQ of ACT is independent of the interferometer efficiency factor ε, the NEQ of DPC-CT is directly proportional to ε² based on Eq. 3.24. Improving ε will reduce the magnitude of the NPS of DPC-CT, thereby, increasing its NEQ. Figure 7 shows the calculated NEQ at different ε values. A larger ε not only increases the magnitude of the DPC-CT NEQ, but also widens the frequency range over which DPC-CT is superior to ACT (Fig. 7). Note that based on Eq. 3.24, the crossover frequency is independent of photon fluence ${\overline{N}}_0$.

Figure 7.

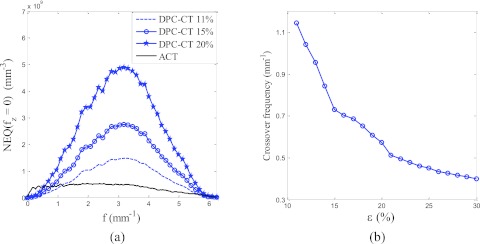
(a) Predicted DPC-CT NEQ(f, f_z = 0) at various interferometer efficiency (ε) values . (b) The crossover frequency of the two modalities' NEQ curves as a function of ε.

Ideal observer detectability index

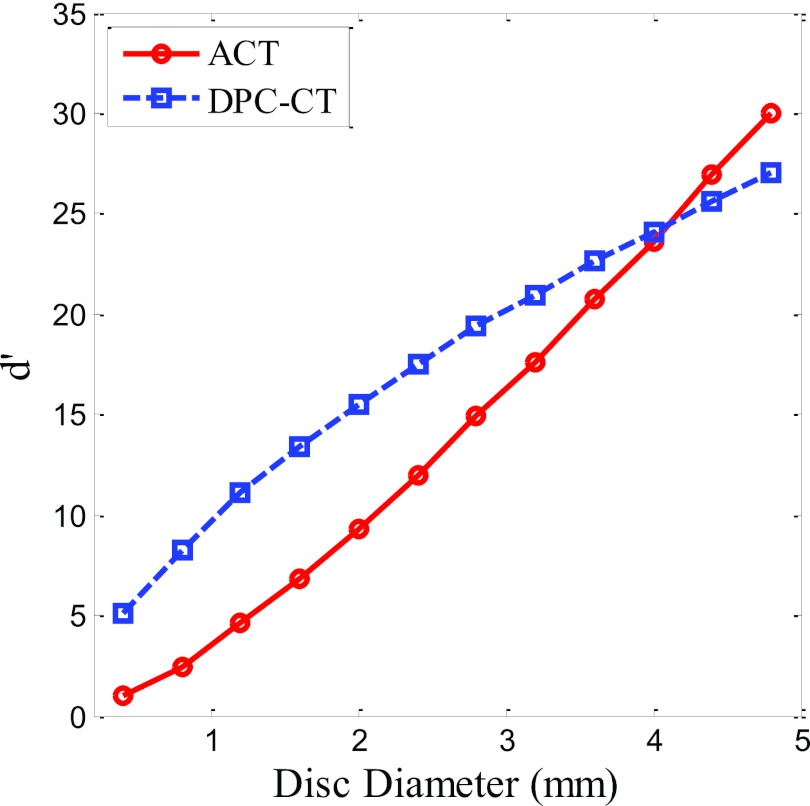
The ideal observer detectability indices for the simple disc-detection tasks are plotted as a function of disc diameters in Fig. 8. When the task contains more high-frequency content (detection of discs with smaller radii), DPC-CT shows better ideal observer performance. In contrast, ACT outperforms DPC-CT for the detection of relatively low frequency objects (discs with larger radii). This result is consistent with a human observer performance study³¹ and a recent study using channelized Hotelling observer model.⁶⁹ Crossover of the two curves is at diameter = 4.0 mm. However, the extent of the agreement between detectability indices in ideal observer model and human observer performance is still not well understood and merits further investigation.

Figure 8.

Ideal observer detectability index (d ^′) of the experimental DPC-CT/ACT system used in this paper. The imaging task is the detection of acrylic discs of various diameters from uniform water background.

DISCUSSION AND CONCLUSIONS

In this paper, we investigated the relationship of noise properties of a grating-based DPC-CT system and the associated ACT system. The results demonstrate that one can predict the noise performance of the DPC-CT system from that of the associated ACT system with the gratings present, or vice versa. In practice, one may want to start with an ACT system without gratings, equivalent to any currently used ACT system in clinical practice, to understand the potential performance of a DPC-CT system with gratings. This can be readily achieved by accounting for the difference in NPS in ACT systems with and without gratings: the final photon fluence at the detector will be reduced by a fraction α due to the presence of the gratings. As a result, the NPS will have to be corrected by a factor of 1/α since the ACT NPS is inversely proportional to the number of photons.^{41, 43} The correction factor α will depend on the quality and design parameters of the gratings, e.g., duty cycle and G₂ material, which can be easily calculated or measured for a given interferometer design. Using this correction factor, the NPS relationship should be adjusted to

$$S^{\mathrm{dpc}}=\frac{1}{\alpha }\frac{C_{\mathrm{g}}}{f^2}{S}_0^{\mathrm{a}},$$ (6.1)

where $S_0^{\mathrm{a}}=\alpha S^{\mathrm{a}}$ is the NPS of the existing single-contrast ACT system without gratings at the same dose level to the image object. For the experimental system used in this paper, the parameter α was measured to be 0.56 ± 0.03. It is worth emphasizing that Eq. 6.1 is only valid under the condition of equivalent dose to the object. This NPS relationship provides a valuable approach for the quantitative modeling, prediction, evaluation, and optimization of the noise performance of proposed DPC-CT systems across a broad range of input parameters (e.g., radiation dose, kVp, beam filtration, magnification, spatial resolution, and quality control parameters for interferometer).

By combining a task function with NEQ, the detection performance for an ideal observer can be calculated following Eq. 2.12 and used to evaluate the benefits of DPC-CT for specific clinically relevant tasks. However, the calculation of the DPC-CT NEQ does require prior knowledge about the interferometer transfer function T_TL. A theoretical model pinpointing the DPC signal transfer process through the Talbot-Lau interferometer would add further insight and deserves to be the subject of future work.

The model presented here does not account for possible limitations caused by the following effects: changes in the NPS due to undersampling,^{23, 24} reduction of the interferometer efficiency ε due to small-angle scattering,⁷⁰ or spatially varying noise behavior due to divergent beams.^{71, 72, 73} These effects would need to be studied in the future, although experimental results presented in this work suggest that their effects may be negligible.

In conclusion, this work provides theoretical analysis and experimental validation of the fundamental relationship between the noise performance of DPC-CT and the associated ACT. The theoretical model highlights a number of characteristics, particularly the efficiency of the Talbot-Lau interferometer, that can affect the noise properties of DPC-CT. The theoretical framework can be applied to the design and optimization of a multicontrast x-ray CT system for potential medical applications.