Origins of Stereoselectivities in Chiral Phosphoric Acid-Catalyzed Allylborations and Propargylations of Aldehydes

Abstract

The chiral BINOL-phosphoric acid catalyzed allylboration and propargylation reactions are studied with density functional theory (B3LYP and B3LYP-D3). Two different models were recently proposed for these reactions by Goodman and our group, respectively. In Goodman's model for allylborations, the catalyst interacts with the boronate pseudo-axial oxygen. By contrast, our model for propargylations predicts that the catalyst interacts with the boronate pseudo-equatorial oxygen. In both models, the phosphoric acid stabilizes the transition state by forming a strong hydrogen bond with the oxygen of the boronate, and is oriented by a formyl hydrogen bond (Goodman model), and by other electrostatic attractions in our model. Both of these models have now been reinvestigated for both allylborations and propargylations. For the most effective catalyst for these reactions, the lowest energy transition state corresponds to Goodman's axial model, while the best transition state leading to minor enantiomer involves the equatorial model. The high enantioselectivity observed with only the bulkiest catalyst arises from the steric interactions between the substrates and the bulky groups on the catalyst, and the resulting necessity for distortion of the catalyst in the disfavored transition state.

Introduction

Asymmetric allylborations of carbonyls are valuable methods in organic synthesis, and occur with high enantioselectivity and diastereoselectivity.¹ The most common method for enantioselective allylboration involves chiral allylboron reagents.² However, the preparation of chiral allylboranes and allyl boronates often requires multiple steps and can be challenging. Enantioselective allylborations involving catalytic chiral Lewis acids³ or Brønsted acids⁴ have now been developed. In particular, chiral BINOL-phosphoric acids that have been employed in many other asymmetric reactions^5,6 were recently demonstrated by Antilla to catalyze the enantioselective allylboration reaction between allylboronate 1 and benzaldehyde 2 (Figure 1).⁷ The homoallylic alcohol 3 was obtained in 99% yield and 93% ee with catalyst PA1 bearing bulky 3,3'-substituents. For other aldehydes, including electron-donating aromatic aldehydes, electron-withdrawing aromatic aldehydes and aliphatic aldehydes, the enantioselectivities vary from 73% to 99% ee. The asymmetric propargylation involving allenyl boronic acid pinacol ester 1' and benzaldehyde 2 was efficiently catalyzed by PA1 as well, which gave homopropargylic alcohol 3' in high yield and ee.⁸ Catalysts where the Ar groups are less bulky gave much lower ee values.

Figure 1.

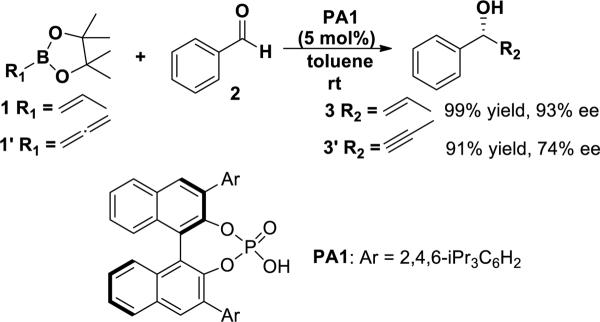
Chiral phosphoric acid-catalyzed allylborations and propargylations of benzaldehyde.

Using computational methods, we recently proposed a model to explain the enantioselectivities in propargylations.⁸ In our model (Figure 2), the phosphoric acid establishes a H-bond with the pseudo-equatorial oxygen of the boronate. The high enantioselectivities observed for PA1 originate from the larger distortion of the catalyst in the disfavored TS, which is the result of avoiding steric interactions between the allenylboronate methyls and the bulky substituents in the catalyst. At almost the same time, Grayson, Pellegrinet, and Goodman published a computational study of allylboration reactions.⁹ In the Goodman et al. work, it was proposed that the hydroxyl group of BINOL phosphoric acid H-bonds to the pseudo-axial oxygen of the boronate, and the phosphoryl oxygen interacts with the aldehyde formyl hydrogen through electrostatic interactions (Figure 2). Due to the large size of the real catalyst, Goodman used ONIOM calculations on the full catalyst PA1. The high enantioselectivities were rationalized from the unfavorable steric clash between the pinacol methyl groups and the large alkyl-substituted aromatic group of the catalyst. Despite the differences in the activation modes of two models, steric effects or the resulting distortions of the catalyst are believed to determine the origins of the stereoselectivites in these reactions.

Figure 2.

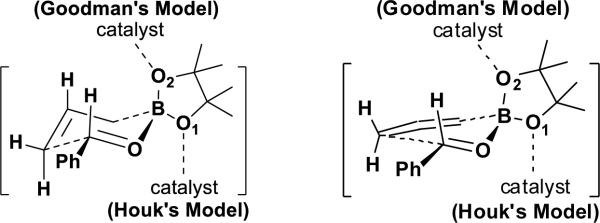
Two models for the chiral phosphoric acid-catalyzed allylborations and propargylations of benzaldehyde.

We have reinvestigated the chiral BINOL-phosphoric acid catalyzed allylboration and propargylation reactions using several levels of DFT calculations. In order to study the enantioselectivity of the catalysis, the two different models were evaluated. In addition, we used B3LYP-D3, which includes dispersion energies,¹⁰ to calculate the transition state energies, which may also be important to such systems. Using biphenol (BIPOL)-derived phosphoric acid as the model catalyst, we found that the two competing models are comparable in energy. The diastereomeric TSs involved in allylborations and propargylations for PA1 were located using fully DFT optimization, and the calculated energies by B3LYP and B3LYP-D3 indicated that both pathways were involved for these systems. Goodman's model with axial coordination has a lower energy for re-face attack TS, which leads to the major enantiomeric product. However, in our calculations, for si-face attack TS, our model is more stable than Goodman's model, which indicated that the minor enantiomeric TS comes from equatorial coordination of the catalyst.

Results and Discussion

Investigation of the reaction mechanism

The allylboration reaction proceeds via a closed six-membered chairlike transition state.¹¹ There are three possible coordination positions for the catalyst hydroxyl group: the two boronate oxygens or the aldehyde oxygen. In Goodman's and our models, the phosphoric acid forms a hydrogen bond with the boronate oxygens: either the pseudo-equatorial oxygen (path i: eq), or the pseudo-axial oxygen (path ii: ax). The other plausible mechanistic pathway is the phosphoric acid forming a H-bond with the oxygen of the aldehyde (path iii).

In order to evaluate these different pathways, we first explored transition states where each of the oxygens was protonated. All calculations were performed with the Gaussian 09 package.¹² Geometries were fully optimized in the gas phase and characterized by frequency calculations using B3LYP functional and 6–31G* basis set. Free energies were calculated for each stationary point. The optimized chairlike transition state structure of the uncatalyzed reaction is shown in Figure 4, and the transition states for the three possible sites of protonation are shown in Figure 5 along with their relative Gibbs free energies.

Figure 4.

Optimized transition state of the uncatalyzed allylboration of benzaldehyde at the B3LYP/6–31G* level of theory.

Figure 5.

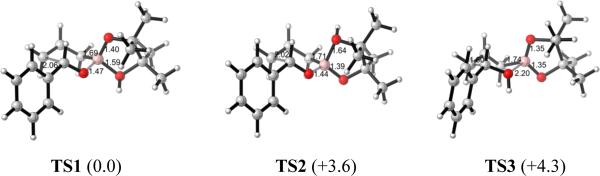
Optimized transition states of different mechanisms at the B3LYP/6–31G* level of theory. Bond lengths are given in Å. Relative free energies (kcal/mol) are shown in parentheses.

As shown in Figure 5, the pathways involving protonation of boronate oxygens (TS1: 0.0 kcal/mol, TS2: +3.6 kcal/mol) are more favorable than TS3 (+4.3 kcal/mol) which involves protonation of the aldehyde oxygen. Protonation of a B–O increases the electrophilicity of the boronate and lowers the activation energy.¹³ This finding is in agreement with Hall's experimental observations¹⁴ and Fujimoto's theoretical studies¹⁵ of similar Lewis acid catalyzed allylboration reactions. Similarly, for propargylations, protonation of boronate oxygens accelerates more than protonation of aldehyde (See Supporting Information).

Model of the phosphoric acid-catalyzed allylboration reaction

The mechanistic studies reported above illustrate that activation of boronate oxygens are more favorable than activation of aldehyde oxygen. This phenomenon is also found in Goodman's model study calculations. In order to better understand the boronate activation pathways, catalyst PA without Ar substituents was then employed to study both paths i and ii in more detail. In order to reduce the computational cost, the biphenol (BIPOL)-derived phosphoric acid was initially used as the model instead of the BINOL-derived phosphoric acid. This kind of truncating has previously been justified by Yamanaka, Akiyama and Goodman in their studies.⁶ Replacement of the binaphthyl backbone with a smaller biaryl does not significantly alter the geometry around the reaction center.

In both pathways i (eq) and ii (ax), the catalyst interacts with the allylboronate by a single hydrogen bond, and the orientation of the phosphate with respect to the substrate is not fixed. As a result, the remaining parts of the catalyst are conformationally flexible, and there are many possible diastereomeric transition state structures with different orientations of the catalyst. To explore all accessible conformations of the transition states, a conformational search was performed (See Supporting Information: Figure S1).

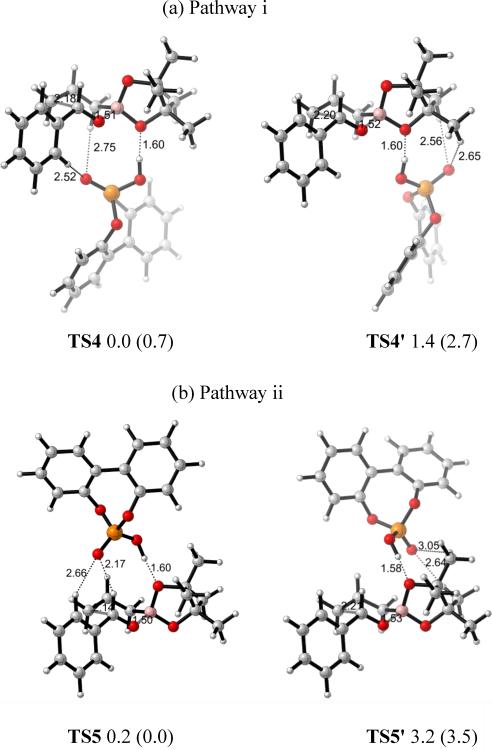
For pathway i, two low energy transition state structures, TS4 and TS4', were located for the phosphoric acid-catalyzed allylboration reaction (Figure 6a). In TS4, the lowest energy minimum for i, the phosphoryl oxygen was near the six-membered transition state; in TS4', the phosphoryl oxygen is away from the six-membered ring, but next to the boronate methyls. TS4' is 1.4 kcal/mol less stable than TS4. Since B3LYP may underestimate the aromatic and dispersion interactions in such systems, a method which is expected to treat such interactions more accurately was used to calculate the energy differences between different transition states as well. The energy difference between TS4 and TS4' is calculated to be 2.0 kcal/mol with B3LYP-D3, which includes a dispersion energy correction. For pathway ii, involving H-bonds to the pseudo-axial boronate oxygen, two different diastereomeric transition state conformers, TS5 and TS5' were also found (Figure 6b). TS5, in which the phosphoryl oxygen is situated over the six-membered ring TS, was more energetically favorable than TS5' by 3.0 kcal/mol. B3LYP-D3 calculation gave an energy difference of 3.5 kcal/mol between TS5 and TS5'. This order of stability between TS5 and TS5' was also observed by Goodman et al.⁹

Figure 6.

Optimized transition state structures of (a) TS4, TS4' in pathway i (eq) and (b) TS5, TS5' in pathway ii (ax) at the B3LYP/6–31G* level of theory. Bond lengths are given in Å. Values next to each structure are energies relative to TS4 in kcal/mol. Values in parentheses are energies relative to TS5 calculated by B3LYP-D3.

In order to study the origin of the energy differences between the different transition state conformers, electrostatic potentials were computed. They are shown for the uncatalyzed reaction transition state TS in Figure 7. The formyl H, allyl Hs and phenyl Hs are more positive than the Hs on boronate methyls. This indicates that there can be stabilizing electrostatic attractions between the phosphoryl oxygen and those positive Hs. The stabilized interactions between electronegative parts of catalysts and the formyl H has been proposed by Corey before,¹⁶ as well as in Goodman's model. Here, TS4 was more stable than TS4' and TS5 was more stable than TS5'. The extra stabilization of TS4 and TS5 comparing to TS4' and TS5' came from the extra attractive P=O∙∙∙H–C interactions, either with the aldehyde H in TS5 or the phenyl and allyl Hs in TS4.

Figure 7.

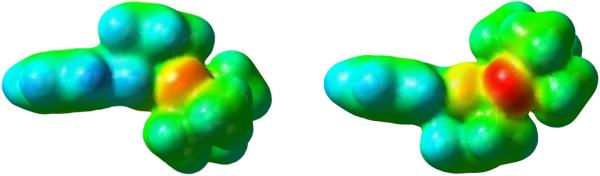
Top and bottom view of electrostatic potential of TS from Figure 4. Red: negative ESP; Blue: positive ESP; Green: neutral.

By comparing the most stable TSs in two pathways, TS4 is calculated to be 0.2 kcal/mol more stable than TS5 by B3LYP, but 0.7 kcal/mol less stable than TS5 using B3LYP-D3. In the Goodman et al. work, when buta-1,3-diene-1,4-diol-phosphoric acid, which contains no aromatic rings was used as the model catalyst, the two competing pathways are differentiated by 2.2 kcal/mol. In our studies, the model catalyst (biphenol-derived phosphoric acid) resembles more the real catalysts in the experiment, and the two different pathways are calculated to be similar in energy. This is likely due to the role of the additional aromatic rings in our model catalyst. The energy differences we calculate are quite small, suggesting that both of them may be involved in the reactions.

On the basis of these investigations, the “two-point binding models” of two different pathways shown in Figure 8 appear to operate for phosphoric acid catalyzed allylborations. The models consider two interactions between the catalyst and the substrates, which provide relative rigidity to the transition state. In what we will refer to as A (for axial), which is the same as Goodman's model, the acidic H of the catalyst forms a hydrogen bond with the pseudo-axial oxygen of boronate. In E (for equatorial), the hydroxyl group of the catalyst H-bonds to the pseudo-equatorial oxygen of boronate. The second interaction comes from the electrostatic attractions between the phosphoryl oxygen and relatively positive Hs.

Figure 8.

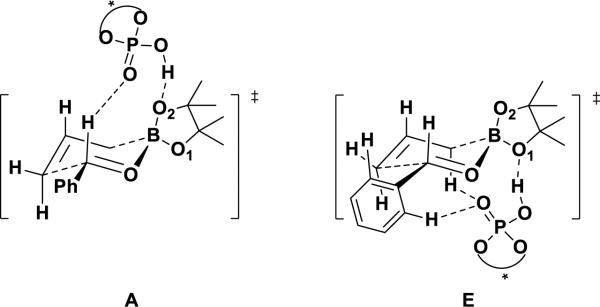
Models for the phosphoric acid-catalyzed allylboration reaction.

Activation barrier for uncatalyzed and catalyzed reactions

Having investigated the mechanism and the model for this chiral phosphoric acid catalyzed allylboration reaction, the issue of the reactivity in the present reaction was then addressed. The uncatalyzed allylboration reaction between allylboronate and benzaldehyde was studied first. The free energy profile is shown in Figure 9. A loose reactant complex C1 is formed with 7.9 kcal/mol free energy higher than the separated reactants. The activation free energy of the uncatalyzed reaction relative to the separated reactants (1+2) was calculated to be high, 26.2 kcal/mol (Figure 9). This is consistent with the low reaction rates observed experimentally for the uncatalyzed allylboration reaction.¹⁷

Figure 9.

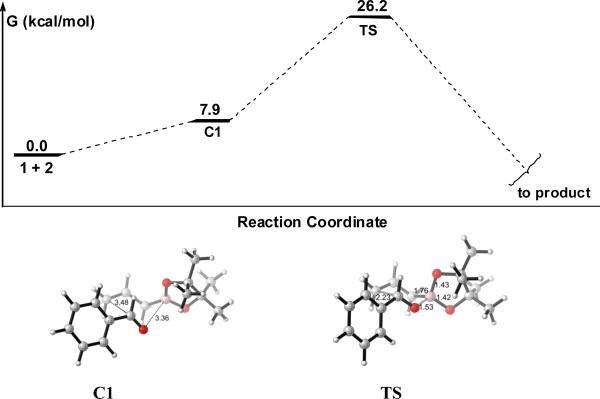
Reaction profile for the uncatalyzed allylboration reaction of 1 with 2 by B3LYP. Free energies relative the reactants in the gas phase. Optimized geometries of the complexes C1 and transition state TS are shown below the reaction profile.

For the phosphoric acid-catalyzed reaction, in the E TS, the catalyst forms a hydrogen bond with the boronate pseudo-equatorial oxygen to afford complex C2 with 0.6 kcal/mol free energy higher than the separated reactants, as shown in Figure 10. The binding of benzaldehyde on C2 leads to the reactant complex C3. In transition state structure TS4, both the forming C-C and B–O bond distances (2.18 Å and 1.51 Å) are shorter than that in the uncatalyzed reaction TS (2.23 Å and 1.53 Å), which indicates the electrophilicity of boron is increased by catalyst activation. The calculated activation barrier of the catalyzed reaction relative to the separated reactants (1+2+catalyst) is 20.2 kcal/mol (Figure 10), 6 kcal/mol lower than the uncatalyzed reaction.

Figure 10.

Reaction profiles for the allylboration reaction of 1 with 2 catalyzed by chiral phosphoric acid using E by B3LYP. Free energies relative the reactants in the gas phase. Optimized geometries of the complexes C2, C3 and transition state TS4 are shown below the reaction profile.

On the other hand, for the A TS, the catalyst forms a hydrogen bond with the boronate pseudo-axial oxygen to afford complex C4, as shown in Figure 11. The binding of benzaldehyde on C4 leads to the reactant complex C5 with 12.8 kcal/mol free energy higher than the separated reactants. In TS5, the electrophilicity of boron is also increased by catalyst activation represented by the shorter C-C and B–O bond distances (2.14 Å and 1.50 Å) than that in the uncatalyzed reaction TS (2.23 Å and 1.53 Å). And the calculated activation barrier is 20.4 kcal/mol (Figure 11), 5.8 kcal/mol lower than the uncatalyzed reaction.

Figure 11.

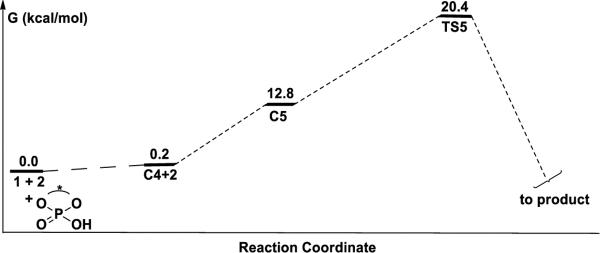
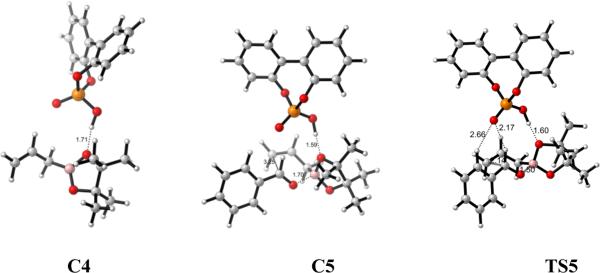
Reaction profiles for the allylboration reaction of 1 with 2 catalyzed by chiral phosphoric acid using A by B3LYP. Free energies relative the reactants in the gas phase. Optimized geometries of the complexes C4, C5 and transition state TS5 are shown below the reaction profile.

The two competing pathways give nearly identical energy profiles towards the catalyzed allylboration reactions, which again indicate the possibility that both two pathways are involved in the actual catalyzed reactions.

Origins of Enantioselectivity

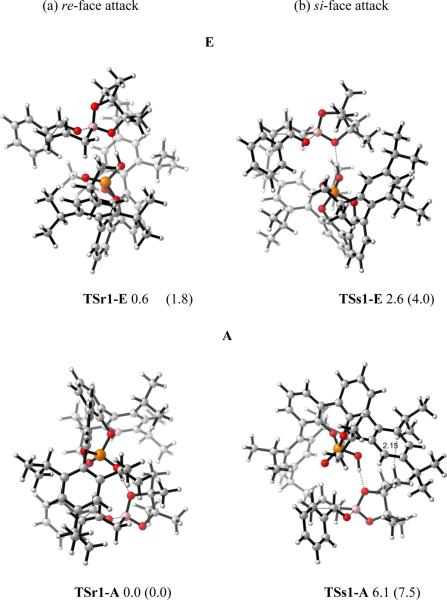
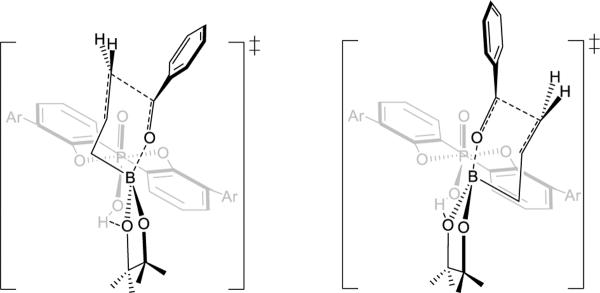
The model studies described above indicated that both of the transition states in the two models, A and E, are likely to be involved in the reactions. To explore the origins of the enantioselectivity of the catalysis, the 3,3'-substituted BIPOL model for the binaphthol catalyst PA1 was employed, and both transition states, A and E, were computed. Catalyst PA1 bearing the 2,4,6-triisopropylphenyl group on the 3,3'-positions gave high enantioselectivity experimentally. The diastereomeric transition states for re-face (r) and si-face attack (s) involving BIPOL model of PA1 were explored. The transition states involved were fully optimized, in contrast to Goodman's ONIOM calculations for these systems, TSr1-E, TSs1-E are located for E and TSr1-A, TSs1-A are located for A. These are shown in Figure 12.

Figure 12.

Optimized structures of TSr1-E and TSs1-E for E, TSr1-A and TSs1-A for A. Values next to each structure are energies relative to TSr1-A in kcal/mol. Values enclosed in parentheses are energies relative to TSr1-A calculated by B3LYP-D3.

In the equatorial coordination model E, the re-face attack TSr1-E is predicted to be more favored than the si-face attack TSs1-E by 2.0 kcal/mol. In the axial coordination model A, TSr1-A is more stable than TSs1-A by 6.1 kcal/mol using B3LYP calculations, which is consistent with Goodman's ONIOM calculations on these two TSs, which gives an energy difference of 6.7 kcal/mol.

In contrast to Goodman's ONIOM calculations that both re and si TSs are substantially energetically preferable in A over E, our fully optimized structure energies show that transition states resembling both models contribute to selectivity. That is, using the B3LYP-D3 energetics, the relative rates of reaction via TSr1-A, TSr1-E, and TSs1-E will be 1:0.05:0.001. Use of A only predicts far too high selectivity. The energy difference between the most stable re-face (r) attack transition state TSr1-A and the most stable si-face (s) attack transition state TSs1-E is 2.6 kcal/mol by B3LYP, which is in close agreement with the 93% ee observed experimentally. Solvation energy calculations using PCM model with toluene as the solvent does not change the energy difference very much, which gives a number of 3.1 kcal/mol.

Based on these calculations, we compare the two competing models for each enantiomeric TS (re or si), respectively. In Goodman's paper, the large preference for A comes from both steric and electronic factors. In the case of re-TSs, our calculations, in agreement with Goodman's results, show A (TSr1-A) is more stable than E (TSr1-E). Inspection of the two diastereomeric TSs show they are both free of steric problems by inspecting all the H-H distances; all H-H distances are 2.4 Å or more. The stabilities between two TSs is then perhaps because formyl H-bond strength inside A (TSr1-A) is stronger than the electrostatic interactions between phosphoryl oxygen and relative positive Hs in E (TSr1-E).

Our calculations show that A (TSs1-A) is much less favorable than E (TSs1-E) for si-TSs. In our fully optimized TS structures TSs1-A and TSs1-E, both of them have an almost linear H-bond arrangement. However, A (TSs1-A) has a longer H-bond distance (1.65 Å) and corresponding weaker H-bond strength than that in E (TSs1-E) (1.59 Å); this is opposite from Goodman's ONIOM calculated structures. We find a steric difference between the two models. Inspection of A (TSs1-A) shows that the pinacol group is orientated toward the bulky pocket of the catalyst, and there is one significant steric repulsion between an isopropyl H on the catalyst and a methyl H on the boronate; separated by only 2.15 Å; such steric repulsions are not found in E (TSs1-E). As a result, both electronic and steric factors make A (TSs1-A) less favorable than E (TSs1-E) in our calculated structures for si-TSs.

After comparing the two competing models, it is then necessary to investigate the origins of different stabilities between re and si TSs in each model, respectively. In A, the stabilities between TSr1-A and TSs1-A are due to steric factors. One significant steric repulsion between isopropyl H on the catalyst and methyl H on the boronate, separated by only 2.15 Å, was found for TSs1-A; by contrast TSr1-A is free of steric congestion. These steric factors are believed to control the stabilities of two diastereomeric TSs in A in Goodman's studies as well.

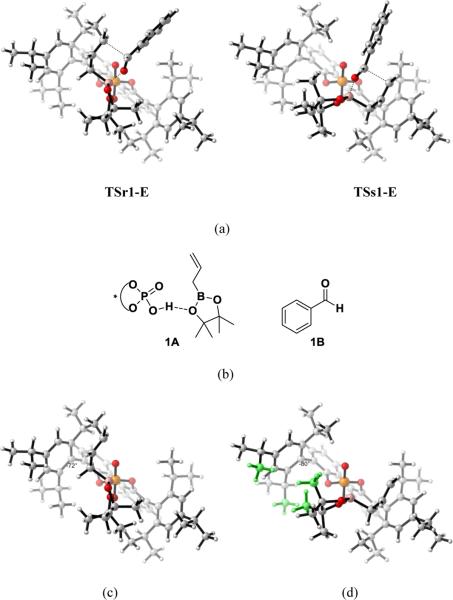
In E, however, as mentioned above, there are no obvious steric differences in the two transition states TSr1-E and TSs1-E. To gain insights into the origins of the energy difference between TSr1-E and TSs1-E, the distortion energy (ΔE_d) and interaction energy (ΔE_i) of the transition states were performed. This method has been used previously to understand 1,3-dipolar and Diels-Alder cycloadditions.¹⁸TSr1-E and TSs1-E are divided into two parts: catalyst-boronate complex 1A and the benzaldehyde 1B (Figure 13b) with the geometries fixed at the transition state geometries. The calculated distortion energy ΔE_d of 1B in TSr1-E (+12.2 kcal/mol) is almost the same as that in TSs1-E (+12.3 kcal/mol). There is also no interaction energy ΔE_i difference between TSr1-E (−41.3 kcal/mol) and TSs1-E (−41.2 kcal/mol) which means all of the stabilizing and destabilizing interactions between 1A and 1B in the two TSs are similar. The preference for re-facial selectivity is therefore the result of the larger distortion of catalyst-boronate complex 1A in TSs1-E. 1A is more heavily distorted in TSs1-E (+33.9 kcal/mol) than in TSr1-E (+32.1 kcal/mol) by 1.8 kcal/mol.

Figure 13.

(a) Side view of TSr1-E and TSs1-E. (b) Structures of 1A and 1B. (c) 3D structures of 1A in TSr1-E. (d) 3D structures of 1A in TSs1-E.

The origins of the differences in distortion energies of 1A in the two TSs can be visualized from the 1A geometries, as shown in Figure 13. In Figure 13d, which shows the 1A structure in TSs1-E, the dioxaborolane ring is on the left, and the methyl groups on the dioxaborolane ring and isopropyl groups of catalysts are close to each other (green atoms in Figure 13d). In order to minimize such steric repulsions, the 2,4,6-triisopropylphenyl substituent is rotated around the bond to the BIPOL phenyl core with a dihedral angle of 80°. This is an 8° rotation away from the dihedral angle in the optimized catalyst (72°). Due to the distortion of the catalyst, the green atoms (Figure 13d) are all far away, resulting in no steric repulsions. In other words, the catalyst undergoes conformational changes to avoid unfavorable steric interactions in TSs1-E. Figure 13c shows the 1A structure in TSr1-E. Here, the dioxaborolane ring is far from the catalyst, and the dihedral angle between 2,4,6-triisopropylphenyl substituent and the BIPOL core is 72°, the same as the dihedral angle of 72° in the optimized catalyst. The asymmetric induction can be rationalized by differences in distortion energies originating from avoiding the steric interactions between the substrates and the bulky 3,3'-substituents on the catalysts.

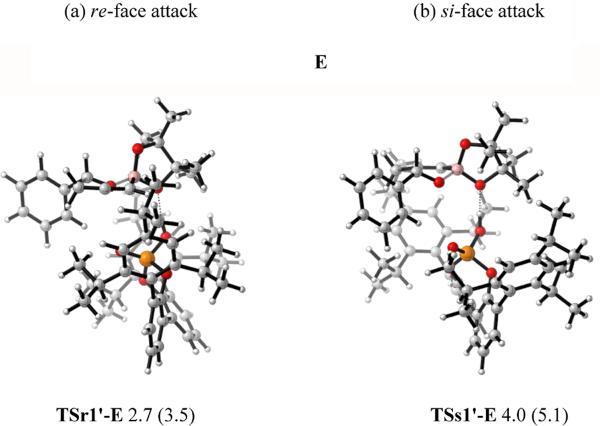
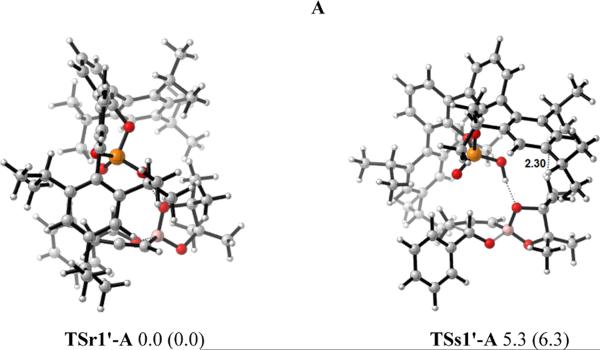
After investigating the allylboration reaction, we then reinvestigated the propargylations. The propargylation proceeds via a six-membered cyclic transition state similar to that for allylborations. Once again, the catalyst could activate the reaction by forming a hydrogen bond with either of the boronate oxygens. The transition state structures of propargylation involving the phosphoric acid catalyst PA1 using both E and A were studied. As before, diastereomeric transition states TSr1'-E and TSs1'-E were located for E, and TSr1'-A and TSs1'-A were located for A (Figure 14).

Figure 14.

Optimized structures of TSr1'-E and TSs1'-E for E, TSr1'-A and TSs1'-A for A. Values next to each structure are energies relative to TSr1'-A in kcal/mol. Values enclosed in parentheses are energies relative to TSr1'-A calculated by B3LYP-D3.

As in the allylboration analysis, for re-face (r) attack, A (TSr1'-A) is more stable than E (TSr1'-E) by 2.7 (or 3.5) kcal/mol. For si-face (s) attack, A (TSs1'-A) is less stable than E (TSs1'-E) by 1.3 (or 1.2) kcal/mol. The energy difference between the most stable re-face (r) attack transition state TSr1'-A and the most stable si-face (s) attack transition state TSs1'-E is 4.0 (or 5.1) kcal/mol, overestimating the stereoselectivities as compared to the 74% ee observed experimentally.

Our studies on propargylations still showed that for re-TSs, A is more favorable; while E is more favorable for si-TSs. The A and E transition states leading to re attack are both lower in energy than E transition state that leads to si attack.

In E, the calculated distortion energy ΔE_d of benzaldehyde in TSr1'-E (+17.4 kcal/mol) is almost the same as that in TSs1'-E (+17.5 kcal/mol), so is the interaction energy ΔE_i for the two transition states. The preference for re-facial selectivity still comes from the larger distortion of catalyst-boronate complex in TSs1'-E. The catalyst-boronate complex is calculated to be more heavily distorted in TSs1'-E (+45.9 kcal/mol) than in TSr1'-E (+44.7 kcal/mol) by 1.2 kcal/mol.

The origin of the differences in distortion energies of catalyst-boronate complex in the two TSs is similar to that in the allylboration reaction. In Figure 15b which shows the complex structures in TSs1'-E, in order to minimize the steric repulsions between the methyl groups on the dioxaborolane ring and isopropyl groups of catalysts (green atoms in Figure 15b), the 2,4,6-triisopropylphenyl substituent is rotated around the bond to the BIPOL phenyl core with a dihedral angle of 78°. In Figure 15a which shows the catalyst-boronate complex structure in TSr1'-E, the dihedral angle between 2,4,6-triisopropylphenyl substituent and the BIPOL core is 74°. The 4° dihedral angle differences of the two complexes accounts for their different distortion energies.

Figure 15.

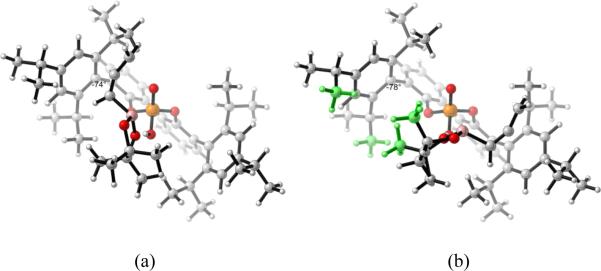
(a) 3D structure of TSr1'-E without the benzaldehyde. (b) 3D structure of TSs1'-E without the benzaldehyde.

Conclusion

Theoretical calculations have been carried out for the chiral phosphoric acid-catalyzed enantioselective allylboration and propargylation reactions. Transition states with either boronate oxygen hydrogen-bonded to the phosphoric acid were studied. The catalyst is able to activate the boronate by forming a hydrogen bond either with the pseudo-equatorial oxygen (E) or the pseudo-axial oxygen (A) of the boronate; the phosphoryl oxygen interacts with relatively positive Hs of the substrate through electrostatic attractions, which provides further stabilization of the TS, and a two-point orientation of the catalyst. Pathway A is investigated in detail in Goodman's model⁹, and our studies focus more on pathway E in this paper.

For re-face attack, both equatorial and axial coordination gives TSs that are free of steric repulsions, with A more favorable than E. The relative stability of A is due to the formyl H-bond strength in A. For si-face attack, to give the minor enantiomer, our calculations showed that A is less favorable than E. Steric factors make the more crowded A less stable than the less crowded E.

Calculations show that the enantioselectivity observed experimentally originates from larger distortions of the catalyst in the minor enantiomeric TS, which is the result of the avoidance of the repulsive interactions between the bulky 3,3'-substituents in the catalyst and the substrates. The pinacol boronate methyls have an important role, and these groups could be altered to influence stereoselectivities. These investigations might help direct future enantioselective catalysis development for allylboration and propargylation reactions.

Figure 3.

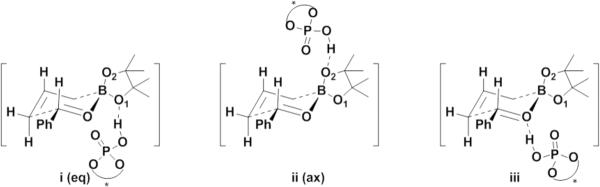
Three possible sites of coordination in the phosphoric acid-catalyzed allylboration reaction.