Predicting ex vivo failure loads in human metatarsals using bone strength indices derived from volumetric quantitative computed tomography

Abstract

We investigated the capacity of bone quantity and bone geometric strength indices to predict ultimate force in the human second metatarsal (Met2) and third metatarsal (Met3). Intact lower extremity cadaver samples were measured using clinical, volumetric quantitative computed tomography (vQCT) with positioning and parameters applicable to in vivo scanning. During processing, raw voxel data (0.4mm isotropic voxels) were converted from Hounsfield units to apparent bone mineral density (BMD) using hydroxyapatite calibration phantoms to allow direct volumetric assessment of whole-bone and subregional metatarsal BMD. Voxel data were realigned to produce cross-sectional slices perpendicular to the longitudinal axes of the metatarsals. Average mid-diaphyseal BMD, bone thickness, and buckling ratio were measured using an optimized threshold to distinguish bone from non-bone material. Minimum and maximum moments of inertia and section moduli were measured in the mid-diaphysis region using both a binary threshold for areal, unit-density measures and a novel technique for density-weighted measures.

BMD and geometric strength indices were strongly correlated to ultimate force measured by ex vivo 3-point bending. Geometric indices were more highly correlated to ultimate force than was BMD; bone thickness and density-weighted minimum section modulus had the highest individual correlations to ultimate force. Density-weighted geometric indices explained more variance than their binary analogs. Multiple regression analyses defined models that predicted 85–89% of variance in ultimate force in Met2 and Met3 using bone thickness and minimum section modulus in the mid-diaphysis. These results have implications for future in vivo imaging to non-invasively assess bone strength and metatarsal fracture risk.

Introduction

The metatarsals are a frequent site of foot fracture, particularly stress fractures occurring without an acute traumatic event. In athletes, roughly 20% of stress fractures occur in the metatarsals, with the majority (14–18%) occurring in either the second metatarsal (Met2) or third metatarsal (Met3) (Hulkko and Orava, 1987; McBryde, Jr., 1985). Additionally, diabetes mellitus with concomitant peripheral neuropathy has been linked to focal osteopenia in the feet and an increased risk of metatarsal fracture (Cundy et al., 1985; Gill et al., 1997) and “silent” bone stress injuries (Chantelau et al., 2007).

Bone mineral density (BMD) in the metatarsal mid-diaphysis correlates with ex vivo bone strength measured via mechanical testing (Courtney et al., 1997; Muehleman et al., 2000). Image-based, in vivo assessment of BMD is more challenging in the metatarsals than in other long bones (e.g. femur or tibia) due to the smaller size, numerous articulations, and obstructed views of foot bones. As a result, previous investigations of metatarsal BMD and bone dimensions (Courtney et al., 1997; Fleischli et al., 1998; Muehleman et al., 2000) have utilized cadaver bones that were excised before making measurements. Recent work by our group allows in vivo measurement of BMD of all foot bones using volumetric quantitative computed tomography (vQCT) (Commean et al., 2009; Hastings et al., 2008; Commean et al., 2011). The vQCT method uses a semiautomatic bone segmentation technique to separate the tarsals and metatarsals from each other and the surrounding soft tissue to compute whole-bone and subregional bone volumes and BMD (Commean et al., 2009).

Though the ability to assess volumetric BMD of foot bones in vivo is a significant technical advancement, the role of BMD as a prospective risk factor for acute or overuse-related pedal fracture is unclear. Research in the tibia and femur suggests a reduction in BMD alone may not lead to increased fracture risk, and that bone geometric strength provide an improved index of fracture risk. For example, ex vivo studies of tibial strength have shown that indices reflecting resistance to compression (such as cross-sectional area, A) and bending (moment of inertia, I, and section modulus, S) are more strongly related to fracture strength than is BMD (Kontulainen et al., 2008; Liu et al., 2007). Similarly, while female military recruits have a 2 to 6 times higher risk of developing a tibial stress fracture than males (Pester and Smith, 1992; Brudvig et al., 1983) a recent study showed that females had 2.0% to 2.7% higher cortical BMD in the tibia than males (Evans et al., 2008). Higher stress fracture incidence despite higher cortical BMD may be explained by females’ significantly lower cross-sectional diameter, A, and I (Evans et al., 2008).

To offset a general age-related decline in BMD, long bones minimize reductions in bending strength by adding bone material to the periosteal surface while a concomitant, larger expansion of the endosteal surface leads to reductions in cortical thickness (Sigurdsson et al., 2006; Ward et al., 2011). This homeostatic expansion leaves bones at elevated risk for focal cortical shell weakness and fractures (Beck, 2007; Kaptoge et al., 2008). Decreased cortical thickness and increased buckling ratio (BR = periosteal radius/cortical thickness) in the femoral neck, both of which reflect a reduced resistance to cortical buckling loads, have been related to an increased risk of hip fracture (LaCroix et al., 2010; Melton, III et al., 2005; Szulc et al., 2006).

The purpose of this study was to assess BMD and geometric strength indices that reflect resistance to compressive, bending, and buckling loads as predictors of ex vivo failure loads in human Met2 and Met3 samples using techniques directly applicable to in vivo clinical imaging. Intact cadaver lower-extremity specimens were imaged using vQCT before excising metatarsals and subjecting the bones to failure testing. We hypothesized that BMD and geometric indices would correlate to metatarsal strength, and that geometric indices would be retained in stepwise regression models predicting metatarsal strength.

2. Methods

Measuring BMD and bone geometric strength indices in the metatarsals using a method applicable to in vivo scanning poses unique challenges. Whereas the femur and tibia can easily be aligned axially within an imaging modality such as high resolution peripheral quantitative computed tomography (HR-pQCT) to produce cross-sectional slices, the metatarsals cannot be simultaneously aligned in true axial position within a vQCT scanner. Using excised cadaver metatarsal samples obviates the need for segmentation or axis realignment but limits clinical relevance. Any method capable of assessing bone geometry in human metatarsals in vivo requires bone segmentation and realignment of image data along the primary axis of each metatarsal in order to produce anatomically relevant cross-sectional image slices.

2.1 Cadaver preparation and vQCT testing

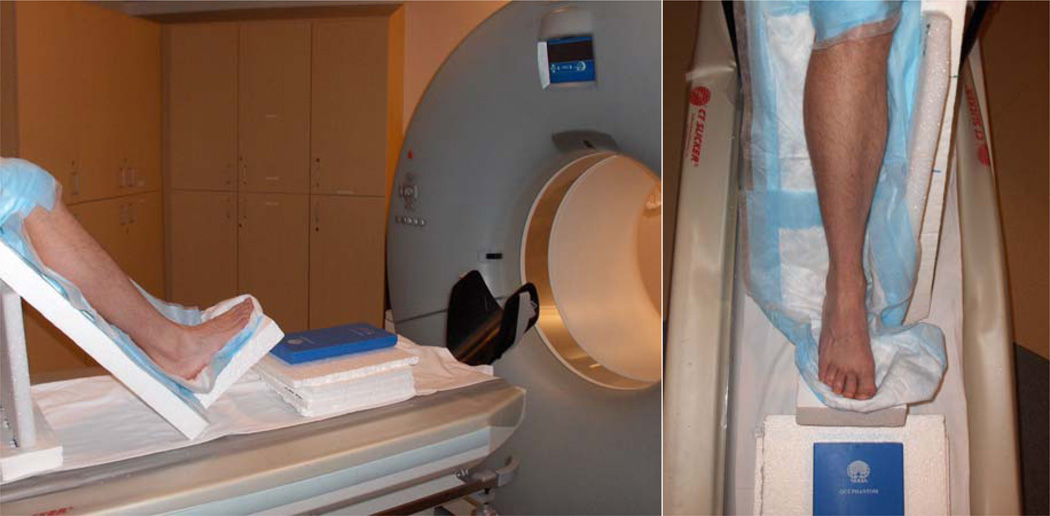
Ten unpaired fresh-frozen cadaver lower limbs were received from the Human Body Donation Program at the Washington University School of Medicine. All samples were right limbs. After thawing (24–36 hours), limbs were disarticulated at the knee and transported to the Center for Clinical Imaging Research for clinical vQCT scans. Cadaver samples were placed in a radiolucent Styrofoam holding apparatus to ensure consistent positioning. The ankle joint was held in a neutral position (90°) with the foot and shank both 45° above the horizontal (Figure 1). This position kept the metatarsals as close to horizontal as possible while allowing clearance of the proximal tibia within the vQCT scanner tube. Additionally, the cadaver positioning closely matches the standard orientation of the lower limb for patients and research subjects at our institution (Commean et al., 2011; Commean et al., 2009). Table height was adjusted so the volume isocenter was approximately at the height of the mid-diaphyseal region of the metatarsals. A QCT Bone Mineral™ hydroxyapatite (HA) calibration phantom (Image Analysis Inc., Columbia, KY, USA) was placed in series with each sample at the same height as the scanner isocenter to allow conversion of CT Hounsfield units (HU) to apparent BMD (mg/cm³ of HA). (Smith et al., 2011)

Figure 1.

Position and orientation of lower extremity sample in Styrofoam fixture during vQCT scanning. Hydroxyapatite calibration phantom is shown in front of the foot, at the height of the talus.

Foot images were acquired using a Siemens SOMATOM Definition CT scanner (Siemens Medical Systems, Malvern, PA, USA) with acquisition parameters of 220 mA·s, 120 kVp, pitch = 1, rotation time 0.33s, and a 512×512 matrix. Raw data were reconstructed at 0.4mm slice reconstruction intervals using a B70f kernel to create vQCT images. Prior to reconstruction, the in-plane field of view was cropped to roughly 200mm × 200mm, resulting in an in-plane resolution of approximately 0.4mm × 0.4mm.

2.2 Bone Segmentation Processing

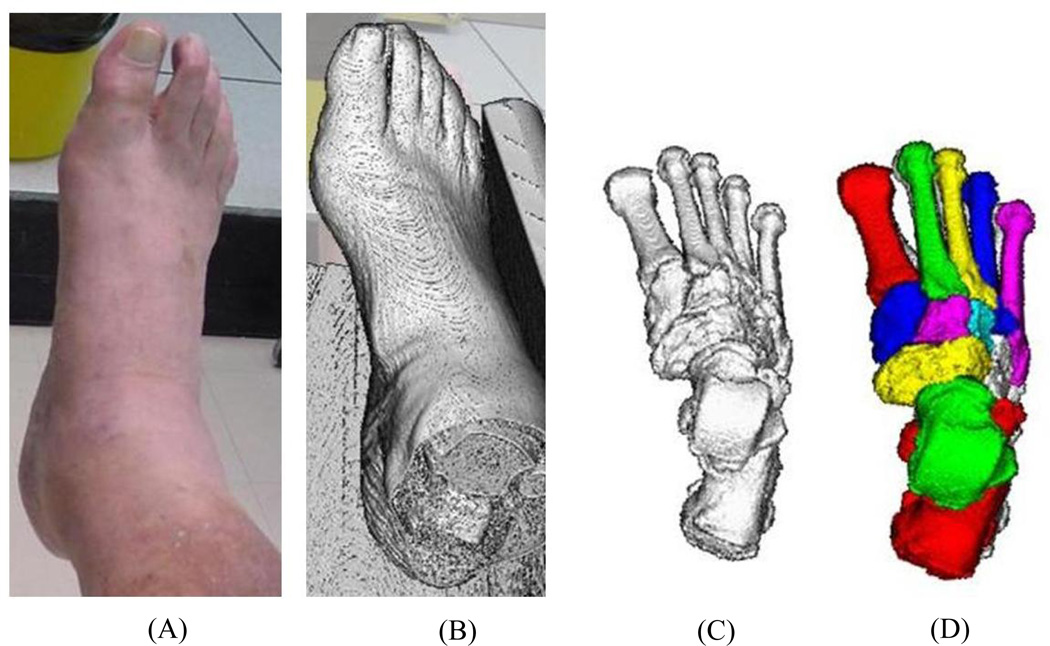
Reconstructed vQCT images were loaded in Digital Imaging and Communications in Medicine (DICOM) format into Analyze® software (Biomedical Imaging Resource, Mayo Clinic, Rochester, MN). Image data were interpolated to isotropic voxels with 0.4mm dimension using a cubic spline function. Full details of the bone segmentation process are described elsewhere (Liu et al., 2008; Commean et al., 2011). In brief, bones were segmented from the surrounding soft tissue using density-based filtering algorithms employed as custom ImageJ plugins (NIH Research Services Branch, rsbweb.nih.gov), Analyze® software to further segment bones from soft tissue (e.g. high density tissues such as tendon and ligament), and a custom graph-cut method to segment bones at their articulating surfaces and create volume-filled object maps (Liu et al., 2008) as shown in Figure 2. Following segmentation, bone object maps were overlaid on the original grayscale volumetric data so that the Met2 and Met3 voxel datasets could be exported for further analysis.

Figure 2.

Bone segmentation processing. (A) photograph of cadaver sample; (B) raw vQCT image; (C) filtered vQCT image to remove soft tissue; (D) segmented, filled bone object maps for tarsals and metatarsals.

2.3 Bone Axis Realignment

Grayscale voxel data for each bone produced during bone segmentation were exported to ImageJ, where the BoneJ plugin (Doube et al., 2010) was used to compute a density-weighted principal components analysis and realign the voxel data perpendicular to each bone’s longitudinal axis. This transformation realigned voxel data from the vQCT scanner coordinate axes into anatomically relevant cross-sectional slices perpendicular to each metatarsal’s longitudinal axis. Realigned data retained 0.4mm isotropic voxel dimensions. Subsequent calculations of BMD and bone geometric strength indices were completed with BoneJ and custom macros in Excel (Microsoft) using the voxel data (XYZ positions and HU values) from realigned cross-sectional slices.

2.4 Bone Geometric Strength Indices

HU values were converted to apparent BMD using the cadaver-specific HA calibration coefficients. Measuring cortical thickness and BR requires a threshold-based binary definition of bone and non-bone material, and Otsu thresholding (Otsu, 1979) of the 20 metatarsals revealed optimal thresholds between 150 and 300 mg/cm³. To maintain consistency across specimens and also reduce the likelihood of overestimating bone material by choosing an erroneously low bone threshold (Hangartner, 2007), a universal threshold of 300 mg/cm³ was applied to all bones to distinguish between bone and non-bone material.

The spatial resolution of vQCT scanning limits the ability to distinguish trabecular and cortical bone material due to spatial averaging. In lieu of measuring cortical thickness directly, average thickness (t_avg) and BR were computed using an assumption that the metatarsal mid-diaphysis is roughly a circular annulus. Total cross-sectional area (A_tot) was computed by summing the entire area (including the medullary cavity) and bone area (A_bone) was computed by summing the area of voxels with BMD ≥ 300 mg/cm³. Average thickness and BR were then calculated based on the outer (R_o) and inner (R_i) radii, as follows:

$$A_{\mathit{\text{tot}}}=\pi *R_o^2$$

$$A_{\mathit{\text{tot}}}-A_{\mathit{\text{bone}}}=\pi *R_i^2$$

$$t_{\mathit{\text{avg}}}=R_o-R_i$$

$$\mathit{\text{BR}}=\frac{R_o}{t_{\mathit{\text{avg}}}}$$

Minimum and maximum moments of inertia (I_min, I_max) and section moduli (S_min, S_max) were computed as indices of bending strength using the BoneJ plugin (Doube et al., 2010) in ImageJ. BoneJ computes I and S as areal measures (I_Area.min, I_Area.max, S_Area.min, S_Area.max) using an assumption of unit density and a threshold-based binary definition of bone and non-bone material, as has been done previously using other analysis software (Courtney et al., 1997; Evans et al., 2008; Muehleman et al., 2000). This binary definition of bone material can be problematic if the threshold is suboptimal (Hangartner, 2007), especially for clinical scanning of small bones such as metatarsals. A density-weighted approach may lessen the effects of limited spatial resolution by improving the density resolution. Thus, in addition to the standard area-based bending strength indices, we also computed novel density-weighted measures (I_ρ.min, I_ρ.max, S_ρ.min, and S_ρ.max) using all voxel data exceeding the 300 mg/cm³ threshold. Computations of the areal and density-weighted measures are provided in the Appendix. Note that the density-weighted calculations for I_ρ and S_ρ require a bone volume rather than a cross-sectional area. To allow for future replication using different imaging techniques with varying voxel dimensions, the values for I_ρ and S_ρ were computed using the 0.4mm isotropic voxel size, but are expressed as volumetric averages across a standard axial length of 1mm.

2.5 Bone Fracture Testing

After vQCT scanning, Met2 and Met3 were excised from the cadaver limbs, taking care to avoid damage to the periosteal surface while denuding the bones of surrounding soft tissue. Bones were wrapped in gauze that had been soaked in 0.9% NaCl solution, then stored in 75mL specimen tubes at −20°C until being thawed prior to fracture testing.

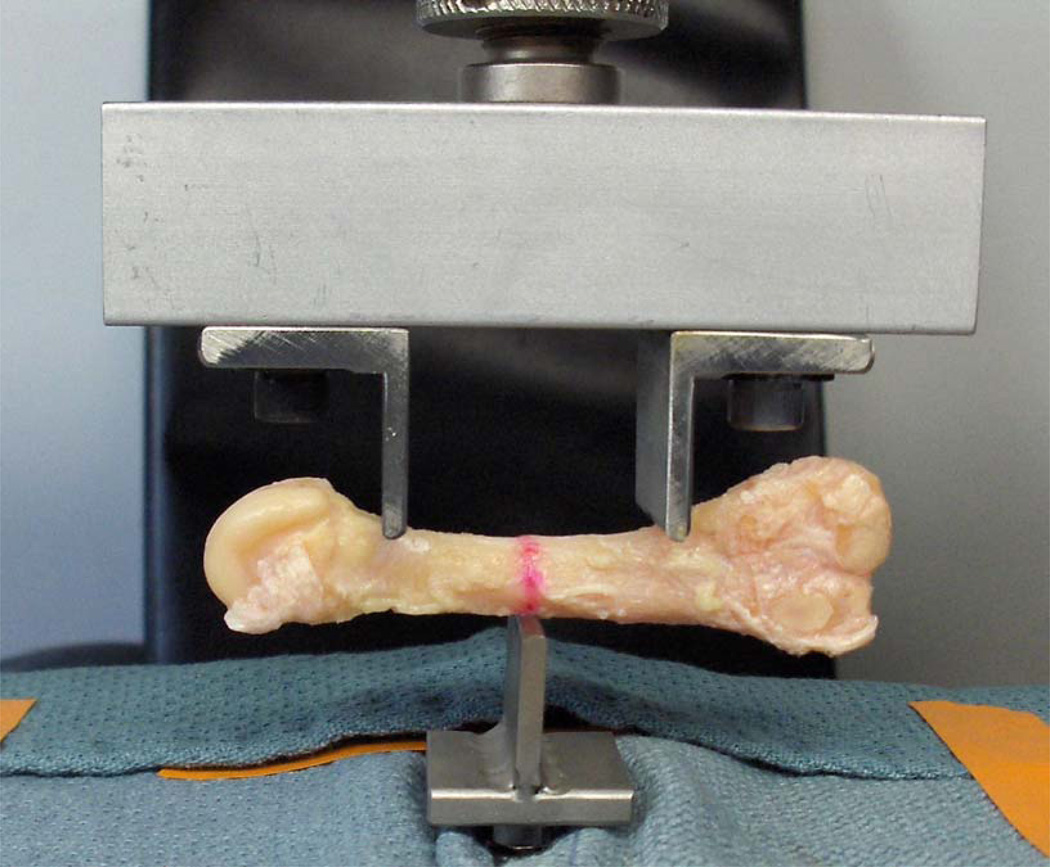
Bones were loaded monotonically to failure in three-point bending using an Instron 8841 materials testing machine (Instron, Canton, MA, USA). While fatigue testing is arguably more physiologically relevant than monotonic loading, it would require some foreknowledge of the appropriate submaximal load magnitudes to utilize during the repetitive loading cycles, typically a percentage of monotonic failure load measured in contralateral limbs or a matched cohort (Warden et al., 2005; Silva and Touhey, 2007). Absent this foreknowledge in our excised metatarsal samples, we elected to utilize monotonic three-point loading to failure as the measure of whole-bone strength. The span length (L) of 33mm was chosen because it was the longest distance that ensured the vertical loading posts would be located within the metatarsal shaft for all bones tested. The central force was applied at the span midpoint on the (inverted) dorsal side of the metatarsal; the two other forces were applied at equal distances from the midpoint on the plantar side of the metatarsal to mimic the predominant loading mode during push-off (Arndt et al., 2002; Donahue and Sharkey, 1999) as shown in Figure 3. Fixture posts for 3-point bending were machined to have a rounded tip with 3mm diameter to minimize the effect of local cortical buckling at the fixture sites and thus help ensure that failure would occur due to bending loads rather than local contact stress.

Figure 3.

Cadaver Met2 sample in 3-point loading configuration. Red line denotes the mid-diaphysis as determined from caliper measurements.

Pre-load was 10N, displacement rate was 0.1 mm/s, and force-displacement data were sampled at 60 Hz. The ultimate force (F_ult, in N) was defined as the maximum force registered between the onset of loading and fracture. To allow for comparison to other loading modes (e.g. 4-point bending or cantilever loading) or differing span lengths, we also report the ultimate bending moment (M_ult in N·m), computed using the equation for bending moment in a 3-point configuration with loading at the mid-diaphysis:

$$M_{\mathit{\text{ult}}}=\frac{F_{\mathit{\text{ult}}}*L}{4}$$

2.6 Statistical Analysis

All statistical analyses were completed using IBM SPSS Statistics 20.0 [IBM, Chicago, IL]. A linear regression comparing the F_ult between Met2 and Met3 showed that bones from the same individual were highly correlated. Therefore we report separate regression analyses for Met2 and Met3. Simple linear regression analyses were performed between F_ult and the independent variables: BMD; t_avg; BR; and areal (I_Area.min, I_Area.max, S_Area.min, and S_Area.max) and density-weighted (I_ρ.min, I_ρ.max, S_ρ.min, and S_ρ.max) indices of bending strength. Note that since L was maintained at 33mm for all metatarsals tested, correlation coefficients between F_ult and the independent variables are identical to the correlation coefficients between M_ult and the independent variables. Lastly, a stepwise multiple regression analysis (α ≤ 0.05 for inclusion,α ≥ 0.10 for removal) was performed to assess the relative roles of potential strength indices in determining F_ult.

3. Results

Cadaver specimens came from 7 females and 3 males who had an average age of 83 years (SD 13, range 56–99) at death. Table 1 shows the average values for ultimate loads, bone quantity, size, and distribution parameters for Met2 and Met3. Univariate correlation coefficients with F_ult are also reported. For both Met2 and Met3, t_avg was the highest correlate of F_ult, and the density-weighted geometric indices of bending strength accounted for a higher proportion of the variance in F_ult than did the unit density analogs of bending strength.

Table 1.

Bone quantity, size, and bending strength parameters. R values represent correlation coefficient with ultimate loads (F_ult or M_ult).

		Met2		Met3
	Units	Mean ± SD	R	Mean ± SD	R
Ultimate loads
Fult	N	572 ± 299	n/a	406 ± 244	n/a
Mult	N*m	4.72 ± 2.47	n/a	3.36 ± 2.01	n/a
Bone quantity parameters
Whole-bone BMD	mg/cm3	403 ± 91	0.770	367 ± 91	0.730
Mid-diaphysis BMD	mg/cm3	806 ± 205	0.705	725 ± 195	0.623
Mid-diaphysis size parameters
Total Area (Atot)	mm2	50.9 ± 11.5	0.464	49.0 ± 9.5	0.713
Buckling Ratio (BR)	unitless	2.29 ± 0.54	−0.801	2.50 ± 0.55	−0.624
Average thickness (tavg)	mm	1.84 ± 0.49	0.923	1.64 ± 0.40	0.829
Areal, unit density bending strength parameters
IArea.min	mm4	156.7 ± 70.0	0.716	133.6 ± 65.3	0.789
IArea.max	mm4	253.3 ± 143.8	0.399	236.1 ± 92.5	0.696
SArea.min	mm3	39.9 ± 13.9	0.704	35.2 ± 13.2	0.824
SArea.max	mm3	50.4 ± 20.9	0.444	47.3 ± 14.1	0.701
Density-weighted bending strength parameters
Iρ.min	mg·mm2	73.7 ± 35.2	0.756	58.9 ± 34.3	0.848
Iρ.max	mg·mm2	119.7 ± 71.6	0.428	108.5 ± 47.0	0.723
Sρ.min	mg·mm	17.8 ± 6.7	0.822	14.5 ± 6.9	0.867
Sρ.max	mg·mm	28.7 ± 13.4	0.460	27.0 ± 10.1	0.678

(Abbreviations: F_ult = ultimate force; M_ult = ultimate moment; BMD = bone mineral density; A_tot = total cross-sectional area; BR = buckling ratio; t_avg = average thickness; I_Area.min = areal, unit-density minimum moment of inertia; I_Area.max = areal, unit-density maximum moment of inertia; S_Area.min = areal, unit-density minimum section modulus; S_Area.max = areal, unit-density maximum section modulus; I_ρ.min = density-weighted minimum moment of inertia; I_ρ.max = density-weighted maximum moment of inertia; S_ρ.min = density-weighted minimum section modulus; S_ρ.max = density-weighted maximum section modulus)

For Met2, all bone quantity and geometric strength parameters except for mid-diaphysis area and bending strength maxima (I_max and S_max) were significantly correlated with F_ult. The strongest individual predictor was mid-diaphysis t_avg (r² = 0.85). Two other variables (BR and S_ρ.min) had univariate values of r² > 0.64. The stepwise multiple regression analysis for Met2 yielded a model that included only mid-diaphysis t_avg (Table 2).

Table 2.

Results of stepwise multiple regressions for F_ult in Met2 and Met3. SEE = standard error of estimate.

	Fult regression equation	R2	Adjusted R2	SEE (in N)
Met 2
Model 1:	Fult = 559 * tavg – 458 N	0.852	0.834	122
Met3
Model 1:	Fult = 30.5 * Sρ.min – 34 N	0.752	0.721	129
Model 2:	Fult = 20.5 * Sρ.min + 302 * tavg – 386 N	0.914	0.889	81

For Met3, all bone quantity and geometric strength parameters were significantly correlated with F_ult. Univariate regression analyses revealed that I_ρ.min and S_ρ.min explained 72% and 75% of variance in F_ult, respectively; mid-diaphysis t_avg explained 69%. The final stepwise model for F_ult included S_ρ.min and mid-diaphysis t_avg and predicted a total of 89% of the variance in F_ult (Table 2).

4. Discussion

Using vQCT scanning and processing methods directly applicable to in vivo testing, we produced findings that compare favorably with previous investigations using excised bones to predict bending strength in human metatarsals. To our knowledge, this is the first attempt to implement bone axis realignment of human vQCT image data, as well as the first use of buckling ratio and density-weighted bending strength indices in foot bones.

In contrast to previous research using metatarsals (Courtney et al., 1997; Muehleman et al., 2000), we found that geometric bending strength indices (I_ρ.min and S_ρ.min) were more predictive of ex vivo ultimate force than BMD. Courtney et al used dual-energy X-ray absorptiometry (DXA) to compute areal BMD at the mid-diaphysis in 11 pairs of excised Met2 and Met3 samples, then conducted fracture testing in a 4-point loading configuration. F_ult values for 3-point and 4-point loading are not directly comparable, but computing M_ult allows comparison between the testing techniques. Our results for M_ult (Met2 = 4.72 ± 2.47 N*m, Met3 = 3.36 ± 2.01 N*m for Met3) are roughly 30% lower for Met2 and 40% lower for Met3 than values computed based on F_ult data in Courtney et al (Met2 = 6.5 ± 3.8 N*m, Met3 = 5.5 ± 3.0 N*m), which can attributed in part to the older age of our cadaver samples (83 ± 13 yrs) compared to an average age of 63 yrs in Courtney et al. The authors also computed areal bone geometric measures (t_avg, I_Area.min, and I_Area.max) using a binary definition of bone and non-bone material based on a digital photograph of a single cross-section near the mid-diaphysis. BMD was a strong predictor of metatarsal strength (r² = 0.81–0.83) whereas geometric properties neither correlated significantly with strength nor contributed additional significance in stepwise multiple regression (Courtney et al., 1997). Another study (Muehleman et al., 2000) compared DXA and pQCT measures of BMD and bone geometry as predictors of failure strength of excised Met2 samples in a cantilever loading configuration and found similar results: BMD was the strongest correlate of failure load for both DXA (r² = 0.40) and pQCT (r² = 0.46), and geometric strength indices did not correlate significantly to bone failure strength.

These previous analyses used areal measures of bending strength based on an assumption of unit density in bone material. Our findings suggest that density-weighted geometric bending parameters were more highly correlated to F_ult than areal measures. A density-weighted approach may lessen the effects of suboptimal spatial resolution by improving the density resolution. Additionally, both papers utilized cadaver metatarsals that were excised before imaging. It is not clear that similar accuracy and precision of BMD and geometric indices would be achieved using in vivo techniques. Future clinical utility of DXA or pQCT rests on the ability to replicate findings using a technique applicable to in vivo testing. Our novel technique allows measurement of cross-sectional strength properties using vQCT scanning and post-processing bone axis realignment.

Numerous bone quantity and geometric strength parameters measured with the novel vQCT method relate strongly to F_ult. For both bones, vQCT-based indices of bending strength accounted for more variance in F_ult than BMD, and density-weighted indices of bending strength were superior to areal unit density indices. Some caution should be taken regarding the findings from the regression analyses, as correlation coefficients are potentially volatile with such a small number of samples relative to the number of independent variables included. The single highest correlate of F_ult in Met2 and Met3 was mid-diaphysis t_avg. The strong relationship between mid-diaphysis t_avg and F_ult is highly relevant to changes that occur due to aging, as bones maintain measures of bending strength (despite age-related loss in BMD) through a process of homeostatic expansion that leaves bones at elevated risk for focal cortical shell weakness and fractures (Beck, 2007). Future analyses may assess whether the strong relationship between t_avg and F_ult persists for younger or athletic populations.

One limitation of this study is that although the vQCT spatial resolution (0.4mm isotropic) is near the current limits of clinical imaging capabilities, it nonetheless leads to partial volume effects that limit the ability to determine cortical thickness directly (Beck, 2007). This spatial averaging of bone and non-bone material makes it more difficult to distinguish bone from marrow, or trabecular bone from cortical bone. If too low of a threshold is chosen, then A_bone and t_avg will be overestimated due to inclusion of voxels that are not predominantly cortical bone. Conversely, choosing a threshold that is too high could lead to apparent (and erroneous) discontinuities in the cortical shell. Other researchers have faced the challenge of thresholding and have independently chosen the same threshold of 300 mg/cm³ (Borggrefe et al., 2010). To adequately distinguish cortical and trabecular bone would require voxel spatial resolution of roughly 100 µm (0.1 mm) (Beck, 2007) which is currently limited to HR-pQCT and micro-computed tomography (µCT) and thus not applicable to in vivo scanning of foot bones. Future investigations may assess the validity of the assumption that the mid-diaphysis is a circular annulus by comparing the vQCT-based measures of t_avg to direct measures of cortical thicknessmade using high resolution µCT (spatial resolution 10–30 µm). This µCT validation may also permit optimization of vQCT thresholds and allow direct measurement of cortical porosity (Zebaze et al., 2010). Similarly, µCT validation of vQCT measures could be used in future research to assess bone quality and fracture risk in tarsal bones, which have predominantly trabecular bone and are subjected to different loading modes than the metatarsals (Diederichs et al., 2009).

A potential future direction using vQCT-based assessment of metatarsal strength indices is to relate the predicted ultimate loading capacity to in vivo loading calculated using plantar pressure measurement. Stokes et al (Stokes et al., 1979) estimated compressive force, shear force, and bending moments in metatarsals using plantar pressure mapping, videographic assessment, and cadaver-based estimates of bone geometry. The methods we report here could be used as direct measures of bone quantity and geometry, in lieu of the estimated geometry calculated by Stokes et al. Furthermore, vQCT-based assessment of metatarsal strength indices could be combined with direct in vivo assessment of metatarsal strain (Arndt et al., 2002) to provide a full representation of the interplay among bone structure, loading, and deformation.

In conclusion, this study represents the novel development and ex vivo validation of a clinically applicable vQCT-based method to assess human metatarsal strength. The methods can be used for in vivo imaging to non-invasively estimate bone strength and fracture risk by providing direct, volumetric measurement of BMD and bone geometric strength indices. Our findings suggest that average mid-diaphysis bone thickness, buckling ratio, minimal moment of inertia and minimal section modulus may be important indices of metatarsal strength in future in vivo studies.

Abbreviations

Met2

second metatarsal

Met3

third metatarsal

BMD

bone mineral density

vQCT

volumetric quantitative computed tomography

BR

buckling ratio

HR-pQCT

high resolution peripheral quantitative computed tomography

HA

hydroxyapatite

HU

Hounsfield unit

DICOM

Digital Imaging and Communications in Medicine

t_avg

average thickness

A_tot

total cross-sectional area

A_bone

cross-sectional area of bone material

R_o

outer radius

R_i

inner radius

I_Area.min

unit density, areal measure of minimum moment of inertia

I_Area.max

unit density, areal measure of maximum moment of inertia

S_Area.min

unit density, areal measure of minimum section modulus

S_Area.max

unit density, areal measure of maximum section modulus

I_ρ.min

density-weighted minimum moment of inertia

I_ρ.max

density-weighted maximum moment of inertia

S_ρ.min

density-weighted minimum section modulus

S_ρ.max

density-weighted minimum section modulus

F_ult

ultimate force

M_ult

ultimate moment

pQCT

peripheral quantitative computed tomography

DXA

dual-energy X-ray absorptiometry

µCT

micro-computed tomography