Potentiating antibacterial activity by predictably enhancing endogenous microbial ROS production

Abstract

The ever-increasing incidence of antibiotic-resistant infections combined with a weak pipeline of new antibiotics has created a global public health crisis¹. Accordingly, novel strategies for enhancing our antibiotic arsenal are needed. As antibiotics kill bacteria in part by inducing reactive oxygen species (ROS)^2–4, we reasoned that targeting microbial ROS production might potentiate antibiotic activity. Here we show that ROS production can be predictably enhanced in Escherichia coli, increasing the bacteria’s susceptibility to oxidative attack. We developed an ensemble, genome-scale metabolic modeling approach capable of predicting ROS production in E. coli. The metabolic network was systematically perturbed and its flux distribution analyzed to identify targets predicted to increase ROS production. In silico–predicted targets were experimentally validated and shown to confer increased susceptibility to oxidants. Validated targets also increased susceptibility to killing by antibiotics. This work establishes a systems-based method to tune ROS production in bacteria and demonstrates that increased microbial ROS production can potentiate killing by oxidants and antibiotics.

Reactive oxygen species (ROS) can damage DNA, RNA, proteins and lipids, resulting in cell death when the level of ROS exceeds an organism’s detoxification and repair capabilities. Despite this danger, aerobically growing bacteria endogenously generate ROS as a metabolic by-product, a risk balanced by an increased efficiency and yield of energy from growth substrates. At least two possible mechanisms exist to manipulate bacterial ROS metabolism and achieve increased sensitivity to oxidative attack: (1) amplification of endogenous ROS production, and (2) impairment of detoxification and repair systems. Whereas removal of detoxification and repair systems has been shown to increase susceptibility to oxidants^{5, 6}, antibiotics⁷ and immunity^{8, 9}, manipulation of endogenous ROS production remains largely unexplored. Endogenous ROS production has long been appreciated as a factor influencing the ability of an organism to survive oxidative stress¹⁰, but an inability to predict the outcome of genetic and environmental perturbations on ROS production¹¹ has hampered exploration of this phenomenon as an antimicrobial adjuvant. This inability derives from a limited systems-level understanding of a potentially, expansive and highly integrated biochemical reaction network. In this study, we sought to tune E. coli metabolism for increased ROS production (specifically, O₂⁻ and H₂O₂) and to determine whether this effect can potentiate oxidative stress and antibiotic activity. Our goal was not to overwhelm the oxidative detoxification and repair capabilities of E. coli with endogenously generated ROS, but rather to increase endogenous production such that the ability of E. coli to cope with exogenous oxidative stress would be compromised. We hypothesized that such a strategy would broadly potentiate antimicrobials that harness oxidative stress and provide a general approach for the discovery of antimicrobial adjuvants. To achieve this goal, we developed an ensemble, genome-scale modeling approach to quantitatively estimate ROS production from E. coli metabolism (Fig. 1).

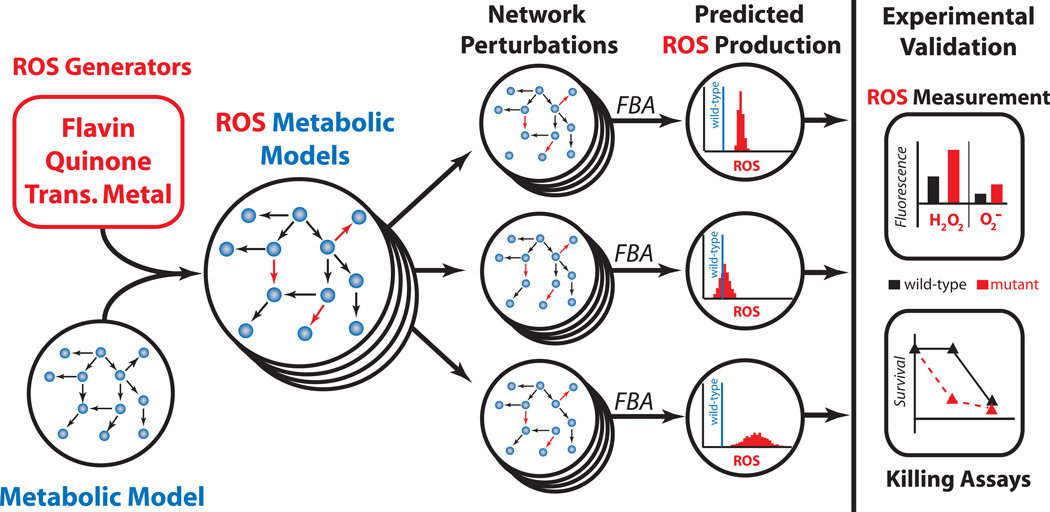
Figure 1.

Systems approach to enhance microbial ROS production. (left) Methodology for the development and validation of an ensemble of systems-level models of E. coli metabolism for estimation of basal ROS production. ROS-generating reactions were incorporated into a metabolic reconstruction and FBA framework¹⁷. Network perturbations via single-gene knockouts were performed in silico using FBA to identify alterations that affect ROS production. (right) In silico predictions were evaluated experimentally by generating mutants and measuring their ROS production and susceptibility to killing by oxidants and antibiotics.

The sources for the majority of endogenous ROS produced by E. coli remain elusive¹¹. The removal of enzymes that generate ROS in vitro has had seemingly little effect on whole-cell ROS production¹¹. This can be explained by the potential scope of ROS generators. Previous studies have demonstrated that O₂⁻ and H₂O₂ can be produced when O₂ abstracts electrons from reduced flavin, quinol and transition metal functional groups^{12, 13}. Inspection of E. coli metabolism for enzymes that use these electron carriers identified 133 reactions, spanning many metabolic pathways, with the potential to generate ROS in the presence of O₂ (see Supplementary Table 1 online). The number of potential ROS-generating reactions is of comparable size to the number of reactions that generate ATP/ADP, NAD/H, and NADP/H, suggesting that ROS could play a crucial, highly integrated role in bacterial metabolism. To predictably modify the production of such highly connected metabolites, a quantitative systems-level approach is required, as even removal of enzymes that endogenously produce ROS may increase or decrease production depending on the redistribution of metabolic flux on the remaining ROS-generating enzymes¹¹.

Systems-level metabolic modeling has been used extensively to optimize the production of desirable metabolites, and has significantly impacted the fields of biotechnology, metabolic discovery and microbiology¹⁴. In this study, we employed flux balance analysis (FBA) with genome-scale metabolic models (GSMM) to simulate systems-level ROS production in E. coli. In FBA, reaction stoichiometries are used to define a metabolic solution space, and linear programming identifies a flux distribution within that space that optimizes an objective function, such as biomass generation. Accuracy within the stoichiometric reaction network is critical to the performance of constraint-based techniques^{15, 16}. Current metabolic reconstructions include consumption reactions, such as superoxide dismutase and catalase, and generation reactions involved in cofactor biosynthesis and alternate carbon metabolism, but are devoid of generation reactions that account for the majority of ROS produced¹⁷. To construct a metabolic model capable of estimating ROS production, we added 266 additional ROS production reactions to the E. coli GSMM¹⁷ one O₂⁻ and one H₂O₂ producing reaction for each of the 133 potential sources (see Methods, Supplementary Methods and Supplementary Table 1 online). These potential ROS sources included all enzymes known to generate H₂O₂ and O₂⁻ in E. coli ^{11, 13, 17, 18}, and this framework allowed separate (independent species balances) but simultaneous modeling of H₂O₂ and O₂⁻ production in E. coli.

Optimization of an objective function is a critical feature of constraint-based techniques, and maximizing for biomass generation has proven to be effective in predicting redistribution of metabolic flux¹⁹. However, when presented with competing pathways, constraint-based methods will identify the most efficient pathway in terms of cellular resources as the one that carries flux. ROS-generating reactions are less efficient competing pathways where reducing equivalents are lost to O₂ instead of being transferred to the intended acceptor. Therefore, addition of ROS-generating reactions to a GSMM is necessary to model ROS metabolism, but insufficient because the reactions will not carry flux (see Supplementary Methods online). To address this, we recognized that ROS-generating reactions are coupled to their more efficient counterpart, in the sense that initial electron transfer from reactant to electron carrier proceeds normally and is dictated by requirements for the intended products, and that it is the promiscuity of the reduced electron carrier with O₂ that generates ROS. Thus, ROS flux is a function of the number of electrons transferred to the electron carrier, and consequently dependent on the reaction flux of the intended reaction. Therefore, in this study, the flux of O₂⁻ and H₂O₂ from ROS-generating enzyme_i was assumed to be proportional to the reaction flux, v_i. This assumption results in proportionality between ROS flux from enzyme_i and the number of electrons transferred by enzyme_i, and is accomplished by coupling the intended enzyme reaction to both its O₂⁻ and H₂O₂ side-reactions (see Methods and Supplementary Methods online). This coupling requires specification of the proportion of electrons that flow to O₂ to form O₂⁻ and H₂O₂ for each of the 133 potential ROS sources. These values vary significantly from enzyme to enzyme^{12, 20}, and are largely undefined owing to the absence of in vivo measurements. With this indeterminacy in mind, we employed an ensemble approach.

Two ensembles of ROS-GSMMs were constructed, each with 1,000 different models (see Supplementary Methods online). The proportions of electron flow from reaction_i to generate O₂⁻ and H₂O₂ were captured by the constants $c_{i,o_2^{-}}$ and c_{i, H2O2} (see Supplementary Methods online). One ensemble derived these constants from a Gaussian distribution in order to model a distributed ROS production network (many significant generators), whereas the other ensemble derived these constants from an exponential distribution to model a centralized ROS production network (few significant generators). Further, it was specified that ROS could only be produced from these reactions and not consumed, with the exception of O₂⁻ attack of Fe-S centers, and that the in silico O₂⁻ and H₂O₂ production rates of the wildtype GSMM had to match the best available experimental estimates (see Methods and Supplementary Methods online). Thus, every stoichiometric reaction network within the ensembles had the exact same production rate of O₂⁻ and H₂O₂ for its wildtype GSMM. Also, the existence of alternative optimal solutions for ROS production of each wildtype network was examined using flux varability analysis (FVA). At a biomass production rate of 100%, all wildtype networks generate a unique solution for the flux of H₂O₂ and O₂⁻ (see Supplementary Methods online).

With these ensembles, we explored in silico how perturbations to the metabolic network alter basal ROS production. We performed a systematic gene-deletion analysis in which genes were removed one at a time and reaction fluxes recalculated, while optimizing for biomass (see Methods and Supplementary Methods online). This provided quantitative distributions of ROS production (H₂O₂ and O₂⁻) from mutant E. coli (Fig. 1) and allowed identification of deletions likely to alter basal ROS production, as measured by the mean ROS production level (Fig. 2a,b andSupplementary Fig. 1a). To account for variable growth rates of mutant strains, we normalized ROS flux by biomass production (BM), and calculations are therefore H₂O₂/BM and O₂⁻/BM (mmol/gDW produced). From our analysis of aerobic glucose minimal media, the gene deletions identified as being most likely to increase ROS production encoded for ATP synthase (atpA-I), pyruvate dehydrogenase (aceEF, lpd), NADH dehydrogenase complex I (nuoABCE-N), glutamate dehydrogenase (gdhA), cytochrome bo (cyoABCD), and triose phosphate isomerase (tpiA). Investigation of the flux distributions for these mutants identified a general trend for ROS production where predicted increases correlated with inefficiencies in the production or usage of ATP.

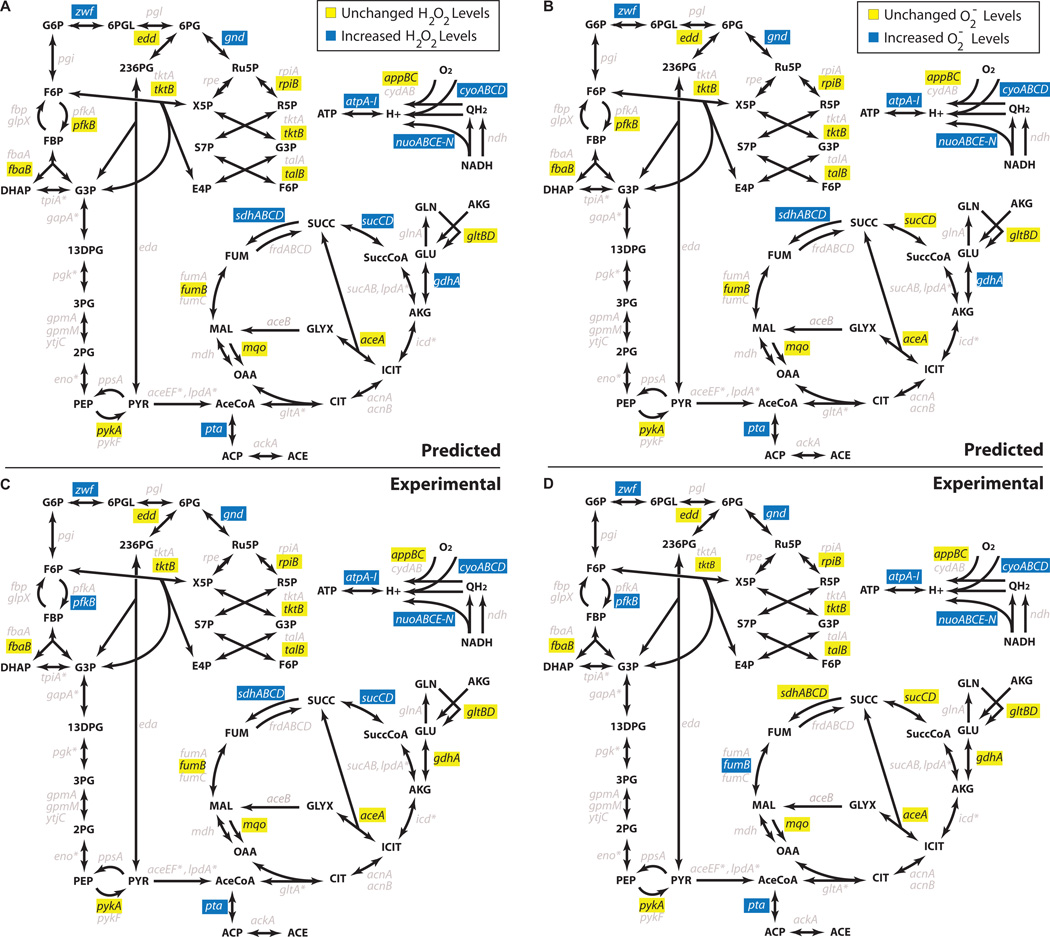
Figure 2.

In silico predictions and experimental measures of H₂O₂ and O₂⁻ levels. (a) Predicted H₂O₂ levels of various mutants compared to wildtype. Blue designates strains whose mean H₂O₂ production levels were simulated to be >5% higher than wildtype over both ensembles, whereas yellow designates strains whose mean H₂O₂ production levels were simulated to be <5% higher than wildtype over both ensembles. (b) Predicted O₂⁻ levels of various mutants compared to wildtype. Blue designates strains whose mean O₂⁻ production levels were simulated to be >5% higher than wildtype over both ensembles, whereas yellow designates strains whose mean O₂⁻ production levels were simulated to be <5% higher than wildtype over both ensembles. (c) Experimentally measured relative fluorescence/OD600 of strains with the H₂O₂-sensitive reporter (dps promoter-gfp). Blue designates strains that were experimentally measured to have increased levels of H₂O₂ compared with wildtype (P-value < 0.05), whereas yellow designates strains that were experimentally measured to have levels of H₂O₂ that do not exceed those of wildtype. (d) Experimentally measured relative fluorescence/OD600 of strains with the O₂⁻-sensitive reporter (soxS promoter-gfp). Blue designates strains that were experimentally measured to have increased levels of O₂⁻ compared with wildtype (P-value < 0.05), whereas yellow designates strains that were experimentally measured to have levels of O₂⁻ that do not exceed those of wildtype. * denotes genes that are essential in our media conditions. Grey denotes genes that were not experimentally examined (for consistency between diagrams, these genes were also denoted by grey in a and b, although in silico predictions were computed).

To validate our approach and in silico analysis, we experimentally tested a series of gene deletions that encode enzymes within glycolysis, the pentose-phosphate pathway, Entner-Doudoroff pathway, TCA cycle, glyoxylate shunt, aerobic respiration, acetate metabolism and glutamate metabolism (Fig. 2c,d and Supplementary Fig. 1b). This collection of enzymes included those predicted to increase ROS (targets) as well as those predicted to leave ROS production unchanged (negative controls). We note that our predictions include all twenty-one genetic mutants tested, both targets and negative controls, and that only those enzymes that were experimentally tested are color-coded in Figure 2 and Supplementary Figure 1. Isozymes selected for testing were based on literature evidence that suggested their removal would most closely reflect model assumptions, and deletions of pyruvate dehydrogenase and triose-phosphate isomerase were not tested owing to an inability to grow in minimal glucose media (see Supplementary Methods online).

To measure O₂⁻, we employed a SoxR-controlled GFP-reporter system, whereas to measure H₂O₂, we used both an OxyR-controlled GFP-reporter system and the direct-sensing HyPer protein (Methods). Our experimental results show between 80–90% qualitative agreement with our in silico predictions of H₂O₂ and O₂⁻ production (Fig. 2 and Supplementary Fig. 1; Correct predictions: dps-GFP: 19/21, soxS-GFP: 17/21, HyPer: 17/21). The probabilities that these levels of agreement would have occurred by chance, using the null hypothesis that random segregation of the 21 genes into targets and negative controls would match experimental results as well as predictions from our modeling approach, are 3.7×10⁻⁴ (dps-GFP), 1.0×10⁻² (soxS-GFP), and 6.2×⁻³ (HyPer) (Methods). These experimental results suggest that our systems-level, ensemble approach enables predictable tuning of ROS production in E. coli.

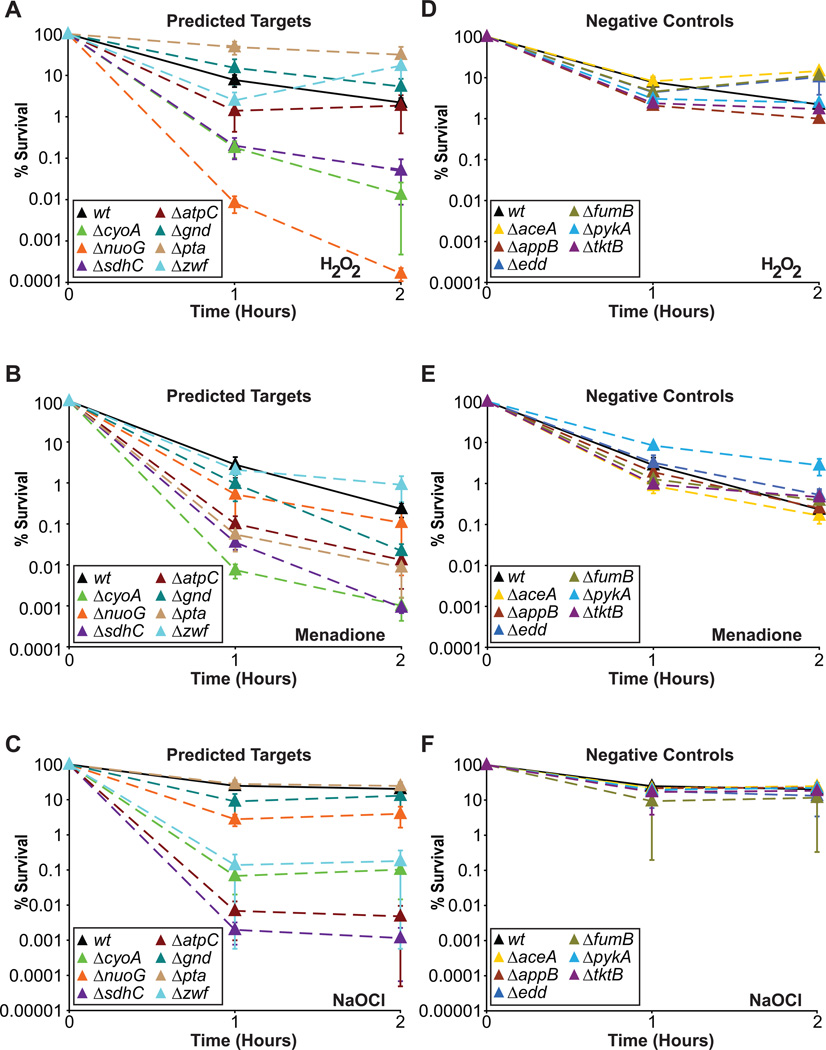
We next sought to determine if increased basal production of O₂⁻ and/or H₂O₂ can translate into increased killing by oxidants. The oxidants we tested were O₂⁻(generated via menadione), H₂O₂, and NaOCl (bleach). O₂⁻ and H₂O₂ were chosen owing to their inclusion in the model and importance for antibiotic action³, and NaOCl was chosen owing to its use as a biocide. Strains chosen for testing of oxidant sensitivity were those with in silico predictions that were confirmed by experimental results (Fig. 2). Our experimental results indicate that increased basal production of O₂⁻ or H₂O₂ generally increases microbial susceptibility to oxidative attack (Fig. 3). Genetic deletions that increase ROS production exhibited increased susceptibility to oxidants, whereas the negative control strains that exhibited wildtype production levels of ROS did not. The probability this enrichment would have been observed by random selection is 2.5×10⁻⁵ (Methods), and demonstrates that increased production of O₂⁻ and H₂O₂ can potentiate killing by oxidants. We note that some predictions conferred increased susceptibility to all oxidants tested (ΔcyoA and ΔsdhC), whereas others exhibited selective increases in sensitivity (e.g., Δzwf), suggesting that sensitivity to one oxidant does not always translate to other oxidants. This is not surprising, and likely derives from the differences in biochemical activity of the oxidants and the distinct cellular death pathways they induce^{20, 21}. Our results clearly demonstrate that increasing endogenous production is a robust strategy to enhance the susceptibility of microbes to oxidative stress.

Figure 3.

Evaluation of susceptibility to killing by oxidants. (a) Time course of predicted target strains and wildtype treated with H₂O₂. (b) Time course of predicted target strains and wildtype treated with menadione. (c) Time course of predicted target strains and wildtype treated with NaOCl. (d) Time course of negative control strains and wildtype treated with H₂O₂. (e) Time course of negative control strains and wildtype treated with menadione. (f) Time course of negative control strains and wildtype treated with NaOCl. Mean ± SEM are shown for all plots.

Bactericidal antibiotics have been shown to share a common mechanism of cell death that involves the production of ROS³. We sought to determine if increased basal production of ROS could potentiate the action of bactericidal antibiotics (the β-lactam ampicillin, the fluoroquinolones ofloxacin and ciprofloxacin, and the aminoglycoside gentamicin) (Fig. 4). Three of the validated targets (ΔcyoA, ΔnuoG, ΔsdhC) exhibited increased sensitivity to both β-lactam and fluoroquinolone antibiotics (Fig. 4a,b and Supplementary Fig. 2a) and one of the targets (Δpta) exhibited increased sensitivity to only fluoroquinolones (Fig. 4b and Supplementary Fig. 2a), whereas all of the negative control strains displayed wildtype sensitivity to both antibiotic classes (Fig. 4c,d and Supplementary Fig. 2b). This results in a correct prediction rate for our approach of greater than 70% for both β-lactams and fluoroquinolone antibiotics. Sensitivity to aminoglycosides was also tested, though we reasoned that increased killing, in general, would not be observed. This expectation was based on the fact that many of the gene deletions that increase basal ROS production negatively impact proton motive force, which is important for aminoglycoside uptake²². As expected, the negative controls had similar sensitivity to gentamicin as wildtype, whereas many targets exhibited decreased sensitivity (see Supplementary Fig. 2c,d online). We note that ΔatpC demonstrated increased sensitivity toward gentamicin, which we believe may be the result of its positive impact on proton motive force²³ as well as its effect on basal ROS production. These data indicate that bactericidal antibiotic primary target interactions must be enabled (e.g., via antibiotic uptake) in order to leverage ROS production as an adjuvant therapy. Accordingly, we expected and demonstrated that the activities of bacteriostatic antibiotics, which do not produce ROS⁶, are unaffected by increases in basal ROS production (see Supplementary Fig. 3 online).

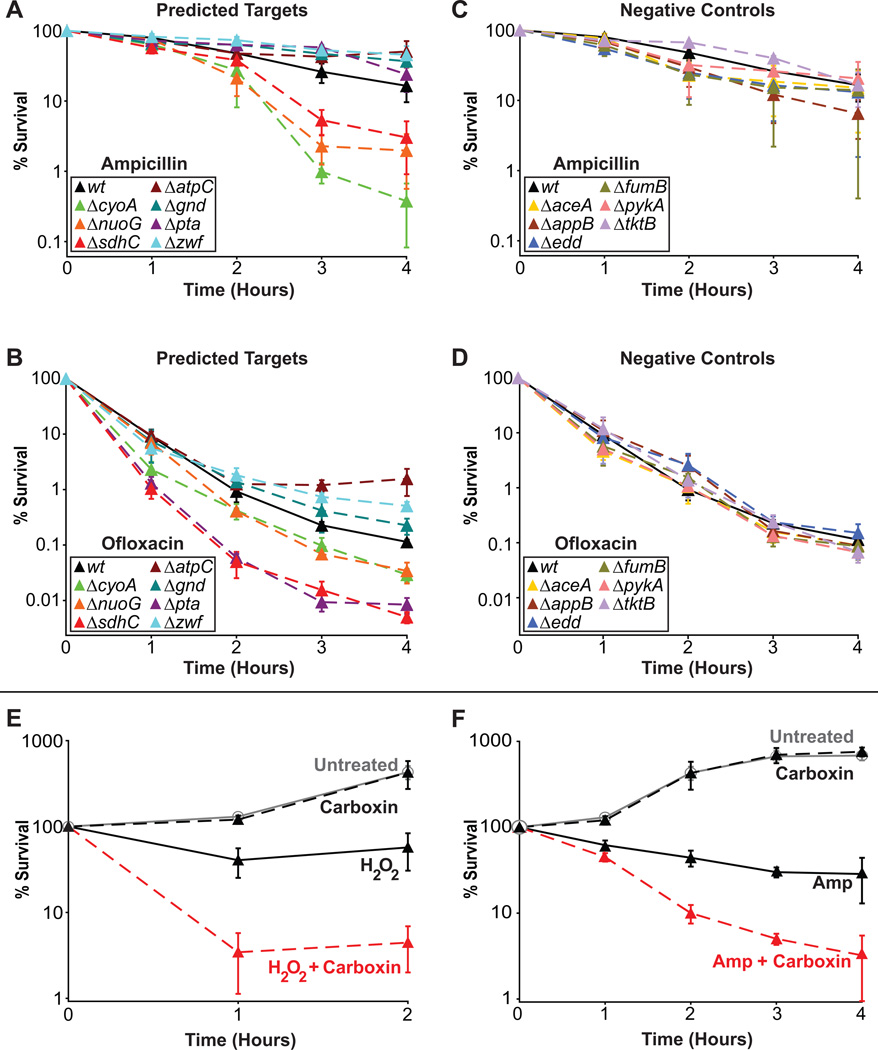
Figure 4.

Evaluation of susceptibility to killing by bactericidal antibiotics and combination treatments with a chemical inhibitor. (a) Time course of predicted target strains and wildtype treated with ampicillin. (b) Time course of predicted target strains and wildtype treated with ofloxacin. (c) Time course of negative control strains and wildtype treated with ampicillin. (d) Time course of negative control strains and wildtype treated with ofloxacin. (e) Time course of wildtype cells treated with carboxin alone, H₂O₂ alone, a combination of carboxin and H₂O₂, or no treatment. (f) Time course of wildtype cells treated with carboxin alone, ampicillin alone, a combination of carboxin and ampicillin, or no treatment. Mean ± SEM are shown for a–f.

We also sought to demonstrate that chemical inhibition of one of the validated targets could increase sensitivity to oxidants and bactericidal antibiotic treatment. To do so, we treated wildtype with carboxin, an inhibitor of succinate dehydrogenase, and measured susceptibility toward H₂O₂ and ampicillin, respectively. Addition of carboxin alone had no effect on the growth of wildtype cells (Fig. 4e, f). However, wildtype cells treated with H₂O₂ and carboxin demonstrated increased sensitivity compared to wildtype cells treated with H₂O₂ alone (Fig. 4e). Similarly, wildtype cells treated with ampicillin and carboxin were significantly more sensitive to the antibiotic than cells treated with ampicillin alone (Fig. 4f). To more fully examine this synergy, we conducted a systematic drug screen spanning five concentrations for each compound (carboxin and ampicillin) including the untreated sample. This allowed us to calculate that carboxin concentrations of 250µM or greater are synergistic with ampicillin concentrations between 7.5–10 µg/mL, using the Bliss Independence and Highest Single Agent models of drug synergism (see Supplementary Fig. 4 online). These results show that chemical inhibition of a predicted and validated target (succinate dehydrogenase) is sufficient to increase sensitivity to oxidative attack and antibiotic treatment. Although carboxin itself is not suitable as an antibiotic adjuvant owing to human toxicity issues²⁴, validation that chemical inhibition of succinate dehydrogenase confers similar sensitivity as genetic perturbation allows translation of this finding to chemical library screening where non-toxic inhibitors of bacterial succinate dehydrogenase and other predicted targets may be found. Chemical libraries have been successfully screened for compounds with antimicrobial properties against pathogenic bacteria²⁵ and our method complements this work by identifying novel enzyme targets for compounds which may have no antimicrobial properties alone, but which enhance the killing efficacy of current antibacterial agents.

Here we established a systems-based method to predictably tune microbial ROS production. By developing genome-scale ROS metabolic models, we were able to predict redistribution of ROS flux resulting from network perturbations and demonstrate experimentally that increased ROS flux can potentiate oxidative attack from antibiotic and biocide treatment. This approach allows rapid identification of antibacterial adjuvant targets, and is translatable to other pathogens of interest, such as Mycobacterium tuberculosis, Staphylococcus aureus, Haemophilus influenzae, and Salmonella typhimurium, where metabolic reconstructions are available^26–29. In addition, the increasingly rapid construction of genome-scale metabolic models will extend the breadth of the technique³⁰, opening up the possibility of using it to target newly identified resistant strains.

Online Methods

Antibiotics and chemicals

All chemicals and antibiotics were purchased from Sigma or Fisher Scientific. Concentrated stock solutions of menadione, H₂O₂, NaOCl, and all antibiotics were prepared fresh daily. H₂O₂, NaOCl, ampicillin, and gentamicin were diluted with or dissolved in sterile deionized water. Ofloxacin and ciprofloxacin were dissolved in 0.1N NaOH. Tetracycline was dissolved in 50% ethanol (v/v). Menadione, carboxin, and chloramphenicol were dissolved in 100% ethanol.

Strains and media

Escherichia coli MG1655 was used in this study. Genetic deletions of aceA, appB, atpC, cyoA, edd, fumB, fbaB, gdhA, gltB, gnd, mqo, nuoG, pfkB, pta, pykA, rpiB, sdhC, sucC, talB, tktB and zwf were transduced from the Keio single-gene deletion knockout library³¹ into MG1655 using the P1 phage method, and confirmed with PCR. The media used for all experiments was M9 minimal media with 10mM glucose as the sole carbon source or MOPS minimal media with 10mM glucose (for the HyPer protein experiments).

Plasmids

The O₂⁻ response sensor used in this study was constructed previously⁷, and utilized the native soxS promoter upstream of the gfpmut2 gene. The H₂O₂ response sensor used the same plasmid backbone and was constructed by PCR-amplifying the native dps promoter and cloning it into the BamHI and XhoI restriction sites, which formerly contained the soxS promoter. The forward primer for PCR was GCGCCTCGAGCCGCTTCAATGGGGTCTACGCT and the reverse primer was GGCCGGATCCTCGGAGACATCGTTGCGGGTAT. The H₂O₂ response sensor was confirmed to increase expression of GFP upon addition of H₂O₂.

GFP reporter assays

Fluorescent measurements were performed on a SpectraMax M5 plate reader (Molecular Devices) using Costar black, clear, flat bottom 96-well plates (Fisher). Each well contained 195µL of M9 minimal glucose media with ampicillin (100µg/mL) and 5µL of overnight culture (plasmids carry an AmpR gene for selection). Overnight cultures were grown in M9 minimal glucose media. Strains were grown in the plate reader at 37°C with shaking. OD₆₀₀ and fluorescence (excitation: 488nm, emission: 520nm, bottom read) were monitored every 10 minutes. Fluorescence/OD₆₀₀ values were calculated using ordinary least squares regression for measurements between OD₆₀₀ = 0.1 and OD₆₀₀ = 0.4. Values reported in Supplementary Table 2 are the relative mean and standard error mean for at least three independent biological replicates. P-values were calculated using a single-tailed, two-sample t-test, assuming unequal variance.

HyPer assays

The HyPer protein is a fluorescent probe that was made by inserting a circularly permuted yellow fluorescent protein into the H₂O₂-sensitive regulatory domain of OxyR³². In the presence of increasing concentrations of H₂O₂, the probe’s excitation peak shifts ratiometrically from 420nm to 500nm, which allows for quantitative measurement of cellular H₂O₂ levels^{32, 33}. HyPer is based on an E. coli H₂O₂-sensing domain, and has been shown to be effective at sensing H₂O₂ within E. coli³². HyPer was provided from the manufacturer (Evrogen) as an IPTG-inducible gene in a pQE30 vector (ampicillin selection marker)³². Single colonies of strains were inoculated into LB media supplemented with 50µg/mL ampicillin and grown overnight at 37°C. The ΔatpC and Δzwf strains were run separately with wildtype because those strains grew significantly slower than the other mutant strains. Strains were inoculated 1:100 into MOPS minimal media plus 10mM Glucose and 50µg/mL ampicillin, and grown to an OD₆₀₀ of 0.2–0.3. All cultures were then diluted with MOPS minimal media plus 50µg/mL ampicillin in a black, clear bottom 96-well plate to a final OD₆₀₀ of 0.05, in a final volume of 200µL per well. 20µL of mineral oil (Sigma Aldrich) was added to each well to prevent evaporation. Strains were grown with and without 75µM IPTG in a SpectraMax M5 plate reader (Molecular Devices) at 37°C with shaking, and OD₆₀₀ and fluorescence (excitation: 420nm and 500nm, emission: 530nm, bottom read) were monitored every 15 minutes for 12 hours. Measurements between OD₆₀₀ = 0.2 and OD₆₀₀ = 0.6 were corrected for background strain fluorescence by subtracting the fluorescence values for un-induced cultures at the same cell density, as measured by OD₆₀₀. The 420nm × 500nm curve was linear over this region, and therefore ordinary least squares regression was used to interpolate between time points. The 500nm excitation fluorescence value that corresponded with 55 fluorescence units from 420nm excitation was calculated and the 500/420 ratio was obtained for all strains. Values reported in Supplementary Table 3 are the relative mean and standard error mean for three independent biological replicates. P-values were calculated using a single-tailed, two-sample t-test, assuming unequal variance.

Antimicrobial sensitivity assays

Strains were grown aerobically from an initial inoculation of OD₆₀₀ = 0.01 to OD₆₀₀ = 0.16–0.20 in 250mL baffled flasks filled to 1/10^th the total volume and shaken at 300rpm at 37°C. For menadione, H₂O₂, and antibiotic sensitivity assays, time-zero samples were collected (200–400µL), then 1mL aliquots were transferred to 14mL test tubes, and appropriate volumes of menadione, H₂O₂, or antibiotic stock solutions, not in excess of 15µL, were added to obtain the final concentrations (1mM menadione, 5mM H₂O₂, 7.5 µg/mL ampicillin, 100 ng/mL ofloxacin, 15ng/mL ciprofloxacin, 500 ng/mL gentamicin, 10 µg/mL tetracycline, and 15 µg/mL chloramphenicol). For NaOCl, due to its reactivity with media components³⁴, 10mL of culture was centrifuged at 3,000 rpm for 10 minutes in a benchtop centrifuge, 9.5mL of the supernatant was removed and the cell pellet was resuspended with 9.5mL of sterile phosphate buffered saline (PBS) at pH 7.2. The suspension was spun down again at 3,000 rpm for 10 minutes, and 9.5mL of the supernatant removed. The cell pellet was resuspended with 4.5mL of sterile PBS. The cell density was adjusted with sterile PBS to achieve an OD₆₀₀ = 0.2. Time-zero samples were collected (200–400µL), 1mL aliquots were transferred to 14mL test tubes, and NaOCl stock solution was added to obtain the final concentration (20µM NaOCl). At the specified times (1, 2 hours for menadione, H₂O₂, NaOCl; 1, 2, 3, 4 hours for antibiotics), sample aliquots were collected (200–400µL). All samples were immediately centrifuged at 10k rpm in a microcentrifuge, 95% of the supernatant was removed, and the cell pellets were resuspended in PBS. Samples were serially-diluted and plated on LB agar plates, which were then incubated overnight at 37°C. Colony forming units were counted approximately 16–18 hours after plating.

Carboxin inhibitor experiments

Strains were grown aerobically from an initial inoculation of OD₆₀₀ = 0.01 to OD₆₀₀ = 0.16–0.20 in 250mL baffled flasks filled to 1/10^th the total volume and shaken at 300 rpm at 37°C. Time-zero samples were collected (200–400µL), then 1mL aliquots were transferred to 14mL test tubes. Carboxin solubilized in 100% ethanol or ethanol alone was added to the tubes. Carboxin was added at a final concentration of 500 µM. H₂O₂ or ampicillin stock solutions were added to obtain the final concentrations of 5 mM H₂O₂ and 10 µg/mL ampicillin. A dose response was also performed of both carboxin (0, 250, 500, 750, and 1000 µM) and ampicillin (0, 5, 7.5, 10, and 15 µg/mL) to determine if the two compounds demonstrate a synergistic interaction. Drug synergism was calculated using the Bliss Independence and Highest Single Agent models^{35, 36}. Specifically, the formula,

$${\text{BIC}}_{\text{AB}}=\mathrm{A}+\mathrm{B}-\text{AB}$$ (1)

was used to calculate synergism with the Bliss Independence model. A and B are the effects of the two drugs in isolation, whereas, BIC_AB is the combined effect of the two drugs as predicted by the Bliss Independence model. If C_AB, the experimentally-determined combined effect of the two drugs, is > BIC_AB, synergy is observed. In contrast, in the Highest Single Agent model, if C_AB > max(A, B) synergy is observed. Since we were monitoring cell death, the quantitative effect of each compound was defined as the fractional reduction of the population, R = 1-CFU_t/CFU₀, where CFU_t is the number of CFUs measured after treatment, and CFU₀ is the number of CFUs measured before treatment. R = 1 indicates complete loss of the population, R = 0 indicates a population in stasis, and R < 0 indicates a growing population. Since carboxin was non-lethal and allowed significant growth, even at concentrations as high as 1mM, the Highest Single Agent model was a much more stringent measure of synergy than the Bliss Independence model. To prove this, let us rewrite the Bliss Independence model as follows,

$${\text{BIC}}_{\text{AB}}=\mathrm{A}(1-\mathrm{B})+\mathrm{B}$$ (2)

If A is a compound that reduces CFUs, such as ampicillin, its effect above the MIC will be 0≤A≤1, whereas if B is a compound that allows growth at all concentrations, its effect will be B < 0 regardless of the concentration. Rearrangement of the above yields,

$${\text{BIC}}_{\text{AB}}/\mathrm{A}=1-\mathrm{B}+\mathrm{B}/\mathrm{A}$$ (3)

Since equation 3 yields BIC_AB/A < 1 for all B<0 and 0<A<1, the Highest Single Agent model requires C_AB/A > 1 and the Bliss Independence model requires C_AB/BIC_AB > 1 for synergy, the Highest Single Agent model will always be a more strict synergy requirement under these conditions. Synergy can readily be observed from the relative survival curves in Supplementary Figure 4 (curves substantially lower than 1) where 7.5 and 10 µg/mL ampicillin synergize with carboxin concentrations from 250–1000µM.

Modeling Escherichia coli ROS metabolism

Systems-level metabolic modeling was performed using FBA and the COBRA Toolbox³⁷. Aerobic E. coli metabolism (O₂ uptake = −18.5 mmol/gDW/hr¹⁷) was modeled using iAF1260 with glucose (glucose uptake = −11 mmol/gDW/hr¹⁷) and ammonia as the sole carbon and nitrogen sources. The model was augmented with ROS-generating reactions as described in the Supplementary Methods. Single-gene deletion analysis was performed using the built-in COBRA function. Complete modeling details are provided in the Supplementary Methods.

Statistical analysis of model performance

Statistical significance was assessed using the null hypothesis that random selection of genes would match experimental results as well as predictions from our modeling approach. For the GFP reporter systems, where N genes exhibited an increased ROS/BM compared to wildtype (p-value < 0.05), and M genes did not (N+M: total number of genes tested), we identified the number of genes, P, our approach predicted to increase ROS/BM. We calculated the (a) total number of ways to pick P genes from N+M, and then calculated the (b) number of ways to pick P genes that would yield C correct predictions, C being defined as the correctly predicted number of genes our approach identified to increase ROS/BM. The ratio of (b)/(a) is the probability that random selection would yield the same frequency of correct predictions as our approach. Agreement was assessed by calculating the number of predictions that agreed with experimental results. For the O₂⁻-sensing GFP reporter, 17 of the 21 genes (81%) experimentally tested qualitatively agreed with predictions, whereas for the H₂O₂-sensing GFP reporter, 19 of the 21 genes (90%) experimentally tested qualitatively agreed with predictions. Identical procedures were used in the analysis of HyPer results, except that a p-value of 0.1 was used to identify genes that exhibited an increased H₂O₂/BM compared to wildtype. For antimicrobial sensitivity assays, statistical significance was assessed similarly, except that N in this case is the number of genes that exhibited a 2-fold increase in susceptibility toward any oxidant after a treatment time of 2 hours.