Entropic force between membranes reexamined

Lipid bilayers serve as model surfaces that are often used to understand the behavior of actual cell membranes. Cell adhesion (1, 2), membrane fusion (1), binding-unbinding transition (3), self-assembly, and related phenomena govern an astounding array of biological functions; for example, sperm-egg fusion is the basis of mammalian reproducion (1). These phenomena are dictated by a complex interplay between the various attractive and repulsive forces that mediate between biological membranes. The key role is played by a repulsive force termed “steric hindrance,” or simply entropic pressure, the origins of which lie in the thermally excited fluctuations of membranes. Nearly four decades ago, in a landmark paper, Wolfgang Helfrich (4) proposed both the concept and the quantitative nature of this force. Freund (5) reexamines this paradigm in PNAS, and finds that the entropic force is of a remarkably different character than hitherto believed.

Ubiquitous van der Waals forces provide the weak attraction between biological surfaces; these vary as 1/c³ for close separations and transition to 1/c⁶ at larger distances (Fig. 1 A and B) (6, 7). Here, c is the mean distance between the interacting membranes. The notable aspect of the attractive force is that it is long-ranged. A catch-all phrase, “hydration forces” (8), is used to denote the repulsive force that becomes operative when membranes are nearly touching each other; this is quite short-ranged and drops off exponentially with distance. The underlying mechanisms of hydration forces are still debated and a subject of active research (9). A notable observation is that both the van der Waals and hydration interactions would be present even if membranes were perfectly rigid. The origins of a third interaction—the so-called “entropic force”—is predicated on the fact that biomembranes are (generally) quite flexible and the energetic cost of elastic bending is low enough that at room temperature, they fluctuate and flap like flags in a strong wind. A single membrane fluctuates freely. As two membranes approach each other, they hinder or diminish each other’s out-of-plane fluctuations. This hindrance decreases the entropy and the ensuing overall increase of the free-energy of the membrane system, which depends on the intermembrane distance, leads to a repulsive force that tends to push the membranes apart. Stated differently, a finite external pressure is required to maintain the mean distance between the interacting membranes. Helfrich (4), using a variety of physical arguments and approximations, postulated that the entropic force varies as 1/c³. In contrast to the other known repulsive forces, this behavior is long-ranged and competes with the van der Waals attraction at all distances (6, 7, 10). Since Helfrich’s proposal (4), biophysicists have used the existence of this repulsive force to explain and understand a variety of phenomena related to membrane interactions.

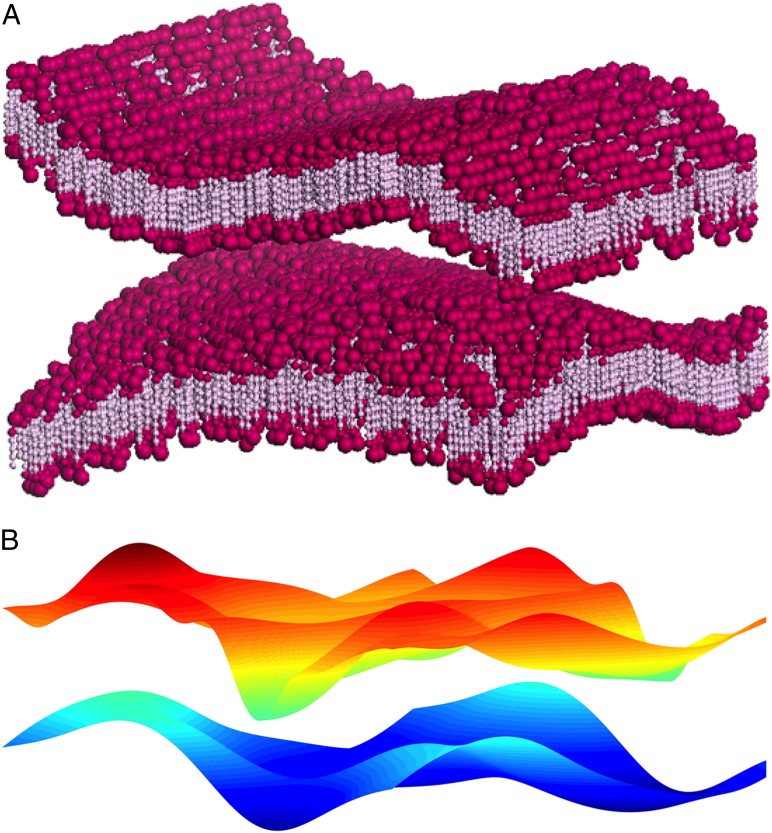
Fig. 1.

(A) Depicts (with some artistic license) a very small patch of interacting and thermally fluctuating lipid bilayers. The areal extent of a membrane at which a continuum analysis is valid is roughly 10–20 times larger in scale than what is shown here. Even in absence of any fluctuations, membranes feel an attractive long-range van der Waals force and a short-range exponentially decaying repulsive hydration force that is attributed to the microscopic structure of lipid-water interface, although the exact physics underlying this repulsion is still under debate (9). (B) The oft-used idealization that replaces the actual (microscopically complex) membranes, as shown in A, by a pair or stack of interacting elastic sheets.

Although lipid bilayers and membranes are microscopically quite complex, their mechanical behavior (under numerous physically relevant circumstances) can be well-described by just a few continuum parameters, such as bending modulus, which sets the energy cost of bending the membrane or an out-of-plane fluctuation. Taking advantage of these parameters, Freund (5), like Helfrich and many other authors preceding him, treats membranes as idealized elastic surfaces and uses classic statistical mechanics to infer the nature of the entropic force caused by interaction with nearby surfaces. Freund’s analysis concludes that across the range of intermembrane separations, the entropic force varies as 1/c, a significant departure from Helfrich’s conclusions (4) and those of others (9). Freund’s work thus appears to be unique in completing a mathematical analysis of this phenomenon.

Despite four decades of work (9) that more or less have found agreement with the results of Helfrich, what leads Freund (5) to this different conclusion? Helfrich (4, 6) views the membrane as consisting of many small elements that fluctuate independently, not unlike how atoms in an ideal gas behave. Drawing further on this analogy and treating the membrane as an ideal gas of valleys and bumps, a pressure ∼1/c³ against the confining medium can be extracted. There are other assumptions buried in the various arguments presented by Helfrich; for example, (i) each independent fluctuating element is considered to have an area that is proportional to c²; (ii) recognizing that it is difficult to handle the statistical mechanics of the point-wise hindrance condition, |h(x, y)| ≤ c, a weaker constraint is used: 〈h²〉 ≤ c². In other words, the hindrance is imposed on the average rather than point-wise. Although the latter argument is a simplification designed to extract analytical insights (a time-honored tradition), the notion that each element fluctuates independently is rooted in the idea that wavelengths below a certain value are energetically very costly, and therefore hardly affect the membrane interaction. The assumption that the area of each independent fluctuating element is related to the intermembrane distance is harder to justify, something that Freund (5) abandons from the outset.

It is precisely with the assumptions mentioned above (and a few that I did not articulate) where Freund (5) departs from Helfrich (4). I have already indicated that in Freund’s work the number of elements making up the membrane are considered to be completely unrelated to intermembrane distance. In his analysis, the elements that constitute the membrane do not fluctuate independently; rather, the elastic deformable membrane responds in its entirety to the external disturbances. Finally, rather than limiting the root mean square fluctuation amplitudes to lie below |c| in an average sense, this constraint is imposed at every single point of the membrane.

In Freund’s (5) analysis, each small piece of the membrane can fluctuate up to c, but it need not. The actual statistical distribution of the fluctuation amplitudes is determined by minimizing the free energy. The final outcome is a set of equations that must be numerically evaluated but yield a rather simple asymptotic relation (for c → 0), but that is seen to be valid across a wide range of interseparation distance: f ∼ n²/c. Here, f is the resultant entropic force and n² can be identified with the number of degrees-of-freedom representing the system. If a representative periodic membrane patch of edge length L is considered, then n = L/λ (i.e., it scales with membrane size). λ is a normalizing length scale but with a meaningful physical interpretation: this is a length scale that is large compared with molecular size, and therefore the use of both a continuum analysis and classic statistical mechanics is justified. A notable feature of this asymptotic result is that the mean pressure f/n² ∼1/c is independent of membrane size, which is what we expect for periodic fluctuations.

As was initially pointed by Helfrich (4), because of reflective symmetry, the problem of a pair of interacting membranes may be replaced by a single membrane confined between two rigid walls. One may, however, consider a softer constraint, for example, parabolic confinement instead of the rigid walls (square confinement). Freund has addressed this problem in a prior work (11). Parabolic confinement is easier to handle analytically, although care must be taken to interpret what exactly is meant by intermembrane distance. Freund’s analysis of the softer confinement corroborates his present calculations (5) and provides some additional insights: in the analysis of fluctuating and interacting membranes, it is tempting to consider only the lowest modes because shorter wavelengths are far less probable as a result of their higher energetic cost. Freund (11) finds that nature of the confinement pressure strongly depends on inclusion of higher modes.

Although a clichéd statement (which does not make it any less true), the test of any new theory comes from careful experiments. However, experiments that purport to isolate the entropic force are easier said than done. Early on, some elegant synchrotron X-ray studies were done by Safinya et al. (12, 13), who concluded that Helfrich’s theory is qualitatively correct. Another notable experimental work is that of Richetti et al. (14). Freund suggests that in the range of intermembrane distances examined in some of the aforementioned experiments, the distinction between 1/c and 1/c³ lies within the error bars. Freund’s thought-provoking reexamination of the widely studied entropic force between membranes will hopefully encourage design of further experimental work that will probe his specific assertions. What are the physical implications of the unique force-law proposed by Freund? I expect the quest for an answer to this question to be an interesting avenue for future research in membrane physics.