Abstract
Using our newly developed explicit three-body (E3B) water model, we simulate the surface of liquid water. We find that the timescale for hydrogen-bond switching dynamics at the surface is about three times slower than that in the bulk. In contrast, with this model rotational dynamics are slightly faster at the surface than in the bulk. We consider vibrational two-dimensional (2D) sum-frequency generation (2DSFG) spectroscopy as a technique for observing hydrogen-bond rearrangement dynamics at the water surface. We calculate the nonlinear susceptibility for this spectroscopy for two different polarization conditions, and in each case we see the appearance of cross-peaks on the timescale of a few picoseconds, signaling hydrogen-bond rearrangement on this timescale. We thus conclude that this 2D spectroscopy will be an excellent experimental technique for observing slow hydrogen-bond switching dynamics at the water surface.
Interfaces play important roles in many disciplines of science. The water liquid/vapor interface, for example, is of great interest in chemistry, biology, and earth science and is an important model system for water in a heterogeneous environment. Of particular interest is understanding the extent to which the structure and dynamics, and ultimately reactivity, of water at the interface differ from those in the bulk. For example, how does the distribution of hydrogen bonds differ between interfacial and bulk water? How anisotropic is the orientation of the water molecules at the interface? In terms of dynamics, how do the diffusion constant, rotational relaxation time, and hydrogen-bond rearrangement time vary as the interface is approached? One can also consider vibrational dynamics processes such as energy relaxation and transfer.
One important technique for addressing these questions is computer simulation. Models used in these calculations for the water surface range from rigid, fixed-point-charge two-body models (1–3), to fluctuating charge or polarizable models (4, 5), to ab initio molecular dynamics calculations (6–10). Regarding static properties, for example, some effort has been expended toward understanding what fraction of H atoms in the surface layer are hydrogen bonded, and what fraction of molecules do not donate any hydrogen bonds (nondonors or “acceptor-only” molecules) (6, 9). In terms of dynamics, it is generally found that diffusion is faster at the interface than in the bulk (1, 4, 10), and rotational relaxation is also faster (3, 6, 7, 10). On the other hand, two studies with fixed-charge two-body models show that hydrogen-bond rearrangement is slower at the interface (2, 3), whereas one study with a fluctuating-charge model shows that hydrogen-bond rearrangement is faster (5). In this latter study the authors conclude that this is generally true for polarizable models.
Because of its surface sensitivity, vibrational sum-frequency generation (SFG) spectroscopy (11, 12) has become one of the most powerful experimental techniques for the study of interfaces, including the one separating liquid water and its vapor (13–28). In a vibrational SFG experiment, infrared (IR) and visible laser pulses are incident on the interface, and the signal is detected at the sum of the frequencies of these incoming beams. For the water liquid/vapor interface one can think of the SFG intensity as the vibrational spectrum of the water molecules near the surface (29, 30). Intensity-level SFG spectra of the OH stretching mode of water show two major features for this system. A sharp peak near 3,700 cm−1 indicates the existence of dangling or “free” OH groups at the water surface. The other broad band in the frequency region from 3,000 to 3,600 cm−1 is interpreted as arising from hydrogen-bonded OHs (13, 14).
Further interpretation of SFG results was catalyzed by two major advances. First, studying the isotopically dilute HOD in D2O (or H2O) system has helped in the interpretation of spectra, because the frequency mismatch of OH and OD stretches largely eliminates the effects of vibrational couplings, which greatly complicate the measured spectra for neat water (31, 32). Second, the invention of phase-sensitive SFG enables the direct measurement of the imaginary part of the second-order complex susceptibility χ2 (whereas the conventional experiments measure |χ2|2) (33, 34). Because Im(χ2) contains only resonant contributions, it is analogous to an absorption spectrum and is easier to interpret and to calculate. Moreover, Im(χ2) is signed, and the sign is related to the projection of the OH (OD) transition dipole onto the surface normal. Recently, Shen and coworkers measured Im(χ2) for both the neat and the isotope-labeled water liquid/vapor interfaces (35, 36). These phase-sensitive SFG results for HOD/D2O show three major features: a sharp positive peak at about 3,700 cm−1 corresponding to the upward-pointing dangling OH bonds and negative and positive bands at about 3,500 and 3,300 cm−1, respectively, attributed to hydrogen-bonded water OHs (36). The latter two peaks were interpreted by the authors as “water-like” molecules with downward-pointing OH bonds and “ice-like” molecules with upward-pointing OH bonds, respectively (36, 37).
As mentioned above, phase-sensitive SFG allows for a better comparison between experimental results and theoretical calculations. Although recent papers by Geissler, Shen, and coworkers show that in principle magnetic-dipole and electric-quadrupole terms should be included in a correct SFG calculation (38–40), in practice nearly all calculations have used the electric-dipole approximation. Most of the widely used two-body water models fail to reproduce the positive band in the low-frequency region of the phase-sensitive SFG spectrum (41–46). Morita and coworkers have developed a polarizable and flexible classical water model that successfully qualitatively reproduces Im(χ2) of the neat H2O surface, and they assigned the positive signal in the hydrogen-bonding region to induced dipoles perpendicular to the water surface (28, 47, 48). This conclusion was also in agreement with their results from hybrid quantum mechanics/molecular mechanics molecular dynamics (MD) simulations (49). Our group has used the newly developed explicit three-body (E3B) water model (50, 51), which includes three-molecule interactions, to calculate Im(χ2) using a mixed quantum/classical approach. The calculations also qualitatively reproduce the experimental spectra. The two features in the hydrogen-bonding region were found to result from canceling contributions from water molecules with different hydrogen-bonding configurations (46, 52), with especially large contributions from four-hydrogen–bonded double-donor molecules and two-hydrogen–bonded single-donor molecules.
Although conventional SFG spectroscopy can provide structural information about an interface, in the case of water, where the spectrum is dominated by inhomogeneous broadening, it is unable to probe the dynamics. To study dynamics, one-dimensional (1D)SFG needs to be extended to two dimensions (2D), much like IR spectroscopy has recently been extended to 2DIR (53). In a time-domain 2DIR experiment, the sample is subjected to three IR pulses, separated by two time intervals t1 and t2, and the signal is heterodyne detected at a time t3 later. The signal is then Fourier transformed in t1 and t3, leading to two frequency dimensions ω1 and ω3. A series of 2DIR spectra is collected as a function of t2, the “waiting time.” Roughly speaking, the 2DIR spectrum can be thought of as the joint probability density that the chromophore has frequency ω1 at time 0 and ω3 at time t2. Thus, the experiment naturally reports on dynamic processes such as spectral diffusion and chemical exchange (53). 2DIR spectroscopy has been widely used to study dynamics in bulk water, including hydrogen-bond dynamics (54–60), rotations (61–63), and vibrational energy transfer (64–69). However, 2DIR, a third-order nonlinear spectroscopy, is not surface sensitive. Therefore, 2DSFG, a fourth-order nonlinear spectroscopy, is needed to study the dynamics at the interfacial region.
In 2DSFG, four laser beams are incident on the sample: three time-delayed IR pulses followed by a visible pulse (70). Although some related and beautiful ultrafast pump-probe SFG and homodyne-detected 2DSFG experiments have been performed to measure vibrational relaxation, rotational dynamics, and vibrational energy transfer at the water surface (71–76), to the best of our knowledge the heterodyne-detected 2DSFG experiment for the air/water interface (and especially desirably, for HOD/D2O or HOD/H2O) has not yet been performed. Indeed, only two heterodyne-detected 2DSFG experiments on any system have been reported (70, 77). Xiong et al. measured the heterodyne-detected 2DSFG spectrum of CO molecules adsorbed on a platinum surface (70), whereas Singh et al. measured the heterodyne-detected 2DSFG spectrum for the interface of HOD/D2O with the positively charged surfactant cetyltrimethylammonium bromide (77). This latter system provides a stronger signal than that for the air/water interface, because the electric field from the surfactant produces substantial alignment of the water molecules. A theoretical 2DSFG calculation by Nagata et al. using a classical approach has appeared for water at a lipid monolayer interface (78).
In this paper, we simulate the liquid/vapor interface using our E3B water model (51, 52). We calculate the hydrogen-bond rearrangement time-correlation function for the surface molecules, finding that it decays on a timescale of about 4 ps, which is significantly slower than the corresponding timescale for the bulk. We can contrast this to the timescale for rotational motion, which for our model is faster at the surface than in the bulk. We also calculate the 2DSFG signal for different polarizations, as a function of waiting time. Cross-peaks grow in on the timescale of the hydrogen-bond rearrangment time. This demonstrates the promise of the 2DSFG technique for an experimental measurement of spectral diffusion and chemical exchange at the water surface and hence an experimental measurement of structural relaxation in the interfacial region.
Molecular Dynamics Simulation
Details of the E3B water model and the MD simulation protocol are described elsewhere (46, 51). Briefly, the MD simulation with the E3B water model is performed in the canonical ensemble. The simulation box consists of 500 water molecules. The size of the rectangular box is 2.46 × 2.46 × 7.39 nm3, producing liquid and vapor slabs. Standard 3D periodic boundary conditions are applied. Electrostatic interactions are calculated using particle-mesh Ewald summation, and the Lennard–Jones interactions are truncated at 9 Å. The system is maintained at constant temperature (298 K) by means of a Berendsen thermostat (79) with coupling parameter τ = 0.5 ps. The equations of motion are propagated with a 1-fs time step. After an equilibration run of 1 ns, the production run of 20 ns is performed and sampled every 10 fs. The GROMACS package (80, 81), home modified for implementing the E3B model, is used to perform the simulation.
We are interested in contrasting the hydrogen-bond rearrangement dynamics for surface and bulk water molecules. To that end, we must first define what we mean by surface molecules. From the simulation one can compute the density profile as a function of, for example, the oxygen position. One finds that it decreases monotonically from the bulk liquid value to the value (essentially zero) for the vapor phase. One often defines the interfacial region to be that where the density decreases from 90 to 10% of the bulk value, which for E3B water is roughly 4 Å wide. Any molecule whose oxygen atom is in this region at a given time is defined to be a surface molecule.
Next we must define what we mean by a hydrogen bond. There are myriad definitions in the literature—we choose an electronic structure-based definition involving the 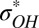 orbital occupancy associated with every H atom (60, 82). When this occupancy, due to charge transfer from lone-pair electrons on a nearby O atom, is above a certain threshold value, we say there is a hydrogen bond between these two atoms. At every instant in time one can then define the number of hydrogen bonds n that a molecule makes with its neighbors. The equilibrium hydrogen-bonding time-correlation function is defined to be (83, 84)
orbital occupancy associated with every H atom (60, 82). When this occupancy, due to charge transfer from lone-pair electrons on a nearby O atom, is above a certain threshold value, we say there is a hydrogen bond between these two atoms. At every instant in time one can then define the number of hydrogen bonds n that a molecule makes with its neighbors. The equilibrium hydrogen-bonding time-correlation function is defined to be (83, 84)
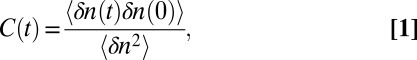 |
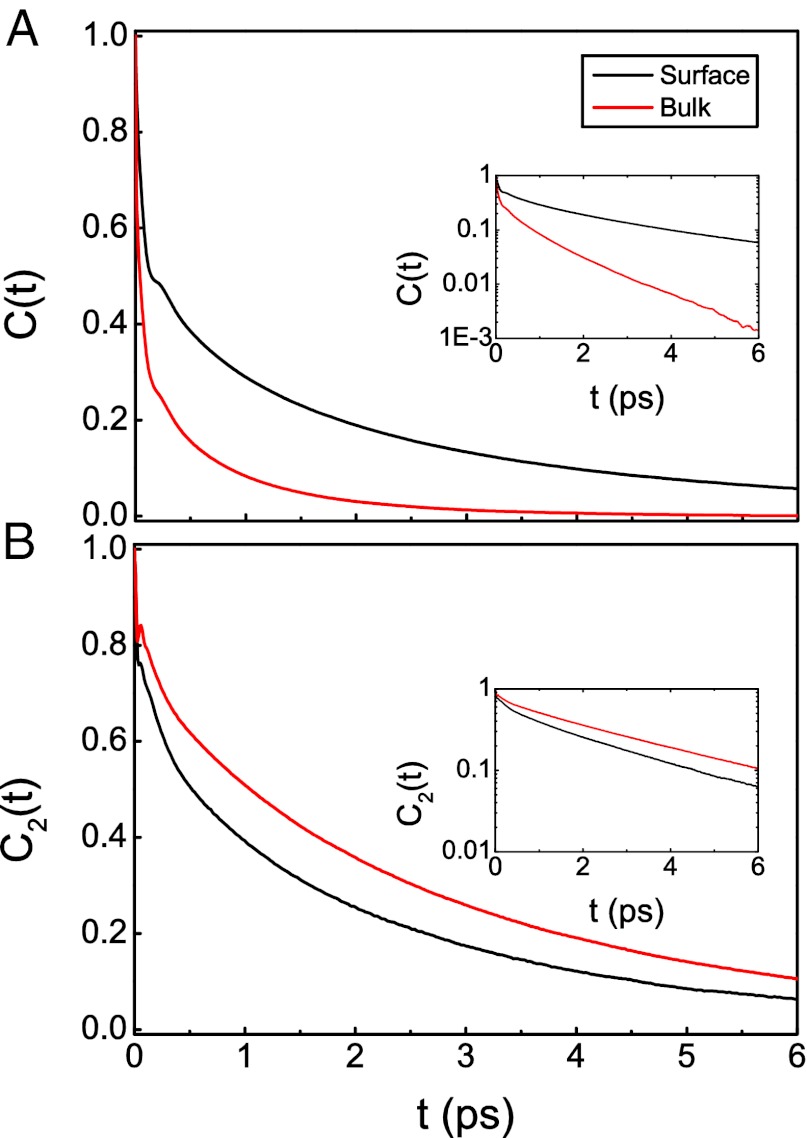
where 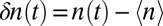 , and〈n〉is the average number of hydrogen bonds. This time-correlation function is calculated for all molecules defined to be in the surface region at both times 0 and t. Fig. 1 displays the hydrogen bond number fluctuations for the surface and the bulk. One sees clearly that the timescale for hydrogen-bond rearrangement is significantly slower at the surface. A rough measure of the decay time can be obtained by fitting each time-correlation function to a single exponential after the initial fast drop. The relaxation times for the time-correlation functions at the interface and in the bulk are 3.7 and 1.2 ps, respectively. Slower switching dynamics at the surface presumably result from the lower density of the interface and the concomitant relative paucity of hydrogen-bond accepting partners (10, 57, 58, 85, 86). Quantitative estimates for the extent of slowdown at the interface depend on the type of hydrogen-bonding time-correlation function used in the calculations (2, 5, 83, 84) and also on the water model [and the associated populations of different hydrogen-bonded species through the interface (8, 46)].
, and〈n〉is the average number of hydrogen bonds. This time-correlation function is calculated for all molecules defined to be in the surface region at both times 0 and t. Fig. 1 displays the hydrogen bond number fluctuations for the surface and the bulk. One sees clearly that the timescale for hydrogen-bond rearrangement is significantly slower at the surface. A rough measure of the decay time can be obtained by fitting each time-correlation function to a single exponential after the initial fast drop. The relaxation times for the time-correlation functions at the interface and in the bulk are 3.7 and 1.2 ps, respectively. Slower switching dynamics at the surface presumably result from the lower density of the interface and the concomitant relative paucity of hydrogen-bond accepting partners (10, 57, 58, 85, 86). Quantitative estimates for the extent of slowdown at the interface depend on the type of hydrogen-bonding time-correlation function used in the calculations (2, 5, 83, 84) and also on the water model [and the associated populations of different hydrogen-bonded species through the interface (8, 46)].
Fig. 1.
(A) Hydrogen-bond number fluctuation time-correlation functions for the water/vapor interface and bulk water. (Inset) Data on a logarithmic scale. (B) P2 reorientational time-correlation function for the surface and the bulk.
We can also calculate the timescale for molecular reorientation through the P2 time-correlation function 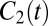 defined by
defined by
where P2 is the second-order Legendre polynomial and 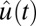 denotes the unit vector along the OH bond. Also shown in Fig. 1 is
denotes the unit vector along the OH bond. Also shown in Fig. 1 is 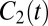 for bulk water and the interface (for molecules in the surface region for both times 0 and t). Both curves have a fast initial decay due to librational motion (62, 63, 87), followed by a slow relaxation. In this case one can clearly see that reorientation dynamics are slightly faster at the interface. After the fast initial drop, the time-correlation function is fit to a single exponential, which gives the relaxation time of 3.0 ps on the surface vs. 3.3 ps in the bulk. The faster reorientational motion on the surface is presumably caused by the lower number of hydrogen bonds and hence fewer constraints on the rotational motion. This interesting situation where the hydrogen-bond switching dynamics are slower at the surface compared with the bulk, whereas the reorientation dynamics are faster, is in agreement with a number of other simulations (1–3, 6, 7, 10).
for bulk water and the interface (for molecules in the surface region for both times 0 and t). Both curves have a fast initial decay due to librational motion (62, 63, 87), followed by a slow relaxation. In this case one can clearly see that reorientation dynamics are slightly faster at the interface. After the fast initial drop, the time-correlation function is fit to a single exponential, which gives the relaxation time of 3.0 ps on the surface vs. 3.3 ps in the bulk. The faster reorientational motion on the surface is presumably caused by the lower number of hydrogen bonds and hence fewer constraints on the rotational motion. This interesting situation where the hydrogen-bond switching dynamics are slower at the surface compared with the bulk, whereas the reorientation dynamics are faster, is in agreement with a number of other simulations (1–3, 6, 7, 10).
2DSFG Spectroscopy
In a 2DSFG spectroscopy experiment, the sample is exposed to four sequential laser pulses. The first three are ultrafast IR pulses with wave vectors 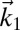 ,
, 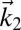 , and
, and 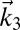 , characterized by a broad range of frequencies. The last one is a visible pulse with wave vector
, characterized by a broad range of frequencies. The last one is a visible pulse with wave vector 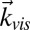 (70, 78). The response of the sample is determined by the incident and scattered light wave vectors and polarizations. The emitted signal reflects the appropriate elements of the fourth-order susceptibility tensor χ4 (11, 12, 70, 78, 88–90). In the present study, we first consider the sspss polarization condition, in which case the signal, visible, and first two IR pulses are polarized perpendicular to the plane of incidence and in the plane of interface (s), whereas the third IR pulse is polarized in the plane of incidence (p). In this case, the measured signal is related only to a single element of the susceptibility tensor
(70, 78). The response of the sample is determined by the incident and scattered light wave vectors and polarizations. The emitted signal reflects the appropriate elements of the fourth-order susceptibility tensor χ4 (11, 12, 70, 78, 88–90). In the present study, we first consider the sspss polarization condition, in which case the signal, visible, and first two IR pulses are polarized perpendicular to the plane of incidence and in the plane of interface (s), whereas the third IR pulse is polarized in the plane of incidence (p). In this case, the measured signal is related only to a single element of the susceptibility tensor 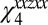 (defining
(defining 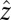 as the direction of the surface normal and the y – z plane as the incident plane), and the normalized line shape is independent of the experimental incident angles (assuming frequency-independent Fresnel factors). We also consider the ssppp signal, which is related to a linear combination of four tensor elements:
as the direction of the surface normal and the y – z plane as the incident plane), and the normalized line shape is independent of the experimental incident angles (assuming frequency-independent Fresnel factors). We also consider the ssppp signal, which is related to a linear combination of four tensor elements: 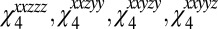 . In this case the precise linear combination depends on the incident angles and Fresnel factors (89–91) (which in turn depend on these angles and the indexes of refraction of the air, water, and interface). For this calculation we choose the incident angles of the first two IR beams to be 56° and the angle of the third IR beam to be 40° (75), and we take the indexes of refraction to be 1, 1.18, and 1.33 for air, the interface, and the liquid, respectively (91). Note that, again assuming frequency-independent Fresnel factors, the linear combination of the four tensor elements is independent of the incident angle of the visible beam.
. In this case the precise linear combination depends on the incident angles and Fresnel factors (89–91) (which in turn depend on these angles and the indexes of refraction of the air, water, and interface). For this calculation we choose the incident angles of the first two IR beams to be 56° and the angle of the third IR beam to be 40° (75), and we take the indexes of refraction to be 1, 1.18, and 1.33 for air, the interface, and the liquid, respectively (91). Note that, again assuming frequency-independent Fresnel factors, the linear combination of the four tensor elements is independent of the incident angle of the visible beam.
The interactions between light and matter can be depicted by double-sided Feynman diagrams in Liouville space (11, 53, 88). 2DSFG spectroscopy follows the same Feynman diagram pathways as 2DIR spectroscopy does, except the last incident visible light excites the system to a “virtual” electronic state (70, 78). Therefore, similarly to 2DIR spectroscopy (92), six Feynman diagram pathways are measured in the experiment, meaning six four-point time-correlation functions need to be computed. They are listed in the Postscript, as is an explicit expression for the observable Im(χ4).
In this paper we consider dilute HOD in H2O and focus on the OD stretch. We choose this system instead of HOD/D2O for two reasons: first, it is primarily H2O, which is of greater interest than D2O; and second, because the OD stretch has a longer lifetime than the OH stretch, experimentally one can obtain signals out to longer waiting times t2. To calculate spectra for dilute HOD in H2O, a simulation should in principle be performed with only one HOD water molecule in a box of H2O. However, a very long trajectory is needed to obtain adequate averaging in this case. Instead, we run a simulation of neat H2O, because the dynamics of an individual HOD molecule in H2O and that of neat H2O are almost indistinguishable (93). Then we treat each OH bond as a putative OD bond and sample over all of the H atoms. More details about the SFG spectroscopy calculations can be found in ref. 46.
The protocols for calculating the frequencies, and transition dipoles and polarizabilities, needed for such spectra have been described elsewhere (46, 94, 95). The 1–0 transition frequency maps are from ref. 94, and the dipole derivative μ′ is taken from ref. 95. The 2DSFG calculation also requires 2–1 transition maps, which have not been reported previously for the E3B model. As a result, we have fitted new ω21 and x21 maps, using the procedure discussed in ref. 94. For the E3B water model, all of the maps used in the present study are given in Table 1. As before, we make the usual approximations regarding adding lifetime effects phenomenologically (53), and we take the OD stretch lifetime to be 1.8 ps (96). The lifetime introduces only minor effects to the spectra so its precise value is not very important.
Table 1.
Electrostatic maps for the E3B water model for the 1–0 and 2–1 transition frequencies ω10 and ω21 (in cm−1), dipole derivative μ′, and 1–0 and 2–1 matrix elements of the oscillator stretching coordinate, x10 and x21, respectively (in atomic units)
| Maps | rms |
| ω10 = 2,748.2 − 2,572.2E − 1.0298 × 105E2 | (47) |
| ω21 = 2,673.0 − 1,763.5E − 1.3853 × 105E2 | (51) |
| x10 = 0.16598 − 2.0752 × 10−5ω10 | |
| x21 = 0.23167 − 2.8596 × 10−5ω21 | |
| μ′ = 0.1646 + 11.39E + 63.42E2 | (0.08) |
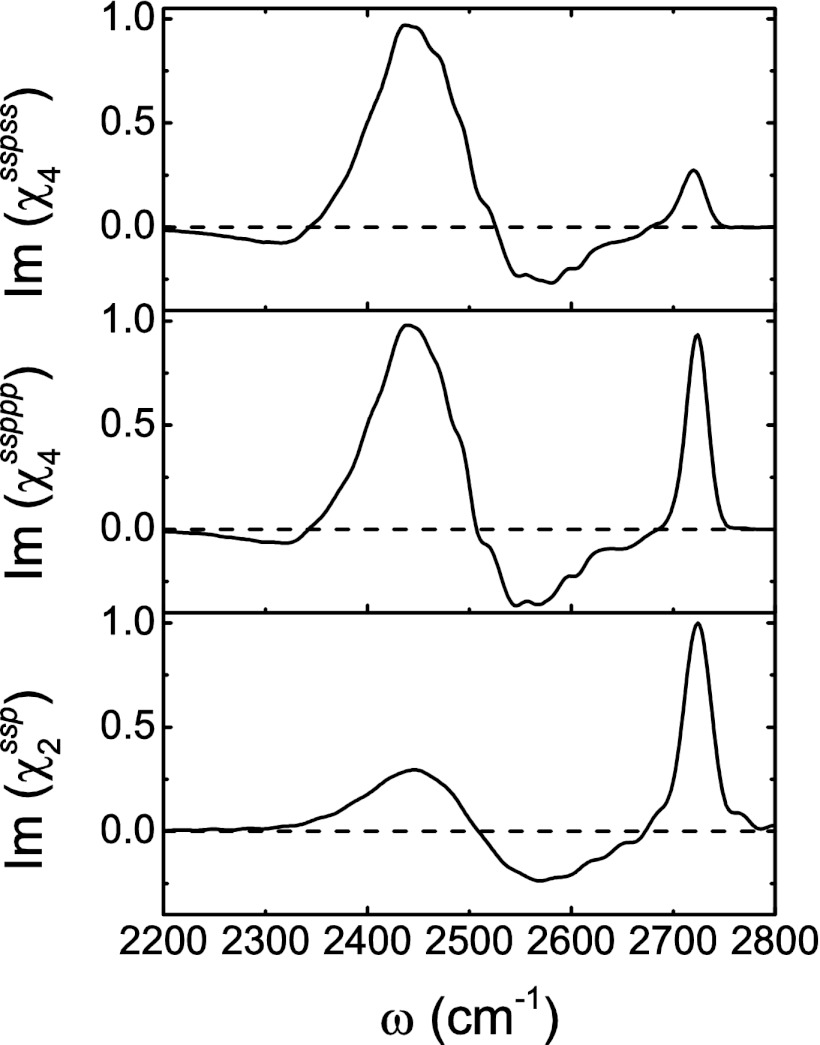
Fig. 2 displays the calculated 2DSFG spectra for waiting times of t2 = 0, 0.8, 2.4, 6, and 12 ps, for the sspss and ssppp polarizations. The spectra have been normalized to the largest (positive or negative) peak at each t2. To interpret these spectra, first consider zero waiting time, when no spectral diffusion or chemical exchange (in this case, transitions between free and hydrogen-bonded OH) takes place. In Fig. 3, the diagonal cuts (ω1 = ω3) of the two spectra are shown and compared with the (1D)SFG spectrum. The amplitude along the diagonal is qualitatively similar to the (1D)SFG spectrum (46) and has a positive peak at about 2,720 cm−1, a negative peak at about 2,575 cm−1, and a positive peak at about 2,450 cm−1. These three peaks correspond precisely to the peaks at about 3,700, 3,500, and 3,300 cm−1, respectively, for HOD/D2O, as discussed in the introductory section. Response functions 1, 2, 4, and 5 produce these peaks. In addition, response functions 3 and 6 produce the three peaks at lower frequency ω3 in Fig. 2. These three peaks come from the 1–2 transitions associated with each of the 0–1 peaks, whose frequencies are red shifted from the 0–1 transitions because of anharmonicity, and like in 2DIR, in each case they have the opposite sign from the 0–1 peaks. The spectra for the two polarization conditions are different because they involve different polarizations for the first two IR pulses. In particular, the sspss amplitude for the free OD peak at about 2,720 cm−1 is much weaker than the ssppp amplitude, because the free OD, with its propensity to point out to the vapor phase, gives a small amplitude with s-polarized (in the plane of the interface) light. However, otherwise the two spectra are qualitatively similar.
Fig. 2.
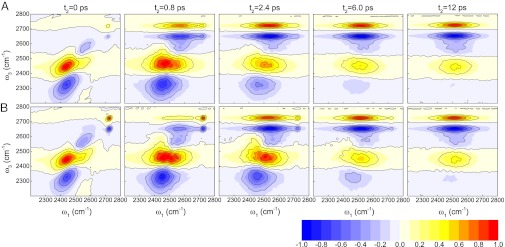
Theoretical 2DSFG spectra for HOD/H2O. The spectra correspond to waiting times t2 = 0, 0.8, 2.4, 6, and 12 ps. (A) sspss polarization; (B) ssppp polarization.
Fig. 3.
(Top) Diagonal cut of the sspss-polarized spectrum at t2 = 0 ps; (Middle) diagonal cut of the ssppp-polarized spectrum at t2 = 0 ps; (Bottom) calculated (1D)SFG spectrum with ssp polarization (46).
At the other extreme we can consider long waiting times—long enough so that the frequencies and orientations of a given OD stretch are uncorrelated at times 0 and t2. This means that each of the response functions factors into two terms. For example, R1 (Eq. 4a) becomes
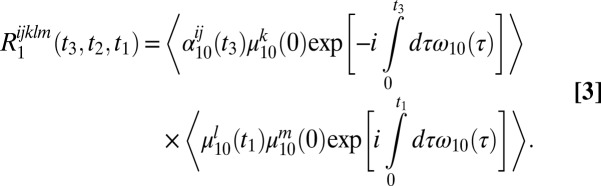 |
The consequence is that the 2DSFG line shape is essentially a product of the 1D ssp SFG line shape in the ω3 direction and the bulk liquid IR line shape in the ω1 direction. This is the case for t2 = 12 ps in Fig. 2. In addition, however, the spectrum in the ω3 direction also has the 1–2 peaks (from R3 and R6), with the appropriate signs. In this case, the 1–2 free-OD peak adds to the (negative) OD peak at about 2,575 cm−1, the 1–2 transition of this latter peak adds to the (positive) OD peak at about 2,450 cm−1, and the 1–2 transition for this latter peak is visible (and is negative) at about 2,325 cm−1. This explains why in the limit of long waiting times the 2DSFG spectrum has four alternating positive and negative bands along the ω3 axis. Also note that the sspss and ssppp 2DSFG spectra are the same in this long waiting-time limit, because the ss and pp bulk IR spectra are, of course, the same.
Finally, we can consider intermediate waiting times such that the frequencies of OD stretches have changed (due to spectral diffusion and/or chemical exchange), but the frequencies and orientations at the two times 0 and t2 are not uncorrelated. For example, on this timescale free-OD and hydrogen-bonded OD stretches may have interconverted. In a 2DIR experiment spectral diffusion is manifest as broadening of all 0–1 peaks, below and above the digaonal, whereas chemical exchange appears as cross-peaks, below and above the diagonal (53). In a 2DSFG experiment, however, this is in general not the case, because the signal is not symmetric with respect to ω1 and ω3, as discussed above. In this case, the cross-peaks are suppressed below the diagonal. For example, in Fig. 2 for t2 = 2.4 ps, both spectra show intense cross-peaks at ω1 = 2,525 cm−1 and ω3 = 2,720 cm−1. These arise from OD stretches that were hydrogen bonded at time 0, but are free ODs at time t2. However, in the cross-peak region below the diagonal (ω1 = 2,720 cm−1 and ω3 = 2,525 cm−1), the signal for the transition from free OD to hydrogen-bonded OD is difficult to observe. The important point is that the growth of the cross-peaks above the diagonal as t2 increases reports directly on the hydrogen-bond rearrangement at the surface. Indeed, one sees that the observed timescale for the growth of these peaks is similar to the surface hydrogen-bond rearrangement time of 3.7 ps as shown in Fig. 1.
Water molecules at the surface are in many different hydrogen-bonding environments. One would like to be able to understand the detailed kinetics of transitions among these environments. However, 2DSFG is an imperfect probe of such kinetics, because it labels frequencies but not necessarily environments. Moreover, as we have seen, SFG involves much cancellation of signals from different types of molecules (46), and 2DSFG involves further cancellation between 0–1 and 1–2 transitions. Therefore, the experimental situation is quite complicated. Still, one would like to know the timescale that a free OD converts into molecules that produce the negative feature [in the (1D)SFG spectrum] at 2,575 cm−1, the timescale for molecules producing the negative feature at 2,575 cm−1 to convert to those that produce the positive feature at 2,450 cm−1, etc. To this end, we have very recently tried again (97) to identify those molecules that produce the various spectral features, and we find that the largest contribution to the free-OD peak comes from 2S molecules [those with one acceptor and one donor hydrogen bond (60)], the largest contribution to the negative peak comes from hydrogen bonds between a 2S donor and a 4D acceptor (a 4D molecule has two donor and two acceptor hydrogen bonds), and the largest contribution to the positive peak at low frequency comes from hydrogen bonds between a 4D donor and a 2S acceptor.
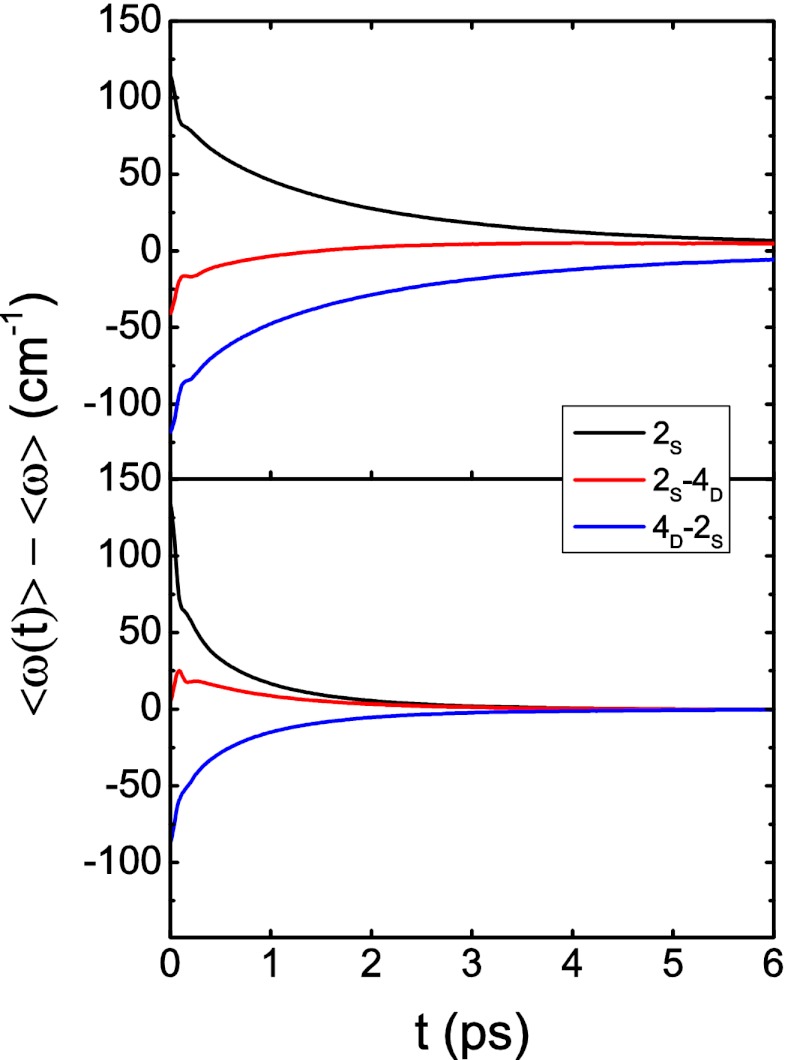
To investigate the kinetics of these three classes (2S, 2S-4D, and 4D-2S) of OD stretches, we consider molecules that are in the surface region and in one particular class at t = 0 and then calculate the nonequilibrium average frequency 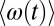 for these molecules as time evolves (but we include only those molecules that are still in the surface region at the later time t). Thus, each of these nonequilibrium averages will decay to the global (surface) average 〈ω〉 as hydrogen-bond rearrangement occurs. The results for
for these molecules as time evolves (but we include only those molecules that are still in the surface region at the later time t). Thus, each of these nonequilibrium averages will decay to the global (surface) average 〈ω〉 as hydrogen-bond rearrangement occurs. The results for 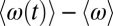 are shown in Fig. 4 (Upper). Interestingly, we see that for the 2S and 4D-2S OD stretches, the nonequilibrium averages decay monotonically to the global surface average, whereas for the 2S-4D OD stretches, the nonequilibrium average goes from below to above the global average before relaxing to equilibrium. This suggests that these 2S-4D OD stretches are first breaking the OD hydrogen bond (to become 2S molecules?) before reaching global (surface) equilibrium. In any case, we see that the timescale for evolution to the average frequency is roughly the same for all three classes, which means that there is probably only a single timescale for hydrogen-bond rearrangement at the surface. 2DSFG spectroscopy should easily be able to determine that timescale. In Fig. 4 (Lower), we also show the analogous results for bulk water, and one again clearly sees that hydrogen-bond rearrangement occurs about three times faster in the bulk than at the surface.
are shown in Fig. 4 (Upper). Interestingly, we see that for the 2S and 4D-2S OD stretches, the nonequilibrium averages decay monotonically to the global surface average, whereas for the 2S-4D OD stretches, the nonequilibrium average goes from below to above the global average before relaxing to equilibrium. This suggests that these 2S-4D OD stretches are first breaking the OD hydrogen bond (to become 2S molecules?) before reaching global (surface) equilibrium. In any case, we see that the timescale for evolution to the average frequency is roughly the same for all three classes, which means that there is probably only a single timescale for hydrogen-bond rearrangement at the surface. 2DSFG spectroscopy should easily be able to determine that timescale. In Fig. 4 (Lower), we also show the analogous results for bulk water, and one again clearly sees that hydrogen-bond rearrangement occurs about three times faster in the bulk than at the surface.
Fig. 4.
Average frequencies as a function of time for OH stretches that were in specific hydrogen-bonding environments at t = 0. (Upper) Interface (molecules must be in the surface region at both times 0 and t); (Lower) bulk.
Conclusions
The E3B model has been developed with the expectation that it will be more accurate than two-body water models for simulating water in heterogeneous environments such as the liquid/vapor interface. This model has shown promise by its ability to reproduce and interpret the (1D)SFG spectrum (46). In this paper, we use the model to investigate molecular dynamics near the interface. We find that the dynamics for hydrogen-bond rearrangement at the surface are a factor of about 3 slower than in the bulk due to the lower density of the surface.
We suggest that heterodyne-detected 2D vibrational sum-frequency generation spectroscopy of isolated HOD in H2O (D2O) may be a useful technique for the experimental measurement of hydrogen-bond rearrangement dynamics at the surface. We calculate the susceptibility for such an experiment, using the E3B model, and find that the appearance of cross-peaks between the free-OH and hydrogen-bonding regions provides a clear signature of this slow hydrogen-bond rearrangement timescale. It appears that heterodyne-detected 2DSFG spectroscopy on the water/vapor interface will be experimentally feasible in the near future. The comparison between theory and this experiment will provide more insight into the nature of the water surface.
Postscript—2DSFG Response Functions
The six 2DSFG response functions for an isolated chromophore are
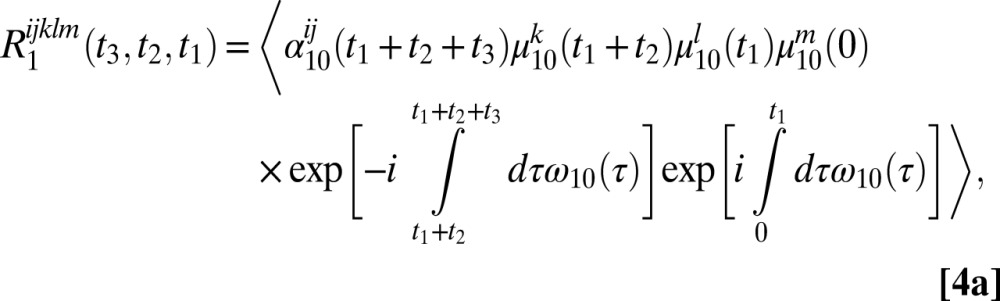 |
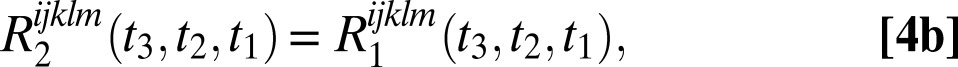 |
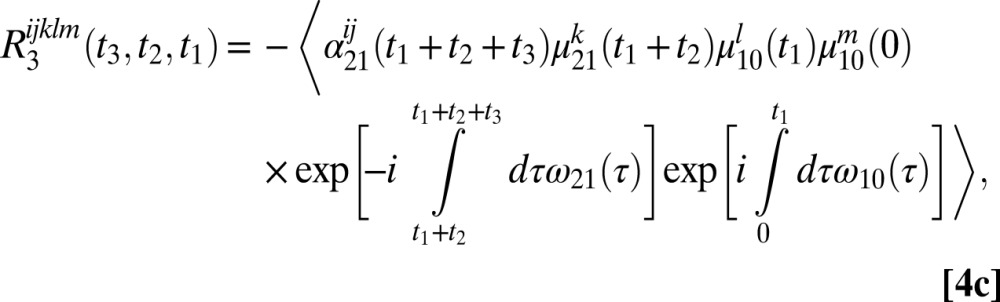 |
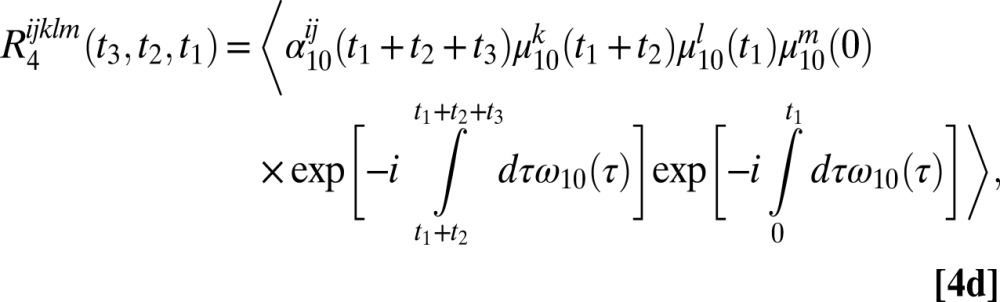 |
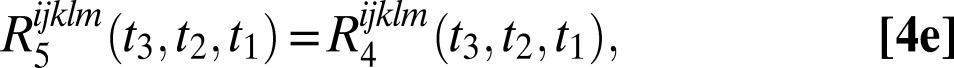 |
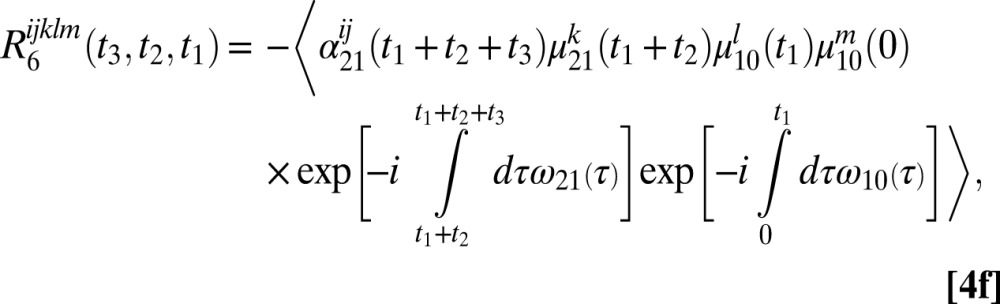 |
where 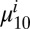 and
and 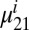 are the projections of the 1–0 and 2–1 transition dipoles along the electric field unit vector
are the projections of the 1–0 and 2–1 transition dipoles along the electric field unit vector 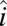 ,
, 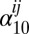 and
and 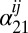 are the 1–0 and 2–1 transition polarizability tensor elements, and ω10 and ω21 are the fluctuating 1–0 and 2–1 transition frequencies. The indexes i, j, k, l, m correspond to
are the 1–0 and 2–1 transition polarizability tensor elements, and ω10 and ω21 are the fluctuating 1–0 and 2–1 transition frequencies. The indexes i, j, k, l, m correspond to 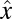 ,
, 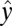 , or
, or 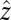 components, as described above.
components, as described above.
2DSFG and 2DIR have the same phase-matching conditions, and therefore the rephasing signal is in the 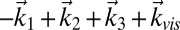 direction and the nonrephasing signal is in the
direction and the nonrephasing signal is in the 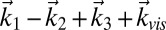 direction. The rephasing and nonrephasing response functions
direction. The rephasing and nonrephasing response functions 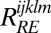 and
and 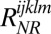 are
are
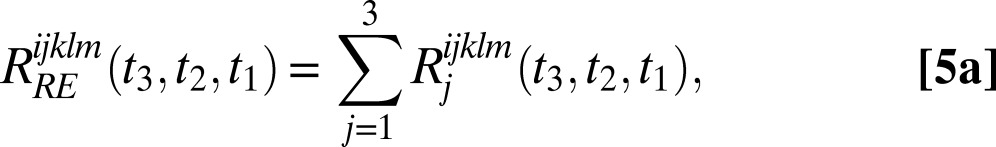 |
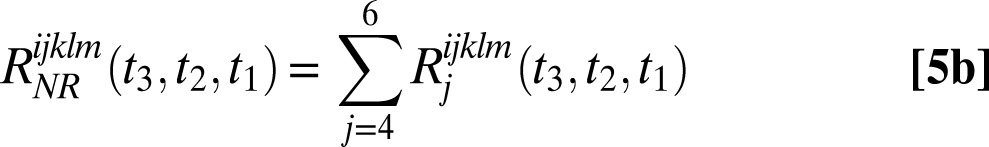 |
The final 2DSFG spectrum is calculated from Fourier transformation of the response functions in both the t1 and the t3 coherence times. The rephasing and nonrephasing parts are added together to eliminate the phase twisting effect (53) and hence generate the absorptive spectrum. Therefore, under the impulsive limit approximation (the incident laser pulses are temporal δ-functions), the 2DSFG spectrum is given by
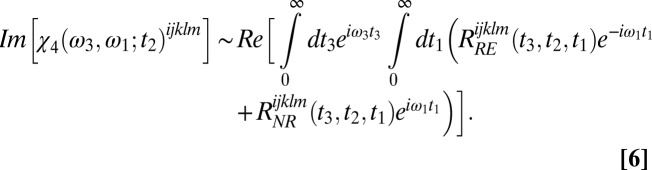 |
Acknowledgments
We acknowledge helpful conversations with Marty Zanni and Jenny Laaser and helpful correspondence with Chris Mundy and Poul Petersen. We thank the National Science Foundation through Grant CHE-1058752 for support.
Footnotes
The authors declare no conflict of interest.
References
- 1.Taylor RS, Dang LX, Garrett BC. Molecular dynamics simulations of the liquid/vapor interface of SPC/E water. J Phys Chem. 1996;100:11720–11725. [Google Scholar]
- 2.Paul S, Chandra A. Hydrogen bond dynamics at vapour-water and metal-water interfaces. Chem Phys Lett. 2004;386:218–224. [Google Scholar]
- 3.Vila Verde A, Bolhuis PG, Campen RK. Statics and dynamics of free and hydrogen-bonded OH groups at the air/water interface. J Phys Chem B. 2012;116(31):9467–9481. doi: 10.1021/jp304151e. [DOI] [PubMed] [Google Scholar]
- 4.Liu P, Harder E, Berne BJ. On the calculation of diffusion coefficients in confined fluids and interfaces with an application to the liquid-vapor interface of water. J Phys Chem B. 2004;108:6595–6602. [Google Scholar]
- 5.Liu P, Harder E, Berne BJ. Hydrogen-bond dynamics in the air-water interface. J Phys Chem B. 2005;109(7):2949–2955. doi: 10.1021/jp046807l. [DOI] [PubMed] [Google Scholar]
- 6.Kuo IFW, Mundy CJ. An ab initio molecular dynamics study of the aqueous liquid-vapor interface. Science. 2004;303(5658):658–660. doi: 10.1126/science.1092787. [DOI] [PubMed] [Google Scholar]
- 7.Kuo IFW, et al. Structure and dynamics of the aqueous liquid-vapor interface: A comprehensive particle-based simulation study. J Phys Chem B. 2006;110(8):3738–3746. doi: 10.1021/jp056330t. [DOI] [PubMed] [Google Scholar]
- 8.Baer MD, et al. Re-examining the properties of the aqueous vapor-liquid interface using dispersion corrected density functional theory. J Chem Phys. 2011;135(12):124712. doi: 10.1063/1.3633239. [DOI] [PubMed] [Google Scholar]
- 9.Kühne TD, Pascal TA, Kaxiras E, Jung Y. New insights into the structure of the vapor/water interface from large-scale first-principles simulations. J Phys Chem Lett. 2011;2:105–113. doi: 10.1021/jz101391r. [DOI] [PubMed] [Google Scholar]
- 10.Chakraborty D, Chandra A. A first principles simulation study of fluctuations of hydrogen bonds and vibrational frequencies of water at liquid-vapor interface. Chem Phys. 2012;392:96–104. [Google Scholar]
- 11.Shen YR. The Principles of Nonlinear Optics. New York: Wiley; 1984. [Google Scholar]
- 12.Boyd RW. Nonlinear Optics. 3rd Ed. Amsterdam: Elsevier; 2008. [Google Scholar]
- 13.Du Q, Superfine R, Freysz E, Shen YR. Vibrational spectroscopy of water at the vapor/water interface. Phys Rev Lett. 1993;70(15):2313–2316. doi: 10.1103/PhysRevLett.70.2313. [DOI] [PubMed] [Google Scholar]
- 14.Du Q, Freysz E, Shen YR. Surface vibrational spectroscopic studies of hydrogen bonding and hydrophobicity. Science. 1994;264(5160):826–828. doi: 10.1126/science.264.5160.826. [DOI] [PubMed] [Google Scholar]
- 15.Miranda PB, Shen YR. Liquid interfaces: A study by sum-frequency vibrational spectroscopy. J Phys Chem B. 1999;103:3292–3307. [Google Scholar]
- 16.Brown MG, Raymond EA, Allen HC, Scatena LF, Richmond GL. The analysis of interference effects in the sum frequency generation of water interfaces. J Phys Chem A. 2000;104:10220–10226. [Google Scholar]
- 17.Shultz MJ, Baldelli S, Schnitzer C, Simonelli D. Aqueous solution/air interfaces probed with sum frequency generation spectroscopy. J Phys Chem B. 2002;106:5313–5324. doi: 10.1021/jp014466v. [DOI] [PubMed] [Google Scholar]
- 18.Richmond GL. Molecular bonding and interactions at aqueous surfaces as probed by vibrational sum frequency spectroscopy. Chem Rev. 2002;102(8):2693–2724. doi: 10.1021/cr0006876. [DOI] [PubMed] [Google Scholar]
- 19.Liu D, Ma G, Levering LM, Allen HC. Vibrational spectroscopy of aqueous sodium halide solutions and air-liquid interfaces: Observation of increased interfacial depth. J Phys Chem B. 2004;108:2252–2260. [Google Scholar]
- 20.Shen YR, Ostroverkhov V. Sum-frequency vibrational spectroscopy on water interfaces: Polar orientation of water molecules at interfaces. Chem Rev. 2006;106(4):1140–1154. doi: 10.1021/cr040377d. [DOI] [PubMed] [Google Scholar]
- 21.Perry A, Neipert C, Space B, Moore PB. Theoretical modeling of interface specific vibrational spectroscopy: Methods and applications to aqueous interfaces. Chem Rev. 2006;106(4):1234–1258. doi: 10.1021/cr040379y. [DOI] [PubMed] [Google Scholar]
- 22.Gan W, Wu D, Zhang Z, Feng RR, Wang HF. Polarization and experimental configuration analyses of sum frequency generation vibrational spectra, structure, and orientational motion of the air/water interface. J Chem Phys. 2006;124(11):114705. doi: 10.1063/1.2179794. [DOI] [PubMed] [Google Scholar]
- 23.Morita A, Ishiyama T. Recent progress in theoretical analysis of vibrational sum frequency generation spectroscopy. Phys Chem Chem Phys. 2008;10(38):5801–5816. doi: 10.1039/b808110g. [DOI] [PubMed] [Google Scholar]
- 24.Fan Y, Chen X, Yang L, Cremer PS, Gao YQ. On the structure of water at the aqueous/air interface. J Phys Chem B. 2009;113(34):11672–11679. doi: 10.1021/jp900117t. [DOI] [PubMed] [Google Scholar]
- 25.Tian CS, Byrnes SJ, Han HL, Shen YR. Surface propensities of atmospherically relevant ions in salt solutions revealed by phase-sensitive sum frequency vibrational spectroscopy. J Phys Chem Lett. 2011;2:1946–1949. [Google Scholar]
- 26.Jubb AM, Hua W, Allen HC. Environmental chemistry at vapor/water interfaces: Insights from vibrational sum frequency generation spectroscopy. Annu Rev Phys Chem. 2012;63:107–130. doi: 10.1146/annurev-physchem-032511-143811. [DOI] [PubMed] [Google Scholar]
- 27.Stiopkin IV, et al. Hydrogen bonding at the water surface revealed by isotopic dilution spectroscopy. Nature. 2011;474(7350):192–195. doi: 10.1038/nature10173. [DOI] [PubMed] [Google Scholar]
- 28.Nihonyanagi S, et al. Unified molecular view of the air/water interface based on experimental and theoretical χ(2) spectra of an isotopically diluted water surface. J Am Chem Soc. 2011;133(42):16875–16880. doi: 10.1021/ja2053754. [DOI] [PubMed] [Google Scholar]
- 29.Benjamin I. Vibrational spectrum of water at the liquid/vapor interface. Phys Rev Lett. 1994;73(15):2083–2086. doi: 10.1103/PhysRevLett.73.2083. [DOI] [PubMed] [Google Scholar]
- 30.Buch V. Molecular structure and OH-stretch spectra of liquid water surface. J Phys Chem B. 2005;109(38):17771–17774. doi: 10.1021/jp052819a. [DOI] [PubMed] [Google Scholar]
- 31.Raymond EA, Tarbuck TL, Richmond GL. Isotopic dilution studies of the vapor/water interface as investigated by vibrational sum-frequency spectroscopy. J Phys Chem B. 2002;106:2817–2820. [Google Scholar]
- 32.Raymond EA, Tarbuck TL, Brown MG, Richmond GL. Hydrogen bonding interactions at the vapor/water interface investigated by vibrational sum-frequency spectroscopy of HOD/H2O/D2O mixtures and molecular dynamics simulations. J Phys Chem B. 2003;107:546–556. [Google Scholar]
- 33.Ostroverkhov V, Waychunas GA, Shen YR. New information on water interfacial structure revealed by phase-sensitive surface spectroscopy. Phys Rev Lett. 2005;94(4):046102. doi: 10.1103/PhysRevLett.94.046102. [DOI] [PubMed] [Google Scholar]
- 34.Stiopkin IV, Jayathilake HD, Bordenyuk AN, Benderskii AV. Heterodyne-detected vibrational sum frequency generation spectroscopy. J Am Chem Soc. 2008;130(7):2271–2275. doi: 10.1021/ja076708w. [DOI] [PubMed] [Google Scholar]
- 35.Ji N, Ostroverkhov V, Tian CS, Shen YR. Characterization of vibrational resonances of water-vapor interfaces by phase-sensitive sum-frequency spectroscopy. Phys Rev Lett. 2008;100(9):096102. doi: 10.1103/PhysRevLett.100.096102. [DOI] [PubMed] [Google Scholar]
- 36.Tian CS, Shen YR. Isotopic dilution study of the water/vapor interface by phase-sensitive sum-frequency vibrational spectroscopy. J Am Chem Soc. 2009;131(8):2790–2791. doi: 10.1021/ja809497y. [DOI] [PubMed] [Google Scholar]
- 37.Tian CS, Shen YR. Sum-frequency vibrational spectroscopic studies of water/vapor interfaces. Chem Phys Lett. 2009;470:1–6. [Google Scholar]
- 38.Noah-Vanhoucke J, Smith JD, Geissler PL. Toward a simple molecular understanding of sum frequency generation at air-water interfaces. J Phys Chem B. 2009;113(13):4065–4074. doi: 10.1021/jp805928h. [DOI] [PubMed] [Google Scholar]
- 39.Byrnes SJ, Geissler PL, Shen YR. Ambiguities in surface nonlinear spectroscopy calculations. Chem Phys Lett. 2011;516:115–124. [Google Scholar]
- 40.Shen YR. Basic theory of surface sum-frequency generation. J Phys Chem C. 2012;116:15505–15509. [Google Scholar]
- 41.Morita A, Hynes JT. A theoretical analysis of the sum frequency generation spectrum of the water surface. Chem Phys. 2000;258:371–390. [Google Scholar]
- 42.Morita A, Hynes JT. A theoretical analysis of the sum frequency generation spectrum of the water surface. II. Time-dependent approach. J Phys Chem B. 2002;106:673–685. [Google Scholar]
- 43.Walker DS, Richmond GL. Understanding the effects of hydrogen bonding at the vapor-water interface: Vibrational sum frequency spectroscopy of H2O/HOD/D2O mixtures studied using molecular dynamics simulations. J Phys Chem C. 2007;111:8321–8330. [Google Scholar]
- 44.Auer BM, Skinner JL. Vibrational sum-frequency spectroscopy of the liquid/vapor interface for dilute HOD in D(2)O. J Chem Phys. 2008;129(21):214705. doi: 10.1063/1.3012568. [DOI] [PubMed] [Google Scholar]
- 45.Auer BM, Skinner JL. Vibrational sum-frequency spectroscopy of the water liquid/vapor interface. J Phys Chem B. 2009;113(13):4125–4130. doi: 10.1021/jp806644x. [DOI] [PubMed] [Google Scholar]
- 46.Pieniazek PA, Tainter CJ, Skinner JL. Interpretation of the water surface vibrational sum-frequency spectrum. J Chem Phys. 2011;135(4):044701. doi: 10.1063/1.3613623. [DOI] [PubMed] [Google Scholar]
- 47.Ishiyama T, Morita A. Vibrational spectroscopic response of intermolecular orientational correlation at the water surface. J Phys Chem C. 2009;113:16299–16302. [Google Scholar]
- 48.Ishiyama T, Morita A. Analysis of anisotropic local field in sum frequency generation spectroscopy with the charge response kernel water model. J Chem Phys. 2009;131(24):244714. doi: 10.1063/1.3279126. [DOI] [PubMed] [Google Scholar]
- 49.Ishiyama T, Takahashi H, Morita A. Vibrational spectrum at a water surface: A hybrid quantum mechanics/molecular mechanics molecular dynamics approach. J Phys Condens Matter. 2012;24(12):124107. doi: 10.1088/0953-8984/24/12/124107. [DOI] [PubMed] [Google Scholar]
- 50.Kumar R, Skinner JL. Water simulation model with explicit three-molecule interactions. J Phys Chem B. 2008;112(28):8311–8318. doi: 10.1021/jp8009468. [DOI] [PubMed] [Google Scholar]
- 51.Tainter CJ, Pieniazek PA, Lin YS, Skinner JL. Robust three-body water simulation model. J Chem Phys. 2011;134(18):184501. doi: 10.1063/1.3587053. [DOI] [PubMed] [Google Scholar]
- 52.Pieniazek PA, Tainter CJ, Skinner JL. Surface of liquid water: Three-body interactions and vibrational sum-frequency spectroscopy. J Am Chem Soc. 2011;133(27):10360–10363. doi: 10.1021/ja2026695. [DOI] [PubMed] [Google Scholar]
- 53.Hamm P, Zanni M. Concepts and Methods of 2D Infrared Spectroscopy. Cambridge, UK: Cambridge Univ Press; 2011. [Google Scholar]
- 54.Asbury JB, et al. Water dynamics: Vibrational echo correlation spectroscopy and comparison to molecular dynamics simulations. J Phys Chem A. 2004;108:1107–1119. [Google Scholar]
- 55.Loparo JJ, Roberts ST, Tokmakoff A. Multidimensional infrared spectroscopy of water. I. Vibrational dynamics in two-dimensional IR line shapes. J Chem Phys. 2006;125(19):194521. doi: 10.1063/1.2382895. [DOI] [PubMed] [Google Scholar]
- 56.Loparo JJ, Roberts ST, Tokmakoff A. Multidimensional infrared spectroscopy of water. II. Hydrogen bond switching dynamics. J Chem Phys. 2006;125(19):194522. doi: 10.1063/1.2382896. [DOI] [PubMed] [Google Scholar]
- 57.Eaves JD, et al. Hydrogen bonds in liquid water are broken only fleetingly. Proc Natl Acad Sci USA. 2005;102(37):13019–13022. doi: 10.1073/pnas.0505125102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Roberts ST, Ramasesha K, Tokmakoff A. Structural rearrangements in water viewed through two-dimensional infrared spectroscopy. Acc Chem Res. 2009;42(9):1239–1249. doi: 10.1021/ar900088g. [DOI] [PubMed] [Google Scholar]
- 59.Nicodemus RA, Ramasesha K, Roberts ST, Tokmakoff A. Hydrogen bond rearrangements in water probed with temperature-dependent 2D IR. J. Phys. Chem. Lett. 2010;1:1068. [Google Scholar]
- 60.Auer BM, Kumar R, Schmidt JR, Skinner JL. Hydrogen bonding and Raman, IR, and 2D-IR spectroscopy of dilute HOD in liquid D2O. Proc Natl Acad Sci USA. 2007;104(36):14215–14220. doi: 10.1073/pnas.0701482104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ramasesha K, Roberts ST, Nicodemus RA, Mandal A, Tokmakoff A. Ultrafast 2D IR anisotropy of water reveals reorientation during hydrogen-bond switching. J Chem Phys. 2011;135(5):054509. doi: 10.1063/1.3623008. [DOI] [PubMed] [Google Scholar]
- 62.Moilanen DE, et al. Water inertial reorientation: Hydrogen bond strength and the angular potential. Proc Natl Acad Sci USA. 2008;105(14):5295–5300. doi: 10.1073/pnas.0801554105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Lin YS, Pieniazek PA, Yang M, Skinner JL. On the calculation of rotational anisotropy decay, as measured by ultrafast polarization-resolved vibrational pump-probe experiments. J Chem Phys. 2010;132(17):174505. doi: 10.1063/1.3409561. [DOI] [PubMed] [Google Scholar]
- 64.Paarmann A, Hayashi T, Mukamel S, Miller RJD. Probing intermolecular couplings in liquid water with two-dimensional infrared photon echo spectroscopy. J Chem Phys. 2008;128(19):191103. doi: 10.1063/1.2919050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Paarmann A, Hayashi T, Mukamel S, Miller RJD. Nonlinear response of vibrational excitons: Simulating the two-dimensional infrared spectrum of liquid water. J Chem Phys. 2009;130(20):204110. doi: 10.1063/1.3139003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Woutersen S, Bakker HJ. Resonant intermolecular transfer of vibrational energy in liquid water. Nature. 1999;402:507–509. [Google Scholar]
- 67.Kraemer D, et al. Temperature dependence of the two-dimensional infrared spectrum of liquid H2O. Proc Natl Acad Sci USA. 2008;105(2):437–442. doi: 10.1073/pnas.0705792105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Piatkowski L, Eisenthal KB, Bakker HJ. Ultrafast intermolecular energy transfer in heavy water. Phys Chem Chem Phys. 2009;11(40):9033–9038. doi: 10.1039/b908975f. [DOI] [PubMed] [Google Scholar]
- 69.Yang M, Li F, Skinner JL. Vibrational energy transfer and anisotropy decay in liquid water: Is the Förster model valid? J Chem Phys. 2011;135(16):164505. doi: 10.1063/1.3655894. [DOI] [PubMed] [Google Scholar]
- 70.Xiong W, Laaser JE, Mehlenbacher RD, Zanni MT. Adding a dimension to the infrared spectra of interfaces using heterodyne detected 2D sum-frequency generation (HD 2D SFG) spectroscopy. Proc Natl Acad Sci USA. 2011;108(52):20902–20907. doi: 10.1073/pnas.1115055108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.McGuire JA, Shen YR. Ultrafast vibrational dynamics at water interfaces. Science. 2006;313(5795):1945–1948. doi: 10.1126/science.1131536. [DOI] [PubMed] [Google Scholar]
- 72.Smits M, Ghosh A, Sterrer M, Müller M, Bonn M. Ultrafast vibrational energy transfer between surface and bulk water at the air-water interface. Phys Rev Lett. 2007;98(9):098302. doi: 10.1103/PhysRevLett.98.098302. [DOI] [PubMed] [Google Scholar]
- 73.Ghosh A, et al. Ultrafast vibrational dynamics of interfacial water. Chem Phys. 2008;350:23–30. [Google Scholar]
- 74.Hsieh CS, et al. Ultrafast reorientation of dangling OH groups at the air-water interface using femtosecond vibrational spectroscopy. Phys Rev Lett. 2011;107(11):116102. doi: 10.1103/PhysRevLett.107.116102. [DOI] [PubMed] [Google Scholar]
- 75.Zhang Z, Piatkowski L, Bakker HJ, Bonn M. Ultrafast vibrational energy transfer at the water/air interface revealed by two-dimensional surface vibrational spectroscopy. Nat Chem. 2011;3(11):888–893. doi: 10.1038/nchem.1158. [DOI] [PubMed] [Google Scholar]
- 76.Zhang Z, Piatkowski L, Bakker HJ, Bonn M. Communication: Interfacial water structure revealed by ultrafast two-dimensional surface vibrational spectroscopy. J Chem Phys. 2011;135(2):021101. doi: 10.1063/1.3605657. [DOI] [PubMed] [Google Scholar]
- 77.Singh PC, Nihonyanagi S, Yamaguchi S, Tahara T. Ultrafast vibrational dynamics of water at a charged interface revealed by two-dimensional heterodyne-detected vibrational sum frequency generation. J Chem Phys. 2012;137(9):094706. doi: 10.1063/1.4747828. [DOI] [PubMed] [Google Scholar]
- 78.Nagata Y, Mukamel S. Spectral diffusion at the water/lipid interface revealed by two-dimensional fourth-order optical spectroscopy: A classical simulation study. J Am Chem Soc. 2011;133(10):3276–3279. doi: 10.1021/ja110748s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. Molecular dynamics with coupling to an external bath. J Chem Phys. 1984;81:3684–3690. [Google Scholar]
- 80.Lindahl E, Hess B, van der Spoel D. Gromacs 3.0: A package for molecular simulation and trajectory analysis. J Mol Model. 2001;7:306–317. [Google Scholar]
- 81.Van Der Spoel D, et al. GROMACS: Fast, flexible, and free. J Comput Chem. 2005;26(16):1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 82.Kumar R, Schmidt JR, Skinner JL. Hydrogen bonding definitions and dynamics in liquid water. J Chem Phys. 2007;126(20):204107. doi: 10.1063/1.2742385. [DOI] [PubMed] [Google Scholar]
- 83.Lawrence CP, Skinner JL. Ultrafast infrared spectroscopy probes hydrogen-bonding dynamics in liquid water. Chem Phys Lett. 2003;369:472–477. [Google Scholar]
- 84.Lawrence CP, Skinner JL. Vibrational spectroscopy of HOD in liquid D2O. III. Spectral diffusion, and hydrogen-bonding and rotational dynamics. J Chem Phys. 2003;118:264–272. [Google Scholar]
- 85.Laage D, Hynes JT. A molecular jump mechanism of water reorientation. Science. 2006;311(5762):832–835. doi: 10.1126/science.1122154. [DOI] [PubMed] [Google Scholar]
- 86.Laage D, Hynes JT. On the molecular mechanism of water reorientation. J Phys Chem B. 2008;112(45):14230–14242. doi: 10.1021/jp805217u. [DOI] [PubMed] [Google Scholar]
- 87.Bakker HJ, Skinner JL. Vibrational spectroscopy as a probe of structure and dynamics in liquid water. Chem Rev. 2010;110(3):1498–1517. doi: 10.1021/cr9001879. [DOI] [PubMed] [Google Scholar]
- 88.Mukamel S. Principles of Nonlinear Optical Spectroscopy. New York: Oxford Univ Press; 1995. [Google Scholar]
- 89.Zhuang X, Miranda PB, Kim D, Shen YR. Mapping molecular orientation and conformation at interfaces by surface nonlinear optics. Phys Rev B. 1999;59:12632–12640. [Google Scholar]
- 90.Roke S, Bonn M, Petukhov AV. Nonlinear optical scattering: The concept of effective susceptibility. Phys Rev B. 2004;70:115106. [Google Scholar]
- 91.Wang HF, Gan W, Lu R, Rao Y, Wu BH. Quantitative spectral and orientational analysis in surface sum frequency generation vibrational spectroscopy (SFG-VS) Int Rev Phys Chem. 2005;24:191–256. [Google Scholar]
- 92.Schmidt JR, et al. Are water simulation models consistent with steady-state and ultrafast vibrational spectroscopy experiments? Chem Phys. 2007;341:143–157. [Google Scholar]
- 93.Corcelli SA, et al. Spectral diffusion in a fluctuating charge model of water. J Chem Phys. 2004;121(18):8897–8900. doi: 10.1063/1.1803532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Li F, Skinner JL. Infrared and Raman line shapes for ice Ih. I. Dilute HOD in H2O and D2O. J Chem Phys. 2010;132(20):204505. doi: 10.1063/1.3430518. [DOI] [PubMed] [Google Scholar]
- 95.Shi L, Gruenbaum SM, Skinner JL. Interpretation of IR and Raman line shapes for H2O and D2O ice Ih. J Phys Chem B. 2012;116(47):13821–13830. doi: 10.1021/jp3059239. [DOI] [PubMed] [Google Scholar]
- 96.Kropman MF, Nienhuys HK, Woutersen S, Bakker HJ. Vibrational relaxation and hydrogen-bond dynamics of HDO:H2O. J Phys Chem A. 2001;105:4622–4626. [Google Scholar]
- 97.Tainter CJ, Ni Y, Shi L, Skinner JL. Hydrogen bonding and OH-stretch spectroscopy in water: Hexamer (cage), liquid surface, liquid, ice. J Phys Chem Lett. 2013;4:12–17. doi: 10.1021/jz301780k. [DOI] [PubMed] [Google Scholar]