Abstract
Myxococcus xanthus is a bacterium capable of complex social organization. Its characteristic social (“S”)-motility mechanism is mediated by type IV pili (TFP), linear actuator appendages that propel the bacterium along a surface. TFP are known to bind to secreted exopolysaccharides (EPS), but it is unclear how M. xanthus manages to use the TFP-EPS technology common to many bacteria to achieve its unique coordinated multicellular movements. We examine M. xanthus S-motility, using high-resolution particle-tracking algorithms, and observe aperiodic stick–slip movements. We show that they are not due to chemotaxis, but are instead consistent with a constant TFP-generated force interacting with EPS, which functions both as a glue and as a lubricant. These movements are quantitatively homologous to the dynamics of earthquakes and other crackling noise systems. These systems exhibit critical behavior, which is characterized by a statistical hierarchy of discrete “avalanche” motions described by a power law distribution. The measured critical exponents from M. xanthus are consistent with mean field theoretical models and with other crackling noise systems, and the measured Lyapunov exponent suggests the existence of highly branched EPS. Such molecular architectures, which are common for efficient lubricants but rare in bacterial EPS, may be necessary for S-motility: We show that the TFP of leading “locomotive” cells initiate the collective motion of follower cells, indicating that lubricating EPS may alleviate the force generation requirements on the lead cell and thus make S-motility possible.
Keywords: biofilm, proteobacteria, sociomicrobiology, twitching, tribology
The soil bacterium myxococcus xanthus is an advanced Gram-negative bacterium that is capable of highly organized social behavior (1). For example, M. xanthus can form predatory “wolf packs” to prey on other species, and under starvation conditions, they can self-organize into macroscopic fruiting bodies to ensure community survival (2). This rudimentary social behavior (3) relies on the gliding ability to move in the direction of the cell’s long axis on solid surfaces, which is regulated by the adventurous (“A”)- and social (“S”)-motility systems (4). As two distinct motility systems, A-motility allows movement of individual and isolated cells, whereas S-motility controls the coordinated motility of large numbers of cells. S-motility in M. xanthus is mechanistically equivalent to the twitching motilities in Pseudomonas aeruginosa and Neisseria gonorrheae (5), which are all driven by type IV pili (TFP) (6). TFP are located at the two bacterial poles and propel the cell by cycles of extension, attachment, and retraction (7, 8). Recently it has been shown that TFP are used to sense the exopolysaccharides (EPS) that are secreted by other cells onto the cell body or the surface (9, 10), which enables M. xanthus to coordinate movement along EPS tracks. Although only one pole is piliated at a time, bacteria are known to reverse direction by disassembling the TFP apparatus on the pole and reassembling it at the other one (11). This reversal behavior, which is driven by chemotaxis, allows cells to retrace their paths and form fruiting bodies (12, 13), which incorporate significant concentrations of EPS within their structures (14, 15). Although it is clear that this coupling between TFP and EPS is critical to the formation of structured fruiting bodies by M. xanthus, it is not known how M. xanthus TFP-EPS technology allows it to achieve its unique coordinated multicellular movements (15, 16), given that TFP and EPS exist in a variety of bacterial species (17) that do not exhibit S-motility.
Because M. xanthus S-motility involves TFP pulling the bacterium along surfaces with heterogeneous coverages of EPS, friction is expected to play an important role. Recently, theoretical models for frictional motion on surfaces have been shown to be widely applicable to slowly sheared materials, ranging from the deformation of slowly sheared nanocrystals to the slip dynamics along geological faults via earthquakes (18–27). These systems exhibit “stick–slip” movement with broadly distributed slip sizes. Theoretical “crackling noise” models show that the observed slip statistics can be used to obtain information about the system. In this work, we first compare the observed slip statistics to crackling noise model predictions and then find a description of the system that is consistent with them. We then use the slip statistics to extract information about the EPS and other properties of the system. S-motility of M. xanthus is known to be slow compared with the motility of other bacterial species and is usually studied using time-lapse microscopy. To get the required data for theoretical comparisons, we do the opposite and investigate the S-motility of M. xanthus on a surface at 250-ms resolution with particle-tracking algorithms (28–30).
Results and Discussion
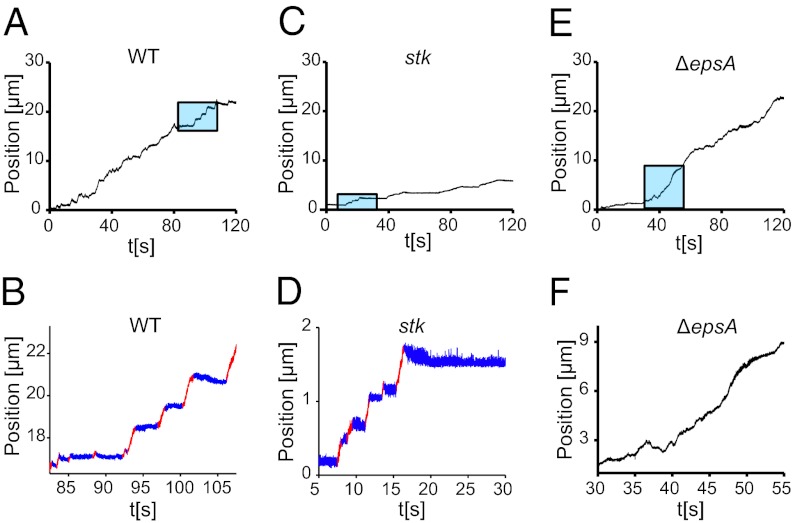
From a visual examination of motile M. xanthus bacteria undergoing TFP-dependent single-cell S-motility, which has been reviewed extensively (1, 6, 7, 9, 10, 13, 31, 32), we see that their trajectories are not smooth, but are characterized by intermittent, aperiodic stick–slip motion; similar “burst” behavior has been observed in other biological systems (33, 34). An example plot of the bacterial displacement is composed of distinct “slips”, where the bacterium moves rapidly, separated by plateaus where the bacterium “sticks” to the surface and appears stationary (Fig. 1 A and B). In a sequence of images evenly spaced in time, the motion appears uneven (Fig. S1). Unlike P. aeruginosa, which exhibits different dynamics at the leading and the lagging pole (30), moving M. xanthus bacteria show little asymmetry between their leading and lagging poles, and so we analyze the trajectory of the bacterial midpoint. In a single slip, the bacterium can move up to several microns; short slips of just above the detection limit (∼0.1 μm) are also observed. The observed duration of individual slips varies from ∼0.01 s to several seconds. Interestingly, the motion is not unidirectional; after a slip, a bacterium may move backward (seen most clearly in Fig. 1 B and D), indicating that there is viscoelastic relaxation in the system. The stick–slip motion found in the wild-type (WT) DK1622 (6) is also observed in the DK3088 (stk) strain that overproduces EPS (35), even though the magnitude of motions is much smaller in the latter case (Fig. 1 C and D). However, stick–slip motion is suppressed in the SW810 (∆epsA) strain (Fig. 1 E and F), which underproduces EPS (9). This strain is still able to move and be stationary on the surface, but does not produce a distinct separation between plateaus and slips. We find that the slips in the WT and stk strains are analogous to the avalanches observed in other crackling noise systems (24). As the TFP exert a force on the bacterium, the trajectory is broken into distinct slips by the friction-like interaction between the cell surface and the substrate, mediated by an EPS layer.
Fig. 1.
Sticks and slips in M. xanthus movement. (A) The trajectory of the centroid of an individual WT cell. The section in the blue box is expanded in B; at a small scale, the trajectory can be broken down into distinct plateaus (blue) and slips (red). These are small compared with the bacterial size. A small backward motion can be discerned at the transition from a slip to a plateau (blue to red) in some of the slips (Methods). (C) The stk mutant that overproduces EPS moves at a lower average velocity. A small section is expanded in D; it displays distinct plateaus and slips. (E and F) The trajectory of the ∆epsA mutant (E) that underproduces EPS (F) has a different appearance on a small scale, with distinct plateaus and slips appearing less frequently.
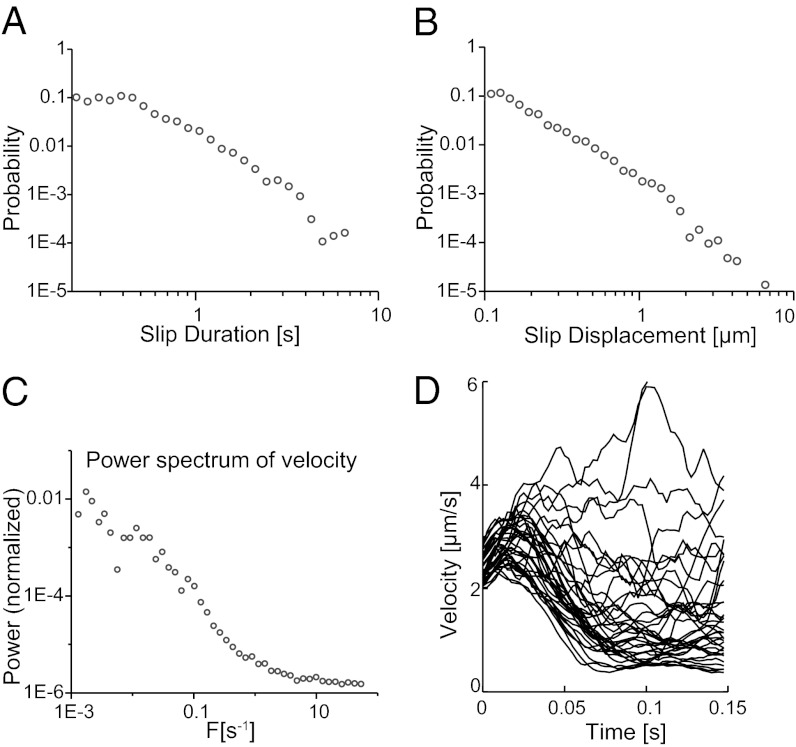
To quantitatively compare the crackling noise model to the M. xanthus system, we algorithmically separate the trajectories into distinct plateaus and slips and examine the distributions of displacements and durations of these slips, as well as the velocities during a slip. The slips are analogous to crackling noise “avalanches”. Many experimental crackling noise systems, especially small systems that exhibit avalanche behavior, exhibit only 1–1.5 decades of power law scaling due to their finite size (36–38). Moreover, we expect any manifestation of crackling noise power laws to be strongly modified by the inherent complexity of a biological system, such as the influence of signaling, or possible variable output of the TFP molecular motor. Surprisingly, power law scaling survives in the M. xanthus system and is observed in the slip duration (Fig. 2A) and slip displacement (Fig. 2B) distributions. However, the apparent slip duration power law breaks down above a cutoff value. Likewise, the power spectrum of the velocity (Fig. 2C) also breaks down above a cutoff frequency. As a useful consistency check, it is interesting to note that these cutoff values correspond closely to typical TFP pull durations (∼4 s) and TFP lengths (∼5 μm) (6, 8).
Fig. 2.
Power law scaling of slips in M. xanthus motion. (A) The distribution of slip durations follows a power law, with an exponent of 2.3. This breaks down at low durations due to the displacement of a single short slip being below the imaging resolution. (B) The distribution of slip displacements follows a power law, with an exponent of 2.0. (C) The power spectrum of the velocity has an exponent of 1.7, with a plateau at high frequency (>1 Hz). (D) A selection of trajectories that start with similar initial velocities and their accelerations quickly diverge due to the chaotic nature of the system.
Given that the number of decades of observable power law behavior is necessarily small, we subject the measured slip distributions to a series of quantitative tests, based on comparisons to a mean field theory of friction. Qualitatively, the contact area between a bacterium and the substrate is modeled as an array of patches, each of which has an individual random slip threshold, taken from a distribution of such thresholds. It can be formally shown that the exact shape and width of the random distribution are not important for the slip statistics on long length scales (22, 24, 39). As the pili retract, the force on each of these patches increases until eventually a weak patch on the contact surface slips. Elastic interactions between the patches on the surface then lead to an increase in the force on the other patches, which can be so large that it causes other patches to slip as well. By the same mechanism, these patches trigger additional slips, resulting in a slip avalanche, which we observe as a single slip of the whole system. This simple model can be solved analytically in mean field theory, using the approximation that every patch interacts equally strongly with every other patch in the system. Mean field theories have been shown to correctly predict the correct avalanche size distributions, duration distributions, and exponent relations for slip statistics on surfaces coupled by full 3D elasticity, as well as the power spectra of the velocity time trace and average temporal avalanche profile, as a function of parameters such as forcing rate and substrate properties (22, 39). The model predicts values of the exponents for the displacement, duration, and power spectrum of velocity and a quantitative relation between these exponents (Table 1), which can be tested against experimental results.
Table 1.
Comparison of exponents observed in M. xanthus to other systems
| Crystal deformation | Earthquake dynamics | M. xanthus behavior | Mean field value | |
| Slip displacement, τ | 1.4–1.6 | 1.3–2.5 | 1.9–2.2 | 3/2 |
| Slip duration, α | — | ∼2 | 2.2–2.6 | 2 |
| Power spectrum of velocity, 1/(σνz) | 2 | 1.8–3.4 | 1.5–1.8 | 2 |
| Exponent relation: |(τ + σνz − 1)/(σνz) – α| | — | — | 0.2–0.5 | 0 |
The measured power law exponents for displacement, duration, and power spectrum of velocity compare well with theoretical crackling noise predictions from mean field models, such as those used to describe friction between two sheared surfaces, and the exponents observed for other crackling noise systems (23, 24, 40–44) (Table 1). We observe slip displacement distribution exponents between 1.9 and 2.2, within the 1.3–2.5 range previously observed for earthquakes and similar to the mean field predictions of 3/2 [or 2, depending on the details of the model (18)]. The slip duration distribution exponent is 2.2–2.6, similar to the mean field prediction of 2. The decay exponent of the power spectrum of the velocity is 1.5–1.8, again similar to the mean field prediction of 2 (24). These measurements provide an excellent test of current theoretical descriptions for crackling noise and allow a variety of exponents to be calculated.
Importantly, the observed general scaling relation between exponents (Table 1) demonstrates self-consistency between the measured quantities. The agreement of multiple observed exponents with the crackling noise model and their internal consistency provides strong support for treating the data as a crackling noise system over the observed range and validates the treatment of the trajectory as a sequence of plateaus and slips. The broad agreement between our experiments and the crackling noise model suggests that M. xanthus motions are derived from a constant TFP-generated force acting against friction. The agreement also implies that the frictional interaction in M. xanthus must take place over the two-dimensional interface between the bacterium and the surface and not just at the leading or lagging pole as in the case of P. aeruginosa (30).
To elucidate the source of the crackling noise behavior, we compare the power law exponents observed for WT M. xanthus with the exponents observed for several mutant strains (Table 2). The mutant strains SW2070 (∆frzD) and SW2071 (∆frzE), which have previously observed defects in chemotaxis-driven reversal behavior (13, 45), have exponents quite similar to those of the WT; moreover, their exponents are the same despite the mutations having opposite effects on reversal behavior, with the ∆frzD strain being a hyperreverser that changes direction every 2.2 min and the ∆frzE strain being reversal deficient and reversing once every 2 h (13). This indicates that the power law exponents do not depend on the chemotactic behavior of M. xanthus and are not influenced by changes on the bacterial reversal timescale of minutes.
Table 2.
Comparison of exponents observed in different M. xanthus mutant strains
| WT | ∆frzD | ∆frzE | stk | ∆epsA | |
| Slip displacement, τ | 1.9–2.2 | 2.0–2.2 | 1.9–2.3 | 1.8–2.0 | 1.3–1.7 |
| Slip duration, α | 2.2–2.6 | 2.3–2.5 | 2.3–2.6 | 2.0–2.4 | 1.4–1.8 |
| Power spectrum of velocity, 1/(σνz) | 1.5–1.8 | 1.7–2.2 | 1.6–2.2 | 1.3–1.7 | 0.9–1.2 |
The EPS overproducer (stk) and the chemotaxis mutants (∆frzD, ∆frzE) all have power law exponents similar to that of the WT. All three indicator exponents for the EPS-deficient strain (∆epsA) are significantly different from the values for the EPS-competent strains, indicating that the presence of EPS produced by M. xanthus is critical for the crackling noise scaling, whereas chemotaxis is not.
To test whether EPS was implicated in the observed exponents, we examined the ∆epsA strain, which is defective in EPS production (9), and the stk strain, which overproduces EPS (35). The EPS overproducer has a lower average velocity than the WT, and individual slips are shorter (Fig. 1 A–D). However, it exhibits very similar crackling noise exponents to the WT, indicating that the frictional interaction is preserved. In contrast, the observed exponent signature of plateaus and slips is suppressed for the EPS underproducer, although its average velocity is similar to the WT. Its stops and starts do not exhibit the characteristic crackling noise exponents observed in the other strains (Table 2). Thus, the crackling noise power laws result from the interaction between the bacterial body and the EPS-covered surface as the bacterium is pulled along by its TFP. This is consistent with crackling noise models in general, in which stick–slip movements are generated by the competition between long-range elastic interactions on the surface, which favors long slips, and heterogeneity in surface contacts, which favors short slips.
Interestingly, we find that the EPS secreted by M. xanthus acts as much like a lubricant as it does like a glue; TFP-driven M. xanthus movement on EPS-covered glass involves the shearing of two smooth surfaces separated by a lubricant, differing from other crackling noise systems like earthquakes. Previously, thin lubricant films of branched hydrocarbons sheared between smooth surfaces have been shown to exhibit chaotic stick–slip behavior, as well as smooth sliding and periodic stick–slip regimes (46). Experiments with hydrocarbon lubricants of linear architecture or those with no lubricants (dry friction) exhibit only periodic stick–slip and smooth sliding. The chaotic stick–slip regime is characterized by irregular, aperiodic velocity oscillations and has been associated with the presence of large, multimolecular domains in an architecturally complex lubricant having a broad band of relaxation times. The TFP-driven stick–slip motions that we observe in M. xanthus span ∼1.5 orders of magnitude in dynamic range before being interrupted by the motility cycle. To determine whether the system exhibits chaotic behavior, we calculate a Lyapunov exponent from these bacterial trajectories (47). We find that the maximal Lyapunov exponent is ∼2.2, indicating that the behavior is indeed chaotic because the exponent is positive and greater than 1 (Fig. 2D). The presence of this chaotic regime suggests that M. xanthus EPS behaves like highly branched molecules, similar to the branched hydrocarbon lubricants that exhibit chaotic stick–slip behavior between smooth surfaces; simpler lubricants do not exhibit this regime. Highly branched molecules are known to be the best low-friction lubricant fluids (48), and it is believed that the reason for this is their inability to pack efficiently at a molecular scale, which gives them a tendency to remain liquid-like instead of “freezing” into solid-like ordered arrangements when confined between two shearing microscopically smooth surfaces (49–51). However, although characterization of bacterial EPS distributions is complex, it is known that highly branched EPS is rare in bacteria (52).
To support these dynamical measurements, we perform a glycosyl composition analysis of purified M. xanthus EPS. As shown in Table S1, the four primary sugars found in the sample were glucose (34.1%), rhamnose (21.9%), mannose (16.0%), and N-acetyl glucosamine (12.0%). Additionally, arabinose, xylose, galactose, and N-acetyl mannosamine were identified but in amounts less than 10%. The analysis also reveals a complex molecule containing a variety of linkages and indicating that the polysaccharide has a number of branches (Table S2). These data suggest that the M. xanthus EPS is a carbohydrate with at least three different types of branches and four different terminating residues. This is consistent with our dynamical findings that also suggested a complex, branched structure for M. xanthus EPS.
The M. xanthus system exhibits several interesting deviations from theoretical crackling noise predictions. A plot of the slip duration against the slip displacement (Fig. 3A) has a slope which is near 1, significantly different from the theoretical value of 2 (53). Additionally, the characteristic velocity profiles for the wide range of observed slips deserve comment. Mean field theory predicts that this velocity profile should be scale invariant and therefore maintain the same shape for all slips. We calculate this profile by rescaling all slips and calculating the average velocity at different time points along the slip and find a subtle difference from the expected behavior. We find instead two characteristic shapes for the large number of slips observed, one for short and one for long slips (Fig. 3B) (24, 37, 38, 54, 55). Slips that are short (<1 s) exhibit a slightly asymmetric shape; although the mean field model predicts a symmetric shape, similar asymmetric avalanche shapes have also been observed in other crackling noise systems (53, 56). However, long slips (>1 s) have a significantly more uniform velocity profile (37). Both of these deviations can be caused either by short slips overlapping in time and merging into long slips, such as due to excessive force generation, or by the slips reaching a peak velocity. We distinguish between these explanations by examining a histogram of the velocities over individual slips (Fig. 3C), which has a distinct peak and does not exhibit power law scaling as predicted by mean field theories, even in the high-velocity tail of the histogram, despite the power law scaling of the displacement and duration individually. The average slip velocity is 0.4 µm/s; this is similar to the retraction velocity of individual M. xanthus TFP, which has been measured as 0.7 µm/s when exerting a force of 60 pN and as 0.2 µm/s when exerting a force of 150 pN (8). We hypothesize that the peak velocity over an individual slip may be limited by the retraction velocity of the TFP motor in M. xanthus, where it exerts a force of 60–150 pN. That slips exhibit self-similar behavior in their velocity profiles, however, is a striking and stringent indication of crackling noise behavior.
Fig. 3.
Deviations from crackling noise behavior. (A) The slip duration vs. displacement plot has an exponent of 1.0, differing from the predicted exponent of 2. (B) Short slips (<1 s, red) have a slightly left-skewed shape (24) and long slips (>1 s, blue) are more uniform. These observations can be explained by the TFP reaching a maximum retraction velocity during individual slips. (C) The histogram of slip velocities exhibits a peak at 0.4 μm/s, consistent with previously measured retraction velocities of individual TFP (8).
The social behavior of M. xanthus can be examined in the context of this observed stick–slip motion, which is exquisitely sensitive to coordination between cells. We imaged bacteria at cell densities where a range of surface-to-surface distances between bacteria are observed, from cell–cell contact to distances comparable to the bacterial length. We located paired bacteria by visually finding cells that maintained a low end-to-end separation (<4 μm) while moving over a long distance (>25 μm). Pairs of bacteria are able to attach end-to-end and move together, with an interbacterial separation of less than 0.2 μm (Fig. 4A). In contrast with this strong coupling, we also observed pairs of bacteria moving along similar trajectories, with interbacterial surface-to-surface separations of 1–4 μm (Fig. 4B). To quantify the spatiotemporal signatures of how pairs of bacteria follow one another during the initiation of social interactions, we calculate the frequency-dependent velocity–velocity correlation between the motions of two paired bacteria. Bacterial motion was first projected onto a straight line. For each frequency bin, we apply a bandpass filter to remove the contributions from all other frequencies; then, the correlation between the velocities of the two bacteria could be calculated directly for each frequency bin as 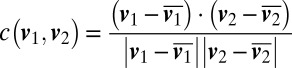 , where
, where  and
and 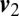 are the frequency-filtered velocity sequences. For bacteria that are in end-to-end contact, there is strong correlation at low frequencies (<1 Hz) that progressively decays at higher frequencies (Fig. 4C). It is interesting to note that for bacteria that are within ∼4 μm, velocity correlations qualitatively similar to those in the case of end-to-end contact are observed, although they are significantly weaker (Fig. 4D). We hypothesize that some of the interactions that act at cell–cell contact already exist at such distances. A fraction of these cell pairs move beyond this initial exploratory engagement and eventually transition to cell–cell contact, so that M. xanthus social interactions occur in a series of “handshaking” steps that involve different mechanical coupling at different distances, progressing from cells that simply follow the same EPS-directed path to those that progressively link and eventually “dock”.
are the frequency-filtered velocity sequences. For bacteria that are in end-to-end contact, there is strong correlation at low frequencies (<1 Hz) that progressively decays at higher frequencies (Fig. 4C). It is interesting to note that for bacteria that are within ∼4 μm, velocity correlations qualitatively similar to those in the case of end-to-end contact are observed, although they are significantly weaker (Fig. 4D). We hypothesize that some of the interactions that act at cell–cell contact already exist at such distances. A fraction of these cell pairs move beyond this initial exploratory engagement and eventually transition to cell–cell contact, so that M. xanthus social interactions occur in a series of “handshaking” steps that involve different mechanical coupling at different distances, progressing from cells that simply follow the same EPS-directed path to those that progressively link and eventually “dock”.
Fig. 4.
Social movement of M. xanthus. (A) A pair of bacteria can move together when attached end-to-end. (Scale bar, 5 μm.) (B) Velocities of bacteria in such pairs are correlated in a frequency-dependent manner up to a frequency of 1 Hz. (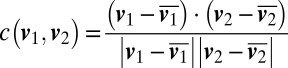 .) (C) Bacteria can also follow each other at small distances. (Scale bar, 5 μm.) (D) However, in this case, their velocities have significantly lower correlation. (E) For attached bacteria, there is a strong correlation in slip times (blue); unattached bacteria show no such correlation in slip times (red). The peak correlation for attached bacteria is at a delay of 50 ms (Upper Inset), indicating that, on average, the leading bacterium has its slips 0.05 s before the lagging bacterium.
.) (C) Bacteria can also follow each other at small distances. (Scale bar, 5 μm.) (D) However, in this case, their velocities have significantly lower correlation. (E) For attached bacteria, there is a strong correlation in slip times (blue); unattached bacteria show no such correlation in slip times (red). The peak correlation for attached bacteria is at a delay of 50 ms (Upper Inset), indicating that, on average, the leading bacterium has its slips 0.05 s before the lagging bacterium.
There has been significant effort aimed at understanding whether the two coupled cells contribute equally to motility and how the dynamics of the coupled cells are coordinated (32). The stick–slip behavior allows us to access this directly. We calculate the correlation between slip times of the leading and lagging bacterium as  , where
, where 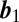 and
and  are sequences that are equal to 1 when the bacterium is in a slip and 0 otherwise. We extend this to a time-dependent correlation by shifting
are sequences that are equal to 1 when the bacterium is in a slip and 0 otherwise. We extend this to a time-dependent correlation by shifting  in time (Fig. 4E). For bacteria in end-to-end contact, this correlation reaches a peak of 0.4; for unattached bacteria, this stays less than 0.1. Importantly, we find that the correlation peak is not centered at zero, but at a lag time of ∼50 ms. By a Granger causality analysis (57), we confirm that for bacteria in end-to-end contact, the motion of the leading cell Granger causes the motion of the lagging cell (P = 0.00003, the P value of the statistical test); for unattached bacteria, Granger causality is not detectable (P = 0.47). These observations show unambiguously that not only do the coupled bacteria move with coordinated slips, but also there is a “locomotive” cell that leads a trailing cell, with the lead cell initiating the motion. This is direct evidence indicating that the TFP of the lead cell pull both cells and determine the trajectory of the pair. The force generation requirements on the locomotive cell become increasingly stringent for the multiply entrained cells observed in late-stage M. xanthus S-motility. This suggests that our observation of lubricating behavior in M. xanthus EPS is an enabling factor in S-motility. That some M. xanthus EPS can have a lubricating function explains the puzzling observation that more EPS often lead to more motility, rather than less motility, as would be the case if EPS were to function only as a “glue”. For example, the highly motile cells that actively drive fruiting body formation move in the presence of high concentrations of EPS (15, 16). M. xanthus alone among bacteria is capable of S-motility. This observation is consistent with the empirical fact that highly branched EPS is rare for bacteria and indicates that small changes in TFP-EPS technology can lead to qualitative differences in bacterial social organization.
in time (Fig. 4E). For bacteria in end-to-end contact, this correlation reaches a peak of 0.4; for unattached bacteria, this stays less than 0.1. Importantly, we find that the correlation peak is not centered at zero, but at a lag time of ∼50 ms. By a Granger causality analysis (57), we confirm that for bacteria in end-to-end contact, the motion of the leading cell Granger causes the motion of the lagging cell (P = 0.00003, the P value of the statistical test); for unattached bacteria, Granger causality is not detectable (P = 0.47). These observations show unambiguously that not only do the coupled bacteria move with coordinated slips, but also there is a “locomotive” cell that leads a trailing cell, with the lead cell initiating the motion. This is direct evidence indicating that the TFP of the lead cell pull both cells and determine the trajectory of the pair. The force generation requirements on the locomotive cell become increasingly stringent for the multiply entrained cells observed in late-stage M. xanthus S-motility. This suggests that our observation of lubricating behavior in M. xanthus EPS is an enabling factor in S-motility. That some M. xanthus EPS can have a lubricating function explains the puzzling observation that more EPS often lead to more motility, rather than less motility, as would be the case if EPS were to function only as a “glue”. For example, the highly motile cells that actively drive fruiting body formation move in the presence of high concentrations of EPS (15, 16). M. xanthus alone among bacteria is capable of S-motility. This observation is consistent with the empirical fact that highly branched EPS is rare for bacteria and indicates that small changes in TFP-EPS technology can lead to qualitative differences in bacterial social organization.
By examining the dynamics of M. xanthus cells at fast timescales, we are able to observe the aperiodic stick–slip movements that are caused by the TFP-generated force acting against EPS-derived friction. At timescales shorter than the motility cycle (the time required for typical TFP pulls), the movements of M. xanthus cells are consistent with a crackling noise model, which has been previously applied to the dynamics of earthquakes (23) and a variety of other nonbiological systems (24, 25). We measure critical exponents for the M. xanthus system and find that they are consistent with mean field theoretical models of crackling noise and with other crackling noise systems (26, 27); additionally, by examining the ∆frzD and ∆frzE mutants, which have defects in reversal behavior, we confirm that the sticks and slips are unaffected by the chemotactic decisions of the bacterium. Interestingly, although EPS is usually thought of as a molecular glue, we find that EPS of M. xanthus can both promote surface adhesion and also function as a lubricant. To analyze the lubricating properties of EPS we estimate the degree of chaos in the system by calculating a Lyapunov exponent and find that it suggests the existence of highly branched EPS, similar to artificial lubricants but different from the EPS of most other bacteria. We hypothesize that this is necessary for S-motility: We show that the TFP of leading locomotive cells initiate the collective motion of follower cells, whose motions lag behind those of the lead cell by ∼50 ms. The unique lubricating properties of M. xanthus EPS may alleviate the force generation requirements on the lead cell and thus make coordinated social motility possible.
Methods
Cell Tracking.
M. xanthus cells were transferred onto a glass slide, overlaid with Mops buffer containing 1% methylcellulose, and recorded at 30 °C (7); these conditions suppress adventurous motility and promote TFP-driven S-motility even in isolated cells and not just aggregates. The cells were given 30–60 min to attach to the surface and initiate S-motility. Thirty-second recordings with a wide field of view (>100 visible bacteria) were taken to identify cells that were motile and not stationary; then, longer movies (2–10 min) of individual motile cells were recorded. Movies were acquired at 400 frames per second, using a Phantom V12.1 camera (Vision Research) on an Olympus microscope with a 60× objective, resulting in images with a resolution of 0.2 μm per pixel. Each image was smoothed by applying a spatial bandpass filter with background subtraction, reducing the bacteria to bright objects on a black background; then a brightness threshold criterion was used to identify them. The centroid position and orientation of each bacterium were calculated from the moments of the backbone distribution (28, 29, 58), and tracking was done using a minimum squared-displacement criterion (59). As M. xanthus moves and changes direction slowly, the leading and lagging poles of the bacterium exhibited the same dynamics as the centroid; the position of the centroid was used as the bacterial position for subsequent analysis.
The noise level of the system was determined by examining an immobile bacterium; position measurements of an immobile bacterium varied by ∼0.2 μm, the width of one pixel. Averaging the position over multiple frames (boxcar smoothing) was used to improve spatial accuracy, at the cost of giving up fast-timescale information. To eliminate high-frequency noise in the velocity and position measurements, the trajectory was first smoothed with a boxcar average of width 0.05 s. At each point in the trajectory, the velocity was calculated as 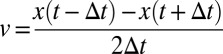 , using ∆t = 0.05 s. Slips were identified by their peak velocity; sections of the trajectory where the smoothed velocity remained below the noise threshold (0.1 μm/s) were labeled as plateaus, whereas sections of the trajectory where the velocity remained higher than the noise threshold were labeled as slips. To calculate the power spectrum of the velocity, segments of the trajectory identified as plateaus were excised; the magnitude of the velocity was calculated at each remaining trajectory point, using the unsmoothed data and a ∆t of 0.0025 s. The fast Fourier transform of this signal was squared to give the power spectrum and then binned logarithmically, and the slope was calculated using a least-squares fit.
, using ∆t = 0.05 s. Slips were identified by their peak velocity; sections of the trajectory where the smoothed velocity remained below the noise threshold (0.1 μm/s) were labeled as plateaus, whereas sections of the trajectory where the velocity remained higher than the noise threshold were labeled as slips. To calculate the power spectrum of the velocity, segments of the trajectory identified as plateaus were excised; the magnitude of the velocity was calculated at each remaining trajectory point, using the unsmoothed data and a ∆t of 0.0025 s. The fast Fourier transform of this signal was squared to give the power spectrum and then binned logarithmically, and the slope was calculated using a least-squares fit.
For each slip, we calculated the displacement as ∆x = xf
− xi, where xi and xf are the positions before and after the slip, respectively; likewise, we calculated the duration as ∆t = tf
− ti, where ti and tf are the start and end times of the slip. The distributions of slip displacements and durations were binned logarithmically for plotting. The power law exponents for these quantities were calculated directly without fitting via 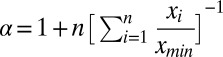 , where the xi are the data points within the power law region (60).
, where the xi are the data points within the power law region (60).
The above calculations were repeated with different parameters to ensure that observed trends were due to physical effects and not analysis artifacts; changing the smoothing widths to ∆t = 0.1 s or ∆t = 0.2 s as well as velocity thresholds to 0.075 μm/s or 0.125 μm/s affected the calculated exponents by 0.1 or less and did not disrupt the power law scaling.
It is worthwhile to point out that a “backward” movement can be discerned after some of the slips. We hypothesize that these movements indicate the existence of a finite a relaxation time in the EPS on the surface and suggest that we may be able to extract more information on the polymeric nature of EPS by using secretion mutants. For the purposes of the present work, we repeated the slip distribution analysis with the postslip backward motion counted as part of the slip and alternately as part of the plateau. We found that the resultant effects on the slip duration and displacement distributions are not large enough to affect the measured exponents.
We calculate the Lyapunov exponent from the sequences of bacterial velocities as follows (47). The program keeps track of an initial point p(i), which is initialized to be the first point on the first bacterial trajectory. Then, the program finds a second point p(j), which may be on the trajectory of a different bacterium, with a similar velocity, differing from the velocity at p(i) by 0.05 μm/s; it looks ahead by ∆t = 0.25 s, comparing the magnitude of the final velocity difference between the two trajectories ∆vf to the initial velocity difference ∆vi and updating the running average of 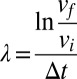 . The next p(i) is selected to be similar, in velocity and direction, to p(i + ∆t), but differing by at least 0.05 μm/s, and the procedure is repeated. This converges to the maximal Lyapunov exponent of the system.
. The next p(i) is selected to be similar, in velocity and direction, to p(i + ∆t), but differing by at least 0.05 μm/s, and the procedure is repeated. This converges to the maximal Lyapunov exponent of the system.
M. xanthus EPS Purification and Analysis.
Wild-type M. xanthus (DK1622) EPS was isolated and purified following a protocol modified from two different sources (61, 62). After overnight incubation to log phase in casitone yeast extract (CYE) liquid medium (63) the bacteria were spread onto five large CYE plates (∼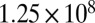 cells per plate) and allowed to grow for 3 d at 32 °C. The cells were then scraped off the plates into 0.9% NaCl solution (∼10 mL per plate). Phenol was added to a final concentration of 5% (vol/vol) and stirred for 5 h at 4 °C. The cells and debris were removed by centrifugation and the EPS was then precipitated from the supernatant with 4 vol of isopropanol. After centrifugation, the pellet was redissolved in water. The precipitation and resuspension were repeated three times. The resulting product was dialyzed first against 0.1 M NaCl and then against water. The EPS solution was lyophilized.
cells per plate) and allowed to grow for 3 d at 32 °C. The cells were then scraped off the plates into 0.9% NaCl solution (∼10 mL per plate). Phenol was added to a final concentration of 5% (vol/vol) and stirred for 5 h at 4 °C. The cells and debris were removed by centrifugation and the EPS was then precipitated from the supernatant with 4 vol of isopropanol. After centrifugation, the pellet was redissolved in water. The precipitation and resuspension were repeated three times. The resulting product was dialyzed first against 0.1 M NaCl and then against water. The EPS solution was lyophilized.
Glycosyl analysis of lyophilized EPS was performed by combined gas chromatography/mass spectrometry (GC/MS) of the per-O-trimethylsilyl (TMS) derivatives of the monosaccharide methyl glycosides produced from the sample by acidic methanolysis (64). For determination of glycosyl linkages, the sample was permethylated, depolymerized, reduced, and acetylated; and the resultant partially methylated alditol acetates (PMAAs) were analyzed by GC/MS.
Supplementary Material
Acknowledgments
We thank Ann Lu and the University of Georgia Complex Carbohydrate Research Center for technical assistance on analyzing glycosyl composition and linkages of M. xanthus EPS. This research was funded by the National Science Foundation (DMR11-06106 and DMR10-05209), the National Institutes of Health (NIH) (1R01HL087920 and NIH GM54666), and the Center for the Physics of Living Cells (PHYS-082261 and PHYS-0822613).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1215089110/-/DCSupplemental.
References
- 1.Kaplan HB. Multicellular development and gliding motility in Myxococcus xanthus. Curr Opin Microbiol. 2003;6(6):572–577. doi: 10.1016/j.mib.2003.10.006. [DOI] [PubMed] [Google Scholar]
- 2.Shimkets LJ. Social and developmental biology of the myxobacteria. Microbiol Rev. 1990;54(4):473–501. doi: 10.1128/mr.54.4.473-501.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dworkin M. Recent advances in the social and developmental biology of the myxobacteria. Microbiol Rev. 1996;60(1):70–102. doi: 10.1128/mr.60.1.70-102.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hodgkin J, Kaiser D. Genetics of gliding motility in Myxococcus xanthus (Myxobacterales): Two gene systems control movement. Mol Gen Genet. 1979;171(2):177–191. [Google Scholar]
- 5.Mattick JS. Type IV pili and twitching motility. Annu Rev Microbiol. 2002;56(1):289–314. doi: 10.1146/annurev.micro.56.012302.160938. [DOI] [PubMed] [Google Scholar]
- 6.Kaiser D. Social gliding is correlated with the presence of pili in Myxococcus xanthus. Proc Natl Acad Sci USA. 1979;76(11):5952–5956. doi: 10.1073/pnas.76.11.5952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sun H, Zusman DR, Shi W. Type IV pilus of Myxococcus xanthus is a motility apparatus controlled by the frz chemosensory system. Curr Biol. 2000;10(18):1143–1146. doi: 10.1016/s0960-9822(00)00705-3. [DOI] [PubMed] [Google Scholar]
- 8.Clausen M, Jakovljevic V, Søgaard-Andersen L, Maier B. High-force generation is a conserved property of type IV pilus systems. J Bacteriol. 2009;191(14):4633–4638. doi: 10.1128/JB.00396-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lu A, et al. Exopolysaccharide biosynthesis genes required for social motility in Myxococcus xanthus. Mol Microbiol. 2005;55(1):206–220. doi: 10.1111/j.1365-2958.2004.04369.x. [DOI] [PubMed] [Google Scholar]
- 10.Li Y, et al. Extracellular polysaccharides mediate pilus retraction during social motility of Myxococcus xanthus. Proc Natl Acad Sci USA. 2003;100(9):5443–5448. doi: 10.1073/pnas.0836639100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nudleman E, Wall D, Kaiser D. Polar assembly of the type IV pilus secretin in Myxococcus xanthus. Mol Microbiol. 2006;60(1):16–29. doi: 10.1111/j.1365-2958.2006.05095.x. [DOI] [PubMed] [Google Scholar]
- 12.McBride MJ, Weinberg RA, Zusman DR. “Frizzy” aggregation genes of the gliding bacterium Myxococcus xanthus show sequence similarities to the chemotaxis genes of enteric bacteria. Proc Natl Acad Sci USA. 1989;86(2):424–428. doi: 10.1073/pnas.86.2.424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Blackhart BD, Zusman DR. “Frizzy” genes of Myxococcus xanthus are involved in control of frequency of reversal of gliding motility. Proc Natl Acad Sci USA. 1985;82(24):8767–8770. doi: 10.1073/pnas.82.24.8767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shimkets LJ. Role of cell cohesion in Myxococcus xanthus fruiting body formation. J Bacteriol. 1986;166(3):842–848. doi: 10.1128/jb.166.3.842-848.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lux R, Li Y, Lu A, Shi W. Detailed three-dimensional analysis of structural features of Myxococcus xanthus fruiting bodies using confocal laser scanning microscopy. Biofilms. 2004;1(04):293–303. [Google Scholar]
- 16.Hendrata M, Yang Z, Lux R, Shi W. Experimentally guided computational model discovers important elements for social behavior in myxobacteria. PLoS ONE. 2011;6(7):e22169. doi: 10.1371/journal.pone.0022169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sutherland IW. Biofilm exopolysaccharides: A strong and sticky framework. Microbiology. 2001;147(Pt 1):3–9. doi: 10.1099/00221287-147-1-3. [DOI] [PubMed] [Google Scholar]
- 18.Friedman N, et al. Statistics of dislocation slip avalanches in nanosized single crystals show tuned critical behavior predicted by a simple mean field model. Phys Rev Lett. 2012;109(9):095507. doi: 10.1103/PhysRevLett.109.095507. [DOI] [PubMed] [Google Scholar]
- 19.Ben-Zion Y, Rice JR, Dmowska R. Interaction of the San Andreas fault creeping segment with adjacent great rupture zones and earthquake recurrence at Parkfield. J Geophys Res. 1993;98:2135–2144. [Google Scholar]
- 20.Ben-Zion Y, Rice JR. Slip patterns and earthquake populations along different classes of faults in elastic solids. J Geophys Res. 1995;100(B7):12959–12983. [Google Scholar]
- 21.Ben-Zion Y. Stress, slip, and earthquakes in models of complex single-fault systems incorporating brittle and creep deformations. J Geophys Res. 1996;101(B3):5677–5706. [Google Scholar]
- 22.Fisher DS, Dahmen K, Ramanathan S, Ben-Zion Y. Statistics of earthquakes in simple models of heterogeneous faults. Phys Rev Lett. 1997;78(25):4885–4888. [Google Scholar]
- 23.Ben-Zion Y, Eneva M, Liu Y. Large earthquake cycles and intermittent criticality on heterogeneous faults due to evolving stress and seismicity. J Geophys Res. 2003;108(B6):2307. [Google Scholar]
- 24.Sethna JP, Dahmen KA, Myers CR. Crackling noise. Nature. 2001;410(6825):242–250. doi: 10.1038/35065675. [DOI] [PubMed] [Google Scholar]
- 25.Travesset A, White RA, Dahmen KA. Crackling noise, power spectra, and disorder-induced critical scaling. Phys Rev B. 2002;66(2):024430. [Google Scholar]
- 26.Sethna JP, et al. Hysteresis and hierarchies: Dynamics of disorder-driven first-order phase transformations. Phys Rev Lett. 1993;70(21):3347–3350. doi: 10.1103/PhysRevLett.70.3347. [DOI] [PubMed] [Google Scholar]
- 27.Houle PA, Sethna JP. Acoustic emission from crumpling paper. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1996;54(1):278–283. doi: 10.1103/physreve.54.278. [DOI] [PubMed] [Google Scholar]
- 28.Conrad JC, et al. Flagella and pili-mediated near-surface single-cell motility mechanisms in P. aeruginosa. Biophys J. 2011;100(7):1608–1616. doi: 10.1016/j.bpj.2011.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gibiansky ML, et al. Bacteria use type IV pili to walk upright and detach from surfaces. Science. 2010;330(6001):197. doi: 10.1126/science.1194238. [DOI] [PubMed] [Google Scholar]
- 30.Jin F, Conrad JC, Gibiansky ML, Wong GCL. Bacteria use type-IV pili to slingshot on surfaces. Proc Natl Acad Sci USA. 2011;108(31):12617–12622. doi: 10.1073/pnas.1105073108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hu W, et al. Exopolysaccharide-independent social motility of Myxococcus xanthus. PLoS ONE. 2011;6(1):e16102. doi: 10.1371/journal.pone.0016102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhang Y, Ducret A, Shaevitz J, Mignot T. From individual cell motility to collective behaviors: Insights from a prokaryote, Myxococcus xanthus. FEMS Microbiol Rev. 2012;36(1):149–164. doi: 10.1111/j.1574-6976.2011.00307.x. [DOI] [PubMed] [Google Scholar]
- 33.Neuman KC, Abbondanzieri EA, Landick R, Gelles J, Block SM. Ubiquitous transcriptional pausing is independent of RNA polymerase backtracking. Cell. 2003;115(4):437–447. doi: 10.1016/s0092-8674(03)00845-6. [DOI] [PubMed] [Google Scholar]
- 34.Svoboda K, Schmidt CF, Schnapp BJ, Block SM. Direct observation of kinesin stepping by optical trapping interferometry. Nature. 1993;365(6448):721–727. doi: 10.1038/365721a0. [DOI] [PubMed] [Google Scholar]
- 35.Dana JR, Shimkets LJ. Regulation of cohesion-dependent cell interactions in Myxococcus xanthus. J Bacteriol. 1993;175(11):3636–3647. doi: 10.1128/jb.175.11.3636-3647.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Colaiori F. Exactly solvable model of avalanches dynamics for Barkhausen crackling noise. Adv Phys. 2008;57(4):287–359. [Google Scholar]
- 37.Papanikolaou S, et al. Universality beyond power laws and the average avalanche shape. Nat Phys. 2011;7(4):316–320. [Google Scholar]
- 38.Dahmen KA, Ben-Zion Y, Uhl JT. A simple analytic theory for the statistics of avalanches in sheared granular materials. Nat Phys. 2011;7(7):554–557. [Google Scholar]
- 39.Dahmen KA, Ben-Zion Y, Uhl JT. Micromechanical model for deformation in solids with universal predictions for stress-strain curves and slip avalanches. Phys Rev Lett. 2009;102(17):175501. doi: 10.1103/PhysRevLett.102.175501. [DOI] [PubMed] [Google Scholar]
- 40.Ben-Zion Y, Lyakhovsky V. Analysis of aftershocks in a lithospheric model with seismogenic zone governed by damage rheology. Geophys J Int. 2006;165(1):197–210. [Google Scholar]
- 41.Ben-Zion Y, Dahmen K, Uhl J. A unifying phase diagram for the dynamics of sheared solids and granular materials. Pure Appl Geophys. 2011;168(12):2221–2237. [Google Scholar]
- 42.Zaiser M. Scale invariance in plastic flow of crystalline solids. Adv Phys. 2006;55(1–2):185–245. [Google Scholar]
- 43.Miguel MC, Vespignani A, Zapperi S, Weiss J, Grasso J-R. Intermittent dislocation flow in viscoplastic deformation. Nature. 2001;410(6829):667–671. doi: 10.1038/35070524. [DOI] [PubMed] [Google Scholar]
- 44.Csikor FF, Motz C, Weygand D, Zaiser M, Zapperi S. Dislocation avalanches, strain bursts, and the problem of plastic forming at the micrometer scale. Science. 2007;318(5848):251–254. doi: 10.1126/science.1143719. [DOI] [PubMed] [Google Scholar]
- 45.Shi W, Yang Z, Sun H, Lancero H, Tong L. Phenotypic analyses of frz and dif double mutants of Myxococcus xanthus. FEMS Microbiol Lett. 2000;192(2):211–215. doi: 10.1111/j.1574-6968.2000.tb09384.x. [DOI] [PubMed] [Google Scholar]
- 46.Drummond C, Israelachvili J. Dynamic phase transitions in confined lubricant fluids under shear. Phys Rev E Stat Nonlin Soft Matter Phys. 2001;63(4 Pt 1):041506. doi: 10.1103/PhysRevE.63.041506. [DOI] [PubMed] [Google Scholar]
- 47.Wolf A, Swift JB, Swinney HL, Vastano JA. Determining Lyapunov exponents from a time series. Physica D. 1985;16(3):285–317. [Google Scholar]
- 48.Gee ML, McGuiggan PM, Israelachvili JN, Homola AM. Liquid to solidlike transitions of molecularly thin films under shear. J Chem Phys. 1990;93(3):1895–1906. [Google Scholar]
- 49.Israelachvili JN. Adhesion forces between surfaces in liquids and condensable vapours. Surf Sci Rep. 1992;14(3):109–159. [Google Scholar]
- 50.Kamei D, et al. Computational chemistry study on the dynamics of lubricant molecules under shear conditions. Tribol Int. 2003;36(4–6):297–303. [Google Scholar]
- 51.Cui ST, Cummings PT, Cochran HD. Effect of branches on the structure of narrowly confined alkane fluids: n-hexadecane and 2,6,11,15-tetramethylhexadecane. J Chem Phys. 2001;114(14):6464–6471. [Google Scholar]
- 52.Dumitriu S. Polysaccharides: Structural Diversity and Functional Versatility. New York: Marcel Dekker; 2005. [Google Scholar]
- 53.Mehta AP, Dahmen KA, Ben-Zion Y. Universal mean moment rate profiles of earthquake ruptures. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;73(5 Pt 2):056104. doi: 10.1103/PhysRevE.73.056104. [DOI] [PubMed] [Google Scholar]
- 54.Kuntz MC, Sethna JP. Noise in disordered systems: The power spectrum and dynamic exponents in avalanche models. Phys Rev B. 2000;62(17):11699–11708. [Google Scholar]
- 55.Mehta AP, Mills AC, Dahmen KA, Sethna JP. Universal pulse shape scaling function and exponents: Critical test for avalanche models applied to Barkhausen noise. Phys Rev E Stat Nonlin Soft Matter Phys. 2002;65(4 Pt 2A):046139. doi: 10.1103/PhysRevE.65.046139. [DOI] [PubMed] [Google Scholar]
- 56.Zapperi S, Castellano C, Colaiori F, Durin G. Signature of effective mass in crackling-noise asymmetry. Nat Phys. 2005;1(1):46–49. [Google Scholar]
- 57.Seth AK. A MATLAB toolbox for Granger causal connectivity analysis. J Neurosci Methods. 2010;186(2):262–273. doi: 10.1016/j.jneumeth.2009.11.020. [DOI] [PubMed] [Google Scholar]
- 58.Mohraz A, Solomon MJ. Direct visualization of colloidal rod assembly by confocal microscopy. Langmuir. 2005;21(12):5298–5306. doi: 10.1021/la046908a. [DOI] [PubMed] [Google Scholar]
- 59.Crocker JC, Grier DJ. Methods of digital video microscopy for colloidal studies. J Colloid Interface Sci. 1996;179:298–310. [Google Scholar]
- 60.Newman MEJ. Power laws, Pareto distributions and Zipf’s law. Contemp Phys. 2005;46(5):323–351. [Google Scholar]
- 61.Cescutti P, et al. Exopolysaccharides produced by a clinical strain of Burkholderia cepacia isolated from a cystic fibrosis patient. Carbohydr Res. 2003;338(23):2687–2695. doi: 10.1016/s0008-6215(03)00384-7. [DOI] [PubMed] [Google Scholar]
- 62.Sutherland IW, Thomson S. Comparison of polysaccharides produced by Myxococcus strains. J Gen Microbiol. 1975;89(1):124–132. doi: 10.1099/00221287-89-1-124. [DOI] [PubMed] [Google Scholar]
- 63.Campos JM, Geisselsoder J, Zusman DR. Isolation of bacteriophage MX4, a generalized transducing phage for Myxococcus xanthus. J Mol Biol. 1978;119:167–178. doi: 10.1016/0022-2836(78)90431-x. [DOI] [PubMed] [Google Scholar]
- 64.McNeil M, Darvill AG, Åman P, Franzén LE, Albersheim P. Structural analysis of complex carbohydrates using high-performance liquid chromatography, gas chromatography, and mass spectrometry. Methods Enzymol. 1982;83:3–45. doi: 10.1016/0076-6879(82)83003-6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.