Elasticity and wrinkled morphology of Bacillus subtilis pellicles

Abstract

Wrinkled morphology is a distinctive phenotype observed in mature biofilms produced by a great number of bacteria. Here we study the formation of macroscopic structures (wrinkles and folds) observed during the maturation of Bacillus subtilis pellicles in relation to their mechanical response. We show how the mechanical buckling instability can explain their formation. By performing simple tests, we highlight the role of confining geometry and growth in determining the symmetry of wrinkles. We also experimentally demonstrate that the pellicles are soft elastic materials for small deformations induced by a tensile device. The wrinkled structures are then described by using the equations of elastic plates, which include the growth process as a simple parameter representing biomass production. This growth controls buckling instability, which triggers the formation of wrinkles. We also describe how the structure of ripples is modified when capillary effects are dominant. Finally, the experiments performed on a mutant strain indicate that the presence of an extracellular matrix is required to maintain a connective and elastic pellicle.

Bacterial biofilms most often refer to communities that self-assemble into a cohesive extracellular matrix on solid surfaces or as pellicles floating on top of liquids. Bacteria self-organize in a collective behavior, giving a large-scale coherence to the system. Biofilms thus represent a protected life mode allowing bacteria to survive in hostile environments and from where they can disperse to colonize new niches (1, 2). A primary characteristic of biofilm formation is the production of exopolymeric substances by some cells. These substances mostly consists of exopolysaccharides (EPS), a few specific proteins, and nucleic acids (3–5), but their exact composition depends on the strain of the bacterium and the type of nutrients present in the culture medium (6, 7). When studied in a laboratory, wild-type strains of Bacillus subtilis are known to produce floating pellicles of rich and complex multiscale architectures (8, 9). The vertical structures range from the local 50-μm-scale “fruiting bodies” (10) to the extended macroscopic patterns illustrated in Fig. 1. As recently suggested in ref. 11, multiscale roughness could play a role in increasing the defense capability of B. subtilis against vapor and liquid antimicrobial agents.

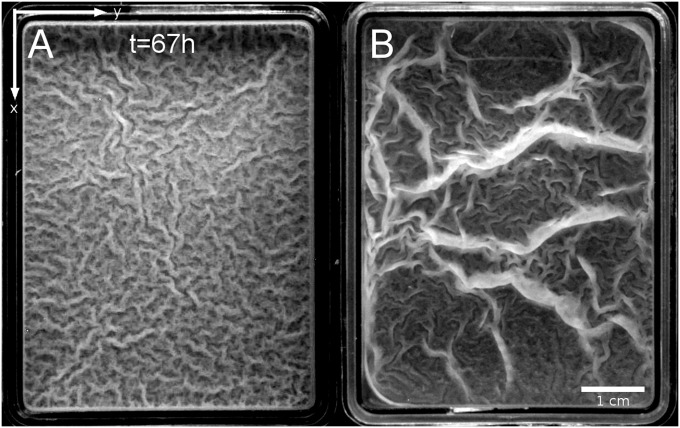
Fig. 1.

Top view of two wild-type B. subtilis pellicles floating on top of liquid culture media after ∼67 h of incubation at 23 °C. (A) NCIB 3610 wild-type strain. (B) DV1 wild-type strain. Grayscale images.

This study centers on the physical forces acting on biofilm and determining their morphologies at the macroscopic scale. To proceed, we restrict our experimental approach to the simplified case where macroscopic pellicles stand on rich static media. We primarily focus on the pellicles formed by the wild-type strain NCIB 3610, but present some features measured on another wild-type strain DV1 to obtain a more complete picture of existing morphologies. Of course the phenotypes are even more complex in nature given the possible multistrain and species coassembly and the diversity of settings and environments.

The two typical phenotypes illustrated in Fig. 1 present intriguing resemblances to patterns and other labyrinth structures reported in various compressed elastic systems (e.g., membranes, synthetic gels, and tissues) (12–15). We propose here that this macroscopic morphology is a consequence of a buckling mechanical instability, as in other systems, and is triggered by growth in a confined space, which strains and hence stresses the pellicles. The growth generates an inner compressive stress able to exceed the critical value of the buckling transition. We first describe the macroscopic emergent structures and then examine the case where periodic parallel undulations of well-defined wavelengths stand up under uniaxial confinement. We also set up a specific device to measure the elastic response of the pellicles and to estimate its elastic constant. The experimental data are then compared with the theoretical expectations of the buckling model. The model allows us to understand the millimeter-length scale of the structures; a comparison with the theoretical prediction hints at the presence of a thin effective elastic layer within the pellicle. Different wavelengths are also observed near the edges, suggesting the contribution of capillary forces to equilibrium as observed in other submicrometer plates (16). This study demonstrates how mechanics can shape biofilms as in many living systems, from plants to animal tissues (17–19).

Results and Discussion

Emergent Vertical Structures.

Fig. 1 illustrates two phenotypes where the vertical structures are different: Fig. 1A shows a typical B. subtilis NCIB 3610 pellicle that exhibits numerous small quasi-periodic undulations (wrinkles), whereas Fig. 1B shows the presence of large vertical structures of localized curvature (folds) coexisting with wrinkles on a DV1 strain pellicle. In the following, we focus our analysis on the wrinkles formation in NCIB 3610 strain; the presence of folds is discussed thereafter. Following the pellicle development (Materials and Methods), we first observe a flat, uniform, yet confined pellicle, suggesting that the growth process is homogeneous and isotropic. Then wrinkles spontaneously arise without any specific symmetry, as observed in the mature state (Fig. 1A). The typical wavelength λ_b of these skeletal wrinkles can be directly measured from the images using fast Fourier transformation (FFT) methods: we obtain ∼1.3 mm in the example illustrated in SI Text, Image Analysis and Wavelength Measurement, and typically 1−2 mm on different biofilms. As shown in SI Text, Temperature and Enriched Medium, the wavelength is not sensitive to the temperature but becomes λ_b ∼3 mm in a twice-enriched medium.

Note that all these structures are not observed in the mutants defective in EPS production (3610 epsA-0::tet). In agreement with a previous finding (5), we observe that the mutant cannot form a macroscopic floating pellicle even after 5 d of incubation.

Morphology in Open and Confined Spaces.

In Fig. 1A, the wrinkled structure is branchy and looks like the labyrinth patterns observed when thin elastic plates set onto solid substrates are biaxially compressed (14, 15, 20). In our geometry, pellicles are confined into rectangular containers whose edges can define the two axes (x, y) of confinement. To understand the key role played by the confinement during the bulk wrinkles formation, we simply cut off the system to change the confinement geometry. In the past, such a process allowed Fung (21) to point out experimentally that the growth process can be modeled by a residual stress in many tissues. We first isolate a square piece of flat pellicle by removing all of the surrounding matter and observe the small portion of pellicle growing homogeneously without any further wrinkle. When we isolate a piece of weakly wrinkled pellicle, it returns to its undeformed flat initial shape. These observations provide direct evidence that the wrinkles originate from growth in a confined space; for small deformations, an elastic-like behavior restores the wrinkled pellicle to its initial flat state.

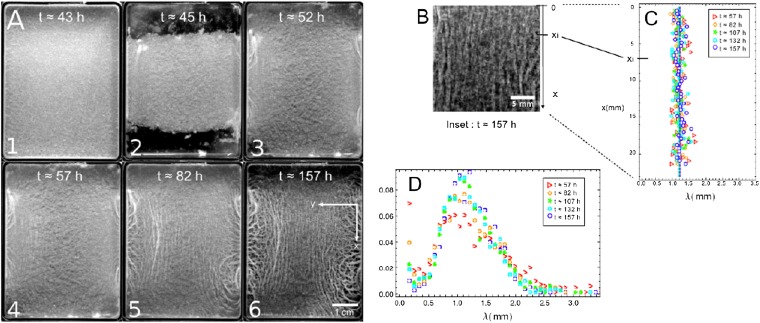
To create an uniaxial symmetry on the final biofilm structure, we cut off and remove the two shorter edges of the pellicle before it starts to wrinkle, 45 h after the bacteria inoculation (Fig. 2 A1 and A2). We thus release the geometrical constraint along the x direction, and the compression is then quasi-uniaxial even though the system grows in both directions. The final structure in Fig. 2 A5 and A6 is then completely different from the biaxially confined pellicle (Fig. 1A). Two types of wrinkles are now clearly visible: (i) the quasi-parallel wrinkles emerging in the bulk and (ii) the wrinkles developed near the edges, which are discussed in another section. Bulk wrinkles align along the x direction perpendicular to the confinement axis y or to the inner compression; this situation is similar to the case of synthetic elastic floating thin films subject to uniaxial mechanical compression (12, 22, 23); their amplitude increases with the incubation time. It is interesting to consider a central part of the grayscale images (Fig. 2B) and measure the wavelengths of these bulk wrinkles along the x direction (Fig. 2C; SI Text, Image Analysis and Wavelength Measurement). Surprisingly, the wavelength turns out to be constant and depends on neither location nor incubation time. A normalized distribution profile of the wrinkles is illustrated in Fig. 2D, and becomes maximal when λ_b = 1.2 mm, with 0.9 mm FWHM. Note that the profiles present a high value at very short distances, especially in the early stages; we interpret this maximum as the signature of the grainy texture in Fig. 2A. If we repeat the same experiment on different biofilms, the wavelength ranges from 1.2 to 2 mm.

Fig. 2.

Evolution of a severed B. subtilis NCIB 3610 pellicle over 7 d in biofilm medium at room temperature (Materials and Methods). (A) The image sequence shows the formation and evolution of quasi-parallel wrinkles in the bulk of the pellicle. (A1) At t ∼43 h: intermediate stage of an initially flat thin pellicle floating on top of liquid. (A2) At t ∼44 h, we carefully remove two strips ∼1.0 cm wide at the shorter edges from the initial pellicle before it wrinkles. (A3) This pellicle continues growing and covers the entire surface at t ∼52 h. (A4) As the growth process is constrained along the y direction, parallel wrinkles arise in the center of the pellicle (t ∼57 h). (A5 and A6) Subsequent evolution after wrinkles formation. (B) Grayscale-magnified image of the bulk wrinkles extracted from A6. (C) As detailed in SI Text, Image Analysis and Wavelength Measurement, at each position x_i of the magnified image (within a band 0.4 mm of thickness), we determine the averaged wavelength λ from consecutive maxima of gray values and report it on a graph (λ, x). This analysis is applied to the magnified images recorded at different incubation times. (D) Distribution profile of distances between two consecutive maxima; the profiles are normalized by the sum of events.

Elastic Response of B. subtilis Pellicles.

The previous experiments indicate that the flat pellicles behave like a growing elastic plate rather than a liquid; to quantify their elastic properties before wrinkling, we measure their mechanical response under uniaxial tensile stress. For this purpose, a specific setup has been built and placed inside a biological safety cabinet (BSC) to ensure sterile conditions during biofilm formation and measurements.

As detailed in SI Text, Force Device and Thickness Estimation, the device consists of two parallel and vertical thin plastic plates separated by a distance L_o; one of the plates is connected to a microtranslation stage and the other to a force sensor. The two plates’ bottom parts are immersed in the biofilm medium. While a biofilm grows at the air/liquid interface, it simultaneously sticks to the two plates with no further surface treatment. Before each measurement, we keep intact the part of the pellicle located in between the two plates and remove the rest from the medium. In that condition, only this biofilm portion is stimulated by a displacement ΔL_o of the plate; the displacement induces a deformation that stresses the biofilm portion to a magnitude that can be detected by the force sensor. To determine accurately the millinewton (mN) force F, we design a sensor based on the deflection measurement of a double-cantilever spring (24). Using such a sensitive system, we are able to obtain the force-displacement curve of the pellicle. In our geometry, a displacement ΔL_o of the translation stage (and therefore of one plate) induces a mechanical strain 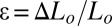. If h and D denote the thickness and width of the biofilm portion, respectively, the stress is related to the measured force through the expression 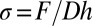. In a typical experiment, the magnitude of the displacement ΔL_o is ∼2 mm and the initial length L_o is ∼14 mm; the speed of the displacement ranges between 50 and 150 μm/s. The width D is fixed at 41 mm, and the thickness is h ∼350 μm, as found by the tests explained in SI Text, Force Device and Thickness Estimation.

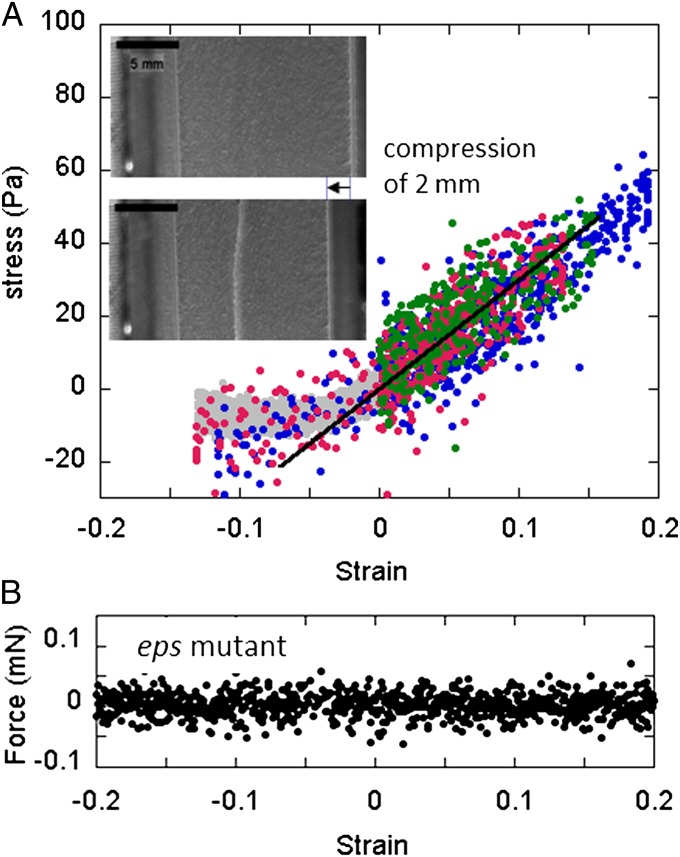
Using all these values and the measured force vs. displacement, we obtain the strain–stress curves presented in Fig. 3A. In the elongation range (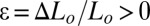), we plot the measurements recorded on three different pellicles. Strains and stresses are found proportional as expected for an elastic material. Denoting Y the elastic modulus of the material with σ = Yɛ, we obtain Y = 300 ± 100 Pascal (Pa) by fitting the data in the range 0 < ɛ < 0.15. This value is between the 10- to 10,000-Pa values reported in the literature (25). Pellicles are therefore very soft materials, softer than the conventional megapascal materials such as swollen agar gel, and comparable to individual living eukaryotic cells (26) or inert cellular materials such as weakly dense polymerized foams (27). We must emphasize here that our Y value depends on the h thickness estimation, i.e., we are measuring the force and deducing the product Yh = 0.105 ± 0.022 Pa.m from a data linear fit; knowing h, we estimate Y in a second step. Note that when the medium is twice enriched, we recover 0.105 Pa.m of Yh value with a slightly bigger thickness of h ∼450 μm.

Fig. 3.

(A) Measurements of the mechanical response of several pellicles (data of different colors) produced by the NCIB 3610 wild-type strain. In the elongation range 0 < ɛ < 0.15, the mechanical strain (ɛ)–stress (σ) curve exhibits a linear elastic-like response σ = Yɛ of elastic modulus Y = 300 Pa (black line). In the compression range ɛ < 0, the stress remains constant above a certain value of confinement. (Insets) Top-view images indicate that the initial flat pellicle (Upper) forms a single invaginated bottom fold when confined (Lower). (B) Force experiments performed on the standing culture of the eps mutant. As recorded, the mechanical force becomes insensitive to any displacements or strains. The lack of EPS prevents the formation of a macroscopic connective pellicle.

As shown in Fig. 3A, we also strain some biofilms by approaching the two plates in the range ɛ < 0 in an attempt to mimic the confinement effects seen in the previous section. We find that the negative stress deviates from the linear fit for very low strain values and becomes constant (approximately −10 Pa). By recording top-view images of the induced deformation, we can see that a single fold parallel to the plates appears instead of multiple periodic undulations. The fold location varies from one biofilm to another but remains an invaginated bottom fold and parallel to the direction of confinement. This surprising effect is discussed further in this article. Note that the growth rate is ∼1 mm/h (0.3 μm/s) for the growth described in Fig. 2, and ∼100 μm/s for the mechanical solicitation. In a few compression experiments, we reduce the translation speed to 5 μm/s (gray data in Fig. 3A) and still observe a single fold.

In a final set of mechanics experiments, we record the force-displacement curve on the standing cultures of the eps mutant. In contrast to the wild-type strain NCIB 3610, we measure a force insensitive to the displacement or to the strain (Fig. 3B). The absence of variation points out the absence of connectivity and of elasticity in these colonies. In turn it highlights the role of the extracellular matrix in the cohesion and in the elasticity of the wild-type B. subtilis pellicles.

Theoretical Approach of Wrinkled Morphology.

Based on the morphology experiments performed in open and confined spaces, we suspect that the wrinkle formation is driven by the compression induced by a constrained growth mechanism as considered in ref. (28). Starting from the classical formalism of the growth process in 3D bodies (29), and doing appropriate scaling assumptions and series expansions, Dervaux and collaborators have proposed an additive decomposition of the growth and of the elastic deformation for 2D systems; we apply here their approach to our system under several required assumptions. We first assume that, at the prewrinkled stage (Fig. 2A1), the pellicle behaves like a solid material in which growth is essentially an isotropic and homogeneous in-plane process. We then neglect the vertical growth and assume a constant pellicle thickness h. Because pellicles are very thin compared with their typical lateral dimensions (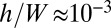), we describe them as growing elastic plates. We consider that the growth can be described by a single parameter—the cumulative growth rate G, which increases as the growth proceeds and is referred to as g in ref. 28. The parameter G compares the excess of length induced by the growth with respect to an initial configuration without stress (G > 0). The 2D growth tensor is 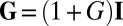, where I denotes the 2D identity tensor and the 2D Cauchy–Green strain tensor ε turns out to be the sum of a growth-induced deformation and the elasticity-induced response of the material (28): 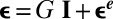. For simplicity, we focus on the bulk unidirectional wrinkles illustrated in Fig. 2A and then consider the strain and stress along the y direction. 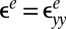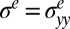These elastic contributions and read

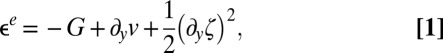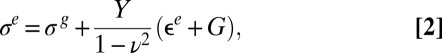where 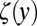and 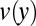represent the out-of-plane and in-plane displacements of the pellicle, respectively; Eq. 1 corresponds to equation 30 in ref. 28. Note that the pellicle is also strained in the x direction due to the growth biaxiality ( and 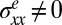). Eq. 2 is simply the 2D Hooke’s law relating the elastic stress and strain in the pellicle of Poisson’s ratio ν. The in-plane growth induces a residual compressive in-plane stress 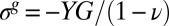in the initial undeformed flat state of the pellicle (ζ = 0).

As sketched in Fig. 4, during in-plane growth, vertical displacements may be first neglected, and the elastic stress compensates the increasing residual compressive stress up to a critical threshold 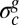. The pellicle keeps growing, and buckles forming extended quasi-periodic structures (v and ζ ≠ 0). The morphological and mechanical properties of this extended pattern can be determined by solving the force balance equations as the pellicle is in mechanical equilibrium:

where 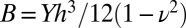is the bending rigidity. Eqs. 3 and 4 are, respectively, the in-plane and out-of-plane equilibrium of forces (per area unit). The functions N and T_y represent the normal and y-tangential component of the external load, accounting for the action of the fluid substrate on the pellicle. In what follows, we consider small deformations and suppose N = Kζ and T_y = 0, 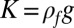being the “stiffness” of the fluid substrate of density ρ_f and g the gravitational acceleration (30). As a consequence, above 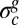and in the absence of any external in-plane force, the elastic stress remains constant (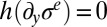) and equal to the critical stress 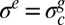. Then when the pellicle continues to grow, the compressive residual stress still increases while the pellicle deforms to keep 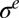constant. Solving Eqs. 3 and 4 leads to a pattern described by the periodic function 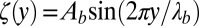of wavelength 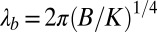and of amplitude A_b (12, 16, 23). Apart from the influence of the fluid substrate density, λ_b only depends on the biofilm parameters such as the Young modulus, thickness, and Poisson's ratio. This undulation appears above a critical stress 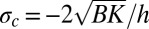, which is reached by the critical residual stress 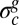at the critical strain 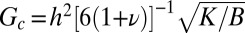. Replacing these relations in Eqs. 1 and 2, we find the undulation magnitude scales .

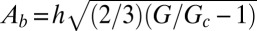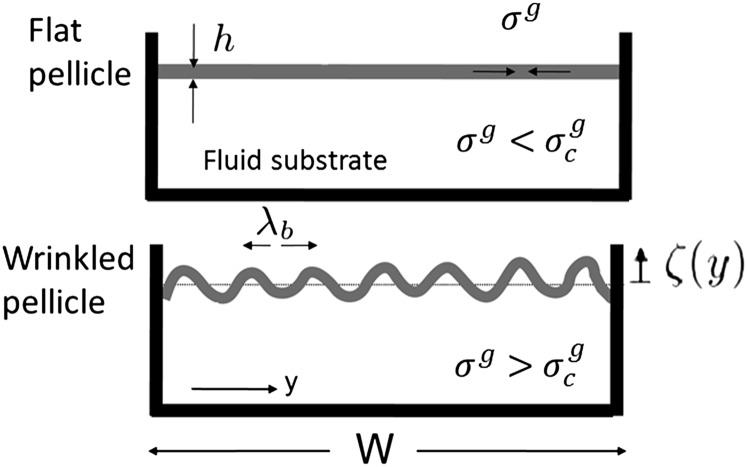
Fig. 4.

Sketch of the wrinkling instability. The pellicle growth proceeds in a confined space and gives rise to an increasing compressive in-plane residual stress 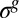. The flat pellicle (Upper) buckles above a critical value 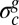(Lower).

Theoretical Expectations vs. Experimental Results.

Because both pellicle and fluid medium are mainly composed of water, we can estimate the fluid parameter K ∼ 10⁴ Pa/m (ρ_f ∼ 10³ kg/m³ and g ∼ 10 m/s²) for the substrate and assume ν ∼ 0.5 for the pellicle. Assuming a thickness h ∼350 μm and a Young modulus Y ∼300 Pa from our experiments, we expect 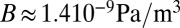and λ_b ∼3.9 mm. Because of the biofilm softness, our approach succeeds in explaining the millimeter wavelength of the wrinkles. Conventional gel plates, such as swollen agar gels, would rather lead to centimeter wavelengths in the same conditions.

Although the theoretical estimation agrees on the magnitude of λ_b, the expected value is still 3× larger than the experimental one, λ_b ∼1.5 mm measured in the standard medium. When the medium is twice enriched, the expected value becomes equal to 4.4 mm, close to the other millimeter experimental length, 3 mm. These discrepancies could be a signature of the limitation of our simplified approach; biofilm can be approximated to a uniform elastic plate up to a first approach only. The real heterogeneous structure would need to refine the approach and to calculate numerically the appropriate wavelength. To reach a wavelength of 1.5 or 3 mm, the ideal elastic film has to be as thin as 50 or 200 μm, respectively, which is not reasonable given the biofilm turbidity and texture (Figs. 1 and 2A), and is outside of our measured range. The low experimental λ_b values rather suggest the existence of a mechanically active layer much thinner than the actual 350- or 450-μm thickness. Indeed, when part of a pellicle incubated in the standard medium is transferred onto a glass slide, it decomposes into large, separated turbid domains that are still connected by a transparent thin layer; this connective layer may be sensitive to mechanical forces. The domains are yet visible in Fig. 2A and correspond to the detected grains in Fig. 2D. We speculate that an increase in nutrient concentration changes the composition of the biofilm and enlarges the connective layer.

Replacing B, h, and K by their measured values, we obtain the cumulative critical rate G_c ∼0.035 and the residual stress 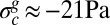. If W denotes the width of the rectangular dish in which cultures have been studied (W = 4.6 cm in Figs. 1 and 2A), biofilm should start buckling at a critical cumulative growth rate 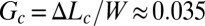or equivalently when the additional length generated by growth ΔL_c becomes ∼1.6 mm. This critical length is very small, and given a growth rate of 1 mm/h, 1 or 2 h would be sufficient for the biofilm to expand 1.6 mm. In other words, if a half day is needed to optically detect the wrinkles, biofilm could, in principle, have already started to buckle long before that, just 1 or 2 h after covering the surface. The heterogeneous structure may also postpone the buckling or simply prevent the detection of wrinkles formed by a too-thin elastic layer. To be detected, wrinkles must reach amplitudes at least higher than the total thickness h; according to the model, they should appear beyond the cumulative rate 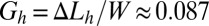and equivalently at least 4 h later. In practice, a half day is needed, which leads to .

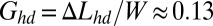It is also tempting to compare the buckling conditions with the experimental confinement performed in our force device. Moreover, the two critical strain and stress parameters (−G_c ∼ −0.035 and 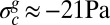) can be directly located along the two axes (ɛ, σ) of Fig. 3. The explored range of applied strain includes the values ɛ_c = −G_c and −G_h, and the compressive stress remains always lower than the threshold value σ_c.

Morphology Near the Edges.

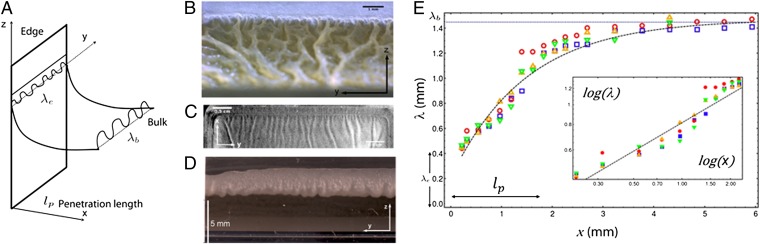
As shown in Figs. 2A and 5B, the NCIB 3610 biofilm exhibits another type of wrinkles near the edges. Similar wrinkles are also formed by the DV1 pellicles, top viewed in Fig. 5C. The pellicle is no longer horizontal in the edges vicinity; it covers the initial fluid meniscus induced by capillary effects, climbs, and adheres to the dish walls. Tiny wrinkles then locate at the edges of the dish and are connected to the bulk wrinkles through a cascade-like phenomenon. In Fig. 5E we report the wavelength variation as a function of the distance x from the edge in different samples and observe undulations, the wavelength λ(x) of which increases progressively as we move away from the edge, reaching values up to 3× larger than at the edge. Averaged values of bulk and edge wavelengths are equal to λ_b ∼1.5 mm and λ_e ∼0.4 mm, respectively. Data are plotted in Fig. 5E together with two types of fits (exponential and power law), although neither laws fit the data well. However the exponential law allows us to estimate the penetration length. We found that the cascade penetrates into the bulk over a length l_p ∼1.5−2 mm. Usually for a liquid, the typical meniscus size is given by the capillary length 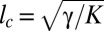, γ being the air/liquid culture surface tension. Knowing ρg ∼10⁴ N/m³ and γ ∼53 mN/m (31), we obtain l_c ∼2.3 mm, which is of the order of our penetration length l_p. Therefore, this cascade-like structure extends over a region roughly delimited by capillary effects where the surface energy must contribute to the mechanical equilibrium of the biofilm.

Fig. 5.

(A) A sketch showing the pellicle configuration near the edge of the Petri dish wall. (B) Perspective view of a NCIB 3610 pellicle showing the cascade-like behavior. The climbing of the pellicle on the dish wall, which follows the meniscus, can also be appreciated. (C) Cascade-like wrinkled morphology is observed in DV1 pellicles (grayscale image). (D) Backside view of a NCIB 3610 pellicle climbed onto the edge. The pellicle bottom in contact with the liquid substrate presents a wavy morphology. (E) Wavelength 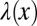as a function of the distance from the edge x (SI Text, Image Analysis and Wavelength Measurement). Data obtained on different DV1 pellicles are differently colored and can be fitted by a simple exponential (black line) or by a power law (Inset). (Inset) Same data but plotted in log-log scale with the power law fit .

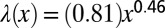Biofilms have this feature in common with synthetic thin elastic systems as recently reported in refs. 16 and 32. When subjected to uniaxial compression, an elastic polymer sheet that floats on a liquid forms a wrinkled structure that becomes thinner near the uncompressed edge than in the bulk (16). As found by Huang et al. (16), the dominant energies are the bending and the tensile ones (via the surface tension) in that region near the edge. Balancing both energy contributions 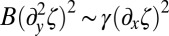for x-dependent undulations, the cascade profile can read 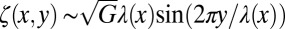. The resulting wavelength scales as 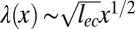, where l_ec defines the elastocapillary length 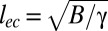(32). Considering the numerical prefactor values, we expect 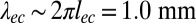. By fitting the data by a power law (Fig. 5E, Inset), we obtain an exponent value 0.46 and a prefactor 0.8, close to the expectations.

Note that similar edge structures have been observed only when the synthetic plates are subjected to a compressive load parallel to the edge. In our case, because the compression comes from the residual stress, the presence of such a structure suggests other effects at the edge of the pellicle (e.g., asymmetric growth, thickness variation, or adhesion influence). Moreover, during the biofilm formation, the emergence of edge wrinkles before the bulk pattern also suggests a critical edge residual stress lower than the bulk value .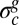

Folds.

In addition to the millimeter bulk and edge wrinkles, the presence of large folds separated by centimeter distances complete the range of vertical structures visible in mature pellicles (Fig. 1B). In Fig. 3, the flat pellicle also folds when compressed mechanically. The so-called folds localize most of the bending energy of the system in small regions of large curvature, relaxing the rest of the surface stress. In principle, when compressed progressively, the film should first wrinkle and then fold (12). In our experiments of mechanical confinement, we did not observe the presence of wrinkles before the fold appearance. In the mature pellicles, however, wrinkles and folds coexist. Indeed, the mechanical and previous growth confinements are not equivalent in terms of fields of strain and stress. Strain field is uniform in the case of growth only.

The recent combination of experiments, simulations, and theories indicate that the transition wrinkles to fold of a floating film allows relaxing at least eight wrinkles into one fold simultaneously (12). These results are consistent with our milli- and centimeter scales of spacing between wrinkles and folds, respectively (Figs. 1A and 3). However, the absence of wrinkles during the mechanical confinement may suggest the presence of spatial heterogeneities such as the ones observed during the early DV1 pellicle development and that may change the stress field. The precise fold location between the two plates varies from one sample to another in our mechanical experiment and may depend on heterogeneities within the pellicle. Finally, when measuring force vs. displacement, force deviates from the elastic behavior in accordance with a stress relaxation accompanying the fold emergence.

Conclusions

We present direct measurements of floating biofilms’ elasticity and consider the presence of wrinkles as a consequence of that elasticity. A simplified analytical model of buckling allows us to explain the presence of wrinkles as well as the order of magnitude of the edge and bulk characteristic wavelengths. Further approaches may refine the model by including the heterogeneous structures of the biofilm and the influence of stress and strain on the growth rate. Similar mechanisms could apply to the wrinkled morphology observed in other bacterial species cultured in the laboratory.

The eps mutant experiments show no elastic response; these results highlight the key role of the extracellular matrix in providing connectivity and elasticity of the pellicle. We speculate that the wrinkles and the mechanical properties may be controlled genetically through the extracellular components production.

Materials and Methods

Strains, Growth, and Biofilm Conditions.

Two wild-type strains of B. subtilis, NCIB 3610 and DV1, were used for this study. DV1 was isolated from a sand sample from the Death Valley desert in the Mesquite Flats Dunes region. 16S rDNA PCR amplification using universal primers 8F and 1492R and sequencing allows the classification of the strain DV1 in the B. subtilis group. The DV1 16S rDNA sequence is available in the National Center for Biotechnology Information database (NCBI accession no. EU362117). For the preparation of pellicles, cells of each strain from freezer stocks were streaked onto agar plates. A single colony was grown overnight in LB medium (10 g/L NaCl, 5 g/L yeast extract, and 10 g/L tryptone) at 30 °C under shaking (140 rpm). Cells were resuspended in a fresh LB medium and incubated in the same conditions up to OD₆₀₀ = 0.1. Cells were then inoculated in regular dishes (inner dimensions of 61 and 46 cm) containing 25 mL of biofilm medium [LB supplemented with 0.1 mM MnCl2 and 3% (vol/vol) glycerol]. The height of liquid into a dish was ∼5 mm. The samples were placed in a chamber maintained at 23 °C or sometimes at room temperature for varying time periods (4–7 d) without shaking. A total of 10 µg/mL of tetracycline was added in LB and biofilm medium in the case of the epsA-0::tet mutant strain.

Image Analysis and Wavelength Measurement.

See SI Text, Image Analysis and Wavelength Measurement.

Force Device and Thickness Estimation.

See SI Text, Force Device and Thickness Estimation.

Temperature and Enriched Medium.

See SI Text, Temperature and Enriched Medium.