Geometric modeling of subcellular structures, organelles, and multiprotein complexes

SUMMARY

Recently, the structure, function, stability, and dynamics of subcellular structures, organelles, and multi-protein complexes have emerged as a leading interest in structural biology. Geometric modeling not only provides visualizations of shapes for large biomolecular complexes but also fills the gap between structural information and theoretical modeling, and enables the understanding of function, stability, and dynamics. This paper introduces a suite of computational tools for volumetric data processing, information extraction, surface mesh rendering, geometric measurement, and curvature estimation of biomolecular complexes. Particular emphasis is given to the modeling of cryo-electron microscopy data. Lagrangian-triangle meshes are employed for the surface presentation. On the basis of this representation, algorithms are developed for surface area and surface-enclosed volume calculation, and curvature estimation. Methods for volumetric meshing have also been presented. Because the technological development in computer science and mathematics has led to multiple choices at each stage of the geometric modeling, we discuss the rationales in the design and selection of various algorithms. Analytical models are designed to test the computational accuracy and convergence of proposed algorithms. Finally, we select a set of six cryo-electron microscopy data representing typical subcellular complexes to demonstrate the efficacy of the proposed algorithms in handling biomolecular surfaces and explore their capability of geometric characterization of binding targets. This paper offers a comprehensive protocol for the geometric modeling of subcellular structures, organelles, and multiprotein complexes.

1. INTRODUCTION

One of major features of biological sciences in the 21st century is their transition from an empirical, qualitative, and phenomenological discipline to a comprehensive, quantitative, and predictive one [1]. Indeed, theoretical description, mathematical modeling, and computer simulation of biological systems have made enormous contribution to the present understanding of biological sciences. The material basis and fundamental underpinning of modern biological sciences are biological macromolecules, especially proteins and nucleic acids, which coil into specific three-dimensional (3D) shapes and are able to carry out most of the functions of cells. The goal of theoretical description, mathematical modeling, and computer simulation is to understand the structure, function, dynamics, and transport of biological macromolecules. A prerequisite to theoretical description, mathematical modeling, and computer simulation of the structure, function, dynamics, and transport of biological macromolecules is the geometric modeling based on their 3D shapes. In addition to straightforward geometric visualization, geometric modeling bridges the gap between imaging and mathematical modeling such that the structural information can be integrated into mathematical models [2].

Macromolecular 3D shapes can be indirectly obtained from a number of experimental means, including macromolecular X-ray crystallography, nuclear magnetic resonance (NMR), electron paramagnetic resonance, cryo-electron microscopy (cryo-EM), multiangle light scattering, confocal laser-scanning microscopy, small angle scattering, ultra fast laser spectroscopy, and others. The main workhorses for single macromolecules are crystallography and NMR. The advanced X-ray crystallography technology is able to provide decisive structural information at Armstrong and sub-Armstrong resolutions, whereas NMR experiments often offer structural information under physiological conditions. Both X-ray crystallography and NMR are technologically relatively well developed, except for their applications in special tasks, such as the crystallization of membrane proteins. However, these approaches are not suitable for proteasomes, subcellular structures, organelles, cells, and tissues. Their study has become one of the major new trends in structural biology. Currently, one of the most powerful tools for subcellular structures, organelles, and large multiprotein complexes is cryo-EM [3].

Cryo-EM, or electron cryo-microscopy, is an increasingly popular transmission EM whose sample is bombarded by electron beams at cryogenic temperatures to improve the signal-to-noise ratio (SNR). Its working principle is based on the projection (thin film) specimen scans collected from many different directions around one or two axes and the creation of 3D images by using the Radon transform. Cryo-EM allows the imaging of specimens in their native environment and is capable of providing 3D mapping of entire cellular proteomes together with their detailed interactions at a nanometer resolution [4–7].

Because most biological specimens are extremely radiation sensitive, they can only sustain the illumination of a limited electron dose. As a result, cryo-EM images are inevitably of low SNR and lead to limited resolutions [3]. In practice, cryo-EM maps often do not contain adequate information to offer unambiguous atomic-scale structural reconstruction of biological specimens. Additional information obtained from other techniques, such as crystallography, NMR, and computer simulation, is utilized to interpret the cryo-EM maps. However, the resolution of cryo-EM maps has been improved dramatically in the past few years, thanks to the technical advances in experimental hardware, noise reduction, and image segmentation techniques. By further taking the advantage of symmetric averaging, many cryo-EM-based virus structures have already achieved a resolution that can be interpreted in terms of an atomic model. Therefore, it is time to utilize cryo-EM images for molecular and atomic-scale mathematical modeling and computer simulation of subcellular structures, organelles, and large multiprotein complexes.

Most 3D imaging data obtained from cryo-EM and many other tomographic modalities are currently presented in a digital format, as a volumetric density distribution, where each Cartesian grid point is assigned with a scalar value associated with the local electron scattering power. For the purpose of visualization, one needs to convert them into images in the form of a series of two-dimensional (2D) images, rendering of the 3D shapes generated by isosurface extraction, or direct volumetric rendering. For the purpose of geometric analysis, structural features in the complex settings of cellular landscapes are further characterized in terms of surface areas, surface-enclosed volumes, and Gaussian and mean curvatures. For the purpose of mathematical modeling and computation, the resulting 3D geometric shape is to be further described in either the Lagrangian representation or the Eulerian representation. The Lagrangian representation is a basis for the Lagrangian formulation of the biological evolution, in which surface elements are directly evolved according to a governing equation or a set of rules [2, 8]. Similarly, the Eulerian representation facilitates the Eulerian formulation of the biological dynamics, in which the biological shape is embedded in a hypersurface function, or a level set function, and such a function is then evolved under prescribed physical and/or biological principles [9–11]. Both Lagrangian and Eulerian approaches have their own pros and cons, and are very useful in mathematical modeling and computation. In the present work, we focus our studies on the Lagrangian representation of 3D imaging data.

Currently, the SNR of 3D imaging data for subcellular structures, organelles, and large multi-protein complexes is typically in the neighborhood of 0.01 [3]. To make the situation worse, the image contrast, which depends on the difference between electron scattering cross sections of cellular components, is also very low in most biological systems. Consequently, appropriate noise reduction is an indispensable process in the structure reconstruction from 3D imaging data. To improve the SNR and image contrast of cryo-EM data, researchers have employed a wide variety of denoising schemes, including wavelet transform techniques [12], nonlinear anisotropic diffusions [13, 14] or Beltrami flow [15], bilateral filter [16–18], and iterative median filtering [19]. Despite much effort, noise reduction of cryo-EM data remains a challenging task and is far from adequate, due to the extremely low SNR and other technical complications [3]. Innovative mathematical approaches are necessary to further tackle this problem [20–22].

Geometric flows, in which the flow motion is governed or influenced by geometric properties, such as curvatures, have become an established approach to image analysis and surface generation in the past few years. Particularly, mean curvature flows have been a popular subject in applied mathematics for image analysis, material design [23–25], and surface processing [26, 27]. The first use of PDEs for image analysis dates back to 1983 [28]. Witkin noticed that the evolution of an image under a diffusion operator is formally equivalent to the standard Gaussian low-pass filter for image denoising [28]. Perona and Malik introduced an anisotropic diffusion equation [29] to protect image edges during the diffusion process. The Perona–Malik equation stimulated much interest in applied mathematics [29–33]. Over the past two decades, many related mathematical techniques, such as the level set formalism devised by Osher and Sethian [25, 34], Mumford–Shah variational functional [35], and the total variation (TV) minimization [36], have been widely used for image analysis [37–41].

To improve the efficiency of noise removing, Wei introduced the first family of arbitrarily high-order nonlinear PDEs for image denoising and restoration in 1999 [31]. Many fourth-order evolution equations were introduced in the literature for image analysis [32, 42–45]. These equations were proposed either as a high-order generalization of the Perona–Malik equation [31, 46] or as an extension of the TV formulation [32, 42–44]. The essential assumption in these high-order evolution equations is that high-order diffusion operators are able to remove high-frequency components more efficiently. High-order geometric PDEs have been widely applied to image and surface analysis [31, 32, 42–48]. Because of the stiffness of high-order nonlinear PDEs, computational techniques for solving higher-order geometric PDEs are of great importance. For instance, alternating direction implicit schemes are developed in the literature for integrating high-order nonlinear PDEs [46, 49].

Image-processing PDEs of the Perona–Malik type and the TV type are mostly designed to function as nonlinear low-pass filters. In 2002, Wei and Jia [33] introduced coupled nonlinear PDEs to behave as high-pass filters. These coupled nonlinear PDEs are demonstrated for image edge detection. The essential idea behind these PDE-based high-pass filters is that when two Perona–Malik type of PDEs evolve at dramatically different speeds, the difference of their solutions gives rise to image edges. This follows from the fact that the difference between an all-pass filter (i.e., identity operator) and a low-pass one is a high-pass filter [33]. The speeds of evolution in these equations are controlled by the appropriate selection of the diffusion coefficients. These PDE-based edge detectors have been shown to work extremely well for images with a large amount of textures [33, 50]. Most recently, the PDE transform is introduced for functional mode decomposition, [51–53] based on arbitrarily high-order PDE high-pass filters. Such an approach has significantly extended the utility of PDEs for image, surface, and data analysis. Similar to wavelet transform, the PDE transform has controllable time-frequency location and perfect reconstruction. The PDE transform has found its success in molecular surface generation of proteins [54].

The use of curvature-controlled PDEs for biomolecular surface construction was initiated in 2005 [55]. Atomic coordinate information of a protein is embedded in 3D Eulerian grids to undergo geometric flow evolution before the protein surface is extracted via the marching cubes method from a level-set type of hypersurface function. This approach was combined with a variational procedure to generate the first variational biomolecular surface model, the minimal molecular surface, for proteins [9, 26]. Molecular interactions were further incorporated in this approach to develop potential and curvature-driven geometric flows for the construction of biomolecular surfaces [46]. Recently, many variational multiscale models have been introduced on the basis of the geometric flow separation of solvent and solute domains [1, 10, 11, 56].

After the surface construction, a further issue in geometric modeling is the surface and volumetric (i.e., boundary and interior) meshing [41, 57, 58]. There are a wide variety of methods that can be used for this purpose. Mesh generation is one of the most important aspects of continuum mechanical analysis [59–63]. Numerous elegant methods, such as the probabilistic methods for centroidal Voronoi tessellations [64, 65], the optimal Delaunay triangulation and graph cut-based variational surface reconstruction [66], and other surface remeshing enhancement methods and technologies [41, 67–70], have been developed for surface reconstruction or surface remeshing during the past two decades. In general, high-quality triangle surface meshes must be low noise, low memory cost, near 60° for majority of element angles and aligned with the physical features. Yu et al. discussed the use of adaptive feature-preserving methods for biomolecular surface meshing [2, 71]. They used the constrained Delaunay triangulation implemented in TetGen [72] for volumetric meshing [2].

Curvature is a measure of how much a curve deviates from being straight or a surface from being flat [73]. Curvature has been used to analyze the stereospecificity of molecular surfaces [74]. Curvature has also been applied for finite element analysis crank mechanisms [75]. The essential idea is that geometries of binding partners are locally complementary to each other at the binding site(s). Curvatures are also used as a geometric descriptor to characterize the shape of known protein binding sites so as to identify matching site(s) in other proteins and ligands. However, in real cases, the effect of stereospecificity may be offset by hydrogen bond, polarization, electrostatics, solvation, and allosteric modulation.

The objective of the present work is to explore the efficient computational methods for the geometric modeling of subcellular structures, organelles, and large multiprotein complexes. Specifically, we study the reconstruction of biological structures from noisy 3D imaging data, examine the geometric representation of complex biological shapes, provide accurate calculation of surface areas and surface-enclosed volumes, and investigate the computational algorithm and surface mapping of Gaussian and mean curvatures of macromolecules. Most geometric modeling is carried out in the Lagrangian representation with triangle meshes on the surface.

The rest of this paper is organized as follows. Section 2 is devoted to computational methods and numerical algorithms for geometric modeling. We give a brief description of high-order geometric PDEs and nonlinear PDE-based high-pass filters. Different surface extraction schemes are discussed. Numerical algorithms for calculating surface areas and surface-enclosed volumes are given in the Lagrangian representation. We introduce the state of the art techniques for volumetric meshing of subcellular structures, organelles, and large multiprotein complexes. Efficient schemes for computing Gaussian and mean curvatures are provided. In Section 3, we carry out extensive numerical experiments to validate the proposed methods, algorithms, and schemes. We design analytical cases to test accuracy and convergent order of the proposed algorithms for area, volume, and curvature calculations. Second-order convergence is found in these schemes. Finally, we apply the proposed methods to six biomolecular examples. Our results demonstrate the usefulness, robustness, and efficiency of the proposed approaches. This paper ends with a conclusion in Section 4.

2. METHODS

This section provides a variety of mathematical and computational methods for geometric modeling. The goal here is to introduce a repertoire of appropriate computational tools for the applications involving volumetric data and the shapes defined in cryo-EM datasets.

2.1. High-order geometric flows

Geometric flows, such as the Laplace–Beltrami flow, play a significant role in image analysis. An important aspect in the geometric flow development is the use of high-order geometric PDEs for image processing or surface analysis. Willmore flow, proposed in 1920s, is a fourth-order geometric PDE that locally minimizes the difference between two principal curvatures (see detailed description on principal curvatures in Section 2.5.1). Therefore, the Willmore flow prefers spherical shapes, which may be undesirable in general applications. Motivated by the hyperdiffusion in the pattern formation in alloys, glasses, polymer, combustion, and biological systems, Wei introduced the first family of arbitrarily high-order geometric PDEs for edge-preserving image restoration in 1999, using Fick’s law [31]

$$\frac{\partial u(\mathbf{r},t)}{\partial t}=-\sum _q\nabla ·{\mathbf{j}}_q+e(u(\mathbf{r},t),\mid \nabla u(\mathbf{r},t)\mid ,t),q=0,1,2,\dots$$ (1)

where the nonlinear hyperflux is given by

$${\mathbf{j}}_q=-d_q(u(\mathbf{r},t),\mid \nabla u(\mathbf{r},t)\mid ,t)\nabla {\nabla }^{2q}u(\mathbf{r},t),q=0,1,2,\dots$$ (2)

where r ∈ ℝⁿ, ∇ = ∂/∂r, u(r, t) is the processed image function, d_q(u(r, t), |∇u(r, t)|, t) are edge sensitive diffusion coefficients, and e(u(r, t), |∇ u(r, t)|, t) is a nonlinear operator. Equation (1) is subject to the initial image data u(r, 0) = X(r) and appropriate boundary conditions. The essential idea of Equation (1) is to accelerate the noise removal in the Perona–Malik equation [29] by higher-order derivatives, which is more efficient in noise dissipation. As a generalization of the Perona–Malik equation, the hyperdiffusion coefficients d_q(u, |∇ u|, t) in Equation (2) can also be chosen as the Gaussian form

$$d_q(u(\mathbf{r},t),\mid \nabla u(\mathbf{r},t)\mid ,t)=d_{q0}exp\left[-\frac{{\mid \nabla u\mid }^2}{2{\sigma }_q^2}\right],$$ (3)

where the values of constant d_q0 depend on the noise level, and σ₀ and σ₁ were chosen as the local statistical variance of u and ∇u

$${\sigma }_q^2(\mathbf{r})=\overline{{\mid {\nabla }^{q}u-\overline{{\nabla }^{q}u}\mid }^2}(q=0,1).$$ (4)

The notation $\overline{Y(\mathbf{r})}$ denotes the local average of Y (r) centered at position r. The measure based on the local statistical variance is important for discriminating image features from noise. As a result, one can bypass the image preprocessing, that is, the convolution of the noise image with a smooth mask in the application of the PDE operator to noisy images. High-order geometric PDEs have found many practical applications [31, 44, 76, 77]. Arbitrarily high-order geometric PDEs are modified for molecular surface formation and evolution [46]

$$\frac{\partial S}{\partial t}={(-1)}^q\sqrt{g(\mid \nabla {\nabla }^{2q}S\mid )}\nabla ·\left(\frac{\nabla ({\nabla }^{2q}S)}{\sqrt{g(\mid \nabla {\nabla }^{2q}S\mid )}}\right)+P(S,\mid \nabla S\mid ),$$ (5)

where S is the hypersurface function, g (|∇ ∇^2qS|) = 1 + |∇ ∇^2qS|² is the generalized Gram determinant, and P is a generalized potential term, including microscopic interactions in biomolecular surface construction. When q = 0 and P = 0, Equation (5) recovers the mean curvature flow used in our earlier construction of minimal molecular surfaces [9]. It reproduces the surface diffusion flow [46] when q = 1 and P = 0. It has been shown that surface generated with the fourth-order geometric PDE demonstrates a morphology distinguished from that obtained with the mean curvature flow or the Laplace–Beltrami flow [46].

2.2. Nonlinear PDE-based high-pass filters

Unfortunately, the studies of geometric flows have been essentially limited to the construction of nonlinear PDE-based low-pass filters. From the point of view of image and signal processing, low-pass filtering is just one specific type of operations, and other filters, such as high-pass filters and band-pass filters, are equally important. An exception is the nonlinear PDE-based high-pass filters introduced by Wei and Jia [33] for image edge detection in 2002,

$$u_t(\mathbf{r},t)=F_1(u,\nabla u,{\nabla }^{2}u,\dots )+{\epsilon }_u(v-u)$$ (6)

$$v_t(\mathbf{r},t)=F_2(v,\nabla v,{\nabla }^{2}v,\dots )+{\epsilon }_v(u-v)$$ (7)

where u(r, t) and v(r, t) are scalar fields, ε_u and ε_v are coupling strengths. Here, F₁ and F₂ are general nonlinear diffusion operators and can be chosen as the Perona–Malik operator F₁ = ∇ · d₁(|∇u|)∇ and F₂ = ∇ · d₂(|∇v|)∇. The initial values for both nonlinear evolution equations are chosen to be the same image, that is, u(r, 0) = v(r, 0) = X(r). As a nonlinear dynamic system, the time evolution of Equations (6) and (7) will eventually lead to a synchronization in the solution for positive nonzero coupling coefficients. For the purpose of image processing, Equations (6) and (7) are designed to evolve at dramatically different time scales, for example, the coefficients d₁ and d₂ are chosen as the Gaussian form in Equation (3) with d₂₀ ≫ d₁₀ ≥ 0. After finite time evolution, the image edges are obtained as the difference [33]

$$w(\mathbf{r},t)=u(\mathbf{r},t)-v(\mathbf{r},t).$$ (8)

It was shown that Equation (8) behaves like a band-pass filter when d₂₀ ≫ d₁₀ ~ 0. The essence of this approach is that when two coupled evolution PDEs are evolving at dramatically different speeds, the difference of two low-pass PDE operators gives rise to a band-pass or high-pass filter. The coupling terms play the role of relative fidelity and balance the disparity of two images. It has been shown that nonlinear PDE-based high-pass filters work extremely well for images with a large number of textures and outperform classical Sobel, Prewitt, and Canny operators [33, 50].

2.3. Surface extraction and meshing

Both the 3D imaging data from cryo-EM and the result of the aforementioned Eulerian geometric flows or PDE-based nonlinear filtering are given as functions sampled on Eulerian grids. For the subsequent use in FEMs or Langrangian geometry processing, the Lagarangian representation is employed, which is often much more efficient than the Eulerian representation due to better adaptivity of the irregular sampling and the reduction from 3D into curved 2D representation. In most geometry processing approaches, h-refinement (more segments) is preferred over p-refinement (degree of the polynomial in each segment), because the modern computer architectures can handle a large number of simple objects more efficiently than a small number of complex objects representing the same surface [78]. In the following, we use the extremal C⁰ case, that is, piecewise flat surface meshes, the de facto standard data structure in current geometry processing.

The conversion from 3D image data to 2D triangle mesh is often implemented by using the widely used marching cubes algorithm [79]. Without loss of generality, we can assume the isosurface to be extracted is the 0 level set. The vertices can be found on edges with opposite field values on both ends. The exact location of the intersection of the isosurface on the edge can be easily computed on the basis of the trilinear interpolation approximation of the continuous underlying field, which reduces to linear interpolation along the edge. The mesh connectivity is then established by examining each cell and constructing triangles with vertices on the edges of that cell by checking in a predetermined lookup table, which contains the connectivity information of the vertices within each cell for the 256 possible sign configurations of the eight grid points of the cell. The actual lookup table is reduced to 15 cases by using symmetry. For some cases, disambiguation based on actual field values is necessary [80].

We recommend the use of marching cubes for applications that do not require well-shaped elements, as this approach is highly parallelizable. On the other hand, for FEM and other applications with stringent requirement on the maximum and minimum angles of each triangle, we propose to use an alternative based on restricted Delaunay triangulation [81]. A sample implementation is available from the Computational Geometry Algorithms Library (CGAL) [82]. It distributes sample points on the surface and then extracts an interpolating triangle mesh through the 3D triangulation of the points. These points are added iteratively following a Delaunay refinement-like step until the sizes and shapes of the mesh triangles meet specified criteria. Other choices include dual contouring for adaptive octree data [83, 84], and the extended marching cubes for models with sharp features [85], which might be rare for cryo-EM datasets though.

2.4. Surface areas and surface-enclosed volumes

Surface area and surface-enclosed volume are crucial components in the mathematical and thermodynamical modeling of biomolecular systems [1, 8, 10, 86]. Given a Lagrangian mesh with piecewise flat segments, it is straightforward to compute the surface area and surface-enclosed volume. For surface area, one simply sums up the area of each surface triangle,

$$A(S)={\int }_{S}1\text{d}A=\sum _{t_l\in T}\mid t_l\mid =\sum _{t_l\in T}\frac{1}{2}\mid ({\mathbf{v}}_k-{\mathbf{v}}_i)\times ({\mathbf{v}}_j-{\mathbf{v}}_i)\mid ,$$ (9)

where S is the surface of the biomolecule, A(S) is the total surface area, and T contains all the surface triangles in a tessellation of S. Here, t_l is a triangle mesh element, with v_i, v_j, and v_k as the coordinates of its three vertices.

To calculate the volume on the mesh, one picks an arbitrary point inside or outside the mesh, for example, the origin, and sums up all the signed volume of the tetrahedron formed by the point and each triangle,

$$V(S)={\int }_S\mathbf{x}·\mathbf{n}\text{d}A=\sum _{t_l\in T}\frac{1}{6}(({\mathbf{v}}_k-{\mathbf{v}}_i)\times ({\mathbf{v}}_j-{\mathbf{v}}_i))·{\mathbf{v}}_i,$$ (10)

where V(S) is the total volume, and n is the outward surface normal at a position x on the surface S. Here, the vertices of each triangle are assumed to be listed in counterclockwise order when viewed from the outside of the surface. Even when a volumetric mesh of the inside is available, summing up the volumes of these thin tetrahedra formed by a fixed point and boundary faces is in general much more efficient than summing up the volumes of all the tetrahedra of the volumetric mesh.

2.5. Curvatures

2.5.1. Brief introduction to the continuous theory

Local geometric shape of the surface can be described by curvatures. A brief description of curvatures in terms of differential geometry theory can be found in Ref. [9]. The curvature for a point on a curve represents how fast the tangent direction turns, or more precisely, the magnitude of the second derivative of the curve in its arc-length parameterization. For a point on the surface, one can create a planar curve through the intersection of the surface and the local plane spanned by the surface normal and a tangent direction. The curvature of this planar curve is called the normal curvature along the chosen tangent direction. We can denote the maximum curvature among these normal curvatures by κ₁ and the minimum curvature by κ₂. These two curvatures are called principal curvatures, and the tangent directions associated with them are called principal directions. Note that these two directions are always orthogonal to each other. It can be further shown that the normal curvature κ along an arbitrary direction can be determined by κ₁ and κ₂ (the principal curvatures) and the angle θ that the chosen tangent direction makes with the maximum curvature direction

$$\kappa ={cos}^2(\theta ){\kappa }_1+{sin}^2(\theta ){\kappa }_2.$$

The second-order approximation (quadric surface patch) around that point will be the same if two principal curvatures are identical. To see this, we describe the neighborhood of a point on the surface by the deviation of the surface from the tangent plane (a height function z = f(x, y) in a local coordinate system with the origin aligned to the point and the xy-plane aligned to the tangent plane). The second-order approximation is

$$z=\frac{1}{2}(\begin{array}{cc}x& y\end{array})\text{Hess}\left(\begin{array}{c}x\\ y\end{array}\right)+\cdots ,$$

where Hess is the Hessian (the symmetric second derivative matrix) of f,

$$\text{Hess}=\left(\begin{array}{cc}\frac{{\partial }^{2}f}{\partial x^2}& \frac{{\partial }^{2}f}{\partial x\partial y}\\ \frac{{\partial }^{2}f}{\partial x\partial y}& \frac{{\partial }^{2}f}{\partial y^2}\end{array}\right).$$

The actual shape of the second-order approximation depends only on the eigenvalues of Hess, because applying a rotation in the tangent plane can diagonalize the Hessian. Thus, we can align two local approximation shapes through a rotation, as along as the diagonalized Hessians are the same. By the definition of curvature, one can immediately see that these eigenvalues are − κ₁ and − κ₂. Here, we follow the convention in which bending towards the normal indicates a negative curvature, and bending away from the normal indicates a positive curvature. In this way, the curvatures for spheres will be positive. Note that some authors use the opposite sign.

Alternatively, it is often advantageous to use the Gaussian curvature and the mean curvature defined by

$$K={\kappa }_1{\kappa }_2,$$ (11)

$$H=\frac{1}{2}({\kappa }_1+{\kappa }_2)$$ (12)

where K is the Gaussian curvature, and H is the mean curvature. They correspond to, respectively, the determinant and half of the trace of the aforementioned Hessian matrix, which is another way of prescribing the rotation invariants.

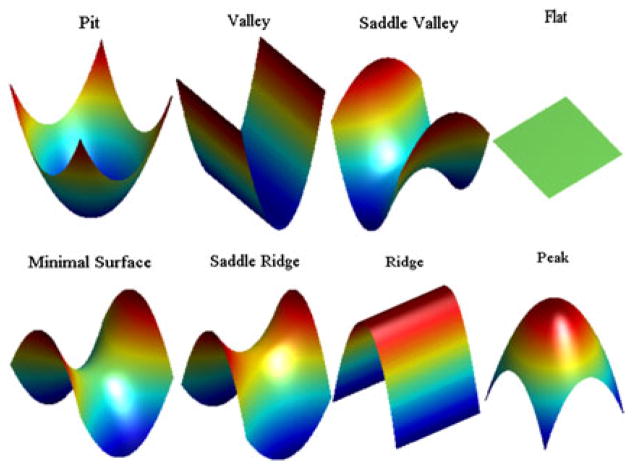
On the basis of the signs of the Gaussian curvature and the mean curvature, the neighborhood of a surface point can be roughly classified as one of the eight different shapes, namely, pit, valley, saddle ridge, flat, minimal surface, saddle valley, ridge, and peak. In Table I, we specify the type of shapes for each possible combination of signs. The actual shapes can be found in Figure 1.

Table I.

Surface types based on signs of Gaussian curvature and mean curvature as illustrated in Figure 1.

	K > 0	K = 0	K < 0
H > 0	Peak	Ridge	Saddle ridge
H = 0	None	Flat	Minimal surface
H < 0	Pit	Valley	Saddle valley

Figure 1.

Representative image gallery of surface types based on signs of Gaussian curvature and mean curvature listed in Table I.

Considering the quadratic approximations they represent, we can see that local shapes with opposite signs of mean curvatures and same signs of Gaussian curvatures may fit together.

To give intuitive descriptions of the shape, another pair of continuous variables, the shape index s and the curvedness c, can also be defined [73]

$$\begin{array}{c}s=-\frac{2}{\pi }arctan\left(\frac{{\kappa }_1+{\kappa }_2}{{\kappa }_1-{\kappa }_2}\right),\\ c=\sqrt{\frac{1}{2}({\kappa }_1^2+{\kappa }_2^2)}.\end{array}$$

Here, s describes the relation between the principal curvatures and c describes how nonflat the shape is.

2.5.2. Curvature estimates on triangle meshes

Meshing is a crucial component in geometric and mechanical analysis [58, 87–94]. In this work, we employ triangle meshes for the geometric representation of macromolecules. Therefore, we discuss schemes for curvature calculation on the triangle meshes.

The integral of Gaussian curvature over a small region and the integral of the geodesic curvature (deviation of a surface curve from a geodesic curve or a locally shortest curve) over its boundary sum up to 2π, according to the Gauss–Bonnet theorem. For a triangle mesh, the integral of the geodesic curvature around the dual loop around a vertex (e.g., the loop in Figure 3) is the same as the sum of the tip angles of triangles containing that vertex. Thus, the Gaussian curvature integral for a dual cell around the vertex is often estimated by the angle defect (or angle deficit), the difference between 2π, and the sum, which is also called the Gauss–Bonnet scheme. To obtain a pointwise estimate, we can divide it by the area of the neighborhood around the vertex, as shown in Figure 2.

Figure 3.

An illustration of dual cells defined around a vertex. Left: the area of the barycentric dual cell around a vertex (the cell formed by connecting consecutive barycenters of the triangles and edges incident to the center vertex v_i ), here l_j is the length of the part of edge e_j inside the neighborhood; Right: the area of the Voronoi dual cell of a vertex (the region containing all points closer to the center vertex v_i than to any other vertices).

Figure 2.

Schematic illustration of curvature algorithms. Left: a typical ‘one-ring’ neighborhood of a vertex (v₀); Middle: flattening the one-ring by ‘cutting open’ along the edge v₀v₁, we can measure the ‘angle deficit’ used in Gaussian curvature estimates, denoted here by $\mathrm{\Delta }\theta =2\pi -{\displaystyle \sum _{i=1}^5}{\theta }_i$. Right: angles used in the cotangent formula for the Laplace–Beltrami estimate of mean curvature.

The mean curvature normal can be estimated by using the Laplace–Beltrami operator applied to the surface description [95], which is essentially an estimate of the trace of the Hessian of the local description of the surface. The neighborhood area of the vertex could be estimated either by barycentric dual cell area (one third of the sum of the neighbor triangles’ area) or the Voronoi dual cell area (the area of the region containing points closer to the vertex than to any other vertices).

The discrete estimates of the curvatures can be formulated as follows:

$$K_i=\frac{1}{A_i}\left(2\pi -\sum _{{\theta }_j\in {\mathrm{\Theta }}_i}{\theta }_j\right),$$ (13)

where K_i is the estimated curvature at vertex i, θ_j is the angle of triangle j at vertex i, Θ_i is a collection of all angles around vertex i as shown in Figure 2, and A_i is one of the dual cell areas (Voronoi dual, barycentric dual, and mixed dual areas) in Figure 3 used to estimate the curvature. As shown in Ref. [95], the Voronoi dual cell area guarantees the least estimated errors for meshes with nonobtuse triangles. The straightforward estimation suggested by the authors for the Voronoi cell area around a vertex on mesh is

$$A_i=\frac{1}{8}\sum _{{\mathbf{v}}_j\in N_i}(cot{\alpha }_{ij}+cot{\beta }_{ij}){\left|\right|{\mathbf{v}}_i-{\mathbf{v}}_j\left|\right|}^2,$$ (14)

where N_i is the collection of all vertices immediately adjacent to vertex v_i, also known as the one-ring neighborhood as shown in Figure 3. For one-ring neighborhoods containing obtuse angles, a modification called mixed area can be applied [95]. In practice, the formula using Voronoi dual area produces better results even when there are negative cotangents.

The mean curvature (H_i ) at vertex i can be computed as

$${\mathbf{H}}_{\mathbf{i}}=\frac{1}{4A_i}\sum _{{\mathbf{v}}_j\in N_i}(cot{\alpha }_{ij}+cot{\beta }_{ij})({\mathbf{v}}_i-{\mathbf{v}}_j),$$ (15)

where H_i = H_i n_i is the mean curvature normal, and n_i is a unit vector representing an estimated surface normal at vertex i. The sign of H_i can be determined by the sign of H_i · n, where n is the normal of any of the triangles incident to vertex i. Here, v_i and v_j are the coordinates of vertex i, and j, α_ij and β_ij are the opposite angles of the same edge in two triangles incident to the edge (see, e.g., Figure 2 right).

If an estimated curvature tensor is required, a commonly used approach is to take the average of the curvature tensor evaluated on the edges inside a certain neighborhood [96]

$$\mathbf{C}({\mathbf{v}}_i)=\frac{1}{A_i^{\prime }}\sum _{{\mathbf{e}}_j\in E({\mathbf{v}}_i)}\beta ({\mathbf{e}}_j)l_j{\overline{\mathbf{e}}}_j{\overline{\mathbf{e}}}_j^T,$$ (16)

where C(v_i) is the estimated curvature tensor at vertex i expressed as a symmetric 3 × 3 matrix in the global Euclidean coordinates, and $A_i^{\prime }$ is the area of a specific neighborhood, for which common choices include, for example, the intersection of a sphere which gives radius around i, a geodesic disk on the surface around i, or the one-ring of vertex i. Here, E(v_i) is the set of all edges intersecting the neighborhood around vertex i, β(e_j) is the signed dihedral angle between the normals of the faces sharing edge e_j (negative when the faces bend towards the surface normal and positive otherwise), ē_j the unit direction along e_j (choosing either orientation of the edge will result in the same tensor), (·)^T denotes the matrix transpose operation, and l_j is the length of the part of edge e_j inside the neighborhood. To find two principal curvatures and two principal directions, one may perform an eigen-decomposition of C(v_i). The eigenvalue with the smallest absolute value is always nearly 0, and the associated eigenvector is an estimate of the local surface normal. Other two eigenvalues are the principal curvatures, and their associated eigenvectors are two principal directions in the tangent plane. The larger the chosen neighborhood is, the less accurate the result is. However, choosing an overly small neighborhood results in noisy estimates when the resolution of the mesh is low.

2.6. Volumetric meshing

Volumetric meshing refers to the interior meshing. It is possible to generate tetrahedron meshes directly from 3D images with theoretical bounds on dihedral angles using algorithms such as isosurface stuffing [97]. Isosurface stuffing uses regular patterns to tetrahedralize grid cells completely inside the surface, followed by a marching-cubes-like boundary treatment, which shifts some of grid points near the boundary for attaining a better element shape. The algorithm is extremely fast, and the surface can approximate smooth isosurfaces well under reasonable assumptions, but the element shape is not optimal, and its adaptivity is restricted to octree-like structures.

Other available popular algorithms include TetGen [72] and NetGen [98], both providing user control on the size and shape of tetrahedra. The NetGen can take either a constructive solid geometry (shapes composed of primitive shapes combined through Boolean operations, i.e, union, intersection, and subtraction) or a boundary surface representation. However, NetGen can be less robust than other algorithms, such as TetGen [99]. TetGen produces tetrahedron meshes through constrained Delaunay tetrahedralization. If the tetrahedron mesh is required to conform to a boundary triangle mesh, the TetGen can be the method of choice. However, restricting the boundary to the given mesh can make the quality of the volumetric mesh dependent on the surface triangle mesh given by the user.

Another recent algorithm using interleaved Delaunay refinement and mesh optimization [100] can generate quality meshes that satisfy a set of user-defined criteria, which can be useful, for example, when importance of the sampling density is determined by the local chemical structure. In the Delaunay refinement step, sample points are inserted to satisfy the user-specified quality requirements. In the optimization step, a target function called the optimal Delaunay triangulation energy is used, whose minimization leads to a high-quality mesh. A final step perturbing the locations of vertices of slivers (flat tetrahedra) further improves the mesh quality.

3. RESULTS AND DISCUSSION

In this section, we examine the accuracy and demonstrate the usefulness of the methods and algorithms presented in the last section. A collection of all cryo-EM data can be found at the EMDataBank (http://emdatabank.org/index.html), which was established to create a global deposition and retrieval network for cryo-EM maps and associated metadata. It also works as a portal of software tools for standardized map format conversion, segmentation, model assessment, visualization, and data integration. A list of EM software can be found in the website (http://emdatabank.org/emsoftware.html). Cryo-EM data are stored as a 3D grid of voxels (volumetric cell), each with a value corresponding to the density of electrons. The data format was developed by the Medical Research Council Laboratory of Molecular Biology and is supported by almost every molecular graphics software that supports volumetric data, such as visual molecular dynamics, PyMOL (http://www.pymol.org/), UCSF Chimera (http://www.cgl.ucsf.edu/chimera/), and so on. The Medical Research Council file format is used in cryo-EM data, and its specifications can be found from the website (http://ami.scripps.edu/software/mrctools/mrc_specification.php).

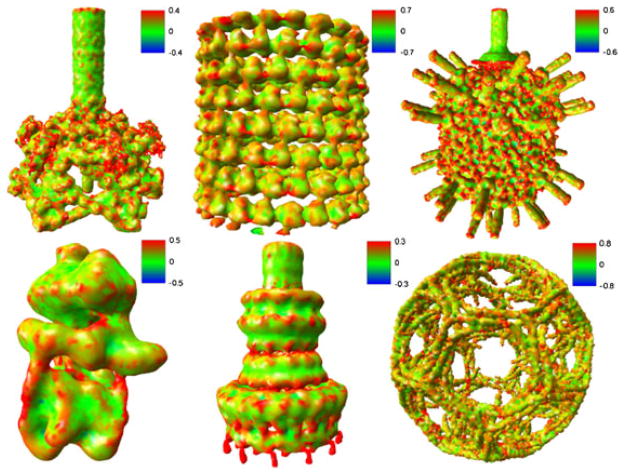
In the present work, we consider six representative cryo-EM maps from the EMDataBank. With the help of visualization tool visual molecular dynamics (http://www.ks.uiuc.edu/Research/vmd/), we extract their surfaces with the recommended iso-values, and the results are displayed in Figure 4. The details of these data are summarized as follows.

Figure 4.

Image gallery of representative cryo-electron microscopy maps used in this study. The visual molecular dynamics is used for visualization.

• Figure 4A (EMD1048): The baseplate of bacteriophage T4. It is a multiprotein molecular machine that controls host cell recognition, attachment, tail sheath contraction, and viral DNA ejection.

• Figure 4B (EMD1129): GDP-tubulin. It is a GDP-bound tubulin. The rope-like polymers of tubulin, which are components of the cytoskeleton, can grow as long as 25 μm and are highly dynamic.

• Figure 4C (EMD1265): Bacteriophage φ29. It is a viral DNA-packaging motor, which translocates and compresses genomic DNA with tremendous velocity into a preformed protein shell (the procapsid).

• Figure 4D (EMD1590): Manduca sexta vacuolar ATPase complex. It is a V-ATPase, which acidifies a wide array of intracellular organelles and pumps protons across the plasma membranes. V-ATPases couple the energy of ATP hydrolysis to proton transport across intracellular and plasma membranes of eukaryotic cells.

• Figure 4E (EMD1617): Shigella flexneri T3SS needle complex. The type three secretion system (T3SS) is a protein appendage found in several Gram-negative bacteria. In pathogenic bacteria, the needle-like structure is used as a sensory probe to detect the presence of eukaryotic organisms and secrete proteins that help the bacteria infect them.

• Figure 4F (EMD5119): Clathrin coats. It is a polyhedral lattice that surrounds the vesicle to safely transport molecules between cells. The endocytosis and exocytosis of vesicles allow cells to transfer nutrients, to import signaling receptors, and to mediate an immune response.

3.1. Data denoising and surface extraction

In this work, we explore our integrated tools on EMD datasets to test the strategies proposed used for geometric modeling. Six different EMD objects shown in Figure 4 are employed for the present study. It can be seen from Figure 4 that the electron tomography sometimes produces extremely noisy and low contrast 3D density maps. The poor signal-to-noise ratio (SNR) hinders visualization and interpretation. Therefore, some noise filtering techniques are indispensable. Many important methods and schemes, like wavelet transform techniques, nonlinear anisotropic diffusions, Beltrami flow, bilateral filter, and iterative median filtering have been used for noise reduction [12, 15–19, 101]. In this work, to improve the noise removal, we make use of the high-order geometric flows. Basically, it is a set of high-order geometric PDE based low-pass filters for image processing or surface analysis. An example of noise removal of EMD1617 is demonstrated in Figure 5. The basic structure of the T3SS needle complex is preserved while the noise amplitude is dramatically reduced. During the process of noise reduction, the surface of the protein is smoothed. Artificial sharp edge and sharp tips are naturally removed. From the energy minimization point of view, these features are not favorable in the biological surface formation [9]. Therefore, the loss of these features does not lead to degradation in accuracy when dealing with biological data.

Figure 5.

Noise reduction of EMD1617. Left: before filtering; right: after filtering by high-order geometric PDEs.

Among those surface extraction methods, shown in Section 2.3, we compare the results of the marching cubes method and CGAL’s Delaunay-based method in Figure 6. The marching cubes method is highly parallelizable because the lookup table used is precomputed and stored. For all the files that we tested, it costs less than 5 s to process a cryo-EM map with up to 200 × 200 × 200 Cartesian grids. The direct result from marching cubes for EMD1590 shows that it may have a large number of skinny triangles, and the overall shape may contain terracing artifacts for a large proportion of the triangles. Many triangles have sharp angles less than 30°. The lack of element quality control is the intrinsic weakness of the marching cubes methods. Thus, the result often needs postprocessing to improve the mesh quality. It may also require a large number of triangles to store (14,170 vertices and 28,360 triangles in the example shown) at a given accuracy due to the lack of adaptivity.

Figure 6.

Comparison of surface meshes. Top: marching cubes result of EMD1590; bottom: Computational Geometry Algorithms Library result of EMD1590.

On the other hand, CGAL’s running time and generated surface mesh quality depend heavily on the criteria chosen for the Delaunay triangulation. The criteria are controlled by three parameters: angular bound for mesh triangles’ minimal angle, radius bound for the maximum surface Delaunay balls’ radius (a surface Delaunay ball circumscribes a mesh triangle and centered on surface), and distance bound for the maximum distance between triangle’s circumcenter and surface Delaunay ball center. However, these parameters can usually be easily tuned to achieve proper results with appropriate triangle shapes and sizes given some domain knowledge of the intended application. We use 30° as the angular bound, 0.8 as the radius bound, and 0.8 as the distance bound to directly extract the EMD1590 surface mesh from its cryo-EM map file. It takes about 4 s to run the algorithm to obtain the extracted surface with 10,100 vertices and 20,220 triangles. If we set smaller parameter values, we will obtain more detailed models but may suffer from longer running time and increased mesh size due to the smaller mesh triangles. Compared with the marching cubes result for EMD1590, the CGAL result gives triangle angles always greater than 30°, triangles with almost the same size, and reduced mesh sizes without losing surface shape accuracy, as shown in Figure 6.

The histograms of the triangle angle for both meshes are given in Figure 7. From the figure, one can see that the angles in the marching cubes results have a large distribution in the low range, which may result in accuracy problems in mathematical modeling involving PDEs. In contrast, CGAL’s results are guaranteed to meet the angle requirements while reducing the mesh size significantly.

Figure 7.

Comparison of surface mesh angle distributions. Left: angle histogram of marching cubes result of EMD1590; Right: angle histogram of Computational Geometry Algorithms Library isosurface extraction result of EMD1590.

3.2. Surface mesh improvement

The surface generated from the marching cubes method or its variants often does not fit the need of applications relying on finite element, finite difference, or finite volume methods, such as geometric reconstruction of the internal structure or numerical simulation of electrostatics [1, 8, 10, 102, 103]. The process of creating a mesh that satisfies the new requirements while remaining close to the original mesh is called remeshing [104]. For instance, the mesh for EMD1590 produced by the marching cubes method can be remeshed into a mesh with rather uniform well-shaped triangles as shown in Figure 8. Even for meshes with well-shaped elements (for triangle meshes, this means nearly equilateral triangles, measured by the ratio of the circumcircle radius to the length of the shortest edge [105]), it is still possible to perform remeshing to reduce vertex count while remaining faithful to the original underlying surface. In this case, the procedure is also called mesh simplification.

Figure 8.

Mesh improvement with Delaunay remeshing. Left: marching cubes result of EMD1590; Right: remeshing result using the result to the left as the input.

Figure 9 presents a collection of meshes of six cryo-EM maps generated by using the CGAL approaches. The bacteriophage φ29 and clathrin lattice have small-scale features. In particular, clathrin lattice data are quite noisy. It is seen from Figure 9 that the CGAL library is very robust and reliable for cryo-EM meshing.

Figure 9.

Computational Geometry Algorithms Library results of surface meshes. From upper left to lower right: EMD1048, bacteriophage T4 baseplate [106]; EMD1129, GDP-tubulin [107]; EMD1265, bacteriophage φ29 [108]; EMD1590, vacuolar ATPase motor [109]; EMD1617, Shigella flexneri T3SS needle complex [110]; and EMD5119, clathrin lattice [111].

3.3. Areas, volumes and curvatures

Surface areas and surface-enclosed volumes are frequently used in mathematical models of biomolecular systems [1, 8, 10, 86]. Accurate estimation of surface areas and surface-enclosed volumes is important in theoretical biology. The validation of the presented numerical methods is described in the succeeding paragraphs.

We compute surface areas and surface-enclosed volumes for spheres with different radii by the proposed methods and give the comparison between the theoretical values and their estimates in Table II. The radii used in our tests are 1, $\sqrt{2}$, and $\sqrt{3}$, whose theoretical values of area and volume are straightforward to compute. It can be seen that the straightforward methods proposed in this work are accurate for the high-quality meshes generated using the proposed methods.

Table II.

Comparison of theoretical values and computer estimate of sphere’s areas and volumes.

Radius	Total area (est.)	Total area (theo.)	Total volume (est.)	Total volume (theo.)
1	12.53	12.57	4.16	4.19
$\sqrt{2}$	25.09	25.13	11.81	11.85
$\sqrt{3}$	37.66	37.70	21.72	21.77

As shown in Section 2.5, the curvature at a point on the surface describes the local geometric feature. Curvature analysis is useful for the identification of protein–protein and protein–ligand interaction sites. It can also be used to help understand the protein–DNA binding specificity. In this work, we first validate the accuracy and convergence order of the numerical methods proposed in Section 2.5. We then demonstrate the usefulness of these methods for cryo-EM data analysis.

As discussed in Section 2.5, around each vertex, the one-ring area can be chosen in two different ways, the barycentric dual cell area and the Voronoi cell area. The accuracy of these approaches are examined by spheres of radii (r) 1, $\sqrt{2}$, and $\sqrt{3}$. Their Gaussian and mean curvatures are given by 1/r² and 1/r, respectively. These spheres are tessellated with triangles of similar sizes. The results of estimated curvatures obtained with the barycentric dual areas are shown in Table III, together with theoretical values. Both our results for both Gaussian and mean curvatures are accurate in the tests. The resulting standard deviations show that the difference between the computed value and the theoretical value is small relative to the mesh size. For a comparison, we also listed our results obtained with the Voronoi dual areas in Table IV, under the same mesh. It is seen that the curvatures computed with the Voronoi dual areas are essentially the same as those with the barycentric dual areas. However, the Voronoi dual area approach offers smaller standard deviations in Gaussian and mean curvature estimations than does the barycentric dual area approach. Therefore, the Voronoi dual area approach performs better and is utilized in the rest of this work.

Table III.

The curvatures estimated using barycentric dual cell area.

radius	μK	${\sigma }_K^2$	Ktheo	μH	${\sigma }_H^2$	Htheo
1	1.003239	0.026352	1	1.000031	0.018632	1
$\sqrt{2}$	0.500804	0.011344	0.5	0.707106	0.011323	0.707107
$\sqrt{3}$	0.333685	0.009292	0.333333	0.577343	0.010881	0.577350

Here, μ_K (resp., μH) is the average of Gaussian curvature K (mean curvature H), ${\sigma }_K^2\left({\sigma }_H^2\right)$ is the standard deviation of K (H), and K_theo (H_theo) is the theoretical value of K (H).

Table IV.

The curvatures estimated using Voronoi cell area.

Radius	μK	${\sigma }_K^2$	Ktheo	μH	${\sigma }_H^2$	Htheo
1	1.003238	0.010534	1	1.000030	0.002627	1
$\sqrt{2}$	0.500804	0.007382	0.5	0.707107	0.003701	0.707107
$\sqrt{3}$	0.333684	0.007158	0.333333	0.577343	0.005481	0.577350

Here, μ_K (resp., μH) is the average of Gaussian curvature K (mean curvature H), ${\sigma }_K^2\left({\sigma }_H^2\right)$ is the standard deviation of K (H), and K_theo (H_theo) is the theoretical value of K (H).

To further explore the accuracy and convergence of our curvature estimate, we design tests on different analytical models with different geometric types, including all cases of the intrinsically nonflat ones, namely, peak, pit, saddle ridge, minimal surface, and saddle valley. The pit type is identical to the peak case because of the symmetry. Specifically, the test results on a patch of a sphere are shown here (Figure 10). The convergence orders of our curvature method are measured by L_∞ and L₂ error norms. Tables V and VI show the orders for Gaussian curvature and mean curvature, respectively. The average L_∞ order is about 1.4, whereas the second accuracy is achieved for the L₂ order. These results indicate the robustness and reliability of the proposed methods for curvature evaluation.

Figure 10.

The analytical geometry model: a patch of a sphere.

Table V.

The convergence orders for Gaussian curvatures on a patch of a sphere.

Maximal edge length	L∞	Order	L2	Order
1.00 × 10−1	8.325 × 10−3		4.815 × 10−3
5.00 × 10−2	2.676 × 10−3	1.64	1.149 × 10−3	2.07
2.50 × 10−2	1.031 × 10−3	1.38	2.803 × 10−4	2.04
1.25 × 10−2	4.544 × 10−4	1.18	6.920 × 10−5	2.02

Table VI.

The convergence orders for mean curvatures on a patch of a sphere.

Maximal edge length	L∞	Order	L2	Order
1.00 × 10−1	1.275 × 10−3		5.228 × 10−4
5.00 × 10−2	3.441 × 10−4	1.89	1.409 × 10−4	1.89
2.50 × 10−2	8.820 × 10−5	1.96	3.623 × 10−5	1.96
1.25 × 10−2	2.226 × 10−5	1.99	9.167 × 10−6	1.98

3.3.1. Applications of curvature estimates cryo-electron microscopy to maps

Having established the accuracy and convergence of proposed numerical methods for curvature estimation, we apply these methods for the curvature calculation of six cryo-EM map entries. Note that these complexes vary in dimensions. The absolute value of curvatures increases as the dimension decreases as shown in the analytically expressions given in the last section.

First, we evaluate Gaussian curvatures and illustrate the results in Figure 11. Because the Gaussian curvature is an intrinsic measure of curvature and does not depend on the surface embedding, it is a convenient tool for identifying peak, pit, saddle ridge, and saddle valley. These features are clearly demonstrated in Figure 11. Taking the Shigella exneri T3SS needle complex as an example, Gaussian curvatures are mostly negative along the ring regions, which can be identified as saddle valleys, whereas Gaussian curvatures are positive on peaks and noisy dots.

Figure 11.

Gaussian curvature estimates for six cryo-electron microscopy map entries.

We next consider the mean curvatures of six cryo-EM map entries. In contrast to the Gaussian curvature, mean curvature is an extrinsic measure of curvature, and it reflects the local characteristic of a surface. Figure 12 plots the mean curvature maps of six biomolecular complexes. Overall, mean curvatures are mostly positive for these complexes, indicating the main geometric features of peaks, ridges, and noisy dots. However, regions with very negative mean curvature can be found for pits and valleys, which are clearly potential binding targets of other smaller compounds.

Figure 12.

Mean curvature estimates for six cryo-electron microscopy map entries.

To further utilize the power of the present curvature estimates, we investigate the behavior of the first and second principal curvatures. The accuracy and convergence of the present curvature estimates established in the last section enable us to accurately compute principal curvatures as well by Equations (11) and (12). The maximum curvatures, κ₁, are plotted in Figure 13. It is interesting to note that the maximum curvature is a very good indicator for peaks and ridges of the biomolecular complex and possible noisy dots. Therefore, with a good confidence, one can exclude these regions with very large positive κ₁ values from being targets of small binding compounds.

Figure 13.

Maximum curvature (κ₁) estimates for six cryo-electron microscopy map entries.

Finally, we investigate the behavior of the minimum curvature, κ₂. Results are depicted in Figure 14 for six cryo-EM entries. As expected, large negative curvatures indicate pits and valleys (pockets), which are potential binding sites of small compounds. We believe that the second principal curvature can be used as a promising binding indicator for practical docking, drug design, and protein design analysis. This aspect, together with the electrostatic analysis, is further analyzed elsewhere for proteins [112].

Figure 14.

Minimum curvature (κ₂) estimates for six cryo-electron microscopy map entries.

3.4. Volumetric meshing

If a Lagrangian surface readily exists, its volumetric meshing is a separate task. There are a number of strategies for volumetric meshing. First, we can tetrahedralize the surface mesh files by using CGAL library functions. To reduce the work load of the tetrahedralization process, we use CGAL to extract the surface mesh with nearly same-sized triangles. Then, we use CGAL’s tetrahedralization functionality to produce the tetrahedron mesh. The CGAL API function has five parameters to fine tune the tetrahedralization process: angular bound for surface mesh triangles’ minimal angle, triangle size bound for the maximum surface Delaunay ball radius, triangle distance bound for the maximum distance between a triangle’s circumcenter and the surface Delaunay ball center, cell radius edge ratio bound for the maximum ratio of the circumradius of a cell to its shortest edge, and cell size bound for the maximum cell circumradius. Setting smaller values for the latter three parameters will lead to more sampling points in the tetrahedralization step, which will increase the number of vertices and tetrahedra in meshes. If the user needs smaller cells near the surface mesh and larger cells far from the surface mesh, a large cell size and small surface triangle size bound could be adopted. The CGAL library tetrahedralization process has provable guarantees on the surface mesh quality, through tetrahedralization of the interior regions with constrained Delaunay triangulation.

TetGen is another popular choice for tetrahedralization step with high performance. The TetGen library has a large number of parameters to easily meet various requirements by the users. The most commonly modified parameters for tetrahedralizing a surface mesh is the maximum volume constraint on tetrahedron and the cell radius edge ratio bound. The default value of the cell radius edge ratio bound is 2.0, which can be lowered by the user to remove most cases of low-quality element shapes. A comparison of the results from TetGen and CGAL is given in Figure 15. As the surface triangle meshes are of similar good quality, both produced satisfiable results.

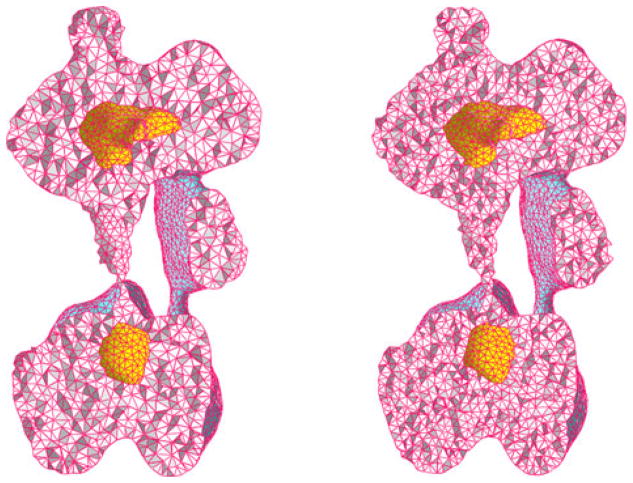
Figure 15.

Comparison of volumetric meshing for an EMD1590 cut open in the middle. Left: TetGen result; Right: Computational Geometry Algorithms Library result.

To observe the quality of the tetrahedron meshes generated by the proposed methods, we can show the planar cross-sectional views of the tetrahedron meshes as in Figure 15. Alternatively, we can also observe the internal structure by generating a cross section by removing a connected piece of volume as shown in Figure 16. For this purpose, we first choose a surface face as a seed face, then use breadth-first search algorithm to find a number of tetrahedra connected to the seed face. If we set a constant number of tetrahedra to remove as the stop criterion, we can expose the internal elements in a curved cross section at approximately the same distance from the seed face. This gives us a cutaway view to illustrate the interior meshing quality after tetrahedralization.

Figure 16.

Cross section view of Computational Geometry Algorithms Library result of EMD1590.

Both CGAL and TetGen share a parameter to tune the cell radius edge ratio bound of a generated tetrahedron. This parameter is highly effective in controlling the quality of the tetrahedra. All well-shaped tetrahedra have small values (less than 3) for the ratio, and most of the badly shaped tetrahedra have large values. This does not mean that the limit can be set arbitrarily small, because the value has a lower bound of 0.612 (the value for an equilateral tetrahedron). The one case of a badly shaped tetrahedron with small (cell radius to shortest edge) ratio is called ‘sliver’, which has a flat and near-degenerate shape. Its cell radius edge ratio can go as low as 0.707. One effective way to prevent slivers from being created is to incorporate a minimum volume constraint or to employ a procedure called sliver exudation as is done in CGAL.

4. CONCLUSION

One of the most important new trends in structural biology is the investigation of the structures, functions, and dynamics of subcellular structures, organelles, and large multiprotein complexes. Currently, a main workhorse for this investigation is the cryo-EM. However, cryo-EM maps are well known for their low resolution and low reliability. Geometric modeling provides tools for improving cryo-EM resolution and bridges the gap between molecular structures and mathematical modeling, which is necessary for the understanding of the function and dynamics of subcellular structures and complexes. This work presents a comprehensive protocol for the geometric modeling of cryo-EM data and other volumetric density distributions used in macromolecules. We first introduce high-order geometric PDEs for noise removal of cryo-EM data and volumetric data. High-order geometric PDEs are more efficient for denoising because they have controllable time-frequency localization and can be tuned up for specific noise distribution. Additionally, we discuss two surface extraction schemes, the regular marching cubes, and the CGAL. Moreover, we explore efficient and reliable algorithms for volumetric meshing of macromolecular complexes, bearing in mind the further needs of other geometric tasks. Furthermore, we discuss some simple but robust schemes for the estimation of surface areas and surface-enclosed volumes based on the Lagrangian triangle-based surface representation. Finally, we introduce barycentric dual cell and Voronoi cell approaches for surface curvature estimations of biological complexes. We present explicit formula for evaluating conventional Gaussian curvature and mean curvature. On the basis of these curvatures, one can calculate the first and second principal curvatures as well.

The computational methods and algorithms introduced in the present work are carefully validated for their accuracy and convergence by analytically solvable systems. We show that the simple methods based on triangle meshes work well for estimating surface area and surface-enclosed volumes. The second-order convergence of Gaussian and mean curvature estimations, particularly in the L₂ norm, has been numerically observed. The L_∞ norm is also of second-order accuracy for the mean curvature calculations. Therefore, the resulting Gaussian and mean curvatures can be directly used for calculating two principal curvatures. The rigorous validations conducted in the present work provide us with empirical evidence in applying the proposed methods to the geometric analysis of cryo-EM data and other volumetric data for biomolecular systems with high-quality meshes, despite the known fact that these curvature estimates do not converge when there is no control over mesh quality.

Extensive applications are considered to cryo-EM data denoising, surface extraction, volumetric meshing, surface area and volume calculation, and curvature analysis. To this end, we utilize a total of six representative cryo-EM complexes, including bacteriophage T4 baseplate [106], GDP-tubulin [107], bacteriophage φ29 [108], vacuolar ATPase motor [109], Shigella flexneri T3SS needle complex [110], and clathrin lattice [111]. We have demonstrated the efficiency of high-order geometric PDEs for noise removal of cryo-EM data. We also investigate the performance of marching cubes and CGAL schemes for surface extraction. Marching cubes method is readily parallelizable and is recommended for applications that do not require well-shaped elements. Whereas, if high-quality meshes are needed, the CGAL is a better choice. The comparison among different methods has been carried out for triangle meshing. Specifically, we analyze the performance of four algorithms, the isosurface stuffing [97], TetGen [72], NetGen [98], and Delaunay refinement and interleaved mesh optimization [100] for the volumetric meshing of biomolecules. TetGen and NetGen both perform well, while the last one is very suitable for quality improvement, capable of remeshing the surface from possibly low-quality surface mesh inputs. Interesting results are found in curvature analysis. It is found that the maximum and minimum curvature maps of cryo-EM complexes can be used for binding site characterization. Specifically, the maximum curvature can also be used to exclude regions from the binding targets of small molecules, whereas the minimum curvature serves a promising indicator of binding targets. These findings will be further investigated by combining curvature and electrostatic characteristics in our future work [112].