Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Dec 1.
Published in final edited form as: J Muscle Res Cell Motil. 2012 Jun 30;33(6):431–437. doi: 10.1007/s10974-012-9310-0

The Velocity of Cardiac Sarcomere Shortening; Mechanisms and Implications

Pieter P de Tombe 1, Henk EDJ ter Keurs 2,*
PMCID: PMC3568939  NIHMSID: NIHMS438990  PMID: 22752243

Abstract

A classical paper published by Michael Barany almost 50 years ago demonstrated a tight correlation between the mechanical parameter of maximal velocity of shortening and the biochemical parameter of myosin ATPase activity in a wide spectrum of species. Here, we review the determinants of muscle dynamics by mechanical load and the relation between sarcomere shortening velocity and cross-bridge dynamics in rat myocardium containing a range of fast and slow myosin. Observations from molecular level to mechanics of the intact human heart suggest that cardiac actin-myosin kinetic properties are matched so as to optimize myocardial strain rate and allow for the maximum rate of hydraulic energy output observed during ejection in the whole ventricle.

Keywords: Sarcomere, Velocity of Muscle Shortening, Heart, Myosin, ATPase, Muscle Mechanics

INTRODUCTION

Barany has convincingly shown that the maximal velocity of muscle shortening tightly correlates with the rate of energy conversion from ATP by the myofibril (Barany, 1967). Further studies have shown that the nature of the myosin heavy chain (MHC) composition dictates the rate of ATP hydrolysis by the cross bridges (Sieck and Regnier, 2001). These finding are basic to the dynamic properties of muscle in general as well as to the properties of cardiac muscle, where mechanical power output of the left ventricle (LV) is finely tuned to the impedance of the arterial system (Toorop et al., 1988).

A few numbers about a slender person (~70 kg) readily illustrate this. This person’s left ventricle (165 g muscle mass) ejects ~70 mL blood in 0.4 s from an end diastolic volume of 115 mL for a cardiac output of 5 litres/minute at rest. The peak ejection rate (.3 L/s; (Bacharach et al., 1979)) is accompanied by a peak circumferential strain rate of ~−1.6/s (Petersen et al., 2011). Laplace’s Law predicts that, if the arterial pressure of this individual is 13.3 kPa, wall stress during peak ejection is ~ 17kPa, or one third of the maximal stress (Kentish et al., 1986). A hyperbolic relationship between muscle shortening velocity and muscle load was described in the first half of the 20th century (Hill, 1938), predicting that power output is maximal when muscle shortens at this level (~1/3 of isometric force) of mechanical loading. Elzinga and collaborators have indeed shown that power transfer from the LV into the arterial bed is kept maximal, even during cardiac hypertrophy (Horn et al., 1985; Petersen et al., 2011). It is evident that mechanical energy output by the myocardial sarcomeres is responsible for these properties.

Sarcomere length (SL) in the heart in vivo – as well as in in vitro experiments- ranges between 1.55 μm and 2.35 μm, which covers the ascending limb of the force length relationship (Rodriguez et al., 1992). In turn, the velocity of sarcomere length change (VSL) is determined by ‘Hill’s’ hyperbolic function and this allows for a balance of force between the billions of sarcomere that are connected in series in the LV wall (ter Keurs et al., 2010). Regulation of this hyperbolic function is achieved by both variation of the maximal VSL, which depends on the MHC composition and by the maximal isometric stress that can be generated in response to inotropic and trophic stimuli (Ricciardi et al., 1986; ter Keurs et al., 1989). Power output, equalling the product of VSL and the developed stress, is consequently regulated by these factors as well (McDonald, 2011).

We will review the factors that dictate VSL in isolated cardiac muscle here and discuss the impact of these factors on the energetics of the heart. Much work on sarcomere shortening has been done on isolated cardiac fascicles or trabeculae that can be found on the endocardial side of the ventricles in many species, including mouse, ferret, cat, pig, rabbit and man, but the main source over the years has been the rat right ventricle (ter Keurs, 2012). Figure 1 illustrates a rat right ventricular trabecula attached to a motor via a hook through the remnant of the tricuspid valve on the right end side, and a platinum basket holding a block of free right ventricular wall tissue that is attached to a force transducer on the left hand side (van Heuningen et al., 1982; de Tombe and ter Keurs, 1990b). It has been shown by Loiselle and collaborators that these trabeculae are virtually identical to the fascicles that comprise the wall of the heart (Loiselle et al., 2008). The attraction of using these thin (usually <200 μm wide and < 100 μm thick), but several mm long free running muscles (cf. Figure 1) is that the mechanical load on the sarcomere is uniform throughout the cross section of the muscle, while the mechanical properties can be studied at sarcomere level by using light diffraction techniques, while loading the specimen with Ca2+ sensitive fluorescent dyes permits continuous measurement of the cytosolic [Ca2+]i. (Backx and ter Keurs, 1993) (Janssen and de Tombe, 1997b).

Figure 1.

Figure 1

Open in a new tab

Isolated rat right ventricular endocardial trabecula attached to a high-speed motor via a hook inserted through a remnant of the tricuspid valve on the right hand side, and a block of free wall ventricular tissue held within a platinum basket attached to a sensitive force transducer on the left hand side. The small axial dimensions (<200 μm wide and <100 μm thin) of these ultra-thin myocardial preparations both ensure adequate oxygenation and waste product removal as well as allow for the measurement of high-speed sarcomere length by laser diffraction techniques; longitudinal uniformity (2–5 mm in length) allow for unambiguous sarcomere mechanics measurement under strict sarcomere length feedback control.

FORCE DEVELOPMENT

The mechanical properties of trabeculae from different species reveal many similarities. The action potential induces rapid Ca2+ release from the sarcoplasmic reticulum, which brings the muscle uniformly from an exquisitely compliant passive structure, to an impressive maximal stress development of ~80 kPa (Kentish et al., 1986). This level of stress development is more than sufficient to generate the end-systolic pressure of the normal LV. Four major factors dictate active force development: [Ca2+]i in the cytosol of the myocytes, the phosphorylation status of contractile proteins, SL and the velocity of sarcomere shortening. The latter two parameters are important to maintenance of force in muscle in which the activation is non-uniform (see below). The relationship between SL and force show little dependence on shortening before peak force of the twitch and forms the basis for the well known end-systolic force-sarcomere length relationship (ter Keurs et al., 1980; Burkhoff et al., 1987; Rodriguez et al., 1992), which underlies the end-systolic Pressure-Volume relationship of the pump chambers of the heart (Suga and Sagawa, 1974). [Ca2+]i and the sensitivity of the contractile proteins to Ca2+ ions dictate force generation at any sarcomere length, and these parameters underlie the inotropic state of the heart. In ‘in vitro’ experiments, sarcomeres shorten during the contraction because they are able to stretch the connections of the muscle with the recording equipment. Measurement and control of SL allows the experimenter to circumvent this confounding factor; when sarcomere shortening is prevented, it is clear that both the magnitude and the time course of the force of contraction are length dependent (ter Keurs et al., 1980) (de Tombe and Little, 1994)

THE FORCE VELOCITY RELATIONSHIP

Cardiac Sarcomeres

VSL measured in trabeculae harvested from rodent hearts, such as the rat that express predominantly the αMHC isoform (Hoh et al., 1978), obeys Hill’s hyperbola quite accurately up to 80% of Po and then declines slightly more rapidly than the hyperbola predicts, a phenomenon that has been observed in skeletal muscle as well (de Tombe and ter Keurs, 1992; Edman, 1988). On the other hand, the force- VSL relationship still obeys a hyperbolic relationship reasonably well if data on force development during stretch are incorporated (ter Keurs et al., 2010). This fundamental property of muscle indicates that mechanical power output by the collective of cross bridges is rigorously controlled (note that VSL reflects twice the sliding velocity of the contractile filaments). Figure 2 illustrates force-sarcomere velocity relationships and force-power relationships determined in rat cardiac trabeculae harvested from euthyroid (αMHC myocardium) and hypothyroid rats (βMHC myocardium); as discussed below, myocardium containing the slower myosin isoform shorten at a slower rate and produce less maximum power at ~30% mechanical loading compared to myocardium containing the faster myosin isoform. These experiments also revealed that instantaneous muscle stiffness varies steeply with the load (de Tombe and ter Keurs, 1992).

Figure 2.

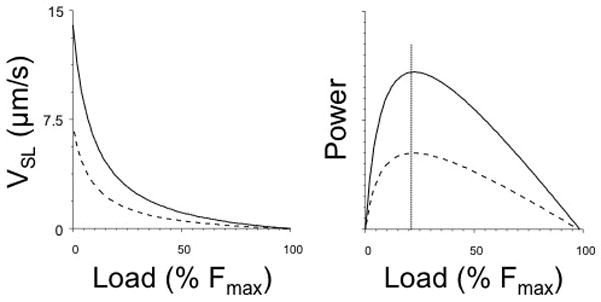
Figure 2

Open in a new tab

Force-sarcomere velocity relationships (left panel) and Force-Power relationships (right panel) determined in isolated rat myocardium composed of predominantly α myosin (solid lines) or β myosin (dashed lines). Expression of the slower β myosin results in reduced sarcomere shortening velocity at all mechanical loads as well as reduced power development. Maximum power is generated at ~30% Fmax as indicated by the vertical dotted line. Modified from (de Tombe and ter Keurs, 1991a).

Cardiac Cross Bridges

Stiffness is a measure of the number of actin-bound cross bridges that collectively move the actin filament during contraction. Variation of muscle stiffness during sarcomere shortening and lengthening, therefore, implies that the number of attached cross bridges also varies. Hence, mechanical power output is controlled by the combined control of the rate of sliding of actin propelled by the cross bridge and by the number of attached and cycling cross bridges itself. Correction for the number of attached cross-bridges generates a tight linear relationship between sliding velocity of actin and the mechanical load of an average single cycling cross bridge (de Tombe and ter Keurs, 1992), as illustrated in Figure 3. Cross bridges composed of αMHC dimers (V1 myosin) as well as cross bridges composed of βMHC (V3 myosin) both obey this simple linear relationship, albeit that the slope of the former is ~2.5 times steeper than that of V3 myosin (ter Keurs et al., 2010), corresponding to the difference in unloaded shortening velocities of V1 and V3 myosin (de Tombe and ter Keurs, 1990b)(de Tombe & ter Keurs, 1991a). A similar linear relationship between VSL and load has been described in skeletal muscle (Haugen, 1988). Hence, the cross bridge of striated muscle behaves like a quasi viscous power generator, which behaviour is dictated by the maximal shortening velocity that can be attained in the absence of a mechanical load and is determined by 1) the MHC composition and its intrinsic biochemical properties, in line with Barany’s 1967 classical observation, and 2) by the maximal force that can be generated by attached and cycling cross-bridges when movement of the actin filament is prevented, which is determined by the force generating capacity of a single cross-bridge and the number of attached and cycling cross bridges. Because of the linearity of the force-velocity relationship of a single cross bridge, maximal power generation of the single cross bridge occurs at 50% of isometric force (cf. Figure 3).

Figure 3.

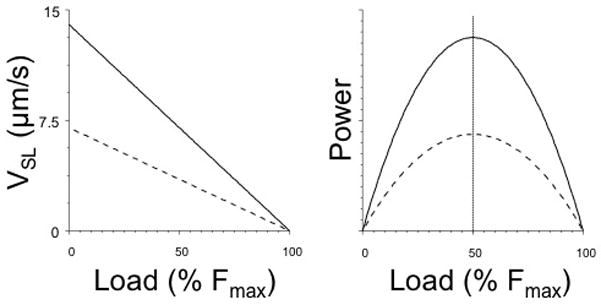
Figure 3

Open in a new tab

Average single cross bridge Force-sarcomere velocity relationships (left panel) and Force-Power relationships (right panel) prediction based on measurement of sarcomere stiffness during sarcomere shortening for α myosin (solid lines) or β myosin (dashed lines). The attached cycling cross bridges behave mechanically as a visco-elastic unit, where shortening velocity is linearly inversely proportional to muscle load. Maximum power at the single cross bridge level is generated at 50% Fmax as indicated by the vertical dotted line. Modified from (de Tombe and ter Keurs, 1992; de Tombe and ter Keurs, 1991a; ter Keurs et al., 2010).

CONTROL OF THE NUMBER OF CROSS BRIDGES

The number of attached cross bridges (K) is determined by the attachment rate (f) and the detachment rate (g) of the bridges in steady state in the form of: K = f/(f + g) (Huxley, 1957). The observation that K is a hyperbolic function of VSL led to the hypothesis that g might be proportional to VSL as: g=go + g1*VSL (Landesberg et al., 2000). Moreover, that study revealed experimentally that linear sarcomere shortening ramps imposed on contracting cardiac muscle result in a force response that is dictated by a rapid component, reflecting the elastic properties of the attached and cycling cross bridges, followed by a decline of the number of attached cross bridges in proportion to the rate of SL shortening, exactly as predicted by the hypothetical parameter g1. This is illustrated in Figure 4 where predicted sarcomere stiffness (solid line) and the measured sarcomere stiffness is plotted as function of sarcomere velocity (Landesberg et al., 2000; de Tombe and ter Keurs, 1992). These studies suggest that Hill’s hyperbola is the product of a linear force-velocity relationship of the average cross bridge and the effect of a velocity dependent variation of the dissociation rate of the attached and cycling cross bridges from actin. The curvature of the hyperbola increases with increasing g1 and as a result the load/isometric force at which maximum power is generated decreases (Landesberg et al., 2000). Interestingly, the magnitude of g1 appears to be the same for the slow (V3) and fast (V1) isoforms of myosin and permit optimal power output at 30% of the isometric force (ter Keurs et al., 2010). Because g1 appears to be similar for fast and slow myosin, the VSLmax of myosin is the main factor that dictates the difference in power output by muscles that generate the same maximal stress. As a result, myosin isoform composition is the main determinant of the mechanical performance of the muscle.

Figure 4.

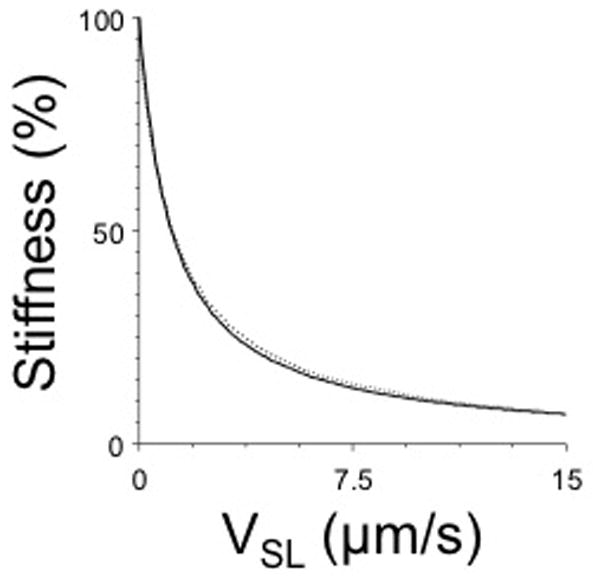
Figure 4

Open in a new tab

Relationship between muscle stiffness and sarcomere shortening velocity. The predicted relationship (solid line) is given by K = f/(go + g1•V); the dotted line indicates experimentally measured sarcomere stiffness. Since muscle stiffness is proportional to the number of attached cycling cross bridges, these data indicate that the number of attached cross-bridges declines (to ~12%) during maximal unloaded sarcomere shortening; a reduced number of cross bridges as function of sarcomere shortening causes the curved, hyperbolic force-sarcomere velocity relationship seen in muscle (cf. figure 2). Modified from (Landesberg et al., 2004; de Tombe and ter Keurs, 1992).

THE MAXIMAL VELOCITY OF SHORTENING (VSLmax)

VSLmax is independent of SL above slack length (1.86μm), but declines below slack length probably as a result of opposing force generated by the elastic structures in the muscle, notably titin and the collagen mesh that envelops the cells (Daniels et al., 1984). VSLmax at a SL = ~2.0 μm, i.e. where the elastic forces are negligible, depends on [Ca2+]o as a result of the viscous drag of the shortening cells (de Tombe and ter Keurs, 1992). These properties hold true when young adult rats with mostly V1 myosin are studied and when rats are studied with predominantly V3 myosin. The unloaded VSLmax for rat –mostly V1 myosin- is ~14 μm/s (at 27 C; [Ca2+]o 1.2 mM), i.e. nearly 2 times higher than the unloaded VSLmax of trabeculae from rats in which βMHC was induced by 1 month exposure to propyl-thiouracil (de Tombe and ter Keurs, 1991a). Moreover, as illustrated in Figure 5, the energetic and mechanical properties of rat myocardium are directly proportional to the relative composition of αMHC and βMHC in terms of maximal sarcomere shortening velocity (VSLmax), ATPase activity during maximal isometric force development (ATPasemax), the ratio of ATPase activity and force development (tension-cost), and the rate of force redevelopment following a mechanical length perturbation (ktr). Unloaded VSLmax varies in proportion to the distribution of fast and slow myosin (α and β MHC respectively). Moreover, it has been suggested that unloaded VSLmax is determined by the ADP dissociation rate of the attached and cycling cross-bridge (Siemankowski et al, 1985). The unloaded VSLmax of cat and ferret in which the heart contains a larger fraction of βMHC cross bridges than rodents is thus predictably 40 % lower than that of rat cardiac trabeculae under comparable conditions (de Tombe and ter Keurs, 1991b). Hence, power output by the heart is mainly regulated in these species by control of the expression of α or β forms of the myosin heavy chains during growth and during the response to hemodynamic loading. Given a certain distribution of isoforms, regulatory factors such as adrenergic drive and increased heart rate modulate excitation contraction coupling and, thereby, regulate power output by modification of intracellular [Ca2+] and the resultant variation in the number of attached and cycling cross bridges. VSLmax of both V3 and V1 myosin in rat cardiac trabeculae appears to be insensitive to beta-adrenergic stimulation, provided that [Ca2+]i in the trabeculae was maximized. This result suggest that PKA dependent phosphorylation of the contractile proteins does not modulate VSLmax (de Tombe and ter Keurs, 1991a; Janssen and de Tombe, 1997a). Whether contractile protein phosphorylation affects intrinsic actin-myosin interaction kinetics is not resolved, however (de Tombe and Stienen, 1995; Biesiadecki et al., 2007). Translation of these experimental data to power output of the heart in vivo requires information about the temperature dependence of VSLmax and g1. Information about temperature dependence of g1 is scarce, but VSLmax and other parameters have been studied in detail. These studies require sarcomere length control to avoid the effects of spurious sarcomere shortening against series elastic elements linking the muscle to the recording apparatus. Furthermore, the effect of raising the temperature of a trabecula is a decrease [Ca2+]i of the force as a result of a reduced sensitivity to extracellular [Ca2+]i. We have seen, in the above, that a viscous load limits VSLmax and this effect is most noticeable at submaximal activation levels. When [Ca2+]i is maximized in order to avoid this effect, the Q10 of VSLmax appears to be ~4.5(de Tombe and ter Keurs, 1990a; de Tombe and Stienen, 2007). Moreover, as is the case for the impact of myosin isoform composition (cf. Figure 5), temperature not only strongly affects VSLmax, but also the other mechano-energetic parameters such as isometric ATPase activity at maximum force development, tension-cost and the mechanical ktr parameter, as is illustrated by the Arrhenius temperature dependence plots of these parameters in Figure 6. Hence, based on these temperature dependence studies, VSLmax for V1 myosin at body temperature would be predicted at ~50 μm/s, and for V3 myosin ~30 μm/s. Maximal power would, therefore, be generated at a predicted circumferential strain rate of ~2/s in a V3 dominated heart such as that of our typical person, close to the maximal strain rate that is estimated for the human heart.

Figure 5.

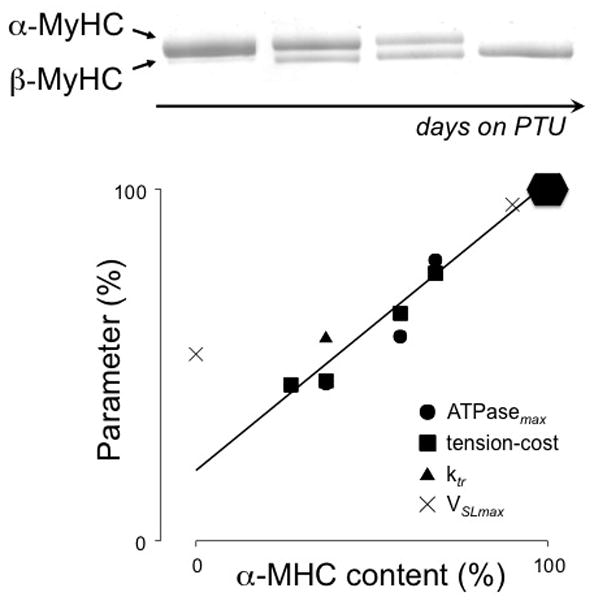
Figure 5

Open in a new tab

Treatment of rats with propyl-thiouracil (PTU) induces hypothyroidism that leads to the gradual replacement over several weeks of α- by β-myosin (MHC) in the heart (top panel). There is a direct proportional relationship between the myosin composition and various mechano-energetic parameters such as the ATPase activity during maximum isometric force development (ATPasemax), the ratio of ATPase activity and force development (tension-cost), the rate of force redevelopment following a sarcomere length perturbation (ktr), and the maximum unloaded velocity of sarcomere shortening (VSLmax). Modified from (de Tombe and ter Keurs, 1991a; Rundell et al., 2005). The 100% level of the various parameters is indicated by the solid hexagonal: ATPasemax = 600 pmol/s; tension-cost = 10 pmol/s/mm3; Ktr = 16/s; VSLmax = 15 μm/s.

Figure 6.

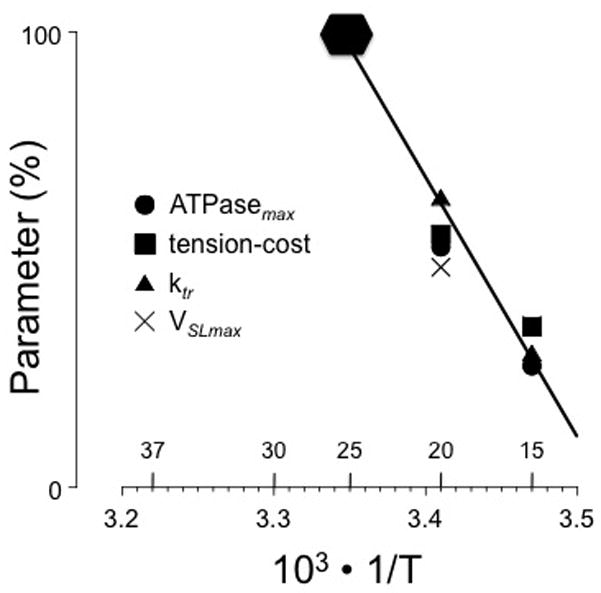
Figure 6

Open in a new tab

Temperature dependence of mechano-energetic parameters in the form of an Arrhenius plot measured in euthyroid isolated rat myocardium; equivalent temperatures in °C are indicated above the abscissa. Temperature strongly affects all parameters (average Q10 = ~ 4; T indicates absolute temperature in K). Modified from (de Tombe and ter Keurs, 1990b; de Tombe and Stienen, 2007). The 100% level of the various parameters is indicated by the solid hexagonal: ATPasemax = 800 pmol/s; tension-cost = 18 pmol/s/mm3; Ktr = 50/s; VSLmax = 25 μm/s.

CONCLUSIONS

About fifty years ago, Barany discovered a striking correlation between the enzymatic ATPase activity of myosin and the mechanical property of maximal shortening velocity. This suggests that these separate properties are the reflection of a uniform underlying structure, just as AV Hill had demonstrated earlier for skeletal muscle mechanics and energetics (Hill, 1938). Here we reviewed recent studies on cardiac muscle that demonstrate, directly, that mechanical power generation by the cardiac sarcomere is determined by the intrinsic biochemical properties of myosin and the number of attached and cycling cross bridges. The former parameter is regulated by variation of the expression of myosin isoforms and contractile protein post-translation modification, while the latter is parameter is determined by the rate of sarcomere length shortening. Together, these factors are finely tuned so as to match the required circumferential strain rate required to provide optimal pump power production by the heart to match the hemodynamic load imposed by the body.

Acknowledgments

This work was supported, in part, by grants from the American Heart Association and the National Institutes of Health (HL62426, HL75494, HL52322, HL58860, and HL66140), as well as grants from the Canadian Institutes for Health Research and the Heart and Stroke Foundation of Alberta the North West Territories and Nunavut. H.E.D.J. ter Keurs is Emeritus Senior Investigator of the Alberta Heritage Foundation for Medical Research.

Reference List

  1. Bacharach SL, Green MV, Borer JS, Hyde JE, Farkas SP, Johnston GS. Left-Ventricular Peak Ejection Rate, Filling Rate, and Ejection Fraction -Frame Rate Requirements at Rest and Exercise -Concise Communication. Journal of Nuclear Medicine. 1979;20:189–193. [PubMed] [Google Scholar]
  2. Backx PH, ter Keurs HEDJ. Fluorescent properties of rat cardiac trabeculae microinjected with fura-2 salt. Am J Physiol. 1993;264:H1098–H1110. doi: 10.1152/ajpheart.1993.264.4.H1098. [DOI] [PubMed] [Google Scholar]
  3. Barany M. ATPase activity of myosin correlated with speed of muscle shortening. J Gen Physiol. 1967;50:197–218. doi: 10.1085/jgp.50.6.197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Biesiadecki BJ, Kobayashi T, Walker JS, John SR, de Tombe PP. The troponin C G159D mutation blunts myofilament desensitization induced by troponin I Ser23/24 phosphorylation. Circ Res. 2007;100:1486–1493. doi: 10.1161/01.RES.0000267744.92677.7f. [DOI] [PubMed] [Google Scholar]
  5. Burkhoff D, Sugiura S, Yue DT, Sagawa K. Contractility-dependent curvilinearity of end-systolic pressure-volume relations. Am J Physiol. 1987;252:H1218–H1227. doi: 10.1152/ajpheart.1987.252.6.H1218. [DOI] [PubMed] [Google Scholar]
  6. Daniels MCG, Noble MIM, ter Keurs HEDJ, Wohlfart B. Velocity of sarcomere shortening in rat cardiac muscle: relationship to force, sarcomere length, calcium, and time. J Physiol. 1984;355:367–381. doi: 10.1113/jphysiol.1984.sp015424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. De Tombe PP, Little WC. Inotropic effects of ejection are myocardial properties. Am J Physiol. 1994;266:H1202–H1213. doi: 10.1152/ajpheart.1994.266.3.H1202. [DOI] [PubMed] [Google Scholar]
  8. De Tombe PP, Stienen GJ. Protein kinase A does not alter economy of force maintenance in skinned rat cardiac trabeculae. Circ Res. 1995:76. doi: 10.1161/01.res.76.5.734. [DOI] [PubMed] [Google Scholar]
  9. De Tombe PP, Stienen GJA. Impact of temperature on cross-bridge cycling kinetics in rat myocardium. Journal of Physiology-London. 2007;584:591–600. doi: 10.1113/jphysiol.2007.138693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. De Tombe PP, ter Keurs HE. Force and velocity of sarcomere shortening in trabeculae from rat heart. Effects of temperature. Circ Res. 1990a;66:1239–1254. doi: 10.1161/01.res.66.5.1239. [DOI] [PubMed] [Google Scholar]
  11. De Tombe PP, ter Keurs HEDJ. Force and velocity of sarcomere shortening in trabeculae from rat heart. Effects of temperature. Circ Res. 1990b;66:1239–1254. doi: 10.1161/01.res.66.5.1239. [DOI] [PubMed] [Google Scholar]
  12. De Tombe PP, ter Keurs HEDJ. Lack of effect of isoproterenol on unloaded velocity of sarcomere shortening in rat cardiac trabeculae. Circ Res. 1991a;68:382–391. doi: 10.1161/01.res.68.2.382. [DOI] [PubMed] [Google Scholar]
  13. De Tombe PP, ter Keurs HEDJ. Sarcomere dynamics in Cat cardiac trabeculae. Circ Res. 1991b;68:588–596. doi: 10.1161/01.res.68.2.588. [DOI] [PubMed] [Google Scholar]
  14. De Tombe PP, ter Keurs HEDJ. an internal viscous element limits unloaded velocity of sarcomere shortening in rat myocardium. J Physiol. 1992;454:619–642. doi: 10.1113/jphysiol.1992.sp019283. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Edman KAP. Double-hyperbolic force-velocity relation in frog muscle fibers. J Physiol. 1988;404:301–321. doi: 10.1113/jphysiol.1988.sp017291. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Haugen P. The stiffness under isotonic releases during a twitch of frog muscle fibre. In: Haugen P, editor. Molecular mechanisms of muscle contraction. New York: Plenum Press; 1988. pp. 461–469. [PubMed] [Google Scholar]
  17. Hill AV. The heat of shortening and the dynamic constants of muscle. Proceedings of the Royal Society of London Series B-Biological Sciences. 1938;126:166–195. doi: 10.1098/rspb.1949.0019. [DOI] [PubMed] [Google Scholar]
  18. Hoh JF, McGrath PA, Hale PT. Electrophoretic analysis of multiple forms of rat cardiac myosin: effects of hypophysectomy and thyroxine replacement. J Mol Cell Cardiol. 1978;10:1053–1076. doi: 10.1016/0022-2828(78)90401-7. [DOI] [PubMed] [Google Scholar]
  19. Horn GJ, Westerhof N, Elzinga G. Optimal power generation by the left ventricle. A study in the anesthetized open thorax cat. Circ Res. 1985;56:252–261. doi: 10.1161/01.res.56.2.252. [DOI] [PubMed] [Google Scholar]
  20. Huxley AF. Muscle structure and theories of contraction. Prog Biophys Biophys Chem. 1957;7:255–318. [PubMed] [Google Scholar]
  21. Janssen PM, de Tombe PP. Protein kinase A does not alter unloaded velocity of sarcomere shortening in skinned rat cardiac trabeculae. Am J Physiol. 1997a;273:H2415–H2422. doi: 10.1152/ajpheart.1997.273.5.H2415. [DOI] [PubMed] [Google Scholar]
  22. Janssen PM, de Tombe PP. Uncontrolled sarcomere shortening increases intracellular Ca2+ transient in rat cardiac trabeculae. Am J Physiol. 1997b;272:H1892–H1897. doi: 10.1152/ajpheart.1997.272.4.H1892. [DOI] [PubMed] [Google Scholar]
  23. Kentish JC, ter Keurs HEDJ, Ricciardi L, Bucx JJJ, Noble MIM. Comparison between the sarcomere length-force relations of intact and skinned trabeculae from rat right ventricle. Circ Res. 1986;58:755–768. doi: 10.1161/01.res.58.6.755. [DOI] [PubMed] [Google Scholar]
  24. Landesberg A, Livshitz L, ter Keurs HE. the effect of sarcomere shortening velocity on force generation, analysis, and verification of models for crossbridge dynamics. Annals of Biomedical Engineering. 2000;28:968–978. doi: 10.1114/1.1321013. [DOI] [PubMed] [Google Scholar]
  25. Landesberg A, Livshitz L, ter Keurs HEDJ. Cross-bridge kinetics is a function of sarcomere velocity. A novel theory of muscle contraction. Biophys J. 2004;86:568A. [Google Scholar]
  26. Loiselle D, Goo S, Gerneke D, Sands G, LeGrice I. At the heart of ventricular trabeculae. J Mol Cell Cardiol. 2008;44:817. [Google Scholar]
  27. McDonald KS. the interdependence of Ca(2+) activation, sarcomere length, and power output in the heart. Pflugers Archiv-European Journal of Physiology. 2011;462:61–67. doi: 10.1007/s00424-011-0949-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Petersen JW, Forder JR, Thomas JD, MOYE LA, Lawson M, Loghin C, Traverse JH, Baraniuk S, Silva G, Pepine CJ. Quantification of Myocardial Segmental Function in Acute and Chronic Ischemic Heart Disease and Implications for Cardiovascular Cell Therapy Trials A Review from the NHLBI-Cardiovascular Cell Therapy Research Network. JACC-Cardiovascular Imaging. 2011;4:671–679. doi: 10.1016/j.jcmg.2011.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ricciardi L, ter Keurs HEDJ, Laarse A, Vliegen HW. Variazoni meccaniche e strutturali nel miocardio ipertrofico di ratti allenati dal nuoto. Boll Soc It Biol Sper. 1986;62:89–93. [PubMed] [Google Scholar]
  30. Rodriguez EK, Hunter WC, Royce MJ, Leppo MK, Douglas AS, Weisman HF. A method to reconstruct myocardial sarcomere lengths and orientations at transmural sites in beating canine hearts. Am J Physiol. 1992;263:H293–H306. doi: 10.1152/ajpheart.1992.263.1.H293. [DOI] [PubMed] [Google Scholar]
  31. Rundell VL, Manaves V, Martin AF, de Tombe PP. Impact of beta-myosin heavy chain isoform expression on cross-bridge cycling kinetics. Am J Physiol Heart Circ Physiol. 2005;288:H896–H903. doi: 10.1152/ajpheart.00407.2004. [DOI] [PubMed] [Google Scholar]
  32. Sieck GC, Regnier M. Plasticity in skeletal, cardiac, and smooth muscle -Invited review: Plasticity and energetic demands of contraction in skeletal and cardiac muscle. Journal of Applied Physiology. 2001;90:1158–1164. doi: 10.1152/jappl.2001.90.3.1158. [DOI] [PubMed] [Google Scholar]
  33. Siemankowski RF, Wiseman MO, White HD. ADP dissociation from actomyosin subfragment 1 is sufficiently slow to limit the unloaded shortening velocity in vertebrate muscle. Proc Natl Acad Sci U S A. 1985;82:658–62. doi: 10.1073/pnas.82.3.658. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Suga H, Sagawa K. Instantaneous pressure-volume relationships and their ratio in the excised, supported canine left ventricle. Circ Res. 1974;35:117–126. doi: 10.1161/01.res.35.1.117. [DOI] [PubMed] [Google Scholar]
  35. Ter Keurs HE, Savage DD, Lester WM, McGee DL. New perspectives on left ventricular hypertrophy: anatomy, physiology, and significance. Clin Cardiol. 1989;12:IV36–IV49. doi: 10.1002/clc.4960121310. [DOI] [PubMed] [Google Scholar]
  36. Ter Keurs HEDJ. The interaction of Ca(2+) with sarcomeric proteins: role in function and dysfunction of the heart. American Journal of Physiology-Heart and Circulatory Physiology. 2012;302:H38–H50. doi: 10.1152/ajpheart.00219.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Ter Keurs HEDJ, Diao N, Deis NP. Nonuniform activation and the mechanics of myocardial trabeculae with fast or slow myosin. Analysis of Cardiac Development: from Embryo to Old Age. 2010;1188:165–176. doi: 10.1111/j.1749-6632.2009.05097.x. [DOI] [PubMed] [Google Scholar]
  38. Ter Keurs HEDJ, Rijnsburger WH, van Heuningen R, Nagelsmit MJ. tension development and sarcomere length in rat cardiac trabeculae. Evidence of length-dependent activation. Circ Res. 1980;46:703–714. doi: 10.1161/01.res.46.5.703. [DOI] [PubMed] [Google Scholar]
  39. Toorop GP, Horn GJ, Elzinga G, Westerhof N. Matching between feline left ventricle and arterial load: optimal external power or efficiency. Am J Physiol. 1988;2544:H279–H285. doi: 10.1152/ajpheart.1988.254.2.H279. [DOI] [PubMed] [Google Scholar]
  40. Van Heuningen R, Rijnsburger WH, ter Keurs HEDJ. sarcomere length control in striated muscle. Am J Physiol. 1982;242:H411–H420. doi: 10.1152/ajpheart.1982.242.3.H411. [DOI] [PubMed] [Google Scholar]

RESOURCES