Measuring the modulus and reverse percolation transition of a degrading hydrogel

Abstract

In light of the growing importance in understanding and controlling the physical cues presented to cells by artificial scaffolds, direct, temporally resolved measurements of the gel modulus are needed. We demonstrate that an interpolation of macro- and microrheology measurements provides a complete history of a hydrogel modulus during degradation through the reverse percolation transition. The latter is identified by microrheology, which captures the critical scaling behavior of reverse percolation, a transition of key importance in controlling cell migration, implant degradation, and tissue regeneration.

Synthetic hydrogelators are frequently used as scaffolds for tissue regeneration and engineering. A seamless transition from the initial network to a tissue requires precise control over the degradation of the synthetic material to match the regeneration time scale of the native tissue. Moreover, the mechanical modulus of the hydrogel influences cellular migration, signaling cues, and ultimately, cell fate.^1–3 Despite the importance of understanding and controlling the time-scale and microenvironment changes during hydrogel degradation, it is currently challenging to characterize the degradation of hydrogel scaffolds in a manner that directly measures changes in the material modulus over long times and a large modulus range. Until now, the only available options were instead to characterize degradation indirectly by measuring the hydrogel mass loss or the cross-linker conversion kinetics.^4–10

Here, we demonstrate that a combination of macro- and microrheology provides complementary measurements that yield precise knowledge of the evolution of hydrogel modulus from the initial gel through the final degradation point. The gel modulus changes nearly five orders of magnitude, over a period of almost 30 days. Furthermore, we demonstrate that the final degradation exhibits critical scaling behavior in a reverse process of the percolation transition that occurs during gelation.^11–13 This scaling provides a precise definition of the degradation time. Before presenting and discussing these results, we briefly review the materials and methods employed in this study.

The hydrogels are composed of a four-arm star poly(ethylene glycol) (PEG) end-functionalized with 3-mercaptopropionic acid (f_PEG ≈ 4) and maleimide-functionalized low molecular weight heparin (LMWH, f_LMWH ≈ 2.6).^14,15 The hydrogels are made with a 1:1 stoichiometric ratio of functional groups equivalent to 2.8 wt% LMWH: 2.2 wt% PEG. The initial rheological properties of the hydrogels were measured by oscillatory bulk rheology, with measurements of hydrogel degradation taken every 5 minutes over 3.5 days. Measurements were performed at 1% strain, which is well below the onset of non-linear response at 10% strain, to avoid potential mechanical degradation.

Multiple particle tracking microrheology (MPT) measurements were collected throughout the 30-day period of degradation. Fluorescently labeled probe particles (diameter 2R = 1.04 ± 0.02 μm, Polysciences, Warrington, PA) were dispersed in the precursor material LMWH solution at a concentration of 0.054% solids per volume prior to gelation. After mixing the precursor solutions, hydrogel samples were formed in polydimethylsiloxane (PDMS) chambers (6 mm diameter by 800 μm height cylinder, Dow Corning) and submerged in 1 × phosphate buffered saline (pH=7.4, Invitrogen) at 37°C. Video microscopy is used to capture the movement of probe particles and their trajectories are determined from the brightness-weighted centroid of each particle using classical tracking algorithms^16,17. The mean-squared displacement (MSD), 〈Δr²(τ)〉, is calculated for each set of data. The Brownian motion of the probe particles provides the creep compliance J(τ) via the Generalized Stokes-Einstein Relation (GSER), J(τ) = πR〈Δr²(τ)〉/k_BT, where k_BT is the thermal energy. The creep compliance is a material property that relates the strain that evolves in a material due to an applied stress.¹⁸ Thus, provided that the GSER is satisfied, the MSD is a rheological measurement. ¹⁹ The equilibrium creep compliance is J_e (τ) = τ/η for the limiting case of a viscoelastic fluid with viscosity η, and J_e (τ) = 1/G_e for a viscoelastic solid with an equilibrium shear modulus G_e. Microrheological characterization is ideal for fundamental studies of model materials that are extracellular matrix (ECM) mimics, since this passive technique can be translated into more complex environments, such as a cell-laden gel.

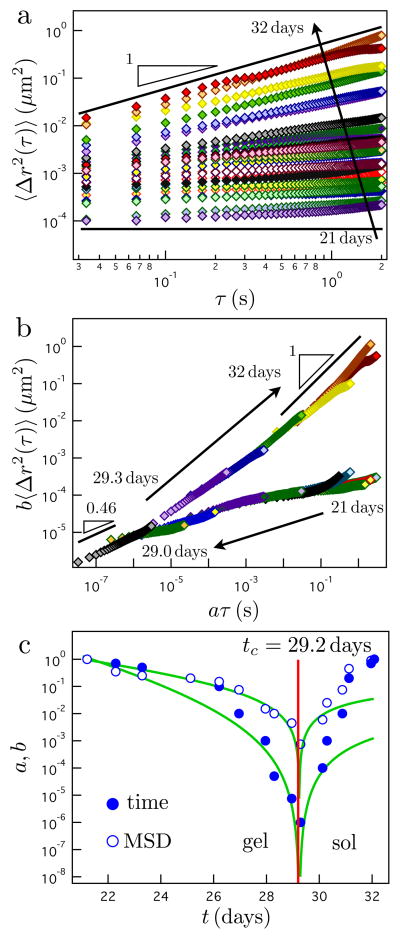
The LMWH-PEG hydrogels that form have moduli, ~2.5kPa, which is above the measurable limit of MPT. Dispersed probe particles exhibit no observable displacement until the 21^st day. The onset of detectable thermal motion indicates that the equilibrium modulus is approaching a value of G_e ~ 10 Pa, the maximum limit resolvable in our MPT microrheology experiment. Over the next ten days the series of MSD curves, shown in Figure 1a, trace the evolution of the hydrogel from a solid to a liquid. As the degradation reaction proceeds, the magnitude of the MSD increases. At 28.3 days, the MSD slope begins to increase, indicating that the gel network is transitioning to a viscoelastic fluid. Finally, the logarithmic slope approaches the value of one, consistent with probe particles diffusing in a viscous fluid.

Figure 1.

The microrheology of hydrogel degradation. (a) The mean-squared displacement (MSD) of probe particles during the last 11 days of degradation. The solid lines have a slope of one and zero to guide the eye. (b) Gel and sol master curves are constructed by empirically shifting the data. (c) The shift factors plotted versus time identify the critical degradation time, t_c. The green lines represent theoretical MSD and time shift factors calculated using first-order rate constants determined from the experimental data and a kinetic model.

Using the self-similar shape of the MSD curves, we empirically construct sol and gel master curves, as shown in Figure 1b, by multiplying the lag time and MSD by shift factors a and b, respectively, analogous to time-cure superposition for a gelation reaction.^11–13 The shift factors represent the critical scaling with respect to the extent of reaction p of the longest relaxation time a ~ ε^y and equilibrium compliance b ~ ε^z, where the extent of reaction p is represented by ε = |p − p_c|/p_c, the distance from the critical extent of reaction at the degradation point, p_c, and y and z are critical scaling exponents. The empirical shifting procedure is possible only if the range of MSD lag times captures the longest relaxation time of the pre- or post-gel state, and hence exhibits curvature on the logarithmic scale. Then, the intersection of the pre- and post-gel master curves identifies the reverse percolation transition.

More precisely, the rapid decrease of the shift factors, identifying a common asymptote (Figure 1c), identifies the degradation time, t_c = 29.2 ± 0.1 days. The error represents the standard deviation of three separate measurements. The asymptotic decrease of the shift factors is a consequence of the divergence of the longest relaxation time and compliance as the hydrogel approaches its reverse percolation point.

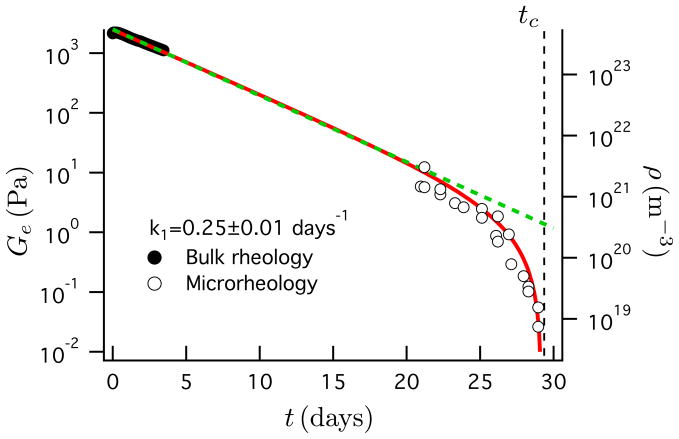
With the degradation point determined, we next combine the microrheology data with bulk rheology measurements taken initially after the gel forms. The complementary data sets are shown in Figure 2. These data establish a complete history of the gel modulus by interpolation.

Figure 2.

A first-order kinetic model of the hydrogel pseudostationary equilibrium modulus (solid red line) interpolates the data obtained from macrorheology over the initial 3.5 days (solid symbols) and microrheology near the percolation transition (open symbols). The green curve is the calculated cross-link density. The black dashed line indicates the time of the reverse percolation transition, t_c = 29.2 days.

A kinetic model of cross-link degradation is derived to construct the interpolation. The cross-link density, ρ, follows first-order reaction kinetics of ester hydrolysis, dρ/dt = −k₁ρ, where k₁ is the rate constant and t is the degradation time.^20,21 With the initial density of ester linkages ρ₀ corresponding to the initial gel modulus G_e0 ~ ρ₀k_BT, this yields ρ(t) = ρ₀e^−k₁t. From the cross-link density the pseudo-stationary equilibrium modulus, defined as the equilibrium modulus were the degradation to be halted at each moment in time, is G_e = ρk_BT(|ρ − ρ_c|/ρ)^z. The modulus is initially proportional to the ester density, G_e ~ ρ, which decays exponentially with time, but diverges to zero as the percolation transition is approached as G_e ~ ε^z for ρ → ρ_c where ρ_c is the critical ester concentration at p_c. The model is shown in Figure 2 with G_e0 = 2500 Pa, k₁ = 0.25 ± 0.01 days⁻¹, z = 1.4, and demonstrates that the gel modulus can be reconstructed over a period of thirty days, as it spans nearly five decades in magnitude. The equilibrium elastic modulus tracks the exponential decay of the cross-link density for approximately 28 days before diverging. The value of the first-order rate constant is consistent with those found in the literature for similar hydrogel chemistries undergoing hydrolytic degradation. Values reported for k₁ range between 0.01 and 0.5 days^−1.20–22

Using the first-order rate constant, the cross-link density is used to calculate the power-law scaling functions of the MSD and lag time shift factors. With the value of z determined above, we find y = 2.9. The calculated shift factors based on these exponents are illustrated by the solid green curves in Figure 1c. Interestingly, beyond the percolation transition, the compliance and relaxation time of the sol increase faster than the scaling law predicts based on the rate of cross-link degradation, possibly due to a rapid loss of polymer. This is in agreement with previous studies, which observe a sudden mass loss after the critical degradation time.^4,20,21 Lastly, the ratio of the critical scaling exponents, which defines the critical relaxation exponent n = z/y, further verifies the identification of the reverse percolation transition. We find n = 0.48, in close agreement with the MSD slope closest to the degradation point, 0.46, as shown in Figure 1b. This consensus verifies the expected power-law dependence of the reverse percolation transition compliance, J(τ) = τⁿ.^12,23

In all, we used the powerful complementarity of macro- and micro- rheological measurements to characterize the modulus of a hydrogel over the entire course of a one-month degradation reaction. Microrheology identified the reverse percolation transition of the hydrogel, which exhibits scaling behavior analogous to a gelation reaction. Interpolation of the rheological data sets produced a complete history of the hydrogel modulus and thus the ability to quantify and direct the physical cues presented to cells by artificial scaffolds and engineer the time scales for implant degradation. Finally, the ability to measure local material rheology using microrheology provides a unique opportunity to study the evolution of the microenvironment in the pericellular region, the material directly around the cell that is remodeled and degraded during cell proliferation and motility.