Abstract
GLIC is a bacterial member of the large family of pentameric ligand-gated ion channels. To study ion conduction through GLIC and other membrane channels, we combine the one-dimensional potential of mean force for ion passage with a Smoluchowski diffusion model, making it possible to calculate single-channel conductance in the regime of low ion concentrations from all-atom molecular dynamics (MD) simulations. We then perform MD simulations to examine sodium ion conduction through the GLIC transmembrane pore in two systems with different bulk ion concentrations. The ion potentials of mean force, calculated from umbrella sampling simulations with Hamiltonian replica exchange, reveal a major barrier at the hydrophobic constriction of the pore. The relevance of this barrier for ion transport is confirmed by a committor function that rises sharply in the barrier region. From the free evolution of Na+ ions starting at the barrier top, we estimate the effective diffusion coefficient in the barrier region, and subsequently calculate the conductance of the pore. The resulting diffusivity compares well with the position-dependent ion diffusion coefficient obtained from restrained simulations. The ion conductance obtained from the diffusion model agrees with the value determined via a reactive-flux rate calculation. Our results show that the conformation in the GLIC crystal structure, with an estimated conductance of ~1 picosiemens at 140 mM ion concentration, is consistent with a physiologically open state of the channel.
INTRODUCTION
By revealing molecular motions with atomic resolution, molecular dynamics (MD) simulations provide a powerful tool for the elucidation of complex biomolecular processes.1 But beyond providing qualitative insights, quantitative MD simulations also establish a direct connection between theory and experiment, as emphasized by van Gunsteren and his collaborators in word and deed.2 In particular, the energies and entropies driving the functional dynamics of biomolecules can be deduced from the thermal averages obtained from MD simulations. By exploiting also the ability to determine dynamic properties, including friction or diffusion coefficients, one can thus obtain accurate estimates of the resulting biomolecular kinetics. Here we exploit these quantitative powers of MD to determine the ion conductivity of a membrane channel.
Pentameric ligand-gated ion channels3 (pLGICs) form a large family of membrane proteins that open or close in response to external signals such as ligand binding. Some members of the family, such as the nicotinic acetylcholine receptor (nAChR), play important roles in neural signal transduction, and are major targets for psychoactive drugs. Following a ~ 4-Å resolution electron microscopy structure of nAChR,4 the structures of two bacterial pLGICs, ELIC and GLIC, were determined by xray crystallography.5-7 GLIC has been characterized as a pH-gated channel8 and serves as a model for the pLGIC family. In subsequent studies the crystal structures of the isolated GLIC extracellular domains,9 and of GLIC bound with anesthetics ligands,10 also became available.
Although the crystal structures5-7 of GLIC and ELIC appear to represent the open and closed conformations, respectively, this interpretation was recently challenged.11,12 Based on mutational and electrophysiological studies of nAChR and GLIC, it was proposed that the crystal structure of ELIC represents a refractory nonconductive state,11 and the GLIC crystal structure corresponds to a desensitized state.11,12 To bridge the gap between the crystallographic and functional studies, it is highly desirable to determine the main physiological properties, i.e., the ion conductivity, of the channel in the conformations described by the crystal structures.
Computer simulations are powerful tools to study ion conduction in channels of known structures. At a coarse-grained level, the current-voltage relation in ELIC and GLIC was calculated in Brownian dynamics simulations.13,14 At an all-atom level, one can similarly introduce a voltage bias or an electrochemical gradient in molecular dynamics (MD) simulations and determine the corresponding electric current directly from the observed ion flux.15-20 To obtain statistically significant results, one needs to observe the passage of multiple ions through the channel during the simulation. For channels with low conductance, this method thus requires very long simulation times. Alternatively, one can estimate the conductance on the basis of the potential of mean force (PMF)21 of an ion along the channel.22,23 Indeed, calculations of ion PMFs in GLIC have recently been reported.14,24 In this study, we first determine an accurate single-ion PMF. In a second step, we determine the friction (or diffusion) coefficient of ion motion along the pore axis in the hydrophobic constriction that gives rise to the energetic barrier for ion passage. By combining these results, we then estimate the single-channel conductance of the GLIC transmembrane pore in the open conformation.
METHODS
In this section, we first describe theories for calculating the channel conductance in the linear-response regime based on the PMF and the Smoluchowski diffusion model. We note that our elementary derivation recovers a number of known results scattered in the literature. Nevertheless, for the sake of completeness, and to understand our implementation of the conductance calculation, we provide an outline of the underlying theories. We then describe the simulation setup used to calculate the conduction of Na+ ions through the GLIC pore.
Linear Response Theory of Channel Crossing Rate
We are interested in the ion current I through a channel under an applied voltage V , which determines the conductance of the channel at the given ion concentration ρ. To address this problem in the context of MD simulations, we consider a simple system in which two reservoirs with equal ion concentration ρ are separated by a membrane with a single channel. We assume that ρ is sufficiently low, such that the probability of finding two or more ions simultaneously inside the channel is negligibly small.
We first consider an equilibrium situation without an applied voltage, in which ions may nonetheless randomly permeate the channel in either direction. We define the crossing rate, k0, as the average number of ions crossing from the left to the right reservoir per unit time. In equilibrium, the crossing rate in the opposite direction, from the right to the left reservoir, is also k0, resulting in zero net ion flux.
The right and left crossing rates, kr and kl, depend on the applied voltage V and will differ for non-zero V. At sufficiently low ion concentrations, an ion is only weakly affected by other ions as it traverses the channel, and the passages of individual ions are not correlated. In such a single-ion conduction scheme, the ion experiences a free energy difference of qV between the two reservoirs, with q the charge of the ion. Detailed balance thus requires that the two crossing rates satisfy
| (1) |
where kB is the Boltzmann constant and T the temperature.
In general, the exact dependence of kr and kl on V depends on a number of factors, such as the position and magnitude of the energetic barrier for the crossing.25 However, for small V, we can expand kr and kl to first order: , i = r, l. Substituting these into Eq. 1 and comparing the first-order terms in V lead to26ar − al = 1. To lowest order in V, the net electric current I is thus given by
| (2) |
We note that Eq. 2 is valid for sufficiently small V, regardless of the specific underlying barrier or other factors. Therefore, in the single-ion conduction scheme, the current induced by a small voltage can be predicted from the equilibrium crossing-rate k0. However, although k0 can in principle be directly obtained from equilibrium simulations, it would require very long simulation times to observe multiple spontaneous crossing events for channels with low conductance. For instance, at a conductance of 1 picosiemens for monovalent ions, we expect a current of one ion every 1.6 μs at 100 mV membrane potential or, in the absence of a potential, a spontaneous ion crossing every 3 s in either direction based on Eq. 2. In the following we instead describe more efficient methods to estimate k0 from the simulations.
Ion Free Energy Profile
Ions exhibit a uniform three-dimensional (3D) density or concentration in the bulk reservoirs. Inside the channel, in contrast, their motions perpendicular to the pore axis are highly restricted by the channel wall. Therefore the thermodynamics of the ions in the channel can often be described by a one-dimensional (1D) PMF along the pore axis. In the following we derive the relationship between the 1D PMF and 3D bulk density, such that the crossing rate k0 can be obtained by solving an equivalent 1D diffusion problem described in the next section.
The 3D bulk density and the 1D free energy profile are related via an effective surface area factor.22,27 Here we establish this connection by exploiting the proportionality of the one-particle densities in the biased and unbiased systems, which provides a basis for future generalizations to 2D and 3D representations. Consider a system of N atoms with a potential energy function V0(r1,...,rN) in a canonical ensemble at inverse temperature β = 1/kBT, with particles 1,...,n being ions of the type we are interested in. Because the n ions are identical, the ion density is equal to n times the probability distribution of a single ion:
| (3) |
where δ(r − r1) is Dirac's delta function. In a simulation in which particle 1 is tagged and restrained by a biasing potential u(r1) that acts exclusively on this one particle, its density becomes
| (4) |
By using the property of the delta function, we can relate the two densities,
| (5) |
where C = n · 〈exp[−βu(r1)]〉0 is a constant. Importantly, in the region where u(r)=0, the two densities of the single tagged ion and of the untagged ions are proportional up to a constant factor.
For membrane channel systems, a flat-bottom lateral potential u(r) = u(x, y) is commonly adopted, having virtually no effect when the tagged ion is inside the channel but laterally confining the ion in the bulk regions. With this lateral restraint, we define the 1D density of the tagged ion as p(1)(z) = ∫ dxdyρ(1)(r), with a constant value in the bulk regions. We then define the 1D free energy (or PMF) G(z) for the tagged ion as
| (6) |
in which z0 can be any point in the bulk region. With this definition, the flat baselines of G(z) at the two ends will be at zero level. According to Eq. 5, and given the density ρ0(r) = ρ in the bulk regions, we have
| (7) |
for any z0 in the bulk regions, where
| (8) |
is the effective cross-sectional area.
Inside the channel, we may similarly define the 1D density for ions in the unbiased system, p0(z) = ∫ dxdyρ0(r). Moreover, in the interior of the channel, u(x, y) is zero at all points accessible to the ion, as mentioned earlier. According to Eq. 5, we have p(1)(z) = p0(z)/C in the channel region. By combining this relation with Eqs. 6 and 7, we obtain the desired result for the unbiased 1D ion density profile inside the channel, in terms of the bulk density and the free energy profile:
| (9) |
where we assumed again that G(z) = 0 in the bulk, without loss of generality. Eq. 9 shows that as far as the channel region is concerned, the equilibrium ion density there in a system with 3D bulk concentration ρ is identical to the density of the tagged ion in a laterally restrained system with 1D bulk concentration ρS and 1D PMF G(z). This equivalence allows us to obtain k0 from the crossing rate of the tagged ion in the laterally restrained system, as described below.
Ion Translocation Kinetics
As mentioned before, it is not practically feasible to obtain the crossing rate directly from free MD simulations for channels with low conductivity. To address the problems of low conductance and slow ion motion through the channel, we assume that a diffusion model can be used to calculate the crossing rate of ions. The diffusion model is parameterized in terms of 1D position-dependent diffusion coefficient D(z) and a 1D free energy surface G(z) as discussed earlier. Here we tacitly assume that motions in the x-y plane parallel to the membrane are fast in comparison to motions into and through the channel. We further assume that channel crossing is slow compared to motions in and out of the regions just outside the openings.
From MD simulations combined with, e.g., umbrella sampling, we can determine the 1D PMF G(z) of a single tagged ion as a function of its z-position, in the range z1 ≤ z ≤ z2 extending beyond the channel openings on both sides. Far from the membrane, we expect G(z) = 0 according to our definition. Under the assumptions of the 1D diffusion model, the time-dependent density distribution p(z,t) of the tagged ion obeys the Smoluchowski equation:
| (10a) |
| (10b) |
where j(z,t) is the particle flux.
To determine the unidirectional ion flux, we assume the bulk density at the left boundary p(z1) = ρS as discussed before. This boundary condition ignores particle exit and entry parallel to the membrane, and could be improved by using a radiation boundary condition28 on the cap covering the openings, suitably incorporated into the 1D model. We assume a vanishing density at the right boundary, p(z2) = 0. The resulting steady-state density satisfies
| (11) |
in which the splitting probability (or committor) ϕ(z) is defined as the probability that an ion starting at z exits the channel at the left opening before reaching the right opening,
| (12) |
The position and time-independent flux29 determines the unidirectional rate of ion crossing,
| (13) |
By substitution into Eq. 2, we obtain the well-known expression for the conductance γ of the channel,
| (14) |
where G(z) = 0 in the bulk. We note that this formalism can also be readily applied to calculate the net diffusional flux js of any solute through the channel under the influence of a bulk concentration (or activity) difference Δρs:
| (15) |
In the above formulas, both the cross-sectional area S and the PMF G(z) depend on the lateral potential u(x, y) used to restrain the tagged ion in the free energy calculation. Because u(x, y) is flat-bottomed and has no effect when the ion is inside the channel, it will only affect the overall offset of G(z) in the channel region, but not its shape. If a different u(x, y) is adopted corresponding to a scaled cross-sectional area aS, the resulting G(z) will be shifted by kBT ln a in the channel region. Therefore, as long as this portion of G(z) makes the predominant contribution to the integral in Eqs. 13-15, thus corresponding to the rate-limiting region, the resulting k0 and γ will not depend significantly on the choice of u(x, y).
High Voltages and Ion Concentrations
In the derivation of Eqs. 2 and 14 we assumed that the applied voltage V is small, such that the ion current I is linearly proportional to V. For large V beyond the linear I -V range, if the single-ion conduction assumption is still valid, one may similarly calculate a single-ion PMF from simulations with an applied voltage.15 The two baselines of this PMF will then differ by qV. By solving the Smoluchowski equation for this biased PMF, one can again obtain the stationary ion flux.
We note that Eq. 14 is only valid under the assumption of single-ion conduction, in which the crossing events of different ions are not correlated. When the ion concentration ρ is sufficiently small, ion-ion interaction can be ignored, and the PMF G(z) does not depend on ρ. The channel conductance is then, as expected, linearly proportional to ρ. As ρ increases, a concentration-dependent G(z) could be determined to account for non-linear effects. At even larger ρ, the channel region will be more frequently occupied and the crossing of multiple ions may be coupled to each other, and consequently Eq. 14 will become inaccurate. A notable example is the family of K+ channels30 whose selectivity filter is constantly occupied by multiple ions at physiological conditions, which move concertedly in a single file. In this case Eq. 14 is clearly invalid, and one needs to explicitly consider ion-ion coupling, e.g., through multiion PMFs31 or by mapping the transport problem on a generalized 1D coordinate.32
Computational Details
Umbrella sampling of Na+ ion conduction
The system (Fig. 1) and the first stage of the simulations were reported in our previous study.33 Briefly, the GLIC transmembrane pore was held in the open conformation by applying restraints on the Cartesian coordinates of 420 selected Cα atoms.33 (These restraints on the protein are consistently applied in all simulations in this study, regardless of whether the ion is restrained or not.) A set of umbrella sampling simulations, 1 ns each, was performed in a total of 153 umbrella windows with a uniform spacing of 0.5 Å, thus covering a distance of 76 Å. In each simulation, the z-coordinate of the Na+ ion was subject to a harmonic restraint with spring constant K = 10 kcal/mol/Å2. In the xy dimensions, a flat-bottom restraint u(x, y) is applied,
| (16) |
with R0 = 6 Å.
Figure 1.
Unit cell of the simulation system. Rendered in VMD.51
In the present study, we extended the simulations above with Hamiltonian replica exchange,34 with a swap between neighboring umbrella windows attempted every 200 fs. At each attempt, assuming that the current z-coordinate of the ion is z1 and z2 in two neighboring windows with reference position of the harmonic restraint at r1 and r2, respectively, the swap would change the combined Hamiltonian by K(z2 − z1)(r2 − r1). According to the Metropolis criterion, we thus accept the swap with a probability of . If the swap is accepted, the first and second simulations will adopt r2 and r1 as the new reference position of the harmonic restraint, respectively. Accepted replica exchanges facilitate the equilibration of the systems, without altering the equilibrium distribution of the z-coordinate in each window. In these simulations we adopted a slightly wider lateral restraint u(x, y) with R0 = 7 Å. The simulations were run for 3 ns per window. Then, out of the 153 umbrella windows, we chose a stretch of 124 windows that cover the entire pore region, and extended the simulations for another 2 ns in each window. In summary, each of the 124 umbrella windows (in the pore region) was run for a total of 6 ns, and other windows (in the bulk region) were run for 4 ns each. The first 2 ns in each window were discarded, and the remaining trajectory was used for the PMF calculation.
To investigate the effect of ionic strength on the single-ion PMF, we built another system, with 48 Na+ and 53 Cl- ions incorporated to represent a bulk NaCl concentration of ~240 mM. The system is identical to the one described above except for the different ion concentrations. For this system we performed 4 ns Hamiltonian replica exchange simulations in each of the 153 umbrella windows, followed by another 2 ns on the 124 windows in the pore region mentioned earlier. In summary, similar to the simulations with zero bulk ion concentration described earlier, here each umbrella window in the pore region and bulk region was run for a total of 6 ns and 4 ns, respectively. The first 2 ns in each window were discarded, and the remaining trajectory was used for the PMF calculation.
To quantify the effect of Hamiltonian replica exchange, we compare the 1-ns simulations in our previous study33 to the first 1 ns of the simulations above. We use the difference between the PMFs calculated from these trajectories and the final converged PMFs as an estimate of the computational error. We find that with Hamiltonian replica exchange implemented here, the mean squared error in the PMF is reduced to ~40% of that in our previous study,33 corresponding to a ~2.5 fold increase in sampling efficiency. A systematic evaluation of the efficiency enhancement by this technique should be of interest in future studies.
Unrestrained simulations at barrier top
As will be discussed later, the ion PMF exhibits a major barrier at location z ≈0 Å. To investigate the dynamics of the ion at the barrier top, we performed a set of simulations with the ion unrestrained. First, 10 frames were manually selected in which the ion is near the barrier top. Each frame was subject to a 1-ns simulation, in which a strong harmonic restraint (250 kcal/mol/Å2) in the z direction was applied to confine the ion at the barrier top. Next, we took 10 frames from the latter half of each simulation above, thus yielding a total of 100 snapshots. Starting from each snapshot, we carried out two 1-ns simulations without the restraint on the ion and with opposite initial velocities. The pair of simulations thus shares identical initial coordinates but reverted initial velocities of the atoms. We then obtained a total of 200 free trajectories, each 1-ns long and starting with the ion at the barrier top.
Calculation of ion PMF
The single-ion PMFs in both systems (with 0 and ~240 mM bulk ions) were calculated using the weighted histogram analysis method (WHAM)35 with a fast numerical algorithm.36 As mentioned before, the PMF is expected to exhibit flat baselines at the two ends, representing the bulk water region. In the absence of a membrane potential, ideally the left and right baselines should match exactly, although this may not be the case in a calculated PMF due to the statistical errors in the finite sampling. A common practice to correct the unmatched baselines in the ion PMF is to force the normalization factors of the two end windows to be equal during WHAM calculations. The effect on the resulting PMF is usually a linear correction over the entire sampled distance. Here we adopt an alternative approach to correct the baseline mismatch, as described below.
Let G1(z) and G2(z) denote the computed PMF G(z) with the zero level shifted to the left and right baselines, respectively, and Gb(z) denote the ideal PMF with both baselines at the zero level. In principle, Gb(z) may be obtained from either G1(z) or G2(z), and in practice it can be estimated from a weighted average of the two. We recently introduced a simple method to estimate the variance in the free energy difference between any two positions in G(z) from the statistical errors of the average z-coordinate in the intermediate umbrella windows.36 Using this method, the variances V1(z) and V2(z) of G1(z) and G2(z), respectively, can be calculated, representing the statistical uncertainty between G(z) and the left or right baseline. The weighted average with the minimal statistical errors is then given by
| (17) |
| (18) |
We thus have a PMF Gb(z) with both baselines at zero level, and with the standard deviation σ[Gb(z)] = var[Gb(z)]1/2.
Our error estimation method36 also gives the estimated variance Vb for the difference between the two baselines, which can be compared to the actual baseline difference ΔG in the original PMF. In both simulations here, we find that ΔG is well within one standard deviation . In case the PMF exhibits hysteresis with ΔG larger than , one could accordingly scale V1(z) and V2(z) by a factor of (ΔG)2/Vb to compensate for the underestimation of the errors.
Calculation of diffusion coefficients
Under a sufficiently narrow harmonic potential, the local diffusion coefficient of the ion can be assumed as a constant, and estimated from37
| (19) |
in which τ is the integrated autocorrelation function of the z-coordinate:
| (20) |
| (21) |
where δz(t) ≡ z(t) − 〈z〉. We note that the local diffusion coefficient can also be calculated from the velocity autocorrelation function.38 Although the two approaches are formally identical, Eq. 19 here enables simpler numerical implementations.
Assuming that n data points with time interval Δt, zi ≡ z(iΔt) (i = 1,... n), are sampled from the simulation, one would use the average coordinate z̄ = ∑ zi/n to replace 〈z〉 in the equations above. For a single trajectory, we note that the estimation of 〈z〉, C(t), and τ will not be reliable unless C(t) vanishes at a time scale much shorter than the trajectory length nΔt. In such cases the variance of z̄, var(z̄), also depends on τ. To see this, we start with the equality39
| (22) |
Under the above assumption that C(iΔt) is essentially zero for large i/ n, the summation in Eq. 22 approximates the sum of the values of C(t) sampled with interval Δt. We thus have
| (23) |
| (24) |
var(z̄) can be estimated by block averages.39 The local diffusion coefficient D can then be obtained from Eqs. 19 and 24, without an explicit calculation of the autocorrelation function C(t). By combining the values of D calculated for each umbrella window, one then obtains an estimate of the position-dependent diffusion coefficients D(z) .
The method above is applicable for continuous trajectories that are not subject to replica exchange. To estimate D(z) for the open conformation, we thus utilized two sets of umbrella sampling simulations from our previous study,33 one of which served as the initial equilibration here, as described before. The two simulation sets are both 1-ns long per window, but with different initial configurations obtained by dragging the ion into the pore along two opposite directions during the preparatory stage.33 For each umbrella window, we calculate D from the last 0.9 ns of each trajectory using the method described here, and then take the average of the two as the local diffusion coefficient.
Simulation protocols
All simulations were performed using the CHARMM force field,40 the TIP3P water model,41 and the NAMD2 program,42 under the periodic boundary conditions with constant temperature (300 K) and volume. Full electrostatics was calculated using the particle mesh Ewald method.43
RESULTS
Results from the umbrella sampling simulations with bulk ion concentrations of 0 and ~240 mM, respectively, are shown in Fig. 2a. In each umbrella window, the Na+ ion is subject to a biasing potential in the z-direction and a flat-bottom lateral restraint in the x-y directions. In the bulk water region the lateral restraint u(x, y) confines the ion in the x-y plane. In contrast, in the narrower interior segment of the pore (bracketed by the vertical dashed lines in Fig. 2a), the ion is confined by the channel wall to a smaller lateral distance and is thus effectively not subject to the repulsive part of u(x, y). As discussed in Methods, although the magnitude of the 1D PMF depends on u(x, y), the shape of the PMF within the interior region will remain essentially unchanged upon using a different lateral potential.
Figure 2.
(a) Free energy (PMF) of the Na+ ion from the systems with 0 (blue) and ~240 mM (green) bulk NaCl concentrations, as described in the text. The two vertical dashed lines indicate the narrower portion of the channel where the maximum lateral distance of the ion to the pore axis during the simulation is smaller than R0 (7 Å). In this segment the ion is thus effectively not subject to the lateral restraint u(x, y) (see Eq. 16). (b) Committor (splitting probability) for the system with 0 bulk ion concentration. The solid curve is calculated according to Eq. 12 using position-dependent diffusion coefficients D(z) (Fig. 3a), and the dashed curve shows , assuming a uniform diffusion coefficient in Eq. 12.
The major barrier is located at z ≈0 Å, well within the interior region. At the barrier, the ion is mainly surrounded by the hydrophobic side chains of Ile232, which form a constriction in the pore radius.33 The barrier divides the pore into two halves with distinctive features. In the extracellular half (z >0 Å), the pore is mostly lined by hydrophobic residues, in particular Ile239 which, along with Ile232, forms the hydrophobic gate of the pore.33 In addition, the pore becomes increasingly wider toward the extracellular entrance, adopting a funnel shape in this half. Consequently, the PMFs in the extracellular half are relatively smooth, and represent an overall downhill profile toward the bulk solvent. In contrast, in the intracellular half (z <0 Å), the pore is almost uniformly narrow, up to another constriction at the intracellular entrance.33 The pore-facing residues in this half are also much more hydrophilic, including Glu221, Thr225, and Ser229. Therefore the ion interacts with the protein residues much more strongly in the intracellular half, resulting in a more rugged PMF with multiple barriers and wells.
The two PMFs at different bulk ion concentrations are close to each other at the major barrier and in the extracellular half of the pore, but exhibit larger deviations in the intracellular half. We note that the statistical errors36 of the PMF in the narrow intracellular half of the pore are significantly larger than in other umbrella windows, presumably because of the stronger coupling between the motions of the ion and of the protein side chains. We indeed observe multiple conformations of the side chains of Thr225 and Ser229 in different simulations, and the transitions between these side chain conformations are not frequent within the nanosecond time scale of a single simulation. Overall, the difference between the PMFs in the two systems is comparable to the estimated statistical errors, and thus appears to arise from the limited sampling of protein side chain motions, rather than directly from the different bulk ion concentrations in these simulations.
To identify the rate-limiting portion of the channel, we calculated the splitting probability (or committors), as shown in Fig. 2b. The committor exhibits a sharp transition at the major barrier (z ≈0 Å), and indicates that in an equilibrium ensemble, most ions on the left and right sides of the barrier come from (and return to) the respective reservoirs. The barrier is thus the major separation between the ions from the two reservoirs, and crossing this barrier is the rate-limiting step in ion conduction. We note that the committor functions calculated with position-dependent and position-independent diffusion coefficients differ noticeably on the intracellular side of the barrier. This difference reflects the reduced diffusivity of the ion in this region, as will be discussed below.
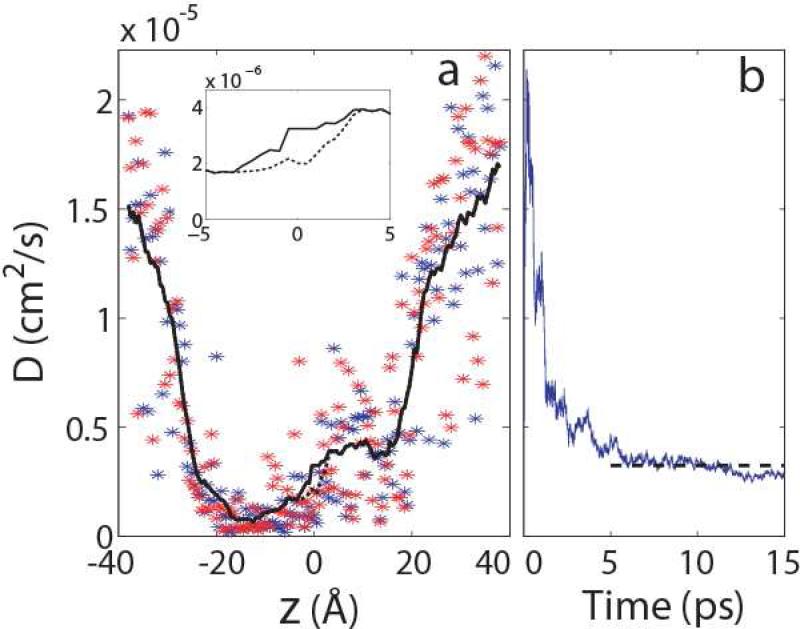
As described in Methods, we calculated the position-dependent diffusion coefficients D(z) from two sets of simulations in our previous study.33 As shown in Fig. 3a, the local diffusion coefficients bear large fluctuations between the two simulations33 in the same umbrella window and between neighboring windows. We thus smoothed the curve by updating the value of each window i with the average over a stretch of 11 windows (from i − 5 to i + 5). In the resulting D(z), the diffusion coefficients inside the pore are significantly reduced, with the minimum at least 20-fold smaller than the bulk values. Moreover, the intracellular half of the pore exhibits smaller diffusion coefficients than the extracellular half, presumably due to the narrower pore radius and stronger ion-protein interactions in this region, as mentioned earlier. We note that the calculated ion diffusion coefficients in K+ channels38 and carbon nanotubes44 are much larger than the values here, probably due in part to the smoother interior of those pores and the lack of friction from floppy side chains.
Figure 3.
(a) The position-dependent diffusion coefficients D(z) , calculated from two sets of 1-ns umbrella sampling simulations with different initial coordinates.33 The blue and red stars represent the local diffusion coefficients in each umbrella window obtained from the two simulations, respectively. The black dashed curve is the smoothed D(z) by applying moving average as described in the text. The black solid curve is obtained by using the optimal diffusion coefficient from (b) to update the D(z) values in the barrier region (highlighted in inset), as described in the text. (b) The optimal diffusion coefficient at the barrier top estimated from 200 unrestrained simulations. At each time step, the distribution of the ion coordinates is obtained from the corresponding snapshots in the 200 trajectories, and an optimal diffusion coefficient is then determined by maximizing the likelihood function L(D) (Eq. 25), as described in the text. The black dashed line indicates the average over the values between 5 ps and 15 ps, which is used to correct the D(z) curve in (a) at the barrier top.
Because D(z) was calculated from trajectories in the early stage of the simulations before the ion was equilibrated further with Hamiltonian replica exchange, we expect additional uncertainties. Furthermore, the Smoluchowski equation in the high friction limit (Eq. 10) is only valid for sufficiently long time intervals such that the memory effect can be ignored, and it remains to be tested whether in such time scales the diffusion coefficient can still be taken as a constant. As discussed earlier, the barrier at z ≈0 Å gives rise to the rate-limiting step in the ion conduction, and the local diffusion coefficient there plays the predominant role in determining the conductance of the pore. We therefore performed additional unrestrained simulations to estimate the local diffusion coefficient at the barrier top and to test the diffusion model.
As described in Methods, we released the ion at the barrier top in 200 independent unrestrained simulations, and observed its free evolution over time. When the ions have not deviated away from the barrier region, we expect that their evolution can be reasonably described by a constant local diffusion coefficient. Given a diffusion coefficient D, along with the initial distribution of the ion positions and the calculated PMF, we can numerically solve the Smoluchowski equation (Eq. 10) to obtain the probability distribution p(z,t | D) of the ion at any time,45 and compare the resulting distribution to the observed distribution of the ion from the simulations. Specifically, we divide each observed histogram into five cells, each with count Ni, i =1,...5. By integrating the calculated p(z,t | D), we also obtain the corresponding probability Pi(D) for the ion to appear in the respective cell. We then numerically search for the optimal D that maximizes the likelihood function
| (25) |
This maximum-likelihood approach of finding D corresponds to that of ref. 37, with the difference that here a strictly constant diffusion coefficient D is assumed and that the underlying PMF is taken from previous umbrella sampling simulations.
The optimal values of D calculated in this way for different lag times, defined as the lapse between the release of the ion and the observation time, are shown in Fig. 3b. As mentioned before, the Smoluchowski equation in the high friction limit (Eq. 10) is only valid at time scales much longer than those required for the velocity autocorrelation function to vanish, such that the memory of the initial velocity is completely lost. Moreover, motions along degrees of freedom other than z need to be relaxed, including motions in the protein coupled to the ion movement. Fig. 3b indeed shows that at smaller lag times, the apparent diffusion coefficient is larger than at longer lag times. In the other limit, for large time lapse, the ions already diffuse away from the barrier top, and a constant diffusion coefficient is no longer sufficient to describe the evolution of the ions. We therefore use lag times between 5 ps and 15 ps and take the average of the corresponding maximum-likelihood diffusion coefficients as the optimal value Db for the barrier (Fig. 3b). The obtained Db =3.2×10-6 cm2/s is somewhat larger than the original value (2.0×10-6 cm2/s) calculated from the simulations with harmonic restraints. We then used Db to modify D(z) near the barrier location (z =0 Å). Specifically, the three windows at -0.5 Å, 0 Å, and 0.5 Å were directly assigned the value Db. Moreover, we applied separate moving averages (over 11 windows, as described before) on the left and the right sections of the curve. When taking the moving average for the left section (z <-0.5 Å), we assumed Db for all windows at the right end (z ≥-0.5 Å). Similarly, the moving average for the right section (z >0.5 Å) was calculated using Db for windows at the left end (z ≥-0.5 Å). The resulting correction (Fig. 3a, inset) thus effectively modified D(z) between -3 Å and 3 Å.
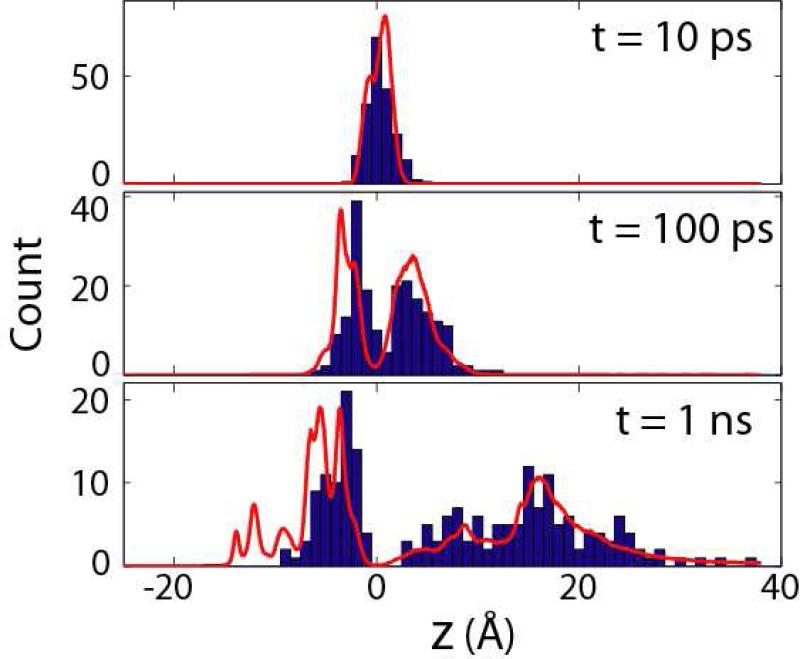
To examine the validity of our diffusion model, we numerically solved the probability distribution p(z,t) using our calculated PMF and position-dependent diffusion coefficients D(z). As shown in Fig. 4, at a time scale larger than ~10 ps, the ions started to fall onto either side of the barrier, and thus were split into two groups with different kinetic behaviors. On the extracellular side, the ions diffuse more easily and spread more widely, with several of them exiting all the way to the bulk solvent. In contrast, on the intracellular side, all ions were still trapped in the local minima inside the pore at the end of the 1-ns trajectories, with none reaching beyond z ≈-10 Å. The slower evolution in the intracellular half of the pore is consistent with a rugged PMF and smaller diffusion coefficients, as discussed before. The predicted probability distributions (red curves, Fig. 4) overall agree reasonably well with the observed histograms, and the match is especially good on the extracellular side. In the intracellular portion, as mentioned before, both the PMF and the D(z) involve larger uncertainty, and consequently the agreement is less accurate. The observed differences indicate that the actual D(z) on the intracellular side of the barrier might be even lower than our estimate obtained by interpolation.
Figure 4.
Histograms for the z -coordinates of the ion in the 200 trajectories, at three lag times (10 ps, 100 ps, 1 ns) after the start of the simulations. The red curves represent the prediction from the numerical solution45 of the diffusion equation (Eq. 10) using the calculated PMF (Fig. 2a) and D(z) (Fig. 3a).
With the PMF G(z) and the diffusion coefficients D(z) known, we can now calculate the conductance of the pore at a physiological Na+ ion concentration of 140 mM, corresponding to a number density of ρ =8.43×10-5/Å3. For the lateral restraint (Eq. 16, with R0 = 7 Å) in our umbrella sampling simulations, the effective cross-sectional area S according to Eq. 8 is equal to ~168 Å2. According to Eq. 13, we obtain k0 ~1.6×105/s for the spontaneous crossing rate. Finally, the conductance γ of the pore is estimated (Eq. 14) to be ~1.0 picosiemens (pS). In comparison, the conductance of GLIC measured in experiments8 is 8 pS.
Given that crossing the barrier at z ≈0 Å is the rate-limiting step in the ion conduction, in principle it is also possible to calculate the transmission coefficient for the ion from our unrestrained simulations, and to subsequently obtain the barrier crossing rate.46 From the initial velocities of the ions at the barrier top and their corresponding positions after the 1-ns free evolution, we obtained a transmission coefficient46 of 0.023, corresponding to a conductance of 3.6 pS, in the same order of magnitude as that obtained from the diffusion model above. However, for diffusive barrier crossing, the small transmission coefficient arises from cancellation of quantities of almost identical magnitudes, and consequently involves large statistical errors (estimated at ~0.1 here for the transmission coefficient). We therefore consider the results from our diffusion model to be more reliable.
DISCUSSION
To evaluate our calculated channel conductance, we first examine the assumptions involved in our calculations. Our simulation system incorporates only the transmembrane domain (TMD) of GLIC, without the extracellular domain (ECD). Because the channel is much narrower and more hydrophobic in the TMD pore than in the ECD vestibule, it is expected that the TMD presents the major obstacle to ion conduction. It thus appears somewhat surprising that in a recent study14 of the full-length GLIC channel, two major peaks in the PMF of Na+ ion were found in the ECD, one of which is even higher than the barrier in the TMD. We note that in the mentioned study, the ion is laterally restrained in the ECD within a radius of ~4 Å, but subject to no lateral restraint in the TMD.14 Because such lateral restraint in the ECD would significantly reduce the accessible area of the ion, the actual ion occupancy in the ECD should be higher than what the so-calculated PMF would predict. Indeed, in a long MD simulation47 of GLIC, the ECD portion of the channel exhibits substantial ion density, in fact with two cation reservoirs observed.47 We therefore believe that the TMD, rather than the ECD, forms the major barrier to ion conduction.
Recent computational studies suggest that the protonation state of Glu221 at the intracellular entrance plays a significant role in the ion PMF and the channel conductance.13,14,24 To determine the proper protonation state of this residue, it is important to note that the protein experiences different solutions on the two sides of the membrane. The single channel conduction of GLIC was measured in cell-attached patch clamp experiments,8 in which GLIC is exposed to the pipette solution with pH ~5-6 on the extracellular side and to the normal cytoplasmic solution on the intracellular side. Accordingly, here we leave Glu221 unprotonated, consistent with previous MD simulations7,10,24,33,47 of GLIC. Although the side chains of Glu221 exhibit flexibility in our simulations, most of the time they are fully accessible to bulk water. Furthermore, according to our diffusion model (Eq. 14) and the calculated PMF (Fig. 2a), the channel conductance is mainly determined by the barrier in the middle of the pore and the local diffusion coefficient there. Therefore, even if some of these hydrated Glu221 side chains were occasionally protonated, they would not be expected to have a significant effect on the barrier region ~20 Å away. Indeed, in the simulation with Glu221 mutated into an alanine,24 the perturbation to the PMF is confined within the vicinity of this residue, with no large deviation observed around Ile232 where the barrier in our PMF is located. However, if all of the five Glu221 side chains are protonated, they could form an H-bonded ring6 and block the pore entrance. The exact protonation state47 of this residue and its effect on the PMF are therefore worth further study.
Different MD studies so far have not reached a consensus with regard to the PMF of the GLIC pore. Near Ile232, e.g., the PMFs from an earlier study14 and from our calculation here both exhibit a prominent barrier, whereas in another study24 the PMF is featureless in this region. We suspect that the variations among these studies may arise from subtle differences in the conformations of the pore, especially in the hydrophobic gate between Ile232 and Ile239. When the radius of this gate decreases by only ~1-2 Å from the open to the closed conformation,33 the barrier height increases substantially. Because an isolated TMD of GLIC undergoes spontaneous closure,33 in this study we need to apply restraints to keep the protein in the open conformation, as also in other simulations of the truncated TMD.24 The artificial restraints might have subtle effects on the geometry of the pore. In our simulations here, we observe that the side chains of Ile239 are more asymmetric than in the crystal structure, making the radius of the hydrophobic gate slightly smaller. If the gate were wider, we would expect a lower barrier in the PMF and a higher conductance of the channel. To obtain a more accurate PMF, it is thus desirable to repeat the calculations here on a fully equilibrated and stable system of the entire GLIC complex with both the TMD and the ECD, thus eliminating the necessity to restrain the protein conformation, and with longer simulation time to fully sample the side chain conformations. Such calculations are worthwhile in future studies with more powerful computational resources.
In this study, the ion PMF is obtained in the absence of an applied voltage V, and the calculated conductance corresponds to the slope of the linear portion of the I-V curve at V = 0. However, because the single-channel measurement of GLIC clearly indeed shows a linear I-V relationship,8 our calculated conductance can be justifiably compared to the measured data.
The conductance of an ion channel is also a function of the bulk ion concentration. Here the two calculated PMFs (Fig. 2a) in the presence of 0 and ~240 mM NaCl, respectively, are quite similar, particularly in the barrier region which is the major determinant of the channel conductance. On this basis, it appears that the conductance of the GLIC pore should have a linear dependence on the ion concentration. However, we note that in all our calculations we have assumed a single-ion conduction mechanism, in which the crossings of different ions are not coupled to each other. Notably, it was reported that a deep attractive well at the intracellular entrance of GLIC with unprotonated Glu221 results in a nonconducting channel.14 If the ion concentration is sufficiently low, such that single-ion conduction is valid (see Methods), an attractive well in the PMF should not decrease the conductance (Eq. 14). Therefore, the observed behavior14 must arise from ion-ion interactions. For example, an ion tightly bound at the pore entrance might block the access to the pore for other ions. However, although our PMF also shows an attractive well at the intracellular entrance consistent with the observed cation reservoir,47 it is not nearly as deep as the reported 22.5 kBT.14 As mentioned before, in our simulations the side chains of the Glu221 ring are normally fully solvated in the bulk water. Although in our simulations with ~240 mM NaCl these side chains are frequently visited by ions from the bulk, the ions usually do not block the entrance of the pore at the symmetry axis. However, our PMFs exhibit another attractive well (Fig. 2a) near the side chains of Thr225, where the pore is narrow and the presence of an ion will interfere with the passage of other ions. Although in our simulations no ion reached this energy well from the bulk, probably due to the limited simulation time, our calculated PMFs indicate that at a bulk concentration of 140 mM, the occupancy of Na+ at this site is ~16%-41%. It thus appears more likely that this attractive well may cause certain deviations from a linear conductance-concentration relationship.
Although the crystal structure of ELIC5 has been generally believed to represent the closed conformation of the protein, it was recently speculated11 that the phenylalanine residues at the hydrophobic gate might play an unusual role in locking ELIC into the observed crystal structure. However, a recent crystal structure48 showed that when that phenylalanine is mutated into an alanine, the protein structure remains unchanged, indicating that the observed ELIC conformation is not solely due to that residue. Indeed, our study showed that GLIC, with an isoleucine (Ile239) residue replacing the ELIC phenylalanine, can also adopt a conformation similar to the ELIC pore, which is highly stable in the simulations and exhibits a conductance33 at least three orders of magnitude lower than in the conformation studied here. The ELIC crystal structure5 and the corresponding conformation of GLIC obtained by simulation33 thus appear to be consistent with the physiologically closed states of the respective proteins observed in functional studies.
In addition to the open and closed states, it has been demonstrated that ELIC and GLIC can also enter a desensitized state.11,12,48 It was then suspected that in the crystal structures6,7 GLIC might be captured in the desensitized state, rather than the previously assumed open state. Although our calculated conductance (~1 pS) of the GLIC pore at 140 mM ion concentration is somewhat lower than the value of ~8 pS measured experimentally,8 the deviation is not significant given the approximations in our calculations, as discussed earlier. On this basis, the GLIC crystal structures appear to be more consistent with the physiologically open state than with the desensitized state. We also note that the recent crystal structure of another pLGIC, the glutamate-gated chloride channel,49 which is believed to be in the open conformation, bears considerable resemblance to the GLIC structures in the transmembrane pore.
The exact correspondence between the structural models and the functional states in GLIC and other pLGICs apparently require more investigations. The channel conductance is arguably the most important quantitative link between the crystal structures and the functional measurements.50 In this study, we apply a consistent method to calculate the channel conductance entirely from fully atomic simulations, in the singleion conduction regime. In addition to GLIC, the method can also be applied to calculate the conductance of different conformations for other pLGICs, such as ELIC, with its activating ligands now known.48 Complementary to the ongoing experimental efforts, such calculations will help resolve the structure-function relationship in this important protein family.
ACKNOWLEDGEMENTS
This work is dedicated to Wilfred F. van Gunsteren on the occasion of his 65th birthday in recognition of his pioneering work in quantitative molecular simulations. This research was supported by the Intramural Research Programs of the NIDDK, NIH, and utilized the high-performance computational capabilities of the Biowulf Linux cluster at the National Institutes of Health, Bethesda, MD (http://biowulf.nih.gov).
REFERENCES
- 1.Hansson T, Oostenbrink C, van Gunsteren WF. Molecular dynamics simulations. Curr. Opin. Struct. Biol. 2002;12:190–6. doi: 10.1016/s0959-440x(02)00308-1. [DOI] [PubMed] [Google Scholar]
- 2.Daura X, Jaun B, Seebach D, van Gunsteren WF, Mark AE. Reversible peptide folding in solution by molecular dynamics simulation. J. Mol. Biol. 1998;280:925–32. doi: 10.1006/jmbi.1998.1885. [DOI] [PubMed] [Google Scholar]
- 3.Sine SM, Engel AG. Recent advances in Cys-loop receptor structure and function. Nature. 2006;440:448–55. doi: 10.1038/nature04708. [DOI] [PubMed] [Google Scholar]
- 4.Unwin N. Refined structure of the nicotinic acetylcholine receptor at 4Å resolution. J. Mol. Biol. 2005;346:967–89. doi: 10.1016/j.jmb.2004.12.031. [DOI] [PubMed] [Google Scholar]
- 5.Hilf RJ, Dutzler R. X-ray structure of a prokaryotic pentameric ligand-gated ion channel. Nature. 2008;452:375–9. doi: 10.1038/nature06717. [DOI] [PubMed] [Google Scholar]
- 6.Hilf RJ, Dutzler R. Structure of a potentially open state of a proton-activated pentameric ligand-gated ion channel. Nature. 2009;457:115–8. doi: 10.1038/nature07461. [DOI] [PubMed] [Google Scholar]
- 7.Bocquet N, Nury H, Baaden M, Le Poupon C, Changeux JP, Delarue M, Corringer PJ. X-ray structure of a pentameric ligand-gated ion channel in an apparently open conformation. Nature. 2009;457:111–4. doi: 10.1038/nature07462. [DOI] [PubMed] [Google Scholar]
- 8.Bocquet N, Prado de Carvalho L, Cartaud J, Neyton J, Le Poupon C, Taly A, Grutter T, Changeux JP, Corringer PJ. A prokaryotic proton-gated ion channel from the nicotinic acetylcholine receptor family. Nature. 2007;445:116–9. doi: 10.1038/nature05371. [DOI] [PubMed] [Google Scholar]
- 9.Nury H, Bocquet N, Le Poupon C, Raynal B, Haouz A, Corringer PJ, Delarue M. Crystal structure of the extracellular domain of a bacterial ligand-gated ion channel. J. Mol. Biol. 2010;395:1114–27. doi: 10.1016/j.jmb.2009.11.024. [DOI] [PubMed] [Google Scholar]
- 10.Nury H, Van Renterghem C, Weng Y, Tran A, Baaden M, Dufresne V, Changeux JP, Sonner JM, Delarue M, Corringer PJ. X-ray structures of general anaesthetics bound to a pentameric ligand-gated ion channel. Nature. 2011;469:428–31. doi: 10.1038/nature09647. [DOI] [PubMed] [Google Scholar]
- 11.Gonzalez-Gutierrez G, Grosman C. Bridging the gap between structural models of nicotinic receptor superfamily ion channels and their corresponding functional states. J. Mol. Biol. 2010;403:693–705. doi: 10.1016/j.jmb.2010.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Parikh RB, Bali M, Akabas MH. Structure of the M2 transmembrane segment of GLIC, a prokaryotic Cys loop receptor homologue from Gloeobacter violaceus, probed by substituted cysteine accessibility. J. Biol. Chem. 2011;286:14098–109. doi: 10.1074/jbc.M111.221895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Song C, Corry B. Ion conduction in ligand-gated ion channels: Brownian dynamics studies of four recent crystal structures. Biophys. J. 2010;98:404–11. doi: 10.1016/j.bpj.2009.10.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cheng MH, Coalson RD, Tang P. Molecular dynamics and brownian dynamics investigation of ion permeation and anesthetic halothane effects on a proton-gated ion channel. J. Am. Chem. Soc. 2010;132:16442–9. doi: 10.1021/ja105001a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Roux B. The membrane potential and its representation by a constant electric field in computer simulations. Biophys. J. 2008;95:4205–16. doi: 10.1529/biophysj.108.136499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Aksimentiev A, Schulten K. Imaging alpha-hemolysin with molecular dynamics: ionic conductance, osmotic permeability, and the electrostatic potential map. Biophys. J. 2005;88:3745–61. doi: 10.1529/biophysj.104.058727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Khalili-Araghi F, Tajkhorshid E, Schulten K. Dynamics of K+ ion conduction through Kv1.2. Biophys. J. 2006;91:L72–4. doi: 10.1529/biophysj.106.091926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sotomayor M, Vasquez V, Perozo E, Schulten K. Ion conduction through MscS as determined by electrophysiology and simulation. Biophys. J. 2007;92:886–902. doi: 10.1529/biophysj.106.095232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jensen MO, Borhani DW, Lindorff-Larsen K, Maragakis P, Jogini V, Eastwood MP, Dror RO, Shaw DE. Principles of conduction and hydrophobic gating in K+ channels. Proc. Natl. Acad. Sci. USA. 2010;107:5833–8. doi: 10.1073/pnas.0911691107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kutzner C, Grubmüller H, de Groot BL, Zachariae U. Computational electrophysiology: the molecular dynamics of ion channel permeation and selectivity in atomistic detail. Biophys. J. 2011;101:809–17. doi: 10.1016/j.bpj.2011.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Trzesniak D, Kunz AP, van Gunsteren WF. A comparison of methods to compute the potential of mean force. Chemphyschem. 2007;8:162–9. doi: 10.1002/cphc.200600527. [DOI] [PubMed] [Google Scholar]
- 22.Allen TW, Andersen OS, Roux B. Molecular dynamics - potential of mean force calculations as a tool for understanding ion permeation and selectivity in narrow channels. Biophys. Chem. 2006;124:251–67. doi: 10.1016/j.bpc.2006.04.015. [DOI] [PubMed] [Google Scholar]
- 23.Beckstein O, Sansom MS. A hydrophobic gate in an ion channel: the closed state of the nicotinic acetylcholine receptor. Phys. Biol. 2006;3:147–59. doi: 10.1088/1478-3975/3/2/007. [DOI] [PubMed] [Google Scholar]
- 24.Fritsch S, Ivanov I, Wang H, Cheng X. Ion selectivity mechanism in a bacterial pentameric ligand-gated ion channel. Biophys. J. 2011;100:390–8. doi: 10.1016/j.bpj.2010.11.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.de Groot BL, Grubmuller H. The dynamics and energetics of water permeation and proton exclusion in aquaporins. Curr. Opin. Struct. Biol. 2005;15:176–83. doi: 10.1016/j.sbi.2005.02.003. [DOI] [PubMed] [Google Scholar]
- 26.Zhu F, Tajkhorshid E, Schulten K. Theory and simulation of water permeation in aquaporin-1. Biophys. J. 2004;86:50–7. doi: 10.1016/S0006-3495(04)74082-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hub JS, de Groot BL. Mechanism of selectivity in aquaporins and aquaglyceroporins. Proc. Natl. Acad. Sci. USA. 2008;105:1198–203. doi: 10.1073/pnas.0707662104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bezrukov SM, Berezhkovskii AM, Szabo A. Diffusion model of solute dynamics in a membrane channel: mapping onto the two-site model and optimizing the flux. J. Chem. Phys. 2007;127:115101. doi: 10.1063/1.2766720. [DOI] [PubMed] [Google Scholar]
- 29.Eisenberg RS, Klosek MM, Schuss Z. Diffusion as a Chemical-Reaction - Stochastic Trajectories between Fixed Concentrations. J. Chem. Phys. 1995;102:1767–1780. [Google Scholar]
- 30.Zhou Y, Morais-Cabral JH, Kaufman A, MacKinnon R. Chemistry of ion coordination and hydration revealed by a K+ channel-Fab complex at 2.0 A resolution. Nature. 2001;414:43–8. doi: 10.1038/35102009. [DOI] [PubMed] [Google Scholar]
- 31.Bernèche S, Roux B. A gate in the selectivity filter of potassium channels. Structure. 2005;13:591–600. doi: 10.1016/j.str.2004.12.019. [DOI] [PubMed] [Google Scholar]
- 32.Berezhkovskii A, Hummer G. Single-file transport of water molecules through a carbon nanotube. Phys. Rev. Lett. 2002;89:064503. doi: 10.1103/PhysRevLett.89.064503. [DOI] [PubMed] [Google Scholar]
- 33.Zhu F, Hummer G. Pore opening and closing of a pentameric ligand-gated ion channel. Proc. Natl. Acad. Sci. USA. 2010;107:19814–9. doi: 10.1073/pnas.1009313107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fukunishi H, Watanabe O, Takada S. On the Hamiltonian replica exchange method for efficient sampling of biomolecular systems: Application to protein structure prediction. J. Chem. Phys. 2002;116:9058–9067. [Google Scholar]
- 35.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. The weighted histogram analysis method for free-energy calculations on biomolecules .1. The method. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 36.Zhu F, Hummer G. Convergence and error estimation in free energy calculations using the weighted histogram analysis method. J. Comput. Chem. 2012;33:453–465. doi: 10.1002/jcc.21989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hummer G. Position-dependent diffusion coefficients and free energies from Bayesian analysis of equilibrium and replica molecular dynamics simulations. New Journal of Physics. 2005;7:34. [Google Scholar]
- 38.Bernèche S, Roux B. A microscopic view of ion conduction through the K+ channel. Proc. Natl. Acad. Sci. USA. 2003;100:8644–8. doi: 10.1073/pnas.1431750100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Flyvbjerg H, Petersen HG. Error-Estimates on Averages of Correlated Data. J. Chem. Phys. 1989;91:461–466. [Google Scholar]
- 40.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 41.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 42.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 44.Peter C, Hummer G. Ion transport through membrane-spanning nanopores studied by molecular dynamics simulations and continuum electrostatics calculations. Biophys. J. 2005;89:2222–34. doi: 10.1529/biophysj.105.065946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bicout DJ, Szabo A. Electron transfer reaction dynamics in non-Debye solvents. J. Chem. Phys. 1998;109:2325–2338. [Google Scholar]
- 46.Roux B, Karplus M. Ion-Transport in a Gramicidin-Like Channel - Dynamics and Mobility. J. Phys. Chem. 1991;95:4856–4868. [Google Scholar]
- 47.Nury H, Poitevin F, Van Renterghem C, Changeux JP, Corringer PJ, Delarue M, Baaden M. One-microsecond molecular dynamics simulation of channel gating in a nicotinic receptor homologue. Proc. Natl. Acad. Sci. USA. 2010;107:6275–80. doi: 10.1073/pnas.1001832107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zimmermann I, Dutzler R. Ligand activation of the prokaryotic pentameric ligand-gated ion channel ELIC. PLoS Biol. 2011;9:e1001101. doi: 10.1371/journal.pbio.1001101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hibbs RE, Gouaux E. Principles of activation and permeation in an anion-selective Cys-loop receptor. Nature. 2011;474:54–60. doi: 10.1038/nature10139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wilson MA, Wei C, Bjelkmar P, Wallace BA, Pohorille A. Molecular dynamics simulation of the antiamoebin ion channel: linking structure and conductance. Biophys. J. 2011;100:2394–402. doi: 10.1016/j.bpj.2011.03.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. J. Mol. Graphics. 1996;14:33–8. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]